Equations ya mistari ya moja kwa moja na curves kwenye ndege. Mlinganyo wa mstari
Sifa za mstari wa moja kwa moja katika jiometri ya Euclidean.
Idadi isiyo na kikomo ya mistari iliyonyooka inaweza kuchorwa kupitia sehemu yoyote.
Kupitia pointi zozote mbili zisizo sanjari mstari mmoja wa moja kwa moja unaweza kuchorwa.
Mistari miwili tofauti katika ndege ama hukatiza katika sehemu moja au iko
sambamba (ifuatayo kutoka kwa uliopita).
Katika nafasi ya pande tatu, kuna chaguzi tatu kwa nafasi ya jamaa ya mistari miwili:
- mistari huingiliana;
- mistari ni sambamba;
- mistari iliyonyooka hukatiza.
Moja kwa moja mstari— curve algebraic ya utaratibu wa kwanza: mstari wa moja kwa moja katika mfumo wa kuratibu wa Cartesian
inatolewa kwenye ndege kwa equation ya shahada ya kwanza (linear equation).
Mlinganyo wa jumla wa mstari wa moja kwa moja.
Ufafanuzi. Mstari wowote wa moja kwa moja kwenye ndege unaweza kubainishwa na mlinganyo wa mpangilio wa kwanza
Shoka + Wu + C = 0,
na mara kwa mara A, B si sawa na sifuri kwa wakati mmoja. Mlingano huu wa mpangilio wa kwanza unaitwa jumla
equation ya mstari wa moja kwa moja. Kulingana na maadili ya mara kwa mara A, B Na NA Kesi maalum zifuatazo zinawezekana:
. C = 0, A ≠0, B ≠ 0- mstari wa moja kwa moja hupitia asili
. A = 0, B ≠0, C ≠0 (Kwa + C = 0)- mstari wa moja kwa moja sambamba na mhimili Oh
. B = 0, A ≠0, C ≠ 0 (Ax + C = 0)- mstari wa moja kwa moja sambamba na mhimili OU
. B = C = 0, A ≠0- mstari wa moja kwa moja unafanana na mhimili OU
. A = C = 0, B ≠0- mstari wa moja kwa moja unafanana na mhimili Oh
Equation ya mstari wa moja kwa moja inaweza kuwasilishwa kwa aina tofauti kulingana na yoyote iliyotolewa
masharti ya awali.
Equation ya mstari wa moja kwa moja kutoka kwa uhakika na vector ya kawaida.
Ufafanuzi. Katika mfumo wa kuratibu wa mstatili wa Cartesian, vekta yenye vipengele (A, B)
perpendicular kwa mstari uliotolewa na equation
Shoka + Wu + C = 0.
Mfano. Tafuta mlinganyo wa mstari unaopita kwenye nukta A(1, 2) perpendicular kwa vector (3, -1).
Suluhisho. Kwa A = 3 na B = -1, hebu tutunge mlinganyo wa mstari ulionyooka: 3x - y + C = 0. Ili kupata mgawo C
Wacha tubadilishe viwianishi vya nukta A kwenye usemi unaosababisha. Tunapata: 3 - 2 + C = 0, kwa hivyo.
C = -1. Jumla: mlinganyo unaohitajika: 3x - y - 1 = 0.
Mlinganyo wa mstari unaopita pointi mbili.
Hebu pointi mbili zipewe katika nafasi M 1 (x 1 , y 1 , z 1) Na M2 (x 2, y 2, z 2), Kisha equation ya mstari,
kupitia pointi hizi:
Ikiwa yoyote kati ya madhehebu ni sifuri, nambari inayolingana inapaswa kuwekwa sawa na sifuri. Washa
ndege, equation ya mstari wa moja kwa moja iliyoandikwa hapo juu imerahisishwa:

Kama x 1 ≠ x 2 Na x = x 1, Kama x 1 = x 2 .
Sehemu = k kuitwa mteremko moja kwa moja.
Mfano. Pata equation ya mstari unaopitia pointi A (1, 2) na B (3, 4).
Suluhisho. Kwa kutumia formula iliyoandikwa hapo juu, tunapata:

Equation ya mstari wa moja kwa moja kwa kutumia uhakika na mteremko.
Ikiwa equation ya jumla ya mstari Shoka + Wu + C = 0 kusababisha:

na kuteua  , basi equation inayotokana inaitwa
, basi equation inayotokana inaitwa
mlinganyo wa mstari ulionyooka na mteremko k.
Equation ya mstari wa moja kwa moja kutoka kwa uhakika na vector ya mwelekeo.
Kwa kulinganisha na hatua ya kuzingatia equation ya mstari wa moja kwa moja kupitia vector ya kawaida, unaweza kuingiza kazi.
mstari wa moja kwa moja kupitia hatua na vector inayoongoza ya mstari wa moja kwa moja.
Ufafanuzi. Kila vekta isiyo ya sifuri (α 1, α 2), ambao vipengele vyake vinakidhi hali hiyo
Aα 1 + Baa 2 = 0 kuitwa kuelekeza vector ya mstari wa moja kwa moja.
Shoka + Wu + C = 0.
Mfano. Pata equation ya mstari wa moja kwa moja na vector ya mwelekeo (1, -1) na kupitia hatua A (1, 2).
Suluhisho. Tutatafuta equation ya mstari unaotaka katika fomu: Ax + Kwa + C = 0. Kulingana na ufafanuzi,
coefficients lazima ikidhi masharti yafuatayo:
1 * A + (-1) * B = 0, i.e. A = B.
Kisha equation ya mstari wa moja kwa moja ina fomu: Shoka + Ay + C = 0, au x + y + C / A = 0.
katika x = 1, y = 2 tunapata C/A = -3, i.e. mlinganyo unaohitajika:
x + y - 3 = 0
Equation ya mstari wa moja kwa moja katika makundi.
Ikiwa katika equation ya jumla ya mstari wa moja kwa moja Ах + Ву + С = 0 С≠0, basi, kugawanya na -С, tunapata:
 au wapi
au wapi

Maana ya kijiometri ya coefficients ni kwamba mgawo a ni uratibu wa hatua ya makutano
moja kwa moja na mhimili Oh, A b- kuratibu hatua ya makutano ya mstari na mhimili OU.
Mfano. Equation ya jumla ya mstari wa moja kwa moja hutolewa x - y + 1 = 0. Tafuta equation ya mstari huu katika sehemu.
C = 1, , a = -1, b = 1.
Mlinganyo wa kawaida wa mstari.
Ikiwa pande zote mbili za equation Shoka + Wu + C = 0 kugawanya kwa nambari  ambayo inaitwa
ambayo inaitwa
sababu ya kawaida, basi tunapata
xcosφ + ysinφ - p = 0 -equation ya kawaida ya mstari.
Ishara ± ya sababu ya kawaida lazima ichaguliwe ili μ*C< 0.
R- urefu wa perpendicular imeshuka kutoka asili hadi mstari wa moja kwa moja;
A φ - angle inayoundwa na perpendicular hii na mwelekeo mzuri wa mhimili Oh.
Mfano. Equation ya jumla ya mstari imetolewa 12x - 5y - 65 = 0. Inahitajika kuandika aina tofauti za milinganyo
mstari ulionyooka huu.
Mlinganyo wa mstari huu katika sehemu:

Equation ya mstari huu na mteremko: (gawanya kwa 5)

Mlinganyo wa mstari:

cos φ = 12/13; dhambi φ= -5/13; p = 5.
Ikumbukwe kwamba sio kila mstari ulionyooka unaweza kuwakilishwa na equation katika sehemu, kwa mfano, mistari iliyonyooka,
sambamba na shoka au kupita asili.
Pembe kati ya mistari iliyonyooka kwenye ndege.
Ufafanuzi. Ikiwa mistari miwili imetolewa y = k 1 x + b 1 , y = k 2 x + b 2, kisha pembe ya papo hapo kati ya mistari hii
itafafanuliwa kama

Mistari miwili ni sambamba ikiwa k 1 = k 2. Mistari miwili ni perpendicular
Kama k 1 = -1/ k 2 .
Nadharia.
Moja kwa moja Shoka + Wu + C = 0 Na A 1 x + B 1 y + C 1 = 0 sambamba wakati coefficients ni sawia
A 1 = λA, B 1 = λB. Ikiwa pia С 1 = λС, basi mistari inalingana. Kuratibu za hatua ya makutano ya mistari miwili
zinapatikana kama suluhisho la mfumo wa milinganyo ya mistari hii.
Mlinganyo wa mstari unaopita kwenye sehemu fulani ya mstari uliopeanwa.
Ufafanuzi. Mstari unaopita kwa uhakika M 1 (x 1, y 1) na perpendicular kwa mstari y = kx + b
kuwakilishwa na equation:

Umbali kutoka kwa uhakika hadi mstari.
Nadharia. Ikiwa hatua imetolewa M(x 0, y 0), kisha umbali wa mstari wa moja kwa moja Shoka + Wu + C = 0 hufafanuliwa kama:

Ushahidi. Hebu uhakika M 1 (x 1, y 1)- msingi wa perpendicular imeshuka kutoka kwa uhakika M kwa kupewa
moja kwa moja. Kisha umbali kati ya pointi M Na M 1:
![]() (1)
(1)
Kuratibu x 1 Na saa 1 inaweza kupatikana kama suluhisho la mfumo wa equations:

Equation ya pili ya mfumo ni equation ya mstari wa moja kwa moja unaopitia hatua fulani M 0 perpendicularly.
kupewa mstari ulionyooka. Ikiwa tutabadilisha equation ya kwanza ya mfumo kuwa fomu:
A(x - x 0) + B(y - y 0) + Shoka 0 + Kwa 0 + C = 0,
basi, kutatua, tunapata:

Kubadilisha misemo hii katika equation (1), tunapata:

Nadharia imethibitishwa.
Mlinganyo wa mstari unaopita katika sehemu fulani katika mwelekeo fulani. Mlinganyo wa mstari unaopita pointi mbili ulizopewa. Pembe kati ya mistari miwili iliyonyooka. Hali ya usawa na perpendicularity ya mistari miwili iliyonyooka. Kuamua hatua ya makutano ya mistari miwili
Mifano ya matatizo na ufumbuzi
Tafuta equation ya mstari unaopitia pointi mbili: (-1, 2) na (2, 1).
Suluhisho.
Kulingana na Eq.
kuamini ndani yake x 1 = -1, y 1 = 2, x 2 = 2, y 2 = 1 (haijalishi ni hatua gani inayozingatiwa kwanza na ni hatua gani inachukuliwa kuwa ya pili), tunapata
baada ya kurahisisha tunapata equation ya mwisho inayohitajika katika fomu
x + 3y - 5 = 0.
Pande za pembetatu hutolewa na milinganyo: (AB ) 2 x + 4 y + 1 = 0, (A.C. ) x - y + 2 = 0, (B.C. ) 3 x + 4 y -12 = 0. Pata kuratibu za wima za pembetatu.
Suluhisho.
Kuratibu za Vertex A tunapata kwa kutatua mfumo unaojumuisha milinganyo ya pande AB Na A.C.:
Tunatatua mfumo wa milinganyo miwili ya mstari na mbili zisizojulikana kwa kutumia mbinu zinazojulikana kutoka algebra ya msingi, na tunapata
Kipeo A ina kuratibu
Kuratibu za Vertex B tutapata kwa kutatua mfumo wa equations wa pande AB Na B.C.:
tunapokea.
Kuratibu za Vertex C tunapata kwa kutatua mfumo wa equations wa pande B.C. Na A.C.:
Kipeo C ina kuratibu.
A (2, 5) sambamba na mstari wa 3x - 4 y + 15 = 0.
Suluhisho.
Hebu tuthibitishe kwamba ikiwa mistari miwili ni sambamba, basi milinganyo yao inaweza daima kuwakilishwa kwa namna ambayo inatofautiana tu katika masharti yao ya bure. Hakika, kutokana na hali ya ulinganifu wa mistari miwili inafuata hivyo.
Wacha tuonyeshe kwa t thamani ya jumla ya mahusiano haya. Kisha
na kutoka kwa hii inafuata hiyo
A 1 = A 2 t, B 1 = B 2 t. (1)
Ikiwa mistari miwili
A 1 x + B 1 y + C 1 = 0 na
A 2 x + B 2 y + C 2 = 0
yanalingana, masharti (1) yanatimizwa, na, kuchukua nafasi ya kwanza ya milinganyo hii A 1 na B 1 kulingana na fomula (1), tutakuwa nayo
A 2 tx + B 2 ty + C 1 = 0,
au, kugawanya pande zote mbili za equation na , tunapata
Kulinganisha equation inayosababisha na equation ya mstari wa pili wa moja kwa moja A 2 x + B 2 y + C 2 = 0, tunaona kwamba milinganyo hii inatofautiana tu katika neno la bure; Kwa hivyo tumethibitisha kile kinachohitajika. Sasa hebu tuanze kutatua tatizo. Tutaandika equation ya mstari unaotaka kwa njia ambayo itatofautiana na equation ya mstari uliopewa tu na neno la bure: tutachukua maneno mawili ya kwanza katika equation inayotaka kutoka kwa equation hii, na tutaashiria yake. muda wa bure na C. Kisha equation inayohitajika itaandikwa kwa fomu
3x - 4y + C = 0, (3)
na kuamuliwa C.
Kutoa kwa mlinganyo (3) thamani C maadili yote yanayowezekana, tunapata seti ya mistari inayofanana na ile iliyotolewa. Kwa hivyo, equation (3) ni mlinganyo si wa mstari mmoja, lakini wa familia nzima ya mistari sambamba na mstari fulani wa 3. x - 4y+ 15 = 0. Kutoka kwa familia hii ya mistari, tunapaswa kuchagua moja ambayo hupita kwa uhakika A(2, 5).
Ikiwa mstari unapita kwa uhakika, basi kuratibu za hatua hii lazima ziwe na usawa wa mstari. Na kwa hivyo tutaamua C, ikiwa katika (3) tunabadilisha badala ya viwianishi vya sasa x Na y kuratibu za uhakika A, i.e. x = 2, y= 5. Tunapata na C = 14.
Thamani iliyopatikana C mbadala katika (3), na mlingano unaohitajika utaandikwa kama ifuatavyo:
3x - 4y + 14 = 0.
Tatizo sawa linaweza kutatuliwa kwa njia nyingine. Kwa kuwa mgawo wa angular wa mistari inayofanana ni sawa kwa kila mmoja, na kwa mstari uliopewa 3 x - 4y+ 15 = 0 mteremko, basi mteremko wa mstari wa moja kwa moja unaotaka pia ni sawa.
Sasa tunatumia equation y - y 1 = k(x - x 1) kundi la mistari iliyonyooka. Nukta A(2, 5) ambayo mstari wa moja kwa moja unapita inajulikana kwetu, na kwa hivyo, kubadilisha katika mlinganyo wa penseli ya mistari iliyonyooka. y - y 1 = k(x - x 1) maadili, tunapata
au baada ya kurahisisha 3 x - 4y+ 14 = 0, yaani sawa na hapo awali.
Tafuta milinganyo ya mistari inayopita kwenye nuktaA (3, 4) kwa pembe ya digrii 60 hadi mstari wa 2 ulionyookax + 3 y + 6 = 0.
Suluhisho.
Ili kutatua tatizo, tunahitaji kuamua coefficients angular ya mistari I na II (angalia takwimu). Wacha tuonyeshe coefficients hizi kwa mtiririko huo k 1 na k 2, na mgawo wa angular wa mstari huu umepitia k. Ni dhahiri kwamba.

Kulingana na ufafanuzi wa pembe kati ya mistari miwili ya moja kwa moja, wakati wa kuamua pembe kati ya mstari uliopewa na mstari wa moja kwa moja, mimi hufuata katika nambari ya sehemu katika fomula.
toa mteremko wa mstari huu, kwa kuwa unahitaji kuzungushwa kinyume cha saa karibu na uhakika C mpaka ilingane na mstari wa moja kwa moja I.
Kwa kuzingatia hilo, tunapata
Wakati wa kuamua angle kati ya mstari wa II na mstari uliopewa, mtu anapaswa kuondoa mgawo wa angular wa mstari wa II katika nambari ya sehemu sawa, i.e. k 2, kwa kuwa mstari wa II unapaswa kuzungushwa kinyume na hatua B mpaka inaendana na mstari huu:
Tafuta mlinganyo wa mstari unaopita kwenye nuktaA (5, -1) perpendicular kwa mstari wa 3x - 7 y + 14 = 0.
Suluhisho.
Ikiwa mistari miwili
A 1 x + B 1 y + C 1 = 0, A 2 x + B 2 y + C 2 = 0
ni perpendicular, basi usawa
A 1 A 2 + B 1 B 2 = 0,
au, ni nini sawa,
A 1 A 2 = -B 1 B 2 ,
na kutoka kwa hii inafuata hiyo
Tunaashiria maana ya jumla ya misemo hii kwa t.
Kisha inafuata hiyo
A 2 = B 1 t, B 2 = -A 1 t.
Kubadilisha maadili haya A 2 na B 2 na equation ya mstari wa pili, tunapata
B 1 tx - A 1 ty + C 2 = 0.
au, kugawanya kwa t pande zote mbili za usawa, tutakuwa nazo
Kulinganisha equation inayotokana na equation ya mstari wa kwanza wa moja kwa moja
A 1 x + B 1 y + C 1 = 0,
tunaona kwamba coefficients yao katika x Na y wamebadilishana mahali, na ishara kati ya maneno ya kwanza na ya pili imebadilika kuwa kinyume, lakini maneno ya bure ni tofauti.
Hebu sasa tuanze kutatua tatizo. Kutaka kuandika mlinganyo wa mstari unaoelekea kwenye mstari wa 3 x - 7y+ 14 = 0, kwa msingi wa hitimisho lililotolewa hapo juu, tutaendelea kama ifuatavyo: tutabadilisha coefficients kwa x Na y, na ubadilishe alama ya minus kati yao kwa ishara ya kuongeza, na uonyeshe neno lisilolipishwa kwa herufi C. Tunapata 7 x + 3y + C= 0. Mlingano huu ni mlingano wa familia ya mistari perpendicular kwa mstari wa 3 x - 7y+ 14 = 0. Fafanua C kutoka kwa hali ambayo mstari unaohitajika unapita kwa uhakika A(5, -1). Inajulikana kuwa ikiwa mstari unapita kwa uhakika, basi kuratibu za hatua hii lazima kukidhi equation ya mstari. Kubadilisha 5 kwa mlinganyo wa mwisho badala ya x na -1 badala yake y, tunapata
Hii ndiyo maana C Badilisha katika mlinganyo wa mwisho na upate
7x + 3y - 32 = 0.
Wacha tusuluhishe shida sawa kwa njia tofauti, kwa kutumia hii equation ya penseli ya mistari iliyonyooka.
y - y 1 = k(x - x 1).
Mteremko wa mstari huu ni 3 x - 7y + 14 = 0
kisha mgawo wa angular wa mstari unaoelekea kwake,
Kubadilisha katika mlinganyo wa penseli ya mistari iliyonyooka , na badala yake x 1 na y Viwianishi 1 vya hatua hii A(5, -1), pata , au 3 y + 3 = -7x+ 35, na hatimaye 7 x + 3y- 32 = 0, yaani sawa na hapo awali.
Milinganyo kuna curves nyingi wakati wa kusoma fasihi ya kiuchumi.Tuonyeshe baadhi ya mikondo hii.
Curve ya kutojali - curve inayoonyesha michanganyiko tofauti ya bidhaa mbili ambazo zina thamani sawa, au matumizi, kwa watumiaji.
Mkondo wa Bajeti ya Watumiaji - Curve inayoonyesha mchanganyiko tofauti wa idadi ya bidhaa mbili ambazo mtumiaji anaweza kununua kwa kiwango fulani cha mapato yake ya pesa.
Curve ya uwezekano wa uzalishaji - Curve inayoonyesha mchanganyiko tofauti wa bidhaa au huduma mbili ambazo zinaweza kuzalishwa chini ya hali ya ajira kamili na pato kamili katika uchumi na usambazaji wa rasilimali mara kwa mara na teknolojia ya mara kwa mara.
Mzunguko wa mahitaji ya uwekezaji - Curve inayoonyesha mienendo ya kiwango cha riba na kiasi cha uwekezaji katika viwango tofauti vya riba.
Mzunguko wa Phillips- Curve inayoonyesha kuwepo kwa uhusiano thabiti kati ya kiwango cha ukosefu wa ajira na kiwango cha mfumuko wa bei.
Laffer Curve- safu inayoonyesha uhusiano kati ya viwango vya ushuru na mapato ya ushuru, inayobainisha kiwango cha ushuru ambacho mapato ya ushuru hufikia kiwango cha juu zaidi.
Tayari uorodheshaji rahisi wa istilahi unaonyesha jinsi ilivyo muhimu kwa wanauchumi kuweza kuunda grafu na kuchanganua milinganyo ya mikunjo, kama vile mistari iliyonyooka na mikondo ya mpangilio wa pili - duara, duaradufu, hyperbola, parabola. Kwa kuongeza, wakati wa kutatua darasa kubwa la matatizo, ni muhimu kuchagua eneo kwenye ndege iliyofungwa na curves baadhi ambayo equations hutolewa Mara nyingi, matatizo haya yanaundwa kama ifuatavyo: pata mpango bora wa uzalishaji kwa rasilimali zilizopewa. Ugawaji wa rasilimali kawaida huchukua aina ya usawa, milinganyo ambayo hutolewa. Kwa hivyo, lazima tutafute maadili makubwa zaidi au madogo zaidi yaliyochukuliwa na kazi fulani katika mkoa ulioainishwa na hesabu za mfumo wa usawa.
Katika jiometri ya uchambuzi mstari kwenye ndege hufafanuliwa kama seti ya pointi ambazo viwianishi vinakidhi mlingano F(x,y)=0. Katika kesi hii, vizuizi vinapaswa kuwekwa kwa kazi F ili, kwa upande mmoja, equation hii iwe na seti isiyo na kipimo ya suluhisho na, kwa upande mwingine, ili seti hii ya suluhisho isijaze "kipande cha ndege. .” Darasa muhimu la mistari ni lile ambalo kitendakazi F(x,y) ni polinomia katika viambishi viwili, ambapo mstari uliofafanuliwa na mlinganyo F(x,y)=0 unaitwa. algebra. Mistari ya aljebra inayofafanuliwa na mlinganyo wa shahada ya kwanza ni mistari iliyonyooka. Mlinganyo wa shahada ya pili, ambayo ina idadi isiyo na kikomo ya suluhu, hufafanua duaradufu, hyperbola, parabola, au mstari unaogawanyika katika mistari miwili iliyonyooka.
Acha mfumo wa kuratibu wa Cartesian wa mstatili ubainishwe kwenye ndege. Mstari wa moja kwa moja kwenye ndege unaweza kutajwa na moja ya hesabu:
10 . Mlingano wa jumla wa mstari
Shoka + Kwa + C = 0. (2.1)
Vekta n(A,B) ni orthogonal kwa mstari, nambari A na B si sawa na sifuri kwa wakati mmoja.
20 . Equation ya mstari wa moja kwa moja na mteremko
y - y o = k (x - x o), (2.2)
ambapo k ni mteremko wa mstari, yaani, k = tg a, wapi a - ukubwa wa pembe inayoundwa na mstari wa moja kwa moja na mhimili wa Ox, M (x o, y o) - hatua fulani ya mstari wa moja kwa moja.
Equation (2.2) inachukua fomu y = kx + b ikiwa M (0, b) ni hatua ya makutano ya mstari wa moja kwa moja na mhimili wa Oy.
thelathini . Mlinganyo wa mstari katika sehemu
x/a + y/b = 1, (2.3)
ambapo a na b ni maadili ya sehemu zilizokatwa na mstari wa moja kwa moja kwenye shoka za kuratibu.
4 0 . Mlinganyo wa mstari unaopitia pointi mbili ulizopewa ni A(x 1, y 1) na B(x 2, y 2):
. (2.4)
50 . Mlinganyo wa mstari unaopita kwenye nukta fulani A(x 1, y 1) sambamba na vekta fulani. a(m, n)
![]() . (2.5)
. (2.5)
6 0 . Mlinganyo wa kawaida wa mstari
rn o - p = 0, (2.6)
Wapi r- radius ya hatua ya kiholela M(x, y) ya mstari huu, n o ni vekta ya kitengo cha orthogonal kwa mstari huu na kuelekezwa kutoka asili hadi mstari; p ni umbali kutoka asili hadi mstari wa moja kwa moja.
Kawaida katika fomu ya kuratibu ina fomu:
x cos a + y sin a - p = 0,
wapi a - ukubwa wa pembe inayoundwa na mstari wa moja kwa moja na mhimili wa Ox.
Mlinganyo wa penseli ya mistari iliyo na kituo katika hatua A(x 1, y 1) ina fomu:
y-y 1 = l (x-x 1),
wapi l - parameter ya boriti. Ikiwa boriti inafafanuliwa na mistari miwili ya moja kwa moja inayoingiliana A 1 x + B 1 y + C 1 = 0, A 2 x + B 2 y + C 2 = 0, basi equation yake ina fomu:
l (A 1 x + B 1 y + C 1) + m (A 2 x + B 2 y + C 2)=0,
wapi l na m - vigezo vya boriti ambazo hazigeuki hadi 0 kwa wakati mmoja.
Pembe kati ya mistari y = kx + b na y = k 1 x + b 1 imetolewa na formula:
tg j = .
Usawa 1 + k 1 k = 0 ni hali ya lazima na ya kutosha kwa perpendicularity ya mistari.
Ili milinganyo miwili
A 1 x + B 1 y + C 1 = 0, (2.7)
A 2 x + B 2 y + C 2 = 0, (2.8)
ikipewa mstari sawa sawa, ni muhimu na ya kutosha kwamba coefficients yao iwe sawia:
A 1 /A 2 = B 1 /B 2 = C 1 /C 2.
Milinganyo (2.7), (2.8) inafafanua mistari miwili tofauti sambamba ikiwa A 1 /A 2 = B 1 /B 2 na B 1 /B 2¹ C1/C2; mistari hukatiza ikiwa A 1 /A 2¹B 1 /B 2 .
Umbali d kutoka hatua ya M o (x o, y o) hadi mstari wa moja kwa moja ni urefu wa perpendicular inayotolewa kutoka kwa uhakika M o hadi mstari wa moja kwa moja. Ikiwa mstari wa moja kwa moja unatolewa na equation ya kawaida, basi d =ê r O n o -r ê , Wapi r o - vector ya radius ya uhakika M o au, kwa fomu ya kuratibu, d =ê x o cos a + y o sin a - р ê .
Mlinganyo wa jumla wa curve ya mpangilio wa pili una fomu
a 11 x 2 + 2a 12 xy + a 22 y 2 + 2a 1 x +2a 2 y +a = 0.
Inachukuliwa kuwa kati ya coefficients ya equation 11, 12, 22 kuna zisizo sifuri.
Mlinganyo wa duara na kituo katika ncha C(a, b) na kipenyo sawa na R:
(x - a) 2 + (y - b) 2 = R 2 . (2.9)
Ellipseni eneo la pointi ambazo jumla ya umbali kutoka pointi mbili zilizotolewa F 1 na F 2 (foci) ni thamani ya mara kwa mara sawa na 2a.
Mlinganyo wa kisheria (rahisi zaidi) wa duaradufu
x 2 /a 2 + y 2 /a 2 = 1. (2.10)
Mviringo uliotolewa na mlingano (2.10) una ulinganifu kwa heshima na shoka za kuratibu. Chaguo a Na b zinaitwa mashimo ya axle duaradufu.
Hebu a>b, basi foci F 1 na F 2 ziko kwenye mhimili wa Ox kwa mbali
c= kutoka asili. Uwiano c/a = e < 1 называется usawa duaradufu. Umbali kutoka kwa uhakika M(x, y) wa duaradufu hadi foci yake (vekta za radius ya focal) huamuliwa na fomula:
r 1 = a - e x, r 2 = a + e x.
Ikiwa a< b, то фокусы находятся на оси Оy, c= ,
e = c/b,
r 1 = b + e x, r 2 = b - e x.
Ikiwa a = b, basi duaradufu ni mduara unaozingatia asili ya radius a.
Hyperboleni eneo la pointi ambazo tofauti ya umbali kutoka kwa pointi mbili zilizotolewa F 1 na F 2 (foci) ni sawa kwa thamani kamili kwa nambari iliyotolewa 2a.
Canonical hyperbola equation
x 2 /a 2 - y 2 /b 2 = 1. (2.11)
Hyperbola inayotolewa na mlingano (2.11) ina ulinganifu kuhusu shoka za kuratibu. Inaingilia mhimili wa Ox kwa pointi A (a,0) na A (-a,0) - wima ya hyperbola na haiingiliani na mhimili wa Oy. Kigezo a kuitwa mhimili wa nusu halisi, b -mhimili wa nusu wa kufikirika. Kigezo c= ni umbali kutoka kwa lengo hadi asili. Uwiano c/a = e > 1 inaitwa usawa hyperboli. Mistari ambayo milinganyo yake ni y =± b/a x wanaitwa asymptotes hyperboli. Umbali kutoka kwa uhakika M(x,y) wa hyperbola hadi foci yake (vekta za radius) huamuliwa na fomula:
r 1 = ê e x - a , r 2 = ê e x + a ê .
Hyperbola ambayo a = b inaitwa usawa, mlinganyo wake x 2 - y 2 = a 2, na mlinganyo wa asymptotes y =±
x. Hyperbolas x 2 / a 2 - y 2 /b 2 = 1 na
y 2 /b 2 - x 2 /a 2 = 1 wanaitwa iliyounganishwa.
Parabolani eneo la pointi kwa usawa kutoka kwa uhakika fulani (lengo) na mstari uliotolewa (directrix).
Mlinganyo wa kisheria wa parabola una aina mbili:
1) y 2 = 2рx - parabola ni ulinganifu kuhusu mhimili wa Ox.
2) x 2 = 2рy - parabola ni ulinganifu kuhusu mhimili wa Oy.
Katika visa vyote viwili, p>0 na vertex ya parabola, ambayo ni, hatua iliyo kwenye mhimili wa ulinganifu, iko kwenye asili.
Parabola ambayo equation y 2 = 2рx ina mwelekeo F (р/2,0) na directrix x = - р/2, vekta ya eneo la msingi la uhakika M(x,y) juu yake ni r = x+ р/ 2.
Parabola ambayo equation x 2 =2рy ina mwelekeo F (0, р/2) na directrix y = - р/2; vector ya radius ya msingi ya uhakika M (x, y) ya parabola ni sawa na r = y + p/2.
Equation F(x, y) = 0 inafafanua mstari unaogawanya ndege katika sehemu mbili au zaidi. Katika baadhi ya sehemu hizi usawa wa F(x, y) unashikilia<0, а в других - неравенство F(x, y)>0. Kwa maneno mengine, mstari
F(x, y)=0 hutenganisha sehemu ya ndege, ambapo F(x, y)>0, kutoka sehemu ya ndege, ambapo F(x, y)<0.
Mstari wa moja kwa moja ambao mlinganyo wake ni Ax+By+C = 0 hugawanya ndege katika nusu-ndege mbili. Kwa mazoezi, ili kujua ni katika nusu-ndege gani tuna Ax+By+C<0, а в какой Ax+By+C>0, njia ya ukaguzi inatumika. Ili kufanya hivyo, chukua hatua ya kudhibiti (bila shaka, sio uongo kwenye mstari wa moja kwa moja ambao equation ni Ax+By+C = 0) na angalia ni ishara gani ya kujieleza Ax+By+C ina katika hatua hii. Ishara hiyo hiyo ina usemi ulioonyeshwa katika nusu-ndege nzima ambapo sehemu ya kudhibiti iko. Katika nusu ya pili ya ndege, Ax+By+C ina ishara kinyume.
Ukosefu wa usawa usio na mstari na mbili zisizojulikana hutatuliwa kwa njia sawa.
Kwa mfano, hebu tusuluhishe ukosefu wa usawa x 2 -4x+y 2 +6y-12 > 0. Inaweza kuandikwa upya kama (x-2) 2 + (y+3) 2 - 25 > 0.
Equation (x-2) 2 + (y+3) 2 - 25 = 0 inafafanua mduara na kituo katika hatua C (2,-3) na radius ya 5. Mduara hugawanya ndege katika sehemu mbili - ndani. na nje. Ili kujua ni nani kati yao kuna ukosefu huu wa usawa, chukua sehemu ya udhibiti katika eneo la ndani, kwa mfano, kituo C(2,-3) cha mduara wetu. Kubadilisha kuratibu za nukta C katika upande wa kushoto wa usawa, tunapata nambari hasi -25. Hii ina maana kwamba katika pointi zote amelazwa ndani ya mduara usawa
x 2 -4x+y 2 +6y-12< 0. Отсюда следует, что данное неравенство имеет место во внешней для окружности области.
Mfano 1.5.Andika milinganyo ya mistari inayopitia hatua A(3,1) na uelekezwe kwenye mstari 2x+3y-1 = 0 kwa pembe ya 45 o.
Suluhisho.Tutafuta katika fomu y=kx+b. Kwa kuwa mstari unapitia hatua A, kuratibu zake zinakidhi equation ya mstari, i.e. 1=k+b 3,Þ
b=1-3k. Ukubwa wa pembe kati ya mistari iliyonyooka
y= k 1 x+b 1 na y= kx+b huamuliwa na fomula tg j = . Kwa kuwa mgawo wa angular k 1 wa mstari wa awali wa moja kwa moja 2x+3y-1=0 ni sawa na - 2/3, na pembe j = 45 o, basi tuna mlinganyo wa kubainisha k:
(2/3 + k)/(1 - 2/3k) = 1 au (2/3 + k)/(1 - 2/3k) = -1.
Tuna maadili mawili ya k: k 1 = 1/5, k 2 = -5. Kupata maadili yanayolingana ya b kwa kutumia formula b = 1-3k, tunapata mistari miwili iliyonyooka inayotaka, hesabu ambazo ni: x - 5y + 2 = 0 na
5x + y - 16 = 0.
Mfano 1.6. Kwa thamani gani ya parameta t ni mistari ambayo milinganyo 3tx-8y+1 = 0 na (1+t)x-2ty = 0 sambamba?
Suluhisho.Mistari iliyofafanuliwa na milinganyo ya jumla ni sambamba ikiwa migawo ya x Na y ni sawia, i.e. 3t/(1+t) = -8/(-2t). Kutatua equation inayosababisha, tunapata t: t 1 = 2, t 2 = -2/3.
Mfano 1.7. Pata equation ya chord ya kawaida ya miduara miwili:
x 2 +y 2 =10 na x 2 +y 2 -10x-10y+30=0.
Suluhisho.Wacha tupate sehemu za makutano ya miduara; kwa kufanya hivyo, suluhisha mfumo wa equations:


 .
.
Kutatua equation ya kwanza, tunapata maadili x 1 = 3, x 2 = 1. Kutoka kwa equation ya pili - maadili yanayolingana. y: y 1 = 1, y 2 = 3. Sasa tunapata equation ya chord ya jumla, tukijua pointi mbili A (3,1) na B (1,3) za mstari huu: (y-1)/(3) -1) = (x-3)/(1-3), au y+ x - 4 = 0.
Mfano 1.8. Ni vipi pointi ziko kwenye ndege ambayo viwianishi vyake vinakidhi masharti (x-3) 2 + (y-3) 2< 8, x >y?
Suluhisho.Usawa wa kwanza wa mfumo huamua mambo ya ndani ya mduara, bila kujumuisha mpaka, i.e. mduara ulio na kituo katikati (3,3) na kipenyo. Ukosefu wa usawa wa pili hufafanua nusu ya ndege iliyoelezwa na mstari ambao equation ni x = y, na, kwa kuwa usawa ni mkali, pointi za mstari yenyewe sio za nusu ya ndege, na pointi zote chini ya mstari huu ni za nusu-ndege. Kwa kuwa tunatafuta pointi zinazokidhi tofauti zote mbili, eneo tunalotafuta ni mambo ya ndani ya semicircle.
Mfano 1.9.Kokotoa urefu wa upande wa mraba ulioandikwa kwenye duaradufu ambao mlinganyo wake ni x 2 /a 2 + y 2 /b 2 = 1.
Suluhisho.Hebu M(s, s)- vertex ya mraba iko katika robo ya kwanza. Kisha upande wa mraba utakuwa sawa na 2 Na. Kwa sababu nukta M ni ya duaradufu, viwianishi vyake vinakidhi equation ya duaradufu c 2 /a 2 + c 2 /b 2 = 1, ilitoka wapi.
c = ab/ ; Hii ina maana kwamba upande wa mraba ni 2ab/.
Mfano 1.10.Kujua equation ya asymptotes ya hyperbola y =± 0.5 x na moja ya pointi zake M(12, 3), hutunga mlinganyo wa hyperbola.
Suluhisho.Hebu tuandike mlinganyo wa kisheria wa hyperbola: x 2 / a 2 - y 2 /b 2 = 1. Dalili za hyperbola hutolewa na milinganyo y =± 0.5 x, ambayo ina maana b/a = 1/2, inatoka wapi a=2b. Kwa sababu ya M ni hatua ya hyperbola, basi kuratibu zake zinakidhi usawa wa hyperbola, i.e. 144/a 2 - 27/b 2 = 1. Kwa kuzingatia kwamba a = 2b, tunapata b: b 2 =9Þ b=3 na a=6. Kisha equation ya hyperbola ni x 2/36 - y 2/9 = 1.
Mfano 1.11.Kuhesabu urefu wa upande wa pembetatu ya kawaida ya ABC iliyoandikwa katika parabola na kigezo R, ikizingatiwa kuwa hatua A inalingana na kipeo cha parabola.
Suluhisho.Mlinganyo wa kisheria wa parabola yenye kigezo R ina fomu y 2 = 2рx, vertex yake inafanana na asili, na parabola ni ulinganifu kuhusu mhimili wa abscissa. Kwa kuwa mstari wa moja kwa moja AB huunda angle ya 30 o na mhimili wa Ox, equation ya mstari wa moja kwa moja ina fomu: y = x. idadi kubwa ya grafu
Kwa hiyo, tunaweza kupata kuratibu za uhakika B kwa kutatua mfumo wa equations y 2 = 2рx, y = x, ambayo x = 6р, y = 2р. Hii ina maana kwamba umbali kati ya pointi A(0,0) na B(6р,2р) ni sawa na 4р.
Mstari unaopita kwa uhakika K(x 0 ; y 0) na sambamba na mstari y = kx + a unapatikana na formula:
y - y 0 = k(x - x 0) (1)
Ambapo k ni mteremko wa mstari.
Njia mbadala:
Mstari unaopita kwenye nukta M 1 (x 1 ; y 1) na sambamba na mstari Ax+By+C=0 inawakilishwa na mlinganyo.
A(x-x 1)+B(y-y 1)=0 . (2)
Mfano Nambari 1. Andika mlinganyo wa mstari ulionyooka unaopita kwenye nukta M 0 (-2,1) na kwa wakati mmoja:a) sambamba na mstari wa moja kwa moja 2x + 3y -7 = 0;
b) perpendicular kwa mstari wa moja kwa moja 2x+3y -7 = 0.
Suluhisho . Hebu fikiria equation na mteremko katika fomu y = kx + a. Ili kufanya hivyo, songa maadili yote isipokuwa y kwa upande wa kulia: 3y = -2x + 7 . Kisha ugawanye upande wa kulia kwa kipengele cha 3. Tunapata: y = -2/3x + 7/3
Wacha tupate equation NK inayopitia hatua K(-2;1), sambamba na mstari wa moja kwa moja y = -2 / 3 x + 7 / 3
Kubadilisha x 0 = -2, k = -2 / 3, y 0 = 1 tunapata:
y-1 = -2 / 3 (x-(-2))
au
y = -2 / 3 x - 1 / 3 au 3y + 2x +1 = 0
Mfano Nambari 2. Andika mlinganyo wa mstari sambamba na mstari wa 2x + 5y = 0 na kuunda, pamoja na shoka za kuratibu, pembetatu ambayo eneo lake ni 5.
Suluhisho
. Kwa kuwa mistari ni sawa, equation ya mstari unaohitajika ni 2x + 5y + C = 0. Eneo la pembetatu ya kulia, ambapo a na b ni miguu yake. Wacha tupate sehemu za makutano ya mstari unaotaka na shoka za kuratibu: 
![]() ;
;
 .
.
Kwa hivyo, A(-C/2,0), B(0,-C/5). Wacha tuibadilishe katika fomula ya eneo:  . Tunapata suluhisho mbili: 2x + 5y + 10 = 0 na 2x + 5y - 10 = 0.
. Tunapata suluhisho mbili: 2x + 5y + 10 = 0 na 2x + 5y - 10 = 0.
Mfano Nambari 3. Andika mlingano wa mstari unaopita kwenye nukta (-2; 5) na sambamba na mstari 5x-7y-4=0.
Suluhisho. Mstari huu wa moja kwa moja unaweza kuwakilishwa na equation y = 5 / 7 x - 4 / 7 (hapa = 5 / 7). Equation ya mstari unaohitajika ni y - 5 = 5 / 7 (x - (-2)), i.e. 7(y-5)=5(x+2) au 5x-7y+45=0 .
Mfano Nambari 4. Baada ya kusuluhisha mfano wa 3 (A=5, B=-7) kwa kutumia fomula (2), tunapata 5(x+2)-7(y-5)=0.
Mfano Nambari 5. Andika mlinganyo wa mstari unaopita kwenye nukta (-2;5) na sambamba na mstari wa 7x+10=0.
Suluhisho. Hapa A=7, B=0. Mfumo (2) unatoa 7(x+2)=0, i.e. x+2=0. Mfumo wa (1) hautumiki, kwa kuwa mlingano huu hauwezi kutatuliwa kwa heshima na y (mstari huu wa moja kwa moja ni sambamba na mhimili wa kuratibu).
 Meli ya vita "Ushindi" - Meli za meli za hadithi
Meli ya vita "Ushindi" - Meli za meli za hadithi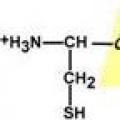 Uundaji wa dhamana ya peptidi Aina mbili zinazofanana
Uundaji wa dhamana ya peptidi Aina mbili zinazofanana Kasatkin Mikhail Alexandrovich (1902-1974) M Kasatkin
Kasatkin Mikhail Alexandrovich (1902-1974) M Kasatkin