คำจำกัดความ 9.3เวกเตอร์ เอ็กซ์ เรียกว่า เวกเตอร์ของตัวเองเมทริกซ์ และหากมีตัวเลขดังกล่าว λ, ที่ความเท่าเทียมกันถือ: และ เอ็กซ์= λ เอ็กซ์, นั่นคือผลลัพธ์ของการสมัคร เอ็กซ์ การแปลงเชิงเส้นที่กำหนดโดยเมทริกซ์ และคือการคูณเวกเตอร์นี้ด้วยจำนวน λ . เบอร์ตัวเอง λ เรียกว่า หมายเลขของตัวเองเมทริกซ์ และ.

การแทนค่าในสูตร (9.3) x` j = λx j ,เราได้ระบบสมการสำหรับกำหนดพิกัดของเวกเตอร์ลักษณะเฉพาะ:

. (9.5)

ระบบเนื้อเดียวกันเชิงเส้นนี้จะไม่มี วิธีแก้ปัญหาเล็กน้อยก็ต่อเมื่อตัวกำหนดหลักของมันคือ 0 (กฎของแครมเมอร์) โดยเขียนเงื่อนไขนี้ในรูปแบบ:

เราได้สมการสำหรับหาค่าลักษณะเฉพาะ λ เรียกว่า สมการคุณลักษณะ. โดยสังเขปสามารถแสดงได้ดังนี้

| เอ-λE | = 0, (9.6)

เนื่องจากด้านซ้ายเป็นตัวกำหนดของเมทริกซ์ เอ-λE. พหุนามที่เกี่ยวกับ เล | เอ-λE| เรียกว่า พหุนามลักษณะเฉพาะเมทริกซ์ ก.

คุณสมบัติของพหุนามลักษณะเฉพาะ:

1) พหุนามลักษณะเฉพาะของการแปลงเชิงเส้นไม่ได้ขึ้นอยู่กับตัวเลือกของพื้นฐาน การพิสูจน์. (ดู (9.4)) แต่ เพราะเหตุนี้, . ดังนั้นจึงไม่ขึ้นอยู่กับการเลือกพื้นฐาน ดังนั้น และ | เอ-λE| ไม่เปลี่ยนแปลงเมื่อเปลี่ยนไปใช้พื้นฐานใหม่

2) ถ้าเมทริกซ์ และการแปลงเชิงเส้นคือ สมมาตร(เหล่านั้น. aij = จิ) ดังนั้นรากทั้งหมดของสมการคุณลักษณะ (9.6) จึงเป็นจำนวนจริง

คุณสมบัติของค่าลักษณะเฉพาะและค่าลักษณะเฉพาะ:

1) ถ้าเราเลือกพื้นฐานจากเวกเตอร์ลักษณะเฉพาะ x 1, x 2, x 3 สอดคล้องกับค่าลักษณะเฉพาะ λ 1 , λ 2 , λ 3เมทริกซ์ และดังนั้น ในพื้นฐานนี้ การแปลงเชิงเส้น A มีเมทริกซ์แนวทแยง:

(9.7) การพิสูจน์คุณสมบัตินี้เป็นไปตามคำจำกัดความของเวกเตอร์ลักษณะเฉพาะ

2) ถ้า ค่าลักษณะเฉพาะการเปลี่ยนแปลง และแตกต่างกันแล้วสอดคล้องกัน เวกเตอร์ไอเกนมีความเป็นอิสระเชิงเส้น

3) ถ้าพหุนามคุณลักษณะของเมทริกซ์ และมีสาม รากที่แตกต่างกันจากนั้นในบางพื้นฐานเมทริกซ์ และมีรูปร่างทแยง

หาของเราเองกันเถอะจำนวนและเวกเตอร์ลักษณะเฉพาะของเมทริกซ์ สมการคุณลักษณะ: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0 λ 1 = -2, λ 2 = 3, λ 3 = 6.

ค้นหาพิกัดของเวกเตอร์ลักษณะเฉพาะที่สอดคล้องกับค่าที่พบแต่ละค่า λ. จาก (9.5) จะได้ว่า ถ้า เอ็กซ์ (1) ={x 1 , x 2 , x 3) เป็นเวกเตอร์ลักษณะเฉพาะที่ตรงกับ λ 1 = -2 แล้ว

-ข้อต่อแต่ ระบบไม่แน่นอน. สามารถเขียนวิธีแก้ปัญหาได้เป็น เอ็กซ์ (1) ={ก,0,-ก) โดยที่ a คือจำนวนใดๆ โดยเฉพาะอย่างยิ่งถ้าคุณต้องการที่ | x (1) |=1, เอ็กซ์ (1) =

ทดแทนเข้าสู่ระบบ (9.5) λ 2 =3 เราได้ระบบสำหรับกำหนดพิกัดของเวกเตอร์ลักษณะเฉพาะที่สอง - x (2) ={y1,y2,y3}:

, ที่ไหน เอ็กซ์ (2) ={ข,-ข,ข) หรือ ให้ | x (2) |=1, x (2) =

สำหรับ λ 3 = 6 หาเวกเตอร์ไอเกน x (3) ={z1, z2, z3}:

, x (3) ={ค,2ค,ค) หรือในเวอร์ชันปกติ

x (3) = จะเห็นได้ว่า เอ็กซ์ (1) เอ็กซ์ (2) = เอบีเอ= 0, x (1) x (3) = ไฟฟ้ากระแสสลับ= 0, x (2) x (3) = พ.ศ- 2พ.ศ. + พ.ศ= 0 ดังนั้น เวกเตอร์ลักษณะเฉพาะของเมทริกซ์นี้จึงเป็นมุมฉากแบบคู่

การบรรยายครั้งที่ 10

รูปแบบกำลังสองและการเชื่อมต่อกับเมทริกซ์สมมาตร คุณสมบัติของเวกเตอร์ลักษณะเฉพาะและค่าลักษณะเฉพาะของเมทริกซ์สมมาตร การลดรูปแบบกำลังสองเป็นรูปแบบบัญญัติ

คำจำกัดความ 10.1แบบฟอร์มกำลังสองตัวแปรจริง x 1, x 2,…, xnพหุนามของดีกรีสองที่เกี่ยวกับตัวแปรเหล่านี้เรียกว่า ซึ่งไม่มีเทอมอิสระและเทอมของดีกรีแรก

ตัวอย่าง แบบฟอร์มกำลังสอง:

(น = 2),

(น = 3). (10.1)

จำคำจำกัดความของเมทริกซ์สมมาตรที่ให้ไว้ในการบรรยายครั้งล่าสุด:

คำจำกัดความ 10.2เมทริกซ์จตุรัส เรียก สมมาตร, ถ้า , นั่นคือถ้าองค์ประกอบเมทริกซ์สมมาตรเทียบกับเส้นทแยงมุมหลักมีค่าเท่ากัน

คุณสมบัติของค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะของเมทริกซ์สมมาตร:

1) ค่าลักษณะเฉพาะทั้งหมดของเมทริกซ์สมมาตรเป็นจริง

หลักฐาน (สำหรับ น = 2).

ให้เมทริกซ์ และดูเหมือนกับ: . มาสร้างสมการคุณลักษณะกันเถอะ:

(10.2) ค้นหาผู้จำแนก:

ดังนั้นสมการจึงมีรากจริงเท่านั้น

2) เวกเตอร์ลักษณะเฉพาะของเมทริกซ์สมมาตรเป็นแบบตั้งฉาก

หลักฐาน (สำหรับ น= 2).

พิกัดของเวกเตอร์ลักษณะเฉพาะและต้องเป็นไปตามสมการ

ระบบสมการเชิงเส้นเอกพันธ์

ระบบที่เป็นเนื้อเดียวกัน สมการเชิงเส้นเรียกว่าระบบรูปแบบ

เป็นที่ชัดเจนว่าในกรณีนี้ , เพราะ องค์ประกอบทั้งหมดของหนึ่งในคอลัมน์ในดีเทอร์มิแนนต์เหล่านี้มีค่าเท่ากับศูนย์

เนื่องจากสูตรพบสิ่งแปลกปลอม ในกรณีเมื่อ Δ ≠ 0 ระบบจะมีวิธีแก้ปัญหาเฉพาะที่เป็นศูนย์ x = ย = ซี= 0 อย่างไรก็ตาม ในหลายปัญหา คำถามที่ว่าระบบเอกพันธ์มีคำตอบอื่นที่ไม่ใช่ศูนย์หรือไม่นั้นเป็นสิ่งที่น่าสนใจ

ทฤษฎีบท.เพื่อให้ระบบเชิงเส้น สมการเอกพันธ์มีวิธีแก้ปัญหาที่ไม่เป็นศูนย์ จำเป็นและเพียงพอที่ Δ ≠ 0

ดังนั้น ถ้าดีเทอร์มีแนนต์คือ Δ ≠ 0 แสดงว่าระบบมีคำตอบเฉพาะ ถ้า Δ ≠ 0 แสดงว่าระบบสมการเนื้อเดียวกันเชิงเส้นมี ชุดที่ไม่มีที่สิ้นสุดโซลูชั่น

ตัวอย่าง.

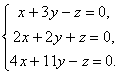
ค่าลักษณะเฉพาะของเวกเตอร์และค่าลักษณะเฉพาะของเมทริกซ์

ให้กำหนดตารางเมทริกซ์ , เอ็กซ์เป็นเมทริกซ์-คอลัมน์ที่มีความสูงตรงกับลำดับของเมทริกซ์ ก. .

ในหลายๆ ปัญหา เราต้องพิจารณาสมการของ เอ็กซ์

โดยที่ λ คือจำนวนจำนวนหนึ่ง เป็นที่ชัดเจนว่าสำหรับ λ สมการนี้มีคำตอบเป็นศูนย์

จำนวน λ ซึ่งสมการนี้มีคำตอบที่ไม่เป็นศูนย์เรียกว่า ค่าลักษณะเฉพาะเมทริกซ์ ก, ก เอ็กซ์สำหรับ λ ดังกล่าวเรียกว่า เวกเตอร์ของตัวเองเมทริกซ์ ก.

มาหาเวกเตอร์ไอเกนของเมทริกซ์กัน ก. เพราะว่า อี∙X=เอ็กซ์สมการเมทริกซ์สามารถเขียนใหม่ได้เป็น หรือ . ในรูปแบบขยาย สมการนี้สามารถเขียนใหม่เป็นระบบสมการเชิงเส้นได้ จริงๆ .

และดังนั้นจึง

ดังนั้นเราจึงได้ระบบสมการเชิงเส้นเอกพันธ์สำหรับกำหนดพิกัด x 1, x2, x 3เวกเตอร์ เอ็กซ์. เพื่อให้ระบบมีโซลูชันที่ไม่เป็นศูนย์ มีความจำเป็นและเพียงพอที่ดีเทอร์มีแนนต์ของระบบจะเท่ากับศูนย์ เช่น

นี่คือสมการดีกรี 3 เทียบกับ λ ก็เรียกว่า สมการคุณลักษณะเมทริกซ์ กและทำหน้าที่หาค่าลักษณะเฉพาะ λ

ค่าลักษณะเฉพาะ λ แต่ละค่าสอดคล้องกับเวกเตอร์ลักษณะเฉพาะ เอ็กซ์ซึ่งพิกัดถูกกำหนดจากระบบด้วยค่าที่สอดคล้องกันของ λ

ตัวอย่าง.

เวกเตอร์พีชคณิต แนวคิดเวกเตอร์

เมื่อศึกษาสาขาต่างๆ ของฟิสิกส์ จะมีปริมาณที่กำหนดโดยการกำหนดค่าตัวเลข เช่น ความยาว พื้นที่ มวล อุณหภูมิ เป็นต้น ค่าดังกล่าวเรียกว่าสเกลาร์ อย่างไรก็ตามนอกเหนือจากนั้นแล้วยังมีปริมาณสำหรับการกำหนดซึ่งนอกเหนือจากค่าตัวเลขแล้วจำเป็นต้องรู้ทิศทางในอวกาศด้วยเช่นแรงที่กระทำต่อร่างกายความเร็วและความเร่ง ของร่างกายเมื่อเคลื่อนที่ไปในอวกาศจะเกิดความตึงเครียด สนามแม่เหล็กณ จุดที่กำหนดในอวกาศ ฯลฯ ปริมาณดังกล่าวเรียกว่าปริมาณเวกเตอร์

ให้เราแนะนำคำจำกัดความที่เข้มงวด

ส่วนทิศทางเรียกกลุ่มหนึ่งซึ่งสัมพันธ์กับส่วนท้ายซึ่งเป็นที่รู้จักกันว่ากลุ่มใดเป็นกลุ่มแรกและกลุ่มใดเป็นกลุ่มที่สอง

เวกเตอร์เรียกว่าส่วนที่กำกับซึ่งมีความยาวที่แน่นอนเช่น นี่คือส่วน ความยาวที่แน่นอนซึ่งจุดสิ้นสุดจุดหนึ่งถือเป็นจุดเริ่มต้นและจุดสิ้นสุดที่สอง ถ้า กเป็นจุดเริ่มต้นของเวกเตอร์ ขเป็นจุดสิ้นสุด จากนั้นเวกเตอร์จะแสดงด้วยสัญลักษณ์ นอกจากนี้ เวกเตอร์มักจะแสดงด้วยตัวอักษรตัวเดียว . ในรูป เวกเตอร์ถูกระบุโดยส่วน และทิศทางของมันด้วยลูกศร

โมดูลหรือ ความยาวเวกเตอร์เรียกว่าความยาวของส่วนที่กำกับที่กำหนด แสดงโดย || หรือ ||.

เวกเตอร์ที่เรียกว่าศูนย์ซึ่งมีจุดเริ่มต้นและจุดสิ้นสุดตรงกันจะถูกเรียกว่าเวกเตอร์ มันถูกทำเครื่องหมาย เวกเตอร์ศูนย์ไม่มีทิศทางแน่นอนและโมดูลัสเท่ากับศูนย์ ||=0

เวกเตอร์และถูกเรียกว่า คอลิเนียร์หากอยู่ในแนวเดียวกันหรือแนวขนานกัน ในกรณีนี้ ถ้าเวกเตอร์และกำกับเท่ากัน เราจะเขียน ตรงกันข้าม

เวกเตอร์ที่อยู่บนเส้นตรงที่ขนานระนาบเดียวกันเรียกว่า ระนาบเดียวกัน.

เวกเตอร์สองตัวและถูกเรียก เท่ากับหากเป็นเส้นตรง มีทิศทางเดียวกัน และยาวเท่ากัน ในกรณีนี้ ให้เขียน .

มันตามมาจากนิยามของความเท่าเทียมกันของเวกเตอร์ว่าเวกเตอร์สามารถเคลื่อนที่ขนานกับตัวมันเองได้โดยวางจุดกำเนิดไว้ที่จุดใดก็ได้ในอวกาศ

ตัวอย่างเช่น.

การดำเนินการเชิงเส้นบนเวกเตอร์

1. การคูณเวกเตอร์ด้วยจำนวน

   ผลคูณของเวกเตอร์คูณด้วยจำนวน λ เป็นเวกเตอร์ใหม่ในลักษณะที่ว่า:

   ผลคูณของเวกเตอร์และตัวเลข λ เขียนแทนด้วย

   

   ตัวอย่างเช่น,คือเวกเตอร์ที่ชี้ไปในทิศทางเดียวกับเวกเตอร์และมีความยาวครึ่งหนึ่งของเวกเตอร์

   การดำเนินการที่ป้อนมีดังต่อไปนี้ คุณสมบัติ:

2. การบวกเวกเตอร์

   อนุญาต และ เป็นเวกเตอร์ตามอำเภอใจสองตัว เอาล่ะ จุดโดยพลการ อและสร้างเวกเตอร์ หลังจากนั้นจากจุด กกันเวกเตอร์ . เวกเตอร์ที่เชื่อมต่อจุดเริ่มต้นของเวกเตอร์แรกกับจุดสิ้นสุดของวินาทีเรียกว่า ผลรวมของเวกเตอร์เหล่านี้และแสดงแทน .

   

   นิยามสูตรของการบวกเวกเตอร์เรียกว่า กฎสี่เหลี่ยมด้านขนานเนื่องจากสามารถหาผลรวมเวกเตอร์ที่เท่ากันได้ดังนี้ แยกออกจากจุด อเวกเตอร์ และ . สร้างสี่เหลี่ยมด้านขนานบนเวกเตอร์เหล่านี้ สกอ. ตั้งแต่เวกเตอร์ แล้วเวกเตอร์ ซึ่งเป็นเส้นทแยงมุมของสี่เหลี่ยมด้านขนานที่ลากจากจุดยอด อ, จะเป็นผลรวมของเวกเตอร์

   

   ง่ายต่อการตรวจสอบดังต่อไปนี้ คุณสมบัติการบวกเวกเตอร์.

3. ความแตกต่างของเวกเตอร์

   เราเรียกเวกเตอร์ที่เรียงตัวเป็นเส้นตรงกับเวกเตอร์ที่กำหนด ซึ่งมีความยาวเท่ากันและมีทิศทางตรงข้ามกัน ตรงข้ามเวกเตอร์สำหรับเวกเตอร์และแสดงโดย . เวกเตอร์ตรงข้ามสามารถพิจารณาได้ว่าเป็นผลมาจากการคูณเวกเตอร์ด้วยจำนวน λ = –1: .

วิธีการวาง สูตรทางคณิตศาสตร์ไปที่เว็บไซต์?

หากคุณต้องการเพิ่มสูตรทางคณิตศาสตร์หนึ่งหรือสองสูตรลงในหน้าเว็บ วิธีที่ง่ายที่สุดในการทำเช่นนี้คือดังที่อธิบายไว้ในบทความ: สูตรทางคณิตศาสตร์สามารถแทรกลงในไซต์ได้อย่างง่ายดายในรูปแบบของรูปภาพที่ Wolfram Alpha สร้างขึ้นโดยอัตโนมัติ นอกจากความเรียบง่ายแล้ว วิธีสากลจะช่วยปรับปรุงการแสดงผลของเว็บไซต์ใน เครื่องมือค้นหา. มันทำงานมานานแล้ว (และฉันคิดว่ามันจะใช้ได้ตลอดไป) แต่มันล้าสมัยทางศีลธรรม

หากคุณใช้สูตรทางคณิตศาสตร์บนเว็บไซต์ของคุณเป็นประจำ ฉันขอแนะนำให้คุณใช้ MathJax ซึ่งเป็นไลบรารี JavaScript พิเศษที่แสดง สัญกรณ์ทางคณิตศาสตร์ในเว็บเบราว์เซอร์โดยใช้มาร์กอัป MathML, LaTeX หรือ ASCIIMathML

มีสองวิธีในการเริ่มต้นใช้งาน MathJax: (1) การใช้โค้ดอย่างง่าย คุณสามารถเชื่อมต่อสคริปต์ MathJax กับเว็บไซต์ของคุณได้อย่างรวดเร็ว ซึ่งจะอยู่ใน ช่วงเวลาที่เหมาะสมดาวน์โหลดโดยอัตโนมัติจากเซิร์ฟเวอร์ระยะไกล (รายการเซิร์ฟเวอร์) (2) อัปโหลดสคริปต์ MathJax จากเซิร์ฟเวอร์ระยะไกลไปยังเซิร์ฟเวอร์ของคุณและเชื่อมต่อกับทุกหน้าในไซต์ของคุณ วิธีที่สองนั้นซับซ้อนและใช้เวลานานกว่า และจะช่วยให้คุณสามารถโหลดหน้าเว็บของไซต์ของคุณได้เร็วขึ้น และหากเซิร์ฟเวอร์หลัก MathJax ไม่สามารถใช้งานได้ชั่วคราวด้วยเหตุผลบางประการ การดำเนินการนี้จะไม่ส่งผลกระทบต่อไซต์ของคุณแต่อย่างใด แม้จะมีข้อดีเหล่านี้ ฉันเลือกวิธีแรกเนื่องจากง่ายกว่า เร็วกว่า และไม่ต้องใช้ทักษะด้านเทคนิค ทำตามตัวอย่างของฉัน และภายใน 5 นาที คุณจะสามารถใช้คุณลักษณะทั้งหมดของ MathJax บนเว็บไซต์ของคุณได้

คุณสามารถเชื่อมต่อสคริปต์ไลบรารี MathJax จากเซิร์ฟเวอร์ระยะไกลโดยใช้ตัวเลือกโค้ดสองตัวที่นำมาจากเว็บไซต์หลัก MathJax หรือจากหน้าเอกสาร:

หนึ่งในตัวเลือกโค้ดเหล่านี้จำเป็นต้องคัดลอกและวางลงในโค้ดของหน้าเว็บของคุณ โดยควรอยู่ระหว่างแท็ก และหรือหลังแท็ก . ตามตัวเลือกแรก MathJax โหลดเร็วขึ้นและทำให้หน้าช้าลง แต่ตัวเลือกที่สองจะติดตามและโหลด MathJax เวอร์ชันล่าสุดโดยอัตโนมัติ หากคุณใส่รหัสแรก จะต้องมีการอัปเดตเป็นระยะ หากคุณวางโค้ดที่สอง หน้าเว็บจะโหลดช้าลง แต่คุณไม่จำเป็นต้องตรวจสอบการอัปเดตของ MathJax อย่างต่อเนื่อง

วิธีที่ง่ายที่สุดในการเชื่อมต่อ MathJax คือใน Blogger หรือ WordPress: ในแผงควบคุมของไซต์ ให้เพิ่มวิดเจ็ตที่ออกแบบมาเพื่อแทรกโค้ด JavaScript ของบุคคลที่สาม คัดลอกเวอร์ชันแรกหรือเวอร์ชันที่สองของโค้ดโหลดด้านบน และวางวิดเจ็ตให้ใกล้กับ จุดเริ่มต้นของเทมเพลต (อย่างไรก็ตาม สิ่งนี้ไม่จำเป็นเลย เนื่องจากสคริปต์ MathJax ถูกโหลดแบบอะซิงโครนัส) นั่นคือทั้งหมด ตอนนี้เรียนรู้ไวยากรณ์มาร์กอัปของ MathML, LaTeX และ ASCIIMathML และคุณก็พร้อมที่จะฝังสูตรทางคณิตศาสตร์ลงในหน้าเว็บของคุณแล้ว

แฟร็กทัลใดๆ ถูกสร้างขึ้นตามกฎบางอย่าง ซึ่งใช้อย่างต่อเนื่องโดยไม่จำกัดจำนวนครั้ง แต่ละครั้งเรียกว่าการวนซ้ำ

ขั้นตอนวิธีวนซ้ำสำหรับการสร้างฟองน้ำ Menger นั้นค่อนข้างง่าย: ลูกบาศก์เดิมที่มีด้าน 1 ถูกแบ่งด้วยระนาบที่ขนานกับใบหน้าออกเป็น 27 ลูกบาศก์เท่าๆ กัน หนึ่งลูกบาศก์กลางและ 6 ลูกบาศก์ที่อยู่ติดกับใบหน้าจะถูกลบออกจากมัน กลายเป็นชุดที่ประกอบด้วยลูกบาศก์ขนาดเล็กที่เหลืออีก 20 ลูก ทำเช่นเดียวกันกับแต่ละลูกบาศก์เหล่านี้ เราจะได้ชุดที่ประกอบด้วยลูกบาศก์ขนาดเล็กกว่า 400 ลูก ดำเนินขั้นตอนนี้ไปเรื่อย ๆ เราจะได้ฟองน้ำ Menger

ค่าลักษณะเฉพาะ (ตัวเลข) และเวกเตอร์ลักษณะเฉพาะ
ตัวอย่างโซลูชัน

เป็นตัวเอง

จากสมการทั้งสอง จะได้ว่า

มาใส่กันเถอะ: .

ผลที่ตามมา: เป็นเวกเตอร์ลักษณะเฉพาะที่สอง

ขอย้ำ จุดสำคัญโซลูชั่น:

– ระบบผลลัพธ์มีแน่นอน การตัดสินใจร่วมกัน(สมการขึ้นอยู่กับเชิงเส้น);

- "Y" ถูกเลือกในลักษณะที่เป็นจำนวนเต็ม และพิกัด "x" แรกเป็นจำนวนเต็ม เป็นบวก และมีขนาดเล็กที่สุด

– เราตรวจสอบว่าโซลูชันนั้นตรงตามสมการแต่ละอย่างของระบบ

ตอบ .

"จุดตรวจ" ระดับกลางนั้นค่อนข้างเพียงพอดังนั้นโดยหลักการแล้วการตรวจสอบความเท่าเทียมกันจึงไม่จำเป็น

ในแหล่งข้อมูลต่างๆ พิกัดของเวกเตอร์ลักษณะเฉพาะมักไม่ได้เขียนเป็นคอลัมน์ แต่เป็นแถว เช่น (และบอกตามตรงว่าผมเองก็เคยเขียนเป็นบรรทัดๆ). ตัวเลือกนี้เป็นที่ยอมรับ แต่ในแง่ของหัวข้อ การแปลงเชิงเส้นสะดวกกว่าในทางเทคนิคในการใช้งาน เวกเตอร์คอลัมน์.

บางทีวิธีแก้ปัญหาอาจดูยาวมากสำหรับคุณ แต่นั่นเป็นเพียงเพราะฉันให้ความเห็นเกี่ยวกับตัวอย่างแรกอย่างละเอียด

ตัวอย่างที่ 2

เมทริกซ์

เราฝึกฝนด้วยตัวเอง! ตัวอย่างโดยประมาณของการออกแบบขั้นสุดท้ายของงานในตอนท้ายของบทเรียน

บางครั้งคุณต้องทำ งานเพิ่มเติมคือ:

เขียนการสลายตัวตามบัญญัติของเมทริกซ์

มันคืออะไร?

ถ้าเมทริกซ์ไอเกนเวกเตอร์ก่อตัวขึ้น พื้นฐานจากนั้นสามารถแสดงเป็น:

เมทริกซ์ที่ประกอบด้วยพิกัดของเวกเตอร์ลักษณะเฉพาะอยู่ที่ไหน – เส้นทแยงมุมเมทริกซ์ที่มีค่าเฉพาะที่สอดคล้องกัน

การสลายเมทริกซ์นี้เรียกว่า เป็นที่ยอมรับหรือ เส้นทแยงมุม.

พิจารณาเมทริกซ์ของตัวอย่างแรก เวกเตอร์ของเธอเอง อิสระเชิงเส้น(non-collinear) และเป็นพื้นฐาน มาสร้างเมทริกซ์จากพิกัดกัน:

บน เส้นทแยงมุมหลักเมทริกซ์ ตามลำดับค่าลักษณะเฉพาะตั้งอยู่และองค์ประกอบที่เหลือมีค่าเท่ากับศูนย์:
- ฉันเน้นย้ำถึงความสำคัญของลำดับอีกครั้ง: "สอง" ตรงกับเวกเตอร์ที่ 1 ดังนั้นจึงอยู่ในคอลัมน์ที่ 1 "สาม" - ไปยังเวกเตอร์ที่ 2

ตามอัลกอริทึมปกติสำหรับการค้นหา เมทริกซ์ผกผันหรือ วิธีเกาส์-จอร์แดนหา . ไม่ นั่นไม่ใช่การพิมพ์ผิด! - ต่อหน้าคุณหายากเช่น สุริยุปราคาเหตุการณ์เมื่อผกผันตรงกับเมทริกซ์เดิม

มันยังคงเขียนการสลายตัวตามบัญญัติของเมทริกซ์:

ระบบแก้ไขได้ด้วย การแปลงเบื้องต้นและในตัวอย่างต่อไปนี้เราจะใช้ วิธีนี้. แต่ที่นี่วิธี "โรงเรียน" ทำงานได้เร็วกว่ามาก จากสมการที่ 3 เราแสดง: - แทนที่ในสมการที่สอง:

เนื่องจากพิกัดแรกเป็นศูนย์ เราจึงได้รับระบบ จากสมการแต่ละสมการซึ่งตามด้วยสมการนั้น

และอีกครั้ง ให้ความสนใจกับการมีอยู่จริงของความสัมพันธ์เชิงเส้น. หากได้รับเพียงวิธีแก้ปัญหาเล็กน้อย จากนั้นพบว่าค่าลักษณะเฉพาะไม่ถูกต้องหรือระบบรวบรวม / แก้ไขโดยมีข้อผิดพลาด

พิกัดที่กะทัดรัดให้คุณค่า

ไอเกนเวกเตอร์:

และอีกครั้งเราตรวจสอบว่าพบวิธีแก้ปัญหา ตอบสนองทุกสมการของระบบ. ในย่อหน้าต่อไปนี้และในงานต่อๆ ไป ฉันขอแนะนำให้ยอมรับความปรารถนานี้เป็นกฎบังคับ

2) สำหรับค่าลักษณะเฉพาะ เราได้รับตามหลักการเดียวกัน ระบบต่อไป:

จากสมการที่ 2 ของระบบ เราแสดง: - แทนที่ในสมการที่สาม:

เนื่องจากพิกัด "ซีตา" เท่ากับศูนย์ เราจึงได้รับระบบ จากสมการแต่ละสมการที่ตามมา การพึ่งพาเชิงเส้น.

ปล่อยให้เป็น

เรามาเช็คกันว่าน้ำยา ตอบสนองทุกสมการของระบบ

ดังนั้น eigen vector: .

3) และสุดท้าย ระบบจะสอดคล้องกับค่าของมันเอง:

สมการที่ 2 ดูง่ายที่สุด เราจึงแสดงสมการนั้นแล้วแทนลงในสมการที่ 1 และ 3:

ทุกอย่างเรียบร้อยดี - มีการเปิดเผยการพึ่งพาเชิงเส้นซึ่งเราแทนที่ด้วยนิพจน์:

เป็นผลให้ "X" และ "Y" แสดงผ่าน "Z": ในทางปฏิบัติ ไม่จำเป็นต้องบรรลุความสัมพันธ์ดังกล่าวเพียงอย่างเดียว ในบางกรณี จะสะดวกกว่าที่จะแสดงออกทั้งผ่าน หรือ และผ่าน หรือแม้กระทั่ง "รถไฟ" เช่น "X" ถึง "Y" และ "Y" ถึง "Z"

มาใส่กันเถอะ:

เราตรวจสอบว่าพบวิธีแก้ปัญหา ตอบสนองแต่ละสมการของระบบและเขียนเวกเตอร์ลักษณะเฉพาะที่สาม

ตอบ: เวกเตอร์ไอเกน:

ในทางเรขาคณิต เวกเตอร์เหล่านี้กำหนดทิศทางเชิงพื้นที่ที่แตกต่างกันสามทิศทาง ("ที่นั่นและกลับมาอีกครั้ง")ตามที่ การแปลงเชิงเส้นแปลงเวกเตอร์ที่ไม่ใช่ศูนย์ (เวกเตอร์ไอเกน) เป็นเวกเตอร์ที่เรียงตัวกัน

หากตามเงื่อนไขแล้วจำเป็นต้องค้นหาการขยายตามรูปแบบบัญญัติของ นี่ก็เป็นไปได้ที่นี่เพราะ ค่าลักษณะเฉพาะที่แตกต่างกันสอดคล้องกับเวกเตอร์ลักษณะเฉพาะที่เป็นอิสระเชิงเส้นที่แตกต่างกัน เราสร้างเมทริกซ์ จากพิกัดของพวกเขา เมทริกซ์แนวทแยง จาก ที่เกี่ยวข้องค่าลักษณะเฉพาะและหา เมทริกซ์ผกผัน .

หากตามเงื่อนไขจำเป็นต้องเขียน เมทริกซ์การแปลงเชิงเส้นบนพื้นฐานของเวกเตอร์ลักษณะเฉพาะแล้วเราให้คำตอบในแบบฟอร์ม มีความแตกต่างและความแตกต่างที่สำคัญ!สำหรับเมทริกซ์นี้คือเมทริกซ์ "de"

ท้าทายมากขึ้น การคำนวณอย่างง่ายสำหรับ โซลูชันอิสระ:

ตัวอย่างที่ 5

ค้นหาเวกเตอร์ลักษณะเฉพาะของการแปลงเชิงเส้นที่กำหนดโดยเมทริกซ์

เมื่อค้นหาตัวเลขของคุณเอง พยายามอย่านำกรณีเป็นพหุนามของดีกรี 3 นอกจากนี้ โซลูชันระบบของคุณอาจแตกต่างจากโซลูชันของฉัน - ไม่มีความคลุมเครือที่นี่ และเวกเตอร์ที่คุณพบอาจแตกต่างจากเวกเตอร์ตัวอย่างตามสัดส่วนของพิกัดที่เกี่ยวข้อง ตัวอย่างเช่น และ . การนำเสนอคำตอบในรูปแบบของ เป็นเรื่องสุนทรีย์มากกว่า แต่ก็ไม่เป็นไรหากคุณหยุดที่ตัวเลือกที่สอง อย่างไรก็ตามทุกอย่างมี ขอบเขตที่สมเหตุสมผลรุ่นที่ดูไม่ค่อยดีนัก

ตัวอย่างสุดท้ายของงานที่มอบหมายในตอนท้ายของบทเรียน

จะแก้ปัญหาในกรณีที่มีค่าเฉพาะหลายค่าได้อย่างไร?

อัลกอริทึมทั่วไปยังคงเหมือนเดิม แต่มีลักษณะเฉพาะของตัวเองและขอแนะนำให้เก็บบางส่วนของโซลูชันไว้ในรูปแบบวิชาการที่เข้มงวดมากขึ้น:

ตัวอย่างที่ 6

ค้นหาค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะ

การตัดสินใจ

แน่นอน ใช้ประโยชน์จากคอลัมน์แรกที่ยอดเยี่ยม:

และหลังการย่อยสลาย สี่เหลี่ยมจตุรัสสำหรับตัวคูณ:

เป็นผลให้ได้รับค่าลักษณะเฉพาะซึ่งสองค่าเป็นทวีคูณ

มาหาเวกเตอร์ไอเกนกัน:

1) เราจะจัดการกับทหารคนเดียวตามรูปแบบ "ง่าย":

จากสมการสองสมการที่ผ่านมา จะเห็นความเท่าเทียมกันอย่างชัดเจน ซึ่งแน่นอนว่าควรแทนที่ลงในสมการที่ 1 ของระบบ:

ไม่มีชุดค่าผสมที่ดีกว่า:
ไอเกนเวกเตอร์:

2-3) ตอนนี้เราลบทหารยามสองสามคน ที่ กรณีนี้มันอาจจะเปิดออก อย่างใดอย่างหนึ่งหรือสองไอเกนเวกเตอร์ โดยไม่คำนึงถึงจำนวนหลายหลากของราก เราแทนค่าในดีเทอร์มีแนนต์ ซึ่งนำเราต่อไปนี้ ระบบเอกพันธ์ของสมการเชิงเส้น:

ไอเกนเวคเตอร์เป็นเวกเตอร์พอดี
ระบบการตัดสินใจพื้นฐาน

อันที่จริง ตลอดบทเรียน เรามีส่วนร่วมในการค้นหาเวกเตอร์ของระบบพื้นฐานเท่านั้น เพียงในขณะนี้ คำนี้ไม่จำเป็นอย่างยิ่ง โดยวิธีการที่นักเรียนที่คล่องแคล่วซึ่งอยู่ในชุดพราง สมการเอกพันธ์จะถูกบังคับให้สูบเดี๋ยวนี้

การดำเนินการเพียงอย่างเดียวคือการลบบรรทัดพิเศษ ผลลัพธ์คือเมทริกซ์ "หนึ่งต่อสาม" โดยมี "ขั้นตอน" อย่างเป็นทางการอยู่ตรงกลาง
– ตัวแปรพื้นฐาน – ตัวแปรอิสระ มีตัวแปรอิสระสองตัว ดังนั้น นอกจากนี้ยังมีเวกเตอร์สองตัวของระบบพื้นฐาน.

แสดงตัวแปรพื้นฐานในรูปของตัวแปรอิสระ: ปัจจัยที่เป็นศูนย์หน้า "x" ช่วยให้สามารถรับค่าใด ๆ ก็ได้ (ซึ่งมองเห็นได้ชัดเจนจากระบบสมการ)

ในบริบทของปัญหานี้ จะสะดวกกว่าที่จะเขียนวิธีแก้ปัญหาทั่วไปที่ไม่ได้อยู่ในแถว แต่ในคอลัมน์:

ทั้งคู่สอดคล้องกับเวกเตอร์ไอเกน:
ทั้งคู่สอดคล้องกับเวกเตอร์ไอเกน:

บันทึก : ผู้อ่านที่เชี่ยวชาญสามารถรับเวกเตอร์เหล่านี้ด้วยปากเปล่า - เพียงแค่วิเคราะห์ระบบ แต่จำเป็นต้องมีความรู้บางอย่างที่นี่: มีสามตัวแปร อันดับเมทริกซ์ของระบบ- หน่วยหมายถึง ระบบการตัดสินใจพื้นฐานประกอบด้วย 3 – 1 = 2 เวกเตอร์ อย่างไรก็ตาม เวกเตอร์ที่พบนั้นสามารถมองเห็นได้อย่างสมบูรณ์แม้จะไม่มีความรู้ด้านนี้ก็ตาม ในระดับที่เข้าใจได้ง่ายเท่านั้น ในกรณีนี้ เวกเตอร์ที่สามจะถูกเขียนให้ "สวยงามยิ่งขึ้น": . อย่างไรก็ตาม คำเตือนในอีกตัวอย่างหนึ่ง เลือกง่ายๆอาจไม่ใช่ ซึ่งเป็นเหตุผลว่าทำไมการจองจึงมีไว้สำหรับผู้มีประสบการณ์ นอกจากนี้ ทำไมไม่ใช้เป็นเวกเตอร์ที่สาม พูดว่า ? ท้ายที่สุดแล้ว พิกัดของมันยังเป็นไปตามสมการแต่ละสมการของระบบและเวกเตอร์ด้วย มีความเป็นอิสระเชิงเส้น โดยหลักการแล้วตัวเลือกนี้เหมาะสม แต่ "คดเคี้ยว" เนื่องจากเวกเตอร์ "อื่น ๆ " เป็นชุดค่าผสมเชิงเส้นของเวกเตอร์ของระบบพื้นฐาน

ตอบ: ค่าลักษณะเฉพาะ: , เวกเตอร์ลักษณะเฉพาะ:

ตัวอย่างที่คล้ายกันสำหรับโซลูชันที่ต้องทำด้วยตัวเอง:

ตัวอย่างที่ 7

ค้นหาค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะ

ตัวอย่างการจบบทเรียนโดยประมาณ

ควรสังเกตว่าทั้งในตัวอย่างที่ 6 และ 7 ได้รับเวกเตอร์ไอเกนอิสระเชิงเส้นสามตัว ดังนั้นเมทริกซ์ดั้งเดิมจึงสามารถแสดงเป็น การสลายตัวตามบัญญัติ. แต่ราสเบอร์รี่ดังกล่าวไม่ได้เกิดขึ้นในทุกกรณี:

ตัวอย่างที่ 8

การตัดสินใจ: เขียนและแก้สมการคุณลักษณะ:

เราขยายปัจจัยโดยคอลัมน์แรก:

เราดำเนินการลดความซับซ้อนเพิ่มเติมตามวิธีการที่พิจารณาโดยหลีกเลี่ยงพหุนามของระดับที่ 3:

เป็นค่าลักษณะเฉพาะ

มาหาเวกเตอร์ไอเกนกัน:

1) ไม่มีปัญหากับรูท:

อย่าแปลกใจที่นอกเหนือจากชุดคิทแล้วยังมีการใช้งานตัวแปรอีกด้วย - ไม่มีความแตกต่างที่นี่

จากสมการที่ 3 เราแสดง - เราแทนสมการที่ 1 และ 2:

จากสมการทั้งสองดังนี้

ให้แล้ว:

2-3) สำหรับหลายค่า เราได้ระบบ .

ให้เราเขียนเมทริกซ์ของระบบและใช้การแปลงเบื้องต้น นำมาเป็นรูปแบบขั้นบันได:

เวกเตอร์ลักษณะเฉพาะของเมทริกซ์กำลังสองคือค่าที่เมื่อคูณด้วย เมทริกซ์ที่กำหนดผลลัพธ์เป็นเวกเตอร์เชิงเส้น ด้วยคำพูดง่ายๆเมื่อเมทริกซ์ถูกคูณด้วยไอเกนเวกเตอร์ เมทริกซ์จะยังคงเหมือนเดิม แต่คูณด้วยจำนวนบางตัว

คำนิยาม

เวกเตอร์ลักษณะเฉพาะคือเวกเตอร์ที่ไม่ใช่ศูนย์ V ซึ่งเมื่อคูณด้วยเมทริกซ์จัตุรัส M จะกลายเป็นตัวมันเอง โดยเพิ่มขึ้นด้วยจำนวน λ ในสัญกรณ์พีชคณิต จะมีลักษณะดังนี้:

M × V = λ × V,

โดยที่ λ เป็นค่าลักษณะเฉพาะของเมทริกซ์ M

พิจารณา ตัวอย่างตัวเลข. เพื่อความสะดวกในการเขียน ตัวเลขในเมทริกซ์จะถูกคั่นด้วยเครื่องหมายอัฒภาค สมมติว่าเรามีเมทริกซ์:

• ม = 0; 4;
• 6; 10.

ลองคูณด้วยเวกเตอร์คอลัมน์:

• V = -2;

เมื่อคูณเมทริกซ์ด้วยเวกเตอร์คอลัมน์ เราจะได้เวกเตอร์คอลัมน์ด้วย เข้มงวด ภาษาคณิตศาสตร์สูตรสำหรับการคูณเมทริกซ์ 2 × 2 ด้วยเวกเตอร์คอลัมน์จะมีลักษณะดังนี้:

• ม × ว = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21

M11 หมายถึงองค์ประกอบของเมทริกซ์ M ซึ่งอยู่ในแถวแรกและคอลัมน์แรก และ M22 เป็นองค์ประกอบที่อยู่ในแถวที่สองและคอลัมน์ที่สอง สำหรับเมทริกซ์ของเรา องค์ประกอบเหล่านี้คือ M11 = 0, M12 = 4, M21 = 6, M22 10 สำหรับเวกเตอร์คอลัมน์ ค่าเหล่านี้คือ V11 = –2, V21 = 1 ตามสูตรนี้ เราได้รับสิ่งต่อไปนี้ ผลลัพธ์ของผลคูณของเมทริกซ์จัตุรัสโดยเวกเตอร์:

• ม × ว = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2

เพื่อความสะดวก เราเขียนเวกเตอร์คอลัมน์ลงในแถว ดังนั้นเราจึงคูณเมทริกซ์กำลังสองด้วยเวกเตอร์ (-2; 1) ซึ่งได้ผลลัพธ์เป็นเวกเตอร์ (4; -2) เห็นได้ชัดว่านี่คือเวกเตอร์เดียวกันคูณด้วย λ = -2 แลมบ์ดาในกรณีนี้หมายถึงค่าลักษณะเฉพาะของเมทริกซ์

เวกเตอร์ลักษณะเฉพาะของเมทริกซ์คือเวกเตอร์เชิงเส้น นั่นคือวัตถุที่ไม่เปลี่ยนตำแหน่งในอวกาศเมื่อคูณด้วยเมทริกซ์ แนวคิดของความเป็นเอกภาพใน พีชคณิตเวกเตอร์คล้ายกับคำว่าความขนานในเรขาคณิต ในการตีความทางเรขาคณิต เวกเตอร์คอลลิเนียร์- เหล่านี้เป็นส่วนกำกับขนานที่มีความยาวต่างกัน ตั้งแต่สมัยของ Euclid เรารู้ว่าเส้นตรงหนึ่งเส้นมีเส้นขนานขนานกันเป็นจำนวนไม่จำกัด ดังนั้นจึงมีเหตุผลที่จะสันนิษฐานว่าแต่ละเมทริกซ์มีจำนวนไอเกนเวกเตอร์เป็นจำนวนไม่สิ้นสุด

จากตัวอย่างที่แล้ว จะเห็นได้ว่าทั้ง (-8; 4) และ (16; -8) และ (32, -16) สามารถเป็นเวกเตอร์ลักษณะเฉพาะได้ ทั้งหมดนี้เป็นเวกเตอร์เชิงเส้นที่สอดคล้องกับค่าลักษณะเฉพาะ λ = -2 เมื่อคูณเมทริกซ์ดั้งเดิมด้วยเวกเตอร์เหล่านี้ เราจะยังได้ผลลัพธ์เป็นเวกเตอร์ซึ่งแตกต่างจากต้นฉบับ 2 เท่า นั่นเป็นเหตุผลว่าทำไม ในการแก้ปัญหาการหาเวกเตอร์ลักษณะเฉพาะ จึงจำเป็นต้องค้นหาวัตถุเวกเตอร์อิสระเชิงเส้นเท่านั้น ส่วนใหญ่แล้ว สำหรับเมทริกซ์ขนาด n × n จะมีจำนวนไอเกนเวกเตอร์เป็นลำดับที่ n เครื่องคิดเลขของเราออกแบบมาเพื่อการวิเคราะห์ เมทริกซ์สี่เหลี่ยมลำดับที่สอง ดังนั้น เกือบทุกครั้งจะพบเวกเตอร์ลักษณะเฉพาะสองตัว ยกเว้นเมื่อพวกมันตรงกัน

ในตัวอย่างข้างต้น เรารู้ล่วงหน้าถึงเวกเตอร์ลักษณะเฉพาะของเมทริกซ์ดั้งเดิมและกำหนดหมายเลขแลมบ์ดาด้วยสายตา อย่างไรก็ตามในทางปฏิบัติทุกอย่างเกิดขึ้นในทางตรงกันข้าม: ในตอนแรกมีค่าลักษณะเฉพาะและจากนั้นเป็นเวกเตอร์ลักษณะเฉพาะ

อัลกอริทึมโซลูชัน

ลองดูเมทริกซ์เดิม M อีกครั้งแล้วลองหาเวกเตอร์ลักษณะเฉพาะทั้งสองตัว ดังนั้นเมทริกซ์จึงมีลักษณะดังนี้:

• ม = 0; 4;
• 6; 10.

ในการเริ่มต้น เราต้องหาค่าลักษณะเฉพาะ λ ซึ่งเราต้องคำนวณดีเทอร์มิแนนต์ของเมทริกซ์ต่อไปนี้:

• (0 − λ); 4;
• 6; (10 − λ).

เมทริกซ์นี้ได้จากการลบ λ ที่ไม่รู้จักออกจากองค์ประกอบบนเส้นทแยงมุมหลัก ดีเทอร์มิแนนต์ถูกกำหนดโดยสูตรมาตรฐาน:

• เดตเอ = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

เนื่องจากเวกเตอร์ของเราต้องไม่เป็นศูนย์ เราจึงใช้สมการผลลัพธ์ว่าขึ้นต่อกันเชิงเส้นและจัดดีเทอร์มีแนนต์ detA เป็นศูนย์

(0 − λ) × (10 − λ) − 24 = 0

เปิดวงเล็บและรับสมการคุณลักษณะของเมทริกซ์:

λ 2 − 10λ − 24 = 0

นี่คือมาตรฐาน สมการกำลังสองซึ่งจะต้องแก้ไขในแง่ของการเลือกปฏิบัติ

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

รากของการเลือกปฏิบัติคือ sqrt(D) = 14 ดังนั้น λ1 = -2, λ2 = 12 ตอนนี้สำหรับค่าแลมบ์ดาแต่ละค่า เราต้องหาเวกเตอร์ลักษณะเฉพาะ ให้เราแสดงค่าสัมประสิทธิ์ของระบบสำหรับ λ = -2

• M − λ × E = 2; 4;
• 6; 12.

ในสูตรนี้ E คือ เมทริกซ์เอกลักษณ์. จากเมทริกซ์ที่ได้รับ เราสร้างระบบสมการเชิงเส้น:

2x + 4y = 6x + 12y

โดยที่ x และ y เป็นองค์ประกอบของเวกเตอร์ลักษณะเฉพาะ

ลองรวบรวม X ทั้งหมดทางซ้ายและ Y ทั้งหมดทางขวา แน่นอน - 4x = 8y หารนิพจน์ด้วย - 4 และรับ x = -2y ตอนนี้เราสามารถหาค่าไอเกนเวกเตอร์แรกของเมทริกซ์ได้โดยการรับค่าใด ๆ ของค่าที่ไม่รู้จัก สมมติว่า y = 1 แล้ว x = -2 ดังนั้นเวกเตอร์ลักษณะเฉพาะตัวแรกจึงดูเหมือน V1 = (–2; 1) กลับไปที่จุดเริ่มต้นของบทความ มันเป็นวัตถุเวกเตอร์ที่เราคูณเมทริกซ์เพื่อแสดงแนวคิดของเวกเตอร์ลักษณะเฉพาะ

ทีนี้มาหาเวกเตอร์ไอเกนสำหรับ λ = 12 กัน

• M - λ × E = -12; 4
• 6; -2.

ให้เราสร้างระบบสมการเชิงเส้นเดียวกัน

• -12x + 4y = 6x − 2y
• -18x = -6ย
• 3x=ย.

ตอนนี้ให้ x = 1 ดังนั้น y = 3 ดังนั้น เวกเตอร์ลักษณะเฉพาะตัวที่สองจึงดูเหมือน V2 = (1; 3) เมื่อคูณเมทริกซ์เดิมด้วย เวกเตอร์ที่กำหนดผลลัพธ์จะเป็นเวกเตอร์เดียวกันคูณด้วย 12 เสมอ ซึ่งจะทำให้อัลกอริทึมการแก้ปัญหาเสร็จสมบูรณ์ ตอนนี้คุณรู้วิธีกำหนดเวกเตอร์ไอเกนของเมทริกซ์ด้วยตนเองแล้ว

• ปัจจัย;
• ติดตาม นั่นคือผลรวมขององค์ประกอบในแนวทแยงหลัก
• อันดับนั่นคือ จำนวนเงินสูงสุดแถว/คอลัมน์อิสระเชิงเส้น

โปรแกรมทำงานตามอัลกอริทึมข้างต้น ลดขั้นตอนการแก้ปัญหา สิ่งสำคัญคือต้องชี้ให้เห็นว่าในโปรแกรมแลมบ์ดาจะแสดงด้วยตัวอักษร "c" มาดูตัวอย่างตัวเลขกัน

ตัวอย่างโปรแกรม

ลองนิยามเวกเตอร์ลักษณะเฉพาะสำหรับเมทริกซ์ต่อไปนี้:

• ม=5; 13;
• 4; 14.

ป้อนค่าเหล่านี้ลงในเซลล์ของเครื่องคิดเลขและรับคำตอบในรูปแบบต่อไปนี้:

• อันดับเมทริกซ์: 2;
• ดีเทอร์มีแนนต์เมทริกซ์: 18;
• การติดตามเมทริกซ์: 19;
• การคำนวณเวกเตอร์ไอเกน: c 2 − 19.00c + 18.00 (สมการลักษณะเฉพาะ);
• การคำนวณเวกเตอร์ไอเกน: 18 (ค่าแลมบ์ดาแรก);
• การคำนวณเวกเตอร์ไอเกน: 1 (ค่าแลมบ์ดาที่สอง);
• ระบบสมการเวกเตอร์ 1: -13x1 + 13y1 = 4x1 − 4y1;
• ระบบสมการเวกเตอร์ 2: 4x1 + 13y1 = 4x1 + 13y1;
• ไอเกนเวกเตอร์ 1: (1; 1);
• ไอเกนเวกเตอร์ 2: (-3.25; 1)

ดังนั้นเราจึงได้รับไอเกนเวกเตอร์สองตัวที่เป็นอิสระเชิงเส้น

บทสรุป

พีชคณิตเชิงเส้นและเรขาคณิตวิเคราะห์เป็นวิชามาตรฐานสำหรับน้องใหม่ ความพิเศษทางเทคนิค. จำนวนมากเวกเตอร์และเมทริกซ์นั้นน่ากลัว และง่ายที่จะทำผิดพลาดในการคำนวณที่ยุ่งยากเช่นนี้ โปรแกรมของเราจะช่วยให้นักเรียนตรวจสอบการคำนวณหรือแก้ปัญหาการหาค่าลักษณะเฉพาะโดยอัตโนมัติ มีเครื่องคำนวณพีชคณิตเชิงเส้นอื่นๆ ในแค็ตตาล็อกของเรา ใช้ในการเรียนหรือทำงานของคุณ