Навіщо потрібні формули диференціювання. Знайти похідну: алгоритм та приклади рішень
Нехай функцію y = f(x) визначено в проміжку X. Похіднийфункції y = f(x) у точці х o називається межа
=
![]() .
.
Якщо ця межа кінцевий,то функція f(x) називається диференційованоїу точці x o; при цьому вона виявляється обов'язковою і безперервною в цій точці.
Якщо ж межа дорівнює (або - ), то за умови, що функція в точці х oбезперервна, говоритимемо, що функція f(x) має у точці х o нескінченну похідну.
Похідна позначається символами
y , f (x o), , .
Знаходження похідної називається диференціюваннямфункції. Геометричний зміст похідноїполягає в тому, що похідна є кутовий коефіцієнт дотичної до кривої y=f(x) у даній точці х o ; фізичний зміст -у тому, що похідна від шляху за часом є миттєва швидкістьрухомої точки при прямолінійному русі s = s(t) у момент t o .
Якщо з - постійне число, і u = u(x), v = v(x) - деякі функції, що диференціюються, то справедливі наступні правила диференціювання:
1) (с) "= 0, (cu) "= cu";
2) (u+v)" = u"+v";
3) (uv)" = u"v+v"u;
4) (u/v)" = (u"v-v"u)/v 2;
5) якщо y = f(u), u = (x), тобто. y = f((x)) - складна функція,або суперпозиція, Складена з диференційованих функцій і f, то , або
6) якщо для функції y = f(x) існує зворотна функція, що диференціюється x = g(y), причому 0, то .
На основі визначення похідної та правил диференціювання можна скласти список табличних похідних основних елементарних функцій.
1. (u )" = u 1 u" ( R).
2. (a u)" = a u lna u".
3. (e u) "= e u u".
4. (log a u)" = u"/(u ln a).
5. (ln u)" = u"/u.
6. (sin u)" = cos u u".
7. (cos u)" = - sin u u".
8. (tg u)" = 1/cos 2 u u".
9. (ctg u)" = - u" / sin 2 u.
10. (arcsin u)" = u" / .
11. (arccos u)" = - u"/.
12. (arctg u)" = u"/(1 + u 2).
13. (arcctg u)" = - u"/(1 + u 2).
Обчислимо похідну статечно-показового виразу y=u v , (u>0), де uі vсуть функції від х, що мають у цій точці похідні u",v".
Прологарифмувавши рівність y=u v , отримаємо ln y = v ln u.
Прирівнюючи похідні по хвід обох частин отриманої рівності за допомогою правил 3, 5 та формули для похідної логарифмічної функції, будемо мати:
y"/y = vu"/u +v" ln u, звідки y" = y (vu"/u +v" ln u).
(u v)"=u v (vu"/u+v" ln u), u > 0.
Наприклад, якщо y = x sin x , то y" = x sin x (sin x/x + cos x ln x).
Якщо функція y = f(x) диференційована у точці x, тобто. має в цій точці кінцеву похідну y", то = y"+, де 0 при х 0; звідси y = y" х + x.
Головна частина збільшення функції, лінійна щодо х, називається диференціалом функціїі позначається dy: dy = y" х. Якщо покласти в цій формулі y=x, то отримаємо dx = x"х = 1х =х, тому dy=y"dx, тобто символ для позначення похідної можна як дроб.
Збільшення функції yє збільшення ординати кривої, а диференціал d yє збільшення ординати дотичної.
Нехай ми знайшли для функції y=f(x) її похідну y = f (x). Похідна від цієї похідної називається похідної другого порядкуфункції f(x), або другий похідний,і позначається ![]() .
.
Аналогічно визначаються та позначаються:
похідна третього порядку
-
![]() ,
,
похідна четвертого порядку -
![]()
і взагалі похідна n-го порядку
-
![]() .
.
Приклад 3.15. Обчислити похідну функції y=(3x 3 -2x+1)sin x.
Рішення.За правилом 3, y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x +1) cos x.
приклад 3.16 . Знайти y", y = tg x +.
Рішення.Використовуючи правила диференціювання суми та частки, отримаємо: y"=(tgx + )" = (tgx)" + ()" = + ![]() =
=
![]()
![]() .
.
Приклад 3.17. Знайти похідну складної функції y = , u = x 4 +1.
Рішення.За правилом диференціювання складної функції, отримаємо: y" x = y " u u" x = ()" u (x 4 +1)" x = (2u + . Так як u = x 4 +1, то (2 x 4 + 2+ ![]() .
.
2. Основні правила диференціювання
Якщо з- постійне число, і u = u(x), v = v(x) - деякі функції, що диференціюються, то справедливі такі правила диференціювання:
1) (с) "= 0, (cu) "= cu";
2) (u+v)" = u"+v";
3) (uv)" = u"v+v"u;
4) (u/v)" = (u"v-v"u)/v 2;
приклад 1.Знайти похідну функції
Рішення. Застосовуючи правила (5) та (8) та формулу (4) диференціювання статечної функціїотримаємо
приклад 2.Знайти похідну функції
![]()
Рішення. Застосуємо правило (7) диференціювання твору, а потім знайдемо похідні співмножників так само, як у прикладі 4. Тоді отримаємо
приклад 3.Знайти похідну функції у =
Рішення. Застосуємо правило (10) диференціювання приватного:
![]()
Потім, як і вище, обчислимо похідні в чисельнику. Маємо
![]()
Текст завдання:
Варіант 1
1. Знайти похідну функції  .
.
2. Знайти похідну функції  .
.
 у точці з абсцисою
у точці з абсцисою  ,
,  .
.
 t
t
Варіант 2
1. Знайти похідну функції  .
.
2. Знайти похідну функції  .
.
3. Написати рівняння щодо графіку функції  у точці з абсцисою
у точці з абсцисою  ,
,  .
.
4. Матеріальна точкарухається згідно із законом  . Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
. Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
Варіант 3
1. Знайти похідну функції  .
.
2. Знайти похідну функції  .
.
3. Написати рівняння щодо графіку функції  у точці з абсцисою
у точці з абсцисою  ,
,  .
.
4. Матеріальна точка рухається згідно із законом  . Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
. Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
Варіант 4
1. Знайти похідну функції  .
.
2. Знайти похідну функції  .
.
3. Написати рівняння щодо графіку функції  у точці з абсцисою
у точці з абсцисою  ,
,  .
.
4. Матеріальна точка рухається згідно із законом  . Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
. Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
Варіант 5
1. Знайти похідну функції  .
.
2. Знайти похідну функції  .
.
3. Написати рівняння щодо графіку функції  у точці з абсцисою
у точці з абсцисою  ,
,  .
.
4. Матеріальна точка рухається згідно із законом  . Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
. Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
Варіант 6
1. Знайти похідну функції  .
.
2. Знайти похідну функції  .
.
3. Написати рівняння щодо графіку функції  у точці з абсцисою
у точці з абсцисою  ,
,  .
.
4. Матеріальна точка рухається згідно із законом  . Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
. Знайти швидкість та прискорення в момент часу t=5 с. (Переміщення вимірюється за метри.)
Практична робота № 16
Тема: Застосування похідної до дослідження функцій та побудови графіків
Мета роботи: закріпити знання та вміння студентів з освоєння теми, формувати навички прикладного використання апарату похідної.
Теоретичне обґрунтування:
Схема дослідження функції та побудова її графіка
I. Знайти область визначення функції.
ІІ. Знайти точки перетину графіка функції з осями координат.
ІІІ. Знайти асимптоти.
IV. Знайти точки можливого екстремуму.
V. Знайти критичні точки.
VI. За допомогою допоміжного малюнка дослідити знак перших похідних. Визначити ділянки зростання та зменшення функції, точки екстремумів.
VII. Побудувати графік з огляду на дослідження, проведене в п.1-6.
Відеокурс «Отримай п'ятірку» включає всі теми, необхідні для успішної здачі ЄДІз математики на 60-65 балів. Цілком всі завдання 1-13 Профільного ЄДІз математики. Підходить також для здачі Базового ЄДІ з математики. Якщо ви хочете здати ЄДІ на 90-100 балів, вам треба вирішувати частину 1 за 30 хвилин і без помилок!
Курс підготовки до ЄДІ для 10-11 класів, а також для викладачів. Все необхідне, щоб вирішити частину 1 ЄДІ з математики (перші 12 завдань) та задачу 13 (тригонометрія). А це понад 70 балів на ЄДІ, і без них не обійтись ні стобальнику, ні гуманітарію.
Уся необхідна теорія. Швидкі способирішення, пастки та секрети ЄДІ. Розібрано всі актуальні завдання частини 1 із Банку завдань ФІПД. Курс повністю відповідає вимогам ЄДІ-2018.
Курс містить 5 великих тем, по 2,5 години кожна. Кожна тема дається з нуля, це просто і зрозуміло.
Сотні завдань ЄДІ. Текстові завданнята теорія ймовірностей. Прості і легко запам'ятовуються алгоритми розв'язання задач. Геометрія. Теорія, довідковий матеріал, розбір всіх типів завдань ЄДІ Стереометрія. Хитрі прийоми рішення, корисні шпаргалки, розвиток просторової уяви. Тригонометрія з нуля - до завдання 13. Розуміння замість зубріння. Наочне пояснення складних понять. Алгебра. Коріння, ступеня та логарифми, функція та похідна. База для вирішення складних завдань 2 частини ЄДІ.
Диференціювання – це обчислення похідної.
1. Формули диференціювання.
Основні формули диференціювання – у таблиці. Їх необов'язково зазубривати. Зрозумівши деякі закономірності, ви можете з одних формул самостійно виводити інші.
1) Почнемо з формули (k x+ m) '= k.
Її окремими випадками є формули x′ = 1 і C′ = 0.
У будь-якій функції виду у = kx + m похідна дорівнює кутовому коефіцієнту k.
Наприклад, дана функція у = 2 х+ 4. Її похідна в будь-якій точці дорівнюватиме 2:
(2 х + 4) '= 2 .
Похідна функції у = 9 х+ 5 у будь-якій точці дорівнює 9 . І т.д.
А давайте знайдемо похідну функції у = 5 х. Для цього уявимо 5 ху вигляді (5 х+ 0). Ми отримали вираз, схожий на попередній. Значить:
(5х)′ = (5 х+ 0) '= 5.
Зрештою, з'ясуємо, чому дорівнює x′.
Застосуємо прийом із попереднього прикладу: представимо ху вигляді 1 х+ 0. Тоді отримаємо:
x′ = (1 х+ 0) '= 1.
Таким чином, ми самостійно вивели формулу з таблиці:
(0 · x+ m) = 0.
Але тоді виходить, що m′ теж дорівнює 0. Нехай m = C, де C – довільна стала. Тоді ми приходимо до ще однієї істини: похідна постійної дорівнює нулю. Тобто одержуємо ще одну формулу з таблиці.
 Переведення десяткового дробу у звичайний і навпаки: правило, приклади
Переведення десяткового дробу у звичайний і навпаки: правило, приклади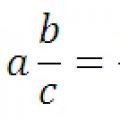 Переведення десяткових чисел у звичайний дріб
Переведення десяткових чисел у звичайний дріб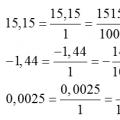 Переведення звичайного дробу в десятковий дріб і назад, правила, приклади
Переведення звичайного дробу в десятковий дріб і назад, правила, приклади