Прості та складові числа. Розкладання на множники 6 складових чисел розкласти на прості множники
Цей онлайн-калькулятор призначений для розкладання функції на множники.
Наприклад, розкласти на множники: x2/3-3x+12. Запишемо як x^2/3-3*x+12. Також можна використовувати цей сервіс, де всі викладки зберігаються у форматі Word.
Наприклад, розкласти на доданки. Запишемо як (1-x^2)/(x^3+x) . Щоб переглянути хід рішення, натискаємо Show steps. Якщо необхідно отримати результат у форматі Word, використовуйте цей сервіс.
Примітка: число "пі" (π) записується як pi; корінь квадратний як sqrt, наприклад, sqrt(3), тангенс tg записується як tan. Щоб переглянути відповідь, див. розділ Alternative.
- Якщо заданий простий вираз, наприклад, 8*d+12*c*d , вираз розкласти на множники означає подати вираз у вигляді співмножників. Для цього потрібно знайти спільні множники. Даний вираз запишемо як: 4*d*(2+3*c) .
- Подати твір у вигляді двох двочленів: x 2 + 21yz + 7xz + 3xy. Тут треба знайти кілька спільних співмножників: x(x+7z) + 3y(x + 7z). Виносимо (x+7z) та отримуємо: (x+7z)(x + 3y) .
див. також Поділ багаточленів куточком (показані всі кроки поділу стовпчиком)
Корисним для вивчення правил розкладання на множники будуть формули скороченого множення, за допомогою яких буде ясно, як розкривати дужки з квадратом:
- (a+b) 2 = (a+b)(a+b) = a 2 +2ab+b 2
- (a-b) 2 = (a-b)(a-b) = a 2 -2ab+b 2
- (a+b)(a-b) = a 2 - b 2
- a 3 +b 3 = (a+b)(a 2 -ab+b 2)
- a 3 -b 3 = (a-b)(a 2 +ab+b 2)
- (a+b) 3 = (a+b)(a+b) 2 = a 3 +3a 2 b + 3ab 2 +b 3
- (a-b) 3 = (a-b)(a-b) 2 = a 3 -3a 2 b + 3ab 2 -b 3
Методи розкладання на множники
Вивчивши кілька прийомів розкладання на множникиможна скласти таку класифікацію рішень:- Використання формул скороченого множення.
- Пошук загального множника.
Все починається з геометричної прогресії. На першій лекції по рядах (див. розділ 18.1. Основні визначення) ми довели, що ця функція є сумою ряду  , і ряд сходиться до функції при
, і ряд сходиться до функції при  . Отже,
. Отже,
 .
.
Випишемо кілька різновидів цього ряду. Замінивши х на - х , отримаємо
при заміні х
на  отримуємо
отримуємо
і т.д.; область збіжності всіх цих рядів та сама:  .
.
2.
 .
.
Усі похідні цієї функції у точці х
=0 рівні  тому ряд має вигляд
тому ряд має вигляд
 .
.
Область збіжності цього ряду - вся числова вісь (приклад 6 розділу 18.2.4.3. Радіус збіжності, інтервал збіжності та область збіжності статечного ряду), тому  при
при  . Як наслідок, залишковий член формули Тейлора
. Як наслідок, залишковий член формули Тейлора  . Тому ряд сходить до
. Тому ряд сходить до
 у будь-якій точці х
.
у будь-якій точці х
.
3.
 .
.
Цей ряд абсолютно сходиться за 
 , і його сума дійсно дорівнює
, і його сума дійсно дорівнює  . Залишковий член формули Тейлора має вигляд
. Залишковий член формули Тейлора має вигляд  , де
, де  або
або  - обмежена функція, а
- обмежена функція, а  (Це загальний член попереднього розкладання).
(Це загальний член попереднього розкладання).
4.
 .
.
Це розкладання можна отримати, як і попередні, послідовним обчисленням похідних, але ми зробимо інакше. Почленно продиференціюємо попередній ряд:
Східність до функції по всій осі випливає з теореми про почленном диференціювання статечного ряду.
5. Самостійно довести, що на всій числовій осі .
6.
 .
.
Ряд цієї функції називається біномним рядом. Тут ми обчислюватимемо похідні.
…Ряд Маклорена має вигляд
Шукаємо інтервал збіжності: отже, інтервал збіжності є  . Дослідження залишкового члена та поведінка ряду на кінцях інтервалу збіжності проводити не будемо; виявляється, що за
. Дослідження залишкового члена та поведінка ряду на кінцях інтервалу збіжності проводити не будемо; виявляється, що за  ряд абсолютно сходиться в обох точках
ряд абсолютно сходиться в обох точках  , при
, при  ряд умовно сходиться у точці
ряд умовно сходиться у точці  і розходиться в точці
і розходиться в точці  , при
, при  розходиться в обох точках.
розходиться в обох точках.
7.
 .
.
Тут ми скористаємося тим, що
 . Оскільки , то, після почленного інтегрування,
. Оскільки , то, після почленного інтегрування,
Область збіжності цього ряду - напівінтервал  , збіжність до функції у внутрішніх точках випливає з теореми про почленное інтегрування статечного ряду, у точці х
=1 - з безперервності і функції, і суми статечного ряду у всіх точках, скільки завгодно близьких до х
=1 зліва. Зазначимо, що взявши х
=1, ми знайдемо суму ряду .
, збіжність до функції у внутрішніх точках випливає з теореми про почленное інтегрування статечного ряду, у точці х
=1 - з безперервності і функції, і суми статечного ряду у всіх точках, скільки завгодно близьких до х
=1 зліва. Зазначимо, що взявши х
=1, ми знайдемо суму ряду .
8.
Почленно інтегруючи ряд , отримаємо розкладання функції  . Виконати всі викладки самостійно, виписати область збіжності.
. Виконати всі викладки самостійно, виписати область збіжності.
9.
Випишемо розкладання функції  за формулою біномного ряду з
за формулою біномного ряду з  : . Знаменник
: . Знаменник  представлений як , подвійний факторіал
представлений як , подвійний факторіал  означає добуток всіх натуральних чисел тієї ж парності, що й
означає добуток всіх натуральних чисел тієї ж парності, що й  , що не перевершують
, що не перевершують  . Розкладання сходиться до функції при
. Розкладання сходиться до функції при  . Почленно інтегруючи його від 0 до х
, Отримаємо . Виявляється, що цей ряд сходиться до функції на всьому відрізку
. Почленно інтегруючи його від 0 до х
, Отримаємо . Виявляється, що цей ряд сходиться до функції на всьому відрізку  ; при х
=1 отримуємо ще одне гарне уявлення числа
; при х
=1 отримуємо ще одне гарне уявлення числа  :
:
 .
.
18.2.6.2. Розв'язання задач на розкладання функцій у ряд.Більшість завдань, в яких потрібно розкласти елементарну функцію в ряд за ступенями  , Вирішується застосуванням стандартних розкладів. На щастя, будь-яка основна елементарна функція має властивість, що дозволяє це зробити. Розглянемо низку прикладів.
, Вирішується застосуванням стандартних розкладів. На щастя, будь-яка основна елементарна функція має властивість, що дозволяє це зробити. Розглянемо низку прикладів.
1. Розкласти функцію  за ступенями
за ступенями  .
.
Рішення. . Ряд сходиться за  .
.
2. Розкласти функцію  за ступенями
за ступенями  .
.
Рішення.  . Область збіжності:
. Область збіжності:  .
.
3. Розкласти функцію  за ступенями
за ступенями  .
.
Рішення. . Ряд сходиться за  .
.
4. Розкласти функцію  за ступенями
за ступенями  .
.
Рішення. . Ряд сходиться за  .
.
5. Розкласти функцію  за ступенями
за ступенями  .
.
Рішення. . Область збіжності  .
.
6. Розкласти функцію  за ступенями
за ступенями  .
.
Рішення. Розкладання до ряду простих раціональних дробів другого типу виходить почленним диференціюванням відповідних розкладів дробів першого типу. У цьому прикладі. Далі почленним диференціюванням можна отримати розкладання функцій  ,
,
 і т.д.
і т.д.
7. Розкласти функцію  за ступенями
за ступенями  .
.
Рішення. Якщо раціональний дріб не є простим, він спочатку подається у вигляді суми простих дробів:  , а потім діємо, як у прикладі 5: , де
, а потім діємо, як у прикладі 5: , де  .
.
Звичайно, такий підхід не застосовується, наприклад, для розкладання функції  за ступенями х
. Тут, якщо треба отримати кілька перших членів ряду Тейлора, найпростіше знайти значення в точці х
=0 необхідної кількості перших похідних.
за ступенями х
. Тут, якщо треба отримати кілька перших членів ряду Тейлора, найпростіше знайти значення в точці х
=0 необхідної кількості перших похідних.
Кожне натуральне число, крім одиниці, має два чи більше дільників. Наприклад, число 7, ділиться без залишку тільки на 1 і на 7, тобто має два дільники. А у числа 8, дільники 1, 2, 4, 8, тобто аж 4 дільники одразу.
Чим відрізняються прості та складові числа
Числа, які мають понад два дільники, називаються складовими. Числа, які мають лише два дільники: одиниця і саме це число, називаються простими числами.
Число 1 має лише один ділити, саме саме це число. Одиниця не відноситься ні до простих, ні до складових чисел.
- Наприклад, число 7 просте, а 8 складове.
Перші 10 простих чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Число 2 єдине парне просте число, всі інші прості числа непарні.
Число 78 складене, оскільки крім 1 і себе, воно ділиться ще й 2. При розподілі на 2 отримаємо 39. Тобто 78= 2*39. У таких випадках говорять, що число розклали на множники 2 та 39.
Будь-яке складове число можна розкласти на два множники, кожен з яких більший за 1. З простим числом такий фокус не прокотить. Такі справи.
Розкладання числа на прості множники
Як зазначалося вище, будь-яке складове число, можна розкласти на два множника. Візьмемо, наприклад, число 210. Це число можна розкласти на два множники 21 і 10. Але числа 21 і 10 теж складові, розкладемо їх на два множники. Отримаємо 10 = 2 * 5, 21 = 3 * 7. І в результаті число 210 розклалося вже на 4 множники: 2,3,5,7. Ці числа вже прості та їх розкласти не можна. Тобто ми розклали число 210 на прості множники.
При розкладанні складених чисел на прості множники, їх зазвичай записують у порядку зростання.
Слід запам'ятати, що будь-яке складове число можна розкласти на прості множники і єдиним чином, з точністю до перестановки.
- Зазвичай при розкладанні числа на прості множники користуються ознаками ділимості.
Розкладемо число 378 на прості множники
Записуватимемо числа, розділяючи їх вертикальною рисою. Число 378 ділиться на 2, оскільки закінчується на 8. При розподілі отримаємо число 189. Сума цифр числа 189 ділиться на 3, отже, і саме число 189 ділиться на 3. У результаті отримаємо 63.
Число 63 теж ділиться на 3, за ознакою подільності. Отримуємо 21, число 21 знову можна поділити на 3, отримаємо 7. Сімка ділиться тільки на себе, отримуємо одиницю. На цьому закінчено поділ. Праворуч після риси вийшли прості множники, куди розкладається число 378.
378|2
189|3
63|3
21|3
Що означає розкласти на звичайні множники? Як це зробити? Що можна дізнатися щодо розкладання числа на прості множники? Відповіді ці питання ілюструються конкретними прикладами.
Визначення:
Простим називають число, яке має рівно два різні дільники.
Складовим називають число, яке має понад два дільники.
Розкласти натуральне число на множники - значить уявити його у вигляді добутку натуральних чисел.
Розкласти натуральне число на прості множники - значить уявити його у вигляді добутку простих чисел.
Зауваження:
- У розкладанні простого числа один із множників дорівнює одиниці, а інший - самому цьому числу.
- Говорити про розкладання одиниці на множники немає сенсу.
- Складове число можна розкласти на множники, кожен із яких відмінний від 1.
|
Розкладемо число 150 на множники. Наприклад, 150 – це 15 помножити на 10. 15 – це складове число. Його можна розкласти на прості множники 5 та 3. 10 – це складове число. Його можна розкласти на прості множники 5 та 2. Записавши замість 15 та 10 їх розкладання на прості множники, ми отримали розкладання числа 150. |
|
|
|
Число 150 можна по-іншому розкласти на множники. Наприклад, 150 - це добуток чисел 5 та 30. 5 – число просте. 30 - це складова. Його можна подати як добуток 10 і 3. 10 – число складове. Його можна розкласти на прості множники 5 та 2. Ми отримали розкладання числа 150 на прості множники в інший спосіб. |
|
Зауважимо, що перше та друге розкладання однакові. Вони відрізняються лише порядком проходження множників. Прийнято записувати множники у порядку зростання. |
|
|
Будь-яке складове число можна розкласти на звичайні множники єдиним чином з точністю до порядку множників. |
|
При розкладанні великих чисел на прості множники використовують запис у стовпчик:
 |
Найменше просте число, яке ділиться 216 - це 2. Розділимо 216 на 2. Отримаємо 108. |
|
Отримане число 108 поділяється на 2. Виконаємо поділ. Отримаємо в результаті 54. |
|
|
Відповідно до ознаки ділимості на 2 число 54 ділиться на 2. Виконавши поділ, отримаємо 27. |
|
|
Число 27 закінчується на непарну цифру 7 . Воно Чи не ділиться на 2. Наступне просте число - це 3. Розділимо 27 на 3. Отримаємо 9. Найменше просте Число, на яке ділиться 9 - це 3. Три - саме є простим числом, воно ділиться на себе і на одиницю. Розділимо 3 на себе. У результаті ми отримали 1. |
|
- Число ділиться лише ті прості числа, які входять до його розкладання.
- Число ділиться лише ті складові числа, розкладання яких у прості множники повністю у ньому міститься.
Розглянемо приклади:
|
4900 ділиться на прості числа 2, 5 і 7. (Вони входять у розкладання числа 4900), але не ділиться, наприклад, на 13. |
|
|
11550 75. Це так, тому що розкладання числа 75 повністю міститься в розкладанні числа 11550. В результаті розподілу буде добуток множників 2, 7 і 11. 11550 не ділиться на 4, тому що в розкладанні чотирьох є зайва двійка. |
Знайти приватне від розподілу числа a на число b, якщо ці числа розкладаються на прості множники наступним чином a=2∙2∙2∙3∙3∙3∙5∙5∙19; b=2∙2∙3∙3∙5∙19
|
Розкладання числа b повністю міститься у розкладанні числа a. |
|
|
Результат поділу a на b - це добуток, що залишилися в розкладанні числа a трьох чисел. Отже, відповідь: 30. |
Список літератури
- Віленкін Н.Я., Жохов В.І., Чесноков А.С., Шварцбурд С.І. Математика 6. – К.: Мнемозіна, 2012.
- Мерзляк А.Г., Полонський В.В., Якір М.С. Математика 6 клас. – Гімназія. 2006.
- Депман І.Я., Віленкін Н.Я. За сторінками підручника з математики. - М: Просвітництво, 1989.
- Рурукін О.М., Чайковський І.В. Завдання з курсу математики 5-6 клас. - М: ЗШ МІФІ, 2011.
- Рурукін О.М., Сочілов С.В., Чайковський К.Г. Математика 5-6. Посібник для учнів 6-х класів заочної школи МІФІ. - М: ЗШ МІФІ, 2011.
- Шеврін Л.М., Гейн А.Г., Коряков І.О., Волков М.В. Математика: Підручник-співрозмовник для 5-6 класів середньої школи. - М: Просвітництво, Бібліотека вчителя математики, 1989.
- Інтернет-портал Matematika-na.ru().
- Інтернет-портал Math-portal.ru().
Домашнє завдання
- Віленкін Н.Я., Жохов В.І., Чесноков А.С., Шварцбурд С.І. Математика 6. – К.: Мнемозіна, 2012. № 127, № 129, № 141.
- Інші завдання: №133, №144.

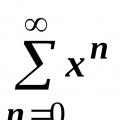 Розкладання на множники 6 складових чисел розкласти на прості множники
Розкладання на множники 6 складових чисел розкласти на прості множники Взаємодія неалельних генів: типи та форми До типів взаємодії алельних генів відноситься
Взаємодія неалельних генів: типи та форми До типів взаємодії алельних генів відноситься Презентація «Правила поведінки у бібліотеці
Презентація «Правила поведінки у бібліотеці