تحليل الأعداد إلى عوامل أولية وطرق وأمثلة للتحلل. الحصول على التحليل القانوني لعدد إلى عوامل أولية

المحاضرة 14 العمليات العشوائية التوسع القانوني للعمليات العشوائية. التحلل الطيفيثابت عملية عشوائية. محاضرة 14
العمليات العشوائية
التوسع الكنسي للعمليات العشوائية.
التحلل الطيفي العشوائي الثابت
عملية. عمليات عشوائية مع مستقلة
أقسام. عمليات ماركوف وسلاسل ماركوف.
العمليات العشوائية العادية. دوريا
العمليات العشوائية غير الثابتة
(أحمدوف س.ك.)

التوسع الكنسي للعمليات العشوائية

أي SP X(t) m.b. المقدمة في
وشكل تحللها، أي. كمجموع
العمليات الأولية:
فك – المتغيرات العشوائية
φk(t) – الدوال غير العشوائية (الجيوب، الأسيات، القدرة
وظائف، الخ.)
حالة خاصة من هذا التحلل هي Canonical
تقسيم
SP X(t)، الذي يحتوي على النموذج
mx(t) = M – التوقع الرياضي لـ SP X(t)
V1، V2…Vk – SVs غير مترابطة ومركزية
D1، D2…Dk- SW التشتت V1، V2…Vk
φk(t) – وظائف غير عشوائية للوسيطة t
المتغيرات العشوائية V1، V2…Vk تسمى معاملات المعيار
تقسيم،
والدوال غير العشوائية φ1(t)، φ2(t) φk(t) - وظائف الإحداثيات
التوسع الكنسي

الخصائص الرئيسية لـ SP المحددة بواسطة التحلل القانوني

M – التوقع الرياضي لـ SP X(t)
ك س (ر، ر ') - وظيفة الارتباطس س (ر)
تعبير
- التوسع الكنسي للارتباط
المهام
إذا كان t = t، فوفقًا للأول
خاصية وظيفة الارتباط
تعبير
دك(ر) –
تشتت
التوسع الكنسي لتباين SP X(t)

التحلل الطيفي لـ SP ثابت

مشروع مشترك ثابت m.b. ممثلة بالتحلل القانوني
Vk وUk - SVs غير مترابطة ومركزة مع التشتت
د = د = دك
ω – قيمة غير عشوائية (التردد)
في هذه الحالة، التوسع القانوني لوظيفة الارتباط
يتم تحديده من خلال التعبير
مُقَدَّم
العنوان الأساسي
تقسيم
مشروع مشترك
X(ر)
مُسَمًّى
التحلل الطيفي لـ SP و
أعرب كما
Θk - المرحلة الاهتزاز التوافقيالابتدائية الثابتة SP,
كونها SW موزعة بشكل موحد في الفترة (0، 2π)؛
Zk – SV، وهي سعة التذبذب التوافقي
الابتدائية الثابتة SP

التحلل الطيفي للثابت SP (2)

المتغيرات العشوائية Θk و Zk تعتمد على ما يلي وينطبق عليهما:
Vk = Zk cos Θk
المملكة المتحدة = Zk خطيئة Θk
مشروع مشترك ثابت m.b. قدم كمجموع من التوافقيات
التذبذبات ذات السعات العشوائية Zk والمراحل العشوائية Θk on
ترددات مختلفة غير عشوائية ωk
وظيفة الارتباط لـ SP X(t) الثابتة متساوية
وظيفة حجتها، أي. ك س (τ) = ك س (- τ). ولذلك، على الفاصل الزمني (-T،
T) يمكن توسيعها إلى سلسلة فورييه في التوافقيات الزوجية (جيب التمام):
إن تباين SP X(t) الثابت يساوي
كمية
الفروق
الجميع
التوافقيات
له
التحلل الطيفي
يسمى الاعتماد Dk = f(wk) بطيف التشتت المنفصل أو
طيف منفصل من SP ثابت.

التحلل الطيفي للثابت SP (3)

في ∆ω
→ 0 سيكون هناك انتقال إلى الطيف المستمر
Sx(ω) - الكثافة الطيفية
وهكذا، فإن وظيفة الارتباط والكثافة الطيفية
ترتبط بواسطة جيب التمام – تحويل فورييه. ولذلك الطيفية
كثافة المشروع المشترك الثابت m.b. يتم التعبير عنها من خلال الارتباط
وظيفة حسب الصيغة

عمليات عشوائية ذات مقاطع عرضية مستقلة

في الهيدرولوجيا، يُعتقد أن السلسلة تتوافق مع نموذج عشوائي
القيم، إذا لم يكن هناك ارتباط كبير بين أعضاء هذه السلسلة
لأي تحول τ.
تعتبر العملية العشوائية ذات المقاطع العرضية المستقلة بمثابة SP لها
عند القيم t و t'
مكس (ر) = مكس
دس (ر) = دس
Kx(t,t') = kx(τ) = (Dx لـ τ = 0 و0 لـ τ ≠ 0)
مثل هذه العملية ثابتة ولها طاقة
ملكية
لمثل هذه العمليات، خصائص قانون التوزيع أحادي البعد
يمكن تقييمها لأي قسم ولأي (بما فيه الكفاية
طويلة الأجل) التنفيذ
مثل هذه العمليات ليس لها أي ارتباط بين الأعضاء داخل أي منها
تطبيق
وبقبول مثل هذا النموذج، يفترض وجود عدد من الكميات الهيدرولوجية
يمثل أحد تنفيذ المشروع المشترك
تسمى أحيانًا عملية عشوائية ذات مقاطع عرضية مستقلة
"الضوضاء البيضاء" قياسا على الضوء الأبيض

عمليات ماركوف وسلاسل ماركوف

عملية عشوائية
ويسمى ماركوفيان إذا كان هناك أي شيء
في الوقت t احتمال كل حالة من حالات النظام في المستقبل
(عند t > t0) يعتمد فقط على حالته في الوقت الحاضر (عند t = t0) وليس
يعتمد على حالته في الماضي (في t< t0)
سلسلة ماركوف أو بسيطة سلسلة ماركوفمُسَمًّى
عملية ماركوف مع حالة منفصلة ووقت منفصل
تم وصف Markov SP بالكامل بقانون ثنائي الأبعاد
توزيعات. لو عملية ماركوفثابت و
Ergodic، فيمكن تقدير خصائصه بناءً على واحد
تطبيق.
الدائرة التي فيها الاحتمالات المشروطةالدول في المستقبل تعتمد
من حالته في عدة خطوات سابقة يسمى معقدا
سلسلة ماركوف.

العمليات العشوائية العادية (الغاوسية).

تسمى العملية العشوائية العادية (الغاوسية) X(t).
SP، حيث يكون SP X(ti) في جميع الأقسام عاديًا
توزيع
المشاريع المشتركة غير الثابتة بشكل دوري
عند الدراسة السنوية والشهرية واليومية وما إلى ذلك. العمليات عادة ما تكون
يتم ملاحظتها سنويًا ، وما إلى ذلك. التقلبات. في هذه الحالة، كما
النموذج الرياضي، يمكنك استخدام النموذج بشكل دوري
عملية عشوائية غير ثابتة (NSRP)
تسمى العملية العشوائية بشكل دوري غير ثابت إذا
خصائصه الاحتمالية ثابتة فيما يتعلق بالتحولات
رقم موجب T. على سبيل المثال، بخطوة منفصلة مدتها شهر واحد
يجب الحفاظ على الثبات عند التحولات 12، 24، 36، إلخ.

تقدم هذه المقالة إجابات على سؤال تحليل رقم على الورقة. دعونا نفكر فكرة عامةحول التحلل مع الأمثلة. دعونا فرزها الشكل الكنسيالتحلل والخوارزمية الخاصة به. سيتم النظر في جميع الطرق البديلة باستخدام علامات القسمة وجداول الضرب.

Yandex.RTB RA-A-339285-1

ماذا يعني تحليل عدد ما إلى عوامل أولية؟

دعونا نلقي نظرة على هذا المفهوم العوامل الأولية. من المعروف أن كل عامل أولي هو عدد أولي. في حاصل ضرب الصورة 2 · 7 · 7 · 23 لدينا 4 عوامل أولية في الصورة 2، 7، 7، 23.

يتضمن التخصيم تمثيله في شكل منتجات الأعداد الأولية. إذا أردنا تحليل الرقم 30، فسنحصل على 2، 3، 5. سيكون الإدخال على الشكل 30 = 2 · 3 · 5. من الممكن أن تتكرر المضاعفات. رقم مثل 144 به 144 = 2 2 2 2 3 3.

ليست كل الأرقام عرضة للانحلال. يمكن تحليل الأعداد الأكبر من 1 والتي تعتبر أعدادًا صحيحة. الأعداد الأولية، عند تحليلها، لا تقبل القسمة إلا على 1 وعلى نفسها، لذلك من المستحيل تمثيل هذه الأعداد كمنتج.

عندما يشير z إلى أعداد صحيحة، يتم تمثيله كمنتج لـ a وb، حيث يتم تقسيم z على a وb. يتم تحليل الأعداد المركبة إلى عوامل أولية باستخدام النظرية الأساسية في الحساب. إذا كان الرقم أكبر من 1، فسيتم تحليله ص 1، ص 2، ...، ص ن تأخذ الشكل a = p 1 , p 2 , … , p n . من المفترض أن يكون التحلل في متغير واحد.

التحليل القانوني لعدد ما إلى عوامل أولية

أثناء التوسع، يمكن تكرار العوامل. وهي مكتوبة بشكل مضغوط باستخدام الدرجات. إذا، عند تحليل الرقم a، لدينا العامل p 1، الذي يتكرر s 1 مرات، وهكذا p n - s n مرات. وبالتالي فإن التوسع سوف يأخذ الشكل أ=ع 1 ق 1 · أ = ع 1 ق 1 · ع 2 ق 2 · … · ع ن ق ن. يُطلق على هذا الإدخال اسم التحليل القانوني لعدد ما إلى عوامل أولية.

عند توسيع الرقم 609840، نحصل على 609840 = 2 2 2 2 3 3 5 7 11 11، وسيكون شكله القانوني 609 840 = 2 4 3 2 5 7 11 2. باستخدام التوسعة الأساسية، يمكنك العثور على كافة قواسم الرقم وعددها.

للتحليل بشكل صحيح، يجب أن يكون لديك فهم للأعداد الأولية والمركبة. النقطة هي الحصول على عدد متسلسل من المقسومات على شكل p 1، p 2، ...، p n أعداد أ، أ 1، أ 2، …، أ ن - 1، وهذا يجعل من الممكن الحصول عليها أ = ص 1 أ 1، حيث أ 1 = أ: ص 1 ، أ = ص 1 · أ 1 = ص 1 · ص 2 · أ 2 ، حيث أ 2 = أ 1: ص 2 ، … ، أ = ص 1 · ع 2 · … · ع ن · ن ، حيث أ ن = أ ن - 1: ص ن. عند الاستلام ن = 1ثم المساواة أ = ص 1 ص 2 … ع ننحصل على التحلل المطلوب للرقم a إلى عوامل أولية. لاحظ أن ص 1 ≥ ص 2 ≥ ص 3 ≥ … ≥ ص ن.

للعثور على أصغر المقسومات المشتركةتحتاج إلى استخدام جدول الأعداد الأولية. يتم ذلك باستخدام مثال العثور على أصغر مقسوم أولي للرقم z. عند أخذ الأعداد الأولية 2، 3، 5، 11 وهكذا، وتقسيم العدد z عليها. منذ ض ليس كذلك رقم اولييجب أن يؤخذ في الاعتبار أن أصغر مقسوم أولي لن يكون أكبر من z. يمكن أن نرى أنه لا توجد مقسومات على z، فمن الواضح أن z عدد أولي.

مثال 1

لننظر إلى مثال الرقم 87. عندما يتم قسمته على 2، نحصل على 87: 2 = 43 والباقي 1. ويترتب على ذلك أن 2 لا يمكن أن يكون مقسوما؛ يجب أن يتم القسمة بالكامل. عند القسمة على 3 نحصل على 87: 3 = 29. ومن هنا الاستنتاج هو أن 3 هو أصغر مقسوم أولي على الرقم 87.

عند تحليل العوامل الأولية، يجب عليك استخدام جدول الأعداد الأولية، حيث أ. عند تحليل 95، يجب استخدام حوالي 10 أعداد أولية، وعند تحليل 846653، يجب استخدام حوالي 1000.

دعونا نفكر في خوارزمية التحلل إلى عوامل أولية:

• إيجاد أصغر عامل للمقسوم عليه p 1 لعدد ما أبالصيغة a 1 = a: p 1، عندما a 1 = 1، فإن a هو رقم أولي ويتم تضمينه في التحليل، عندما لا يساوي 1، ثم a = p 1 · a 1 وتابع إلى النقطة أدناه؛
• إيجاد المقسوم عليه الأولي p2 للرقم a1 عن طريق تعداد الأعداد الأولية بالتسلسل باستخدام a 2 = a 1: p 2 , عندما 2 = 1 , عندها سوف يأخذ التوسيع الشكل a = p 1 p 2 , عندما يكون a 2 = 1، فإن a = p 1 p 2 a 2 , وننتقل إلى الخطوة التالية؛
• البحث من خلال الأعداد الأولية وإيجاد المقسوم عليه ص 3أعداد 2وفقًا للصيغة أ 3 = أ 2: ص 3 عندما يكون أ 3 = 1 , ثم نحصل على أن أ = ص 1 ص 2 ص 3 , عندما لا يساوي 1، فإن a = p 1 p 2 p 3 a 3 والانتقال إلى الخطوة التالية؛
• تم العثور على المقسوم عليه الأولي ص نأعداد ن - 1عن طريق تعداد الأعداد الأولية مع ع - 1، و أ ن = أ ن - 1: ص ن، حيث n = 1، تكون الخطوة نهائية، ونتيجة لذلك نحصل على أن a = p 1 · p 2 · … · p n .

تتم كتابة نتيجة الخوارزمية على شكل جدول يحتوي على العوامل المتحللة بشريط عمودي بشكل تسلسلي في عمود. النظر في الشكل أدناه.

يمكن تطبيق الخوارزمية الناتجة عن طريق تحليل الأرقام إلى عوامل أولية.

عند تحليل العوامل الأولية، ينبغي اتباع الخوارزمية الأساسية.

مثال 2

حلل العدد 78 إلى عوامل أولية.

حل

للعثور على أصغر مقسوم أولي، عليك مراجعة جميع الأعداد الأولية في 78. أي 78: 2 = 39. القسمة بدون باقي تعني أن هذا هو المقسوم البسيط الأول، والذي نشير إليه بالرمز p 1. نحصل على أن أ 1 = أ: ص 1 = 78: 2 = 39. وصلنا إلى مساواة بالشكل a = p 1 · a 1 , حيث 78 = 239. ثم 1 = 39، أي أننا يجب أن ننتقل إلى الخطوة التالية.

دعونا نركز على إيجاد المقسوم عليه الأولي ص2أعداد أ 1 = 39. يجب عليك مراجعة الأعداد الأولية، أي 39: 2 = 19 (الواحد المتبقي). بما أن القسمة على باقي فإن 2 ليس مقسومًا عليه. عند اختيار الرقم 3 نحصل على 39: 3 = 13. هذا يعني أن ع 2 = 3 هو أصغر مقسوم أولي على 39 على أ 2 = أ 1: ع 2 = 39: 3 = 13. نحصل على المساواة في النموذج أ = ص 1 ص 2 أ 2في الصيغة 78 = 2 3 13. لدينا أن 2 = 13 لا يساوي 1، إذن علينا المضي قدمًا.

تم العثور على أصغر مقسوم أولي للرقم a 2 = 13 من خلال البحث في الأرقام بدءًا من الرقم 3. نحصل على 13: 3 = 4 (الباقي 1). من هذا يمكننا أن نرى أن 13 لا يقبل القسمة على 5، 7، 11، لأن 13: 5 = 2 (الباقي 3)، 13: 7 = 1 (الباقي 6) و 13: 11 = 1 (الباقي 2) . يمكن أن نرى أن 13 هو عدد أولي. وفقًا للصيغة تبدو كما يلي: أ 3 = أ 2: ص 3 = 13: 13 = 1. وجدنا أن 3=1 مما يعني اكتمال الخوارزمية. الآن تتم كتابة العوامل بالشكل 78 = 2 · 3 · 13 (أ = ع 1 · ع 2 · ع 3) .

إجابة: 78 = 2 3 13.

مثال 3

قم بتحليل الرقم 83006 إلى عوامل أولية.

حل

الخطوة الأولى تنطوي على التخصيم ص 1 = 2و أ 1 = أ: ع 1 = 83,006: 2 = 41,503حيث 83,006 = 2 · 41,503.

تفترض الخطوة الثانية أن 2 و3 و5 ليست قواسم أولية للرقم a 1 = 41,503، ولكن 7 هو مقسوم أولي، لأن 41,503: 7 = 5,929. نحصل على أن ع 2 = 7، أ 2 = أ 1: ع 2 = 41503: 7 = 5929. من الواضح أن 83,006 = 2 7 5 929.

إيجاد أصغر مقسوم أولي لـ p 4 للعدد a 3 = 847 هو 7. يمكن أن نرى أن أ 4 = أ 3: ص 4 = 847: 7 = 121، وبالتالي 83 006 = 2 7 7 7 121.

للعثور على المقسوم الأولي للرقم أ 4 = 121، نستخدم الرقم 11، أي ص 5 = 11. ثم نحصل على تعبير عن النموذج أ 5 = أ 4: ص 5 = 121: 11 = 11و 83,006 = 2 7 7 7 11 11.

للرقم أ 5 = 11رقم ص 6 = 11هو أصغر المقسوم عليه. وبالتالي أ 6 = أ 5: ص 6 = 11: 11 = 1. ثم 6 = 1. يشير هذا إلى اكتمال الخوارزمية. سيتم كتابة العوامل بالشكل 83006 = 2 · 7 · 7 · 7 · 11 · 11.

سيكون التدوين القانوني للإجابة بالشكل 83 006 = 2 · 7 3 · 11 2.

إجابة: 83006 = 2 7 7 7 11 11 = 2 7 3 11 2.

مثال 4

عامل الرقم 897,924,289.

حل

للعثور على العامل الأولي الأول، ابحث في الأعداد الأولية بدءًا من الرقم 2. نهاية البحث تكون عند الرقم 937. ثم ص 1 = 937، أ 1 = أ: ع 1 = 897 924 289: 937 = 958 297 و 897 924 289 = 937 958 297.

الخطوة الثانية من الخوارزمية هي التكرار على الأعداد الأولية الأصغر. أي أننا نبدأ بالرقم 937. يمكن اعتبار الرقم 967 أوليًا لأنه مقسوم أولي على الرقم أ 1 = 958,297. من هنا نحصل على أن ع 2 = 967، ثم أ 2 = أ 1: ع 1 = 958 297: 967 = 991 و 897 924 289 = 937 967 991.

الخطوة الثالثة تقول أن 991 هو عدد أولي، لأنه لا يحتوي على عامل أولي واحد لا يتجاوز 991. القيمة التقريبية للتعبير الجذري هي 991< 40 2 . Иначе запишем как 991 < 40 2 . وهذا يدل على أن ع 3 = 991 و أ 3 = أ 2: ع 3 = 991: 991 = 1. نجد أن تحليل الرقم 897924289 إلى عوامل أولية يتم الحصول عليه على النحو التالي: 897924289 = 937967991.

إجابة: 897924289 = 937967991.

استخدام اختبارات قابلية القسمة للتحليل إلى عوامل أولية

لتحليل عدد إلى عوامل أولية، عليك اتباع خوارزمية. عندما تكون الأعداد صغيرة، يجوز استخدام جدول الضرب وعلامات القسمة. دعونا ننظر إلى هذا مع الأمثلة.

مثال 5

إذا كان من الضروري تحليل 10، فإن الجدول يوضح: 2 · 5 = 10. الأرقام الناتجة 2 و 5 هي أعداد أولية، لذا فهي عوامل أولية للرقم 10.

مثال 6

إذا كان من الضروري تحليل الرقم 48، فإن الجدول يوضح: 48 = 6 8. لكن 6 و 8 ليسا عاملين أوليين، حيث يمكن أيضًا توسيعهما إلى 6 = 2 3 و 8 = 2 4. ثم التحلل الكاملوبالتالي يصبح 48 = 6 8 = 2 3 2 4. سيكون التدوين الأساسي بالشكل 48 = 2 4 · 3.

مثال 7

عند تحليل الرقم 3400، يمكنك استخدام علامات القسمة. في في هذه الحالةمعايير القسمة على 10 و 100 ذات صلة. من هنا نحصل على 3,400 = 34 · 100، حيث يمكن قسمة 100 على 10، أي كتابتها بالشكل 100 = 10 · 10، مما يعني أن 3,400 = 34 · 10 · 10. بناءً على اختبار قابلية القسمة، نجد أن 3400 = 34 10 10 = 2 17 2 5 2 5. جميع العوامل أولية. التوسع الكنسي يأخذ الشكل 3400 = 2 3 5 2 17.

عندما نجد العوامل الأولية، نحتاج إلى استخدام اختبارات قابلية القسمة وجداول الضرب. إذا كنت تتخيل الرقم 75 كمنتج للعوامل، فأنت بحاجة إلى مراعاة قاعدة القسمة على 5. نحصل على 75 = 5 15، و15 = 3 5. أي أن التمدد المطلوب هو مثال على شكل المنتج 75 = 5 · 3 · 5.

إذا لاحظت وجود خطأ في النص، فيرجى تحديده والضغط على Ctrl+Enter

يسمى المتغير العشوائي V تركزت ، إذا كان توقعها الرياضي يساوي 0. العملية العشوائية المتمركزة الأولية هي نتاج متغير عشوائي متمركز V ودالة غير عشوائية φ(t):X(t)=Vφ(t). تتميز العملية العشوائية المتمركزة الأولية بالخصائص التالية:

التعبير عن النموذج
، حيث φ ك ( ر ), ك =1;2;…-وظائف غير عشوائية؛ , ك =1;2;…- متغيرات عشوائية مركزية غير مترابطة، تسمى بالتوسيع القانوني للعملية العشوائيةX ( ر )، بينما المتغيرات العشوائية تسمى معاملات التوسع الكنسي. والوظائف غير العشوائية φ ك ( ر ) - تنسيق وظائف التوسعة القانونية.

دعونا ننظر في خصائص العملية العشوائية

منذ بشرط
الذي - التي

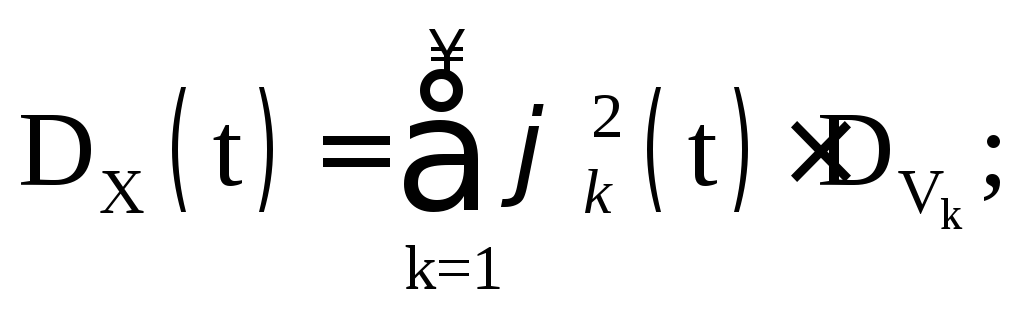
ومن الواضح أن نفس العملية العشوائية لديها أنواع مختلفةالتوسع الكنسي اعتمادا على اختيار وظائف الإحداثيات. علاوة على ذلك، حتى مع اختيار وظائف الإحداثيات، هناك تعسف في توزيع المتغيرات العشوائية V k. في الممارسة العملية، بناءً على نتائج التجارب، يتم الحصول على تقديرات للتوقع الرياضي ووظيفة الارتباط:
. بعد التحلل
في سلسلة فورييه مزدوجة في وظائف الإحداثيات φ إلى (t):

الحصول على قيم التباين
المتغيرات العشوائية V ك .

4.2. مفهوم الوظيفة المعممة. دالة دلتا ديراك. التمثيل القانوني المتكامل للعمليات العشوائية.

وظيفة معممة يُطلق عليه حد تسلسل عائلة ذات معلمة واحدة من الوظائف المستمرة.

دالة دلتا ديراك
- هذه دالة معممة ناتجة عن المرور إلى الحد عند
في عائلة من الوظائف

من بين الخصائص - وظائف نلاحظ ما يلي:

2.

3. إذا و(ر)- وظيفة مستمرة، الذي - التي

عملية عشوائية X( ر ) ، وظيفة الارتباط لها شكل يسمى "الضوضاء البيضاء" غير الثابتة. لو دبليو ( ر 1 )= دبليو - مقدار ثابت ثم اكس( ر )- "الضوضاء البيضاء" الثابتة.

على النحو التالي من التعريف، لا يوجد ارتباط بين قسمين، بغض النظر عن مدى قربهما، من أقسام "الضوضاء البيضاء". يسمى التعبير W(t). شدة "الضوضاء البيضاء".

التمثيل القانوني المتكامل للعملية العشوائية X( ر ) يسمى تعبيرا عن النموذج
أين
- وظيفة عشوائية تتمحور حول؛
- وظيفة غير عشوائية للوسائط المستمرة

وظيفة الارتباط لمثل هذه العملية العشوائية لها الشكل:

يمكن إثبات أن هناك دالة غير عشوائية G() هكذا

حيث G( 1) هي كثافة التشتت؛ δ(x) هي دالة دلتا ديراك. نحن نحصل

وبالتالي فإن تباين العملية العشوائية X(t):

.

4.3. التحولات الخطية وغير الخطية للعمليات العشوائية

يتم أخذ المشكلة التالية بعين الاعتبار: يتم توفير "إشارة دخل" ذات طبيعة عملية عشوائية X(t) إلى مدخلات النظام (الجهاز، المحول) S. يقوم النظام بتحويلها إلى "إشارة خرج" Y(t):

.

رسميًا، يمكن وصف تحويل العملية العشوائية X(t) إلى Y(t) باستخدام ما يسمى بمشغل النظام A t:

ص(ر)=أ ر (X(ر)).

يشير الفهرس t إلى أن هذا المشغل يقوم بتحويل الوقت. الصياغات التالية لمشكلة تحويل عملية عشوائية ممكنة.

قوانين التوزيع معروفة أو الخصائص العامةالعملية العشوائية X(t) عند إدخال النظام S، يتم إعطاء المشغل A t للنظام S، من الضروري تحديد قانون التوزيع أو الخصائص العامة للعملية العشوائية Y(t) عند إخراج النظام س.

قوانين التوزيع (الخصائص العامة) للعملية العشوائية X(t) ومتطلبات العملية العشوائية Y(t) معروفة؛ من الضروري تحديد نوع المشغل A t للنظام S الذي يلبي المتطلبات المحددة kY(t) على أفضل وجه.

قوانين التوزيع (الخصائص العامة) للعملية العشوائية Y(t) معروفة ويتم إعطاء المشغل A t للنظام S؛ مطلوب تحديد قوانين التوزيع أو الخصائص العامة للعملية العشوائية X(t).

ص رينياتا التصنيف القادمالمشغلين A t للنظام S:

مشغلي النظام

الخطي Lغير الخطيN

خطي متجانس L 0 خطي غير متجانس L n

دعونا نفكر في تأثير النظام الخطي غير المتجانس

ل ن (...)=ل 0 (...)+φ(ر)

إلى عملية عشوائية X(t) ذات التوسعة الأساسية التالية:

.

نحن نحصل:

دعونا نقدم التدوين

ثم يأخذ التوسيع القانوني لـ Y(t) الشكل:

.

التوقع الرياضي للعملية العشوائية Y(t):

دالة الارتباط للعملية العشوائية Y(t):

لذلك،

على الجانب الآخر

تباين العملية العشوائية Y(t):

وفي ختام هذه الفقرة نلاحظ أن عوامل التمايز والتكامل للعمليات العشوائية متجانسة خطيا.

2. يعتبر التحول التربيعي:

ص(ر)=(س(ر)) 2 ,

متغيرات عشوائية تتمحور حول V k ولها توزيع متماثل حول الصفر؛ كل أربعة منهم مستقلون بشكل مشترك. ثم

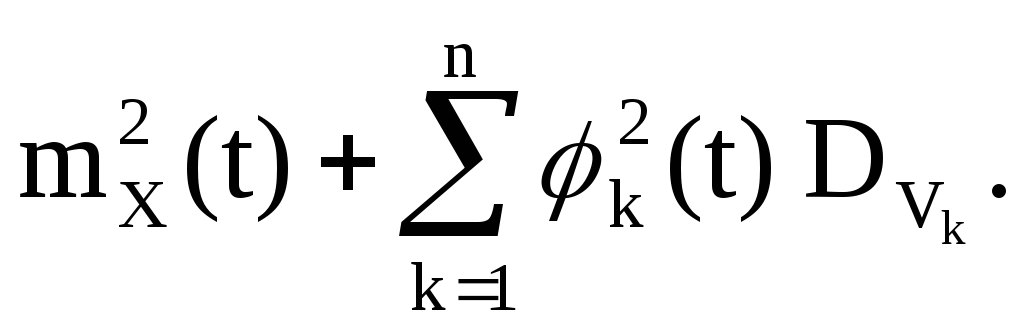
دعونا نقدم وظائف غير عشوائية

والمتغيرات العشوائية

ثم تأخذ العملية العشوائية Y(t) الشكل

يتم الحصول على التوسع المتعارف عليه للعملية العشوائية Y(t). وظيفة الارتباط Y (ر):

صياغة.منح عدد طبيعي ن(ن > 1). الحصول على تحليلها القانوني إلى عوامل بسيطة، أي تقديمها كمنتج لعوامل بسيطة. وفي هذه الحالة يجوز الإشارة إلى عامل 1 في التوسيع، على سبيل المثال 264 = 2 * 2 * 2 * 3 * 11 (يمكن للبرنامج أن ينتج الإجابة 264 = 1 * 2 * 2 * 2 * 3 *). 11).

حل. هذه المهمةلديه حل جميل جدا.

من النظرية الأساسية للحسابمن المعروف أنه بالنسبة لأي عدد طبيعي أكبر من 1، هناك تحليل قانوني إلى عوامل أولية، وهذا التحليل فريد حتى ترتيب العوامل. أي، على سبيل المثال، 12 = 2 * 2 * 2 و 12 = 3 * 2 * 2 هما نفس التوسعات.

خذ بعين الاعتبار الشكل القانوني لأي رقم مثال محدد. على سبيل المثال، 264 = 2 * 2 * 2 * 3 * 11. كيف يمكن التعرف على هذه البنية؟ للإجابة على هذا السؤال، دعونا نذكر ما ورد في أي دورة المدرسةقواعد الجبر لتقسيم أحاديات الحد، متخيلًا أن الأعداد في التوسعة القانونية هي متغيرات. كما تعلم، إذا قمت بتقسيم تعبير إلى متغير موجود بدرجة ما في هذا التعبير بنفس الدرجة، فسيتم شطبه في تدوينه.

وهذا هو، إذا قسمنا 264 على 2، فسيكون هناك واحد اثنان في توسيعه القانوني. ثم يمكننا التحقق مما إذا كان الناتج قابلاً للقسمة مرة أخرى على 2. ستكون الإجابة نعم، ولكن في المرة الثالثة ستعطي القسمة باقيًا. ثم عليك أن تأخذ في الاعتبار الرقم الطبيعي التالي 3 - سيتم قسمة الناتج عليه مرة واحدة. ونتيجة لذلك، بتمرير خط الأعداد في الاتجاه الموجب سنصل إلى الرقم 11، وبعد القسمة على 11 نسيصبح مساوياً لـ 1، مما سيشير إلى الحاجة إلى إكمال الإجراء.

لماذا، مع هذا "الشطب" للعوامل الموجودة، لا نحصل على قابلية القسمة على أرقام مركبة؟ في الواقع، كل شيء بسيط هنا - أي رقم مركب هو حاصل ضرب عوامل أولية أصغر منه. ونتيجة لذلك، اتضح أننا سوف نعبر نجميع عوامل أي عدد مركب، حتى نصل إليه في سلسلة القسمة. على سبيل المثال، مع مثل هذا البحث الشامل نلن يتم تقسيمها أبدًا على 4، نظرًا لأننا سنحذف "في الطريق" إلى هذا الرقم نجميع العوامل اثنان.

الخوارزمية باللغة الطبيعية:

1) الإدخال ن;

2) الإسناد إلى متغير صأرقام 2؛

3) إخراج الرقم نوعلامة المساواة والوحدة لإضفاء الطابع الرسمي على التوسع؛

4) بدء حلقة بشرط مسبق ن< > 1 . في حلقة:

1. لو معصريع = 0، ثم اعرض علامة الضرب والمتغير p، ثم قسمة نعلى صوإلا قم بزيادة القيمة أنابنسبة 1؛

1. برنامج PrimeFactors؛
2. ن، ع: كلمة؛
3. يبدأ
4. ص:= 2;
5. readln(n);
6. اكتب (ن، ' = 1')؛
7. بينما ن<>1 تبدأ
8. إذا (n mod p) = 0 ثم ابدأ
9. اكتب('*',ص);
10. ن:= ن شعبة ص
11. آخر تبدأ
12. المؤتمر الوطني العراقي (ع)