Какво означава цели изрази. Урок „Алгебрични дроби, рационални и дробни изрази
„Урок по многочлен“ - И проверете: 2. Извършете умножението на полиноми: 4. Извършете разделянето на полинома A (x) на B (x). 3. Факторизиране на полинома. 1. Извършете събиране и изваждане на полиноми: P(x)=-2x3 + x2 -x-12 и Q(x)= x3 -3x2 -4x+1. Действия с полиноми. Урок 15
„Преобразуване на цяло число в полином“ – Развиване на изчислителните умения на учениците. Въведете понятието цял израз. Преобразуване на цели числа. Полиномите и по-специално мономите са цели числа. Упражнете учениците да въвеждат подобни термини. Примери за цели числа са: 10y?+(3x+y)(x?-10y?), 2b(b?-10c?)-(b?+2c?), 3a?-(a(a+2c) ) /5+2.5ac.
"Полиномно умножение" - -x6+3x7-2x4+5x2 3 -1 0 -2 0 5 0 0 7 -8 3 5 -6 7x4-8x3+3x2+5x-6. Презентация. Позиционният номер на полином. Умножение на полиноми с позиционно число. Рябов Павел Юриевич. Ръководител: Калетурина А. С.
„Полином със стандартна форма“ – Стандартната форма на полином. Примери. 3x4 + 2x3 - x2 + 5. Събиране на полиноми. Подготовка за s / r № 6. Речник. Глава 2, §1б. За полиноми с една буква водещият член е еднозначно дефиниран. Проверете себе си. 6x4 - x3y + x2y2 + 2y4.
„Полиноми“ – моном се счита за полином, състоящ се от един член. Изваждане на общия множител извън скоби. Алгебра. Полиноми. Умножете полинома a+b по полинома c+d. Произведение на моном и полином Умножение на моном по многочлен. Подобни термини са членове 2 и -7, които нямат буквена част. Членовете на полинома 4xz-5xy+3x-1 са 4xz, -5xy, 3x и -1.
„Факторинг на урока“ – Приложение на FSU. Формули за съкратено умножение. Тема на урока: Отговори: var 1: b, d, b, d, c; вариант 2: a, d, c, b, a; вариант 3: c, c, c, a, b; Вариант 4: d, d, c, b, d. И как? Изваждане на общия множител извън скоби. 3. Завършете разлагането на множители: Групова работа: Поставете общия множител извън скоби. 1. Завършете разлагането на множители: а).
Благодарение на курса по алгебра е известно, че всички изрази изискват трансформация за по-удобно решение. Дефинирането на целочислени изрази насърчава идентични трансформации като начало. Ще трансформираме израза в полином. В заключение нека да разгледаме няколко примера.
Определение и примери за цели числа
Определение 1Целочислени изразиса числа, променливи или изрази със събиране или изваждане, които се записват като степен с естествен показател, които също имат скоби или деление, различно от нула.
Въз основа на дефиницията имаме примери за цели числа: 7 , 0 , − 12 , 7 11 , 2 , 73 , - 3 5 6 и т.н., и променливи във формата a , b , p , q , x , z се считат за цели числа. След преобразуването им на сборове, разлики, произведения, изразите ще придобият формата
x + 1 , 5 y 3 2 3 7 − 2 y − 3 , 3 − x y z 4 , - 6 7 , 5 (2 x + 3 y 2) 2 − - ( 1 − x) (1 + x) (1 + х 2)
Ако изразът съдържа деление на число, различно от нула, във формата x: 5 + 8: 2: 4 или (x + y) : 6, тогава делението може да бъде означено с наклонена черта, като x + 3 5 - 3 , 2 x + 2 . Когато разглеждаме изрази от формата x: 5 + 5: x или 4 + a 2 + 2 a - 6 a + b + 2 c, е ясно, че такива изрази не могат да бъдат цели числа, тъй като в първия има деление на променлива x, а във втория към израз с променлива.
Полином и моном са цели числа, които срещаме в училище, когато работим с рационални числа. С други думи, целочислените изрази не включват ирационални дроби. Друго име са цели ирационални изрази.
Какви трансформации на цели числа са възможни?
Целочислените изрази се разглеждат при решаване като основни тъждествени трансформации, отваряне на скоби, групиране, редуциране на подобни.
Пример 1
Отворете скобите и пренесете подобни членове в 2 · (a 3 + 3 · a · b − 2 · a) − 2 · a 3 − (5 · a · b − 6 · a + b) .
Решение
Първо трябва да приложите правилото за отваряне на скоби. Получаваме израз на формата 2 (a 3 + 3 a b − 2 a) − 2 a 3 − (5 a b − 6 a + b) = = 2 a 3 + 2 3 a b + 2 (− 2 a) − 2 a 3 − 5 a b + 6 a − b = = 2 a 3 + 6 a b − 4 a − 2 a 3 − 5 a b + 6 a − b
Тогава можем да добавим подобни термини:
2 a 3 + 6 a b − 4 a − 2 a 3 − 5 a b + 6 a − b = = (2 a 3 − 2 a 3) + (6 a b − 5 a b) + (− 4 a + 6 a) − b = = 0 + a b + 2 a − b = a b + 2 a − b .
След редуцирането им се получава полином от вида a · b + 2 · a − b .
Отговор: 2 (a 3 + 3 a b − 2 a) − 2 a 3 − (5 a b − 6 a + b) = a b + 2 a − b.
Пример 2
Направете трансформации (x - 1) : 2 3 + 2 · (x 2 + 1) : 3: 7 .
Решение
Съществуващото деление може да се замени с умножение, но с реципрочната стойност на числото. След това е необходимо да се извършат трансформации, след което изразът ще приеме формата (x - 1) · 3 2 + 2 · (x 2 + 1) · 1 3 · 1 7 . Сега трябва да се заемем с намаляването на подобни условия. Разбираме това
(x - 1) 3 2 + 2 (x 2 + 1) 1 3 1 7 = 3 2 (x - 1) + 2 21 x 2 + 1 = = 3 2 x - 3 2 + 2 21 x 2 + 2 21 = 2 21 x 2 + 3 2 x - 59 42 = 2 21 x 2 + 1 1 2 x - 1 17 42
Отговор: (x - 1) : 2 3 + 2 (x 2 + 1) : 3 : 7 = 2 21 x 2 + 1 1 2 x - 1 17 42 .
Пример 3
Изразете израза 6 x 2 y + 18 x y − 6 y − (x 2 + 3 x − 1) (x 3 + 4 x) като произведение.
Решение
След като разгледахме израза, става ясно, че първите три члена имат общ фактор от формата 6 · y , който трябва да бъде изваден от скоби по време на трансформацията. Тогава разбираме това 6 x 2 y + 18 x y − 6 y − (x 2 + 3 x − 1) (x 3 + 4 x) = = 6 y (x 2 + 3 x − 1) - (x 2 + 3 x - 1) (x 3 + 4 x)
Вижда се, че получихме разликата на два израза от формата 6 y (x 2 + 3 x - 1) и (x 2 + 3 x - 1) (x 3 + 4 x) с общ множител x 2 + 3 x − 1 , което трябва да бъде извадено от скоби. Разбираме това
6 y (x 2 + 3 x − 1) − (x 2 + 3 x − 1) (x 3 + 4 x) = = (x 2 + 3 x − 1) (6 y − (x 3 + 4 x) )
След като отворихме скобите, имаме израз от вида (x 2 + 3 x - 1) (6 y - x 3 - 4 x) , който трябваше да се намери по условие.
Отговор:6 x 2 y + 18 x y − 6 y − (x 2 + 3 x − 1) (x 3 + 4 x) = = (x 2 + 3 x − 1) ( 6 y − x 3 − 4 x)
Идентичните трансформации изискват стриктно спазване на реда на операциите.
Пример 4
Преобразуване на израз (3 2 − 6 2: 9) 3 (x 2) 4 + 4 x: 8.
Решение
Първо изпълнявате действията в скоби. Тогава имаме това 3 2 - 6 2: 9 = 3 2 - 3 6: 9 = 6 - 4 = 2. След трансформации изразът става 2 3 · (x 2) 4 + 4 · x: 8 . Известно е, че 2 3 = 8 И (x 2) 4 = x 2 4 = x 8, тогава можете да стигнете до израз като 8 x 8 + 4 x: 8 . Вторият член изисква замяна на делението с умножение от 4x:8. Групирайки факторите, получаваме това
8 x 8 + 4 x: 8 = 8 x 8 + 4 x 1 8 = 8 x 8 + 4 1 8 x = 8 x 8 + 1 2 x
Отговор:(3 2 − 6 2: 9) 3 (x 2) 4 + 4 x: 8 = 8 x 8 + 1 2 x .
Преобразуване на полином
Повечето от преобразуванията на цели числа са полиномиални представяния. Всеки израз може да бъде представен като полином Всеки израз може да се разглежда като полином, свързан с аритметични знаци. Всяка операция върху полиноми води до полином.
За да се представи изразът като полином, е необходимо да се извършат всички действия с полиноми, съгласно алгоритъма.
Пример 5
Изразете като полином 2 · (2 · x 3 − 1) + (2 · x − 1) 2 · (3 − x) + (4 · x − x · (15 · x + 1)) .
Решение
В този израз започнете трансформациите с израз от формата 4 x - x (15 x + 1) и според правилото в началото, като извършите умножение или деление, след което събиране или изваждане. Умножете - x по 15 x + 1, тогава получаваме 4 x - x (15 x + 1) = 4 x - 15 x 2 - x = (4 x - x) - 15 x 2 = 3 x - 15 x 2. Даденият израз ще приеме формата 2 (2 x 3 - 1) + (2 x - 1) 2 (3 - x) + (3 x - 15 x 2) .
След това трябва да повдигнете полинома на 2-ра степен 2x-1, получаваме израз на формата (2 x − 1) 2 = (2 x − 1) (2 x − 1) = 4 x 2 + 2 x (− 1) − 1 2 x − 1 (− 1 ) = = 4 x 2 − 4 x + 1
Сега можем да преминем към гледката 2 (2 x 3 - 1) + (4 x 2 - 4 x + 1) (3 - x) + (3 x - 15 x 2).
Нека да разгледаме умножението. Може да се види, че 2 (2 x 3 - 1) = 4 x 3 - 2 и (4 x 2 - 4 x + 1) (3 - x) = 12 x 2 - 4 x 3 - 12 x + 4 x 2 + 3 - x = = 16 x 2 - 4 x 3 - 13 x + 3
тогава можете да направите преход към израз на формата (4 x 3 - 2) + (16 x 2 - 4 x 3 - 13 x + 3) + (3 x - 15 x 2).
Извършваме събиране, след което стигаме до израза:
(4 x 3 - 2) + (16 x 2 - 4 x 3 - 13 x + 3) + (3 x - 15 x 2) = = 4 x 3 - 2 + 16 x 2 − 4 x 3 − 13 x + 3 + 3 x − 15 x 2 = = (4 x 3 − 4 x 3) + (16 x 2 − 15 x 2) + (− 13 x + 3 x) + (− 2 + 3) = = 0 + x 2 − 10 x + 1 = x 2 − 10 x + 1 .
От това следва, че оригиналният израз има формата x 2 − 10 x + 1.
Отговор: 2 (2 x 3 - 1) + (2 x - 1) 2 (3 - x) + (4 x - x (15 x + 1)) = x 2 - 10 x + 1.
Умножението и степенуването на полином показва, че е необходимо да се използват съкратени формули за умножение, за да се ускори процеса на преобразуване. Това допринася за това, че действията ще се извършват рационално и правилно.
Пример 6
Преобразувайте 4 · (2 · m + n) 2 + (m − 2 · n) · (m + 2 · n) .
Решение
От квадратната формула получаваме това (2 m + n) 2 = (2 m) 2 + 2 (2 m) n + n 2 = 4 m 2 + 4 m n + n 2, тогава произведението (m − 2 n) (m + 2 n) е равно на разликата на квадратите m и 2 n, следователно е равно на m 2 − 4 n 2. Получаваме, че оригиналният израз приема формата 4 (2 m + n) 2 + (m − 2 n) (m + 2 n) = 4 (4 m 2 + 4 m n + n 2) + (m 2 − 4 n 2) = = 16 m 2 + 16 m n + 4 n 2 + m 2 − 4 n 2 = 17 m 2 + 16 m n
Отговор: 4 (2 m + n) 2 + (m − 2 n) (m + 2 n) = 17 m 2 + 16 m n.
За да не бъде прекалено дълго преобразуването, е необходимо дадения израз да се приведе в стандартния вид.
Пример 7
Опростете израза (2 a (− 3) a 2 b) (2 a + 5 b 2) + a b (a 2 + 1 + a 2) (6 a + 15 b 2 ) + (5 a b (− 3) b 2)
Решение
Най-често полиномите и мономите не са дадени в стандартна форма, така че трябва да извършите трансформации. Трябва да се преобразува, за да се получи израз на формата − 6 a 3 b (2 a + 5 b 2) + a b (2 a 2 + 1) (6 a + 15 b 2) − 15 a b 3. За да се приведат подобни, е необходимо първо да се извърши умножение по правилата за преобразуване на сложен израз. Получаваме израз като
− 6 a 3 b (2 a + 5 b 2) + a b (2 a 2 + 1) (6 a + 15 b 2) − 15 a b 3 = = − 12 a 4 b − 30 a 3 b 3 + (2 a 3 b + a b) (6 a + 15 b 2) − 15 a b 3 = = − 12 a 4 b − 30 a 3 b 3 + 12 a 4 b + 30 a 3 b 3 + 6 a 2 b + 15 a b 3 − 15 a b 3 = = (− 12 a 4 b + 12 a 4 b) + (− 30 a 3 b 3 + 30 a 3 b 3) + 6 a 2 b + (15 a b 3 − 15 a b 3) = 6 a 2 b
Отговор: (2 a (− 3) a 2 b) (2 a + 5 b 2) + a b (a 2 + 1 + a 2) (6 a + 15 b 2 ) + + (5 a b (− 3) b 2) = 6 a 2 b
Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter
"Алгебрични дроби, рационални и дробни изрази."
Цели на урока:
Образователни: въвеждане на концепцията за алгебрична дроб, рационални и дробни изрази, диапазон от допустими стойности,
Развитие: формиране на умения за критично мислене, самостоятелно търсене на информация, изследователски умения.
Образователни: възпитание на съзнателно отношение към работата, формиране на комуникативни умения, формиране на самочувствие.
По време на часовете
1. Организационен момент:
Поздравления. Обявяване на темата на урока.
2. Мотивация на урока.
Германците имат такава поговорка „Да влезеш в удара“, което означава да попаднеш в задънена улица, трудна ситуация. Това се обяснява с факта, че дълго време действията с дробни числа, които понякога се наричаха "прекъснати линии", се смятаха с право за много сложни.
Но сега е обичайно да се разглеждат не само числови, но и алгебрични дроби, които ще направим днес.
Нека мотото на нашия урок днес са следните думи:
Успехът не е дестинация. Това движение
Т. По-бързо.
3. Актуализиране на опорни знания.
предна анкета.
Какво представляват целочислените изрази? От какво са направени? Целочисленият израз има смисъл за всякакви стойности на неговите променливи.
Дай примери.
Какво е дроб?
Какво означава да намалиш дроб?
Какво означава да факторизирам?
Какви методи на разлагане познавате?
Колко е квадратът на сбора (разликата)?
Каква е разликата между квадратите?

4. Учене на нов материал.
В 8. клас ще се запознаем с дробни изрази.
Те се различават от целите числа по това, че съдържат действието деление на израз с променлива.
Ако даден алгебричен израз е съставен от числа и променливи, като се използват операциите събиране, изваждане, умножение, степенуване с естествен показател и деление, както и използване на деление на изрази с променливи, тогава той се нарича дробен израз.

Дробните изрази нямат смисъл за тези стойности на променливи, които превръщат знаменателя в нула.
Домейнът на допустимите стойности (ODV) на алгебричен израз е множеството от всички допустими набори от стойности на буквите, включени в този израз.
Целочислените и дробните изрази се наричат рационални изрази
отделен вид рационален израз е рационална дроб. Това е дроб, чийто числител и знаменател са полиноми.
Кои изрази са цели числа и кои са дробни? (или #1)

5. Физическа минутка
6. Затвърдяване на нов материал.
Решете #2, 3(1), 5(1, 3, 4, 6, 7, 9, 10, 11), 7(1).
7. Самостоятелна работа на учениците (в групи).
Решете #3(2), 5(2, 5, 8, 12), 7(2).
8. Отражение.
Труден ли беше материалът на урока?
На кой етап от урока беше най-трудно, най-лесно?
Какво ново научихте в урока? Какво научи?
Работихте ли усилено в клас?
Колко емоционално се почувствахте по време на урока?
D / z: научете т. 1, въпроси стр. 7, решете № 4, 6, 8.
Sincwine.
Всяка група прави синквин за думата "фракция".
Ако знаете дроби
За да разберем точното им значение
Дори трудните задачи стават лесни.
Целочисленият израз е математически израз, съставен от числа и буквални променливи, използващи операциите събиране, изваждане и умножение. Целите числа също включват изрази, които включват деление на някакво число, различно от нула.
Примери за целочислени изрази
По-долу са дадени някои примери за цели числа:
1. 12*a^3 + 5*(2*a -1);
3. 4*y-((5*y+3)/5) -1;
Дробни изрази
Ако изразът съдържа деление на променлива или на друг израз, съдържащ променлива, тогава такъв израз не е цяло число. Такъв израз се нарича дробен израз. Нека дадем пълна дефиниция на дробен израз.
Дробният израз е математически израз, който в допълнение към операциите събиране, изваждане и умножение, извършвани с числа и буквени променливи, както и деление на число, което не е равно на нула, съдържа и деление на изрази с буквални променливи.
Примери за дробни изрази:
1. (12*a^3 +4)/a
3. 4*x- ((5*y+3)/(5-y)) +1;
Дробните и целочислените изрази съставляват два големи набора от математически изрази. Ако тези множества се комбинират, тогава получаваме ново множество, което се нарича рационални изрази. Тоест всички рационални изрази са цели и дробни изрази.
Знаем, че целите изрази имат смисъл за всякакви стойности на променливите, които са включени в тях. Това следва от факта, че за да се намери стойността на цяло число, е необходимо да се извършат действия, които винаги са възможни: събиране, изваждане, умножение, деление на число, различно от нула.
Дробните изрази, за разлика от целочислените, може да нямат смисъл. Тъй като има операция деление на променлива или израз, съдържащ променливи, и този израз може да се превърне в нула, но делението на нула е невъзможно. Стойностите на променливите, за които дробният израз ще има смисъл, се наричат валидни стойности на променливи.
рационална дроб
Един от специалните случаи на рационални изрази ще бъде дроб, чиито числител и знаменател са полиноми. За такава дроб в математиката има и име - рационална дроб.
Една рационална дроб ще има смисъл, ако нейният знаменател не е равен на нула. Тоест всички стойности на променливи, за които знаменателят на дробта е различен от нула, ще бъдат валидни.
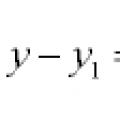 Уравнения на прави и криви в равнината
Уравнения на прави и криви в равнината Обобщено хомогенно уравнение Обобщени хомогенни уравнения от втори ред
Обобщено хомогенно уравнение Обобщени хомогенни уравнения от втори ред Благодарение на запетаята Поради факта, че в техните
Благодарение на запетаята Поради факта, че в техните