Изчисляване на производни на неявни функции, дадени чрез система от уравнения.
Дадена е система от уравнения
или за краткоЕ(х, г)=0 (1)
Определение. Система (1) дефинира неявно дефинирана функцияг= f(х) Над Р н
 ,
,
Ако х д : Е(х , f(х)) = 0.
Теорема (съществуване и уникалност на преобразуване, имплицитно определено от система от уравнения). Позволявам

После в някой кварталU (х 0 ) има уникална функция (картографиране), дефинирана в този кварталг = f(х), така че
х U (х 0 ) : Е(х, f(х))=0 иг 0 = f(х 0 ).
Тази функция е непрекъснато диференцируема в някаква околност на точкатах 0 .
5. Изчисляване на производни на неявни функции, дадени чрез система от уравнения
Дадена система
 (1)
(1)
Ще приемем, че условията на теоремата за съществуване и уникалност за неявната функция, дадена от тази система от уравнения, са изпълнени. Означаваме тази функция г= f(х) . След това в някакъв квартал на точката х 0 идентичностите
 (F(x, f(x))=0) (2)
(F(x, f(x))=0) (2)
Разграничаването на тези идентичности по отношение на х й получаваме
 =0 (3)
=0 (3)
Тези равенства могат да бъдат записани в матрична форма
 ,
(3)
,
(3)
или разширена
 .
.
Имайте предвид, че преходът от равенство Е(х,
f(х))=0
Да се  ,
отговаря на правилата за диференциация за случая, когато х
И гса точки в едномерното пространство. Матрица
,
отговаря на правилата за диференциация за случая, когато х
И гса точки в едномерното пространство. Матрица  не е изродено по предположение, така че матричното уравнение
не е изродено по предположение, така че матричното уравнение  има решение
има решение  . По този начин могат да се намерят частични производни от първи ред на неявни функции
. По този начин могат да се намерят частични производни от първи ред на неявни функции  . За да намерим диференциалите, означаваме
. За да намерим диференциалите, означаваме
dy
=
 ,dx
=
,dx
=
 , диференциране на равенствата (2)
получаваме
, диференциране на равенствата (2)
получаваме
 =0
,
=0
,
или в матрична форма
 .
(4)
.
(4)
Разширено
 .
.
Както в случая с частичните производни, формулата (4)
имаме същата форма, както в случая на едномерни пространства н=1,
стр=1.
Решението на това матрично уравнение може да бъде записано като  . За да се намерят частични производни от втори ред, ще е необходимо да се разграничат тъждествата (3)
(за да изчислите диференциали от втори ред, трябва да разграничите идентичностите (4)
). Така получаваме
. За да се намерят частични производни от втори ред, ще е необходимо да се разграничат тъждествата (3)
(за да изчислите диференциали от втори ред, трябва да разграничите идентичностите (4)
). Така получаваме
 ,
,
къде през А
посочени са термините, които не съдържат желаните  .
.
Матрицата на коефициентите на тази система за определяне на производните  е якобиевата матрица
е якобиевата матрица  .
.
Подобна формула може да се получи за диференциали. Във всеки от тези случаи ще получите матрично уравнениесъс същата матрица на коефициента  в система от уравнения за определяне на желаните производни или диференциали. Същото ще се случи при следните диференциации.
в система от уравнения за определяне на желаните производни или диференциали. Същото ще се случи при следните диференциации.
Пример 1. Намерете  ,
, ,
, в точката u=1,
v=1.
в точката u=1,
v=1.

Решение. Продиференцирайте дадените равенства
 (5)
(5)
Имайте предвид, че според формулировката на проблема трябва да разглеждаме като независими променливи х, г. Тогава функциите ще бъдат z, u, v. Така системата (5) да вземе решение за неизвестното ду, дв, дз . В матрична форма изглежда така
 .
.
Нека решим тази система с помощта на правилото на Крамър. Детерминанта на матрицата на коефициента
 , Третата "заменена" детерминанта за дз
ще бъде равно на (изчислява се чрез разширяване на последната колона)
, Третата "заменена" детерминанта за дз
ще бъде равно на (изчислява се чрез разширяване на последната колона)
 , Тогава
, Тогава
дз
=
 ,
И
,
И  ,
, .
.
Разграничаване (5) отново ( х, г – независими променливи)



Матрицата на коефициента на системата е същата, третата детерминанта

Решавайки тази система, получаваме израз за д 2 z където можете да намерите желаната производна.
Както знаете, имплицитно дадена функция на една променлива се дефинира по следния начин: функция на независима променлива x се нарича имплицитна, ако е дадена от уравнение, което не е разрешено по отношение на y:
Пример 1.11.
Уравнението

имплицитно дефинира две функции:
И уравнението

не дефинира никаква функция.
Теорема 1.2 (съществуване на неявна функция).
Нека функцията z \u003d f (x, y) и нейните частни производни f "x и f" y са дефинирани и непрекъснати в някакъв квартал UM0 на точката M0 (x0y0). В допълнение, f(x0,y0)=0 и f"(x0,y0)≠0, тогава уравнение (1.33) дефинира в околност на UM0 неявна функция y= y(x), непрекъсната и диференцируема в някакъв интервал D с център в точка x0 и y(x0)=y0.
Без доказателства.
От теорема 1.2 следва, че на този интервал D:
тоест има идентичност в
където "общата" производна се намира съгласно (1.31)
Тоест, (1.35) дава формула за намиране на производната на имплицитно дадена функция на една променлива x.
Неявна функция на две или повече променливи се дефинира по подобен начин.
Например, ако в някакъв регион V на пространството Oxyz е вярно следното уравнение:
тогава при определени условия върху функцията F той неявно дефинира функцията
![]()
В същото време, по аналогия с (1.35), частните му производни се намират, както следва:

Пример 1.12. Ако приемем, че уравнението
имплицитно дефинира функция
![]()
намерете z "x, z" y.

следователно, съгласно (1.37), получаваме отговора.

11. Използване на частни производни в геометрията.
12. Екстремуми на функция на две променливи.
Концепциите за максимум, минимум, екстремум на функция на две променливи са подобни на съответните концепции на функция на една независима променлива (вижте раздел 25.4).
Нека функцията z = ƒ(х;у) е дефинирана в някаква област D, точката N(x0;y0) н D.
Точка (x0; y0) се нарича максимална точка на функцията z=ƒ(x; y), ако има такава d-околност на точката (x0; y0), че за всяка точка (x; y), различна от (xo; yo), този квартал удовлетворява неравенството ƒ(х;у)<ƒ(хо;уо).
А  минималната точка на функцията е дефинирана логически: за всички точки (x; y), различни от (x0; y0), следващото неравенство е в сила от d-околността на точката (xo; yo): ƒ(x; y) >ƒ(x0; y0).
минималната точка на функцията е дефинирана логически: за всички точки (x; y), различни от (x0; y0), следващото неравенство е в сила от d-околността на точката (xo; yo): ƒ(x; y) >ƒ(x0; y0).
На фигура 210: N1 е максималната точка, а N2 е минималната точка на функцията z=ƒ(x;y).
Стойността на функцията в точката на максимум (минимум) се нарича максимум (минимум) на функцията. Максимумът и минимумът на една функция се наричат нейни екстремуми.
Обърнете внимание, че по силата на дефиницията екстремната точка на функцията се намира вътре в областта на функцията; максимумът и минимумът имат локален (местен) характер: стойността на функцията в точката (x0; y0) се сравнява с нейните стойности в точки, достатъчно близки до (x0; y0). В регион D функцията може да има няколко екстремума или нито един.
46.2. Необходими и достатъчни условияекстремум
Разгледайте условията за съществуване на екстремум на функция.
Теорема 46.1 (необходими условия за екстремум). Ако в точката N (x0; y0) диференцируемата функция z \u003d ƒ (x; y) има екстремум, тогава нейните частични производни в тази точка са равни на нула: ƒ "x (x0; y0) \u003d 0, ƒ" y (x0; y0 )=0.
Коригираме една от променливите. Да предположим, например, y=y0. Тогава получаваме функцията ƒ(x; y0)=φ(x) на една променлива, която има екстремум при x = x0. Следователно, според необходимото условие за екстремума на функция на една променлива (вижте параграф 25.4), φ "(x0) \u003d 0, т.е. ƒ "x (x0; y0) \u003d 0.
По същия начин може да се покаже, че ƒ "y (x0; y0) \u003d 0.
Геометрично равенствата ƒ "x (x0; y0) \u003d 0 и ƒ "y (x0; y0) \u003d 0 означават, че в точката на екстремума на функцията z \u003d ƒ (x; y), допирателната равнина към повърхността, изобразяваща функцията ƒ (x; y ), е успоредна на равнината Oxy, тъй като уравнението на допирателната равнина е z=z0 (виж формула (45.2)).
У  Забележка. Една функция може да има екстремум в точки, където поне една от частните производни не съществува. Например функцията
Забележка. Една функция може да има екстремум в точки, където поне една от частните производни не съществува. Например функцията ![]() има максимум в точка O (0; 0) (виж Фиг. 211), но няма частични производни в тази точка.
има максимум в точка O (0; 0) (виж Фиг. 211), но няма частични производни в тази точка.
Точката, в която частичните производни от първи ред на функцията z ≈ ƒ(x; y) са равни на нула, т.е. f "x=0, f" y=0, се нарича стационарна точка на функцията z.
Стационарни точки и точки, в които не съществува поне една частична производна, се наричат критични точки.
В критични точки функцията може или не може да има екстремум. Равенството на нула на частните производни е необходимо, но не достатъчно условие за съществуването на екстремум. Да разгледаме например функцията z = xy. За нея точката O (0; 0) е критична (в нея z "x \u003d y и z" y - x изчезват). Функцията z=xy обаче няма екстремум в нея, тъй като в достатъчно малка околност на точката O(0; 0) има точки, за които z>0 (точки I и III на четвъртините) и z< 0 (точки II и IV четвертей).
По този начин, за да се намерят екстремумите на функцията в дадена област, е необходимо всяка критична точка на функцията да бъде подложена на допълнително изследване.
Теорема 46.2 (достатъчно условие за екстремум). Нека влезе неподвижна точка(xo; yo) и някаква нейна близост, функцията ƒ(x; y) има непрекъснати частни производни до втори ред включително. Нека изчислим в точката (x0;y0) стойностите A=f""xx(x0;y0), B=ƒ""xy(x0;y0), C=ƒ""yy(x0;y0) . Обозначете

1. ако Δ > 0, тогава функцията ƒ(x; y) в точката (x0; y0) има екстремум: максимум, ако A< 0; минимум, если А > 0;
2. ако Δ< 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.
В случай на Δ = 0 може да има или да няма екстремум в точката (x0; y0). Необходими са повече изследвания.
ЗАДАЧИ
1.
Пример.Намерете интервалите на нарастване и намаляване на функцията. Решение.Първата стъпка е намиране на областта на дефинициите на функцията. В нашия пример изразът в знаменателя не трябва да изчезва, следователно, . Нека да преминем към производната функция:  За да определим интервалите на нарастване и намаляване на функция по достатъчен критерий, решаваме неравенствата и в областта на дефиниция. Нека използваме обобщение на интервалния метод. Единственият истински корен на числителя е х=2, а знаменателят изчезва при х=0. Тези точки разделят дефиниционната област на интервали, в които производната на функцията запазва своя знак. Нека отбележим тези точки на числовата ос. С плюсове и минуси условно означаваме интервалите, на които производната е положителна или отрицателна. Стрелките по-долу схематично показват нарастването или намаляването на функцията на съответния интервал.
За да определим интервалите на нарастване и намаляване на функция по достатъчен критерий, решаваме неравенствата и в областта на дефиниция. Нека използваме обобщение на интервалния метод. Единственият истински корен на числителя е х=2, а знаменателят изчезва при х=0. Тези точки разделят дефиниционната област на интервали, в които производната на функцията запазва своя знак. Нека отбележим тези точки на числовата ос. С плюсове и минуси условно означаваме интервалите, на които производната е положителна или отрицателна. Стрелките по-долу схематично показват нарастването или намаляването на функцията на съответния интервал.  По този начин,
По този начин,  И
И  . В точката х=2функцията е дефинирана и непрекъсната, така че трябва да се добави както към нарастващия, така и към намаляващия интервал. В точката х=0функцията не е дефинирана, така че тази точка не е включена в необходимите интервали. Представяме графиката на функцията, за да сравним получените резултати с нея.
. В точката х=2функцията е дефинирана и непрекъсната, така че трябва да се добави както към нарастващия, така и към намаляващия интервал. В точката х=0функцията не е дефинирана, така че тази точка не е включена в необходимите интервали. Представяме графиката на функцията, за да сравним получените резултати с нея.  Отговор:функцията се увеличава с
Отговор:функцията се увеличава с ![]() , намалява на интервала (0;
2]
.
, намалява на интервала (0;
2]
.
2.
Примери.
Задайте интервали за изпъкналост и вдлъбнатост на крива г = 2 – х 2 .
Да намерим г"" и определете къде втората производна е положителна и къде е отрицателна. г" = –2х, г"" = –2 < 0 на (–∞; +∞), следовательно, функция всюду выпукла.
г = д х. защото г"" = д x > 0 за всяко х, тогава кривата е вдлъбната навсякъде.



г = х 3 . защото г"" = 6х, Че г"" < 0 при х < 0 и г"" > 0 когато х> 0. Следователно при х < 0 кривая выпукла, а при х> 0 е вдлъбнат.
3.



4. Дадена е функция z=x^2-y^2+5x+4y, вектор l=3i-4j и точка A(3,2). Намерете dz/dl (доколкото разбирам, производната на функцията по посока на вектора), gradz(A), |gradz(A)|. Намерете частичните производни: z(in x)=2x+5 z(in y)=-2y+4 Намерете стойностите на производните в точка A(3,2): z(in x)(3,2)= 2*3+ 5=11 z(по y)(3,2)=-2*2+4=0 ^2)=11 Производна на функцията z по посока на вектора l: dz/dl=z( в x)*cosa+z(в y)*cosb, a,b-векторни ъгли l с координатни оси. cosa=lх/|l|, cosb=ly/|l|, |l|=sqrt(lx^2+ly^2) lx=3, ly=-4, |l|=5. cosa=3/5, cosb=(-4)/5. dz/dl=11*3/5+0*(-4)/5=6,6.
Ще се научим да намираме производни на функции, които са дадени имплицитно, т.е. дадени от някои уравнения, които свързват променливи една с друга хИ г. Примери за имплицитно дефинирани функции:
![]() ,
,
![]() ,
,
Производни на неявни функции или производни на неявни функции са доста лесни за намиране. Сега нека анализираме съответното правило и пример и след това да разберем защо изобщо е необходимо това.
За да се намери производната на функция, дадена имплицитно, е необходимо да се диференцират двете страни на уравнението по отношение на x. Членовете, в които присъства само x, ще се превърнат в обичайната производна на функция от x. И термините с Y трябва да се диференцират с помощта на правилото за диференциация сложна функция, тъй като y е функция на x. Ако е съвсем просто, тогава в получената производна на термина с x трябва да се окаже: производната на функцията от y, умножена по производната от y. Например, производната на термина ще бъде написана като , производната на термина ще бъде написана като . Освен това, от всичко това е необходимо да се изрази тази "у линия" и желаната производна на функцията, дадена имплицитно, ще бъде получена. Нека да разгледаме това с пример.
Пример 1
Решение. Разграничаваме двете страни на уравнението по отношение на x, като приемаме, че y е функция на x:
От тук получаваме производната, която се изисква в задачата:
Сега нещо за двусмисленото свойство на неявно дефинираните функции и защо са необходими специални правила за тяхното диференциране. В някои случаи може да се провери дали заместването в дадено уравнение(вижте примерите по-горе) вместо y, изразът му чрез x води до факта, че това уравнение се превръща в идентичност. Така. горното уравнение имплицитно дефинира следните функции:
След като заместим израза y на квадрат през x в оригиналното уравнение, получаваме идентичността:
![]() .
.
Изразите, които заместихме, бяха получени чрез решаване на уравнението за y.
Ако трябваше да диференцираме съответната изрична функция
тогава ще получим отговор като в пример 1 - от функция, указана имплицитно:
Но не всяка функция, дадена имплицитно, може да бъде представена във формата г = f(х) . Така например неявно дефинираните функции
![]()
не се изразява чрез елементарни функции, тоест тези уравнения не могат да бъдат решени по отношение на играча. Следователно има правило за диференциране на функция, дадена имплицитно, което вече сме изучавали и ще бъде последователно прилагано в други примери.
Пример 2Намерете производната на функция, дадена имплицитно:
![]() .
.
Изразяваме простото число y и - на изхода - производната на функцията, дадена имплицитно:
Пример 3Намерете производната на функция, дадена имплицитно:
![]() .
.
Решение. Диференцирайте двете страни на уравнението по отношение на x:
 .
.
Пример 4Намерете производната на функция, дадена имплицитно:
![]() .
.
Решение. Диференцирайте двете страни на уравнението по отношение на x:
![]() .
.
Изразяваме и получаваме производната:
 .
.
Пример 5Намерете производната на функция, дадена имплицитно:
Решение. Прехвърляме членовете от дясната страна на уравнението в лявата страна и оставяме нула отдясно. Диференцирайте двете страни на уравнението по отношение на x.
Неявни функции, определени от система от уравнения
Дадена е система от уравнения
или за кратко Е(x,y)= 0. (6.7)
Определение. Система(6.7)определя имплицитно дадена функция y=f(х)към DÌR n
ако "xОД:Е(x, f(х)) = 0.
Теорема (съществуване и уникалност на преобразуване, имплицитно определено от система от уравнения).Позволявам
1) F i(x,y)от (6.4) са дефинирани и имат непрекъснати частни производни от първи ред, (i= 1,…,p, k= 1,…,n, j= 1,…,p) в квартал U(М 0)точки М 0 (х 0 ,г 0), х 0 = , y 0 =
2) Е(М 0)=0,
3) дет.
Тогава в някакъв квартал У(х 0)има уникална функция (картографиране), дефинирана в този квартал y = f(х), така че
"xО U(х 0) :Е(x, f(х))=0и y 0 = f(х 0).
Тази функция е непрекъснато диференцируема в някаква околност на точката x 0 .
Дадена система
Ще приемем, че условията на теоремата за съществуване и уникалност за неявната функция, дадена от тази система от уравнения, са изпълнени. Означаваме тази функция y=f(х) . След това в някакъв квартал на точката х 0 идентичностите са верни
Разграничаването на тези идентичности по отношение на x jполучаваме
= 0.(6.9)
Тези равенства могат да бъдат записани в матрична форма
или разширена
Имайте предвид, че преходът от равенство Е(x, f(х))=0k , отговаря на правилата за диференциация за случая, когато хИ гса точки в едномерното пространство. Матрицата не е изродена по условие, така че матричното уравнение има решение. По този начин е възможно да се намерят частични производни от първи ред на неявни функции. За да намерим диференциалите, означаваме
dy= , dx=, диференцирайки равенства (6.8), получаваме
или в матрична форма
Разширено
Точно както в случая на частичните производни, формулата (6.10) има същия вид, както в случая на едномерните пространства n= 1, p= 1. Решението на това матрично уравнение може да бъде записано като За да се намерят частични производни от втори ред, ще е необходимо да се диференцират идентичности (6.9) (за да се изчислят диференциали от втори ред, е необходимо да се диференцират идентичности (6.10)). Така получаваме
къде през Атермините, които не съдържат желаните, са обозначени.
Матрицата на коефициента на тази система за определяне на производните е матрицата на Якоби.
Подобна формула може да се получи за диференциали. Във всеки от тези случаи ще бъде получено матрично уравнение със същата матрица от коефициенти в системата от уравнения за определяне на желаните производни или диференциали. Същото ще се случи при следните диференциации.
Пример 1Намерете, в точка u= 1,v= 1.
Решение. Продиференцирайте дадените равенства
Забележете, че от условието на задачата следва, че трябва да разглеждаме като независими променливи x, y.Тогава функциите ще бъдат z, u, v.Следователно системата (6.11) трябва да бъде решена по отношение на неизвестните ду, дв, дз.В матрична форма изглежда така
Нека решим тази система с помощта на правилото на Крамър. Детерминанта на матрицата на коефициента
Третият "заменен" определител за дзще бъде равно на (изчислява се чрез разширяване на последната колона)
dz = ,И, .
Отново диференцираме (6.11) ( х, у-независими променливи)
Матрицата на коефициента на системата е същата, третата детерминанта
Решавайки тази система, получаваме израз за d2zкъдето можете да намерите желаната производна.
6.3. Диференцируеми преобразувания
Производни преобразувания. Редовни дисплеи. Необходими и достатъчни условия за функционална зависимост.
Нека функцията е дадена имплицитно с помощта на уравнението
(1)
.
И нека това уравнение, за някаква стойност, има уникално решение. Нека функцията е диференцируема функция в точка , и
.
Тогава за тази стойност има производна, която се определя по формулата:
(2)
.
Доказателство
За доказателство разгледайте функцията като сложна функция на променливата:
.
Прилагаме правилото за диференциране на сложна функция и намираме производната по отношение на променливата отляво и десни частиуравнения
(3)
:
.
Тъй като производната на константата е равна на нула и , тогава
(4)
;
.
Формулата е доказана.
Производни от по-високи разряди
Нека пренапишем уравнение (4), използвайки друга нотация:
(4)
.
Освен това и са сложни функции на променливата:
;
.
Зависимостта определя уравнението (1):
(1)
.
Намираме производната по отношение на променливата от лявата и дясната страна на уравнение (4).
Според формулата за производна на сложна функция имаме:
;
.
Според формулата на производния продукт:
.
Според формулата на производната сума:
.
Тъй като производната на дясната страна на уравнение (4) е равна на нула, тогава
(5)
.
Като заместим производната тук, получаваме стойността на производната от втори ред в неявна форма.
Диференцирайки уравнение (5) по подобен начин, получаваме уравнение, съдържащо производна от трети ред:
.
Замествайки тук намерените стойности на производните от първи и втори ред, намираме стойността на производната от трети ред.
Продължавайки диференциацията, може да се намери производна от произволен ред.
Примери
Пример 1
Намерете първата производна на функцията, дадена имплицитно от уравнението:
(P1) .
Формула 2 решение
Намираме производната по формула (2):
(2)
.
Нека преместим всички променливи в лявата страна, така че уравнението да приеме формата .
.
Оттук.
Намираме производната по отношение на , като приемем, че е постоянна.
;
;
;
.
Намираме производната по отношение на променливата, като приемем, че променливата е постоянна.
;
;
;
.
По формула (2) намираме:
.
Можем да опростим резултата, ако отбележим, че според първоначалното уравнение (A.1), . Заместник:
.
Умножете числителя и знаменателя по:
.
Решение по втория начин
Нека решим този пример по втория начин. За да направим това, намираме производната по отношение на променливата на лявата и дясната част на оригиналното уравнение (P1).
Прилагаме:
.
Прилагаме формулата за производна на дроб:
;
.
Прилагаме формулата за производна на сложна функция:
.
Диференцираме първоначалното уравнение (P1).
(P1) ;
;
.
Умножете по и групирайте термините.
;
.
Заместител (от уравнение (P1)):
.
Нека умножим по:
.
Отговор
Пример 2
Намерете производната от втори ред на функцията, дадена имплицитно, като използвате уравнението:
(P2.1) .
Решение
Диференцирайте оригиналното уравнение по отношение на променливата, като приемете, че е функция на:
;
.
Прилагаме формулата за производна на сложна функция.
.
Ние диференцираме оригиналното уравнение (A2.1):
;
.
От първоначалното уравнение (A2.1) следва, че . Заместник:
.
Разгънете скобите и групирайте членовете:
;
(P2.2) .
Намираме производната от първи ред:
(P2.3) .
За да намерим производната от втори ред, диференцираме уравнение (A2.2).
;
;
;
.
Заменяме израза за производната от първи ред (A2.3):
.
Нека умножим по:
;
.
От тук намираме производната от втори ред.
Отговор
Пример 3
Намерете производната от трети ред за на функцията, дадена имплицитно, като използвате уравнението:
(P3.1) .
Решение
Диференцирайте оригиналното уравнение по отношение на променливата, като приемете, че е функция на .
;
;
;
;
;
;
(P3.2) ;
Ние диференцираме уравнение (A3.2) по отношение на променливата.
;
;
;
;
;
(P3.3) .
Диференцираме уравнение (A3.3).
;
;
;
;
;
(P3.4) .
От уравнения (A3.2), (A3.3) и (A3.4) намираме стойностите на производните при .
;
;
.
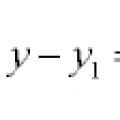 Уравнения на прави и криви в равнината
Уравнения на прави и криви в равнината Обобщено хомогенно уравнение Обобщени хомогенни уравнения от втори ред
Обобщено хомогенно уравнение Обобщени хомогенни уравнения от втори ред Благодарение на запетаята Поради факта, че в техните
Благодарение на запетаята Поради факта, че в техните