Kako pronaći centar gravitacije figure nepravilnog oblika. Položaji težišta nekih figura

Pravougaonik. Pošto pravougaonik ima dve ose simetrije, njegovo težište se nalazi na preseku osi simetrije, tj. u tački preseka dijagonala pravougaonika.

Trougao. Težište leži u tački preseka njegovih medijana. Iz geometrije je poznato da se medijane trougla sijeku u jednoj tački i dijele u omjeru 1:2 od osnove.

Krug. Budući da kružnica ima dvije ose simetrije, njeno težište je na presjeku osi simetrije.

Polukrug. Polukrug ima jednu os simetrije, tada težište leži na ovoj osi. Druga koordinata centra gravitacije izračunava se po formuli: .

Mnogi konstrukcijski elementi izrađeni su od standardnih valjanih proizvoda - uglovi, I-grede, kanali i drugi. Sve dimenzije, kao i geometrijske karakteristike valjanih profila, su tabelarni podaci koji se mogu naći u referentnoj literaturi u standardnim tablicama asortimana (GOST 8239-89, GOST 8240-89).

Primjer 1 Odredite položaj težišta figure prikazane na slici.

Rješenje:

Koordinatne osi biramo tako da os Ox prolazi krajnje donje ukupne dimenzije, a osa Oy - duž krajnje lijeve ukupne dimenzije.

Složenu figuru razbijamo na minimalni broj jednostavnih figura:

pravougaonik 20x10;

trougao 15x10;

krug R=3 cm.

Izračunavamo površinu svake jednostavne figure, njene koordinate centra gravitacije. Rezultati proračuna se unose u tabelu

Slika br.	Područje slike A	Koordinate centra gravitacije

odgovor: C(14,5; 4,5)

Primjer 2 . Odredite koordinate težišta kompozitnog presjeka koji se sastoji od lima i valjanih profila.

Rješenje.

Odabiremo koordinatne ose, kao što je prikazano na slici.

Brojke označavamo brojevima i ispisujemo potrebne podatke iz tabele:

Slika br.	Područje slike A	Koordinate centra gravitacije

Izračunavamo koordinate centra gravitacije figure koristeći formule:

odgovor: C(0; 10)

Laboratorijski rad br. 1 "Određivanje težišta složenih ravnih figura"

Cilj: Eksperimentalnim i analitičkim metodama odredite težište date ravne kompleksne figure i uporedite njihove rezultate.

Radni nalog

Nacrtajte u bilježnicama svoju ravnu figuru u veličini, označavajući koordinatne ose.

Odredite analitički centar gravitacije.

1. Razbijte figuru na minimalni broj figura, čije težište znamo kako odrediti.

   Navedite brojeve područja i koordinate težišta svake figure.

   Izračunajte koordinate težišta svake figure.

   Izračunajte površinu svake figure.

   Izračunajte koordinate težišta cijele figure koristeći formule (stavite položaj težišta na crtežu figure):

Instalacija za eksperimentalno određivanje koordinata centra gravitacije ovjesom sastoji se od vertikalnog nosača 1 (vidi sl.) na koji je pričvršćena igla 2 . ravna figura 3 Izrađen od kartona koji se lako probija kroz rupu. rupe ALI i AT probušene na nasumično lociranim tačkama (po mogućnosti na najudaljenijim jedna od druge). Ravna figura je okačena na iglu, prvo na jednoj tački ALI , a zatim u tački AT . Uz pomoć viska 4 , pričvršćena na istu iglu, na slici je nacrtana okomita linija olovkom koja odgovara liniji viska. Centar gravitacije OD figura će se nalaziti na presjeku vertikalnih linija povučenih kada se figura vješa u tačkama ALI i AT .

centar gravitacije Kruto tijelo je geometrijska tačka koja je kruto povezana s ovim tijelom i predstavlja centar paralelnih sila gravitacije koje se primjenjuju na pojedinačne elementarne čestice tijela (slika 1.6).

Radijus vektor ove tačke

Slika 1.6

Za homogeno tijelo položaj težišta tijela ne ovisi o materijalu, već je određen geometrijskim oblikom tijela.

Ako je specifična težina homogenog tijela γ , težina elementarne čestice tijela

P k = γΔV k (P = γV ) zamijenite formulu za određivanje r C , imamo

Odakle, projektujući na osi i prelazeći do granice, dobijamo koordinate težišta homogenog volumena

Slično, za koordinate težišta homogene površine sa površinom S (Slika 1.7, a)

Slika 1.7

Za koordinate težišta homogene dužine L (Slika 1.7, b)

Metode za određivanje koordinata centra gravitacije

Na osnovu ranije dobijenih općih formula, moguće je naznačiti metode za određivanje koordinata težišta čvrstih tijela:

1 Analitički(integracijom).

2 Metoda simetrije. Ako tijelo ima ravan, os ili centar simetrije, onda njegovo težište leži u ravni simetrije, osi simetrije ili u centru simetrije.

3 Eksperimentalno(metoda ovjesa tijela).

4 razdvajanje. Tijelo je podijeljeno na konačan broj dijelova, za svaki od kojih je položaj centra gravitacije C i područje S poznato. Na primjer, projekcija tijela na ravan xOy (Slika 1.8) može se predstaviti kao dvije ravne figure sa površinama S 1 i S 2 (S=S 1 +S 2 ). Centri gravitacije ovih figura su u tačkama C 1 (x 1 ,y 1 ) i C 2 (x 2 ,y 2 ) . Tada su koordinate centra gravitacije tijela

Slika 1.8

5Dodatak(metoda negativnih površina ili volumena). Poseban slučaj metode particioniranja. Primjenjuje se na tijela sa izrezima ako su poznati centri gravitacije tijela bez izreza i izreza. Na primjer, trebate pronaći koordinate težišta ravne figure (slika 1.9):

Slika 1.9

Težišta najjednostavnijih figura

Slika 1.10

1 trougao

Težište površine trougla poklapa se sa tačkom preseka njegovih medijana (slika 1.10, a).

DM=MB , CM= (1/3)AM .

2 Luk kruga

Luk ima os simetrije (slika 1.10, b). Težište leži na ovoj osi, tj. y C = 0 .

dl – lučni element, dl = Rdφ , R je polumjer kružnice, x = Rcosφ , L= 2aR ,

posljedično:

x C = R(sinα/α) .

3 Kružni sektor

Sektor radijusa R sa centralnim uglom 2 α ima os simetrije Ox , na kojoj se nalazi centar gravitacije (slika 1.10, c).

Sektor dijelimo na elementarne sektore, koji se mogu smatrati trokutima. Centri gravitacije elementarnih sektora nalaze se na luku kružnice poluprečnika (2/3) R .

Težište sektora poklapa se sa težištem luka AB :

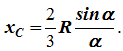
14. Metode za određivanje kretanja tačke.

Sa vektorskom metodom specificiranja kretanja, pozicija tačke je određena vektorom radijusa koji je povučen iz fiksne tačke u odabranom referentnom sistemu.

Sa koordinatnom metodom specificiranja kretanja, koordinate tačke su specificirane kao funkcija vremena:

Ovo su parametarske jednadžbe putanje pokretne tačke, u kojima vrijeme igra ulogu parametra t . Da bismo zapisali njegovu jednačinu u eksplicitnom obliku, potrebno je isključiti iz njih t .

Prirodnom metodom određivanja kretanja, putanje tačke, ishodišta na putanji sa naznakom pozitivnog smjera reference postavlja se zakon promjene koordinata luka: s=s(t) . Ova metoda je pogodna za korištenje ako je putanja točke unaprijed poznata.

15. 1.2 Tačkasta brzina

Razmotrite kretanje tačke u kratkom vremenskom periodu Δt :

prosječna brzina tačke u određenom vremenskom periodu Dt . Brzina tačke u datom trenutku

Tačkasta brzina je kinematička mjera njenog kretanja, jednaka vremenskoj derivaciji radijus vektora ove tačke u referentnom okviru koji se razmatra. Vektor brzine je usmjeren tangencijalno na putanju točke u smjeru kretanja.

Autor: Uzmimo tijelo proizvoljnog oblika. Da li je moguće objesiti ga na konac tako da nakon vješanja zadrži svoj položaj (tj. da ne počne da se okreće) kada bilo koji početna orijentacija (sl. 27.1)?

Drugim riječima, postoji li takva tačka u odnosu na koju bi zbir momenata sila gravitacije koje djeluju na različite dijelove tijela bio jednak nuli pri bilo koji orijentacija tijela u prostoru?

Reader: Da, mislim da jeste. Takva tačka se zove centar gravitacije tela.

Dokaz. Radi jednostavnosti, razmotrimo tijelo u obliku ravne ploče proizvoljnog oblika proizvoljno orijentirano u prostoru (slika 27.2). Uzmite koordinatni sistem X 0at sa ishodištem u centru mase - tačkom OD, onda x C = 0, u C = 0.

Ovo tijelo predstavljamo kao skup velikog broja masa tačaka m i, položaj svakog od njih je dat radijus vektorom .

Po definiciji centra mase , i koordinata x C = .

Pošto u našem koordinatnom sistemu x C= 0, tada . Pomnožimo ovu jednačinu sa g i dobiti

Kao što se može vidjeti sa sl. 27.2, | x i| je rame snage. I ako x i> 0, zatim moment sile M i> 0, i ako x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x i moment sile će biti M i = m i gx i . Tada je jednakost (1) ekvivalentna , gdje M i je moment gravitacije. A to znači da će s proizvoljnom orijentacijom tijela zbir momenata sila gravitacije koje djeluju na tijelo biti jednak nuli u odnosu na njegovo središte mase.

Da bi tijelo koje razmatramo bilo u ravnoteži, potrebno je primijeniti na njega u tački OD sila T = mg usmjereno okomito prema gore. Trenutak ove sile oko tačke OD jednako nuli.

Pošto naše razmišljanje ni na koji način nije zavisilo od toga kako je telo tačno orijentisano u prostoru, dokazali smo da se težište poklapa sa centrom mase, što je i trebalo dokazati.

Problem 27.1. Pronađite težište bestežinskog štapa dužine l, na čijim su krajevima pričvršćene dvije tačkaste mase t 1 i t 2 .

t 1 t 2 l	Rješenje. Nećemo tražiti centar gravitacije, već centar mase (pošto su jedno te isto). Hajde da predstavimo osovinu X(Sl. 27.3). Rice. 27.3
x C =?

Odgovori: daleko od mase t 1 .

STOP! Odlučite sami: B1-B3.

Izjava 1 . Ako homogeno ravno tijelo ima os simetrije, težište je na toj osi.

Zaista, za bilo koju masu tačke m i, koji se nalazi desno od ose simetrije, nalazi se ista tačka mase koja se nalazi simetrično u odnosu na prvu (slika 27.4). U ovom slučaju, zbroj momenata sila .

Budući da se cijelo tijelo može predstaviti kao podijeljeno na slične parove tačaka, ukupni moment gravitacije u odnosu na bilo koju tačku koja leži na osi simetrije je nula, što znači da se i težište tijela nalazi na ovoj osi. Ovo dovodi do važnog zaključka: ako tijelo ima nekoliko osi simetrije, onda težište leži na sjecištu ovih osa(Sl. 27.5).

Rice. 27.5

Izjava 2. Ako dva tijela sa masama t 1 i t 2 spojeni u jedno, onda će težište takvog tijela ležati na pravoj liniji koja spaja težište prvog i drugog tijela (slika 27.6).

Rice. 27.6 Rice. 27.7

Dokaz. Složimo složeno tijelo tako da segment koji povezuje težišta tijela bude okomit. Zatim zbir momenata gravitacije prvog tijela u odnosu na tačku OD 1 je jednak nuli, a zbir momenata gravitacije drugog tijela oko tačke OD 2 je nula (slika 27.7).

primeti, to ramena gravitacije bilo koje mase tačke t i isto u odnosu na bilo koju tačku na segmentu OD 1 OD 2, a time i moment gravitacije u odnosu na bilo koju tačku koja leži na segmentu OD 1 OD 2 su ista. Stoga je gravitacija cijelog tijela nula u odnosu na bilo koju tačku na segmentu OD 1 OD 2. Dakle, težište kompozitnog tijela leži na segmentu OD 1 OD 2 .

Izjava 2 implicira važan praktični zaključak, koji je jasno formulisan u obliku instrukcija.

instrukcija,

kako pronaći težište krutog tijela ako se može slomiti

na dijelove, od kojih su pozicije težišta svakog od njih poznate

1. Zamijenite svaki dio masom koja se nalazi u centru gravitacije tog dijela.

2. Pronađite centar gravitacije(a ovo je isto kao i centar gravitacije) rezultirajućeg sistema masa tačaka, birajući prikladan koordinatni sistem X 0at, prema formulama:

Zaista, postavimo složeno tijelo na takav način da segment OD 1 OD 2 je bio horizontalan, a mi ćemo ga objesiti na niti na tačkama OD 1 i OD 2 (Sl. 27.8, a). Jasno je da će tijelo biti u ravnoteži. I ova ravnoteža neće biti poremećena ako svako tijelo zamijenimo tačkastim masama t 1 i t 2 (Sl. 27.8, b).

Rice. 27.8

STOP! Odlučite sami: C3.

Problem 27.2. Kuglice mase postavljene su u dva vrha jednakostraničnog trougla t svaki. Treći vrh sadrži kuglu mase 2 t(Sl. 27.9, a). Strana trougla a. Odredite centar gravitacije ovog sistema.

t 2t a	Rice. 27.9
x C = ? u C = ?

Rješenje. Uvodimo koordinatni sistem X 0at(Sl. 27.9, b). Onda

,

.

Odgovori: x C = a/2; ; centar gravitacije je na polovini visine AD.

Sposobnost da ostanete u ravnoteži bez napora je veoma važna za efikasnu meditaciju, jogu, čigong, a takođe i za trbušni ples. To je prvi zahtjev sa kojim se suočavaju početnici u ovakvim aktivnostima i jedan od razloga zašto je teško napraviti prve korake bez instruktora. Pitanje koje sugerira da osoba ne poznaje svoj centar gravitacije može izgledati nešto drugačije. U qigongu, na primjer, osoba će se pitati kako da bude opuštena i da ipak izvodi pokrete stojeći, orijentalni plesač početnik neće razumjeti kako da odvoji i uskladi pokrete donjeg i gornjeg dijela tijela, au oba slučaja ljudi će se prenapregnuti i često izgubiti ravnotežu. Njihovi pokreti će biti nesigurni, nespretni.

Stoga je važno razumjeti kako sami pronaći svoj centar gravitacije, to zahtijeva i mentalni rad i vještinu, ali s vremenom ta vještina prelazi na instinktivni nivo.

Što treba učiniti kako ne bi naprezali mišiće i istovremeno ne koristili vanjske potpore. Odgovor je očigledan, morate pomjeriti potporu prema unutra. Preciznije, oslonite se na uslovnu unutrašnju os. Gdje ide ova osovina? Koncept centra gravitacije je uslovan, ali se ipak koristi u fizici. Tamo je uobičajeno da se definiše kao tačka primene rezultujućih sila gravitacije. Rezultirajuća sila gravitacije je ukupnost svih sila gravitacije, uzimajući u obzir smjer njihovog djelovanja.

Je li teško do sada? Zapremite se strpljenjem.

Odnosno, tražimo tačku u našem tijelu koja će nam omogućiti da ne padnemo, a da se svjesno ne borimo protiv gravitacije. To znači da Zemljina gravitacija mora biti usmjerena tako da konvergira s ostalim silama koje djeluju negdje u centru našeg tijela.

Takav smjer sila stvara uvjetnu os u samom centru našeg tijela, vertikalnu površinu, to je vertikala centra gravitacije. Taj dio tijela na koji se naslanjamo na tlo je otisak našeg stopala (stopalama se oslanjamo na tlo).Na mjestu gdje se ova vertikala naslanja na podlogu na kojoj stojimo, odnosno oslanjamo se na tlo, ovo je centar gravitacije unutar otiska stopala. Ako se vertikala pomeri sa ovog mesta, izgubićemo ravnotežu i pasti. Što je sama površina potpore veća, to nam je lakše da ostanemo blizu njenog centra, pa ćemo svi instinktivno napraviti dug korak dok stojimo na nestabilnoj površini. Odnosno, područje oslonca nije samo stopala, već i prostor između njih.

Također je važno znati da širina područja oslonca utječe više od dužine. U slučaju čovjeka, to znači da je veća vjerovatnoća da ćemo pasti na bok nego unazad, a još više naprijed. Stoga nam je prilikom trčanja teže održati ravnotežu, isto se može reći i za štikle. Ali u širokim, stabilnim cipelama, naprotiv, lakše je odoljeti, čak lakše nego potpuno bosi. Međutim, aktivnosti spomenute na početku zahtijevaju vrlo mekanu, laganu obuću ili je uopće nemaju. Stoga si cipelama ne možemo pomoći.

Dakle, veoma je važno pronaći središnju tačku okomite linije na svom stopalu. Obično se ne nalazi u centru stopala, kako neki automatski pretpostavljaju, već bliže peti, negdje na pola puta od centra stopala, do pete.
Ali to nije sve.

Pored vertikalne linije centra gravitacije, postoji i horizontalna, kao i posebna za udove.
Horizontalna linija za žene i muškarce teče malo drugačije.

Naprijed, kod žena, prolazi niže, a kod muškaraca više. Kod muškaraca ide negdje 4-5 prstiju ispod pupka, a kod žena otprilike 10. Iza ženske linije teče gotovo koopčik, a muška linija je oko pet prstiju viša od nje. Osim toga, za stabilnost u vrijeme meditacije, važno je obratiti pažnju na čistu liniju težišta koljena. Nalazi se malo iznad kosti (potkoljenice), ali dva ili tri prsta ispod hrskavice.

Tokom meditacije, kao i tokom trbušnog plesa, nije baš dobro širiti stopala, maksimalna širina obično odgovara širini ramena.

Stoga si morate malo pomoći koljenima, pokušavajući da okomitu os izgradite što je moguće ravnije. Stanite ispred ogledala, pronađite sve opisane tačke na sebi. Stavite stopala u širinu ramena. Opustite mišiće nogu i tijela. Zatim ispravite leđa bez naprezanja tijela, opustite noge uz lagano savijanje u koljenima. Zamislite tri okomite linije, od kojih svaka ide u odgovarajućoj tački u stražnjem dijelu torza, ispred njega i oko koljena. Pokušajte rasporediti tačke tako da prednja os trupa bude otprilike na pola puta između ose leđa i koljena. U tom slučaju koljena ne treba savijati tako da izlaze preko nožnog prsta, već samo blago savijena i dobro opuštena. Po mogućnosti iznad centra gravitacije unutar područja oslonca koje smo pronašli na stopalu. U isto vrijeme, ruke se mogu slobodno postaviti na bogove ili staviti dlanove na bokove.

Kako ćete znati da ste pronašli svoj centar gravitacije?

Osjetit ćete lagano ljuljanje, ali u isto vrijeme sigurno ćete znati da nećete pasti.

Predavanje 4. Težište.

Ovo predavanje pokriva sljedeća pitanja

1. Težište krutog tijela.

2. Koordinate centara gravitacije nehomogenih tijela.

3. Koordinate težišta homogenih tijela.

4. Metode za određivanje koordinata centara gravitacije.

5. Težišta nekih homogenih tijela.

Proučavanje ovih pitanja neophodno je u budućnosti za proučavanje dinamike kretanja tijela, uzimajući u obzir trenje klizanja i trenja kotrljanja, dinamiku centra mase mehaničkog sistema, kinetičke momente, za rješavanje zadataka iz discipline. "Čvrstoća materijala".

Dovođenje paralelnih sila.

Nakon što smo razmotrili svođenje na centar ravnog sistema i proizvoljnog prostornog sistema sila, ponovo se vraćamo na razmatranje posebnog slučaja sistema paralelnih sila.

Dovođenje dve paralelne sile.

U toku razmatranja ovakvog sistema sila moguća su sljedeća tri slučaja redukcije.

1. Sistem dvije kolinearne sile. Razmotrimo sistem od dvije paralelne i usmjerene u istom smjeru sila P i Q, primijenjen na tačkama ALI i AT. Pretpostavićemo da su sile okomite na ovaj segment (slika 1, a).

OD, koji pripada segmentu AB i ispunjava uslov:

AC/SW = Q/P.(1)

Glavni sistemski vektor RC = P + Q modul je jednak zbiru ovih sila: RC = P + Q.

OD uzimajući u obzir (1) jednako je nuli:MC = P ∙ AC- Q∙ SW = 0.

Tako smo kao rezultat glumačke ekipe dobili: RC ≠ 0, MC= 0. To znači da je glavni vektor ekvivalentan rezultantu koji prolazi kroz centar redukcije, odnosno:

Rezultanta kolinearnih sila je po apsolutnoj vrijednosti jednaka njihovom zbiru, a njena linija djelovanja dijeli segment koji povezuje tačke njihove primjene, obrnuto proporcionalno modulima ovih sila iznutra.

Imajte na umu da je pozicija tačke OD neće se promijeniti ako sile R i Q skrenite za ugaoα . Dot OD, koji ima ovo svojstvo se zove centar paralelnih sila.

2. Sistem od dva antikolinearno a nisu jednake po modulu sila. Neka snage P i Q, primijenjen na tačkama ALI i AT, paralelni, usmjereni u suprotnim smjerovima i nejednaki po modulu (sl. 1, b).

Odaberimo tačku kao referentni centar OD, koji i dalje zadovoljava relaciju (1) i leži na istoj pravoj liniji, ali izvan segmenta AB.

Glavni vektor ovog sistema RC = P + Q modulo će sada biti jednak razlici između modula vektora: RC = Q - P.

Glavni momenat o centru OD je i dalje nula:MC = P ∙ AC- Q∙ SW= 0, dakle

Rezultat antikolinearno a sile koje nisu jednake po apsolutnoj vrijednosti jednaka je njihovoj razlici, usmjerena je prema većoj sili, a njena linija djelovanja dijeli segment koji povezuje tačke njihove primjene, obrnuto proporcionalno modulima ovih sila spolja.

Fig.1

3. Sistem od dva antikolinearno i sile jednake po modulu. Uzmimo prethodni slučaj redukcije kao početni. Popravimo struju R, i sila Q hajde da se trudimo po modulu na silu R.

Zatim u Q → R u formuli (1) omjer AC/SW → 1. To znači da AC → SW, odnosno udaljenost AC →∞ .

U ovom slučaju, modul glavnog vektora RC → 0, a modul glavnog momenta ne ovisi o položaju centra redukcije i ostaje jednak prvobitnoj vrijednosti:

MC = P ∙ AC- Q∙ SW = P ∙ ( AC- SW) =P ∙ ALIB.

Tako smo u limitu dobili sistem sila za koji RC = 0, MC≠ 0, a centar redukcije se uklanja u beskonačnost, što se ne može zamijeniti rezultantom. U ovom sistemu nije teško pronaći par sila, dakle par sila nema rezultantu.

Centar sistema paralelnih sila.

Razmotrite sistem n snage Pi, primijenjen na tačkamaA i (x i , y i , z i) i paralelno sa osomOv sa vektorom l(Sl. 2).

Ako unaprijed isključimo slučaj sistema koji je ekvivalentan paru sila, nije teško dokazati, na osnovu prethodnog stava, postojanje njegove rezultante.R.

Odredite koordinate centraC(x c, y c, z c) paralelne sile, odnosno koordinate tačke primjene rezultante ovog sistema.

U tu svrhu koristimo Varignonovu teoremu na osnovu koje:

M0 (R) = Σ M0(Pi).

Fig.2

Vektorski moment sile može se predstaviti kao unakrsni proizvod, dakle:

M 0 (R) = rc× R = Σ M0i(Pi) = Σ ( r i× Pi ).

S obzirom na to R = Rv ∙ l, a Pi = P vi ∙ l i koristeći svojstva vektorskog proizvoda, dobijamo:

rc × Rv ∙ l = Σ ( r i × P vi ∙ l),

rc ∙ R v × l = Σ ( r i ∙ P vi × l) = Σ ( r i ∙ P vi ) × l,

ili:

[ r c R v - Σ ( r i P vi )] × l= 0.

Posljednji izraz vrijedi samo ako je izraz u uglastim zagradama nula. Stoga se izostavlja indeksva s obzirom da je rezultantaR = Σ Pi , odavde dobijamo:

rc = (Σ Pi r i )/(Σ Pi ).

Projektujući posljednju vektorsku jednakost na koordinatnu osu, dobijamo željenu izraz koordinata centra paralelnih sila:

x c = (Σ Pi x i)/(Σ Pi );

y c = (Σ Pi y i )/(Σ Pi );(2)

z c = (Σ Pi z i )/(Σ Pi ).

Težište tijela

Koordinate težišta homogenog tijela.

Zamislite vaganje krutog tijela P i volumen V u koordinatnom sistemu Oxyz, gdje su sjekire x i y povezan sa zemljinom površinom i osovinom z usmjerena u zenit.

Ako tijelo razbijemo na elementarne dijelove sa zapreminom∆ V i , tada će sila privlačenja djelovati na svaki njegov dio∆ Piusmerena ka centru zemlje. Pretpostavimo da su dimenzije tela mnogo manje od dimenzija Zemlje, onda se sistem sila primenjenih na elementarne delove tela može smatrati ne konvergentnim, već paralelnim (slika 3), a svi zaključci prethodnog poglavlja su primjenjivi na njega.

Fig.3

Definicija . Težište krutog tijela je centar paralelnih sila gravitacije elementarnih dijelova ovog tijela.

Prisjetite se toga specifična gravitacija elementarni dio tijela naziva se odnos njegove težine∆ Pi na zapreminu ∆ V i : γ i = ∆ Pi/ ∆ V i . Za homogeno tijelo ova vrijednost je konstantna:γ i = γ = P/ V.

Zamjena u (2) ∆ Pi = γ i ∙∆ V i umjesto Pi, uzimajući u obzir posljednju napomenu i smanjivši brojnik i nazivnik zag, dobijamo izrazi za koordinate težišta homogenog tijela:

x c = (Σ ∆ Vi∙ x i)/(Σ ∆ Vi);

y c = (Σ ∆ Vi∙ y i )/(Σ ∆ Vi);(3)

z c = (Σ ∆ Vi∙ z i )/(Σ ∆ Vi).

Nekoliko teorema je korisno za određivanje centra gravitacije.

1) Ako homogeno tijelo ima ravan simetrije, onda je njegovo težište u ovoj ravni.

Ako osi X i at postavljena u ovu ravan simetrije, zatim za svaku tačku sa koordinatama. i koordinirati prema (3), biće jednak nuli, jer ukupno sve termini suprotnih predznaka se eliminišu u parovima. Dakle, centar gravitacije je u ravni simetrije.

2) Ako homogeno tijelo ima os simetrije, onda se težište tijela nalazi na toj osi.

Zaista, u ovom slučaju, ako je osznacrtati duž ose simetrije, za svaku tačku sa koordinatamamožete pronaći tačku sa koordinatama i koordinate i izračunato po formulama (3) biće jednako nuli.

Treća teorema se dokazuje slično.

3) Ako homogeno tijelo ima centar simetrije, tada se težište tijela nalazi u ovoj tački.

I još nekoliko napomena.

Prvo. Ako se tijelo može podijeliti na dijelove za koje su poznati težina i položaj težišta, onda nema potrebe razmatrati svaku tačku, već u formulama (3) Pi – određuje se kao težina relevantnog dijela ikao koordinate njegovog centra gravitacije.

Sekunda. Ako je tijelo homogeno, onda je težina njegovog zasebnog dijela, gdje je specifična težina materijala od kojeg je tijelo napravljeno, i Vi - zapremina ovog dela tela. I formule (3) će poprimiti prikladniji oblik. Na primjer,

I slično, gdje - zapremina celog tela.

Treća nota. Neka tijelo izgleda kao tanka ploča s površinom F i debljina t leži u avionu Oxy. Zamjena u (3)∆ V i =t ∙ ∆F i , dobijamo koordinate težišta homogene ploče:

x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

y c = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).

z c = (Σ ∆ F i∙ z i ) / (Σ ∆ F i).

gdje – koordinate težišta pojedinih ploča;je ukupna površina tijela.

Četvrta nota. Za tijelo u obliku tanke krivolinijske šipke dužine L sa površinom poprečnog presjeka a elementarni volumen∆ V i = a ∙∆ L i , zbog toga koordinate centra gravitacije tankog krivolinijskog štapaće biti jednako:

x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);

y c = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)

z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).

gdje – koordinate centra gravitacijei-th section; .

Imajte na umu da je, prema definiciji, centar gravitacije geometrijska tačka; također može ležati izvan granica datog tijela (na primjer, za prsten).

Bilješka.

U ovom dijelu kursa ne pravimo razliku između gravitacije, gravitacije i tjelesne težine. U stvarnosti, gravitacija je razlika između Zemljine gravitacije i centrifugalne sile uzrokovane njenom rotacijom.

Koordinate centara gravitacije nehomogenih tijela.

Koordinate centra gravitacije nehomogena čvrsta materija(Sl. 4) u odabranom referentnom sistemu definirani su na sljedeći način:

Fig.4

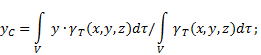
gdje - težina po jedinici zapremine tela (specifična težina)

- cele telesne težine.

neravnu površinu(Sl. 5), tada se koordinate centra gravitacije u odabranom referentnom sistemu određuju na sljedeći način:

Sl.5

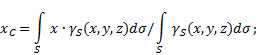
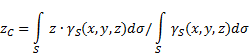
gdje - težina po jedinici površine tijela

- cele telesne težine.

Ako je čvrsta materija heterogena linija(Sl. 6), tada se koordinate centra gravitacije u odabranom referentnom sistemu određuju na sljedeći način:

Fig.6

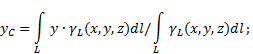
gdje - Jedinična težina tjelesne dužine,

Cela telesna težina.

Metode za određivanje koordinata centra gravitacije.

Na osnovu gore dobijenih općih formula, moguće je naznačiti specifične metode određivanje koordinata težišta tijela.

1. Simetrija. Ako homogeno tijelo ima ravan, os ili centar simetrije (slika 7), onda njegovo težište leži u ravni simetrije, osi simetrije ili u centru simetrije.

Fig.7

2. Razdvajanje. Tijelo je podijeljeno na konačan broj dijelova (slika 8), za svaki od kojih je poznat položaj težišta i površina.

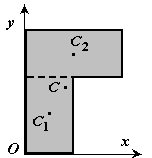
Fig.8

S \u003d S 1 + S 2.

3.Metoda negativnih područja. Poseban slučaj metode particioniranja (slika 9). Primjenjuje se na tijela sa izrezima ako su poznati centri gravitacije tijela bez izreza i izreza. Tijelo u obliku ploče s izrezom predstavljeno je kombinacijom čvrste ploče (bez izreza) s površinom S1 i područje izrezanog dijela S2.

Fig.9

S \u003d S 1 - S 2.

4.metod grupisanja. Dobar je dodatak posljednje dvije metode. Nakon što se figura razbije na sastavne elemente, može biti zgodno ponovo kombinovati neke od njih, kako bi se pojednostavilo rješenje uzimajući u obzir simetriju ove grupe.

Težišta nekih homogenih tijela.

1) Težište kružnog luka. Uzmite u obzir luk AB radijusR sa centralnim uglom. Zbog simetrije, težište ovog luka leži na osiOx(Sl. 10).

Fig.10

Nađimo koordinate prema formuli . Da biste to učinili, odaberite na luku AB element MM ’ dugo, čiji je položaj određen uglom. Koordinate X element MM' bice. Zamjena ovih vrijednosti X i d l a imajući u vidu da se integral mora produžiti cijelom dužinom luka, dobijamo:

gdje je L dužina luka AB jednaka .

Odavde konačno nalazimo da težište kružnog luka leži na njegovoj osi simetrije na udaljenosti od centra Oh jednaki

gdje je ugao mjereno u radijanima.

2) Težište površine trougla. Zamislite trougao koji leži u ravni Oxy, čije su koordinate temena poznate: A i (x i,y i ), (i= 1,2,3). Razbijanje trokuta na uske trake paralelne sa strane ALI 1 ALI 2, dolazimo do zaključka da težište trougla mora pripadati medijani ALI 3 M 3 (sl.11) .

Fig.11

Razbijanje trougla na trake paralelne sa stranicom ALI 2 ALI 3, možete biti sigurni da mora ležati na medijani ALI 1 M jedan . Na ovaj način, težište trougla leži u tački preseka njegovih medijana, koji, kao što znate, odvaja treći dio od svake medijane, računajući od odgovarajuće strane.

Posebno za medijanu ALI 1 M 1 dobijamo, s obzirom da su koordinate tačke M 1 - je aritmetička sredina koordinata vrhova ALI 2 i ALI 3 :

x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.

Dakle, koordinate centra gravitacije trokuta su aritmetička sredina koordinata njegovih vrhova:

x c =(1/3) Σ x i ; y c =(1/3) Σ y i .

3) Težište područja kružnog sektora. Razmotrimo sektor kruga radijusa R sa centralnim uglom 2α , koji se nalazi simetrično oko ose Ox (Sl. 12) .

Očigledno je da y c = 0, a udaljenost od centra kruga iz kojeg je ovaj sektor isječen do njegovog težišta može se odrediti formulom:

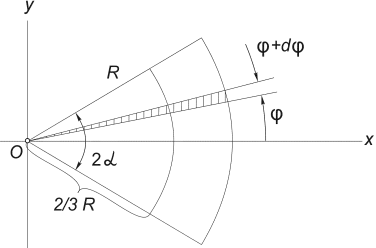
Fig.12

Najlakši način za izračunavanje ovog integrala je podjelom domene integracije na elementarne sektore sa uglom dφ . Do infinitezimala prvog reda, takav sektor se može zamijeniti trouglom sa osnovom jednakom R × dφ i visina R. Površina takvog trougla dF =(1/2)R 2 ∙ dφ , a težište mu je 2/3 R odozgo, pa u (5) stavljamo x = (2/3)R∙ cos. Zamjena u (5) F= α R 2, dobijamo:

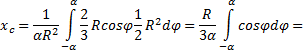
Koristeći posljednju formulu, izračunavamo, posebno, udaljenost do centra gravitacije polukrug.

Zamjenom u (2) α = π /2 dobijamo: x c = (4 R)/(3 π ) ≅ 0,4 R .

Primjer 1Odredimo težište homogenog tijela prikazanog na sl. 13.

Fig.13

Rješenje.Tijelo je homogeno, sastoji se od dva dijela simetričnog oblika. Koordinate njihovih centara gravitacije:

Njihove količine:

Dakle, koordinate centra gravitacije tijela

Primjer 2 Pronađite težište ploče savijene pod pravim uglom. Dimenzije - na crtežu (sl. 14).

Fig.14

Rješenje. Koordinate centara gravitacije:

0.

kvadrati:

Zbog toga:

Primjer 3 Na kvadratnom listu cm izrezana kvadratna rupa vidi (sl. 15). Pronađite težište lista. Primjer 4 Pronađite položaj težišta ploče prikazane na sl. 16. Dimenzije su date u centimetrima.

Fig.16

Rješenje. Ploču podijelimo na figure (slika 17), centričija je težina poznata.

Područja ovih figura i koordinate njihovih centara gravitacije:

1) pravougaonik sa stranicama 30 i 40 cm,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; at 1 \u003d 20 cm.

2) pravougli trougao sa osnovom 50 cm i visinom 40 cm;S 2 =0,5 ∙ 50 ∙ 40= 1000 cm 2 ; X 2 = 30 + 50 / 3 = 46,7 cm; y 2 =40/3 =13,3 cm;

3) polukrug polukruga r = 20 cm;S 3 =0,5 ∙π∙ 20 2 = 628 cm 2 ; X 3 =4 R /3 π =8,5 cm; at

Rješenje. Podsjetimo da je u fizici gustina tijelaρ i njegovu specifičnu težinugpovezano omjerom:γ = ρ g , gdjeg - ubrzanje gravitacije. Da biste pronašli masu takvog homogenog tijela, morate pomnožiti gustinu s njegovom zapreminom.

Fig.19

Izraz "linearna" ili "linearna" gustoća znači da se za određivanje mase šipke za rešetke, linearna gustoća mora pomnožiti s dužinom ove šipke.

Da biste riješili problem, možete koristiti metodu particioniranja. Predstavljajući datu rešetku kao zbir 6 pojedinačnih šipki, dobijamo:

gdjeL i dužinai -th štap farme, ix i , y i - koordinate njegovog centra gravitacije.

Rješenje ovog problema može se pojednostaviti grupiranjem posljednjih 5 rešetkastih šipki. Lako je uočiti da čine lik sa centrom simetrije koji se nalazi u sredini četvrtog štapa, gdje se nalazi težište ove grupe štapova.

Dakle, data rešetka može biti predstavljena kombinacijom samo dvije grupe šipki.

Prvu grupu čini prvi štap, za njuL 1 = 4 m,x 1 = 0 m,y 1 = 2 m. Drugu grupu štapova čini pet štapova, za kojeL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.

Koordinate centra gravitacije farme nalaze se po formuli:

x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Imajte na umu da centar OD leži na liniji koja spaja OD 1 i OD 2 i dijeli segment OD 1 OD 2 u vezi: OD 1 OD/SS 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.

Pitanja za samoispitivanje

Šta je centar paralelnih sila?

- Kako se određuju koordinate centra paralelnih sila?

- Kako odrediti centar paralelnih sila čija je rezultanta nula?

Koje je svojstvo centra paralelnih sila?

- Koje formule se koriste za izračunavanje koordinata centra paralelnih sila?

Šta je težište tijela?

- Zašto se sile privlačenja Zemlje, koje djeluju na tačku tijela, mogu uzeti kao sistem paralelnih sila?

- Zapišite formulu za određivanje položaja težišta nehomogenih i homogenih tijela, formulu za određivanje položaja težišta ravnih presjeka?

- Zapišite formulu za određivanje položaja težišta jednostavnih geometrijskih oblika: pravougaonik, trokut, trapez i pola kruga?

Šta se naziva statički moment površine?

- Navedite primjer tijela čije se težište nalazi izvan tijela.

- Kako se svojstva simetrije koriste za određivanje centara gravitacije tijela?

- Koja je suština metode negativnih pondera?

Gdje se nalazi težište kružnog luka?

Kako možete grafički pronaći centar gravitacije trougla?

- Zapišite formulu koja određuje težište kružnog sektora.

- Koristeći formule koje određuju težište trougla i kružnog sektora, izvedite sličnu formulu za kružni segment.

- Koje formule se koriste za izračunavanje koordinata težišta homogenih tijela, ravnih figura i linija?

- Kako se naziva statički moment površine ravne figure u odnosu na osu, kako se izračunava i koju dimenziju ima?

- Kako odrediti položaj težišta područja, ako je poznat položaj težišta pojedinih njegovih dijelova?

- Koje se pomoćne teoreme koriste za određivanje položaja težišta?