Naći matrice inverzne datoj matrici a. Pronalaženje inverzne matrice na mreži

Pronalaženje inverzne matrice- problem koji se najčešće rješava na dva načina:

metoda algebarskih sabiranja, u kojoj je potrebno pronaći determinante i transponirati matrice;
Gaussova metoda eliminacije, koja zahtijeva elementarne transformacije matrica (dodavanje redova, množenje redova istim brojem, itd.).

Za one koji su posebno znatiželjni, postoje i druge metode, na primjer, metoda linearnih transformacija. U ovoj lekciji ćemo analizirati tri navedene metode i algoritme za pronalaženje inverzne matrice ovim metodama.

inverzna matrica ALI, takva matrica se zove

ALI
. (1)

inverzna matrica , koje je potrebno pronaći za datu kvadratnu matricu ALI, takva matrica se zove

proizvod kojim su matrice ALI desno je matrica identiteta, tj.
. (1)

Matrica identiteta je dijagonalna matrica u kojoj su svi dijagonalni unosi jednaki jedan.

Teorema.Za svaku nesingularnu (nesingularnu, nesingularnu) kvadratnu matricu može se pronaći inverzna matrica, i štaviše, samo jedna. Za specijalnu (degenerisanu, singularnu) kvadratnu matricu, inverzna matrica ne postoji.

Kvadratna matrica se zove nespecijalan(ili nedegenerisan, ne-jednina) ako njegova determinanta nije jednaka nuli, i poseban(ili degenerisati, singular) ako je njegova determinanta nula.

Inverzna matrica se može naći samo za kvadratnu matricu. Naravno, inverzna matrica će također biti kvadratna i istog reda kao i data matrica. Matrica za koju se može naći inverzna matrica naziva se invertibilna matrica.

Za inverzna matrica postoji prikladna analogija s recipročnim brojem. Za svaki broj a, koji nije jednak nuli, postoji broj b da je posao a i b jednako jedan: ab= 1 . Broj b naziva se recipročna vrednost broja b. Na primjer, za broj 7, inverzni je broj 1/7, jer je 7*1/7=1.

Pronalaženje inverzne matrice metodom algebarskih sabiranja (matrica sindikata)

Za nesingularnu kvadratnu matricu ALI inverz je matrica

gdje je determinanta matrice ALI, a je matrica pridružena matrici ALI.

Povezano sa kvadratnom matricom A je matrica istog reda čiji su elementi algebarski komplementi odgovarajućih elemenata determinante matrice transponirane u odnosu na matricu A. Dakle, ako

onda

Algoritam za pronalaženje inverzne matrice metodom algebarskih sabiranja

1. Pronađite determinantu ove matrice A. Ako je determinanta jednaka nuli, pronalaženje inverzne matrice prestaje, jer je matrica degenerirana i za nju ne postoji inverzna.

2. Pronađite matricu transponovanu u odnosu na A.

3. Izračunajte elemente matrice unije kao algebarske komplemente marite pronađene u koraku 2.

4. Primijeniti formulu (2): pomnožiti recipročnu vrijednost determinante matrice A, na matricu ujedinjenja koja se nalazi u koraku 4.

5. Provjerite rezultat dobiven u koraku 4 množenjem ove matrice A na inverznu matricu. Ako je proizvod ovih matrica jednak matrici identiteta, tada je inverzna matrica pronađena ispravno. U suprotnom pokrenite postupak rješenja ponovo.

Primjer 1 Za matricu

pronađite inverznu matricu.

Rješenje. Da biste pronašli inverznu matricu, potrebno je pronaći determinantu matrice ALI. Po pravilu trouglova nalazimo:

Dakle, matrica ALI je nesingularan (nedegenerisan, nesingularan) i za njega postoji inverz.

Nađimo matricu pridruženu datoj matrici ALI.

Nađimo matricu transponovanu u odnosu na matricu A:

Izračunavamo elemente matrice unije kao algebarske komplemente matrice transponovane u odnosu na matricu A:

Dakle, matrica je konjugirana sa matricom A, ima oblik

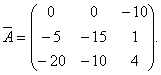
Komentar. Redoslijed izračunavanja elemenata i transpozicije matrice može biti različit. Prvo se mogu izračunati algebarski komplementi matrice A, a zatim transponirati matricu algebarskih komplementa. Rezultat bi trebali biti isti elementi matrice sindikata.

Primjenom formule (2) nalazimo matricu inverznu matrici ALI:

Pronalaženje inverzne matrice Gaussovom eliminacijom nepoznanica

Prvi korak za pronalaženje inverzne matrice Gaussovom eliminacijom je pripisivanje matrici A matrica identiteta istog reda, odvajajući ih okomitom crtom. Dobijamo dualnu matricu. Pomnožite oba dijela ove matrice sa , onda ćemo dobiti

Algoritam za pronalaženje inverzne matrice Gaussovom eliminacijom nepoznatih

1. Na matricu A dodijeliti matricu identiteta istog reda.

2. Transformirajte rezultirajuću dualnu matricu tako da se matrica identiteta dobije u njenom lijevom dijelu, tada će se inverzna matrica automatski dobiti u desnom dijelu umjesto matrice identiteta. Matrix A na lijevoj strani se pretvara u matricu identiteta elementarnim transformacijama matrice.

2. Ako je u procesu transformacije matrice A u matricu identiteta u bilo kojem retku ili u bilo kojoj koloni bit će samo nule, tada je determinanta matrice jednaka nuli i, prema tome, matrica Aće biti degenerisan i nema inverznu matricu. U ovom slučaju, daljnje pronalaženje inverzne matrice prestaje.

Primjer 2 Za matricu

pronađite inverznu matricu.

a mi ćemo ga transformirati tako da se matrica identiteta dobije na lijevoj strani. Započnimo transformaciju.

Pomnožite prvi red lijeve i desne matrice sa (-3) i dodajte ga drugom redu, a zatim pomnožite prvi red sa (-4) i dodajte ga trećem redu, onda ćemo dobiti

Tako da, ako je moguće, ne postoje razlomci tokom narednih transformacija, prvo ćemo kreirati jedinicu u drugom redu na lijevoj strani dualne matrice. Da biste to učinili, pomnožite drugi red sa 2 i oduzmite treći red od njega, a zatim dobijemo

Dodajmo prvi red drugom, a zatim pomnožimo drugi red sa (-9) i dodajmo ga trećem redu. Onda dobijamo

Zatim podijelite treći red sa 8

Pomnožite treći red sa 2 i dodajte ga drugom redu. Ispada:

Zamenivši mesta drugog i trećeg reda, konačno dobijamo:

Vidimo da je matrica identiteta dobijena na lijevoj strani, dakle, inverzna matrica se dobija na desnoj strani. Na ovaj način:

Ispravnost proračuna možete provjeriti množenjem originalne matrice pronađenom inverznom matricom:

Rezultat bi trebao biti inverzna matrica.

Primjer 3 Za matricu

pronađite inverznu matricu.

Rješenje. Sastavljanje dualne matrice

i mi ćemo ga transformisati.

Pomnožimo prvi red sa 3, a drugi sa 2, i oduzmemo od drugog, a zatim prvi red pomnožimo sa 5, a treći sa 2 i oduzmemo od trećeg reda, onda dobijemo

Prvi red pomnožimo sa 2 i dodamo ga drugom, a zatim oduzmemo drugi od trećeg reda i dobijemo

Vidimo da su u trećem redu na lijevoj strani svi elementi ispali jednaki nuli. Dakle, matrica je degenerisana i nema inverznu matricu. Zaustavljamo dalje pronalaženje obrnute marije.

Metode za pronalaženje inverzne matrice, . Razmotrimo kvadratnu matricu

Označimo Δ = det A.

Kvadratna matrica A se naziva nedegenerisan, ili nespecijalan ako je njegova determinanta različita od nule, i degenerisati, ili poseban, akoΔ = 0.

Kvadratna matrica B postoji za kvadratnu matricu A istog reda ako je njihov proizvod A B = B A = E, gdje je E matrica identiteta istog reda kao i matrice A i B.

Teorema . Da bi matrica A imala inverznu matricu, potrebno je i dovoljno da njena determinanta bude različita od nule.

Inverzna matrica prema matrici A, označena sa A- 1 pa B = A - 1 a izračunava se po formuli

, (1)

gdje je A i j - algebarski komplementi elemenata a i j matrice A..

Izračunavanje A -1 po formuli (1) za matrice visokog reda je vrlo naporno, pa je u praksi zgodno pronaći A -1 metodom elementarnih transformacija (EP). Bilo koja nesingularna matrica A može se reducirati pomoću EP samo stupaca (ili samo redova) na matricu identiteta E. Ako se EP-ovi izvedeni na matrici A primjenjuju istim redoslijedom na matricu identiteta E, tada je rezultat inverzna matrica. Pogodno je izvesti EP na matricama A i E istovremeno, pišući obje matrice jednu do druge kroz liniju. Još jednom napominjemo da se prilikom traženja kanonskog oblika matrice, da bismo ga pronašli, mogu koristiti transformacije redova i stupaca. Ako trebate pronaći inverznu matricu, trebali biste koristiti samo redove ili samo stupce u procesu transformacije.

Primjer 2.10. Za matricu naći A -1 .

Rješenje.Prvo ćemo pronaći determinantu matrice A
tako da inverzna matrica postoji i možemo je pronaći po formuli: , gdje je A i j (i,j=1,2,3) - algebarski komplementi elemenata a i j originalne matrice.

Gdje .

Primjer 2.11. Koristeći metodu elementarnih transformacija, pronađite A -1 za matricu: A=.

Rješenje.Originalnoj matrici s desne strane dodjeljujemo matricu identiteta istog reda: . Uz pomoć elementarnih transformacija stupaca, lijevu “polovinu” reduciramo na identičnu, istovremeno obavljajući upravo takve transformacije na desnoj matrici.
Da biste to učinili, zamijenite prvi i drugi stupac: ~ . Dodamo prvu u treću kolonu, a prvu pomnoženu sa -2 u drugu: . Od prve kolone oduzimamo udvostručeni drugi, a od trećeg - drugi pomnožen sa 6; . Dodajmo treću kolonu prvom i drugom: . Pomnožite posljednju kolonu sa -1: . Kvadratna matrica dobijena desno od vertikalne trake je inverzna matrica datoj matrici A. Dakle,
.

U prvom dijelu razmatrana je metoda za pronalaženje inverzne matrice korištenjem algebarskih sabiranja. Ovdje opisujemo još jednu metodu za pronalaženje inverznih matrica: korištenjem Gaussove i Gauss-Jordan transformacije. Često se ova metoda pronalaženja inverzne matrice naziva metodom elementarnih transformacija.

Metoda elementarnih transformacija

Za primjenu ove metode, data matrica $A$ i matrica identiteta $E$ upisuju se u jednu matricu, tj. formiraju matricu oblika $(A|E)$ (ova matrica se naziva i proširena matrica). Nakon toga, uz pomoć elementarnih transformacija izvedenih sa redovima proširene matrice, matrica lijevo od linije postaje jedinica, a proširena matrica poprima oblik $\left(E| A^(-1) \right )$. Elementarne transformacije u ovoj situaciji uključuju sljedeće radnje:

Zamjena dvije linije.
Množenje svih elemenata niza nekim brojem koji nije nula.
Dodavanje elementima jednog reda odgovarajućih elemenata drugog reda, pomnoženih bilo kojim faktorom.

Ove elementarne transformacije mogu se primijeniti na različite načine. Obično se bira Gaussova metoda ili Gauss-Jordan metoda. Generalno, Gauss i Gauss-Jordan metode su namijenjene za rješavanje sistema linearnih algebarskih jednačina, a ne za pronalaženje inverznih matrica. Izraz "primjena Gaussove metode za pronalaženje inverza matrice" ovdje treba shvatiti kao "primjena operacija svojstvenih Gauss metodi na pronalaženje inverza matrice."

Numeracija primjera je nastavljena iz prvog dijela. U primjerima se razmatra i upotreba Gaussove metode za pronalaženje inverzne matrice, a u primjerima se analizira upotreba Gauss-Jordan metode. Treba napomenuti da ako se tokom rješavanja svi elementi nekog reda ili stupca matrice koji se nalaze prije linije postave na nulu, tada inverzna matrica ne postoji.

Primjer #5

Pronađite matricu $A^(-1)$ ako je $A=\left(\begin(array) (ccc) 7 & 4 & 6 \\ 2 & 5 & -4 \\ 1 & -1 & 3 \end( niz )\desno)$.

U ovom primjeru, inverzna matrica će se naći pomoću Gaussove metode. Proširena matrica, koja je općenito $(A|E)$, u ovom primjeru ima sljedeći oblik: $ \left(\begin(array) (ccc|ccc) 7 & 4 & 6 & 1 & 0 & 0 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 1 & -1 & 3 & 0 & 0 & 1 \end(array) \right)$.

Svrha: koristeći elementarne transformacije, dovedite proširenu matricu u oblik $\left(E|A^(-1) \right)$. Primjenjujemo iste operacije koje se koriste u rješavanju sistema linearnih jednačina Gaussovom metodom. Za primjenu Gaussove metode zgodno je kada je prvi element prvog reda proširene matrice jedan. Da bismo to postigli, mijenjamo prvi i treći red proširene matrice, koji postaje: $ \left(\begin(array) (ccc|ccc) 1 & -1 & 3 & 0 & 0 & 1 \\ 2 & 5 & - 4 & 0 & 1 & 0 \\ 7 & 4 & 6 & 1 & 0 & 0 \end(niz) \desno)$.

Hajdemo sada do rješenja. Gaussova metoda je podijeljena u dvije faze: naprijed i nazad (detaljan opis ove metode za rješavanje sistema jednačina dat je u primjerima odgovarajuće teme). Ista dva koraka će se primijeniti u procesu pronalaženja inverzne matrice.

udar naprijed

Prvi korak

Uz pomoć prvog reda resetujemo elemente prvog stupca koji se nalazi ispod prvog reda:

Dozvolite mi da malo prokomentarišem šta sam uradio. Oznaka $II-2\cdot I$ znači da su odgovarajući elementi prvog reda, prethodno pomnoženi sa dva, oduzeti od elemenata drugog reda. Ova akcija se može zasebno napisati na sljedeći način:

Akcija $III-7\cdot I$ se izvodi na potpuno isti način. Ako postoje poteškoće s izvođenjem ovih operacija, one se mogu izvesti odvojeno (slično $II-2\cdot I$ radnji prikazanoj gore), a rezultat se zatim unosi u proširenu matricu.

Drugi korak

Uz pomoć drugog reda, resetujemo element drugog stupca koji se nalazi ispod drugog reda:

Podijelite treći red sa 5:

Pravo trčanje je završeno. Svi elementi koji se nalaze ispod glavne dijagonale matrice do linije su vraćeni na nulu.

Obrnuto

Prvi korak

Uz pomoć trećeg reda, resetujemo elemente treće kolone koja se nalazi iznad trećeg reda:

Prije nego pređete na sljedeći korak, podijelite drugi red sa $7$:

Drugi korak

Uz pomoć drugog reda, resetujemo elemente drugog stupca koji se nalazi iznad drugog reda:

Transformacije su završene, inverzna matrica je pronađena Gaussovom metodom: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \ \ 7/5 & -11/5 & -27/5 \end(niz) \desno)$. Provjera, ako je potrebno, može se izvršiti na isti način kao u prethodnim primjerima. Ako preskočite sva objašnjenja, rješenje će poprimiti oblik:

Odgovori: $A^(-1)=\left(\begin(niz) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/ 5 & -27/5 \end(niz) \desno)$.

Primjer #6

Pronađite matricu $A^(-1)$ ako je $A=\left(\begin(array) (cccc) -5 & 4 & 1 & 0 \\ 2 & 3 & -2 & 1 \\ 0 & 7 & - 4 & -3 \\ 1 & 4 & 0 & 6 \end(niz) \desno)$.

Da bismo pronašli inverznu matricu u ovom primjeru, koristit ćemo iste operacije koje se koriste u rješavanju sistema linearnih jednadžbi pomoću Gaussove metode. Detaljna objašnjenja su data, ali se ovdje ograničavamo na kratke komentare. Napišimo proširenu matricu: $\left(\begin(array) (cccc|cccc) -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \end(niz) \desno)$. Zamijenite prvi i četvrti red ove matrice: $\left(\begin(array) (cccc|cccc) 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \end(niz) \desno)$.

udar naprijed

Forward run transformacije su završene. Svi elementi koji se nalaze ispod glavne dijagonale matrice lijevo od linije su postavljeni na nulu.

Obrnuto

Pronađen Gausov inverz, $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & - 117/ 16 & 49/16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \ end( niz)\desno)$. Provjera se, ako je potrebno, vrši na isti način kao u primjerima br. 2 i br. 3.

Odgovori: $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49 /16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \end(niz) \ desno)$.

Primjer #7

Pronađite matricu $A^(-1)$ ako je $A=\left(\begin(array) (ccc) 2 & 3 & 4 \\ 7 & 1 & 9 \\ -4 & 5 & -2 \end( niz )\desno)$.

Da bismo pronašli inverznu matricu, primjenjujemo operacije karakteristične za Gauss-Jordanovu metodu. Razlika od Gaussove metode, razmatrane u prethodnim primjerima i , je u tome što se rješenje izvodi u jednoj fazi. Da vas podsjetim da je Gaussova metoda podijeljena u 2 faze: pomak naprijed ("pravimo" nule ispod glavne dijagonale matrice do šipke) i obrnuti potez (resetujemo elemente iznad glavne dijagonale matrice do bara). Za izračunavanje inverzne matrice Gauss-Jordan metodom nisu potrebne dvije faze rješenja. Prvo, napravimo proširenu matricu: $(A|E)$:

$$ (A|E)=\left(\begin(array) (ccc|ccc) 2 & 3 & 4 & 1 & 0 & 0\\ 7 & 1 & 9 & 0 & 1 & 0\\ -4 & 5 & -2 &0 & 0 & 1 \end(niz) \desno) $$

Prvi korak

Postavite sve elemente prve kolone na nulu osim jednog. U prvoj koloni svi elementi su različiti od nule, tako da možemo odabrati bilo koji element. Uzmimo, na primjer, $(-4)$:

Odabrani element $(-4)$ nalazi se u trećem redu, tako da koristimo treći red za nuliranje odabranih elemenata prve kolone:

Napravimo prvi element trećeg reda jednakim jedan. Da bismo to učinili, dijelimo elemente trećeg reda proširene matrice sa $(-4)$:

Sada počnimo s nuliranjem odgovarajućih elemenata prve kolone:

U daljnjim koracima više neće biti moguće koristiti treći red, jer smo ga već primijenili u prvom koraku.

Drugi korak

Odaberimo neki element drugog stupca koji nije nula i postavimo sve ostale elemente druge kolone na nulu. Možemo izabrati bilo koji od dva elementa: $\frac(11)(2)$ ili $\frac(39)(4)$. Element $\left(-\frac(5)(4) \right)$ ne može se odabrati jer se nalazi u trećem redu, što smo koristili u prethodnom koraku. Odaberimo element $\frac(11)(2)$, koji se nalazi u prvom redu. Promijenimo $\frac(11)(2)$ u jedan u prvom redu:

Sada postavimo odgovarajuće elemente druge kolone na nulu:

U daljem rezonovanju, prvi red se ne može koristiti.

Treći korak

Potrebno je resetirati sve elemente treće kolone osim jednog. Moramo izabrati neki element koji nije nula iz treće kolone. Međutim, ne možemo uzeti $\frac(6)(11)$ ili $\frac(13)(11)$ jer se ti elementi nalaze u prvom i trećem redu koje smo koristili ranije. Izbor je mali: ostaje samo element $\frac(2)(11)$, koji se nalazi u drugom redu. Podijelite sve elemente drugog reda sa $\frac(2)(11)$:

Sada postavimo odgovarajuće elemente treće kolone na nulu:

Transformacije Gauss-Jordan metodom su završene. Ostaje samo da matrica do linije postane jedinica. Da biste to učinili, morate promijeniti redoslijed redova. Prvo, zamijenite prvi i treći red:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \\ 0 & 1 & 0 & 11/2 & -3 & -5/2 \end(niz) \desno) $$

Sada zamenimo drugi i treći red:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 1 & 0 & 11/2 & -3 & - 5/2 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \end(niz) \desno) $$

Dakle $A^(-1)=\left(\begin(array) (ccc) 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ - 39 /4 & 11/2 & 19/4 \end(niz) \desno)$. Naravno, rješenje se može izvesti na drugačiji način, odabirom elemenata na glavnoj dijagonali. Obično je to upravo ono što oni rade, jer u ovom slučaju, na kraju rješenja, linije neće morati biti zamijenjene. Prethodno rješenje sam dao samo s jednom svrhom: da pokažem da izbor reda u svakom koraku nije fundamentalan. Ako biramo dijagonalne elemente u svakom koraku, rješenje će biti sljedeće.

Neka je data kvadratna matrica. Potrebno je pronaći inverznu matricu.

Prvi način. U teoremi 4.1 o postojanju i jedinstvenosti inverzne matrice, naznačen je jedan od načina da se ona nađe.

1. Izračunajte determinantu date matrice. Ako, onda inverzna matrica ne postoji (matrica je degenerirana).

2. Sastaviti matricu od algebarskih komplemenata matričnih elemenata.

3. Transponirajući matricu, dobijamo pridruženu matricu .

4. Pronađite inverznu matricu (4.1) dijeljenjem svih elemenata pridružene matrice determinantom

Drugi način. Za pronalaženje inverzne matrice mogu se koristiti elementarne transformacije.

1. Sastavite blok matricu dodjeljivanjem datoj matrici matricu identiteta istog reda.

2. Uz pomoć elementarnih transformacija izvedenih na redovima matrice, dovedite njen lijevi blok u najjednostavniji oblik. U ovom slučaju, blok matrica se svodi na oblik, gdje je kvadratna matrica dobivena kao rezultat transformacija iz matrice identiteta.

3. Ako je , tada je blok jednak inverznoj matrici, tj. Ako, onda matrica nema inverznu.

Zaista, uz pomoć elementarnih transformacija redova matrice, njen lijevi blok se može svesti na pojednostavljeni oblik (vidi sliku 1.5). U ovom slučaju, blok matrica se transformira u oblik, gdje je elementarna matrica koja zadovoljava jednakost. Ako je matrica nesingularna, tada se, prema tački 2. napomene 3.3, njen pojednostavljeni oblik poklapa s matricom identiteta. Tada iz jednakosti slijedi da. Ako je matrica degenerirana, tada se njen pojednostavljeni oblik razlikuje od matrice identiteta, a matrica nema inverz.

11. Matrične jednadžbe i njihovo rješenje. Matrična notacija SLAE. Matrična metoda (metoda inverzne matrice) za rješavanje SLAE i uslovi njene primjenljivosti.

Matrične jednačine su jednačine oblika: A*X=C; X*A=C; A*X*B=C gdje su matrice A, B, C poznate, matrica X nije poznata, ako matrice A i B nisu degenerisane, tada će rješenja originalnih matrica biti zapisana u odgovarajućem obliku: X=A -1 *C; X=C*A -1; X \u003d A -1 * C * B -1 Matrični oblik pisanja sistema linearnih algebarskih jednačina. Nekoliko matrica može biti povezano sa svakim SLAE; štaviše, sam SLAE se može napisati kao matrična jednačina. Za SLAE (1), razmotrite sljedeće matrice:

Matrica A se zove sistemska matrica. Elementi ove matrice su koeficijenti date SLAE.

Matrica A˜ se zove prošireni matrični sistem. Dobiva se dodavanjem u sistemsku matricu kolone koja sadrži slobodne članove b1,b2,...,bm. Obično je ova kolona odvojena okomitom linijom, radi jasnoće.

Poziva se matrica stupca B matrica slobodnih članova, a matrica stupaca X je matrica nepoznatih.

Koristeći prethodno uvedenu notaciju, SLAE (1) se može napisati u obliku matrične jednačine: A⋅X=B.

Bilješka

Matrice povezane sa sistemom mogu se pisati na različite načine: sve zavisi od redosleda varijabli i jednačina razmatrane SLAE. Ali u svakom slučaju, redoslijed nepoznanica u svakoj jednadžbi date SLAE mora biti isti.

Matrična metoda je pogodna za rješavanje SLAE u kojima se broj jednačina poklapa sa brojem nepoznatih varijabli i determinanta glavne matrice sistema nije nula. Ako sistem sadrži više od tri jednačine, tada pronalaženje inverzne matrice zahtijeva značajan računski napor, stoga je u ovom slučaju preporučljivo koristiti za rješavanje Gaussova metoda.

12. Homogene SLAE, uslovi postojanja njihovih nenultih rješenja. Svojstva parcijalnih rješenja homogenih SLAE.

Linearna jednačina se naziva homogenom ako je njen slobodni član jednak nuli, a inače nehomogena. Sistem koji se sastoji od homogenih jednačina naziva se homogenim i ima opšti oblik:

13 .Koncept linearne nezavisnosti i zavisnosti parcijalnih rješenja homogene SLAE. Fundamentalni sistem odlučivanja (FSR) i njegov nalaz. Reprezentacija općeg rješenja homogene SLAE u terminima FSR-a.

Funkcijski sistem y 1 (x ), y 2 (x ), …, y n (x ) se zove linearno zavisna na intervalu ( a , b ) ako postoji skup konstantnih koeficijenata koji nisu jednaki nuli istovremeno, tako da je linearna kombinacija ovih funkcija identično jednaka nuli na ( a , b ): za . Ako je jednakost za moguća samo za , Sistem funkcija y 1 (x ), y 2 (x ), …, y n (x ) se zove linearno nezavisna na intervalu ( a , b ). Drugim riječima, funkcije y 1 (x ), y 2 (x ), …, y n (x ) linearno zavisna na intervalu ( a , b ) ako postoji nula na ( a , b ) njihova netrivijalna linearna kombinacija. Funkcije y 1 (x ),y 2 (x ), …, y n (x ) linearno nezavisna na intervalu ( a , b ) ako je samo njihova trivijalna linearna kombinacija identično jednaka nuli na ( a , b ).

Sistem fundamentalnih odluka (FSR) homogena SLAE je osnova ovog sistema kolona.

Broj elemenata u FSR-u jednak je broju nepoznatih u sistemu minus rang sistemske matrice. Svako rješenje originalnog sistema je linearna kombinacija rješenja FSR-a.

Teorema

Opće rješenje nehomogene SLAE jednako je zbiru posebnog rješenja nehomogene SLAE i opšteg rješenja odgovarajuće homogene SLAE.

1 . Ako su kolone rješenja homogenog sistema jednačina, onda je svaka njihova linearna kombinacija također rješenje homogenog sistema.

Zaista, iz jednakosti slijedi da

one. linearna kombinacija rješenja je rješenje za homogeni sistem.

2. Ako je rang matrice homogenog sistema , tada sistem ima linearno nezavisna rješenja.

Zaista, prema formulama (5.13) općeg rješenja homogenog sistema, možemo pronaći posebna rješenja dodjeljivanjem sljedećeg slobodnim varijablama zadani setovi vrijednosti (svaki put pod pretpostavkom da je jedna od slobodnih varijabli jednaka jedan, a ostale jednake nuli):

koje su linearno nezavisne. Zaista, ako se matrica formira iz ovih stupaca, tada njeni posljednji redovi čine matricu identiteta. Dakle, minor koji se nalazi u zadnjim redovima nije jednak nuli (jednak je jedan), tj. je osnovno. Stoga će rang matrice biti jednak. Dakle, svi stupci ove matrice su linearno nezavisni (vidjeti teoremu 3.4).

Bilo koja zbirka linearno nezavisnih rješenja homogenog sistema naziva se osnovni sistem (skup) rješenja .

14 Minor th reda, osnovni mol, matrični rang. Proračun ranga matrice.

Red k minor matrice A je determinanta neke njene kvadratne podmatrice reda k.

U m x n matrici A, minor reda r naziva se osnovnim ako je različit od nule, a svi minori većeg reda, ako postoje, jednaki su nuli.

Stupci i redovi matrice A, na čijem se presjeku nalazi bazni minor, nazivaju se osnovni stupci i redovi matrice A.

Teorema 1. (O rangu matrice). Za bilo koju matricu, manji rang je jednak rangu reda i jednak rangu stupca.

Teorema 2. (O osnovnom molu). Svaki stupac matrice se razlaže u linearnu kombinaciju svojih osnovnih stupaca.

Rang matrice (ili manji rang) je red baznog minora ili, drugim riječima, najveći red za koji postoje minori različiti od nule. Rang nulte matrice se, po definiciji, smatra 0.

Uočavamo dva očigledna svojstva minornog ranga.

1) Rang matrice se ne mijenja prilikom transponiranja, jer kada se matrica transponira, sve njene podmatrice se transponiraju i minori se ne mijenjaju.

2) Ako je A' podmatrica matrice A, onda rang A' ne prelazi rang A, pošto je minor koji nije nula uključen u A' takođe uključen u A.

15. Koncept -dimenzionalnog aritmetičkog vektora. Vektorska jednakost. Akcije na vektore (sabiranje, oduzimanje, množenje brojem, množenje matricom). Linearna kombinacija vektora.

Naručena kolekcija n realni ili kompleksni brojevi se nazivaju n-dimenzionalni vektor. Zovu se brojevi vektorske koordinate.

Dva (ne-nula) vektora a i b jednaki su ako su jednakosmjerni i imaju isti modul. Svi nulti vektori se smatraju jednakim. U svim ostalim slučajevima vektori nisu jednaki.

Sabiranje vektora. Postoje dva načina za dodavanje vektora.1. pravilo paralelograma. Da bismo dodali vektore i, stavljamo početak oba u istu tačku. Dopunjavamo paralelogram i crtamo dijagonalu paralelograma iz iste tačke. Ovo će biti zbir vektora.

2. Drugi način za dodavanje vektora je pravilo trougla. Uzmimo iste vektore i . Dodamo početak drugog na kraj prvog vektora. Sada spojimo početak prvog i kraj drugog. Ovo je zbroj vektora i . Po istom pravilu možete dodati nekoliko vektora. Pričvršćujemo ih jedan po jedan, a zatim povezujemo početak prvog s krajem posljednjeg.

Oduzimanje vektora. Vektor je usmjeren suprotno od vektora. Dužine vektora su jednake. Sada je jasno šta je oduzimanje vektora. Razlika vektora i je zbir vektora i vektora .

Pomnožite vektor brojem

Množenjem vektora brojem k dobije se vektor čija je dužina k puta različita od dužine. Kosmjeran je s vektorom ako je k veći od nule, a usmjeren suprotno ako je k manji od nule.

Skalarni proizvod vektora je proizvod dužina vektora i kosinusa ugla između njih. Ako su vektori okomiti, njihov dot proizvod je nula. I ovako se skalarni proizvod izražava u smislu koordinata vektora i .

Linearna kombinacija vektora

Linearna kombinacija vektora vektor poziva

gdje - koeficijenti linearne kombinacije. Ako a kombinacija se naziva trivijalna ako je netrivijalna.

16 .Skalarni proizvod aritmetičkih vektora. Dužina vektora i ugao između vektora. Koncept ortogonalnosti vektora.

Skalarni proizvod vektora a i b je broj

Skalarni proizvod se koristi za izračunavanje: 1) pronalaženja ugla između njih; 2) pronalaženja projekcije vektora; 3) izračunavanja dužine vektora; 4) uslova okomitosti vektora.

Dužina segmenta AB je rastojanje između tačaka A i B. Ugao između vektora A i B naziva se ugao α = (a, c), 0≤ α ≤P. Pri čemu je potrebno rotirati 1 vektor tako da se njegov smjer poklapa s drugim vektorom. Pod uslovom da im se počeci poklope.

Orth a je vektor a koji ima jediničnu dužinu i smjer a.

17. Sistem vektora i njegova linearna kombinacija. Koncept linearne zavisnosti i nezavisnosti sistema vektora. Teorema o potrebnim i dovoljnim uslovima za linearnu zavisnost sistema vektora.

Sistem vektora a1,a2,...,an naziva se linearno zavisnim ako postoje brojevi λ1,λ2,...,λn takvi da je barem jedan od njih različit od nule i λ1a1+λ2a2+...+λnan=0 . Inače, sistem se naziva linearno nezavisnim.

Dva vektora a1 i a2 nazivaju se kolinearni ako su im smjerovi isti ili suprotni.

Tri vektora a1,a2 i a3 nazivaju se komplanarnim ako su paralelni nekoj ravni.

Geometrijski kriterijumi za linearnu zavisnost:

a) sistem (a1,a2) je linearno zavisan ako i samo ako su vektori a1 i a2 kolinearni.

b) sistem (a1,a2,a3) je linearno zavisan ako i samo ako su vektori a1,a2 i a3 koplanarni.

teorema. (Neophodan i dovoljan uslov za linearnu zavisnost sistemima vektori.)

Vektorski sistem vektor prostor je linearno zavisno ako i samo ako je jedan od vektora sistema linearno izražen u terminima ostalih vektor ovaj sistem.

Posljedica.1. Sistem vektora u vektorskom prostoru je linearno nezavisan ako i samo ako nijedan od vektora sistema nije linearno izražen u terminima drugih vektora ovog sistema.2. Vektorski sistem koji sadrži nulti vektor ili dva jednaka vektora je linearno zavisan.

Za bilo koju nesingularnu matricu A postoji jedinstvena matrica A -1 takva da

A*A -1 =A -1 *A = E,

gdje je E matrica identiteta istih redova kao i A. Matrica A -1 se naziva inverzna matrici A.

Ako je neko zaboravio, u matrici identiteta, osim dijagonale popunjene jedinicama, sve ostale pozicije su popunjene nulama, primjer matrice identiteta:

Pronalaženje inverzne matrice metodom spojene matrice

Inverzna matrica je definirana formulom:

gdje je A ij - elementi a ij .

One. Da biste izračunali inverznu vrijednost matrice, morate izračunati determinantu ove matrice. Zatim pronađite algebarske dodatke za sve njegove elemente i napravite novu matricu od njih. Zatim morate prenijeti ovu matricu. I podijelite svaki element nove matrice determinantom originalne matrice.

Pogledajmo nekoliko primjera.

Naći A -1 za matricu

Rješenje: Naći A -1 metodom adjuktirane matrice. Imamo det A = 2. Nađimo algebarske komplemente elemenata matrice A. U ovom slučaju, algebarski komplementi elemenata matrice će biti odgovarajući elementi same matrice, uzeti sa predznakom u skladu sa formula

Imamo A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Formiramo pridruženu matricu

Prevozimo matricu A*:

Inverznu matricu nalazimo po formuli:

Dobijamo:

Koristite metodu spojene matrice da pronađete A -1 if

Rješenje Prije svega izračunavamo datu matricu da bismo bili sigurni da inverzna matrica postoji. Imamo

Ovdje smo elementima drugog reda dodali elemente trećeg reda, prethodno pomnožene sa (-1), a zatim proširili determinantu za drugi red. Pošto je definicija ove matrice drugačija od nule, onda postoji matrica inverzna njoj. Da bismo konstruisali pridruženu matricu, nalazimo algebarske komplemente elemenata ove matrice. Imamo

Prema formuli

transportiramo matricu A*:

Zatim prema formuli

Pronalaženje inverzne matrice metodom elementarnih transformacija

Pored metode pronalaženja inverzne matrice, koja slijedi iz formule (metoda pridružene matrice), postoji i metoda za pronalaženje inverzne matrice koja se zove metoda elementarnih transformacija.

Elementarne matrične transformacije

Sljedeće transformacije se nazivaju transformacije elementarnih matrica:

1) permutacija redova (kolona);

2) množenje reda (kolone) brojem koji nije nula;

3) dodavanjem elementima reda (kolone) odgovarajućih elemenata drugog reda (kolone), prethodno pomnoženih određenim brojem.

Da bismo pronašli matricu A -1, konstruiramo pravougaonu matricu B = (A | E) redova (n; 2n), dodjeljujući matrici A na desnoj strani matricu identiteta E kroz razdjelničku liniju:

Razmotrimo primjer.

Koristeći metodu elementarnih transformacija, pronaći A -1 if

Rješenje Formiramo matricu B:

Označimo redove matrice B kroz α 1 , α 2 , α 3 . Izvršimo sljedeće transformacije na redovima matrice B.