Podjela koordinatne ravni na četvrtine. Koordinatna ravan: šta je to? Kako označiti tačke i graditi oblike na koordinatnoj ravni? Primjeri koordinatnih ravnina
Ovo matematički kalkulator online pomoći riješiti jednadžbu ili nejednačinu s modulima. Program za rješavanje jednačina i nejednačina sa modulima ne samo da daje odgovor na problem, već i vodi detaljno rješenje sa objašnjenjima, tj. prikazuje proces dobijanja rezultata.
Ovaj program može biti koristan za srednjoškolce opšteobrazovne škole u pripremi za kontrolni rad i ispite, prilikom provjere znanja prije ispita, roditelji kontroliraju rješavanje mnogih zadataka iz matematike i algebre. Ili vam je možda preskupo unajmiti nastavnika ili kupiti nove udžbenike? Ili samo želite da to završite što je prije moguće? zadaća matematika ili algebra? U tom slučaju možete koristiti i naše programe sa detaljnim rješenjem.
Dakle, možete izvršiti svoje vlastitu obuku i/ili obučavanje njihovih mlađa braća ili sestre, dok se nivo obrazovanja iz oblasti zadataka koji se rješavaju povećava.
|x| ili abs(x) - modul xUnesite jednadžbu ili nejednakost s modulima
Utvrđeno je da neke skripte potrebne za rješavanje ovog zadatka nisu učitane i program možda neće raditi.
Možda imate omogućen AdBlock.
U tom slučaju, onemogućite ga i osvježite stranicu.
JavaScript mora biti omogućen da bi se rješenje pojavilo.
Evo instrukcija kako da omogućite JavaScript u vašem pretraživaču.
Jer Ima puno ljudi koji žele riješiti problem, vaš zahtjev je u redu.
Nakon nekoliko sekundi, rješenje će se pojaviti ispod.
Pričekajte sec...
Ako ti uočio grešku u rješenju, onda o tome možete pisati u Obrascu za povratne informacije.
Nemoj zaboraviti naznačiti koji zadatak ti odluči šta unesite u polja.
Naše igre, zagonetke, emulatori:
Malo teorije.
Jednačine i nejednačine sa modulima
U osnovnom školskom kursu algebre možete upoznati najjednostavnije jednačine i nejednačine sa modulima. Da biste ih riješili, možete primijeniti geometrijsku metodu zasnovanu na činjenici da je \(|x-a| \) udaljenost na brojevnoj pravoj između tačaka x i a: \(|x-a| = \rho (x;\; a) ) \). Na primjer, da biste riješili jednačinu \(|x-3|=2 \), morate pronaći tačke na brojevnoj pravoj koje su udaljene 2 od tačke 3. Postoje dvije takve tačke: \(x_1=1 \) i \(x_2=5 \) .
![]()
Rješavanje nejednakosti \(|2x+7| ![]()
Ali glavni način rješavanja jednadžbi i nejednakosti s modulima povezan je s takozvanim "proširenjem modula po definiciji":
ako je \(a \geq 0 \), onda \(|a|=a \);
if \(a Po pravilu, jednačina (nejednakost) sa modulima se svodi na skup jednačina (nejednačina) koje ne sadrže predznak modula.
Pored gornje definicije, koriste se sljedeće tvrdnje:
1) Ako je \(c > 0 \), onda je jednadžba \(|f(x)|=c \) ekvivalentna skupu jednačina: \(\left[\begin(array)(l) f(x) )=c \\ f(x)=-c \end(niz)\desno.\)
2) Ako je \(c > 0 \), onda je nejednakost \(|f(x)| 3) Ako je \(c \geq 0 \), onda je nejednakost \(|f(x)| > c \) ekvivalentno skupu nejednakosti: \(\left[\begin(array)(l) f(x) c \end(array)\right. \)
4) Ako obje strane nejednakosti \(f(x) PRIMJER 1. Riješite jednačinu \(x^2 +2|x-1| -6 = 0 \).
Ako je \(x-1 \geq 0 \), onda \(|x-1| = x-1 \) i zadata jednačina poprima oblik
\(x^2 +2(x-1) -6 = 0 \Strelica desno x^2 +2x -8 = 0 \).
Ako je \(x-1 \(x^2 -2(x-1) -6 = 0 \Strelica desno x^2 -2x -4 = 0 \).
Dakle, datu jednačinu treba posmatrati posebno u svakom od dva navedena slučaja.
1) Neka je \(x-1 \geq 0 \), tj. \(x \geq 1 \). Iz jednačine \(x^2 +2x -8 = 0 \) nalazimo \(x_1=2, \; x_2=-4\). Uslov \(x \geq 1 \) zadovoljava samo vrijednost \(x_1=2\).
2) Neka \(x-1 odgovor: \(2; \;\; 1-\sqrt(5) \)
PRIMJER 2. Riješite jednačinu \(|x^2-6x+7| = \frac(5x-9)(3) \).
Prvi način(proširenje modula po definiciji).
Argumentirajući kao u primjeru 1, zaključujemo da se data jednačina mora razmatrati odvojeno pod dva uslova: \(x^2-6x+7 \geq 0 \) ili \(x^2-6x+7
1) Ako je \(x^2-6x+7 \geq 0 \), onda \(|x^2-6x+7| = x^2-6x+7 \) i data jednadžba postaje \(x^2 -6x+7 = \frac(5x-9)(3) \Strelica desno 3x^2-23x+30=0 \). Rešavanje kvadratna jednačina, dobijamo: \(x_1=6, \; x_2=\frac(5)(3) \).
Hajde da saznamo da li vrednost \(x_1=6 \) zadovoljava uslov \(x^2-6x+7 \geq 0 \). Da biste to učinili, zamijenite navedenu vrijednost u kvadratna nejednakost. Dobijamo: \(6^2-6 \cdot 6+7 \geq 0 \), tj. \(7 \geq 0 \) je ispravna nejednakost. Dakle, \(x_1=6 \) je korijen date jednadžbe.
Hajde da saznamo da li vrijednost \(x_2=\frac(5)(3) \) zadovoljava uvjet \(x^2-6x+7 \geq 0 \). Da bismo to učinili, zamjenjujemo naznačenu vrijednost u kvadratnu nejednakost. Dobijamo: \(\left(\frac(5)(3) \right)^2 -\frac(5)(3) \cdot 6 + 7 \geq 0 \), tj. \(\frac(25)(9) -3 \geq 0 \) je nevažeća nejednakost. Dakle, \(x_2=\frac(5)(3) \) nije korijen date jednadžbe.
2) Ako \(x^2-6x+7 vrijednost \(x_3=3\) zadovoljava uvjet \(x^2-6x+7), vrijednost \(x_4=\frac(4)(3) \) ispunjava ne zadovoljava uslov \ (x^2-6x+7 Dakle, data jednadžba ima dva korijena: \(x=6, \; x=3 \).
Drugi način. Zadana jednačina \(|f(x)| = h(x) \), tada za \(h(x) \(\left[\begin(array)(l) x^2-6x+7 = \frac (5x-9)(3) \\ x^2-6x+7 = -\frac(5x-9)(3) \end(niz)\desno. \)
Obje ove jednadžbe su gore riješene (prvom metodom rješavanja date jednačine), njihovi korijeni su sljedeći: \(6,\; \frac(5)(3),\; 3,\; \frac(4) )(3) \). Uslov \(\frac(5x-9)(3) \geq 0 \) ovih četiri vrijednosti zadovoljavaju samo dva: 6 i 3. Dakle, data jednadžba ima dva korijena: \(x=6, \; x=3 \).
Treći način(grafički).
1) Nacrtajmo funkciju \(y = |x^2-6x+7| \). Prvo konstruišemo parabolu \(y = x^2-6x+7\). Imamo \(x^2-6x+7 = (x-3)^2-2 \). Grafikon funkcije \(y = (x-3)^2-2 \) može se dobiti iz grafa funkcije \(y = x^2 \) pomicanjem za 3 jedinice skale udesno (na x-osa) i 2 jedinice skale prema dolje (duž y-ose). Prava linija x=3 je osa parabole koja nas zanima. Kao kontrolne tačke za preciznije crtanje, zgodno je uzeti tačku (3; -2) - vrh parabole, tačku (0; 7) i tačku (6; 7) simetričnu u odnosu na osu parabole.
Da biste sada izgradili graf funkcije \(y = |x^2-6x+7| \), morate ostaviti nepromijenjene one dijelove konstruirane parabole koji ne leže ispod x-ose i ogledati dio parabole parabola koja leži ispod x-ose oko x-ose.
2) Napravimo graf linearna funkcija\(y = \frac(5x-9)(3) \). Pogodno je uzeti tačke (0; –3) i (3; 2) kao kontrolne tačke.

Bitno je da se tačka x = 1,8 presjeka prave linije s osom apscise nalazi desno od lijeve točke presjeka parabole s osom apscise - to je tačka \(x=3-\ sqrt(2) \) (pošto \(3-\sqrt(2 ) 3) Sudeći po crtežu, grafovi se sijeku u dvije tačke - A (3; 2) i B (6; 7). Zamjena apscisa ovih tačke x = 3 i x = 6 u datoj jednadžbi, osiguravamo da obje druge vrijednosti daju ispravnu numeričku jednakost. Dakle, naša hipoteza je potvrđena - jednadžba ima dva korijena: x = 3 i x = 6 Odgovor: 3; 6.
Komentar. Grafički način uz svu svoju eleganciju, nije baš pouzdan. U razmatranom primjeru, funkcioniralo je samo zato što su korijeni jednadžbe cijeli brojevi.
PRIMJER 3. Riješite jednačinu \(|2x-4|+|x+3| = 8 \)
Prvi način
Izraz 2x–4 postaje 0 u tački x = 2, a izraz x + 3 u tački x = –3. Ove dvije tačke dijele brojevnu pravu na tri intervala: \(x
![]()
Razmotrite prvi interval: \((-\infty; \; -3) \).
Ako je x Razmotrite drugi interval: \([-3; \; 2) \).
Ako \(-3 \leq x Uzmite u obzir treći interval: \(
Drugi važna činjenica: modul nikada nije negativan. Koji god broj da uzmemo - čak pozitivan, čak i negativan - njegov modul se uvijek pokaže pozitivnim (ili u ekstremnim slučajevima nula). Zbog toga se modul često naziva apsolutna vrijednost broja.
Osim toga, ako kombiniramo definiciju modula za pozitivan i negativan broj, onda ćemo dobiti globalnu definiciju modula za sve brojeve. Naime: modul broja jednak je samom ovom broju, ako je broj pozitivan (ili nula), ili jednak suprotan broj ako je broj negativan. Ovo možete napisati kao formulu:
Postoji i modul od nule, ali je uvijek jednak nuli. Osim toga, nula jednina, koji nema suprotnosti.
Dakle, ako uzmemo u obzir funkciju $y=\left| x \right|$ i pokušajte da nacrtate njegov graf, dobićete takvu "guu":
Grafikon modula i primjer rješenja jednadžbe
Sa ove slike možete odmah vidjeti da je $\left| -m \desno|=\lijevo| m \right|$, a dijagram modula nikada ne pada ispod x-ose. Ali to nije sve: crvena linija označava ravnu liniju $y=a$, koja nam, sa pozitivnim $a$, daje dva korijena odjednom: $((x)_(1))$ i $((x) _(2)) $, ali o tome ćemo kasnije. :)
Pored čisto algebarske definicije, postoji i geometrijska. Recimo da postoje dvije tačke na brojevnoj pravoj: $((x)_(1))$ i $((x)_(2))$. U ovom slučaju, izraz $\left| ((x)_(1))-((x)_(2)) \right|$ je samo udaljenost između navedenih tačaka. Ili, ako želite, dužina segmenta koji povezuje ove tačke:
 Modul je rastojanje između tačaka na brojevnoj pravoj
Modul je rastojanje između tačaka na brojevnoj pravoj Iz ove definicije također slijedi da je modul uvijek nenegativan. Ali dosta definicija i teorije - pređimo na stvarne jednadžbe. :)
Osnovna formula
U redu, shvatili smo definiciju. Ali nije bilo lakše. Kako riješiti jednadžbe koje sadrže upravo ovaj modul?
Mirno, samo mirno. Počnimo od najjednostavnijih stvari. Razmotrite nešto poput ovoga:
\[\lijevo| x\desno|=3\]
Dakle, modul$x$ je 3. Čemu može biti jednako $x$? Pa, sudeći po definiciji, $x=3$ će nam sasvim odgovarati. stvarno:
\[\lijevo| 3\desno|=3\]
Ima li drugih brojeva? Čini se da Cap nagoveštava da postoji. Na primjer, $x=-3$ — $\left| -3 \right|=3$, tj. tražena jednakost je zadovoljena.
Pa možda ako tražimo, razmislimo, nađemo još brojeva? I evo pauze: više brojeva br. Jednačina $\left| x \right|=3$ ima samo dva korijena: $x=3$ i $x=-3$.
Sada da malo zakomplikujemo zadatak. Neka umjesto varijable $x$ funkcija $f\left(x \right)$ visi ispod predznaka modula, a na desnoj strani, umjesto trojke, stavimo proizvoljan broj $a$. Dobijamo jednačinu:
\[\lijevo| f\lijevo(x \desno) \desno|=a\]
Pa, kako se odlučuješ? Da vas podsjetim: $f\left(x \right)$ je proizvoljna funkcija, $a$ je bilo koji broj. One. bilo koji uopšte! Na primjer:
\[\lijevo| 2x+1 \desno|=5\]
\[\lijevo| 10x-5 \desno|=-65\]
Pogledajmo drugu jednačinu. Za njega možete odmah reći: on nema korijene. Zašto? Tako je: jer zahtijeva da modul bude jednak negativan broj, što se nikada ne dešava, pošto već znamo da je modul uvek pozitivan broj, ili u ekstremnim slučajevima nula.
Ali s prvom jednačinom sve je zabavnije. Postoje dvije opcije: ili postoji pozitivan izraz ispod znaka modula, a zatim $\left| 2x+1 \right|=2x+1$, ili je ovaj izraz i dalje negativan, u kom slučaju $\left| 2x+1 \desno|=-\levo(2x+1 \desno)=-2x-1$. U prvom slučaju, naša jednačina će biti prepisana kao:
\[\lijevo| 2x+1 \desno|=5\Strelica desno 2x+1=5\]
I odjednom se ispostavi da je izraz podmodula $2x+1$ zaista pozitivan - jednak je broju 5. To jest, možemo bezbedno da rešimo ovu jednačinu - rezultujući koren će biti deo odgovora:
Oni koji su posebno nepovjerljivi mogu pokušati zamijeniti pronađeni korijen u originalnu jednačinu i uvjeriti se da će modul zaista biti pozitivan broj.
Pogledajmo sada slučaj negativnog izraza podmodula:
\[\left\( \begin(align)& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\\end(align) \right.\Rightarrow -2x-1=5 \Strelica desno 2x+1=-5\]
Ups! Opet, sve je jasno: pretpostavili smo da je $2x+1 \lt 0$, i kao rezultat dobili smo da je $2x+1=-5$ - zaista, ovaj izraz je manji od nule. Rješavamo rezultirajuću jednadžbu, a već sigurno znamo da će nam pronađeni korijen odgovarati:
Ukupno smo ponovo dobili dva odgovora: $x=2$ i $x=3$. Da, ispostavilo se da je količina proračuna malo veća nego u vrlo jednostavnoj jednačini $\left| x \right|=3$, ali u osnovi se ništa nije promijenilo. Pa možda postoji neka vrsta univerzalnog algoritma?
Da, takav algoritam postoji. A sada ćemo to analizirati.
Uklanjanje znaka modula
Neka nam je data jednadžba $\left| f\left(x \right) \right|=a$, i $a\ge 0$ (inače, kao što već znamo, nema korijena). Tada se možete riješiti modulo znaka prema sljedećem pravilu:
\[\lijevo| f\left(x \right) \right|=a\Strelica desno f\left(x \right)=\pm a\]
Tako se naša jednadžba s modulom dijeli na dva, ali bez modula. To je cela tehnologija! Pokušajmo riješiti nekoliko jednačina. Počnimo s ovim
\[\lijevo| 5x+4 \desno|=10\Strelica desno 5x+4=\pm 10\]
Posebno ćemo razmotriti kada je desetica sa plusom na desnoj strani, a posebno kada je sa minusom. Imamo:
\[\begin(align)& 5x+4=10\Strelica desno 5x=6\Strelica desno x=\frac(6)(5)=1,2; \\& 5x+4=-10\Strelica desno 5x=-14\Strelica desno x=-\frac(14)(5)=-2.8. \\\end(poravnati)\]
To je sve! Imamo dva korijena: $x=1.2$ i $x=-2.8$. Cijelo rješenje je trajalo doslovno dva reda.
Ok, nema sumnje, hajde da pogledamo nešto malo ozbiljnije:
\[\lijevo| 7-5x \desno|=13\]
Ponovo otvorite modul sa plusom i minusom:
\[\begin(align)& 7-5x=13\Rightarrow -5x=6\Rightarrow x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Strelica desno -5x=-20\Strelica desno x=4. \\\end(poravnati)\]
Opet par redova - i odgovor je spreman! Kao što sam rekao, u modulima nema ništa komplikovano. Treba samo zapamtiti nekoliko pravila. Stoga idemo dalje i nastavljamo sa zaista težim zadacima.
Varijabilna desna kutija
Sada razmotrite ovu jednačinu:
\[\lijevo| 3x-2 \desno|=2x\]
Ova jednačina se suštinski razlikuje od svih prethodnih. Kako? A činjenica da je izraz $2x$ desno od znaka jednakosti - i ne možemo unaprijed znati da li je pozitivan ili negativan.
Kako biti u tom slučaju? Prvo, to moramo shvatiti jednom za svagda ako je desna strana jednadžbe negativna, tada jednačina neće imati korijena- već znamo da modul ne može biti jednak negativnom broju.
I drugo, ako je desni dio još uvijek pozitivan (ili jednak nuli), onda možete nastaviti na potpuno isti način kao i prije: samo otvorite modul odvojeno sa znakom plus i odvojeno sa znakom minus.
Dakle, formulišemo pravilo za proizvoljne funkcije$f\left(x \right)$ i $g\left(x \right)$ :
\[\lijevo| f\left(x \right) \right|=g\left(x \right)\Rightarrow \left\( \begin(align)& f\left(x \right)=\pm g\left(x \right) ), \\& g\left(x \right)\ge 0. \\\end(align) \right.\]
S obzirom na našu jednačinu, dobijamo:
\[\lijevo| 3x-2 \right|=2x\Rightarrow \left\( \begin(align)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(align) \right.\]
Pa, možemo nekako podnijeti zahtjev za $2x\ge 0$. Na kraju, možemo glupo zamijeniti korijene koje dobijemo iz prve jednadžbe i provjeriti da li nejednakost vrijedi ili ne.
Dakle, riješimo samu jednačinu:
\[\begin(align)& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\Strelica desno 3x=0\Strelica desno x=0. \\\end(poravnati)\]
Pa, koji od ova dva korijena zadovoljava zahtjev $2x\ge 0$? Da, oboje! Dakle, odgovor će biti dva broja: $x=(4)/(3)\;$ i $x=0$. To je rešenje. :)
Sumnjam da je jednom od učenika već počelo da se dosađuje? Pa, razmotrimo još složeniju jednačinu:
\[\lijevo| ((x)^(3))-3((x)^(2))+x \desno|=x-((x)^(3))\]
Iako izgleda zločesto, u stvari je sve ista jednadžba oblika "modul jednak funkcija":
\[\lijevo| f\lijevo(x \desno) \desno|=g\lijevo(x \desno)\]
I rješava se na isti način:
\[\lijevo| ((x)^(3))-3((x)^(2))+x \desno|=x-((x)^(3))\Strelica desno \levo\( \begin(align)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \desno), \\& x-((x )^(3))\ge 0. \\\end(poravnaj) \desno.\]
Kasnije ćemo se pozabaviti nejednakošću - ona je nekako previše opaka (zapravo jednostavno, ali je nećemo riješiti). Za sada, pogledajmo rezultirajuće jednačine. Razmotrimo prvi slučaj - to je kada se modul proširi znakom plus:
\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]
E, tu je neozbiljno da treba sakupiti sve što je lijevo, donijeti slične i vidjeti šta će biti. I evo šta se dešava:
\[\begin(align)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\end(poravnati)\]
Stavljajući zajednički faktor $((x)^(2))$ iz zagrade, dobijamo vrlo jednostavnu jednačinu:
\[((x)^(2))\left(2x-3 \right)=0\Strelica desno \levo[ \begin(align)& ((x)^(2))=0 \\& 2x-3 =0 \\\kraj (poravnaj) \desno.\]
\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1.5.\]
Ovdje smo koristili važna imovina proizvod, radi čega smo rastavili na faktore originalni polinom: proizvod je jednak nuli kada je barem jedan od faktora jednak nuli.
Sada ćemo se na isti način pozabaviti drugom jednadžbom, koja se dobija proširenjem modula sa predznakom minus:
\[\begin(align)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \desno); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\lijevo(-3x+2 \desno)=0. \\\end(poravnati)\]
Opet, ista stvar: proizvod je nula kada je barem jedan od faktora nula. Imamo:
\[\left[ \begin(align)& x=0 \\& -3x+2=0 \\\end(align) \right.\]
Pa, imamo tri korijena: $x=0$, $x=1.5$ i $x=(2)/(3)\;$. Pa, šta će ući u konačni odgovor iz ovog skupa? Da biste to učinili, zapamtite da imamo dodatno ograničenje nejednakosti:
Kako uzeti u obzir ovaj zahtjev? Zamijenimo pronađene korijene i provjerimo vrijedi li nejednakost za ove $x$ ili ne. Imamo:
\[\begin(align)& x=0\Strelica desno x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Strelica desno x-((x)^(3))=1,5-((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Rightarrow x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\end(poravnati)\]
Dakle, korijen $x=1.5$ nam ne odgovara. I samo će dva korijena ići kao odgovor:
\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]
Kao što vidite, čak ni u ovom slučaju nije bilo ništa teško - jednadžbe s modulima se uvijek rješavaju prema algoritmu. Samo trebate dobro razumjeti polinome i nejednakosti. Stoga prelazimo na složenije zadatke - već će postojati ne jedan, već dva modula.
Jednačine sa dva modula
Do sada smo proučavali samo najviše jednostavne jednačine- bio je jedan modul i nešto drugo. Ovo “nešto drugo” smo poslali u drugi dio nejednakosti, dalje od modula, da bi se na kraju sve svelo na jednadžbu poput $\left| f\left(x \right) \right|=g\left(x \right)$ ili još jednostavnije $\left| f\levo(x \desno) \desno|=a$.
Ali vrtić gotovo - vrijeme je da razmislite o nečem ozbiljnijem. Počnimo sa ovakvim jednadžbama:
\[\lijevo| f\lijevo(x \desno) \desno|=\lijevo| g\lijevo(x \desno) \desno|\]
Ovo je jednadžba oblika "modulo jednak modulu". U osnovi važna tačka je odsustvo drugih pojmova i faktora: samo jedan modul lijevo, još jedan modul desno - i ništa više.
Netko bi sada pomislio da je takve jednačine teže riješiti od onoga što smo do sada proučavali. Ali ne: ove jednačine se rješavaju još lakše. Evo formule:
\[\lijevo| f\lijevo(x \desno) \desno|=\lijevo| g\left(x \right) \right|\Rightarrow f\left(x \right)=\pm g\left(x \right)\]
Sve! Jednostavno izjednačavamo izraze podmodula tako što jednom od njih stavimo prefiks sa znakom plus ili minus. A onda rješavamo rezultirajuće dvije jednadžbe - i korijeni su spremni! Nema dodatna ograničenja, nema nejednakosti itd. Sve je vrlo jednostavno.
Pokušajmo riješiti ovaj problem:
\[\lijevo| 2x+3 \desno|=\lijevo| 2x-7 \desno|\]
Elementary Watson! Otvaranje modula:
\[\lijevo| 2x+3 \desno|=\lijevo| 2x-7 \desno|\Strelica desno 2x+3=\pm \levo(2x-7 \desno)\]
Razmotrimo svaki slučaj posebno:
\[\begin(align)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\lijevo(2x-7 \desno)\Strelica desno 2x+3=-2x+7. \\\end(poravnati)\]
Prva jednadžba nema korijen. Jer kada je $3=-7$? Za koje vrijednosti $x$? „Šta je jebote $x$? Jeste li naduvani? Uopšte ne postoji $x$,” kažete. I bićeš u pravu. Dobili smo jednakost koja ne zavisi od varijable $x$, a istovremeno je i sama jednakost netačna. Zato nema korena.
Sa drugom jednačinom sve je malo zanimljivije, ali i vrlo, vrlo jednostavno:
Kao što vidite, sve je odlučeno bukvalno u par redova - ništa drugo nismo ni očekivali od linearne jednačine. :)
Kao rezultat, konačni odgovor je: $x=1$.
Pa, kako? Tesko? Naravno da ne. Hajde da probamo nešto drugo:
\[\lijevo| x-1 \desno|=\lijevo| ((x)^(2))-3x+2 \desno|\]
Opet imamo jednačinu poput $\left| f\lijevo(x \desno) \desno|=\lijevo| g\levo(x \desno) \desno|$. Stoga ga odmah prepisujemo, otkrivajući znak modula:
\[((x)^(2))-3x+2=\pm \levo(x-1 \desno)\]
Možda će neko sada pitati: „Hej, kakve gluposti? Zašto je plus-minus na desnoj, a ne na lijevoj strani? Smiri se, sve ću ti objasniti. Zaista, na dobar način, trebali smo prepisati našu jednačinu na sljedeći način:
Zatim morate otvoriti zagrade, pomaknuti sve članove u jednom smjeru od znaka jednakosti (pošto će jednadžba, očito, u oba slučaja biti kvadratna), a zatim pronaći korijene. Ali morate priznati: kada je “plus ili minus” ispred tri pojma (posebno kada je jedan od ovih pojmova kvadratni izraz), ovo nekako izgleda komplikovanije od situacije kada je „plus ili minus“ samo ispred dva pojma.
Ali ništa nas ne sprječava da originalnu jednačinu prepišemo na sljedeći način:
\[\lijevo| x-1 \desno|=\lijevo| ((x)^(2))-3x+2 \desno|\Strelica desno \levo| ((x)^(2))-3x+2 \desno|=\lijevo| x-1 \desno|\]
Šta se desilo? Da, ništa posebno: samo promijenio lijevo i desna strana mjesta. Sitnica, koja će nam na kraju malo pojednostaviti život. :)
Općenito, rješavamo ovu jednačinu, uzimajući u obzir opcije s plusom i minusom:
\[\begin(align)& ((x)^(2))-3x+2=x-1\Strelica desno ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\lijevo(x-1 \desno)\Strelica desno ((x)^(2))-2x+1=0. \\\end(poravnati)\]
Prva jednadžba ima korijene $x=3$ i $x=1$. Drugi je općenito tačan kvadrat:
\[((x)^(2))-2x+1=((\lijevo(x-1 \desno))^(2))\]
Prema tome, ima jedan korijen: $x=1$. Ali mi smo već ranije primili ovaj korijen. Dakle, samo dva broja će ući u konačni odgovor:
\[((x)_(1))=3;\quad ((x)_(2))=1.\]
Misija završena! Možete ga uzeti sa police i pojesti pitu. Ima ih 2, tvoj prosek. :)
Važna napomena. Imaju iste korijene različite opcije proširenje modula znači da se originalni polinomi razlažu na faktore, a među tim faktorima će nužno postojati i zajednički. stvarno:
\[\begin(align)& \left| x-1 \desno|=\lijevo| ((x)^(2))-3x+2 \desno|; \\&\lijevo| x-1 \desno|=\lijevo| \levo(x-1 \desno)\levo(x-2 \desno) \desno|. \\\end(poravnati)\]
Jedno od svojstava modula: $\left| a\cdot b \desno|=\lijevo| a \right|\cdot \left| b \right|$ (tj. modul proizvoda jednak je proizvodu modula), tako da se originalna jednačina može prepisati na sljedeći način:
\[\lijevo| x-1 \desno|=\lijevo| x-1 \desno|\cdot \levo| x-2 \desno|\]
Kao što vidite, zaista imamo zajednički faktor. Sada, ako sakupite sve module na jednoj strani, onda možete izvaditi ovaj množitelj iz zagrade:
\[\begin(align)& \left| x-1 \desno|=\lijevo| x-1 \desno|\cdot \levo| x-2 \desno|; \\&\lijevo| x-1 \desno|-\lijevo| x-1 \desno|\cdot \levo| x-2 \right|=0; \\&\lijevo| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\\end(poravnati)\]
Pa, sada se prisjećamo da je proizvod jednak nuli kada je barem jedan od faktora jednak nuli:
\[\left[ \begin(align)& \left| x-1 \desno|=0, \\& \levo| x-2 \right|=1. \\\kraj (poravnaj) \desno.\]
Tako je originalna jednadžba sa dva modula svedena na dvije najjednostavnije jednadžbe o kojima smo govorili na samom početku lekcije. Takve jednačine se mogu riješiti u samo par redova. :)
Ova primjedba može izgledati nepotrebno komplikovana i neprimjenjiva u praksi. Međutim, u stvarnosti možete naići na mnogo više izazovni zadaci od onih o kojima danas razgovaramo. U njima se moduli mogu kombinovati sa polinomima, aritmetičkim korijenima, logaritmi itd. I u takvim situacijama, mogućnost snižavanja ukupnog stepena jednačine stavljanjem nečega izvan zagrade može biti vrlo, vrlo zgodna. :)
Sada bih želeo da analiziram još jednu jednačinu, koja na prvi pogled može izgledati suludo. Mnogi studenti se toga “drže” – čak i oni koji vjeruju da dobro razumiju module.
Međutim, ovu jednačinu je još lakše riješiti od onoga što smo ranije razmatrali. I ako možete shvatiti zašto, dobićete još jedan pogodak brza odluka jednačine sa modulima.
Dakle, jednačina je:
\[\lijevo| x-((x)^(3)) \desno|+\lijevo| ((x)^(2))+x-2 \desno|=0\]
Ne, ovo nije greška u kucanju: to je plus između modula. I treba da nađemo za koje je $x$ zbir dva modula jednak nuli. :)
Šta je problem? A problem je što je svaki modul pozitivan broj, ili u ekstremnim slučajevima nula. Šta se dešava kada saberete dva pozitivna broja? Očigledno, opet pozitivan broj:
\[\begin(align)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(align)\]
Posljednji red može vam dati ideju: jedini slučaj u kojem je zbroj modula nula je ako je svaki modul jednak nuli:
\[\lijevo| x-((x)^(3)) \desno|+\lijevo| ((x)^(2))+x-2 \right|=0\Strelica desno \levo\( \begin(align)& \left| x-((x)^(3)) \right|=0, \\& \left|((x)^(2))+x-2 \right|=0. \\\end(align) \desno.\]
Kada je modul jednak nuli? Samo u jednom slučaju - kada je izraz podmodula jednak nuli:
\[((x)^(2))+x-2=0\Strelica desno \levo(x+2 \desno)\levo(x-1 \desno)=0\Strelica desno \levo[ \begin(align)& x=-2 \\& x=1 \\\end(poravnati) \desno.\]
Dakle, imamo tri tačke u kojima je prvi modul postavljen na nulu: 0, 1 i −1; kao i dvije tačke u kojima se drugi modul nuli: −2 i 1. Međutim, potrebno je da oba modula budu nulirana u isto vrijeme, tako da među pronađenim brojevima trebamo izabrati one koji su uključeni u oba skupa. Očigledno, postoji samo jedan takav broj: $x=1$ - ovo će biti konačni odgovor.
metoda cijepanja
Pa, već smo pokrili gomilu zadataka i naučili mnogo trikova. Mislite li da je to to? Ali ne! Sada ćemo razmotriti konačnu tehniku - i istovremeno najvažniju. Govorit ćemo o dijeljenju jednačina s modulom. O čemu će se raspravljati? Vratimo se malo unazad i razmotrimo neku jednostavnu jednačinu. Na primjer, ovo:
\[\lijevo| 3x-5\desno|=5-3x\]
U principu, već znamo kako riješiti takvu jednačinu, jer je standardna $\left| f\left(x \right) \right|=g\left(x \right)$. Ali hajde da pokušamo da sagledamo ovu jednačinu iz malo drugačijeg ugla. Preciznije, razmotrite izraz pod znakom modula. Da vas podsjetim da modul bilo kojeg broja može biti jednak samom broju, ili može biti suprotan ovom broju:
\[\lijevo| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end(align) \right.\]
Zapravo, ta nejasnoća je cijeli problem: pošto se broj ispod modula mijenja (zavisi od varijable), nije nam jasno da li je pozitivan ili negativan.
Ali šta ako u početku zahtijevamo da ovaj broj bude pozitivan? Na primjer, zahtijevajmo da je $3x-5 \gt 0$ - u ovom slučaju zagarantovano ćemo dobiti pozitivan broj pod znakom modula i možemo se potpuno riješiti ovog modula:
Tako će se naša jednačina pretvoriti u linearnu, koja se lako rješava:
Istina, sva ova razmatranja imaju smisla samo pod uslovom $3x-5 \gt 0$ - sami smo uveli ovaj zahtjev kako bismo nedvosmisleno otkrili modul. Dakle, zamijenimo pronađeni $x=\frac(5)(3)$ u ovaj uslov i provjerimo:
Ispostavilo se da kada specificirana vrijednost$x$ naš zahtjev nije zadovoljen, jer Ispostavilo se da je izraz jednak nuli, a potrebno je da bude striktno Iznad nule. Tužan. :(
Ali to je u redu! Na kraju krajeva, postoji još jedna opcija $3x-5 \lt 0$. Štaviše: postoji i slučaj $3x-5=0$ - ovo se takođe mora uzeti u obzir, inače će rješenje biti nepotpuno. Dakle, razmotrite slučaj $3x-5 \lt 0$:
Očigledno je da će se modul otvoriti sa znakom minus. Ali tada nastaje čudna situacija: isti izraz će stajati i s lijeve i s desne strane u izvornoj jednadžbi:
Pitam se za šta će takav $x$ izraz $5-3x$ biti jednak izrazu $5-3x$? Iz ovakvih jednadžbi bi se i Kapetan očito ugušio pljuvačkom, ali znamo da je ova jednačina identitet, tj. to je istina za bilo koju vrijednost varijable!
A to znači da će nam odgovarati bilo koji $x$. Međutim, imamo ograničenje:
Drugim riječima, odgovor neće biti jedan broj, već cijeli interval:
Konačno, ostaje još jedan slučaj za razmatranje: $3x-5=0$. Ovdje je sve jednostavno: ispod modula će biti nula, a modul nule je također jednak nuli (ovo direktno slijedi iz definicije):
Ali onda originalna jednadžba $\left| 3x-5 \right|=5-3x$ će se prepisati ovako:
Već smo dobili ovaj korijen iznad kada smo razmatrali slučaj $3x-5 \gt 0$. Štaviše, ovaj korijen je rješenje jednadžbe $3x-5=0$ - ovo je ograničenje koje smo sami uveli da poništimo modul. :)
Tako ćemo, osim intervala, biti zadovoljni i brojem koji leži na samom kraju ovog intervala:
 Kombiniranje korijena u jednadžbi s modulom
Kombiniranje korijena u jednadžbi s modulom Ukupan konačni odgovor: $x\in \left(-\infty ;\frac(5)(3) \right]$. Nije baš uobičajeno vidjeti takvo sranje u odgovoru na prilično jednostavnu (u suštini linearnu) jednačinu sa modulom Pa, naviknite se na to: složenost modula leži u činjenici da odgovori u takvim jednadžbama mogu biti potpuno nepredvidivi.
Mnogo važnije je nešto drugo: upravo smo demontirali univerzalni algoritam za rješavanje jednadžbe s modulom! A ovaj algoritam se sastoji od sljedećih koraka:
- Izjednačite svaki modul u jednačini sa nulom. Hajde da dobijemo neke jednačine;
- Riješite sve ove jednačine i označite korijene na brojevnoj pravoj. Kao rezultat toga, ravna linija će biti podijeljena na nekoliko intervala, na svakom od kojih su svi moduli jedinstveno prošireni;
- Riješite originalnu jednačinu za svaki interval i kombinirajte odgovore.
To je sve! Ostaje samo jedno pitanje: šta učiniti sa samim korijenima, dobivenim u prvom koraku? Recimo da imamo dva korijena: $x=1$ i $x=5$. Oni će razbiti brojevnu pravu na 3 dijela:
 Dijeljenje brojevne prave na intervale pomoću tačaka
Dijeljenje brojevne prave na intervale pomoću tačaka Dakle, koji su intervali? Jasno je da ih ima tri:
- Krajnje lijevo: $x \lt 1$ - sama jedinica nije uključena u interval;
- Centralno: $1\le x \lt 5$ - ovdje je jedan uključen u interval, ali pet nije uključeno;
- Krajnji desni: $x\ge 5$ — pet je uključeno samo ovdje!
Mislim da već razumete obrazac. Svaki interval uključuje lijevi kraj i ne uključuje desni kraj.
Na prvi pogled takav zapis može izgledati neugodno, nelogično i općenito neka vrsta ludila. Ali vjerujte mi: nakon malo prakse, vidjet ćete da je ovo najpouzdaniji pristup i da u isto vrijeme ne ometa nedvosmisleno otkrivanje modula. Bolje je koristiti takvu shemu nego svaki put razmišljati: dati lijevi / desni kraj trenutnom intervalu ili ga "baciti" sljedećem.
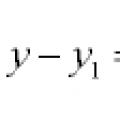 Jednačine linija i krivulja u ravni
Jednačine linija i krivulja u ravni Uopštene homogene jednačine Generalizovane homogene jednačine drugog reda
Uopštene homogene jednačine Generalizovane homogene jednačine drugog reda Hvala zarezu Zbog činjenice da je u njihovoj
Hvala zarezu Zbog činjenice da je u njihovoj