What are the basic properties of the indefinite integral. The simplest properties of integrals
In this article we will list the main properties of the definite integral. Most of these properties are proven based on the concepts of the Riemann and Darboux definite integral.
The calculation of the definite integral is very often done using the first five properties, so we will refer to them when necessary. The remaining properties of the definite integral are mainly used to evaluate various expressions.
Before moving on basic properties of the definite integral, let us agree that a does not exceed b.
For the function y = f(x) defined at x = a, the equality is true.
That is, the value of a definite integral with the same limits of integration is equal to zero. This property is a consequence of the definition of the Riemann integral, since in this case each integral sum for any partition of the interval and any choice of points is equal to zero, since, therefore, the limit of integral sums is zero.
For a function integrable on an interval,  .
.
In other words, when the upper and lower limits of integration change places, the value of the definite integral changes to the opposite. This property of a definite integral also follows from the concept of the Riemann integral, only the numbering of the partition of the segment should begin from the point x = b.
 for functions integrable on an interval y = f(x) and y = g(x) .
for functions integrable on an interval y = f(x) and y = g(x) .
Proof.
Let's write down the integral sum of the function ![]() for a given partition of a segment and a given choice of points:
for a given partition of a segment and a given choice of points: 
where and are the integral sums of the functions y = f(x) and y = g(x) for a given partition of the segment, respectively.
Going to the limit at ![]() we obtain that, by the definition of the Riemann integral, is equivalent to the statement of the property being proved.
we obtain that, by the definition of the Riemann integral, is equivalent to the statement of the property being proved.
The constant factor can be taken out of the sign of the definite integral. That is, for a function y = f(x) integrable on an interval and an arbitrary number k, the following equality holds:  .
.
The proof of this property of the definite integral is absolutely similar to the previous one: 
Let the function y = f(x) be integrable on the interval X, and ![]() and then
and then  .
.
This property is true for both , and or .
The proof can be carried out based on the previous properties of the definite integral.
If a function is integrable on an interval, then it is integrable on any internal interval.
The proof is based on the property of Darboux sums: if new points are added to an existing partition of a segment, then the lower Darboux sum will not decrease, and the upper one will not increase.
If the function y = f(x) is integrable on the interval and for any value of the argument, then  .
.
This property is proven through the definition of the Riemann integral: any integral sum for any choice of points of partition of the segment and points at will be non-negative (not positive).
Consequence.
For functions y = f(x) and y = g(x) integrable on an interval, the following inequalities hold: 
This statement means that integration of inequalities is permissible. We will use this corollary to prove the following properties.
Let the function y = f(x) be integrable on the interval , then the inequality holds  .
.
Proof.
It's obvious that ![]() . In the previous property, we found out that the inequality can be integrated term by term, therefore, it is true
. In the previous property, we found out that the inequality can be integrated term by term, therefore, it is true  . This double inequality can be written as
. This double inequality can be written as  .
.
Let the functions y = f(x) and y = g(x) be integrable on the interval and for any value of the argument , then  , Where
, Where ![]() And
And ![]() .
.
The proof is carried out similarly. Since m and M are the smallest and largest values of the function y = f(x) on the segment , then ![]() . Multiplying the double inequality by a non-negative function y = g(x) leads us to the following double inequality. Integrating it on the interval , we arrive at the statement being proved.
. Multiplying the double inequality by a non-negative function y = g(x) leads us to the following double inequality. Integrating it on the interval , we arrive at the statement being proved.
In differential calculus the problem is solved: under this function ƒ(x) find its derivative(or differential). Integral calculus solves the inverse problem: find the function F(x), knowing its derivative F "(x)=ƒ(x) (or differential). The sought function F(x) is called the antiderivative of the function ƒ(x).
The function F(x) is called antiderivative function ƒ(x) on the interval (a; b), if for any x є (a; b) the equality
F " (x)=ƒ(x) (or dF(x)=ƒ(x)dx).
For example, the antiderivative of the function y = x 2, x є R, is the function, since
![]()
Obviously, any functions will also be antiderivatives

where C is a constant, since
Theorem 29. 1. If the function F(x) is an antiderivative of the function ƒ(x) on (a;b), then the set of all antiderivatives for ƒ(x) is given by the formula F(x)+C, where C is a constant number.
▲ The function F(x)+C is an antiderivative of ƒ(x).
Indeed, (F(x)+C) " =F " (x)=ƒ(x).
Let Ф(х) be some other antiderivative of the function ƒ(x), different from F(x), i.e. Ф "(x)=ƒ(х). Then for any x є (а;b) we have
And this means (see Corollary 25.1) that
where C is a constant number. Therefore, Ф(x)=F(x)+С.▼
The set of all antiderivative functions F(x)+С for ƒ(x) is called indefinite integral of the function ƒ(x) and is denoted by the symbol ∫ ƒ(x) dx.
Thus, by definition 
∫ ƒ(x)dx= F(x)+C.
Here ƒ(x) is called integrand function, ƒ(x)dx — integrand expression, X - integration variable, ∫ -sign of the indefinite integral.
The operation of finding the indefinite integral of a function is called integrating this function.
Geometrically, the indefinite integral is a family of “parallel” curves y=F(x)+C (each numerical value of C corresponds to a specific curve of the family) (see Fig. 166). The graph of each antiderivative (curve) is called integral curve.
Does every function have an indefinite integral?
There is a theorem stating that “every function continuous on (a;b) has an antiderivative on this interval,” and, consequently, an indefinite integral.
Let us note a number of properties of the indefinite integral that follow from its definition.
1. The differential of the indefinite integral is equal to the integrand, and the derivative of the indefinite integral is equal to the integrand:
d(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) " =ƒ(x).
Indeed, d(∫ ƒ(x) dx)=d(F(x)+C)=dF(x)+d(C)=F " (x) dx =ƒ(x) dx
(∫ ƒ (x) dx) " =(F(x)+C)"=F"(x)+0 =ƒ (x).
Thanks to this property, the correctness of integration is checked by differentiation. For example, equality
∫(3x 2 + 4) dx=х з +4х+С
true, since (x 3 +4x+C)"=3x 2 +4.
2. The indefinite integral of the differential of a certain function is equal to the sum of this function and an arbitrary constant:
∫dF(x)= F(x)+C.
Really,
3. The constant factor can be taken out of the integral sign:
α ≠ 0 is a constant.
Really,
(put C 1 / a = C.)
4. The indefinite integral of the algebraic sum of a finite number of continuous functions is equal to the algebraic sum of the integrals of the summands of the functions:
Let F"(x)=ƒ(x) and G"(x)=g(x). Then

where C 1 ±C 2 =C.
5. (Invariance of the integration formula).
If ![]() , where u=φ(x) is an arbitrary function with a continuous derivative.
, where u=φ(x) is an arbitrary function with a continuous derivative.
▲ Let x be an independent variable, ƒ(x) be a continuous function and F(x) be its antiderivative. Then
![]()
Let us now set u=φ(x), where φ(x) is a continuously differentiable function. Consider the complex function F(u)=F(φ(x)). Due to the invariance of the form of the first differential of the function (see p. 160), we have
From here▼
Thus, the formula for the indefinite integral remains valid regardless of whether the variable of integration is the independent variable or any function of it that has a continuous derivative.
So, from the formula ![]() by replacing x with u (u=φ(x)) we get
by replacing x with u (u=φ(x)) we get ![]()
In particular,

Example 29.1. Find the integral ![]()
![]()
![]()
where C=C1+C 2 +C 3 +C 4.
Example 29.2. Find the integral Solution:
![]()
![]()
- 29.3. Table of basic indefinite integrals
Taking advantage of the fact that integration is the inverse action of differentiation, one can obtain a table of basic integrals by inverting the corresponding formulas of differential calculus (table of differentials) and using the properties of the indefinite integral.
For example, because
d(sin u)=cos u . du
The derivation of a number of formulas in the table will be given when considering the basic methods of integration.
The integrals in the table below are called tabular. They should be known by heart. In integral calculus there are no simple and universal rules for finding antiderivatives of elementary functions, as in differential calculus. Methods for finding antiderivatives (i.e., integrating a function) are reduced to indicating techniques that bring a given (sought) integral to a tabular one. Therefore, it is necessary to know table integrals and be able to recognize them.
Note that in the table of basic integrals, the integration variable can denote both an independent variable and a function of the independent variable (according to the invariance property of the integration formula).
The validity of the formulas below can be verified by taking the differential on the right side, which will be equal to the integrand on the left side of the formula.
Let us prove, for example, the validity of formula 2. The function 1/u is defined and continuous for all values of and other than zero.
If u > 0, then ln|u|=lnu, then ![]() That's why
That's why
If u<0, то ln|u|=ln(-u). Но![]() Means
Means
So, formula 2 is correct. Similarly, let's check formula 15:
Table of main integrals


Friends! We invite you to discuss. If you have your own opinion, write to us in the comments.
These properties are used to carry out transformations of the integral in order to reduce it to one of the elementary integrals and further calculation.
1. The derivative of the indefinite integral is equal to the integrand:
2. The differential of the indefinite integral is equal to the integrand:
3. The indefinite integral of the differential of a certain function is equal to the sum of this function and an arbitrary constant:
4. The constant factor can be taken out of the integral sign:
Moreover, a ≠ 0
5. The integral of the sum (difference) is equal to the sum (difference) of the integrals:
6. Property is a combination of properties 4 and 5:
Moreover, a ≠ 0 ˄ b ≠ 0
7. Invariance property of the indefinite integral:
If , then
8. Property:
If , then
In fact, this property is a special case of integration using the variable change method, which is discussed in more detail in the next section.
Let's look at an example:
First we applied property 5, then property 4, then we used the table of antiderivatives and got the result.
The algorithm of our online integral calculator supports all the properties listed above and will easily find a detailed solution for your integral.
Antiderivative and indefinite integral.
An antiderivative of a function f(x) on the interval (a; b) is a function F(x) such that the equality holds for any x from the given interval.
If we take into account the fact that the derivative of the constant C is equal to zero, then the equality is true ![]() . Thus, the function f(x) has a set of antiderivatives F(x)+C, for an arbitrary constant C, and these antiderivatives differ from each other by an arbitrary constant value.
. Thus, the function f(x) has a set of antiderivatives F(x)+C, for an arbitrary constant C, and these antiderivatives differ from each other by an arbitrary constant value.
The entire set of antiderivatives of the function f(x) is called the indefinite integral of this function and is denoted ![]() .
.
The expression is called the integrand, and f(x) is called the integrand. The integrand represents the differential of the function f(x).
The action of finding an unknown function given its differential is called indefinite integration, because the result of integration is not one function F(x), but a set of its antiderivatives F(x)+C.
Table integrals

The simplest properties of integrals
1. The derivative of the integration result is equal to the integrand.
![]()
2. The indefinite integral of the differential of a function is equal to the sum of the function itself and an arbitrary constant.
3. The coefficient can be taken out of the sign of the indefinite integral.
![]()
4. The indefinite integral of the sum/difference of functions is equal to the sum/difference of the indefinite integrals of functions.
Intermediate equalities of the first and second properties of the indefinite integral are given for clarification.
To prove the third and fourth properties, it is enough to find the derivatives of the right-hand sides of the equalities:

These derivatives are equal to the integrands, which is a proof due to the first property. It is also used in the last transitions.
Thus, the problem of integration is the inverse of the problem of differentiation, and there is a very close connection between these problems:
the first property allows one to check integration. To check the correctness of the integration performed, it is enough to calculate the derivative of the result obtained. If the function obtained as a result of differentiation turns out to be equal to the integrand, this will mean that the integration was carried out correctly;
the second property of the indefinite integral allows one to find its antiderivative from a known differential of a function. The direct calculation of indefinite integrals is based on this property.
1.4.Invariance of integration forms.
Invariant integration is a type of integration for functions whose arguments are elements of a group or points of a homogeneous space (any point in such a space can be transferred to another by a given action of the group).
function f(x) reduces to calculating the integral of the differential form f.w, where
An explicit formula for r(x) is given below. The agreement condition has the form ![]() .
.
here Tg means the shift operator on X using gОG: Tgf(x)=f(g-1x). Let X=G be a topology, a group acting on itself by left shifts. I. and. exists if and only if G is locally compact (in particular, on infinite-dimensional groups I.I. does not exist). For a subset of I. and. characteristic function cA (equal to 1 on A and 0 outside A) specifies the left Xaar measure m(A). The defining property of this measure is its invariance under left shifts: m(g-1A)=m(A) for all gОG. The left Haar measure on a group is uniquely defined up to a positive scalar factor. If the Haar measure m is known, then I. and. function f is given by the formula ![]() . The right Haar measure has similar properties. There is a continuous homomorphism (map preserving the group property) DG of the group G into the group (with respect to multiplication) posit. numbers for which
. The right Haar measure has similar properties. There is a continuous homomorphism (map preserving the group property) DG of the group G into the group (with respect to multiplication) posit. numbers for which
where dmr and dmi are the right and left Haar measures. The function DG(g) is called module of the group G. If , then the group G is called. unimodular; in this case the right and left Haar measures coincide. Compact, semisimple and nilpotent (in particular, commutative) groups are unimodular. If G is an n-dimensional Lie group and q1,...,qn is a basis in the space of left-invariant 1-forms on G, then the left Haar measure on G is given by the n-form. In local coordinates for calculation
forms qi, you can use any matrix realization of the group G: the matrix 1-form g-1dg is left invariant, and its coefficient. are left-invariant scalar 1-forms from which the required basis is selected. For example, the complete matrix group GL(n, R) is unimodular and the Haar measure on it is given by the form. Let ![]() X=G/H is a homogeneous space for which the locally compact group G is a transformation group, and the closed subgroup H is the stabilizer of a certain point. In order for an i.i. to exist on X, it is necessary and sufficient that for all hОH the equality DG(h)=DH(h) holds. In particular, this is true in the case when H is compact or semisimple. Complete theory of I. and. does not exist on infinite-dimensional manifolds.
X=G/H is a homogeneous space for which the locally compact group G is a transformation group, and the closed subgroup H is the stabilizer of a certain point. In order for an i.i. to exist on X, it is necessary and sufficient that for all hОH the equality DG(h)=DH(h) holds. In particular, this is true in the case when H is compact or semisimple. Complete theory of I. and. does not exist on infinite-dimensional manifolds.
Replacing variables.

The main task of differential calculus is to find the derivative f'(x) or differential df=f'(x)dx functions f(x). In integral calculus the inverse problem is solved. According to a given function f(x) you need to find such a function F(x), What F'(x)=f(x) or dF(x)=F'(x)dx=f(x)dx.
Thus, the main task of integral calculus is the restoration of function F(x) by the known derivative (differential) of this function. Integral calculus has numerous applications in geometry, mechanics, physics and technology. It gives a general method for finding areas, volumes, centers of gravity, etc.
Definition. FunctionF(x), , is called the antiderivative of the functionf(x) on the set X if it is differentiable for any andF'(x)=f(x) ordF(x)=f(x)dx.
Theorem. Any continuous line on the interval [a;b] functionf(x) has an antiderivative on this segmentF(x).
Theorem. IfF 1 (x) andF 2 (x) – two different antiderivatives of the same functionf(x) on the set x, then they differ from each other by a constant term, i.e.F 2 (x)=F 1x)+C, where C is a constant.
- Indefinite integral, its properties.
Definition. TotalityF(x)+From all antiderivative functionsf(x) on the set X is called an indefinite integral and is denoted:
- (1)In formula (1) f(x)dx called integrand expression,f(x) – integrand function, x – integration variable, A C – integration constant.
Let us consider the properties of the indefinite integral that follow from its definition.
1. The derivative of the indefinite integral is equal to the integrand, the differential of the indefinite integral is equal to the integrand:
And .2. The indefinite integral of the differential of a certain function is equal to the sum of this function and an arbitrary constant:
3. The constant factor a (a≠0) can be taken out as the sign of the indefinite integral:
4. The indefinite integral of the algebraic sum of a finite number of functions is equal to the algebraic sum of the integrals of these functions:
5. IfF(x) – antiderivative of the functionf(x), then:
6 (invariance of integration formulas). Any integration formula retains its form if the integration variable is replaced by any differentiable function of this variable:
Whereu is a differentiable function.
- Table of indefinite integrals.
Let's give basic rules for integrating functions.
Let's give table of basic indefinite integrals.(Note that here, as in differential calculus, the letter u can be designated as an independent variable (u=x), and a function of the independent variable (u=u(x)).)
(n≠-1). (a >0, a≠1). (a≠0). (a≠0). (|u| > |a|).(|u|< |a|).
Integrals 1 – 17 are called tabular.
Some of the above formulas in the table of integrals, which do not have an analogue in the table of derivatives, are verified by differentiating their right-hand sides.
- Change of variable and integration by parts in the indefinite integral.
Integration by substitution (variable replacement). Let it be necessary to calculate the integral
, which is not tabular. The essence of the substitution method is that in the integral the variable X replace with a variable t according to the formula x=φ(t), where dx=φ’(t)dt.Theorem. Let the functionx=φ(t) is defined and differentiable on a certain set T and let X be the set of values of this function on which the function is definedf(x). Then if on the set X the functionf(
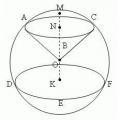 Sphere, ball, segment and sector
Sphere, ball, segment and sector Specialty "Nursing" (bachelor's degree)
Specialty "Nursing" (bachelor's degree) The simplest properties of integrals
The simplest properties of integrals