Matrix rank. The concept of matrix rank How to calculate the rank of a square matrix
§3. Matrix rank
Determining the rank of a matrix
Linearly dependent strings
Elementary matrix transformations
Equivalent matrices
Algorithm for finding the rank of a matrix using elementary transformations
§4. First, second and third order determinants
First order determinant
Second order determinant
Third order determinant
Sarrus rule
§5. Calculation of determinants of large orders
Algebraic complement
Laplace's theorem
Determinant of a triangular matrix
Application. The concept of a determinant P-th order in general.
§ 3. Matrix rank
Each matrix is characterized by a certain number that is important when solving systems of linear equations. This number is called matrix rank.
Matrix rank is equal to the number of its linearly independent rows (columns), through which all its other rows (columns) are linearly expressed.
The rows (columns) of a matrix are called linearly dependent, if their corresponding elements are proportional.
In other words, the elements of one of the linearly dependent rows are equal to the elements of the other, multiplied by the same number. For example, rows 1 and 2 of the matrix A are linearly dependent if , where (λ is some number).
Example. Find the rank of a matrix

Solution.
The second line is obtained from the first if its elements are multiplied by -3, the third is obtained from the first if its elements are multiplied by 0, and the fourth line cannot be expressed through the first. It turns out that the matrix has two linearly independent rows, because The first and fourth rows are not proportional, therefore the rank of the matrix is 2.
Matrix rank A denoted by rank A or r(A).
From the definition of matrix rank it follows:
1. The rank of the matrix does not exceed the smallest of its dimensions, i.e. for matrix A m × n .
2. The rank of a matrix is zero only if it is a zero matrix.
In the general case, determining the rank of a matrix is quite labor-intensive. To facilitate this task, transformations that preserve the rank of the matrix are used, which are called elementary transformations:
1) discarding the zero row (column);
2) multiplying all elements of a row (column) by a number other than zero;
3) changing the order of rows (columns);
4) adding to the elements of one row (column) the corresponding elements of another row (column), multiplied by any number;
5) matrix transposition.
The two matrices are called equivalent, if one is obtained from the other using a finite number of elementary transformations.
The equivalence of matrices is indicated by the sign “~” (equivalent).
Using elementary transformations, any matrix can be reduced to a triangular form, then calculating its rank is not difficult.
The process of calculating the rank of a matrix using elementary transformations Let's look at an example.
Example. Find the rank of a matrix
A = 
Solution.
Our task is to bring the matrix to a triangular form, i.e. Using elementary transformations, ensure that there are only zeros below the main diagonal in the matrix.
1. Consider the first line. If element A 11 = 0, then when rearranging rows or columns we ensure that A 11 ¹ 0. In our example, let’s swap places, for example, the first and second rows of the matrix:
A = 
Now the element A 11 ¹ 0. By multiplying the first row by suitable numbers and adding with other rows, we will ensure that all elements of the first column (except A 11) were equal to zero.

2. Now consider the second line. If element A 22 = 0, then when rearranging rows or columns we ensure that A 22 ¹ 0. If the element A 22 ¹ 0 (and we have A 22 = –1 ¹ 0), then by multiplying the second row by suitable numbers and adding with other rows, we will ensure that all elements of the second column (except A 22) were equal to zero.

3. If the transformation process results in rows (columns) consisting entirely of zeros, then discard them. In our example, we will discard lines 3 and 4:

The last matrix has a stepped form and contains two rows. They are linearly independent, therefore the rank of the matrix is 2.
§ 4. First, second and third order determinants
Among the variety of matrices, square matrices are distinguished separately. This type of matrix is good because:
1. Unit matrices are square.
2. You can multiply and add any square matrices of the same order, resulting in a matrix of the same order.
3. Square matrices can be raised to powers.
In addition, only for square matrices can the determinant be calculated.
Matrix determinant is a special number calculated according to some rule. Matrix determinant A denoted by:
Or straight brackets: ,
Or with the capital Greek letter delta: Δ( A),
Or the “determinant” symbol: det ( A).
Determinant of a first order matrix A= (A 11) or first order determinant, is a number equal to a matrix element:
Δ 1 = ![]() =A 11
=A 11
Determinant of a second order matrix ![]() or second order determinant
or second order determinant
Example:
Determinant of a third-order matrix  or third order determinant, is a number that is calculated by the formula:
or third order determinant, is a number that is calculated by the formula:
The third order determinant can be calculated using Sarrus' rule .
Sarrus rule. To the third-order determinant on the right, sign the first two columns and with a plus sign (+) take the sum of the products of three elements located on the main diagonal of the determinant and on “straight lines” parallel to the main diagonal, with a minus sign (–) take the sum of the products of elements located on the second diagonal and on “straight lines” parallel to it.
Example:

It is easy to see that the number of terms in the determinant increases with its order. In general, in the determinant P of the th order the number of terms is 1·2·3·…· P = P!.
Let's check: for Δ 1 the number of terms is 1! = 1,
for Δ 2 the number of terms is 2! = 1 2 = 2,
for Δ 3 the number of terms is 3! = 1·2·3 = 6.
It follows that for a 4th order determinant the number of terms is 4! = 1·2·3·4 = 24, which means that calculating such a determinant is quite labor-intensive, not to mention determinants of a higher order. Taking this into account, they try to reduce the calculation of determinants of large orders to the calculation of determinants of the second or third order.
§ 5. Calculation of determinants of large orders
Let us introduce a number of concepts.
Let a square matrix be given A n-th order:
| A= |  |
Minor M element ij a ij is called the determinant ( P– 1)th order obtained from the matrix A by crossing out i-th line and j th column.
For example, the minor element A 12 third order matrices will be:
Algebraic complement A element ij a ij is its minor, taken with the sign (−1) i + j:
A ij = (−1) i + jM ij
In other words, A ij = M ij if i+j even number,
A ij = − M ij if i+j odd number.
Example. Find the algebraic complements of the elements of the second row of the matrix

Solution.
Using algebraic additions, it is possible to calculate determinants of large orders, based on Laplace's theorem.
Laplace's theorem. The determinant of a square matrix is equal to the sum of the products of the elements of any of its rows (columns) and their algebraic complements:
– expansion along the i-th row;
( – expansion in the jth column).
Example. Calculate the determinant of a matrix  expansion along the first row.
expansion along the first row.
Solution.
Thus, a determinant of any order can be reduced to the calculation of several determinants of a lower order. Obviously, for decomposition it is convenient to choose a row or column containing as many zeros as possible.
Let's look at another example.
Example. Calculate the determinant of a triangular matrix 
Solution.
Got that the determinant of a triangular matrix is equal to the product of the elements of its main diagonal .
This important derivation makes it easy to calculate the determinant of any triangular matrix. This is all the more useful since, if necessary, any determinant can be reduced to triangular form. In this case, some properties of determinants are used.
Application
The concept of a determinant P-th order in general.
In general, it is possible to give a strict definition for the determinant of a matrix P-order, but for this it is necessary to introduce a number of concepts.
Rearrangement numbers 1, 2, ..., n Any arrangement of these numbers in a certain order is called. In elementary algebra it is proved that the number of all permutations that can be formed from n numbers equals 12...n = n!. For example, from three numbers 1, 2, 3 you can form 3! = 6 permutations: 123, 132, 312, 321, 231, 213.
They say that in this permutation the numbers i And j make up inversion(mess) if i> j, But i comes earlier in this permutation j, that is, if the larger number is to the left of the smaller one.
The permutation is called even(or odd), if it has an even (odd) total number of inversions.
An operation by which one passes from one permutation to another composed of the same n numbers is called substitution n th degree.
A substitution that transforms one permutation into another is written in two lines in common brackets, and the numbers occupying the same places in the permutations under consideration are called corresponding and are written one below the other. For example, the symbol
denotes a substitution in which 3 goes to 4, 1 goes to 2, 2 goes to 1, 4 goes to 3. A substitution is called even (or odd) if the total number of inversions in both rows of the substitution is even (odd). Any substitution n-th power can be written as
those. with natural numbers in the top line.
Let us be given a square matrix of order n

Let's consider all possible products according to n elements of this matrix, taken one and only one from each row and each column, i.e. works of the form:
![]() ,
,
where are the indices q 1 , q 2 ,..., qn make up some permutation of numbers
1, 2,..., n. The number of such products is equal to the number of different permutations from n characters, i.e. equals n!. Work mark ![]() , equal to (–1) q, Where q– the number of inversions in the permutation of the second indices of elements.
, equal to (–1) q, Where q– the number of inversions in the permutation of the second indices of elements.
Determinant n-th order is the algebraic sum of all possible products with respect to n matrix elements taken one and only one from each row and each column, i.e. works of the form: ![]() . In this case, the sign of the product
. In this case, the sign of the product ![]() equal to (–1) q, Where q– the number of inversions in the permutation of the second indices of elements.
equal to (–1) q, Where q– the number of inversions in the permutation of the second indices of elements.
Linear algebra
Previously for a square matrix  th order the concept of minor was introduced
th order the concept of minor was introduced  element
element  . Let us recall that this is the name given to the determinant of order
. Let us recall that this is the name given to the determinant of order  , obtained from the determinant
, obtained from the determinant  by crossing out
by crossing out  th line and
th line and  th column.
th column.
Let us now introduce the general concept of minor. Let's consider some not necessarily square matrix  . Let's choose some
. Let's choose some  line numbers
line numbers  And
And  column numbers
column numbers  .
.
Definition.
Minor order  matrices
matrices  (corresponding to the selected rows and columns) is called the order determinant
(corresponding to the selected rows and columns) is called the order determinant  , formed by elements located at the intersection of selected rows and columns, i.e. number
, formed by elements located at the intersection of selected rows and columns, i.e. number
 .
.
Each matrix has as many minors of a given order  , in how many ways can you select line numbers
, in how many ways can you select line numbers  and columns
and columns  .
.
Definition. In the matrix  sizes
sizes  minor order
minor order  called basic, if it is nonzero and all minors are of order
called basic, if it is nonzero and all minors are of order  equal to zero or minor order
equal to zero or minor order  at the matrix
at the matrix  absolutely not.
absolutely not.
It is clear that a matrix can have several different basis minors, but all basis minors have the same order. Indeed, if all minors are of order  are equal to zero, then all minors of the order are equal to zero
are equal to zero, then all minors of the order are equal to zero  , and, consequently, all higher orders.
, and, consequently, all higher orders.
Definition. Matrix rank The order of the basis minor is called, or, in other words, the largest order for which minors other than zero exist. If all elements of a matrix are equal to zero, then the rank of such a matrix, by definition, is considered zero.
Matrix rank  we will denote by the symbol
we will denote by the symbol  . From the definition of rank it follows that for the matrix
. From the definition of rank it follows that for the matrix  sizes
sizes  the ratio is correct.
the ratio is correct.
Two ways to calculate the rank of a matrix
A) Bordering minor method
Let a minor be found in the matrix 
 -th order, different from zero. Let's consider only those minors
-th order, different from zero. Let's consider only those minors  -th order, which contain (edge) a minor
-th order, which contain (edge) a minor  : if they are all equal to zero, then the rank of the matrix is
: if they are all equal to zero, then the rank of the matrix is  . Otherwise, among the bordering minors there is a non-zero minor
. Otherwise, among the bordering minors there is a non-zero minor  -th order, and the whole procedure is repeated.
-th order, and the whole procedure is repeated.
Example 9
. Find the rank of a matrix  by the method of bordering minors.
by the method of bordering minors.

Let's choose a second order minor  . There is only one third-order minor, bordering the selected minor
. There is only one third-order minor, bordering the selected minor  . Let's calculate it.
. Let's calculate it.

So it's minor  basic, and the rank of the matrix is equal to its order, i.e.
basic, and the rank of the matrix is equal to its order, i.e. 
It is clear that iterating through the minors in this way in search of the basis is a task associated with large calculations, if the dimensions of the matrix are not very small. There is, however, a simpler way to find the rank of a matrix - using elementary transformations.
b) Elementary transformation method
Definition. Elementary matrix transformations The following transformations are called:
multiplying a string by a number other than zero;
adding another line to one line;
rearrangement of lines;
the same column transformations.
Transformations 1 and 2 are performed element by element.
By combining transformations of the first and second types, we can add a linear combination of the remaining strings to any string.
Theorem. Elementary transformations do not change the rank of the matrix.
(No proof)
The idea of a practical method for calculating the rank of a matrix

is that with the help of elementary transformations this matrix  lead to the appearance
lead to the appearance
 ,
(5)
,
(5)
in which the "diagonal" elements  are different from zero, and the elements located below the “diagonal” ones are equal to zero. Let's agree to call the matrix
are different from zero, and the elements located below the “diagonal” ones are equal to zero. Let's agree to call the matrix  this type of triangular (otherwise, it is called diagonal, trapezoidal or ladder). After matrix reduction
this type of triangular (otherwise, it is called diagonal, trapezoidal or ladder). After matrix reduction  to the triangular form we can immediately write that
to the triangular form we can immediately write that  .
.
Indeed,  (since elementary transformations do not change the rank). But the matrix
(since elementary transformations do not change the rank). But the matrix  there is a non-zero minor order
there is a non-zero minor order  :
:
 ,
,
and any minor of order  contains the null string and is therefore equal to zero.
contains the null string and is therefore equal to zero.
Let us now formulate the practical rank calculation rule matrices  using elementary transformations: to find the rank of the matrix
using elementary transformations: to find the rank of the matrix  it should be brought to a triangular form using elementary transformations
it should be brought to a triangular form using elementary transformations  . Then the rank of the matrix
. Then the rank of the matrix  will be equal to the number of non-zero rows in the resulting matrix
will be equal to the number of non-zero rows in the resulting matrix  .
.
Example 10.
Find the rank of a matrix  by the method of elementary transformations
by the method of elementary transformations

Solution.
Let's swap the first and second lines (since the first element of the second line is −1 and it will be convenient to perform transformations with it). As a result, we obtain a matrix equivalent to this one.


Let's denote  -that row of the matrix –
-that row of the matrix –  . We need to reduce the original matrix to triangular form. We will consider the first line to be the leading line; it will participate in all transformations, but itself remains unchanged.
. We need to reduce the original matrix to triangular form. We will consider the first line to be the leading line; it will participate in all transformations, but itself remains unchanged.
At the first stage, we will perform transformations that allow us to get zeros in the first column, except for the first element. To do this, subtract the first line from the second line, multiplied by 2  , add the first to the third line
, add the first to the third line  , and from the third we subtract the first, multiplied by 3
, and from the third we subtract the first, multiplied by 3  We obtain a matrix whose rank coincides with the rank of this matrix. Let's denote it with the same letter
We obtain a matrix whose rank coincides with the rank of this matrix. Let's denote it with the same letter  :
:
 .
.
Since we need to reduce the matrix to form (5), we subtract the second from the fourth row. In this case we have:
 .
.
A matrix of triangular form is obtained, and we can conclude that  , i.e. the number of non-zero lines. Briefly, the solution to the problem can be written as follows:
, i.e. the number of non-zero lines. Briefly, the solution to the problem can be written as follows:


Let some matrix be given:
 .
.
Let us select in this matrix  arbitrary strings and
arbitrary strings and  arbitrary columns
arbitrary columns  . Then the determinant
. Then the determinant  th order, composed of matrix elements
th order, composed of matrix elements  , located at the intersection of selected rows and columns, is called a minor
, located at the intersection of selected rows and columns, is called a minor  th order matrix
th order matrix  .
.
Definition 1.13. Matrix rank  is the largest order of the non-zero minor of this matrix.
is the largest order of the non-zero minor of this matrix.
To calculate the rank of a matrix, one should consider all its minors of the lowest order and, if at least one of them is different from zero, proceed to considering the minors of the highest order. This approach to determining the rank of a matrix is called the bordering method (or the method of bordering minors).
Problem 1.4. Using the method of bordering minors, determine the rank of the matrix  .
.
 .
.
Consider first-order edging, for example,  . Then we move on to consider some second-order edging.
. Then we move on to consider some second-order edging.
For example,  .
.
Finally, let's analyze the third-order bordering.
 .
.
So the highest order of a non-zero minor is 2, hence  .
.
When solving Problem 1.4, you can notice that a number of second-order bordering minors are nonzero. In this regard, the following concept applies.
Definition 1.14. A basis minor of a matrix is any non-zero minor whose order is equal to the rank of the matrix.
Theorem 1.2.(Basis minor theorem). The basis rows (basis columns) are linearly independent.
Note that the rows (columns) of a matrix are linearly dependent if and only if at least one of them can be represented as a linear combination of the others.
Theorem 1.3. The number of linearly independent matrix rows is equal to the number of linearly independent matrix columns and is equal to the rank of the matrix.
Theorem 1.4.(Necessary and sufficient condition for the determinant to be equal to zero). In order for the determinant  -th order
-th order  was equal to zero, it is necessary and sufficient that its rows (columns) be linearly dependent.
was equal to zero, it is necessary and sufficient that its rows (columns) be linearly dependent.
Calculating the rank of a matrix based on its definition is too cumbersome. This becomes especially important for matrices of high orders. In this regard, in practice, the rank of a matrix is calculated based on the application of Theorems 10.2 - 10.4, as well as the use of the concepts of matrix equivalence and elementary transformations.
Definition 1.15. Two matrices  And
And  are called equivalent if their ranks are equal, i.e.
are called equivalent if their ranks are equal, i.e.  .
.
If matrices  And
And  are equivalent, then note
are equivalent, then note 
 .
.
Theorem 1.5. The rank of the matrix does not change due to elementary transformations.
We will call elementary matrix transformations  any of the following operations on a matrix:
any of the following operations on a matrix:
Replacing rows with columns and columns with corresponding rows;
Rearranging matrix rows;
Crossing out a line whose elements are all zero;
Multiplying a string by a number other than zero;
Adding to the elements of one line the corresponding elements of another line multiplied by the same number  .
.
Corollary of Theorem 1.5. If matrix  obtained from matrix
obtained from matrix  using a finite number of elementary transformations, then the matrix
using a finite number of elementary transformations, then the matrix  And
And  are equivalent.
are equivalent.
When calculating the rank of a matrix, it should be reduced to a trapezoidal form using a finite number of elementary transformations.
Definition 1.16. We will call trapezoidal a form of matrix representation when in the bordering minor of the highest order non-zero, all elements below the diagonal ones vanish. For example:
 .
.

Here  , matrix elements
, matrix elements  go to zero. Then the form of representation of such a matrix will be trapezoidal.
go to zero. Then the form of representation of such a matrix will be trapezoidal.
As a rule, matrices are reduced to a trapezoidal shape using the Gaussian algorithm. The idea of the Gauss algorithm is that, by multiplying the elements of the first row of the matrix by the corresponding factors, it is achieved that all elements of the first column located below the element  , would turn to zero. Then, multiplying the elements of the second column by the corresponding factors, we ensure that all elements of the second column located below the element
, would turn to zero. Then, multiplying the elements of the second column by the corresponding factors, we ensure that all elements of the second column located below the element  , would turn to zero. Then proceed in the same way.
, would turn to zero. Then proceed in the same way.
Problem 1.5. Determine the rank of a matrix by reducing it to a trapezoidal shape.
 .
.
To make it easier to use the Gaussian algorithm, you can swap the first and third lines.





 .
.
It's obvious that here  . However, to bring the result to a more elegant form, you can further continue transforming the columns.
. However, to bring the result to a more elegant form, you can further continue transforming the columns.







 .
.
Consider a matrix A of size .
A=  Let us select k rows and k columns (
Let us select k rows and k columns (  ).
).
Definition 26:Minor The kth order of a matrix A is the determinant of a square matrix obtained from a given one by selecting it.
krows and kcolumns.
Definition 27:Rank of a matrix is called the largest of the non-zero orders of its minors, r(A).
Definition 28: A minor whose order coincides with its rank is called basic minor.
Statement:
1. Rank is expressed as an integer.(  )
)
2. r=0,  , when A is zero.
, when A is zero.
Elementary transformations of matrices.
Elementary matrix transformations include the following:
1) multiplying all elements of any row (column) of a matrix by the same number.
2) adding to the elements of any row (column) of the matrix the corresponding elements of another row (column) multiplied by the same number;
3) rearranging the rows (columns) of the matrix;
4) discarding the zero row (column);
5) replacing the rows of the matrix with the corresponding columns.
Definition 29: Matrices resulting from one another under elementary transformations are called equivalent matrices and are denoted by “~“
The main property of equivalent matrices: The ranks of equivalent matrices are equal.
Example 18: Calculate r(A), 
Solution: Multiply the first line step by step by (-4)(-2)
(-7) and then add to the second, third and fourth lines respectively.
~
swap the second and fourth lines  multiply the second line by (-2) and add it to the fourth line; Let's add the second and third lines.
multiply the second line by (-2) and add it to the fourth line; Let's add the second and third lines.
 Let's add the third and fourth lines.
Let's add the third and fourth lines.
~ remove the zero line
remove the zero line
~ r(A)=3
r(A)=3  rank of the original matrix
rank of the original matrix
equals three.
Definition 30: Let's call matrix A stepwise if all elements of the main diagonal  0, and the elements under the main diagonal are zero.
0, and the elements under the main diagonal are zero.
Offer:
1) the rank of a step matrix is equal to the number of its rows;
2) any matrix can be reduced to echelon form using elementary transformations.
Example 19: At what values matrix  has a rank equal to one?
has a rank equal to one?
Solution: The rank is equal to one if the second-order determinant is equal to zero, i.e.

§6. Systems of linear equations of general form.
View system  ---(9) is called a system of general form.
---(9) is called a system of general form.
Definition 31: Two systems are called equivalent if each solution of the first system is a solution of the second and vice versa.
In system (1) matrix A=  we call it the main matrix of the system, and
we call it the main matrix of the system, and  =
= extended matrix system
extended matrix system
Theorem. Kronecker-Capelli
For system (9) to be compatible, it is necessary and sufficient that the rank of the main matrix of the system is equal to the rank of the extended matrix, i.e. r(A)=r(  )
)
Theorem 1. If the rank of the matrix of a joint system is equal to the number of unknowns, then the system has a unique solution.
Theorem 2. If the rank of the matrix of a joint system is less than the number of unknowns, then the system has an infinite number of solutions.
Rule for solving an arbitrary system of linear equations:
1) find the ranks of the main and extended matrices of the system. If  , then the system is not compatible.
, then the system is not compatible.
2) If  =r, then the system is consistent. Find some basic minor of order r. We will call the minor minor on the basis of which the rank of the matrix was determined.
=r, then the system is consistent. Find some basic minor of order r. We will call the minor minor on the basis of which the rank of the matrix was determined.
The unknowns whose coefficients are included in the basic minor are called principal (basic) and are left on the left, while the remaining unknowns are called free and transferred to the right side of the equation.
3) Find expressions of the main unknowns using free ones. A general solution of the system is obtained.
Example 20: Investigate the system and, if it is compatible, find either a unique or general solution 
Solution: 1) according to T. Kronecker-Capelli, we find the ranks of the extended and main matrices of the system:
 ~
~ ~
~
~ ~
~ the rank of the main matrix is two
the rank of the main matrix is two
2)
find the rank of the extended matrix  ~
~ ~
~ ~
~
3) Conclusion: =2, then the system is consistent.
=2, then the system is consistent.
But 
 the system is uncertain and has countless solutions.
the system is uncertain and has countless solutions.
4) Basic unknowns  And
And  , since they belong to the basis minor, and
, since they belong to the basis minor, and  - free unknown.
- free unknown.
Let  =c, where c is any number.
=c, where c is any number.
5) The last matrix corresponds to the system 


6)Answer: 
7) Check: into any of the equations of the original system, where all the unknowns are present, we substitute the found values.
This article will discuss such a concept as the rank of a matrix and the necessary additional concepts. We will give examples and proofs of finding the rank of a matrix, and also tell you what a matrix minor is and why it is so important.
Matrix minor
To understand what the rank of a matrix is, you need to understand the concept of matrix minor.
Definition 1
Minorkth order of the matrix is the determinant of a square matrix of order k×k, which is composed of elements of matrix A located in pre-selected k-rows and k-columns, while maintaining the position of the elements of matrix A.
Simply put, if in matrix A you delete (p-k) rows and (n-k) columns, and from those elements that remain, create a matrix, preserving the arrangement of the elements of matrix A, then the determinant of the resulting matrix is the order k minor of matrix A.
From the example it follows that the first-order minors of matrix A are the matrix elements themselves.
We can give several examples of 2nd order minors. Let's select two rows and two columns. For example, 1st and 2nd row, 3rd and 4th column.
With this choice of elements, the second order minor will be - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2
Another 2nd order minor of matrix A is 0 0 1 1 = 0
Let us provide illustrations of the construction of second-order minors of matrix A:
A 3rd order minor is obtained by crossing out the third column of matrix A:
0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9
Illustration of how the 3rd order minor of matrix A is obtained:
For a given matrix, there are no minors higher than 3rd order, because
k ≤ m i n (p , n) = m i n (3 , 4) = 3
How many minors of order k are there for matrix A of order p×n?
The number of minors is calculated using the following formula:
C p k × C n k , where e C p k = p ! k! (p - k) ! and C n k = n ! k! (n - k) ! - the number of combinations from p to k, from n to k, respectively.
After we have determined what the minors of matrix A are, we can proceed to determining the rank of matrix A.
Matrix rank: methods of finding
Definition 2Matrix rank - the highest order of the matrix other than zero.
Designation 1
Rank (A), Rg (A), Rang (A).
From the definition of the rank of a matrix and the minor of a matrix, it becomes clear that the rank of a zero matrix is equal to zero, and the rank of a nonzero matrix is different from zero.
Finding the rank of a matrix by definition
Definition 3Method of enumerating minors - a method based on determining the rank of a matrix.
Algorithm of actions using the method of enumerating minors :
It is necessary to find the rank of a matrix A of order p× n. If there is at least one non-zero element, then the rank of the matrix is at least equal to one ( because there is a 1st order minor that is not equal to zero).
Next comes the enumeration of 2nd order minors. If all 2nd order minors are equal to zero, then the rank is equal to one. If there is at least one non-zero minor of the 2nd order, it is necessary to move on to enumerating the minors of the 3rd order, and the rank of the matrix, in this case, will be equal to at least two.
We will do the same with the rank of the 3rd order: if all the minors of the matrix are equal to zero, then the rank will be equal to two. If there is at least one non-zero minor of the 3rd order, then the rank of the matrix is at least three. And so on, by analogy.
Example 2
Find the rank of the matrix:
A = - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7
Since the matrix is non-zero, its minimum rank is one.
The 2nd order minor - 1 1 2 2 = (- 1) × 2 - 1 × 2 = 4 is non-zero. It follows that the rank of matrix A is at least two.
We sort out the 3rd order minors: C 3 3 × C 5 3 = 1 5! 3! (5 - 3) ! = 10 pieces.
1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (- 1) × 6 × 3 = 0
1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 - (- 1) × 0 × 11 = 0
1 1 - 2 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (- 1) × 0 × 3 = 0
1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0
1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0
1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0
1 - 2 0 6 0 - 4 11 1 - 7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0
Minors of the 3rd order are equal to zero, so the rank of the matrix is two.
Answer : Rank (A) = 2.
Finding the rank of a matrix using the bordering minors method
Definition 3Bordering minor method - a method that allows you to get results with less computational work.
Edge minor - minor M o k (k + 1) of the th order of the matrix A, which borders the minor M of order k of the matrix A, if the matrix that corresponds to the minor M o k “contains” the matrix that corresponds to the minor M.
Simply put, the matrix that corresponds to the bordering minor M is obtained from the matrix corresponding to the bordering minor M o k by deleting the elements of one row and one column.
Example 3
Find the rank of the matrix:
A = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5
To find the rank we take the 2nd order minor M = 2 - 1 4 1
We write down all the bordering minors:
1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .
To justify the method of bordering minors, we present a theorem, the formulation of which does not require a proof.
Theorem 1
If all minors bordering the kth order minor of a matrix A of order p by n are equal to zero, then all minors of order (k+1) of the matrix A are equal to zero.
Algorithm of actions :
To find the rank of a matrix, it is not necessary to go through all the minors, just look at the bordering ones.
If the bordering minors are equal to zero, then the rank of the matrix is zero. If there is at least one minor that is not equal to zero, then we consider bordering minors.
If they are all zero, then Rank(A) is two. If there is at least one non-zero bordering minor, then we proceed to consider its bordering minors. And so on, in the same way.
Example 4
Find the rank of a matrix using the edge minors method
A = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14
How to solve?
Since element a 11 of matrix A is not equal to zero, we take a minor of the 1st order. Let's start looking for a bordering minor that is different from zero:
2 1 4 2 = 2 × 2 - 1 × 4 = 0 2 0 4 1 = 2 × 1 - 0 × 4 = 2
We found a bordering minor of the 2nd order not equal to zero 2 0 4 1 .
Let's enumerate the bordering minors - (there are (4 - 2) × (5 - 2) = 6 pieces).
2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0
Answer : Rank(A) = 2.
Finding the rank of a matrix using the Gaussian method (using elementary transformations)
Let's remember what elementary transformations are.
Elementary transformations:
- by rearranging the rows (columns) of the matrix;
- by multiplying all elements of any row (column) of the matrix by an arbitrary non-zero number k;
by adding to the elements of any row (column) elements that correspond to another row (column) of the matrix, which are multiplied by an arbitrary number k.
Definition 5
Finding the rank of a matrix using the Gaussian method - a method that is based on the theory of matrix equivalence: if matrix B is obtained from matrix A using a finite number of elementary transformations, then Rank(A) = Rank(B).
The validity of this statement follows from the definition of the matrix:
- If the rows or columns of a matrix are rearranged, its determinant changes sign. If it is equal to zero, then when rearranging rows or columns it remains equal to zero;
- in the case of multiplying all elements of any row (column) of the matrix by an arbitrary number k that is not equal to zero, the determinant of the resulting matrix is equal to the determinant of the original matrix, which is multiplied by k;
in the case of adding to the elements of a certain row or column of a matrix the corresponding elements of another row or column, which are multiplied by the number k, does not change its determinant.
The essence of the method of elementary transformations : reduce the matrix whose rank needs to be found to a trapezoidal one using elementary transformations.
For what?
The rank of matrices of this type is quite easy to find. It is equal to the number of lines that have at least one non-zero element. And since the rank does not change when carrying out elementary transformations, this will be the rank of the matrix.
Let's illustrate this process:
- for rectangular matrices A of order p by n, the number of rows of which is greater than the number of columns:
A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 n 0 0 0 ⋯ 0 1 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 , R a n k (A) = n
A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k
- for rectangular matrices A of order p by n, the number of rows of which is less than the number of columns:
A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b p p + 1 ⋯ b p n , R a n k (A) = p
A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0
- for square matrices A of order n by n:
A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 n 0 0 0 ⋯ 0 1 , R a n k (A) = n
A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k (A) = k , k< n
Example 5
Find the rank of matrix A using elementary transformations:
A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11
How to solve?
Since element a 11 is different from zero, it is necessary to multiply the elements of the first row of matrix A by 1 a 11 = 1 2:
A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~
We add to the elements of the 2nd line the corresponding elements of the 1st line, which are multiplied by (-3). To the elements of the 3rd line we add the elements of the 1st line, which are multiplied by (-1):
~ A (1) = 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ A (2) = = 1 1 2 - 1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =
1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10
Element a 22 (2) is non-zero, so we multiply the elements of the 2nd row of matrix A by A (2) by 1 a 22 (2) = - 2 3:
A (3) = 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ A (4) = 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0
- To the elements of the 3rd row of the resulting matrix we add the corresponding elements of the 2nd row, which are multiplied by 3 2;
- to the elements of the 4th line - the elements of the 2nd line, which are multiplied by 9 2;
- to the elements of the 5th row - the elements of the 2nd row, which are multiplied by 3 2.
All row elements are zero. Thus, using elementary transformations, we brought the matrix to a trapezoidal form, from which it can be seen that R an k (A (4)) = 2. It follows that the rank of the original matrix is also equal to two.
Comment
If you carry out elementary transformations, then approximate values are not allowed!
If you notice an error in the text, please highlight it and press Ctrl+Enter
 Projections of the displacement vector Module of body displacement over time
Projections of the displacement vector Module of body displacement over time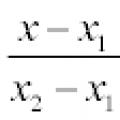 Equation of a line - types of equation of a line: passing through a point, general, canonical, parametric, etc.
Equation of a line - types of equation of a line: passing through a point, general, canonical, parametric, etc. Uniformly accelerated motion: formulas, examples
Uniformly accelerated motion: formulas, examples