Fibonacci series. Key
The text of the work is placed without images and formulas.
The full version of the work is available in the "Job Files" tab in PDF format
THE HIGHEST PURPOSE OF MATHEMATICS IS TO FIND THE HIDDEN ORDER IN THE CHAOS THAT SURROUNDS US.
Viner N.
A person strives for knowledge all his life, tries to study the world around him. And in the process of observation, he has questions that need to be answered. Answers are found, but new questions appear. In archaeological finds, in the traces of civilization, distant from each other in time and space, one and the same element is found - a pattern in the form of a spiral. Some consider it a symbol of the sun and associate it with the legendary Atlantis, but its true meaning is unknown. What do the shapes of a galaxy and an atmospheric cyclone, the arrangement of leaves on a stem and seeds in a sunflower have in common? These patterns come down to the so-called "golden" spiral, the amazing Fibonacci sequence, discovered by the great Italian mathematician of the 13th century.
History of Fibonacci Numbers
For the first time about what Fibonacci numbers are, I heard from a mathematics teacher. But, besides, how the sequence of these numbers is formed, I did not know. This is what this sequence is actually famous for, how it affects a person, and I want to tell you. Little is known about Leonardo Fibonacci. There is not even an exact date of his birth. It is known that he was born in 1170 in the family of a merchant, in the city of Pisa in Italy. Fibonacci's father was often in Algiers on business, and Leonardo studied mathematics there with Arab teachers. Subsequently, he wrote several mathematical works, the most famous of which is the "Book of the abacus", which contains almost all the arithmetic and algebraic information of that time. 2
Fibonacci numbers are a sequence of numbers with a number of properties. Fibonacci discovered this numerical sequence by accident when he tried to solve a practical problem about rabbits in 1202. “Someone placed a pair of rabbits in a certain place, enclosed on all sides by a wall, in order to find out how many pairs of rabbits will be born during the year, if the nature of rabbits is such that in a month a pair of rabbits gives birth to another pair, and rabbits give birth from the second months after his birth. When solving the problem, he took into account that each pair of rabbits gives birth to two more pairs during their life, and then dies. This is how the sequence of numbers appeared: 1, 1, 2, 3, 5, 8, 13, 21, ... In this sequence, each next number is equal to the sum of the two previous ones. It's called the Fibonacci sequence. Mathematical properties of a sequence
I wanted to explore this sequence, and I identified some of its properties. This rule is of great importance. The sequence slowly approaches some constant ratio of about 1.618, and the ratio of any number to the next is about 0.618.
One can notice a number of curious properties of Fibonacci numbers: two neighboring numbers are coprime; every third number is even; every fifteenth ends in zero; every fourth is a multiple of three. If you choose any 10 neighboring numbers from the Fibonacci sequence and add them together, you will always get a number that is a multiple of 11. But that's not all. Each sum is equal to the number 11 multiplied by the seventh member of the given sequence. And here is another interesting feature. For any n, the sum of the first n members of the sequence will always be equal to the difference of the (n + 2) -th and first member of the sequence. This fact can be expressed by the formula: 1+1+2+3+5+…+an=a n+2 - 1. Now we have the following trick: to find the sum of all terms
sequence between two given members, it suffices to find the difference of the corresponding (n+2)-x members. For example, a 26 + ... + a 40 \u003d a 42 - a 27. Now let's look for a connection between Fibonacci, Pythagoras and the "golden section". The most famous evidence of the mathematical genius of mankind is the Pythagorean theorem: in any right triangle, the square of the hypotenuse is equal to the sum of the squares of its legs: c 2 \u003d b 2 + a 2. From a geometric point of view, we can consider all the sides of a right triangle as the sides of three squares built on them. The Pythagorean theorem says that the total area of the squares built on the legs of a right triangle is equal to the area of the square built on the hypotenuse. If the lengths of the sides of a right triangle are integers, then they form a group of three numbers called Pythagorean triples. Using the Fibonacci sequence, you can find such triples. Take any four consecutive numbers from the sequence, for example, 2, 3, 5 and 8, and construct three more numbers as follows: 1) the product of the two extreme numbers: 2*8=16; 2) the double product of the two numbers in the middle: 2* (3 * 5) \u003d 30; 3) the sum of the squares of two average numbers: 3 2 +5 2 \u003d 34; 34 2 =30 2 +16 2 . This method works for any four consecutive Fibonacci numbers. Predictably, any three consecutive numbers of the Fibonacci series behave in a predictable way. If you multiply the two extremes of them and compare the result with the square of the average number, then the result will always differ by one. For example, for numbers 5, 8 and 13 we get: 5*13=8 2 +1. If we consider this property from the point of view of geometry, we can notice something strange. Divide the square
size 8x8 (total 64 small squares) into four parts, the lengths of the sides of which are equal to the Fibonacci numbers. Now from these parts we will build a rectangle measuring 5x13. Its area is 65 small squares. Where does the extra square come from? The thing is that a perfect rectangle is not formed, but tiny gaps remain, which in total give this additional unit of area. Pascal's triangle also has a connection with the Fibonacci sequence. You just need to write the lines of Pascal's triangle one under the other, and then add the elements diagonally. Get the Fibonacci sequence.
Now consider a "golden" rectangle, one side of which is 1.618 times longer than the other. At first glance, it may seem like an ordinary rectangle to us. However, let's do a simple experiment with two ordinary bank cards. Let's put one of them horizontally and the other vertically so that their lower sides are on the same line. If we draw a diagonal line in a horizontal map and extend it, we will see that it will pass exactly through the upper right corner of the vertical map - a pleasant surprise. Maybe this is an accident, or maybe such rectangles and other geometric shapes using the "golden ratio" are especially pleasing to the eye. Did Leonardo da Vinci think about the golden ratio while working on his masterpiece? This seems unlikely. However, it can be argued that he attached great importance to the connection between aesthetics and mathematics.
Fibonacci numbers in nature
The connection of the golden section with beauty is not only a matter of human perception. It seems that nature itself has allocated a special role to F. If squares are sequentially inscribed in the "golden" rectangle, then an arc is drawn in each square, then an elegant curve is obtained, which is called a logarithmic spiral. It is not a mathematical curiosity at all. 5
On the contrary, this wonderful line is often found in the physical world: from the shell of a nautilus to the arms of galaxies, and in the elegant spiral of the petals of a full-blown rose. The connections between the golden ratio and Fibonacci numbers are numerous and unexpected. Consider a flower that looks very different from a rose - a sunflower with seeds. The first thing we see is that the seeds are arranged in two kinds of spirals: clockwise and counterclockwise. If we count the clockwise spirals, we get two seemingly ordinary numbers: 21 and 34. This is not the only example when you can find Fibonacci numbers in the structure of plants.
Nature gives us numerous examples of the arrangement of homogeneous objects described by Fibonacci numbers. In the various spiral arrangements of small plant parts, two families of spirals can usually be seen. In one of these families, the spirals curl clockwise, and in the other - counterclockwise. Spiral numbers of one type and another often turn out to be neighboring Fibonacci numbers. So, taking a young pine twig, it is easy to notice that the needles form two spirals, going from bottom left to right up. On many cones, the seeds are arranged in three spirals, gently winding around the stem of the cone. They are arranged in five spirals, winding steeply in the opposite direction. In large cones, it is possible to observe 5 and 8, and even 8 and 13 spirals. The Fibonacci spirals are also clearly visible on the pineapple: there are usually 8 and 13 of them.
The chicory shoot makes a strong ejection into space, stops, releases a leaf, but already shorter than the first one, again makes an ejection into space, but of less force, releases an even smaller leaf and ejection again. Its growth impulses gradually decrease in proportion to the "golden" section. To appreciate the huge role of Fibonacci numbers, just look at the beauty of the nature around us. Fibonacci numbers can be found in quantity
branches on the stem of each growing plant and in the number of petals.
Let's count the petals of some flowers - the iris with its 3 petals, the primrose with 5 petals, the ragweed with 13 petals, the daisy with 34 petals, the aster with 55 petals, and so on. Is this a coincidence, or is it the law of nature? Look at the stems and flowers of the yarrow. Thus, the total Fibonacci sequence can easily interpret the pattern of manifestations of the "Golden" numbers found in nature. These laws operate regardless of our consciousness and the desire to accept them or not. The patterns of "golden" symmetry are manifested in the energy transitions of elementary particles, in the structure of some chemical compounds, in planetary and space systems, in the gene structures of living organisms, in the structure of individual human organs and the body as a whole, and also manifest themselves in biorhythms and the functioning of the brain and visual perception.
Fibonacci numbers in architecture
The Golden Ratio also manifests itself in many remarkable architectural creations throughout the history of mankind. It turns out that even ancient Greek and Egyptian mathematicians knew these coefficients long before Fibonacci and called them the "golden section". The principle of the "golden section" was used by the Greeks in the construction of the Parthenon, the Egyptians - the Great Pyramid of Giza. Advances in building technology and the development of new materials opened up new possibilities for 20th-century architects. American Frank Lloyd Wright was one of the main proponents of organic architecture. Shortly before his death, he designed the Solomon Guggenheim Museum in New York, which is an inverted spiral, and the interior of the museum resembles a nautilus shell. Polish-Israeli architect Zvi Hecker also used spiral structures in the design of the Heinz Galinski School in Berlin, completed in 1995. Hecker started with the idea of a sunflower with a central circle, from where
all architectural elements diverge. The building is a combination
orthogonal and concentric spirals, symbolizing the interaction of limited human knowledge and controlled chaos of nature. Its architecture mimics a plant that follows the movement of the sun, so the classrooms are lit up throughout the day.
In Quincy Park, located in Cambridge, Massachusetts (USA), the "golden" spiral can often be found. The park was designed in 1997 by artist David Phillips and is located near the Clay Mathematical Institute. This institution is a well-known center for mathematical research. In Quincy Park, you can walk among the "golden" spirals and metal curves, reliefs of two shells and a rock with a square root symbol. On the plate is written information about the "golden" proportion. Even bike parking uses the F symbol.
Fibonacci numbers in psychology
In psychology, there are turning points, crises, upheavals that mark the transformation of the structure and functions of the soul on a person's life path. If a person has successfully overcome these crises, then he becomes able to solve problems of a new class, which he had not even thought about before.
The presence of fundamental changes gives reason to consider the time of life as a decisive factor in the development of spiritual qualities. After all, nature measures time for us not generously, “no matter how much it will be, so much will be,” but just enough so that the development process materializes:
in the structures of the body;
in feelings, thinking and psychomotor - until they acquire harmony necessary for the emergence and launch of the mechanism
creativity;
in the structure of human energy potential.
The development of the body cannot be stopped: the child becomes an adult. With the mechanism of creativity, everything is not so simple. Its development can be stopped and its direction changed.
Is there a chance to catch up with time? Undoubtedly. But for this you need to do a lot of work on yourself. What develops freely, naturally, does not require special efforts: the child develops freely and does not notice this enormous work, because the process of free development is created without violence against oneself.
How is the meaning of the life path understood in everyday consciousness? The inhabitant sees it like this: at the foot - the birth, at the top - the prime of life, and then - everything goes downhill.
The wise man will say: everything is much more complicated. He divides the ascent into stages: childhood, adolescence, youth ... Why is that? Few people are able to answer, although everyone is sure that these are closed, integral stages of life.
To find out how the mechanism of creativity develops, V.V. Klimenko used mathematics, namely the laws of Fibonacci numbers and the proportion of the "golden section" - the laws of nature and human life.
Fibonacci numbers divide our life into stages according to the number of years lived: 0 - the beginning of the countdown - the child was born. He still lacks not only psychomotor skills, thinking, feelings, imagination, but also operational energy potential. He is the beginning of a new life, a new harmony;
1 - the child has mastered walking and masters the immediate environment;
2 - understands speech and acts using verbal instructions;
3 - acts through the word, asks questions;
5 - "age of grace" - the harmony of psychomotor, memory, imagination and feelings, which already allow the child to embrace the world in all its integrity;
8 - feelings come to the fore. They are served by imagination, and thinking, by the forces of its criticality, is aimed at supporting the internal and external harmony of life;
13 - the mechanism of talent begins to work, aimed at transforming the material acquired in the process of inheritance, developing one's own talent;
21 - the mechanism of creativity has approached a state of harmony and attempts are being made to perform talented work;
34 - harmony of thinking, feelings, imagination and psychomotor skills: the ability to brilliant work is born;
55 - at this age, subject to the preserved harmony of soul and body, a person is ready to become a creator. And so on…
What are Fibonacci serifs? They can be compared to dams on the path of life. These dams await each of us. First of all, it is necessary to overcome each of them, and then patiently raise your level of development, until one day it falls apart, opening the way to the next free flow.
Now that we understand the meaning of these nodal points of age development, let's try to decipher how it all happens.
At 1 year the child learns to walk. Before that, he knew the world with the front of his head. Now he knows the world with his hands - the exclusive privilege of man. The animal moves in space, and he, cognizing, masters the space and masters the territory on which he lives.
2 years understands the word and acts in accordance with it. It means that:
the child learns the minimum number of words - meanings and patterns of action;
yet does not separate itself from the environment and is merged into integrity with the environment,
Therefore, he acts on someone else's instructions. At this age, he is the most obedient and pleasant for parents. From a man of the senses, the child turns into a man of knowledge.
3 years- action with the help of one's own word. The separation of this person from the environment has already taken place - and he is learning to be an independently acting person. Hence he:
consciously opposes the environment and parents, kindergarten teachers, etc.;
is aware of its sovereignty and fights for independence;
tries to subjugate close and well-known people to his will.
Now for a child, a word is an action. This is where the acting person begins.
5 years- Age of Grace. He is the personification of harmony. Games, dances, dexterous movements - everything is saturated with harmony, which a person tries to master with his own strength. Harmonious psychomotor contributes to bringing to a new state. Therefore, the child is directed to psychomotor activity and strives for the most active actions.
Materialization of the products of the work of sensitivity is carried out through:
the ability to display the environment and ourselves as part of this world (we hear, see, touch, smell, etc. - all sense organs work for this process);
ability to design the outside world, including yourself
(creation of a second nature, hypotheses - to do both tomorrow, build a new machine, solve a problem), by the forces of critical thinking, feelings and imagination;
the ability to create a second, man-made nature, products of activity (implementation of the plan, specific mental or psychomotor actions with specific objects and processes).
After 5 years, the imagination mechanism comes forward and begins to dominate the rest. The child does a gigantic job, creating fantastic images, and lives in the world of fairy tales and myths. The hypertrophy of the child's imagination causes surprise in adults, because the imagination does not correspond to reality in any way.
8 years- feelings come to the fore and their own measurements of feelings (cognitive, moral, aesthetic) arise when the child unmistakably:
evaluates the known and the unknown;
distinguishes the moral from the immoral, the moral from the immoral;
beauty from what threatens life, harmony from chaos.
13 years- the mechanism of creativity begins to work. But that doesn't mean it's working at full capacity. One of the elements of the mechanism comes to the fore, and all the others contribute to its work. If even in this age period of development harmony is preserved, which almost all the time rebuilds its structure, then the lad will painlessly get to the next dam, overcome it imperceptibly and will live at the age of a revolutionary. At the age of a revolutionary, the youth must take a new step forward: to separate from the nearest society and live in it a harmonious life and activity. Not everyone can solve this problem that arises before each of us.
21 years old If a revolutionary has successfully overcome the first harmonious peak of life, then his mechanism of talent is capable of fulfilling a talented
work. Feelings (cognitive, moral or aesthetic) sometimes overshadow thinking, but in general all elements work in harmony: feelings are open to the world, and logical thinking is able to name and find measures of things from this peak.
The mechanism of creativity, developing normally, reaches a state that allows it to receive certain fruits. He starts to work. At this age, the mechanism of feelings comes forward. As the imagination and its products are evaluated by feelings and thinking, antagonism arises between them. Feelings win. This ability is gradually gaining power, and the boy begins to use it.
34 years- balance and harmony, productive effectiveness of talent. Harmony of thinking, feelings and imagination, psychomotor skills, which is replenished with optimal energy potential, and the mechanism as a whole - an opportunity is born to perform brilliant work.
55 years- a person can become a creator. The third harmonious peak of life: thinking subdues the power of feelings.
Fibonacci numbers name the stages of human development. Whether a person goes through this path without stopping depends on parents and teachers, the educational system, and then on himself and on how a person will learn and overcome himself.
On the path of life, a person discovers 7 objects of relationships:
From birthday to 2 years - the discovery of the physical and objective world of the immediate environment.
From 2 to 3 years - the discovery of oneself: "I am Myself."
From 3 to 5 years - speech, the effective world of words, harmony and the "I - You" system.
From 5 to 8 years old - the discovery of the world of other people's thoughts, feelings and images - the "I - We" system.
From 8 to 13 years old - the discovery of the world of tasks and problems solved by the geniuses and talents of mankind - the system "I - Spirituality".
From 13 to 21 years old - the discovery of the ability to independently solve well-known tasks, when thoughts, feelings and imagination begin to work actively, the "I - Noosphere" system arises.
From 21 to 34 years old - the discovery of the ability to create a new world or its fragments - the realization of the self-concept "I am the Creator".
The life path has a space-time structure. It consists of age and individual phases, determined by many parameters of life. A person masters to a certain extent the circumstances of his life, becomes the creator of his history and the creator of the history of society. A truly creative attitude to life, however, does not appear immediately and not even in every person. There are genetic links between the phases of the life path, and this determines its natural character. It follows that, in principle, it is possible to predict future development on the basis of knowledge of its early phases.
Fibonacci numbers in astronomy
It is known from the history of astronomy that I. Titius, a German astronomer of the 18th century, using the Fibonacci series, found regularity and order in the distances between the planets of the solar system. But one case seemed to be against the law: there was no planet between Mars and Jupiter. But after the death of Titius at the beginning of the XIX century. concentrated observation of this part of the sky led to the discovery of the asteroid belt.
Conclusion
In the process of research, I found out that Fibonacci numbers are widely used in the technical analysis of stock prices. One of the simplest ways to use Fibonacci numbers in practice is to determine the length of time after which an event will occur, for example, a price change. The analyst counts a certain number of Fibonacci days or weeks (13,21,34,55, etc.) from the previous similar event and makes a forecast. But this is too hard for me to figure out. Although Fibonacci was the greatest mathematician of the Middle Ages, the only monuments to Fibonacci are the statue in front of the Leaning Tower of Pisa and two streets that bear his name, one in Pisa and the other in Florence. And yet, in connection with everything I have seen and read, quite natural questions arise. Where did these numbers come from? Who is this architect of the universe who tried to make it perfect? What will be next? Finding the answer to one question, you get the next. If you solve it, you get two new ones. Deal with them, three more will appear. Having solved them, you will acquire five unresolved ones. Then eight, thirteen, and so on. Do not forget that there are five fingers on two hands, two of which consist of two phalanges, and eight of which consist of three.
Literature:
Voloshinov A.V. "Mathematics and Art", M., Enlightenment, 1992
Vorobyov N.N. "Fibonacci numbers", M., Nauka, 1984
Stakhov A.P. "The Da Vinci Code and the Fibonacci Series", Peter Format, 2006
F. Corvalan “The Golden Ratio. Mathematical language of beauty”, M., De Agostini, 2014
Maksimenko S.D. "Sensitive periods of life and their codes".
"Fibonacci numbers". Wikipedia
There are still many unsolved mysteries in the universe, some of which scientists have already been able to identify and describe. Fibonacci numbers and the golden ratio form the basis for unraveling the world around us, building its shape and optimal visual perception by a person, with the help of which he can feel beauty and harmony.
golden ratio
The principle of determining the size of the golden section underlies the perfection of the whole world and its parts in its structure and functions, its manifestation can be seen in nature, art and technology. The doctrine of the golden ratio was founded as a result of research by ancient scientists on the nature of numbers.
It is based on the theory of the proportions and ratios of segment divisions, which was made by the ancient philosopher and mathematician Pythagoras. He proved that when dividing a segment into two parts: X (smaller) and Y (larger), the ratio of the larger to the smaller will be equal to the ratio of their sum (of the entire segment):
The result is an equation: x 2 - x - 1=0, which is solved as x=(1±√5)/2.
If we consider the ratio 1/x, then it is equal to 1,618…
Evidence of the use of the golden ratio by ancient thinkers is given in the book of Euclid's "Beginnings", written back in the 3rd century. BC, who used this rule to construct regular 5-gons. Among the Pythagoreans, this figure is considered sacred, since it is both symmetrical and asymmetrical. The pentagram symbolized life and health.
Fibonacci numbers
The famous book Liber abaci by the Italian mathematician Leonardo of Pisa, who later became known as Fibonacci, was published in 1202. In it, the scientist for the first time gives a pattern of numbers, in a series of which each number is the sum of the 2 previous digits. The sequence of Fibonacci numbers is as follows:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, etc.
The scientist also cited a number of patterns:
- Any number from the series, divided by the next, will be equal to a value that tends to 0.618. Moreover, the first Fibonacci numbers do not give such a number, but as you move from the beginning of the sequence, this ratio will be more and more accurate.
- If you divide the number from the series by the previous one, then the result will tend to 1.618.
- One number divided by the next one will show a value tending to 0.382.
The application of the connection and patterns of the golden section, the Fibonacci number (0.618) can be found not only in mathematics, but also in nature, in history, in architecture and construction, and in many other sciences.
Spiral of Archimedes and golden rectangle
Spirals, very common in nature, were explored by Archimedes, who even derived her equation. The shape of the spiral is based on the laws of the golden ratio. When it is untwisted, a length is obtained to which proportions and Fibonacci numbers can be applied, the step increase occurs evenly.
The parallel between the Fibonacci numbers and the golden ratio can also be seen by constructing a "golden rectangle" whose sides are proportional as 1.618:1. It is built by moving from a larger rectangle to smaller ones so that the lengths of the sides will be equal to the numbers from the row. Its construction can be done in the reverse order, starting with the square "1". When connecting the corners of this rectangle with lines in the center of their intersection, a Fibonacci or logarithmic spiral is obtained.

The history of the use of golden proportions
Many ancient architectural monuments of Egypt were erected using golden proportions: the famous pyramids of Cheops and others. The architects of Ancient Greece widely used them in the construction of architectural objects, such as temples, amphitheatres, stadiums. For example, such proportions were used in the construction of the ancient Parthenon temple (Athens) and other objects that became masterpieces of ancient architecture, demonstrating harmony based on mathematical regularity.
In later centuries, interest in the golden ratio subsided, and the patterns were forgotten, but again resumed in the Renaissance, along with the book of the Franciscan monk L. Pacioli di Borgo "Divine Proportion" (1509). It included illustrations by Leonardo da Vinci, who fixed the new name "golden section". Also, 12 properties of the golden ratio were scientifically proven, and the author talked about how it manifests itself in nature, in art and called it "the principle of building the world and nature."
Vitruvian Man Leonardo
The drawing by which Leonardo da Vinci illustrated the book of Vitruvius in 1492 depicts a figure of a man in 2 positions with arms extended to the sides. The figure is inscribed in a circle and a square. This drawing is considered to be the canonical proportions of the human body (male), described by Leonardo based on their study in the treatises of the Roman architect Vitruvius.
The center of the body as an equidistant point from the end of the arms and legs is the navel, the length of the arms is equal to the height of a person, the maximum width of the shoulders = 1/8 of the height, the distance from the top of the chest to the hair = 1/7, from the top of the chest to the top of the head = 1/6 etc.

Since then, the drawing has been used as a symbol showing the internal symmetry of the human body.
The term "Golden Ratio" was used by Leonardo to denote proportional relationships in the human figure. For example, the distance from the waist to the feet is related to the same distance from the navel to the top of the head in the same way as the height to the first length (from the waist down). This calculation is done similarly to the ratio of the segments when calculating the golden ratio and tends to 1.618.
All these harmonious proportions are often used by artists to create beautiful and impressive works.
Studies of the golden ratio in the 16th-19th centuries
Using the golden ratio and Fibonacci numbers, research work on the issue of proportions has been going on for more than one century. In parallel with Leonardo da Vinci, the German artist Albrecht Dürer was also developing the theory of the correct proportions of the human body. For this, he even created a special compass.
In the 16th century the question of the connection between the Fibonacci number and the golden section was devoted to the work of the astronomer I. Kepler, who first applied these rules to botany.
A new "discovery" awaited the golden ratio in the 19th century. with the publication of "Aesthetic Research" by the German scientist Professor Zeisig. He raised these proportions to the absolute and announced that they are universal for all natural phenomena. He conducted studies of a huge number of people, or rather their bodily proportions (about 2 thousand), as a result of which conclusions were drawn about statistically confirmed patterns in the ratios of various parts of the body: the length of the shoulders, forearms, hands, fingers, etc.
Art objects (vases, architectural structures), musical tones, sizes when writing poems were also studied - Zeisig displayed all this through the lengths of segments and numbers, he also introduced the term "mathematical aesthetics". After receiving the results, it turned out that the Fibonacci series is obtained.

Fibonacci number and golden ratio in nature
In the plant and animal world, there is a tendency to form in the form of symmetry, which is observed in the direction of growth and movement. The division into symmetrical parts in which golden proportions are observed is a pattern inherent in many plants and animals.
The nature around us can be described using Fibonacci numbers, for example:
- the arrangement of leaves or branches of any plants, as well as the distances, are related to the series of given numbers 1, 1, 2, 3, 5, 8, 13 and so on;
- sunflower seeds (scales on cones, pineapple cells), arranged in two rows in twisted spirals in different directions;
- the ratio of the length of the tail and the entire body of the lizard;
- the shape of the egg, if you draw a line conditionally through its wide part;
- the ratio of the size of the fingers on the human hand.

And, of course, the most interesting forms are the spiraling snail shells, the patterns on the web, the movement of the wind inside a hurricane, the double helix in DNA, and the structure of galaxies - all of which include a sequence of Fibonacci numbers.
The use of the golden ratio in art
Researchers looking for examples of the use of the golden section in art examine in detail various architectural objects and paintings. Famous sculptural works are known, the creators of which adhered to golden proportions - the statues of Olympian Zeus, Apollo Belvedere and
One of the creations of Leonardo da Vinci - "Portrait of Mona Lisa" - has been the subject of research by scientists for many years. They found that the composition of the work entirely consists of "golden triangles", united together into a regular pentagon-star. All the works of da Vinci are evidence of how deep his knowledge of the structure and proportions of the human body was, thanks to which he was able to catch the incredibly mysterious smile of the Mona Lisa.

The golden ratio in architecture
As an example, scientists studied architectural masterpieces created according to the rules of the "golden section": the Egyptian pyramids, the Pantheon, the Parthenon, Notre Dame de Paris Cathedral, St. Basil's Cathedral, etc.
The Parthenon, one of the most beautiful buildings in Ancient Greece (5th century BC), has 8 columns and 17 on different sides, the ratio of its height to the length of the sides is 0.618. The protrusions on its facades are made according to the "golden section" (photo below).

One of the scientists who invented and successfully applied the improvement of the modular system of proportions for architectural objects (the so-called "modulor") was the French architect Le Corbusier. The modulor is based on a measuring system associated with a conditional division into parts of the human body.
The Russian architect M. Kazakov, who built several residential buildings in Moscow, as well as the buildings of the Senate in the Kremlin and the Golitsyn Hospital (now the 1st Clinical named after N.I. Pirogov), was one of the architects who used laws in the design and construction about the golden ratio.
Applying proportions in design
In fashion design, all fashion designers make new images and models, taking into account the proportions of the human body and the rules of the golden ratio, although by nature not all people have ideal proportions.
When planning landscape design and creating volumetric park compositions with the help of plants (trees and shrubs), fountains and small architectural objects, the patterns of "divine proportions" can also be applied. After all, the composition of the park should be focused on creating an impression on the visitor, who will be able to freely navigate in it and find the compositional center.
All elements of the park are in such proportions that, with the help of geometric structure, mutual arrangement, lighting and light, they give the impression of harmony and perfection on a person.
Application of the golden section in cybernetics and technology
The laws of the golden section and Fibonacci numbers are also manifested in energy transitions, in processes occurring with elementary particles that make up chemical compounds, in space systems, in the DNA gene structure.
Similar processes occur in the human body, manifesting itself in the biorhythms of his life, in the action of organs, for example, the brain or vision.
Algorithms and patterns of golden proportions are widely used in modern cybernetics and informatics. One of the simple tasks that beginner programmers are given to solve is to write a formula and determine the sum of Fibonacci numbers up to a certain number using programming languages.
Modern research on the theory of the golden ratio
Since the middle of the 20th century, interest in the problems and influence of the laws of the golden proportions on human life has increased dramatically, and from many scientists of various professions: mathematicians, ethnos researchers, biologists, philosophers, medical workers, economists, musicians, etc.
Since the 1970s, The Fibonacci Quarterly has been published in the United States, where works on this topic are published. Works appear in the press in which the generalized rules of the golden section and the Fibonacci series are used in various branches of knowledge. For example, for coding information, chemical research, biological, etc.

All this confirms the conclusions of ancient and modern scientists that the golden ratio is multilaterally connected with the fundamental issues of science and manifests itself in the symmetry of many creations and phenomena of the world around us.
Fibonacci numbers are elements of a numerical sequence.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, in which each subsequent number is equal to the sum of the previous two numbers. The name is named after the medieval mathematician Leonardo of Pisa (or Fibonacci), who lived and worked as a merchant and mathematician in the Italian city of Pisa. He is one of the most celebrated European scientists of his time. Among his greatest achievements is the introduction of Arabic numerals to replace Roman numerals. Fn=Fn-1+Fn-2
The mathematical series asymptotically (that is, approaching more and more slowly) tends to a constant ratio. However, this attitude is irrational; it has an endless, unpredictable sequence of decimal values lining up after it. It can never be expressed exactly. If each number that is part of the series is divided by the previous value (for example, 13-^8 or 21-FROM), the result of the action is expressed in a ratio that fluctuates around the irrational number 1.61803398875, slightly more or slightly less than the neighboring ratios of the series. The ratio will never, indefinitely, be accurate to the last digit (even with the most powerful computers built in our time). For the sake of brevity, we will use the number 1.618 as the Fibonacci ratio and ask readers not to forget about this error.
Fibonacci numbers are also important when performing analysis. Euclid's algorithm for determining the greatest common divisor of two numbers. The Fibonacci numbers come from Pascal's triangle diagonal formula (binomial coefficients).
Fibonacci numbers have been linked to the Golden Ratio.
The golden ratio was known in ancient Egypt and Babylon, in India and China. What is the "golden section"? The answer is still unknown. Fibonacci numbers are really relevant for the theory of practice in our time. The rise in importance occurred in the 20th century and continues to this day. The use of Fibonacci numbers in economics and computer science attracted masses of people to their study.
The methodology of my research consisted in studying the specialized literature and summarizing the information received, as well as conducting my own research and identifying the properties of numbers and the scope of their use.
In the course of scientific research, she determined the very concept of Fibonacci numbers, their properties. I also found out interesting patterns in wildlife, directly in the structure of sunflower seeds.
On a sunflower, the seeds line up in spirals, and the number of spirals going in the other direction is different - they are consecutive Fibonacci numbers.
This sunflower has 34 and 55.
The same is observed on the fruits of pineapple, where there are 8 and 14 spirals. Corn leaves are associated with the unique property of Fibonacci numbers.
Fractions of the form a/b, corresponding to the helical arrangement of the leaves of the stem legs of a plant, are often ratios of successive Fibonacci numbers. For hazel this ratio is 2/3, for oak 3/5, for poplar 5/8, for willow 8/13, etc.
Considering the arrangement of leaves on the stem of plants, you can see that between each pair of leaves (A and C) the third is located in the place of the golden section (B)
Another interesting property of the Fibonacci number is that the product and the quotient of any two different Fibonacci numbers other than one is never a Fibonacci number.
As a result of the research, I came to the following conclusions: Fibonacci numbers are a unique arithmetic progression that appeared in the 13th century AD. This progression does not lose its relevance, which was confirmed in the course of my research. The Fibonacci number is also found in programming and economic forecasts, in painting, architecture and music. The paintings of such famous artists as Leonardo da Vinci, Michelangelo, Raphael and Botticelli hide the magic of the golden ratio. Even I. I. Shishkin used the golden ratio in his painting “Pine Grove”.
It's hard to believe, but the golden ratio is also found in the musical works of such great composers as Mozart, Beethoven, Chopin, etc.
Fibonacci numbers are also found in architecture. For example, the golden ratio was used in the construction of the Parthenon and Notre Dame Cathedral.
I have found that Fibonacci numbers are being used in our area as well. For example, platbands of houses, gables.
The surrounding world, starting with the smallest invisible particles, and ending with distant galaxies of boundless space, is fraught with many unsolved mysteries. However, the veil of mystery has already been lifted over some of them thanks to the inquisitive minds of a number of scientists.
One such example is golden ratio and Fibonacci numbers that form its basis. This pattern has been displayed in mathematical form and is often found in the nature surrounding a person, once again excluding the possibility that it arose as a result of chance.
Fibonacci numbers and their sequence
Fibonacci number sequence called a series of numbers, each of which is the sum of the previous two:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 …
A feature of this sequence is the numerical values that are obtained by dividing the numbers of this series by each other.
A series of Fibonacci numbers has its own interesting patterns:
- In the Fibonacci series, each number divided by the next will show a value tending towards 0,618 . The farther the numbers are from the beginning of the series, the more accurate the ratio will be. For example, the numbers taken at the beginning of the row 5 And 8 will show 0,625 (5/8=0,625 ). If we take the numbers 144 And 233 , then they will show the ratio 0.618 .
- In turn, if in a series of Fibonacci numbers we divide the number by the previous one, then the result of the division will tend to 1,618 . For example, the same numbers were used as mentioned above: 8/5=1,6 And 233/144=1,618 .
- The number divided by the next one after it will show a value approaching 0,382 . And the farther from the beginning of the series the numbers are taken, the more accurate the value of the ratio: 5/13=0,385 And 144/377=0,382 . Dividing the digits in reverse order will give the result 2,618 : 13/5=2,6 And 377/144=2,618 .
Using the above calculation methods and increasing the gaps between the numbers, you can display the following series of values: 4.235, 2.618, 1.618, 0.618, 0.382, 0.236, which is widely used in Fibonacci tools in the forex market.
Golden Ratio or Divine Proportion
The “golden section” and Fibonacci numbers are very clearly represented by the analogy with a segment. If segment AB is divided by point C in such a ratio that the condition is met:
AC / BC \u003d BC / AB, then it will be the "golden section"

READ ALSO THE FOLLOWING ARTICLES:
Surprisingly, it is this ratio that can be traced in the series of Fibonacci numbers. Taking a few numbers from the series, you can check by calculation that this is so. For example, such a sequence of Fibonacci numbers ... 55, 89, 144 ... Let the number 144 be the whole segment AB, which was mentioned above. Since 144 is the sum of the two previous numbers, then 55+89=AC+BC=144.
Dividing the segments will show the following results:
AC/BC=55/89=0.618
BC/AB=89/144=0.618
If we take the segment AB as a whole, or as a unit, then AC \u003d 55 will be 0.382 of this whole, and BC \u003d 89 will be equal to 0.618.
Where are Fibonacci numbers found?
The regular sequence of Fibonacci numbers was known to the Greeks and Egyptians long before Leonardo Fibonacci himself. This number series acquired such a name after the famous mathematician ensured the wide distribution of this mathematical phenomenon in scientific ranks.
It is important to note that the golden Fibonacci numbers are not just science, but a mathematical representation of the world around them. Many natural phenomena, representatives of the flora and fauna have the "golden section" in their proportions. These are spiral curls of the shell, and the arrangement of sunflower seeds, cacti, pineapples.

The spiral, the proportions of the branches of which are subject to the laws of the "golden section", underlies the formation of a hurricane, the weaving of a web by a spider, the shape of many galaxies, the interweaving of DNA molecules and many other phenomena.
The length of the lizard's tail to its body has a ratio of 62 to 38. The chicory shoot, before releasing a leaf, makes a release. After the first sheet is released, a second ejection occurs before the release of the second sheet, equal in strength to 0.62 of the conditionally accepted unit of force of the first ejection. The third outlier is 0.38 and the fourth is 0.24.
It is also of great importance for a trader that the price movement in the Forex market is often subject to the patterns of golden Fibonacci numbers. Based on this sequence, a number of tools have been created that a trader can use in his arsenal.

Often used by traders, the instrument "" can accurately show the price movement targets, as well as the levels of its correction.

Fibonacci sequence, known to everyone from the film "The Da Vinci Code" - a series of numbers described as a riddle by the Italian mathematician Leonardo of Pisa, better known by the nickname Fibonacci, in the 13th century. Briefly, the essence of the riddle:
Someone placed a pair of rabbits in a certain closed space to find out how many pairs of rabbits would be born during the year, if the nature of the rabbits is such that every month a pair of rabbits produces another pair, and the ability to produce offspring appears on reaching two months old.

The result is a series of numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 , where the number of pairs of rabbits in each of the twelve months is shown, separated by commas. It can be continued indefinitely. Its essence is that each next number is the sum of the previous two.
This series has several mathematical features that must be touched upon. It asymptotically (approaching more and more slowly) tends to some constant ratio. However, this ratio is irrational, that is, it is a number with an infinite, unpredictable sequence of decimal digits in the fractional part. It cannot be expressed exactly.
So the ratio of any member of the series to the one preceding it fluctuates around the number 1,618 , sometimes surpassing it, sometimes not reaching it. The ratio to the following similarly approaches the number 0,618 , which is inversely proportional 1,618 . If we divide the elements through one, then we get the numbers 2,618 And 0,382 , which are also inversely proportional. These are the so-called Fibonacci ratios.
Why all this? So we are approaching one of the most mysterious phenomena of nature. The savvy Leonardo, in fact, did not discover anything new, he simply reminded the world of such a phenomenon as Golden Section, which is not inferior in importance to the Pythagorean theorem.
We distinguish all the objects around us, including in form. We like some more, some less, some completely repulse the eye. Sometimes interest can be dictated by a life situation, and sometimes by the beauty of the observed object. The symmetrical and proportional shape contributes to the best visual perception and evokes a sense of beauty and harmony. A holistic image always consists of parts of different sizes, which are in a certain relationship with each other and the whole. golden ratio- the highest manifestation of the perfection of the whole and its parts in science, art and nature.
If on a simple example, then the Golden Section is the division of a segment into two parts in such a ratio in which the larger part relates to the smaller one, as their sum (the entire segment) to the larger one.

If we take the entire segment c
behind 1
, then the segment a
will be equal to 0,618
, line segment b
- 0,382
, only in this way the condition of the Golden Section will be met (0,618/0,382=1,618
; 1/0,618=1,618
)
. Attitude c
To a
equals 1,618
, A With
To b
2,618
. These are all the same, already familiar to us, Fibonacci coefficients.
Of course, there is a golden rectangle, a golden triangle, and even a golden cuboid. The proportions of the human body in many respects are close to the Golden Section.
Image: marcus-frings.de

But the most interesting begins when we combine the knowledge gained. The figure clearly shows the relationship between the Fibonacci sequence and the Golden Ratio. We start with two squares of the first size. From above we add a square of the second size. We paint next to a square with a side equal to the sum of the sides of the previous two, the third size. By analogy, a square of the fifth size appears. And so on until you get bored, the main thing is that the length of the side of each next square is equal to the sum of the lengths of the sides of the two previous ones. We see a series of rectangles whose side lengths are Fibonacci numbers, and oddly enough they are called Fibonacci rectangles.
If we draw a smooth line through the corners of our squares, we get nothing more than an Archimedes spiral, the increase in the pitch of which is always uniform.

Doesn't it remind you of anything?

Photo: ethanhein on Flickr
And not only in the shell of a mollusk you can find the spirals of Archimedes, but in many flowers and plants, they are just not so obvious.
Aloe multileaf:

Photo: brewbooks on Flickr
 Photo: beart.org.uk
Photo: beart.org.uk
 Photo: esdrascalderan on Flickr
Photo: esdrascalderan on Flickr
 Photo: manj98 on Flickr
Photo: manj98 on Flickr

And then it's time to remember the Golden Section! Are any of the most beautiful and harmonious creations of nature depicted in these photographs? And that's not all. Looking closely, you can find similar patterns in many forms.
Of course, the statement that all these phenomena are built on the Fibonacci sequence sounds too loud, but the trend is on the face. And besides, she herself is far from perfect, like everything else in this world.
There is speculation that the Fibonacci series is nature's attempt to adapt to a more fundamental and perfect golden section logarithmic sequence, which is practically the same, just starts from nowhere and goes nowhere. Nature, on the other hand, definitely needs some kind of whole beginning, from which you can push off, it cannot create something out of nothing. The ratios of the first members of the Fibonacci sequence are far from the Golden Section. But the further we move along it, the more these deviations are smoothed out. To determine any series, it is enough to know three of its members, going one after another. But not for the golden sequence, two are enough for it, it is a geometric and arithmetic progression at the same time. You might think that it is the basis for all other sequences.
Each member of the golden logarithmic sequence is a power of the Golden Ratio ( z). Part of the row looks something like this: ... z -5 ; z-4; z-3; z-2; z -1 ; z0; z1; z2; z3; z4; z 5 ... If we round the value of the Golden Ratio to three decimal places, we get z=1.618, then the row looks like this: ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Each next term can be obtained not only by multiplying the previous one by 1,618 , but also by adding the two previous ones. Thus, exponential growth is achieved by simply adding two neighboring elements. This is a series without beginning and end, and it is precisely this that the Fibonacci sequence tries to be like. Having a well-defined beginning, it strives for the ideal, never reaching it. That is life.
And yet, in connection with everything seen and read, quite natural questions arise:
Where did these numbers come from? Who is this architect of the universe who tried to make it perfect? Was it ever the way he wanted it to be? And if so, why did it fail? Mutations? Free choice? What will be next? Is the coil twisting or untwisting?
Finding the answer to one question, you get the next. If you solve it, you get two new ones. Deal with them, three more will appear. Having solved them, you will acquire five unresolved ones. Then eight, then thirteen, 21, 34, 55...
Sources: ; ; ;
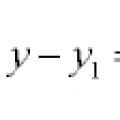 Equations of lines and curves in the plane
Equations of lines and curves in the plane Generalized homogeneous equation Generalized homogeneous equations of the second order
Generalized homogeneous equation Generalized homogeneous equations of the second order Thanks to the comma Due to the fact that in their
Thanks to the comma Due to the fact that in their