Hvordan legge til matriser. Grunnleggende operasjoner på matriser (addisjon, multiplikasjon, transposisjon) og deres egenskaper
1. år, høyere matematikk, studerer matriser og grunnleggende handlinger på dem. Her systematiserer vi de grunnleggende operasjonene som kan utføres med matriser. Hvor skal man begynne å bli kjent med matriser? Selvfølgelig, fra de enkleste ting - definisjoner, grunnleggende konsepter og enkle operasjoner. Vi forsikrer deg om at matrisene vil bli forstått av alle som bruker minst litt tid på dem!
Matrisedefinisjon
Matrise er en rektangulær tabell med elementer. Vel, enkelt sagt - en talltabell.
Vanligvis er matriser angitt med store latinske bokstaver. For eksempel matrise EN , matrise B og så videre. Matriser kan ha forskjellige størrelser: rektangulære, kvadratiske, og det finnes også rad- og kolonnematriser som kalles vektorer. Størrelsen på matrisen bestemmes av antall rader og kolonner. La oss for eksempel skrive en rektangulær matrise av størrelse m på n , Hvor m – antall linjer, og n - Antall kolonner.

Varer for hvilke i=j (a11, a22, .. ) danner hoveddiagonalen til matrisen og kalles diagonal.
Hva kan du gjøre med matriser? Legg til/trekk fra, gange med et tall, formere seg mellom seg, transponere. Nå om alle disse grunnleggende operasjonene på matriser i rekkefølge.
Matriseaddisjons- og subtraksjonsoperasjoner
La oss umiddelbart advare deg om at du bare kan legge til matriser av samme størrelse. Resultatet vil være en matrise av samme størrelse. Å legge til (eller trekke fra) matriser er enkelt - du trenger bare å legge sammen de tilsvarende elementene . La oss gi et eksempel. La oss legge til to matriser A og B med størrelse to og to.

Subtraksjon utføres analogt, bare med motsatt fortegn.
Enhver matrise kan multipliseres med et vilkårlig tall. Å gjøre dette, du må multiplisere hvert av elementene med dette tallet. La oss for eksempel multiplisere matrisen A fra det første eksemplet med tallet 5:

Matrisemultiplikasjonsoperasjon
Ikke alle matriser kan multipliseres sammen. For eksempel har vi to matriser - A og B. De kan bare multipliseres med hverandre hvis antall kolonner i matrise A er lik antall rader i matrise B. I dette tilfellet hvert element i den resulterende matrisen, plassert i den i-te raden og den j-te kolonnen, vil være lik summen av produktene til de tilsvarende elementene i den i-te raden i den første faktoren og den j-te kolonnen til den andre. For å forstå denne algoritmen, la oss skrive ned hvordan to kvadratiske matriser multipliseres:

Og et eksempel med reelle tall. La oss multiplisere matrisene:

Matrisetransponeringsoperasjon
Matrisetransponering er en operasjon der de tilsvarende radene og kolonnene byttes. La oss for eksempel transponere matrisen A fra det første eksemplet:

Matrisedeterminant
Determinant, eller determinant, er et av de grunnleggende begrepene i lineær algebra. Det var en gang folk kom opp med lineære ligninger, og etter dem måtte de komme med en determinant. Til syvende og sist er det opp til deg å takle alt dette, så det siste dyttet!
Determinanten er en numerisk karakteristikk av en kvadratisk matrise, som er nødvendig for å løse mange problemer.
For å beregne determinanten til den enkleste kvadratiske matrisen, må du beregne forskjellen mellom produktene til elementene i hoved- og sekundærdiagonalene.
Determinanten til en matrise av første orden, det vil si bestående av ett element, er lik dette elementet.
Hva om matrisen er tre ganger tre? Dette er vanskeligere, men du kan klare det.
For en slik matrise er verdien av determinanten lik summen av produktene til elementene i hoveddiagonalen og produktene til elementene som ligger på trekantene med en flate parallelt med hoveddiagonalen, hvorfra produktet av elementer av sekundærdiagonalen og produktet av elementene som ligger på trekantene med forsiden av den parallelle sekundære diagonalen trekkes fra.
Heldigvis er det i praksis sjelden nødvendig å beregne determinanter for matriser av store størrelser.
Her så vi på grunnleggende operasjoner på matriser. Selvfølgelig, i det virkelige liv vil du kanskje aldri støte på en antydning til et matrisesystem av ligninger, eller tvert imot, du kan støte på mye mer komplekse tilfeller når du virkelig må pusse hjernen din. Det er for slike saker det finnes profesjonelle studenttjenester. Be om hjelp, få en detaljert løsning av høy kvalitet, nyt akademisk suksess og fritid.
I dette emnet vil vi vurdere konseptet med en matrise, samt typer matriser. Siden det er mange begreper i dette emnet, vil jeg legge til en kort oppsummering for å gjøre det lettere å navigere i stoffet.
Definisjon av en matrise og dens element. Notasjon.
Matrise er en tabell med $m$ rader og $n$ kolonner. Elementene i en matrise kan være objekter av en helt annen karakter: tall, variabler eller for eksempel andre matriser. For eksempel inneholder matrisen $\left(\begin(array) (cc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right)$ 3 rader og 2 kolonner; dens elementer er heltall. Matrisen $\left(\begin(array) (cccc) a & a^9+2 & 9 & \sin x \\ -9 & 3t^2-4 & u-t & 8\end(array) \right)$ inneholder 2 rader og 4 kolonner.
Ulike måter å skrive matriser på: vis\skjul
Matrisen kan skrives ikke bare i runde, men også i firkantede eller doble rette parenteser. Det vil si at oppføringene nedenfor betyr den samme matrisen:
$$ \left(\begin(array) (cc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right);\;\; \left[ \begin(array) (cc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right]; \;\; \left \Vert \begin(array) (cc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right \Vert $$
Produktet $m\ ganger n$ kalles matrisestørrelse. For eksempel, hvis en matrise inneholder 5 rader og 3 kolonner, snakker vi om en matrise med størrelse $5\ ganger 3$. Matrisen $\left(\begin(array)(cc) 5 & 3\\0 & -87\\8 & 0\end(array)\right)$ har størrelse $3 \ ganger 2$.
Vanligvis er matriser merket med store bokstaver i det latinske alfabetet: $A$, $B$, $C$ og så videre. For eksempel, $B=\left(\begin(array) (ccc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right)$. Linjenummerering går fra topp til bunn; kolonner - fra venstre til høyre. For eksempel inneholder den første raden i matrisen $B$ elementene 5 og 3, og den andre kolonnen inneholder elementene 3, -87, 0.
Elementer i matriser er vanligvis angitt med små bokstaver. For eksempel er elementene i matrisen $A$ betegnet med $a_(ij)$. Den doble indeksen $ij$ inneholder informasjon om posisjonen til elementet i matrisen. Tallet $i$ er radnummeret, og tallet $j$ er kolonnenummeret, i skjæringspunktet mellom elementet $a_(ij)$. For eksempel, i skjæringspunktet mellom den andre raden og den femte kolonnen i matrisen $A=\left(\begin(array) (cccccc) 51 & 37 & -9 & 0 & 9 & 97 \\ 1 & 2 & 3 & 41 & 59 & 6 \ \ -17 & -15 & -13 & -11 & -8 & -5 \\ 52 & 31 & -4 & -1 & 17 & 90 \end(array) \right)$ element $a_(25)= $59:
På samme måte, i skjæringspunktet mellom den første raden og den første kolonnen, har vi elementet $a_(11)=51$; i skjæringspunktet mellom den tredje raden og den andre kolonnen - elementet $a_(32)=-15$ og så videre. Legg merke til at oppføringen $a_(32)$ lyder "a tre to", men ikke "en trettito".
For å forkorte matrisen $A$, hvis størrelse er $m\ ganger n$, brukes notasjonen $A_(m\ ganger n)$. Du kan skrive det litt mer detaljert:
$$ A_(m\ ganger n)=(a_(ij)) $$
hvor notasjonen $(a_(ij))$ angir elementene i matrisen $A$. I sin fullt utvidede form kan matrisen $A_(m\ ganger n)=(a_(ij))$ skrives som følger:
$$ A_(m\ ganger n)=\left(\begin(array)(cccc) a_(11) & a_(12) & \ldots & a_(1n) \\ a_(21) & a_(22) & \ldots & a_(2n) \\ \ldots & \ldots & \ldots & \ldots \\ a_(m1) & a_(m2) & \ldots & a_(mn) \end(array) \right) $$
La oss introdusere et annet begrep - like matriser.
To matriser av samme størrelse $A_(m\ ganger n)=(a_(ij))$ og $B_(m\ ganger n)=(b_(ij))$ kalles lik, hvis deres tilsvarende elementer er like, dvs. $a_(ij)=b_(ij)$ for alle $i=\overline(1,m)$ og $j=\overline(1,n)$.
Forklaring på oppføringen $i=\overline(1,m)$: show\hide
Notasjonen "$i=\overline(1,m)$" betyr at parameteren $i$ varierer fra 1 til m. For eksempel indikerer notasjonen $i=\overline(1,5)$ at parameteren $i$ tar verdiene 1, 2, 3, 4, 5.
Så for at matriser skal være like, må to betingelser være oppfylt: sammenfall av størrelser og likhet mellom de tilsvarende elementene. For eksempel er matrisen $A=\left(\begin(array)(cc) 5 & 3\\0 & -87\\8 & 0\end(array)\right)$ ikke lik matrisen $B=\left(\ begin(array)(cc) 8 & -9\\0 & -87 \end(array)\right)$ fordi matrise $A$ har størrelse $3\ ganger 2$ og matrise $B$ har størrelse $2\ ganger $2. Dessuten er ikke matrise $A$ lik matrise $C=\left(\begin(array)(cc) 5 & 3\\98 & -87\\8 & 0\end(array)\right)$ , siden $a_( 21)\neq c_(21)$ (dvs. $0\neq 98$). Men for matrisen $F=\left(\begin(array)(cc) 5 & 3\\0 & -87\\8 & 0\end(array)\right)$ kan vi trygt skrive $A= F$ fordi både størrelsene og de tilsvarende elementene i matrisene $A$ og $F$ er sammenfallende.
Eksempel nr. 1
Bestem størrelsen på matrisen $A=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \\ -6 & 8 & 23 \\ 11 & -12 & -5 \ \4 & 0 & -10 \\ \end(array) \right)$. Angi hva elementene $a_(12)$, $a_(33)$, $a_(43)$ er lik.
Denne matrisen inneholder 5 rader og 3 kolonner, så størrelsen er $5\ ganger 3$. Du kan også bruke notasjonen $A_(5\ ganger 3)$ for denne matrisen.
Element $a_(12)$ er i skjæringspunktet mellom den første raden og den andre kolonnen, så $a_(12)=-2$. Element $a_(33)$ er i skjæringspunktet mellom tredje rad og tredje kolonne, så $a_(33)=23$. Element $a_(43)$ er i skjæringspunktet mellom fjerde rad og tredje kolonne, så $a_(43)=-5$.
Svar: $a_(12)=-2$, $a_(33)=23$, $a_(43)=-5$.
Typer matriser avhengig av størrelse. Hoved- og sekundærdiagonaler. Matrisespor.
La en viss matrise $A_(m\ ganger n)$ gis. Hvis $m=1$ (matrisen består av en rad), kalles den gitte matrisen matrise-rad. Hvis $n=1$ (matrisen består av én kolonne), kalles en slik matrise matrise-kolonne. For eksempel er $\left(\begin(array) (ccccc) -1 & -2 & 0 & -9 & 8 \end(array) \right)$ en radmatrise, og $\left(\begin(array) ) (c) -1 \\ 5 \\ 6 \end(array) \right)$ er en kolonnematrise.
Hvis matrisen $A_(m\ ganger n)$ tilfredsstiller betingelsen $m\neq n$ (dvs. antall rader er ikke lik antall kolonner), så sies det ofte at $A$ er en rektangulær matrise. For eksempel har matrisen $\left(\begin(array) (cccc) -1 & -2 & 0 & 9 \\ 5 & 9 & 5 & 1 \end(array) \right)$ størrelse $2\ ganger 4 $, de. inneholder 2 rader og 4 kolonner. Siden antall rader ikke er lik antall kolonner, er denne matrisen rektangulær.
Hvis matrisen $A_(m\ ganger n)$ tilfredsstiller betingelsen $m=n$ (dvs. antall rader er lik antall kolonner), så sies $A$ å være en kvadratisk matrise av orden $ n$. For eksempel er $\left(\begin(array) (cc) -1 & -2 \\ 5 & 9 \end(array) \right)$ en andreordens kvadratmatrise; $\left(\begin(array) (ccc) -1 & -2 & 9 \\ 5 & 9 & 8 \\ 1 & 0 & 4 \end(array) \right)$ er en tredjeordens kvadratmatrise. Generelt kan kvadratmatrisen $A_(n\ ganger n)$ skrives som følger:
$$ A_(n\ ganger n)=\left(\begin(array)(cccc) a_(11) & a_(12) & \ldots & a_(1n) \\ a_(21) & a_(22) & \ldots & a_(2n) \\ \ldots & \ldots & \ldots & \ldots \\ a_(n1) & a_(n2) & \ldots & a_(nn) \end(array) \right) $$
Elementene $a_(11)$, $a_(22)$, $\ldots$, $a_(nn)$ sies å være på hoveddiagonal matriser $A_(n\ ganger n)$. Disse elementene kalles diagonale hovedelementer(eller bare diagonale elementer). Elementene $a_(1n)$, $a_(2 \; n-1)$, $\ldots$, $a_(n1)$ er på side (mindre) diagonal; de kalles side diagonale elementer. For eksempel, for matrisen $C=\left(\begin(array)(cccc)2&-2&9&1\\5&9&8& 0\\1& 0 & 4 & -7 \\ -4 & -9 & 5 & 6\end( array) \right)$ vi har:

Elementene $c_(11)=2$, $c_(22)=9$, $c_(33)=4$, $c_(44)=6$ er de viktigste diagonale elementene; elementene $c_(14)=1$, $c_(23)=8$, $c_(32)=0$, $c_(41)=-4$ er diagonale sideelementer.
Summen av de viktigste diagonale elementene kalles etterfulgt av matrisen og er betegnet med $\Tr A$ (eller $\Sp A$):
$$ \Tr A=a_(11)+a_(22)+\ldots+a_(nn) $$
For eksempel, for matrisen $C=\left(\begin(array) (cccc) 2 & -2 & 9 & 1\\5 & 9 & 8 & 0\\1 & 0 & 4 & -7\\- 4 & -9 & 5 & 6 \end(array)\right)$ har vi:
$$ \Tr C=2+9+4+6=21. $$
Konseptet med diagonale elementer brukes også for ikke-kvadratiske matriser. For eksempel, for matrisen $B=\left(\begin(array) (ccccc) 2 & -2 & 9 & 1 & 7 \\ 5 & -9 & 8 & 0 & -6 \\ 1 & 0 & 4 & - 7 & -6 \end(array) \right)$ de diagonale hovedelementene vil være $b_(11)=2$, $b_(22)=-9$, $b_(33)=4$.
Typer matriser avhengig av verdiene til elementene deres.
Hvis alle elementene i matrisen $A_(m\ ganger n)$ er lik null, kalles en slik matrise null og er vanligvis betegnet med bokstaven $O$. For eksempel, $\left(\begin(array) (cc) 0 & 0 \\ 0 & 0 \\ 0 & 0 \end(array) \right)$, $\left(\begin(array) (ccc) 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end(array) \right)$ - null matriser.
La matrisen $A_(m\ ganger n)$ ha følgende form:

Da kalles denne matrisen trapesformet. Den inneholder kanskje ikke nullrader, men hvis de finnes, er de plassert nederst i matrisen. I en mer generell form kan en trapesformet matrise skrives som følger:

Igjen, etterfølgende null-linjer er ikke nødvendig. De. Formelt sett kan vi skille mellom følgende forhold for en trapesformet matrise:
- Alle elementer under hoveddiagonalen er null.
- Alle elementer fra $a_(11)$ til $a_(rr)$ som ligger på hoveddiagonalen er ikke lik null: $a_(11)\neq 0, \; a_(22)\neq 0, \ldots, a_(rr)\neq 0$.
- Enten er alle elementene i de siste $m-r$-radene null, eller $m=r$ (dvs. det er ingen null-rader i det hele tatt).
Eksempler på trapesformede matriser:

La oss gå videre til neste definisjon. Matrisen $A_(m\ ganger n)$ kalles tråkket, hvis den oppfyller følgende betingelser:

For eksempel vil trinnmatriser være:

Til sammenligning, matrisen $\left(\begin(array) (cccc) 2 & -2 & 0 & 1\\0 & 0 & 8 & 7\\0 & 0 & 4 & -7\\0 & 0 & 0 & 0 \end(array)\right)$ er ikke echelon fordi den tredje raden har samme nulldel som den andre raden. Det vil si at prinsippet "jo lavere linjen er, jo større nulldelen" brytes. Jeg vil legge til at en trapesformet matrise er et spesielt tilfelle av en trinnvis matrise.
La oss gå videre til neste definisjon. Hvis alle elementene i en kvadratisk matrise som ligger under hoveddiagonalen er lik null, kalles en slik matrise øvre trekantet matrise. For eksempel, $\left(\begin(array) (cccc) 2 & -2 & 9 & 1 \\ 0 & 9 & 8 & 0 \\ 0 & 0 & 4 & -7 \\ 0 & 0 & 0 & 6 \end(array) \right)$ er en øvre trekantet matrise. Merk at definisjonen av en øvre trekantet matrise ikke sier noe om verdiene til elementene som ligger over hoveddiagonalen eller på hoveddiagonalen. De kan være null eller ikke - det spiller ingen rolle. For eksempel er $\left(\begin(array) (ccc) 0 & 0 & 9 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end(array) \right)$ også en øvre trekantet matrise.
Hvis alle elementene i en kvadratisk matrise plassert over hoveddiagonalen er lik null, kalles en slik matrise nedre trekantmatrise. For eksempel, $\left(\begin(array) (cccc) 3 & 0 & 0 & 0 \\ -5 & 1 & 0 & 0 \\ 8 & 2 & 1 & 0 \\ 5 & 4 & 0 & 6 \ end(array) \right)$ - nedre trekantmatrise. Merk at definisjonen av en lavere trekantet matrise ikke sier noe om verdiene til elementene som ligger under eller på hoveddiagonalen. De kan være null eller ikke - det spiller ingen rolle. For eksempel, $\left(\begin(array) (ccc) -5 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 9 \end(array) \right)$ og $\left(\ begynne (matrise) (ccc) 0 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end(matrise) \right)$ er også lavere trekantede matriser.
Den kvadratiske matrisen kalles diagonal, hvis alle elementene i denne matrisen som ikke ligger på hoveddiagonalen er lik null. Eksempel: $\left(\begin(array) (cccc) 3 & 0 & 0 & 0 \\ 0 & -2 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 6 \ end(array)\right)$. Elementene på hoveddiagonalen kan være hva som helst (lik null eller ikke) - det spiller ingen rolle.
Den diagonale matrisen kalles enkelt, hvis alle elementene i denne matrisen på hoveddiagonalen er lik 1. For eksempel $\left(\begin(array) (cccc) 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end(array)\right)$ - fjerdeordens identitetsmatrise; $\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array)\right)$ er andreordens identitetsmatrise.
DEFINISJON AV MATRIKSE. TYPER MATRISKER
Matrise av størrelse m× n kalt et sett m·n tall ordnet i en rektangulær tabell av m linjer og n kolonner. Denne tabellen er vanligvis vedlagt i parentes. For eksempel kan matrisen se slik ut:
For korthets skyld kan en matrise betegnes med en enkelt stor bokstav, for eksempel, EN eller I.
Generelt en matrise av størrelse m× n skriv det slik
 .
.
Tallene som utgjør matrisen kalles matriseelementer. Det er praktisk å gi matriseelementer med to indekser en ij: Den første angir radnummeret og den andre angir kolonnenummeret. For eksempel, en 23– elementet er i 2. rad, 3. kolonne.
Hvis en matrise har samme antall rader som antall kolonner, kalles matrisen torget, og antallet rader eller kolonner kalles i rekkefølge matriser. I eksemplene ovenfor er den andre matrisen kvadratisk - rekkefølgen er 3, og den fjerde matrisen er rekkefølgen 1.
En matrise der antall rader ikke er lik antall kolonner kalles rektangulær. I eksemplene er dette den første matrisen og den tredje.
Det finnes også matriser som bare har én rad eller én kolonne.
En matrise med bare én rad kalles matrise - rad(eller streng), og en matrise med bare én kolonne matrise - kolonne.
En matrise der alle elementene er null kalles null og er betegnet med (0), eller ganske enkelt 0. For eksempel,
 .
.
Hoveddiagonal av en kvadratisk matrise kaller vi diagonalen som går fra øvre venstre til nedre høyre hjørne.
En kvadratisk matrise der alle elementene under hoveddiagonalen er lik null kalles trekantet matrise.
 .
.
En kvadratisk matrise der alle elementene, kanskje unntatt de på hoveddiagonalen, er lik null, kalles diagonal matrise. For eksempel eller.
En diagonal matrise der alle diagonale elementer er lik én kalles enkelt matrise og er betegnet med bokstaven E. For eksempel har 3. ordens identitetsmatrisen formen  .
.
HANDLINGER PÅ MATRISKER
Matrise-likhet. To matriser EN Og B sies å være like hvis de har samme antall rader og kolonner og deres tilsvarende elementer er like en ij = b ij. Så hvis  Og
Og  , Det A=B, Hvis a 11 = b 11, a 12 = b 12, a 21 = b 21 Og a 22 = b 22.
, Det A=B, Hvis a 11 = b 11, a 12 = b 12, a 21 = b 21 Og a 22 = b 22.
Transponer. Tenk på en vilkårlig matrise EN fra m linjer og n kolonner. Det kan assosieres med følgende matrise B fra n linjer og m kolonner, der hver rad er en matrisekolonne EN med samme tall (derfor er hver kolonne en rad i matrisen EN med samme nummer). Så hvis  , Det
, Det  .
.
Denne matrisen B kalt transponert matrise EN, og overgangen fra EN Til B transponering.
Transponering er således en reversering av rollene til radene og kolonnene i en matrise. Matrise transponert til matrise EN, vanligvis betegnet En T.
Kommunikasjon mellom matrise EN og transponeringen kan skrives i formen .
For eksempel. Finn matrisen som er transponert av den gitte.

Matrisetillegg. La matrisene EN Og B bestå av samme antall rader og like antall kolonner, dvs. ha samme størrelser. Deretter for å legge til matriser EN Og B nødvendig for matriseelementer EN legge til matriseelementer B står på de samme stedene. Altså summen av to matriser EN Og B kalt en matrise C, som bestemmes av regelen, for eksempel,
![]()
Eksempler. Finn summen av matriser:

Det er lett å verifisere at matriseaddisjon overholder følgende lover: kommutativ A+B=B+A og assosiativ ( A+B)+C=EN+(B+C).
Multiplisere en matrise med et tall.Å multiplisere en matrise EN per nummer k hvert element i matrisen er nødvendig EN gange med dette tallet. Dermed matriseproduktet EN per nummer k det er en ny matrise, som bestemmes av regelen  eller .
eller .
For alle tall en Og b og matriser EN Og B følgende likheter gjelder:
Eksempler.

Matrisemultiplikasjon. Denne operasjonen utføres i henhold til en særegen lov. Først og fremst merker vi at størrelsen på faktormatrisene må være konsistente. Du kan bare multiplisere de matrisene der antall kolonner i den første matrisen sammenfaller med antall rader i den andre matrisen (dvs. lengden på den første raden er lik høyden på den andre kolonnen). Arbeidet matriser EN ikke en matrise B kalt den nye matrisen C=AB, hvis elementer er sammensatt som følger:
Således, for eksempel, for å oppnå produktet (dvs. i matrisen C) element plassert i 1. rad og 3. kolonne fra 13, må du ta den første raden i den første matrisen, den tredje kolonnen i den andre, og deretter multiplisere radelementene med de tilsvarende kolonneelementene og legge til de resulterende produktene. Og andre elementer i produktmatrisen oppnås ved å bruke et lignende produkt av radene i den første matrisen og kolonnene i den andre matrisen.
Generelt, hvis vi multipliserer en matrise A = (a ij) størrelse m× n til matrisen B = (b ij) størrelse n× s, så får vi matrisen C størrelse m× s, hvis elementer beregnes som følger: element c ij oppnås som et resultat av produktet av elementer Jeg raden i matrisen EN til de tilsvarende elementene j matrisekolonnen B og deres tillegg.
Av denne regelen følger det at du alltid kan multiplisere to kvadratiske matriser av samme rekkefølge, og som et resultat får vi en kvadratisk matrise av samme rekkefølge. Spesielt kan en kvadratisk matrise alltid multipliseres med seg selv, dvs. kvadrat det.
Et annet viktig tilfelle er multiplikasjonen av en radmatrise med en kolonnematrise, og bredden på den første må være lik høyden på den andre, noe som resulterer i en førsteordens matrise (dvs. ett element). Egentlig,
 .
.
Eksempler.

Dermed viser disse enkle eksemplene at matriser generelt sett ikke pendler med hverandre, dvs. A∙B ≠ B∙A . Derfor, når du multipliserer matriser, må du nøye overvåke rekkefølgen på faktorene.
Det kan verifiseres at matrisemultiplikasjon følger assosiative og distributive lover, dvs. (AB)C=A(BC) Og (A+B)C=AC+BC.
Det er også enkelt å sjekke det når man multipliserer en kvadratisk matrise EN til identitetsmatrisen E av samme rekkefølge får vi igjen en matrise EN, og AE=EA=A.
Følgende interessante faktum kan bemerkes. Som du vet er ikke produktet av 2 tall som ikke er null lik 0. For matriser er dette kanskje ikke tilfellet, dvs. produktet av 2 matriser som ikke er null kan vise seg å være lik nullmatrisen.
For eksempel, Hvis  , Det
, Det
![]() .
.
KONSEPTET BESTEMMENDE
La det gis en annenordens matrise - en kvadratisk matrise som består av to rader og to kolonner  .
.
Andre ordens determinant som tilsvarer en gitt matrise er tallet oppnådd som følger: a 11 a 22 – a 12 a 21.
Determinanten er angitt med symbolet  .
.
Så, for å finne andreordens determinanten, må du trekke produktet av elementene langs den andre diagonalen fra produktet av elementene i hoveddiagonalen.
Eksempler. Beregn andreordens determinanter.
På samme måte kan vi vurdere en tredjeordens matrise og dens tilsvarende determinant.
Tredje ordens determinant, som tilsvarer en gitt kvadratisk matrise av tredje orden, er tallet angitt og oppnådd som følger:
 .
.
Dermed gir denne formelen utvidelsen av tredjeordens determinanten når det gjelder elementene i den første raden en 11, en 12, en 13 og reduserer beregningen av tredjeordens determinanten til beregningen av andreordens determinantene.
Eksempler. Regn ut tredjeordens determinant.

På samme måte kan man introdusere begrepene determinanter for den fjerde, femte, etc. bestillinger, redusere rekkefølgen ved å utvide inn i elementene i den første raden, med "+" og "–" tegnene til begrepene vekslende.
Så, i motsetning til en matrise, som er en talltabell, er en determinant et tall som er tilordnet matrisen på en bestemt måte.
Denne håndboken vil hjelpe deg å lære hvordan du utfører operasjoner med matriser: addisjon (subtraksjon) av matriser, transponering av en matrise, multiplikasjon av matriser, finne den inverse matrisen. Alt materiale presenteres i en enkel og tilgjengelig form, relevante eksempler er gitt, slik at selv en uforberedt person kan lære å utføre handlinger med matriser. For egenkontroll og selvtesting kan du laste ned en matrisekalkulator gratis >>>.
Jeg vil prøve å minimere teoretiske beregninger; noen steder er forklaringer "på fingrene" og bruk av ikke-vitenskapelige termer mulig. Elskere av solid teori, vennligst ikke delta i kritikk, vår oppgave er lære å utføre operasjoner med matriser.
For SUPERRASK forberedelse til temaet (hvem er «tennende») er det et intensivt pdf-kurs Matrise, determinant og test!
En matrise er en rektangulær tabell av noen elementer. Som elementer vi vil vurdere tall, det vil si numeriske matriser. ELEMENT er et begrep. Det er lurt å huske begrepet, det vil dukke opp ofte, det er ingen tilfeldighet at jeg brukte fet skrift for å fremheve det.
Betegnelse: matriser er vanligvis merket med store latinske bokstaver
Eksempel: Tenk på en to-av-tre-matrise:
![]()
Denne matrisen består av seks elementer:
Alle tall (elementer) inne i matrisen eksisterer på egen hånd, det vil si at det ikke er snakk om noen subtraksjon: ![]()
Det er bare en tabell (sett) med tall!
Vi er også enige ikke omorganiser tall, med mindre annet er angitt i forklaringene. Hvert nummer har sin egen plassering og kan ikke stokkes!
Den aktuelle matrisen har to rader: 
og tre kolonner: 
STANDARD: når man snakker om matrisestørrelser, da først angi antall rader, og først da antall kolonner. Vi har nettopp brutt ned to-av-tre-matrisen.
Hvis antall rader og kolonner i en matrise er det samme, kalles matrisen torget, For eksempel:  – en tre-av-tre-matrise.
– en tre-av-tre-matrise.
Hvis en matrise har én kolonne eller én rad, kalles også slike matriser vektorer.
Faktisk har vi kjent konseptet med en matrise siden skolen; tenk for eksempel på et punkt med koordinatene "x" og "y": . I hovedsak er koordinatene til et punkt skrevet inn i en en-og-to-matrise. Her er forresten et eksempel på hvorfor rekkefølgen på tallene betyr noe: og er to helt forskjellige punkter på flyet.
La oss nå gå videre til å studere operasjoner med matriser:
1) Akt én. Fjerne et minus fra matrisen (introdusere et minus i matrisen).
La oss gå tilbake til matrisen vår  . Som du sikkert har lagt merke til, er det for mange negative tall i denne matrisen. Dette er veldig upraktisk med tanke på å utføre forskjellige handlinger med matrisen, det er upraktisk å skrive så mange minuser, og det ser rett og slett stygt ut i design.
. Som du sikkert har lagt merke til, er det for mange negative tall i denne matrisen. Dette er veldig upraktisk med tanke på å utføre forskjellige handlinger med matrisen, det er upraktisk å skrive så mange minuser, og det ser rett og slett stygt ut i design.
La oss flytte minus utenfor matrisen ved å endre fortegnet til HVERT element i matrisen:
Ved null, som du forstår, endres ikke tegnet; null er også null i Afrika.
Omvendt eksempel:  . Det ser stygt ut.
. Det ser stygt ut.
La oss introdusere et minus i matrisen ved å endre tegnet til HVERT element i matrisen:

Vel, det ble mye finere. Og viktigst av alt, det vil være LETTERE å utføre alle handlinger med matrisen. Fordi det er et slikt matematisk folketegn: jo flere minuser, jo mer forvirring og feil.
2) Akt to. Multiplisere en matrise med et tall.
Eksempel:
![]()
Det er enkelt, for å multiplisere en matrise med et tall, trenger du hver matriseelement multiplisert med et gitt tall. I dette tilfellet - en treer.
Et annet nyttig eksempel:
 – multiplisere en matrise med en brøk
– multiplisere en matrise med en brøk
La oss først se på hva vi skal gjøre INGEN BEHOV:
Det er IKKE NØDVENDIG å legge inn en brøk i matrisen; for det første kompliserer det bare ytterligere handlinger med matrisen, og for det andre gjør det det vanskelig for læreren å sjekke løsningen (spesielt hvis  – endelig svar på oppgaven).
– endelig svar på oppgaven).
Og spesielt, INGEN BEHOV del hvert element i matrisen med minus syv:

Fra artikkelen Matematikk for dummies eller hvor du skal begynne, husker vi at i høyere matematikk prøver de å unngå desimalbrøker med komma på alle mulige måter.
Det eneste er helst Det du skal gjøre i dette eksemplet er å legge til et minus i matrisen:

Men hvis bare ALLE matriseelementer ble delt på 7 uten et spor, da ville det vært mulig (og nødvendig!) å dele.
Eksempel:

I dette tilfellet kan du TRENGER Å multipliser alle matriseelementer med , siden alle matrisetall er delbare med 2 uten et spor.
Merk: i teorien om matematikk på høyere skole er det ikke noe begrep om "divisjon". I stedet for å si «dette delt på det», kan du alltid si «dette multiplisert med en brøkdel». Det vil si at divisjon er et spesielt tilfelle av multiplikasjon.
3) Tredje akt. Matrix Transponere.
For å transponere en matrise, må du skrive dens rader inn i kolonnene i den transponerte matrisen.
Eksempel:
Transponer matrise
Det er bare én linje her, og i henhold til regelen må den skrives i en kolonne:
– transponert matrise.
En transponert matrise er vanligvis indikert med et hevet skrift eller et primtall øverst til høyre.
Eksempel trinn for trinn:
Transponer matrise 
Først omskriver vi den første raden til den første kolonnen:

Så skriver vi om den andre linjen til den andre kolonnen: 
Og til slutt, omskriver vi den tredje raden til den tredje kolonnen:

Klar. Grovt sett betyr transponering å snu matrisen på siden.
4) Akt fire. Sum (forskjell) av matriser.
Summen av matriser er en enkel operasjon.
IKKE ALLE MATRISKER KAN BETES. For å utføre addisjon (subtraksjon) av matriser, er det nødvendig at de har SAMME STØRRELSE.
For eksempel, hvis en to-til-to-matrise er gitt, kan den bare legges til med en to-til-to-matrise og ingen andre! 
Eksempel:
Legg til matriser ![]() Og
Og ![]()
For å legge til matriser, må du legge til de tilsvarende elementene:

For forskjellen av matriser er regelen lik, det er nødvendig å finne forskjellen mellom de tilsvarende elementene.
Eksempel:
Finn matriseforskjell ![]() ,
, ![]()

Hvordan kan du løse dette eksemplet lettere, for ikke å bli forvirret? Det er tilrådelig å kvitte seg med unødvendige minuser; for å gjøre dette, legg til et minus til matrisen:

Merk: i teorien om matematikk på høyere skole er det ikke noe konsept for "subtraksjon". I stedet for å si "trekk dette fra dette", kan du alltid si "legg til et negativt tall til dette." Det vil si at subtraksjon er et spesielt tilfelle av addisjon.
5) Akt fem. Matrisemultiplikasjon.
Hvilke matriser kan multipliseres?
For at en matrise skal multipliseres med en matrise, er det nødvendig slik at antall matrisekolonner er lik antall matriserader.
Eksempel:
Er det mulig å multiplisere en matrise med en matrise?

Dette betyr at matrisedata kan multipliseres.
Men hvis matrisene omorganiseres, er multiplikasjon i dette tilfellet ikke lenger mulig!

Derfor er multiplikasjon ikke mulig:

Det er ikke så sjeldent å møte oppgaver med et triks, når eleven blir bedt om å multiplisere matriser, hvis multiplikasjon åpenbart er umulig.
Det skal bemerkes at det i noen tilfeller er mulig å multiplisere matriser på begge måter.
For eksempel for matriser, og både multiplikasjon og multiplikasjon er mulig
Matrisetillegg$ A $ og $ B $ er en aritmetisk operasjon, som et resultat av hvilken matrisen $ C $ skal oppnås, hvor hvert element er lik summen av de tilsvarende elementene i matrisene som legges til:
$$ c_(ij) = a_(ij) + b_(ij) $$
I detaljer Formelen for å legge til to matriser ser slik ut:
$$ A + B = \begin(pmatrix) a_(11) & a_(12) & a_(13) \\ a_(21) & a_(22) & a_(23) \\ a_(31) & a_( 32) & a_(33) \end(pmatrix) + \begin(pmatrix) b_(11) & b_(12) & b_(13) \\ b_(21) & b_(22) & b_(23) \\ b_(31) & b_(32) & b_(33) \end(pmatrix) = $$
$$ = \begin(pmatrix) a_(11) + b_(11) & a_(12)+b_(12) & a_(13)+b_(13) \\ a_(21)+b_(21) & a_ (22)+b_(22) & a_(23)+b_(23) \\ a_(31)+b_(31) & a_(32)+b_(32) & a_(33)+b_(33) \ end(pmatrix) = C$$
Vær oppmerksom på at du bare kan legge til og trekke fra matriser med samme dimensjon. Med summen eller differansen vil resultatet bli en matrise $ C $ av samme dimensjon som leddene (trukket fra) til matrisene $ A $ og $ B $. Hvis matrisene $ A $ og $ B $ avviker fra hverandre i størrelse, vil det være en feil å legge til (subtrahere) slike matriser!
Formelen legger til 3 x 3 matriser, noe som betyr at resultatet skal være en 3 x 3 matrise.
Subtraksjon av matriser helt lik addisjonsalgoritmen, bare med et minustegn. Hvert element i den nødvendige matrisen $C$ oppnås ved å subtrahere de tilsvarende elementene i matrisene $A$ og $B$:
$$ c_(ij) = a_(ij) - b_(ij) $$
La oss skrive ned det detaljerte formel for å subtrahere to matriser:
$$ A - B = \begin(pmatrix) a_(11) & a_(12) & a_(13) \\ a_(21) & a_(22) & a_(23) \\ a_(31) & a_( 32) & a_(33) \end(pmatrix) - \begin(pmatrix) b_(11) & b_(12) & b_(13) \\ b_(21) & b_(22) & b_(23) \\ b_(31) & b_(32) & b_(33) \end(pmatrix) = $$
$$ = \begin(pmatrix) a_(11) - b_(11) & a_(12)-b_(12) & a_(13)-b_(13) \\ a_(21)-b_(21) & a_ (22)-b_(22) & a_(23)-b_(23) \\ a_(31)-b_(31) & a_(32)-b_(32) & a_(33)-b_(33) \ end(pmatrix) = C$$
Det er også verdt å merke seg at du ikke kan addere og subtrahere matriser med vanlige tall, så vel som med noen andre elementer
Det vil være nyttig å kjenne egenskapene til addisjon (subtraksjon) for videre løsninger på problemer med matriser.
Egenskaper
- Hvis matrisene $ A,B,C $ er like store, gjelder assosiativitetsegenskapen for dem: $$ A + (B + C) = (A + B) + C $$
- For hver matrise er det en nullmatrise, betegnet $ O $, ved addisjon (subtraksjon) som den opprinnelige matrisen ikke endres med: $$ A \pm O = A $$
- For hver ikke-null matrise $ A $ er det en motsatt matrise $ (-A) $ hvis sum forsvinner: $ $ A + (-A) = 0 $ $
- Når man adderer (subtraherer) matriser, tillates egenskapen kommutativitet, det vil si at matrisene $ A $ og $ B $ kan byttes: $$ A + B = B + A $$ $$ A - B = B - A $$
Eksempler på løsninger
| Eksempel 1 |
|
Gitte matriser $ A = \begin(pmatrix) 2&3 \\ -1& 4 \end(pmatrix) $ og $ B = \begin(pmatrix) 1&-3 \\ 2&5 \end(pmatrix) $. Utfør matriseaddisjon og deretter subtraksjon. |
| Løsning |
|
Først av alt sjekker vi matrisene for dimensjonalitet. Matrisen $ A $ har dimensjon $ 2 \ ganger 2 $, den andre matrisen $ B $ har dimensjon $ 2 \ ganger 2 $. Dette betyr at med disse matrisene er det mulig å utføre en felles operasjon av addisjon og subtraksjon. Husk at for summen er det nødvendig å utføre parvis addisjon av de tilsvarende elementene i matrisene $ A \text( og ) B $. $$ A + B = \begin(pmatrix) 2&3 \\ -1& 4 \end(pmatrix) + \begin(pmatrix) 1&-3 \\ 2&5 \end(pmatrix) = $$ $$ = \begin(pmatrix) 2 + 1 & 3 + (-3) \\ -1 + 2 & 4 + 5 \end(pmatrix) = \begin(pmatrix) 3 & 0 \\ 1 & 9 \end( pmatrix) $$ På samme måte som summen finner vi forskjellen mellom matrisene ved å erstatte "pluss"-tegnet med et "minus": $$ A - B = \begin(pmatrix) 2&3 \\ -1& 4 \end(pmatrix) + \begin(pmatrix) 1&-3 \\ 2&5 \end(pmatrix) = $$ $$ = \begin(pmatrix) 2 - 1 & 3 - (-3) \\ -1 - 2 & 4 - 5 \end(pmatrix) = \begin(pmatrix) 1 & 6 \\ -3 & -1 \ end(pmatrix) $$ Hvis du ikke kan løse problemet, send det til oss. Vi vil gi en detaljert løsning. Du vil kunne se fremdriften til beregningen og få informasjon. Dette vil hjelpe deg med å få karakteren din fra læreren din i tide! |
| Svar |
|
$$ A + B = \begin(pmatrix) 3 & 0 \\ 1 & 9 \end(pmatrix); A - B = \begin(pmatrix) 1 & 6 \\ -3 & -1 \end(pmatrix) $$ |
I artikkelen: «Addisjon og subtraksjon av matriser» ble det gitt definisjoner, regler, kommentarer, egenskaper ved operasjoner og praktiske eksempler på løsninger.
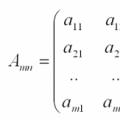 Grunnleggende operasjoner på matriser (addisjon, multiplikasjon, transposisjon) og deres egenskaper
Grunnleggende operasjoner på matriser (addisjon, multiplikasjon, transposisjon) og deres egenskaper Rapport om gjennomføring av forskerpraksis (mastergrad)
Rapport om gjennomføring av forskerpraksis (mastergrad) Mgpi im. Evseviev. FGBOU VPO Mordovian State Pedagogical Institute
Mgpi im. Evseviev. FGBOU VPO Mordovian State Pedagogical Institute