Betydningen av sfærisk trigonometri i Great Soviet Encyclopedia, bse. Astronomi - Sfærisk og sfærisk trigonometri i antikken og i middelalderens øst Formler for sfærisk trigonometri
Sfærisk trigonometri matematisk disiplin som studerer forholdet mellom vinkler og sider av sfæriske trekanter (se Sfærisk geometri). La EN, B, C - hjørner og a, b, c - motsatte sider av en sfærisk trekant ABC(cm. ris.
). Vinklene og sidene til en sfærisk trekant er forbundet med følgende grunnleggende formler for S. t.: cos EN= cos b cos Med+ synd b synd Med cos EN, (2) cos A=- cos B fordi C+ synd B synd MED cos en, (2 1) synd en cos B = cosb synd c- synd b cos Med cos EN, (3) synd EN cos b= cos B synd C+ synd B cos MED cos en; (3 1) i disse formlene a, b, c målt ved de tilsvarende sentrale vinklene, er lengdene på disse sidene lik, henholdsvis aR, bR, cR, Hvor R- kuleradius. Endre betegnelsene på hjørnene (og sidene) i henhold til den sirkulære permutasjonsregelen: EN→I→MED→EN(EN→b→Med→EN),
det er mulig å skrive andre formler for S. t., lik de som er angitt. Formlene til sfæriske trekanter gjør det mulig å bestemme de resterende tre elementene fra hvilke som helst tre elementer i en sfærisk trekant (for å løse trekanten). For rettvinklede sfæriske trekanter ( EN= 90°, A - hypotenuse, b, c - ben) formler for S. t. er forenklet, for eksempel: synd b= synd en synd I, (1") cos a = cos b cos c, (2") synd en cos B= cos b synd c.
(3") For å få formler som forbinder elementene i en rettvinklet sfærisk trekant, kan du bruke følgende mnemoniske regel (Napiers regel): hvis du erstatter bena til en rettvinklet sfærisk trekant med deres komplementer og ordner elementene i trekanten (unntatt den rette vinkelen EN)
i en sirkel i den rekkefølgen de er i en trekant (det vil si som følger: Du, 90° - b, 90 ° - c), så er cosinus til hvert element lik produktet av sinusene til ikke-tilstøtende elementer, for eksempel, cos EN= synd (90° - Med) synd (90° - b) eller, etter transformasjon, cos a = cos b cos Med(formel 2"). Når du løser problemer, er følgende Delambre-formler praktiske, som forbinder alle seks elementene i en sfærisk trekant: Når du løser mange problemer med sfærisk astronomi, avhengig av den nødvendige nøyaktigheten, er det ofte tilstrekkelig å bruke omtrentlige formler: for små sfæriske trekanter (det vil si de hvis sider er små sammenlignet med sfærens radius), kan du bruke formlene av plan trigonometri; for smale sfæriske trekanter (det vil si de med én side, for eksempel EN, liten sammenlignet med andre) bruk følgende formler:
(3’’) eller mer presise formler: S. t. oppsto mye tidligere enn flat trigonometri. Egenskapene til rettvinklede sfæriske trekanter, uttrykt med formlene (1")-(3"), og forskjellige tilfeller av løsningen deres var kjent selv for de greske forskerne Menelaus (1. århundre) og Ptolemaios (2. århundre). Greske forskere reduserte løsningen av skrå sfæriske trekanter til løsningen av rektangulære. Den aserbajdsjanske forskeren Nasiraddin Tuei (1200-tallet) undersøkte systematisk alle tilfeller av å løse skrå sfæriske trekanter, og indikerte for første gang løsningen i to av de vanskeligste tilfellene. De grunnleggende formlene for skrå sfæriske trekanter ble funnet av den arabiske vitenskapsmannen Abul-Vefa (10. århundre) [formel (1)], den tyske matematikeren I. Regiomontan (midten av 1400-tallet) [formler som (2)], og franskmennene matematikeren F. Viet (2. halvdel av 1500-tallet) [formler av typen (2 1)] og L. Euler (Russland, 1700-tallet) [formler av typen (3) og (3 1)]. Euler (1753 og 1779) ga hele systemet med formler for S. T. Noen formler for S. T. praktiske for praksis ble etablert av den skotske matematikeren J. Napier (slutten av 1500-tallet - begynnelsen av 1600-tallet), den engelske matematikeren G. 1600-tallet), russisk astronom A. I. Leksel (andre halvdel av 1700-tallet), den franske astronomen J. Delambre (slutten av 1700-tallet - begynnelsen av 1800-tallet), og andre. Stor sovjetisk leksikon. - M.: Sovjetisk leksikon.
1969-1978
.
![]()
![]()

Se hva "Spherical Trigonometry" er i andre ordbøker:
Sfærisk trigonometri er en del av trigonometri som studerer forholdet mellom vinkler og sidelengder til sfæriske trekanter. Det brukes til å løse ulike geodetiske og astronomiske problemer. Innhold 1 Historie ... Wikipedia
En gren av matematikken som studerer forholdet mellom sidene og vinklene til sfæriske trekanter (det vil si trekanter på overflaten av en sfære) dannet når tre storsirkler krysser hverandre. Sfærisk trigonometri er nært beslektet med ... ... Stor encyklopedisk ordbok
Utforsker egenskapene til en trekant., Tegnet på en sfærisk. overflater dannet på ballen av sirkelbuer. Ordbok med utenlandske ord inkludert i det russiske språket. Pavlenkov F., 1907 ... Ordbok for utenlandske ord i det russiske språket
En gren av matematikken som studerer forholdet mellom sidene og vinklene til sfæriske trekanter (det vil si trekanter på overflaten av en sfære) dannet når tre storsirkler krysser hverandre. Sfærisk trigonometri er nært beslektet med ... ... encyklopedisk ordbok
Matematisk disiplin som studerer forholdet mellom vinkler og sider av sfæriske trekanter (se sfærisk geometri). La A, B, C være vinkler og a, b, c motsatte sider av en sfærisk trekant ABC. Vinkler og sider er sfæriske. triangel... Matematisk leksikon
Matematikkområdet, der avhengighetene mellom sidene og vinklene til den sfæriske studeres. trekanter (dvs. trekanter på overflaten av en kule) dannet i skjæringspunktet mellom tre storsirkler. S. t. er nært beslektet med sfærisk. astronomi... Naturvitenskap. encyklopedisk ordbok
Sfærisk trekant Kurtosis av en sfærisk trekant, eller sfærisk oververdi i sf ... Wikipedia
Legendres teorem i sfærisk trigonometri gjør det mulig å forenkle løsningen av en sfærisk trekant hvis man vet at sidene er små nok sammenlignet med radiusen til kulen den befinner seg på. Ordlyd ... Wikipedia
En rettvinklet sfærisk trekant med hypotenusen c, ben a og b og rett vinkel C. Den sfæriske Pythagoras teorem er et teorem som fastslår forholdet mellom sidene til en rektangulær ... Wikipedia
Storsirkelen deler alltid kulen i to like halvdeler. Sentrum av den store sirkelen sammenfaller med sentrum av sfæren ... Wikipedia
Bøker
- Sfærisk trigonometri, Stepanov N.N. , Kurset for sfærisk trigonometri av N. N. Stepanova er en lærebok for studenter: astronomer, geodesister, topografer, gruvemålere; Samtidig kan det tjene en hensikt... Kategori: Matematikk Utgiver: YoYo Media, Produsent: YoYo Media,
- Sfærisk trigonometri, Stepanov N.N. , Kurset for sfærisk trigonometri av N. N. Stepanova er en lærebok for studenter: astronomer, geodesister, topografer, gruvemålere; samtidig kan det tjene formålene... Kategori:
4)Side cosinus formel.
Koordinatsystemer
Koordinatsystem - et sett med definisjoner som implementerer koordinatmetoden, det vil si en måte å bestemme posisjonen til et punkt eller en kropp ved hjelp av tall eller andre symboler. Settet med tall som bestemmer posisjonen til et bestemt punkt kalles koordinatene til dette punktet. I matematikk er koordinater et sett med tall knyttet til punktene til en manifold i et kart over et bestemt atlas. I elementær geometri er koordinater størrelser som bestemmer posisjonen til et punkt på et plan og i rommet. På et plan bestemmes posisjonen til et punkt oftest av avstandene fra to rette linjer (koordinatakser) som skjærer hverandre i ett punkt (origo) i rett vinkel; en av koordinatene kalles ordinaten og den andre kalles abscissen. I rommet, i henhold til Descartes-systemet, bestemmes posisjonen til et punkt av avstandene fra tre koordinatplan som skjærer hverandre i ett punkt i rette vinkler på hverandre, eller av sfæriske koordinater, der opprinnelsen er i sentrum av kulen. I geografi er koordinatene breddegrad, lengdegrad og høyde over et kjent fellesnivå (for eksempel havet). Se geografiske koordinater I astronomi er koordinater størrelser som bestemmer posisjonen til en stjerne, for eksempel rett oppstigning og deklinasjon Himmelkoordinater er tall som bestemmer posisjonen til lyskilder og hjelpepunkter på himmelsfæren. I astronomi brukes forskjellige systemer med himmelkoordinater. Hver av disse er i hovedsak et system av polare koordinater på en kule med en passende valgt pol. Det himmelske koordinatsystemet er satt av en stor sirkel av himmelsfæren (eller dens pol, 90 ° vekk fra et hvilket som helst punkt i denne sirkelen), som indikerer startpunktet til en av koordinatene. Avhengig av valget av denne sirkelen, ble de himmelske koordinatsystemene kalt horisontale, ekvatoriale, ekliptiske og galaktiske. Når du løser et bestemt matematisk eller fysisk problem ved hjelp av koordinatmetoden, kan du bruke forskjellige koordinatsystemer, og velge det der problemet løses enklere eller mer praktisk i dette spesielle tilfellet.
11) krumningsradier for parallell-, meridian- og normalsnittet.
Gjennom et vilkårlig punkt på overflaten av jordens ellipsoide kan man tegne et uendelig antall vertikale plan som danner normale snitt med overflaten til ellipsoiden. To av dem: meridianen og delen av den første vertikale vinkelrett på den - kalles hovednormalseksjonene. Krumningen av overflaten til jordens ellipsoide på de forskjellige punktene er forskjellig. Dessuten, på samme punkt, har alle normale seksjoner forskjellige krumninger. Krumningsradiene til hovednormalseksjonene ved et gitt punkt er ekstreme, dvs. de største og minste blant alle andre krumningsradier til normalseksjonene. Verdiene av krumningsradiene til meridianen M og den første vertikale N i en gitt breddegrad φ bestemmes av formlene: M = a(1-e²)/ (1 - e²*sin² φ) 3/ 2; N = a / (1 - e²*sin² φ) ½
Krumningsradius r for en vilkårlig parallell av ellipsoiden er relatert til krumningsradiusen til seksjonen av den første vertikalen ved forholdet r = N cos φ. Verdiene til krumningsradiene til hovedseksjonene til ellipsoiden M og N karakteriserer formen nær et gitt punkt. For et vilkårlig punkt på overflaten av ellipsoiden, forholdet mellom radiene
M / N = 1 - e² / 1 - e²*sin² φ
12) Lengden på buene av paralleller og meridianer.
L \u003d 2pR \u003d 2. 3.14 6371 "40000 km.
Ved å bestemme lengden på storsirkelen kan du finne lengden på meridianen (ekvator) buen i 1° eller i 1¢:1° av meridianen (ekvator) buen = L/360°= 111 km, 1¢ av meridianen (ekvator) buen 111/60¢ = 1,853 km Lengden på hver parallell er mindre enn lengden på ekvator og avhenger av stedets breddegrad.
Det er lik L par \u003d L eq cosj par. Posisjonen til et punkt på overflaten av jordens ellipsoide kan bestemmes av geodetiske koordinater - geodetisk breddegrad og geodetisk lengdegrad. For å bestemme posisjonen til et punkt på overflaten av geoiden, brukes astronomiske koordinater, oppnådd ved matematisk behandling av resultatene av astronomiske målinger. Men i noen tilfeller, når det ikke er nødvendig å ta hensyn til forskjellene i geodetiske og astronomiske koordinater, brukes begrepet geografiske koordinater for å bestemme posisjonen til et punkt i flynavigasjon Geografisk breddegrad j er vinkelen mellom ekvatorialen. planet og normalen til ellipsoidoverflaten ved et gitt punkt. Breddegrad måles fra ekvatorplanet til polene fra 0 til 90° nord eller sør. Nordlig breddegrad anses som positiv, sørlig - negativ.
13) Koordinattransformasjon.
Transformasjonen av koordinatsystemet er overgangen fra ett koordinatsystem til et annet.Med en slik utskifting er det nødvendig å etablere formler som gjør det mulig, ved å bruke de kjente koordinatene til et punkt i ett koordinatsystem, å bestemme dets koordinater i et annet.
Hovedmålet med koordinattransformasjon er å bestemme et slikt koordinatsystem der likningen til en gitt linje blir den enkleste. Ved en god plassering av koordinataksene er det mulig å sikre at kurvens ligning tar den enkleste formen. Dette er viktig for å studere egenskapene til en kurve.
14) Geodetisk linje. Direkte og omvendt geodetisk problem.
Geodesisk linje, kurve, hvor hovednormalene for alle punkter sammenfaller med normalene til overflaten den er plassert på. Den korteste avstanden mellom to punkter på overflaten er en G.-linje, men ikke alltid det motsatte Det geodetiske problemet er knyttet til å bestemme den relative plasseringen av punkter på jordoverflaten og er delt inn i direkte og omvendte problemer. Direkte G. z. kalt beregning av geodetiske koordinater - breddegraden og lengdegraden til et bestemt punkt som ligger på jordens ellipsoide, i henhold til koordinatene til et annet punkt og langs lengden og asimuten til den geodetiske linjen som forbinder disse punktene. Omvendt G. h. består i å bestemme de geodetiske koordinatene til to punkter på jordens ellipsoide, lengden og asimuten til den geodetiske linjen mellom disse punktene
15) Konvergens av meridianer Konvergens meridianer på et eller annet punkt av jordens ellipsoide - vinkelen g s mellom tangenten til meridianen til dette punktet og tangenten til ellipsoiden, tegnet i samme punkt parallelt med planet til en innledende meridian. C. m. g s er en funksjon av forskjellen mellom lengdegradene l til de indikerte meridianene, breddegraden B til punktet og parametrene til ellipsoiden. Omtrent er S. m. uttrykt med formelen g s \u003d lsin. S. m. på planet til en geodesisk projeksjon, eller kartografisk projeksjon (eller Gaussisk S. m.) er vinkelen g, som danner en tangent til bilde av en hvilken som helst meridian med den første koordinataksen (abscissen) til denne projeksjonen, som vanligvis er et bilde av den midtre (aksiale) meridianen til det viste territoriet.
16) Det generelle prinsippet om å avbilde overflater ved utfolding.
Utviklingen av en overflate til en annen ved hjelp av bøyning er en slik transformasjon av den første overflaten, der elementene i dens indre geometri er bevart, dvs. vinkler. KVADRAT, Gaussisk krumning av overflaten, og dermed forblir egenskapen til de korteste linjene kortest.Krumningsradiene Ch. normale seksjoner kalles Ch. krumningsradier ved et gitt punkt på overflaten..R=1/R1*R2- Gaussisk krumning av overflaten
Elementer av sfærisk trigonometri
Sfærisk trigonometri omhandler studiet av forholdet mellom sidene og vinklene til sfæriske trekanter (for eksempel på jordoverflaten og på himmelsfæren) Sfæriske trekanter. På overflaten av en ball måles den korteste avstanden mellom to punkter langs omkretsen av en stor sirkel, det vil si en sirkel hvis plan går gjennom midten av ballen. Toppunktene til en sfærisk trekant er skjæringspunktene til tre stråler som kommer ut fra midten av ballen og den sfæriske overflaten. Sidene a, b, c i en sfærisk trekant er de vinklene mellom strålene som er mindre enn 180 (hvis en av disse vinklene er 180, degenererer den sfæriske trekanten til en halvsirkel av en stor sirkel). Hver side av trekanten tilsvarer en bue av en stor sirkel på overflaten av ballen (se figur).
Vinklene A, B, C i en sfærisk trekant, motstående sider a, b, c, henholdsvis, er per definisjon mindre enn 180, vinklene mellom buer av storsirkler som tilsvarer sidene i trekanten, eller vinklene mellom plan definert av disse strålene Geometri på overflaten av ballen er ikke-euklidsk; i hver sfærisk trekant er summen av sidene mellom 0 og 360, summen av vinklene er mellom 180 og 540. I hver sfærisk trekant er det en større vinkel på motsatt side av den større siden. Summen av to sider er større enn den tredje siden, summen av to vinkler er mindre enn 180 pluss den tredje vinkelen. En sfærisk trekant er unikt definert (opp til en symmetritransformasjon): 1) tre sider, 2) tre vinkler, 3) to sider og innelukket mellom dem en vinkel, 4) en side og to vinkler ved siden av den.
4)Side cosinus formel.
Sidecosinusformelen relaterer tre sider og en av vinklene til en sfærisk trekant. Praktisk for å finne en ukjent vinkel eller side motsatt denne vinkelen, og lyder som følger: «i en sfærisk trekant er cosinus til en side lik produktet av cosinus til de to andre sidene pluss produktet av sinusene til disse sidene og cosinus til vinkelen mellom dem"
For noen av våre kunder er kjøp av spesiallagde smykker en lønnsom investering i familiekapital, i en stabil fremtid for barn og barnebarn. For andre kunder, spesielt vakre damer, er eksklusive smykker en annen måte å understreke deres stil, skjønnhet og misunnelsesverdige sosiale status. For menn - et alternativ for å demonstrere kjærlighet og oppmerksomhet til den utvalgte.
G.P. Matvievskaya Sfærisk og sfærisk trigonometri i antikken og i middelalderens øst / Utvikling av metoder for astronomisk forskning. Utgave 8, Moskva-Leningrad, 1979G.P. Matvievskaya
Kuler og sfærisk trigonometri i antikken og i middelalderens øst
1. I antikken og i middelalderen fungerte astronomiens behov som den viktigste stimulansen for utviklingen av mange grener, matematikk og fremfor alt sfærisk trigonometri, som var et matematisk apparat for å løse spesifikke astronomiske problemer. Med utviklingen av astronomi, kompleksiteten til problemene og økningen i kravene til nøyaktigheten av beregninger, ble dette apparatet gradvis forbedret, og følgelig ble innholdet av sfærisk trigonometri beriket. Det ble forklart både i astronomiske avhandlinger - som en innledende del av astronomi - og i spesielle matematiske arbeider.
Av spesiell betydning for historien til sfærisk trigonometri er gamle greske skrifter om sfæren - en vitenskap som inkluderte elementer av astronomi, geometri på en sfære og trigonometri. Innen det 4. århundre. f.Kr e. den var fullt utviklet og betraktet som en astronomisk hjelpedisiplin. De tidligste kjente verkene om sfæren ble skrevet i perioden på 400-tallet f.Kr. f.Kr e. - Jeg århundre. n. e. slike fremragende forskere fra antikken som Autolik, Euclid, Theodosius, Hypsicles, Menelaus.
Disse verkene lar deg visuelt bli kjent med den innledende fasen i utviklingen av sfærisk trigonometri.
Alle resultatene oppnådd av grekerne innen astronomi og trigonometri ble som kjent generalisert i det 2. århundre f.Kr. i Ptolemaios sitt verk med tittelen En matematisk samling i 13 bøker. Senere, sannsynligvis på 300-tallet, ble den kalt den "store" boken, hvorfra navnet "Almagest", som ble allment akseptert, kom fra i middelalderen: dette er hvordan ordet "al-majisti" ble uttalt i Latin - en arabisert form fra "megiste" (den mest store).
I motsetning til den "store" boken til Ptolemaios, ble skriftene til forgjengerne hans, nødvendige for astronomiske beregninger og kombinert i den sene hellenistiske perioden (senest på 400-tallet) i én samling, kalt "Small Astronomy". De måtte studeres etter Euklids elementer, slik at Almagest kunne bli forstått. I arabisk litteratur vises de derfor under navnet "mellombøker" (kutub al-mutawasita).
Denne samlingen inkluderer verkene til Euclid "Data", "Optics", "Phenomena" og den pseudo-euklidiske "Katoptrik", verkene til Archimedes ("På ballen og sylinderen", "Måling av sirkelen", "Lemmas" "), Aristarchus ("Om mengder og avstander Sol og Måne"), Hypsikler ("På oppstigningen av stjernebildene langs ekliptikken"), Autolika ("Om den bevegelige sfæren", "Om oppgangen og nedgangen til fiksstjernene "), Theodosius ("Sfære", "På dager og netter", "Om boliger") og Menelaus ("Sfære"). Arbeidet til Menelaos ble lagt til Minor Astronomy, muligens på et senere tidspunkt.
Den arabiske oversettelsen av de "midtste" bøkene, inkludert verk om sfæren, dukket opp blant de første oversettelsene av verkene til klassikerne av gresk vitenskap. Senere ble de gjentatte ganger kommentert. Blant oversetterne og kommentatorene kan man nevne slike fremragende vitenskapsmenn som Kosta ibn Luka (IX århundre), al-Makhani (IX århundre), Sabit ibn Korra (X århundre), Ibn Irak (X-XI århundrer), Nasir ad -Din kl. -Tusi (XIII århundre) og andre.
Til den greske "Minor Astronomy" la østlige lærde senere verkene "On the Measurement of Figures" av Banu Musa, "Data" og "The Book of the Complete Quadrilateral" av Sabit ibn Korra, "Treatise on the Complete Quadrilateral" av Nasir ad-Din at-Tusi.
Behovet for et dypt kjennskap til «midt»-bøker ble godt anerkjent av østlige matematikere og astronomer og ble understreket selv på 1600-tallet. i det kjente bibliografiske leksikonet til Hajji Khalifa "Fjerne sløret fra titlene til bøker og vitenskaper". Teksten til disse avhandlingene, så vel som kommentarer til dem, er bevart i en rekke arabiske manuskripter. Disse inkluderer for eksempel en håndskrevet samling som ennå ikke er studert av noen, oppbevart i Statens folkebibliotek. M. E. Saltykov-Shchedrin i Leningrad (samling av Khanykov, nr. 144).
Tilbake i 1902 bemerket den kjente matematikkhistorikeren A. Bjornbo med beklagelse at det ble viet for lite oppmerksomhet til det området av antikkens vitenskap, som kan defineres som en "introduksjon til astronomi" og som gjenspeiles i "gjennomsnittlig "bøker. Spesielt insisterte han på behovet for en fullverdig kritisk utgave av teksten til verkene og reiste i forbindelse med dette spørsmålet om å studere deres arabiske versjoner. En stor fortjeneste i studiet av "liten astronomi" tilhører A. Bjornbo selv, samt F. Gulch, I.L. Geiberg, P. Tannery, A. Chvalina, J. Mozhene m.fl.. Men langt fra alt har blitt gjort i denne retningen så langt. Dette gjelder spesielt "midtbøkene" i den arabiske tolkningen.
Forskere fra den østlige middelalderen gjorde ofte betydelige tillegg til greske verk, tilbød sine egne bevis på teoremer og introduserte noen ganger nye ideer i den gamle teorien. Fra dette synspunktet fortjener de arabiske versjonene av verkene viet til sfæren stor oppmerksomhet. Av spesiell betydning er studiet av kommentarene til arbeidet til Menelaus, satt sammen av Abu Nasr ibn Iraq og Nasir ad-Din at-Tusi, som spilte en betydelig rolle i historien til sfærisk trigonometri.
2. De eldste skriftene om sfæren som har kommet ned til oss - og generelt sett fra grekernes matematiske skrifter - er avhandlingene til Autolik fra Pitana (ca. 310 f.Kr.) "On the Revolving Sphere" og "On Sunrises" og solnedganger». Begge tar for seg spørsmål om geometri på en sfære brukt på astronomi.
Autolik studerer en kule som roterer rundt en akse og sirkulære seksjoner på den: store sirkler som går gjennom begge polene, små sirkler oppnådd ved å kutte kulen med plan vinkelrett på aksen, og store sirkler som passerer på skrå til den. Bevegelsen av punktene til disse sirklene vurderes i forhold til et eller annet fast sekantplan som går gjennom sentrum. Det er lett å se her en modell av himmelsfæren med himmelmeridianer, paralleller, ekvator, ekliptikk og horisont. Presentasjonen er imidlertid gjennomført i et rent geometrisk språk og astronomiske termer brukes ikke.
I essayet med 12 setninger "On a Moving Sphere" introduserer Autolik konseptet med jevn bevegelse ("et punkt beveger seg jevnt hvis det går like veier på like ganger") og bruker dette konseptet på en roterende sfære. Først og fremst viser han at punkter på overflaten som ikke ligger på aksen, under jevn rotasjon, beskriver parallelle sirkler med samme poler som kulen, og med plan vinkelrett på aksen (proposisjon 1). Videre er det bevist at i lik tid beskriver alle punktene på overflaten like buer (proposisjon 2) og omvendt, dvs. hvis to buer med parallelle sirkler krysses i lik tid, så er de like (proposisjon 3).
Ved å introdusere konseptet med horisonten - en stor sirkel som skiller den delen av denne sfæren som er synlig for en observatør som ligger i sentrum av sfæren fra den usynlige - vurderer Autolik bevegelsen av overflatepunkter i forhold til den. Ulike mulige posisjoner av horisonten undersøkes, når den er vinkelrett på aksen, passerer gjennom polene og skråner mot aksen. I det første tilfellet (som finner sted ved den terrestriske polen), vil intet punkt på overflaten av sfæren, med jevn rotasjon, være stigende eller sette seg; alle punktene på den synlige delen forblir alltid synlige, og alle punktene til den usynlige delen forblir usynlige (Proposisjon 4).
I det andre tilfellet, som finner sted ved jordens ekvator, stiger og setter alle punkter på overflaten av sfæren seg, og er samtidig over og under horisonten (proposisjon 5).
Til slutt, i det siste - generelle - tilfellet, berører horisonten to like parallelle sirkler, hvorav den ene som ligger ved den synlige polen alltid er synlig, og den andre alltid er usynlig (proposisjon 6). Overflatepunkter mellom disse sirklene stiger og setter seg, og passerer alltid gjennom de samme punktene i horisonten, og beveger seg i sirkler vinkelrett på aksen og skrånende mot horisonten i samme vinkel (Proposisjon 7). Hver stor sirkel festet på overflaten av sfæren, som berører de samme parallelle sirkler som horisonten, vil falle sammen med horisonten når sfæren roterer (Proposisjon 8). I tillegg har det blitt fastslått at hvis horisonten er skråstilt til aksen, vil av de to punktene som stiger samtidig, det ene som er nærmere den synlige polen settes senere; hvis to punkter settes samtidig, så det som ligger nærmere den synlige polen stiger tidligere.
Ved å vise videre at i tilfellet når horisonten er skråstilt til aksen, vil storsirkelen som går gjennom polene til sfæren (dvs. meridianen) to ganger være vinkelrett på horisonten under dens revolusjon (forslag 10), formulerer og beviser Autolik teoremet (proposisjon 11), som i hovedsak omhandler ekliptikken. Vi snakker om hvordan stigningen og innstillingen av punktene som ligger på denne store sirkelen avhenger av dens posisjon i forhold til horisonten. Det er bevist at hvis begge er skråstilt til aksen, og ekliptikken berører to sirkler på sfæren parallelt med hverandre og vinkelrett på aksen, større enn de som horisonten berører, så vil punktene til ekliptikken alltid har sine stigninger og sett på segmentet av horisonten som ligger mellom parallelle sirkler som tangerer ekliptikken.
Den siste setningen sier: Hvis en fast sirkel på overflaten av en kule alltid halverer en annen sirkel som roterer med kulen, som begge ikke er vinkelrett på aksen og ikke går gjennom polene, så er det storsirkler.
Autoliks avhandling "Om soloppganger og solnedganger", bestående av to bøker, er basert på det anmeldte essayet. Den beskriver bevegelsen til fiksstjernene (bok 1), med spesiell oppmerksomhet til de tolv stjernebildene som befinner seg på; ekliptikk (bok II). Det viser seg når stjernene stiger og går ned, har forskjellige posisjoner på himmelsfæren, og under hvilke omstendigheter de er synlige eller usynlige.
Autoliks skrifter om sfæren, som hadde karakter av elementære lærebøker, mistet ikke sin relevans verken i antikken eller i middelalderen. Innholdet i avhandlingen "On the Moving Sphere" ble skissert i den sjette boken i hans "Matematisk samling" av Pappus av Alexandria (3. århundre e.Kr.). Betydningen av rollen til Autolik i utviklingen av vitenskapen ble skrevet på 600-tallet. Simplicius og John Philopon. Den greske teksten til begge verkene hans er fullstendig bevart til i dag.
Verkene til Autolik ble oversatt til arabisk på 900- og begynnelsen av 1000-tallet. blant de første greske skriftene som vekket interessen hos østlige lærde. Oversettelsen av avhandlingen «On the Moving Sphere» fra originalgresk ble utført av den kjente oversetteren Ishaq ibn Hunayn (d. 910/911). Hans samtidige astronom, filosof og lege Kusta ibn Luka al-Baalbaki (d. 912) oversatte avhandlingen Om soloppganger og solnedganger. Disse oversettelsene ble deretter revidert av den berømte matematikeren og astronomen Thabit ibn Korra (d. 901). Senere, i XIII århundre. verkene til Autolik ble kommentert av den fremragende vitenskapsmannen, leder av Maraga-observatoriet Nasir ad-Din at-Tusi (1201 - 1274).
I Europa ble arabiske versjoner av Autoliks verk kjent på 1100-tallet. På dette tidspunktet ble den latinske oversettelsen av avhandlingen "On the Moving Sphere" laget av den største middelalderoversetteren Gerardo av Cremona (1114-1187).
Den greske teksten til Autoliks skrifter, bevart i flere manuskripter fra det 10.-15. århundre, vakte oppmerksomhet fra vitenskapsmenn på 1500-tallet, da en nøye studie av den antikke vitenskapelige arven startet i Europa under påvirkning av humanistiske ideer. Første gang latin; oversettelsen av begge avhandlingene fra det originale greske ble publisert i leksikonet til den italienske læreren George Balla (G. Valla, ca. 1447-1500) i 1501, og deretter i samlingen av gamle skrifter om sfæren, som ble utgitt i 1558 i Messina av Francesco Mavrolico (F. Maurolico, 1494-1575).
Aktivt arbeid med publisering av matematiske og astronomiske verk av eldgamle forfattere ble utført i denne perioden i Frankrike, hvor det ble initiert av en av de fremtredende skikkelsene fra den franske renessansen, en lidenskapelig propagandist for antikkens vitenskap P. Ramus (P. Ramus) , Pierre de la Ramée, 1515-1572 ); Han var dedikert til den første greske utgaven av verkene til Autolik, utført av Conrad Dasipodius (Dasypodius, Conrad Rauchfuss, 1532-1600); den ble utgitt i 1572 i Strasbourg, sammen med en latinsk oversettelse. En annen elev av Ramus P. Forcadel (Pierre Forcadel, ca. 1520-1574) publiserte i 1572 en fransk oversettelse av begge Autoliks avhandlinger.
I 1587-1588. en annen latinsk utgave dukket opp, laget av I. Auria (I. Auria) på flere greske manuskripter fra Vatikanets bibliotek, og i 1644 publiserte M. Mersenne (M. Megsenn, 1588-1648) en forkortet latinsk oversettelse av verkene til Autolik andre Greske skrifter om matematikk og astronomi.
En fullstendig kritisk utgave av den greske teksten til Autoliks avhandlinger, sammen med en latinsk oversettelse, ble utført i 1855 av F. Gulch. Det var grunnlaget for den tyske oversettelsen av A. Chvalina, utgitt i 1931.
Til slutt ble en ny utgave av den greske teksten, basert på en grundig studie av alle bevarte manuskripter, foretatt av J. Maugenet i 1950; teksten innledes med en grundig studie av historien til europeiske utgaver av Autoliks verk. I 1971 ble en engelsk oversettelse av denne teksten publisert i Beirut, som imidlertid skapte alvorlig kritikk av O. Neugebauer.
Autoliks skrifter har tiltrukket seg oppmerksomheten til mange historikere innen astronomi og matematikk. Både Autoliks teori og teksten i hans forfatterskap studeres. Det vises for eksempel at de to bøkene som utgjør «Om soloppgang og solnedgang», etter all sannsynlighet er to versjoner av samme verk.
De arabiske versjonene av Autolik-avhandlingene, som var blant "mellombøkene", er fortsatt de minst studerte, selv om de finnes i en rekke manuskripter lagret i forskjellige biblioteker i Europa og Asia.
3. I andre halvdel av det 4. århundre. f.Kr e. et annet essay om sfæren dukket opp, nært innhold til verkene til Autolik og skrevet av hans yngre samtidige Euclid, den berømte forfatteren av begynnelsen. I denne avhandlingen, med tittelen «Fenomener», gjentar Euklid i stor grad sin forgjenger, men sammenhengen mellom sfæren og praktisk astronomi kommer mye tydeligere til uttrykk hos ham.
Euklids «Fenomener» består av 18 setninger. Den første formulerer utsagnet som ligger til grunn for det geosentriske systemet i verden om at Jorden er tatt som sentrum av universet. Siden observatørens posisjon på jordoverflaten bør betraktes som vilkårlig, følger det av denne uttalelsen at, i forhold til hele universet, anses Jorden som punktet der observatøren befinner seg.
Etter å ha gjentatt i den andre og tredje setningen den syvende teoremet til Autolik fra avhandlingen "On the Moving Sphere", fortsetter Euclid med studiet av stigningen og innstillingen av dyrekretsens tegn - 12 konstellasjoner lokalisert på ekliptikken, det vil si, hver av de tolv buene, ekliptikken, lik 30 ° og betinget tilsvarer disse konstellasjonene. Han beviser (proposisjon 4) at hvis ekliptikken ikke skjærer den største av de alltid synlige sirklene på himmelsfæren, dvs. hvis breddegraden til observasjonsstedet er mindre enn 66 °, vil stjernebildene som stiger først også settes først ; hvis den krysser den, det vil si hvis breddegraden til observasjonsstedet er større enn 66 °, stiger stjernebildene mot nord tidligere og setter senere enn de som ligger i sør (forslag 5). Dermed avhenger egenskapene til stjernebildets stigning og innstilling av breddegraden til observasjonsstedet, det vil si størrelsen på vinkelen mellom verdens akse og horisonten.
Etter å ha vist videre at stigningen og settingen av stjerner lokalisert ved motsatte ender av diameteren til ekliptikken er motsatte av hverandre (proposisjon 6), forklarer Euklid den ellevte teoremet fra Autoliks avhandling "On a Moving Sphere": stjerner plassert på ekliptikken , mens de stiger og setter seg, krysser en del av horisonten som er innelukket mellom tropene, og dette skjæringspunktet skjer ved konstante punkter (proposisjon 7).
Så beviser han at like buer av stjernetegnene stiger og setter seg på ulik buer i horisonten, jo større, jo nærmere jevndøgnene de er plassert; samtidig stiger buer like langt fra ekvator og setter seg på like horisontale buer (proposisjon 8).
Følgende teoremer gjelder varigheten av soloppgangene og solnedgangene til de forskjellige stjernetegnene. Først ble det slått fast at tiden som kreves for å heve halvparten av ekliptikken vil være forskjellig avhengig av posisjonen til referansepunktet (proposisjon 9). Dette tilsvarer utsagnet om ulike lengder på dag og natt i ulike årstider, når solen står i ulike stjernetegn. Deretter vurderes tiden som kreves for oppreisning og innstilling av like og motsatte tegn på dyrekretsen.
Løsningen av spørsmålene som ble reist av Euklid var ekstremt viktig for de gamle astronomene, siden det gjaldt metoder for å bestemme timen på dagen og natten, etablere en kalender osv.
4. I de vurderte verkene til Autolik og Euclid ble derfor grunnlaget for de gamle greske sfærene skissert, både teoretiske og praktiske. Begge forfatterne fulgte imidlertid et tidligere mønster, for de kom med en rekke påstander om sfæren uten bevis, antagelig ansett for å være kjent. Det er mulig at forfatteren av et slikt verk om sfæren, generelt anerkjent på den tiden, var den store matematikeren og astronomen Eudoxus av Cnidus (ca. 408-355 f.Kr.).
Dette tapte verket er nå bedømt av Theodosius' Sphere, skrevet senere, men som utvilsomt gjentar innholdet i hovedsak.
5. Det er forskjellige meninger om livet og biografien til Theodosius, basert på de ofte motstridende rapportene fra gamle historikere, som feilaktig kombinerte flere skikkelser som bar dette navnet i en person. Det er nå slått fast at forfatteren av The Sphere kom fra Bithynia, og ikke fra Tripoli, som tidligere ble antatt og antydet i titlene på mange utgaver av verkene hans. Han levde trolig i 2. halvdel av 2. århundre f.Kr. f.Kr e. selv om han vanligvis ble kalt en samtidig av Cicero (ca. 50 f.Kr.).
I tillegg til sfærene er ytterligere to skrifter av Theodosius, også inkludert i antall "mellombøker", bevart på originalgresk. Den største avhandlingen "Om boliger" inkluderer 12 setninger og er viet til beskrivelsen av stjernehimmelen fra synspunktet til observatører som befinner seg på forskjellige geografiske breddegrader. Den andre avhandlingen, med tittelen "Om dager og netter" og består av to bøker, tar for seg ekliptikkens bue som solen reiser gjennom på en dag, og undersøker betingelsene som er nødvendige, for eksempel for at dag og natt virkelig skal like hverandre ved jevndøgn.
Disse skriftene ble studert og kommentert av mange arabiske forskere, og vakte oppmerksomhet i Europa på 1500-tallet, da deres greske manuskripter ble oppdaget. Den første av dem ble utgitt i latinsk oversettelse i 1558 av F. Mavroliko, sammen med en rekke andre arbeider om sfæren, og deretter i 1572 av K. Dasipodius publiserte de greske og latinske formuleringene av teoremene fra denne avhandlingen i boken nevnt ovenfor. Samme år, 1572, ble en fransk oversettelse av Theodosius' verk utgitt i versjonen av Dasipodius, laget av P. Forcadel. De neste latinske utgavene ble laget i 1587 (I. Auria) og i 1644 (M, Mersenne). Den fullstendige greske teksten til avhandlingen "Om boliger" sammen med den latinske oversettelsen ble utgitt først i 1927 av R. Fecht. Den samme utgaven gjengir også for første gang den originale teksten til verket «On Days and Nights» og dets latinske oversettelse. Tidligere var det kjent takket være ordlyden av setninger på gresk og latin utgitt i 1572 av K. Dasipodius og en fullstendig latinsk oversettelse i utgivelsen av I. Auria.
Theodosius' mest kjente verk var hans "Sfære", som inntar en viktig plass i historien til astronomi, sfærisk trigonometri og ikke-euklidisk geometri.
Theodosius studerer i detalj egenskapene til linjer på overflaten av en kule oppnådd ved å kutte den med forskjellige plan. Det bør understrekes at den sfæriske trekanten ennå ikke vises i ham. Verket er modellert etter Euklids «Begynnelser» og består av tre bøker. Den første boken, som inneholder 23 setninger, begynner med seks definisjoner. Kulen er definert som "en solid figur avgrenset av en overflate, slik at alle rette linjer som faller på den fra ett punkt som ligger inne i figuren er like hverandre", dvs. lik hvordan sirkelen er definert i "Prinsippene" (bok I, 15. definisjon); det er interessant å merke seg at Euklid selv i bok XI av "Begynnelsene" definerer sfæren på en annen måte - som en kropp dannet ved rotasjonen av en halvsirkel rundt en fast diameter (bok XI, 14. definisjon). Videre er definisjonen av sfærens sentrum, dens akse og poler gitt. Polen til en sirkel tegnet på en kule er definert som. et punkt på overflaten av en kule slik at alle linjer trukket gjennom den til sirkelens omkrets er like. Til slutt gjelder den sjette definisjonen sirkler på sfæren like langt fra midten: ifølge Theodosius er disse sirkler slik at perpendikulære trukket fra sfærens sentrum til planene deres er like med hverandre.
Setningene i bok 1 er ganske elementære: bevist; spesielt at enhver seksjon av en sfære ved et plan er en sirkel, at en rett linje trukket fra senteret av sfæren til senteret av en sirkulær seksjon er vinkelrett på planet til denne seksjonen, at sfæren og planet har ett kontaktpunkt osv.
Bok 2 av Theodosius' sfærer begynner med en definisjon av to sirkler på en kule som berører hverandre og inneholder 23 setninger om egenskapene til sirkler som er tilbøyelige til hverandre.
Den tredje boken består av 14 setninger, mer komplekse enn de foregående, og som omhandler systemer med parallelle og kryssende sirkler på en kule. Her klargjøres sfærens tjenesterolle i forhold til astronomi, selv om alle teoremene er formulert og bevist rent geometrisk.
Theodosius «Sfære» ble nøye studert både i antikken og i middelalderen. Det ble kommentert av Pappus av Alexandria (3. århundre) i den sjette boken i hans matematiske samling. I det VI århundre. John Philopon, med tanke på skriftene om sfæren til Euclid, Autolik og Theodosius, bemerker at sistnevnte gir den mest generelle abstrakte presentasjonen av emnet, fullstendig abstrahert fra virkelige astronomiske objekter. Autolik vurderer etter hans mening et mer spesielt tilfelle, siden "selv om forfatteren ikke har noe spesifikt objekt i tankene, så nærmer han seg virkeligheten takket være kombinasjonen av en sfærisk figur og bevegelse." Det mest spesielle problemet behandles i "Fenomenene" til Euklid, siden objektene som er studert av astronomi - himmelen, solen, stjerner, planeter - er ganske ekte.
Theodosius oversatte først «sfæren» til arabisk på 900-tallet. Kusta ibn Luka al-Baalbaki; oversettelsen hans, brakt opp til 5. setning i bok II, ble fullført av Thabit ibn Korra al-Harrani.
Det er mange kommentarer om dette, så vel som om andre skrifter av Theodosius, satt sammen av østlige lærde fra 1200- og 1400-tallet. , blant dem fremtredende matematikere og astronomer som Nasir ad-Din at-Tusi (1201 - 1274), Yahya ibn Muhammad ibn Abi Shukr Mukhi ad-Din al-Maghribi (d. ca. 1285), Muhammad ibn Ma "ruf ibn Ahmad Taqi Din (1525/1526-1585) m.fl.
Behandling av Theodosius 'sfære, eid av en representant for den berømte Maraga vitenskapelige skolen på 1200-tallet. Muhi ad-Din al-Maghribi, ble undersøkt og delvis oversatt til fransk av B. Kappa de Vaux. Denne avhandlingen trekker oppmerksomheten mot astronomisk terminologi, som brukes i presentasjonen og beviset på Theodosius' teoremer. Så her, enda tydeligere enn i den greske originalen, vises forbindelsen mellom sfæren og astronomi, noe som forklarer dens relevans for østlig vitenskap.
I Europa ble Theodosius' sfære kjent på 1100-tallet, da to latinske oversettelser av dette verket fra dets arabiske versjon dukket opp. De ble laget av de eminente oversetterne som jobbet i Spania, Gerardo av Cremona og Platon av Tivoli. Oversettelsen av sistnevnte ble utgitt i 1518 i Venezia, deretter utgitt på nytt i 1529 i utgaven av I. Voegelin (I. Voegelin, død i 1549), og i 1558 - den nevnte boken av F. Mavroliko.
Den greske teksten til "Sfærene" ble først utgitt i 1558 av J. Pena sammen med en latinsk oversettelse. Denne utgaven gjorde det mulig å klargjøre forskjellen mellom den arabiske versjonen av Theodosius' verk og originalen og å fastslå hvilke tillegg og endringer i beviset for teoremer som ble gjort av østlige forskere. Imidlertid led det greske manuskriptet som ble brukt av Pena av mange mangler. Derfor, i 1707 i Oxford, foretok I. Hunt en ny og forbedret utgave, og gjorde noen rettelser på andre manuskripter. Deretter ble den greske teksten til verket (også med en latinsk oversettelse) gjengitt to ganger til: i 1862 av E. Nice og i 1927 av I. Geiberg.
Fra andre halvdel av 1500-tallet begynte forkortede og tilpassede utgaver av Spheres å dukke opp på latin, der teoremer ble forklart ved hjelp av nye matematiske konsepter og ved bruk av sfærisk trigonometri. I 1586 ble en utgave av X. Clavius (Ch. Clavius) utgitt i Roma, og på 1600-tallet. den ble fulgt av flere andre, inkludert utgavene av M. Mersenne (1644) og I. Barrow (1675).
I 1826 ble The Sphere utgitt i en tysk oversettelse av E. Nice. Den andre tyske utgaven av verket ble utført i 1931 av A. Chvalina (sammen med avhandlingene til Autolik). Den første franske oversettelsen av «Spheres», laget av D. Henrion, ble utgitt i 1615, den neste, eid av J.B. Dugamel (J. V. Du Hamel), - i 1660; endelig, i 1927, dukket det opp en moderne oversettelse av P. Ver Eecke.
Arbeidene til mange matematikkhistorikere (A. Knock, I. Geiberg, F. Gulch, P. Tannery, A. Bjornbo, etc.) er viet studiet av teksten og innholdet i Theodosius' sfære. i III- VII århundrer. og bevart i greske manuskripter fra en senere tid, ble forholdet mellom Theodosius "Sfære" og Euklids "Fenomener" og andre verk av gamle forfattere vurdert. Resultatene av disse studiene gjorde det mulig å avklare en rekke spørsmål angående matematikkens og astronomiens historie, samt biografiene til Euclid, Autolik, Theodosius og noen kommentatorer om deres verk.
6. Innholdet i de greske verkene om sfæren er nær det lille verket til Hypsicles fra Alexandria (levde mellom 200 og 100 f.Kr.), med tittelen «På oppstigningen av stjernebildene langs ekliptikken» («Anaforisk»). Hypsikler er best kjent som forfatteren av en avhandling om vanlige polyedre, inkludert i Euklids elementer som bok XIV; et annet av hans verk, om polygonale tall, som ikke har overlevd, er sitert i Diophantus' Arithmetic.
I avhandlingen "På oppstigningen av stjernebildene på ekliptikken", som består av seks setninger, er problemet løst med å bestemme tiden som kreves for å stige eller sette opp hvert tegn i dyrekretsen, som opptar 1/12 av ekliptikken, eller "grad", dvs. 1/30 deler av ekliptikken. Hun spilte en viktig rolle i astrologisk resonnement og nøt derfor stor popularitet i antikken og i middelalderen. Problemet kan løses ved hjelp av sfærisk trigonometri, men Hypsicles, som ennå ikke hadde slike midler, løste det omtrent ved å bruke teoremene om polygonale tall kjent for ham. I dette verket er det for første gang en inndeling av omkretsen av en sirkel i 360 deler, noe som ikke var tilfellet med hans forgjengere og spesielt med Autolik.
Avhandlingen om Hypsikler var en av "mellombøkene" og ble oversatt til arabisk på 900-tallet. Det er mange manuskripter av denne oversettelsen, men den forble uutforsket i lang tid, og det var ikke nøyaktig fastslått om Kusta ibn Luka, al-Kindi eller Ishaq ibn Hunayn utførte den. Han oversatte den arabiske versjonen av verket til latin på 1100-tallet. Gerardo av Cremona.
En kritisk utgave av den greske originalen og den latinske oversettelsen av Gerardo av Cremona ble utført i 1888 av K. Manitius. Den andre utgaven, utgitt i 1966, inkluderer den greske teksten, scholia og oversettelse av W. De Falco, den arabiske teksten og tysk oversettelse av M. Krause, og en innledende artikkel av O. Neugebauer.
7. Av alle de gamle skriftene om sfæren ble den største rollen i vitenskapens historie spilt av "Sfæren" til Menelaos, som arbeidet i Alexandria i det 1. århundre f.Kr. n. e. og oppsummerer alle resultatene som er oppnådd på dette området før ham. I hans arbeid er ikke bare geometrien på sfæren oppgitt, men den sfæriske trekanten ble introdusert for første gang, teoremene som fungerte som grunnlaget for sfærisk trigonometri ble suksessivt bevist, og det teoretiske grunnlaget for trigonometriske beregninger ble opprettet.
Informasjon om livet til Menelaos er ekstremt lite. Det er kjent at han i 98 gjorde astronomiske observasjoner i Roma. The Sphere, hans hovedverk, er ikke bevart på originalgresk og er bare kjent fra middelalderske arabiske oversettelser.
The Sphere består av tre bøker og er modellert etter Euklids elementer. Først av alt introduseres definisjoner av grunnleggende begreper, inkludert konseptet om en sfærisk trekant, som ikke finnes i tidligere greske verk. En betydelig del av arbeidet er viet til studiet av egenskapene til denne figuren.
Når han beviser påstander om egenskapene til linjer og figurer på en sfære, støtter han seg på definisjoner og teoremer fra Theodosius' sfære. I den andre boken er disse teoremene, samt påstandene formulert i astronomisk form i Euclids Phenomena og Hypsicles' Anaforica, systematisert og forsynt med nye strenge bevis.
En spesielt viktig rolle i trigonometriens historie ble spilt av den første setningen i bok III, kjent som "menelaos teoremer" (så vel som "setninger om den komplette firkanten", "reglene for seks størrelser", "teoremer om tverrgående setninger" ”). Med A. Braunmühls ord var det «grunnlaget for hele grekernes sfæriske trigonometri».
Menelaos' setning for plantilfellet er formulert som følger: la gjensidig kryssende linjer AB, AC, BE og CD, som danner figuren ACGB (fig. 1), gis; da gjelder følgende forhold:
CE / AE = CG / DG * DB / AB, CA / AE = CD / DG * GB / BE
For det sfæriske tilfellet, i teoremet, som det var vanlig i gresk trigonometri, vises akkordene til doble buer. Hvis tallet ACGB (fig. 2) er gitt, dannet av buer av storsirkler på overflaten av en kule, så er relasjonene gyldige:
akkord(2CE) / akkord(2AE) = akkord(2CG) / akkord(2DG) * akkord(2DB) / akkord(2AB)
akkord(2AC) / akkord(2AE) = akkord(2CD) / akkord(2DG) * akkord(2GB) / akkord(2BE)

Menelaus beviste også flere andre teoremer av grunnleggende betydning for utviklingen av sfærisk trigonometri. Disse inkluderer den såkalte «regelen om fire størrelser» (2. setning i bok III); hvis to sfæriske trekanter ABC og DEG er gitt (fig. 3), som henholdsvis har like (eller summerer opp til 180°) vinkler A og D, C og G, da
akkord (2AB) / akkord (2BC) = akkord (2DE) / akkord (2EG)
Den tredje setningen i III-boken om "Sfærene" til Menelaos, som senere fikk navnet "tangensregler", lyder; hva om to rettvinklede sfæriske trekanter ABC og DEG (fig. 4) er gitt, for hvilke akkord (2AB) / akkord (2AC) = akkord (2ED) / akkord (2GD) * akkord (2BH) / akkord (2ET) 1. Geiberg I.L. Naturvitenskap og matematikk i den klassiske antikken. Oversettelse fra ham. S.P. Kondratiev, red. med forord A.P. Yushkevich, M-L., ONTI, 1936. 2. Sarton G. Vurdering av antikkens og middelaldervitenskapen under renessansen, Philadelphia, 1953. 3 Steinschneider M. Die "mittleren" Bücher der Araber und ihre Bearbeiter, "Zeitschr. für Math. u. Phys.", Bd 10, 1.865, 456-498. 4. Suter H. Die Mathematiker und Astronomen der Araber und ihre Werke, "Abhandl. zur Gesch. d. math. Wiss.", N. 10, Leipzig, 1900. 5. Björnbo A. Studienüber Menelaus Sphärik. Beiträge zur Geschichte der Sphärik und Trigonometrie der Griechen, "Abhandl. zur Gesch. d. math. Wiss.", H. 14, Leipzig, 1902. 6. Mogenet J. Autolycos de Pitane. Histoire du texte, suivie de l "édition critique des traités de la Sphère en mouvement et des levers et couchers, Louvain, 1950. 7. Theodosii Shpaericorum elementorum Libri III. Ex traditione Mauro-lyci... Menelai Sphaericorum lib. III. Ex traditione eiusdem. Maurolyci, Sphaericorum libri II. Autolyci. De sphaera quae movetur liber. Theodosii. De habitationibus. Euclidis Phaenomena brevissime demonstrata. Demonstratio et praxis trium tabellarum scilicet sinus recti, foecundae, et beneficae ad spheraiia triangula pertinentum. Compendium mathematicae mira brevitate ex clarissimis authoribus. Maurolyci de sphaera sermo. Messanae, 1558. 8. Mersenne M. Universae geometriae mixtaeque mathematicae synopsis, Parisiis, 1644. 9. Auto1yci. De Sphaera quae movetur liber. D.e ortibus et occasibus libri duo, willow cum scholiis antiquis o libris manuscriptis edidit, latina interpretatione et commentariis instruxit F. Hultsch, Leipzig, 1885. 10. Euclidis. Opera omnia. Ed. J. L. Heiberg et H. Menge, t. VIII. Phaenomena et scripta musica, Leipzig, 1916. 11. Tannery P. Recherches sur l "histoire sur l" astronomie ancienne, Paris, 1893. 12. Carra de Vaux B. Notice sur deux manuscrits arabes. I. Remaniement des sphériques de Théodose par labia ibn Muhammad ihn Abi Schukr Almaghribi Aiandalusî, "Journal asiatique", 8. sér., t. 17, 1894, 287-295. 13. Theodosius Tripolites. Sphaerica. Hrsg, von J. L. Heiberg, "Abhandl. d. G.es. d. Wissenschaften zu Göttihgen", fil. hist, Klasse, N. F., Bd 19, No 3, Berlin, 1927. 14. Hypsikles Die Aufgangszeiten der Gestirne, hrsg. und übers, von V. De Falco og M. Krause. Einführung von O. Neugebauer, "Abhandl. d. Akademie d. Wiss. zu Göttingen", phil-hist. Kl., F. 3, No 62, Göttingen, 1966. 15. Krause M. Die Sphärik von Menelaos von Alexandrien in der Verbesserung von Abu Nasr Mansur f. Ali b. Irak mit Untersuchungen zur Geschichte des Textes bei den islamischen Mathematikern, Berlin, 1936. Notater En kopi av denne sjeldne utgaven er tilgjengelig i biblioteket. I OG. Lenin. En kopi er tilgjengelig i biblioteket til USSR Academy of Sciences. SFERISK TRIGONOMETRI trigonometri, den matematiske disiplinen som studerer forholdet mellom vinkler og sider av sfæriske trekanter (se sfærisk geometri). La A, B, C være vinklene og a, b, c de motsatte sidene av den sfæriske trekanten ABC (se figur). Vinklene og sidene til en sfærisk trekant er forbundet med følgende grunnleggende formler for S. t.: cos a cos b cos c + sin b sin c cos A, (2) cos A - cos B cos C + sin B sin C cos a, (21) sin a cos B cos b sin c - sin b cos c cos A, (3) sin A cos b cos B sin C + sin B cos C cos a; (31) i disse formlene er sidene a, b, c målt med de korresponderende sentrale vinklene, lengdene på disse sidene er henholdsvis aR, bR, cR, hvor R er radiusen til kulen. Ved å endre betegnelsene på vinklene (og sidene) i henhold til den sirkulære permutasjonsregelen: A - B - C - A (a - b - c - a), kan du skrive andre S. t.-formler som ligner på de som er angitt. Formlene til sfæriske trekanter gjør det mulig å bestemme de resterende tre elementene fra hvilke som helst tre elementer i en sfærisk trekant (for å løse trekanten). For rettvinklede sfæriske trekanter (A 90 |, a - hypotenuse, b, c - ben), er S. t.-formlene forenklet, for eksempel: sin b sin a sin V,(1") cos a cos b cos c, (2") sin a cos B cos b sin c .(3") For å få formler som forbinder elementene i en rettvinklet sfærisk trekant, kan du bruke følgende mnemoniske regel (Napiers regel): hvis du erstatter bena til en rettvinklet sfærisk trekant med deres komplementer og ordner elementene i trekanten (unntatt rett vinkel A) rundt sirkelen i den rekkefølgen de er i trekanten (det vil si som følger: B, a, C, 90 | - b, 90 | - c), så er cosinus til hvert element lik produktet av sinusene til ikke-tilstøtende elementer, for eksempel, cos a sin (90| - c) sin (90 | - b) eller, etter transformasjon, cos a cos b cos c (formel 2"). Når du løser problemer, er følgende Delambre-formler praktiske, som forbinder alle seks elementene i en sfærisk trekant: Når du løser mange problemer med sfærisk astronomi, avhengig av den nødvendige nøyaktigheten, er det ofte tilstrekkelig å bruke omtrentlige formler: for små sfæriske trekanter (det vil si de hvis sider er små sammenlignet med sfærens radius), kan du bruke formlene av plan trigonometri; for smale sfæriske trekanter (det vil si de der en side, for eksempel a, er liten sammenlignet med de andre), gjelder følgende formler: eller mer presise formler: S. t. oppsto mye tidligere enn flat trigonometri. Egenskapene til rettvinklede sfæriske trekanter, uttrykt med formlene (1")-(3"), og forskjellige tilfeller av løsningen deres var kjent selv for de greske forskerne Menelaus (1. århundre) og Ptolemaios (2. århundre). Greske forskere reduserte løsningen av skrå sfæriske trekanter til løsningen av rektangulære. Den aserbajdsjanske forskeren Nasiraddin Tuei (1200-tallet) undersøkte systematisk alle tilfeller av å løse skrå sfæriske trekanter, og indikerte for første gang løsningen i to av de vanskeligste tilfellene. De grunnleggende formlene for skrå sfæriske trekanter ble funnet av den arabiske vitenskapsmannen Abul-Vefa (10. århundre) [formel (1)], den tyske matematikeren I. Regiomontan (midten av 1400-tallet) [formler som (2)], og franskmennene matematiker F. Viet (2. halvdel av 1500-tallet) [formler av typen (21)] og L. Euler (Russland, 1700-tallet) [formler av typen (3) og (31)]. Euler (1753 og 1779) ga hele systemet med formler for S. T. Noen formler for S. T. praktiske for praksis ble etablert av den skotske matematikeren J. Napier (slutten av 1500-tallet - begynnelsen av 1600-tallet), den engelske matematikeren G. 1600-tallet), russisk astronom A. I. Leksel (andre halvdel av 1700-tallet), den franske astronomen J. Delambre (slutten av 1700-tallet - begynnelsen av 1800-tallet), og andre. Tent. se på Art. sfærisk geometri. Great Soviet Encyclopedia, TSB.
2012
Sfærisk trigonometri i Encyclopedic Dictionary: Definisjon av "Sfærisk trigonometri" av TSB: i disse formlene er sidene a, b, c målt med de korresponderende sentrale vinklene, lengdene på disse sidene er henholdsvis aR, bR, cR, der R er radiusen til kulen. Endre betegnelsene på hjørnene (og sidene) i henhold til den sirkulære permutasjonsregelen: For å få formler som relaterer elementene til en rettvinklet sfærisk trekant, kan du bruke følgende mnemoniske regel (Napiers regel): hvis du erstatter bena til en rettvinklet sfærisk trekant med komplementene deres og ordner elementene i trekanten (unntatt rett vinkel A) rundt sirkelen i den rekkefølgen de er i trekanten (det vil si som følger: B, a, C, 90° - b, 90° - c), så er cosinus til hvert element lik produktet av sinusene til ikke-tilstøtende elementer, for eksempel, sin 1⁄2a sin 1⁄2(B−C) = cos 1⁄2A sin 1⁄2(b−c) cos 1⁄2a cos 1⁄2(B+C) = sin 1⁄2A cos 1⁄2(b+c) cos 1⁄2a sin 1⁄2(B+C) = cos 1⁄2A cos 1⁄2(b−c) S. t. oppsto mye tidligere enn flat trigonometri. Egenskapene til rettvinklede sfæriske trekanter, uttrykt ved formler (1)-(3), og forskjellige tilfeller av løsningen deres var kjent selv for de greske forskerne Menelaos (1. århundre) og Ptolemaios (2. århundre). Greske forskere reduserte løsningen av skrå sfæriske trekanter til løsningen av rektangulære. Den aserbajdsjanske forskeren Nasiraddin Tuei (1200-tallet) undersøkte systematisk alle tilfeller av å løse skrå sfæriske trekanter, og indikerte for første gang løsningen i to av de vanskeligste tilfellene. De grunnleggende formlene for skrå sfæriske trekanter ble funnet av den arabiske vitenskapsmannen Abul-Vefa (10. århundre) [formel (1)], den tyske matematikeren I. Regiomontan (midten av 1400-tallet) [formler som (2)], og franskmennene matematiker F. Viet (2. halvdel av 1500-tallet) [formler av typen (21)] og L. Euler (Russland, 1700-tallet) [formler av typen (3) og (31)]. Euler (1753 og 1779) ga hele systemet med formler for S. T. Noen formler for S. T. praktiske for praksis ble etablert av den skotske matematikeren J. Napier (slutten av 1500-tallet - begynnelsen av 1600-tallet), den engelske matematikeren G. 1600-tallet), russisk astronom A. I. Leksel (andre halvdel av 1700-tallet), den franske astronomen J. Delambre (slutten av 1700-tallet - begynnelsen av 1800-tallet), og andre. 
LITTERATUR
Se også tolkninger, synonymer, betydninger av ordet og hva som er SFERISK TRIGONOMETRI på russisk i ordbøker, leksikon og oppslagsverk:
en gren av matematikken som studerer forholdet mellom sidene og vinklene til sfæriske trekanter (det vil si trekanter på overflaten av en sfære) dannet når ...
(fra gresk trigonon - triangel og ... metrikk) en gren av matematikk som studerer trigonometriske funksjoner og deres anvendelser til ...
(fra gresk. trigonon - trekanter - metrikk), en gren av matematikken som studerer trigonometriske funksjoner og deres anvendelser på geometri. …
(fra gresk trigonon - trekant og ... meter), en gren av matematikk som studerer trigonometriske funksjoner og deres anvendelser på geometri. Skill…
og pl. nei, w. Matematikkens gren som studerer forholdet mellom sidene og vinklene i en trekant. Trigonometrisk - knyttet til trigonometri.||Jfr. ALGEBRA, ...
, -i, f. Matematikkens gren som studerer forholdet mellom sidene og vinklene i en trekant. II adj. trigonometrisk, -th, ...
TRIGONOMETRI (fra gresk. trigonon - en trekant og ... metrikk), en seksjon av matematikk, der trigonometri studeres. funksjoner og deres applikasjoner til ...
SFERISK TRIGONOMETRI, en gren av matematikken der forholdet mellom sider og vinkler til sfæriske objekter studeres. trekanter (dvs. trekanter på overflaten av en kule) dannet av ...
SFERISK GEOMETRI, en gren av matematikken der geom studeres. figurer på sfæren. Utvikling S.g. i antikk antikken var assosiert med oppgaver ...
SFERISK ASTRONOMI, en gren av astronomi som utvikler matematikk. metoder for å løse problemer knyttet til studiet av den tilsynelatende plasseringen og bevegelsen av rommet. kropper (stjerner, sol, ...
SFERISK ABERRASJON, bildeforvrengning i optisk. systemer på grunn av det faktum at lysstrålene fra en punktkilde plassert på optikken. økser...
trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, trigonometri, ...
(gr. trigonon triangle + ... metrics) en gren av matematikk som studerer trigonometriske funksjoner og deres anvendelse for å løse problemer, kap. arr. geometrisk; …
[gr. trigonon triangle + ... metrics] gren av matematikk som studerer trigonometriske funksjoner og deres anvendelse for å løse problemer, kap. arr. geometrisk; T. …
trigonometri...
trigonomi ʻetria, ...
grenen av matematikk som studerer forholdet mellom sider og vinkler...
gresk matematikk av trekanter; vitenskapen om å beregne det ved å konstruere trekanter. -trisk oppmåling og triangulering, oppmåling av terrenget iht ...
(fra gresk trigonon - triangel og ... metrikk), en gren av matematikk som studerer trigonometriske funksjoner og deres anvendelser til ...
trigonometri, pl. nei, w. (fra gresk trigonos - trekant og metreo - mål) (mat.). Institutt for geometri om forholdet mellom sidene ...
trigonometri En gren av matematikk som studerer trigonometriske funksjoner og deres anvendelse for å løse ...
og. En gren av matematikk som studerer trigonometriske funksjoner og deres anvendelse for å løse ...
og. En gren av matematikk som studerer trigonometriske funksjoner og deres anvendelse for å løse ...
geometri, en matematisk disiplin som studerer geometriske bilder som er på en kule, akkurat som planimetri studerer geometriske bilder som er på et plan. Hver…
Bonsai-stiler I naturen er utseendet til trær dannet avhengig av deres vekststed og under påvirkning av naturlige faktorer. Stamme...
SFERISK - se kulekule ...
- en sfærisk overflate plassert over takskjegget i rommet. Polstringen skaper en overgang fra veggens plan til overflaten...
, en slekt av fisk. ansjos neg. sild. 8 arter, fordelt i kystnære havvann i de tropiske og tempererte sonene på begge halvkuler. …
Chumakov (Fyodor Ivanovich) - professor i anvendt matematikk ved Moskva universitet (1782 - 1837). Sønnen til en kaptein, han ble akseptert i nummeret ...
Savich (Aleksey Nikolaevich, 1810 - 1883) - berømt russisk astronom, medlem av Vitenskapsakademiet (siden 1862); i 1829 tok han eksamen ...
Green (Semyon Ilyich) - Admiral (1810 - 1892). Han ble oppdratt i marinekorpset. Han fullførte sin astronomiske utdanning i Yuryev, under veiledning av ...
rettlinjet, en del av et plan avgrenset av tre linjestykker (sidene av en T.), som har parvis én felles ende (toppunkter av en T.). T., som har...
trekant, en geometrisk figur dannet av buene til tre store sirkler som kobler sammen i par tre alle punkter på kulen. På eiendommene til S. t. og ...
(matematisk), en lukket overflate, der alle punkter er like langt fra ett punkt (sentrum av S.). Et segment som forbinder sentrum av S. med noen av dets ...
(Tysk Super-Schmidt-Spiegel), et speil-linse-teleskopsystem der den sfæriske aberrasjonen til et konkavt sfærisk speil korrigeres av en kompleks kombinasjon av en Schmidt-korreksjonsplate (se ...
Sfærisk trigonometri er en gren av matematikken som studerer forholdet mellom sidene og vinklene til sfæriske trekanter (dvs. trekanter på overflaten av en sfære) dannet når tre store sirkler krysser hverandre. Sfærisk trigonometri er nært beslektet med sfærisk astronomi.
Sfærisk trigonometri er en matematisk disiplin som studerer forholdet mellom vinkler og sider av sfæriske trekanter (se Sfærisk geometri ). La A, B, C være vinklene og a, b, c de motsatte sidene av den sfæriske trekanten ABC (se figur). Vinklene og sidene til en sfærisk trekant er forbundet med følgende grunnleggende formler for S. t.:
synd a
synd A =
synd b
synd B =
synd c
synd C,
(1)
cos a = cos b cos c + sin b sin c cos A,(2)
cos A = − cos B cos C + sin B sin C cos a,(21)
sin a cos B = cos b sin c - sin b cos c cos A,(3)
sin A cos b = cos B sin C + sin B cos C cos a;(31)
A → B → C → A (a → b → c → a), man kan skrive andre S. t.-formler som ligner på de som er angitt. Formlene til sfæriske trekanter gjør det mulig å bestemme de resterende tre elementene fra hvilke som helst tre elementer i en sfærisk trekant (for å løse trekanten).
For rettvinklede sfæriske trekanter (A \u003d 90 °, a er hypotenusen, b, c er bena), forenkles S. t.-formlene, for eksempel:
synd b \u003d synd a synd B,(1')
cos a = cos b cos c,(2')
sin a cos B = cos b sin c.(3')
cos a \u003d sin (90 ° - c) sin (90 ° - b)
eller, etter transformasjon,
cos a = cos b cos c (formel 2′).
Når du løser problemer, er følgende Delambre-formler praktiske, som forbinder alle seks elementene i en sfærisk trekant:
sin 1⁄2a cos 1⁄2(B−C) = sin 1⁄2A sin 1⁄2(b+c)
Når du løser mange problemer med sfærisk astronomi, avhengig av den nødvendige nøyaktigheten, er det ofte tilstrekkelig å bruke omtrentlige formler: for små sfæriske trekanter (det vil si de hvis sider er små sammenlignet med sfærens radius), kan du bruke formlene av plan trigonometri; for smale sfæriske trekanter (det vil si de der en side, for eksempel a, er liten sammenlignet med de andre), gjelder følgende formler: (1'")
a cos B ≈ c−b
+
aІ
2
synd B
tg c.
(3′″)
Tent. se på Art. sfærisk geometri.
Ris. til Art. Sfærisk trigonometri.
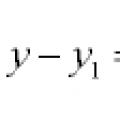 Ligninger av linjer og kurver i planet
Ligninger av linjer og kurver i planet Generalisert homogen likning Generaliserte homogene likninger av andre orden
Generalisert homogen likning Generaliserte homogene likninger av andre orden Takket være kommaet På grunn av det faktum at i deres
Takket være kommaet På grunn av det faktum at i deres