Nambari zinazolingana modulo 7. Moduli ya kulinganisha nambari asilia
Kulinganisha na moja isiyojulikana x inaonekana kama
Wapi. Kama a n haiwezi kugawanywa na m, hiyo ndiyo inaitwa shahada kulinganisha.
Kwa uamuzi kulinganisha ni nambari yoyote x 0 , kwa ambayo
Kama X 0 inakidhi ulinganisho, basi, kulingana na mali ya kulinganisha 9, nambari zote kulinganishwa na x 0 moduli m. Kwa hivyo, suluhisho zote za kulinganisha za modulo ya darasa moja la mabaki T, tutazingatia kama suluhisho moja. Kwa hivyo, ulinganisho una masuluhisho mengi kama vile kuna vipengele vya mfumo kamili wa mabaki unaokidhi.
Ulinganisho ambao seti za suluhisho zinalingana huitwa sawa.
2.2.1 Ulinganisho wa shahada ya kwanza
Shahada ya kwanza kulinganisha na moja haijulikani X inaonekana kama
![]() (2.2)
(2.2)
Nadharia 2.4. Ili kulinganisha iwe na angalau suluhisho moja, ni muhimu na ya kutosha kwamba nambari b kugawanywa na GCD ( a, m).
Ushahidi. Kwanza tunathibitisha hitaji. Hebu d
=
GCD( a,
m)
Na X 0
- suluhisho la kulinganisha. Kisha ![]() , yaani tofauti Oh 0
−
b
kugawanywa na T. Kwa hivyo kuna nambari kamili kama hiyo q,
Nini Oh 0
−
b
=
qm.
Kutoka hapa b= ah 0
−
qm.
Na tangu d,
kama kigawanyiko cha kawaida, hugawanya nambari A Na T, kisha minuend na subtrahend zimegawanywa na d,
na kwa hiyo b
kugawanywa na d.
, yaani tofauti Oh 0
−
b
kugawanywa na T. Kwa hivyo kuna nambari kamili kama hiyo q,
Nini Oh 0
−
b
=
qm.
Kutoka hapa b= ah 0
−
qm.
Na tangu d,
kama kigawanyiko cha kawaida, hugawanya nambari A Na T, kisha minuend na subtrahend zimegawanywa na d,
na kwa hiyo b
kugawanywa na d.
Sasa tuthibitishe utoshelevu. Hebu d- mgawanyiko mkubwa zaidi wa nambari A Na T, Na b kugawanywa na d. Halafu, kwa ufafanuzi wa mgawanyiko, kuna nambari kamili zifuatazo a 1 , b 1 ,T 1 , Nini .
Kwa kutumia algorithm iliyopanuliwa ya Euclidean, tunapata uwakilishi wa mstari wa nambari 1 = gcd( a 1 , m 1 ):
![]()
kwa baadhi x 0 , y 0 . Hebu tuzidishe pande zote mbili za usawa wa mwisho kwa b 1 d:
au, ni nini sawa,
,
yaani, na ndio suluhisho la ulinganisho. □
Mfano 2.10. Ulinganisho wa 9 X= 6 (mod 12) ina suluhu kwani gcd(9, 12) = 3 na 6 inaweza kugawanywa na 3. □
Mfano 2.11. Kulinganisha 6x= 9 (mod 12) haina suluhu, kwani gcd(6, 12) = 6, na 9 haiwezi kugawanywa na 6. □
Nadharia 2.5. Acha kulinganisha (2.2) iweze kutatuliwa na d = GCD( a, m). Kisha seti ya ufumbuzi wa kulinganisha (2.2) inajumuisha d madarasa ya mabaki ya modulo T, yaani ikiwa X 0 - moja ya suluhisho, basi suluhisho zingine zote ni
Ushahidi. Hebu X 0
- suluhisho la kulinganisha (2.2), yaani ![]() Na ,
.
Kwa hivyo kuna kitu kama hicho q, Nini Oh 0
−
b
=
qm.
Sasa kubadilisha katika usawa wa mwisho badala ya X 0
ufumbuzi wa kiholela wa fomu, ambapo, tunapata kujieleza
Na ,
.
Kwa hivyo kuna kitu kama hicho q, Nini Oh 0
−
b
=
qm.
Sasa kubadilisha katika usawa wa mwisho badala ya X 0
ufumbuzi wa kiholela wa fomu, ambapo, tunapata kujieleza
, kugawanywa na m. □
Mfano 2.12. Ulinganisho wa 9 X=6 (mod 12) ina masuluhisho matatu haswa, kwani gcd(9, 12)=3. Suluhu hizi: X 0 = 2, x 0 + 4 = 6, X 0 + 2∙4=10.□
Mfano 2.13. Ulinganisho wa 11 X=2 (mod 15) ina suluhisho la kipekee X 0 = 7, tangu GCD(11,15)=1. □
Tutakuonyesha jinsi ya kutatua ulinganisho wa shahada ya kwanza. Bila upotezaji wa kawaida, tutafikiria kuwa GCD( a, t) = 1. Kisha suluhisho la kulinganisha (2.2) linaweza kutafutwa, kwa mfano, kwa kutumia algorithm ya Euclidean. Kwa kweli, kwa kutumia algorithm iliyopanuliwa ya Euclidean, tunawakilisha nambari 1 kama mchanganyiko wa nambari. a Na T:
Hebu tuzidishe pande zote mbili za usawa huu kwa b, tunapata: b = abq + Bw, wapi abq - b = - Bw, hiyo ni a ∙ (bq) = b(moduli m) Na bq- suluhisho la kulinganisha (2.2).
Suluhisho lingine ni kutumia nadharia ya Euler. Tena tunaamini kwamba GCD(a, T)= 1. Tunatumia nadharia ya Euler: ![]() . Zidisha pande zote mbili za kulinganisha kwa b:
. Zidisha pande zote mbili za kulinganisha kwa b:
![]() .
Kuandika upya usemi wa mwisho kama
.
Kuandika upya usemi wa mwisho kama  , tunapata hiyo ni suluhisho la kulinganisha (2.2).
, tunapata hiyo ni suluhisho la kulinganisha (2.2).
Wacha sasa GCD( a, m) = d>1. Kisha a = atd, m = mtd, wapi GCD ( A 1 , m 1) = 1. Kwa kuongeza, ni muhimu b = b 1 d, ili kulinganisha kutatuliwa. Kama X 0 - suluhisho la kulinganisha A 1 x = b 1 (moduli m 1), na ya pekee, tangu GCD( A 1 , m 1) = 1, basi X 0 itakuwa suluhisho na kulinganisha A 1 xd = db 1 (moduli m 1), yaani, ulinganisho wa awali (2.2). Pumzika d- Suluhu 1 zinapatikana na Theorem 2.5.
Mradi wa hesabu juu ya mada
"Moduli ya kulinganisha"
Zaripova Aisylu
Wilaya ya Sovetsky ya Kazan
MBOU "Shule ya Sekondari No. 166", 7a daraja
Msimamizi wa kisayansi: Antonova N.A.
Jedwali la yaliyomo
Utangulizi ______________________________________________________________________3
Ulinganisho ni nini __________________________________________________4
Dhana ya modulo za ulinganishi____________________________________4
Historia ya kuibuka kwa dhana ya ulinganishi modulo_____4
Sifa za kulinganisha_________________________________________________4
Matumizi rahisi zaidi ya ulinganisho wa modulo ni kuamua mgawanyiko wa nambari ___________________________________________6
Jukumu moja la kulinganisha ___________________________________8
Matumizi ya ulinganisho wa modulo katika shughuli za kitaaluma________________________________________________9
Kutumia ulinganifu kwa utatuzi wa matatizo______________________________6
Hitimisho________________________________________________________________10
Orodha ya fasihi iliyotumika ______________________________________11
Utangulizi.
Mada: Ulinganisho wa Modulo.
Tatizo: Wanafunzi wengi wanakabiliwa na matatizo wakati wa kujiandaa kwa Olympiads, suluhisho ambalo linatokana na ujuzi wa masalio kutoka kwa kugawanya nambari kwa idadi asilia. Tulipendezwa na aina hizi za shida na njia zinazowezekana za kuzitatua. Inabadilika kuwa zinaweza kutatuliwa kwa kutumia kulinganisha modulo.
Kusudi: Jua kiini cha ulinganisho wa modulo, njia kuu za kufanya kazi na ulinganisho wa modulo.
Malengo: pata nyenzo za kinadharia juu ya mada hii, fikiria shida ambazo zinatatuliwa kwa kulinganisha modulo, onyesha njia za kawaida za kutatua shida kama hizo, fanya hitimisho.
Mada ya utafiti: nadharia ya nambari.
Mada ya utafiti: nadharia ya ulinganisho wa modulo.
Kazi hii inahusiana na utafiti wa kinadharia na inaweza kutumika katika maandalizi ya Olympiads za hisabati. Maudhui yake yanaonyesha dhana za msingi za ulinganisho wa modulo na sifa zao kuu, na hutoa mifano ya kutatua matatizo juu ya mada hii.
I . Ulinganisho ni nini?
Dhana ya ulinganisho wa modulo.
Nambari na inasemekana kulinganishwa katika moduli ikiwa zinaweza kugawanywa na, kwa maneno mengine, a na b zina masalio sawa wakati zimegawanywa na.
Uteuzi
Mifano:
12 na 32 zinalinganishwa modulo 5, kwani 12 ikigawanywa na 5 ina salio ya 2 na 32 ikigawanywa na 2 ina salio ya 2. Imeandikwa12 ;
101 na 17 zinalinganishwa modulo 21;
Historia ya kuibuka kwa dhana ya ulinganisho wa modulo.
Nadharia ya mgawanyiko iliundwa kwa kiasi kikubwa na Euler. Ufafanuzi wa kulinganisha uliandaliwa katika kitabu na K.F. Gauss "Masomo ya Hesabu". Kazi hii, iliyoandikwa kwa Kilatini, ilianza kuchapishwa mnamo 1797, lakini kitabu hicho kilichapishwa mnamo 1801 tu kwa sababu ya ukweli kwamba mchakato wa uchapishaji wakati huo ulikuwa wa kazi kubwa na wa muda mrefu. Sehemu ya kwanza ya kitabu cha Gauss inaitwa: "Juu ya kulinganisha nambari." Alikuwa Gauss ambaye alipendekeza ishara ya ulinganisho wa modulo ambayo imeanzishwa katika hisabati.
Tabia za kulinganisha.
Kama
Uthibitisho:
Ikiwa tunaongeza pili kwa usawa wa kwanza, tunapata
ni jumla ya nambari mbili kamili, kwa hivyo ni nambari kamili, kwa hivyo.
Ikiwa tunaondoa ya pili kutoka kwa usawa wa kwanza, tunapata
hii ndio tofauti ya nambari mbili kamili, ambayo inamaanisha kuwa ni nambari kamili, kwa hivyo.
Fikiria usemi:
Hii ni tofauti ya bidhaa za integers, ambayo ina maana ni integer, kwa hiyo.
Hii ni matokeo ya mali ya tatu ya kulinganisha.
Q.E.D.
5) Kama.
Uthibitisho: Wacha tupate jumla ya maneno haya mawili:
ni jumla ya nambari mbili kamili, kwa hivyo ni nambari kamili, kwa hivyo.
Q.E.D.
6) Ikiwa ni nambari kamili, basi
Ushahidi:, wapiuk– nambari kamili, zidisha usawa huu kwa, tunapata: . Kwa kuwa ni bidhaa ya nambari kamili, hiyo ndiyo ilihitaji kuthibitishwa.
7) Kama
Uthibitisho: hoja ni sawa na uthibitisho wa mali 6.
8) Kama - nambari za coprime, basi
Uthibitisho: , gawanya usemi huu kwa, tunapata: - nambari za coprime, ambayo inamaanisha kuwa zinagawanywa kwa nambari kamili, i.e. =. Na hii ina maana kwamba kile kilichohitajika kuthibitishwa.
II . Kutumia kulinganisha kwa kutatua shida.
2.1. Matumizi rahisi zaidi ya ulinganisho wa modulo ni kuamua mgawanyiko wa nambari.
Mfano. Tafuta 2 iliyobaki 2009 saa 7.
Suluhisho: Zingatia nguvu za 2:
kuinua kulinganisha kwa nguvu ya 668 na kuzidisha kwa, tunapata:.
Jibu: 4.
Mfano. Thibitisha kuwa 7+7 2 +7 3 +…+7 4 n inaweza kugawanywa na 100 kwa yoyotenkutoka kwa seti ya nambari kamili.
Suluhisho: Fikiria kulinganisha
na kadhalika. Asili ya mzunguko wa mabaki inaelezewa na sheria za kuzidisha nambari kwenye safu. Kuongeza kulinganisha nne za kwanza, tunapata:
Hii ina maana kwamba kiasi hiki kinagawanywa na 100 bila salio. Vile vile, kwa kuongeza ulinganisho ufuatao kama nne, tunapata kwamba kila jumla kama hiyo inaweza kugawanywa na 100 bila salio. Hii ina maana kwamba jumla yote inayojumuisha 4nmasharti yanaweza kugawanywa na 100 bila salio. Q.E.D.
Mfano. Amua kwa thamani ganinusemi huo unaweza kugawanywa na 19 bila salio.
Suluhisho:.
Wacha tuzidishe ulinganisho huu kwa 20. Tunapata.
Wacha tuongeze kulinganisha, basi. . Kwa hivyo, upande wa kulia wa kulinganisha daima hugawanywa na 19 kwa nambari yoyote ya asilin, ambayo inamaanisha usemi asilia unaweza kugawanywa na 19 kwa asilin.
Jibu n - nambari yoyote ya asili.
Mfano. Nambari inaisha na tarakimu gani?
Suluhisho. Ili kutatua tatizo hili, tutafuatilia tu tarakimu ya mwisho. Fikiria nguvu za nambari 14:
Unaweza kutambua kwamba ikiwa kielelezo ni isiyo ya kawaida, thamani ya shahada inaisha kwa 4, na ikiwa kielelezo ni sawa, kinaisha kwa 6. Kisha inaisha kwa 6, i.e. ni nambari sawa. Kwa hivyo itaisha mnamo 6.
Jibu 6.
2.2. Kazi moja ya kulinganisha.
Makala ya N. Vilenkin "Kulinganisha na madarasa ya mabaki" inatoa tatizo ambalo lilitatuliwa na mwanafizikia maarufu wa Kiingereza Dirac wakati wa miaka ya mwanafunzi wake.
Pia kuna suluhisho fupi la shida hii kwa kutumia ulinganisho wa modulo. Lakini tulikutana na shida kadhaa kama hizo. Kwa mfano.
Mpita njia mmoja alipata rundo la tufaha karibu na mti ambao tumbili alikuwa ameketi. Baada ya kuzihesabu, aligundua kuwa ikiwa tumbili 1 atapewa tumbili, basi idadi ya maapulo iliyobaki itagawanywa katika n bila kuwaeleza. Baada ya kumpa tumbili tumbili lile la ziada, alichukua 1/ n apples iliyobaki na kushoto. Baadaye, mpita-njia aliyefuata alikaribia rundo, kisha ijayo, nk. Kila mpita njia aliyefuata, baada ya kuhesabu maapulo, aligundua kuwa idadi yao wakati imegawanywa na n anatoa salio 1 na, baada ya kumpa tumbili apple ya ziada, alichukua 1 kwa ajili yake mwenyewe n apples iliyobaki na kuendelea. Baada ya yule wa mwisho kuondoka, n mpita njia, idadi ya tufaha iliyobaki kwenye rundo iligawanywa na n bila kuwaeleza. Ni tufaha mangapi zilikuwa kwenye rundo hapo kwanza?
Kwa kutekeleza hoja sawa na Dirac, tulipata fomula ya jumla ya kutatua darasa la shida zinazofanana: , ambapon- nambari ya asili.
2.3. Utumiaji wa kulinganisha kwa moduli katika shughuli za kitaalam.
Nadharia ya kulinganisha inatumika kwa nadharia ya usimbaji, kwa hivyo watu wote wanaochagua taaluma inayohusiana na kompyuta watasoma, na ikiwezekana kutumia ulinganisho katika shughuli zao za kitaaluma. Kwa mfano, idadi ya dhana za nadharia ya nambari, ikijumuisha ulinganisho wa modulo, hutumiwa kuunda algoriti za usimbaji funguo za umma.
Hitimisho.
Kazi inaeleza dhana na sifa za kimsingi za ulinganisho wa modulo na inaonyesha matumizi ya ulinganisho wa modulo na mifano. Nyenzo hizo zinaweza kutumika katika kuandaa olympiads katika hisabati na Mtihani wa Jimbo la Umoja.
Orodha iliyotolewa ya marejeleo inaruhusu, ikiwa ni lazima, kuzingatia baadhi ya vipengele changamano zaidi vya nadharia ya ulinganisho wa modulo na matumizi yake.
Orodha ya fasihi iliyotumika.
Alfutova N.B. Nadharia ya aljebra na nambari./N.B.Alfutova, A.V.Ustinov. M.:MCNMO, 2002, 466 p.
Bukhshtab A.A. Nadharia ya nambari. /A.A.Bukhshtab. M.: Elimu, 1960.
Vilenkin N. Ulinganisho na madarasa ya mabaki./N. Vilenkin.//Quantum. - 1978.- 10.
Fedorova N.E. Utafiti wa algebra na uchambuzi wa hisabati. Daraja la 10.http:// www. prosv. ru/ vitabu vya kielektroniki/ Fedorova_ Aljebra_10 kl/1/ xht
ru. wikipedia. org/ wiki/Comparison_modulo.
Ufafanuzi 1. Ikiwa nambari mbili ni 1) a Na b ikigawanywa na uk toa salio sawa r, basi nambari kama hizo huitwa equiremainder au kulinganishwa katika moduli uk.
Kauli 1. Hebu uk nambari fulani chanya. Kisha kila nambari a daima na, zaidi ya hayo, kwa njia pekee inaweza kuwakilishwa katika fomu
Lakini nambari hizi zinaweza kupatikana kwa kuweka r sawa na 0, 1, 2,..., uk−1. Kwa hivyo sp+r=a itapata nambari zote kamili zinazowezekana.
Wacha tuonyeshe kuwa uwakilishi huu ni wa kipekee. Hebu kujifanya hivyo uk inaweza kuwakilishwa kwa njia mbili a=sp+r Na a=s 1 uk+r 1 . Kisha
| (2) |
Kwa sababu r 1 inakubali moja ya nambari 0,1, ..., uk−1, kisha thamani kamili r 1 −r kidogo uk. Lakini kutoka (2) inafuata hiyo r 1 −r nyingi uk. Kwa hivyo r 1 =r Na s 1 =s.
Nambari r kuitwa kuondoa nambari a moduli uk(kwa maneno mengine, nambari r aliita nambari iliyobaki a juu uk).
Kauli 2. Ikiwa nambari mbili a Na b kulinganishwa katika moduli uk, Hiyo a-b kugawanywa na uk.
Kweli. Ikiwa nambari mbili a Na b kulinganishwa katika moduli uk, basi ikigawanywa na uk kuwa na salio sawa uk. Kisha
kugawanywa na uk, kwa sababu upande wa kulia wa equation (3) imegawanywa na uk.
Kauli 3. Ikiwa tofauti ya nambari mbili imegawanywa na uk, basi nambari hizi zinalinganishwa katika moduli uk.
Ushahidi. Wacha tuonyeshe kwa r Na r Sehemu 1 iliyobaki a Na b juu uk. Kisha
Mifano 25≡39 (mod 7), −18≡14 (mod 4).
Kutoka kwa mfano wa kwanza inafuata kwamba 25 wakati imegawanywa na 7 inatoa salio sawa na 39. Hakika, 25 = 3 · 7 + 4 (salio 4). 39=3 · 7+4 (salio 4). Wakati wa kuzingatia mfano wa pili, unahitaji kuzingatia kwamba salio lazima iwe nambari isiyo hasi chini ya moduli (yaani 4). Kisha tunaweza kuandika: -18=−5·4+2 (salio 2), 14=3·4+2 (salio 2). Kwa hivyo, -18 ikigawanywa na 4 huacha salio 2, na 14 ikigawanywa na 4 huacha salio la 2.
Sifa za ulinganisho wa modulo
Mali 1. Kwa mtu yeyote a Na uk Kila mara
hakuna kulinganisha kila wakati
Wapi λ ndiye mgawanyiko mkubwa zaidi wa nambari m Na uk.
Ushahidi. Hebu λ mgawanyiko mkubwa zaidi wa nambari m Na uk. Kisha
Kwa sababu m(a-b) kugawanywa na k, Hiyo
Kwa hivyo
Na m ni moja ya vigawanyiko vya nambari uk, Hiyo
Wapi h=pqs.
Kumbuka kwamba tunaweza kuruhusu kulinganisha kulingana na moduli hasi, i.e. kulinganisha a≡b mod( uk) inamaanisha katika kesi hii kwamba tofauti a-b kugawanywa na uk. Sifa zote za kulinganisha zinabaki kutumika kwa moduli hasi.
Ulinganisho wa shahada ya kwanza na usiyojulikana una fomu:
f(x) 0 ( mod m); f(X) = Oh + na n. (1)
Tatua ulinganisho- inamaanisha kupata maadili yote ya x ambayo yanakidhi. Ulinganisho mbili ambazo zinakidhi maadili sawa ya x huitwa sawa.
Ikiwa ulinganisho (1) umeridhika na yoyote x = x 1, kisha (kulingana na 49) nambari zote kulinganishwa na x 1, moduli m: x x 1 ( mod m) Darasa hili lote la nambari linachukuliwa kuwa suluhisho moja. Kwa makubaliano kama haya, hitimisho lifuatalo linaweza kutolewa.
66.C alignment (1) itakuwa na suluhisho nyingi kama idadi ya mabaki ya mfumo kamili unaokidhi.
Mfano. Kulinganisha
6x- 4 0 (mod 8)
Kati ya nambari 0, 1, 2, 3, 4, 5, 6, 7, nambari mbili zinakidhi mfumo kamili wa mabaki modulo 8: X= 2 na X= 6. Kwa hivyo, ulinganisho huu una masuluhisho mawili:
x 2 (moduli 8), X 6 (moduli 8).
Ulinganisho wa shahada ya kwanza kwa kusonga neno la bure (na ishara kinyume) kwa upande wa kulia inaweza kupunguzwa kwa fomu.
shoka b(moduli m). (2)
Fikiria ulinganisho unaokidhi hali ( A, m) = 1.
Kulingana na 66, ulinganisho wetu una masuluhisho mengi kama vile kuna mabaki ya mfumo kamili unaokidhi. Lakini lini x huendesha kupitia mfumo kamili wa mabaki ya modulo T, Hiyo Oh hupitia mfumo kamili wa makato (kati ya 60). Kwa hiyo, kwa thamani moja na moja tu X, kuchukuliwa kutoka kwa mfumo kamili, Oh italinganishwa na b. Kwa hiyo,
67. Wakati (a, m) = shoka 1 la kulinganisha b(moduli m)ina suluhisho moja.
Wacha sasa ( a, m) = d> 1. Kisha, ili kulinganisha (2) kuwa na suluhu, ni muhimu (kati ya 55) kwamba. b kugawanywa na d, vinginevyo kulinganisha (2) haiwezekani kwa nambari yoyote x . Kwa kudhani b nyingi d, tuweke a = a 1 d, b = b 1 d, m = m 1 d. Kisha kulinganisha (2) itakuwa sawa na hii (iliyofupishwa na d): a 1 x b 1 ( mod m), ambayo tayari ( A 1 , m 1) = 1, na kwa hivyo itakuwa na modulo moja ya suluhisho m 1 . Hebu X 1 – mabaki madogo yasiyo hasi ya modulo hii ya modulo m 1 , basi nambari zote ni x , kutengeneza suluhisho hili hupatikana katika fomu
x x 1 ( mod m 1). (3)
Modulo m, nambari (3) haziunda suluhisho moja, lakini zaidi, suluhisho nyingi kama vile kuna nambari (3) kwenye safu 0, 1, 2, ..., m - Masalio 1 angalau yasiyo hasi ya modulo m. Lakini nambari zifuatazo (3) zitaanguka hapa:
x 1 , x 1 + m 1 , x 1 + 2m 1 , ..., x 1 + (d – 1) m 1 ,
hizo. Jumla d nambari (3); kwa hivyo kulinganisha (2) ina d maamuzi.
Tunapata nadharia:
68. Acha (a, m) = d. Axe ya kulinganisha b ( mod m) haiwezekani ikiwa b haijagawanywa na d. Wakati b ni mgawo wa d, ulinganisho una masuluhisho d.
69. Njia ya kutatua ulinganisho wa shahada ya kwanza, kwa kuzingatia nadharia ya sehemu zinazoendelea:
Kupanua katika sehemu inayoendelea uhusiano m:a,

na ukiangalia sehemu mbili za mwisho zinazolingana:

kulingana na mali ya sehemu zinazoendelea (kulingana na 30 ) tuna

Kwa hivyo kulinganisha kuna suluhisho
kupata, ambayo inatosha kuhesabu P n- 1 kulingana na njia iliyoainishwa katika 30.
Mfano. Wacha tusuluhishe ulinganisho
111x= 75 (mod 321). (4)
Hapa (111, 321) = 3, na 75 ni nyingi ya 3. Kwa hiyo, kulinganisha kuna ufumbuzi tatu.
Kugawanya pande zote mbili za kulinganisha na moduli na 3, tunapata kulinganisha
37x= 25 (mod 107), (5)
ambayo tunapaswa kutatua kwanza. Tuna
| q | |||||
| P 3 |

Kwa hiyo, katika kesi hii n = 4, P n - 1 = 26, b= 25, na tuna suluhisho la kulinganisha (5) katika fomu
x–26 ∙ 25 99 (mod 107).
Kwa hivyo masuluhisho ya kulinganisha (4) yanawasilishwa kama ifuatavyo:
X 99; 99 + 107; 99 + 2 ∙ 107 (mod 321),
Xº99; 206; 313 (mod 321).
Uhesabuji wa kipengele kinyume na modulo fulani
70.Kama nambari ni nambari kamili a Na n ni coprime, basi kuna idadi a′, kuridhisha kulinganisha a ∙ a′ ≡ 1 (moduli n) Nambari a′ kuitwa kinyume cha kuzidisha cha modulo n na nukuu iliyotumika kwake ni a- 1 ( mod n).
Hesabu ya viwango vya kubadilishana modulo thamani fulani inaweza kufanywa kwa kutatua ulinganisho wa shahada ya kwanza na ile isiyojulikana, ambayo x nambari imekubaliwa a′.
Ili kupata suluhisho la kulinganisha
a∙x≡ 1 (moduli m),
Wapi ( a,m)= 1,
unaweza kutumia kanuni ya Euclid (69) au nadharia ya Fermat-Euler, ambayo inasema kwamba ikiwa ( a,m) = 1, basi
a φ( m) ≡ 1(moduli m).
x ≡ a φ( m)-1 (Mod m).
Vikundi na mali zao
Vikundi ni mojawapo ya madarasa ya taxonomic yanayotumiwa katika uainishaji wa miundo ya hisabati yenye sifa za kawaida. Vikundi vina vipengele viwili: kundi la (G) Na shughuli() imefafanuliwa kwenye seti hii.
Dhana za kuweka, kipengele na uanachama ni dhana za msingi zisizofafanuliwa za hisabati ya kisasa. Seti yoyote inaelezwa na vipengele vilivyojumuishwa ndani yake (ambayo, kwa upande wake, inaweza pia kuweka). Kwa hivyo, tunasema kwamba seti imefafanuliwa au inatolewa ikiwa kwa kipengele chochote tunaweza kujua ikiwa ni ya seti hii au la.
Kwa seti mbili A, B kumbukumbu B A, B A, B∩ A, B A, B \ A, A × B kwa mtiririko huo maana yake B ni sehemu ndogo ya seti A(yaani kipengele chochote kutoka B pia yamo ndani A, kwa mfano, seti ya nambari za asili zinazomo katika seti ya nambari halisi; zaidi ya hayo, daima A A), B ni sehemu ndogo inayofaa ya seti A(hizo. B A Na B ≠ A), makutano ya wengi B Na A(yaani vitu vyote kama hivyo ambavyo viko ndani kwa wakati mmoja A, na katika B, kwa mfano, makutano ya nambari na nambari chanya halisi ni seti ya nambari asilia), umoja wa seti. B Na A(yaani seti inayojumuisha vitu ambavyo viko ndani A, ama ndani B), weka tofauti B Na A(yaani seti ya vipengele vilivyomo B, lakini usilale ndani A), Bidhaa ya Cartesian ya seti A Na B(yaani seti ya jozi za fomu ( a, b), Wapi a A, b B) Kupitia | A| nguvu ya kuweka daima inaashiria A, i.e. idadi ya vipengele katika seti A.
Operesheni ni sheria kulingana na ambayo vipengele viwili vya seti G(a Na b) inalinganishwa na kipengele cha tatu kutoka kwa G: a b.
Vipengele vingi G na operesheni inaitwa kikundi, ikiwa masharti yafuatayo yatatimizwa.
Saa n wanatoa mabaki sawa.
Miundo sawa: a na b kulinganishwa katika moduli n ikiwa tofauti zao a - b inagawanywa na n, au ikiwa a inaweza kuwakilishwa kama a = b + kn , Wapi k- idadi kamili. Kwa mfano: 32 na −10 zinalinganishwa modulo 7, tangu
Taarifa "a na b zinalinganishwa modulo n" imeandikwa kama:
Tabia za usawa za Modulo
Uhusiano wa kulinganisha wa modulo una sifa
Nambari kamili mbili a Na b kulinganishwa modulo 1.
Ili kwa nambari a Na b zililinganishwa katika moduli n, ni muhimu na ya kutosha kwamba tofauti yao inaweza kugawanywa na n.
Ikiwa nambari na zinalinganishwa kwa jozi katika moduli n, basi hesabu zao na , pamoja na bidhaa na pia zinalinganishwa katika moduli n.
Ikiwa nambari a Na b kulinganishwa katika moduli n, kisha digrii zao a k Na b k pia zinalinganishwa katika moduli n chini ya asili yoyote k.
Ikiwa nambari a Na b kulinganishwa katika moduli n, Na n kugawanywa na m, Hiyo a Na b kulinganishwa katika moduli m.
Ili kwa nambari a Na b zililinganishwa katika moduli n, iliyotolewa kwa namna ya mtengano wake wa kisheria katika mambo rahisi uk i
muhimu na ya kutosha
Uhusiano wa kulinganisha ni uhusiano wa usawa na una sifa nyingi za usawa wa kawaida. Kwa mfano, zinaweza kuongezwa na kuzidishwa: ikiwa
Ulinganisho, hata hivyo, hauwezi, kwa ujumla, kugawanywa kwa kila mmoja au kwa nambari nyingine. Mfano: , hata hivyo, kupunguza kwa 2, tunapata kulinganisha kwa makosa:. Sheria za ufupisho za kulinganisha ni kama ifuatavyo.
Pia huwezi kufanya shughuli kwenye ulinganisho ikiwa moduli zao hazilingani.
Tabia zingine:
Ufafanuzi unaohusiana
Madarasa ya kupunguzwa
Seti ya nambari zote zinazolinganishwa na a moduli n kuitwa darasa la kupunguzwa a moduli n , na kwa kawaida huashiria [ a] n au . Kwa hivyo, kulinganisha ni sawa na usawa wa madarasa ya mabaki [a] n = [b] n .
Tangu kulinganisha modulo n ni uhusiano wa usawa kwenye seti ya nambari kamili, kisha madarasa ya mabaki modulo n kuwakilisha madarasa ya usawa; idadi yao ni sawa n. Seti ya modulo za madarasa yote ya mabaki n iliyoashiriwa na au.
Shughuli za kuongeza na kuzidisha kwa kushawishi shughuli zinazolingana kwenye seti:
[a] n + [b] n = [a + b] nKuhusiana na shughuli hizi seti ni pete ya mwisho, na ikiwa n rahisi - shamba finite.
Mifumo ya kupunguzwa
Mfumo wa mabaki unakuwezesha kufanya shughuli za hesabu kwenye seti ya mwisho ya nambari bila kwenda zaidi ya mipaka yake. Mfumo kamili wa makato modulo n ni seti yoyote ya n nambari kamili ambazo hazilinganishwi modulo n. Kwa kawaida, mabaki madogo zaidi yasiyo hasi huchukuliwa kama mfumo kamili wa mabaki modulo n.
0,1,...,n − 1au makato madogo kabisa yanayojumuisha nambari
,katika kesi isiyo ya kawaida n na nambari
katika kesi ya hata n .
Kutatua ulinganisho
Ulinganisho wa shahada ya kwanza
Katika nadharia ya nambari, maandishi ya maandishi na nyanja zingine za sayansi, shida ya kupata suluhisho la kulinganisha kwa kiwango cha kwanza cha fomu mara nyingi hutokea:
Kutatua ulinganisho kama huo huanza na kuhesabu gcd (a, m)=d. Katika kesi hii, kesi 2 zinawezekana:
- Kama b sio nyingi d, basi kulinganisha hakuna suluhisho.
- Kama b nyingi d, basi kulinganisha kuna modulo ya kipekee ya suluhisho m / d au, ni nini sawa, d suluhisho za modulo m. Katika kesi hii, kama matokeo ya kupunguza ulinganisho wa asili na d kulinganisha ni:
Wapi a 1 = a / d , b 1 = b / d Na m 1 = m / d ni nambari kamili, na a 1 na m 1 ni ya juu kiasi. Kwa hivyo nambari a 1 inaweza kugeuzwa modulo m 1, yaani, pata nambari kama hiyo c, hiyo (kwa maneno mengine,). Sasa suluhisho linapatikana kwa kuzidisha kulinganisha kwa matokeo c:
Uhesabuji wa thamani wa vitendo c inaweza kutekelezwa kwa njia tofauti: kwa kutumia nadharia ya Euler, algorithm ya Euclid, nadharia ya sehemu zinazoendelea (tazama algorithm), nk. Hasa, nadharia ya Euler inakuwezesha kuandika thamani. c kama:
Mfano
Kwa kulinganisha tunayo d= 2, kwa hivyo modulo 22 ulinganisho una masuluhisho mawili. Wacha tubadilishe 26 kwa 4, kulinganishwa nayo modulo 22, kisha tupunguze nambari zote 3 kwa 2:
Kwa kuwa 2 ni coprime kwa modulo 11, tunaweza kupunguza pande za kushoto na kulia kwa 2. Matokeo yake, tunapata suluhisho moja modulo 11: , sawa na ufumbuzi mbili modulo 22: .
Ulinganisho wa shahada ya pili
Kusuluhisha ulinganisho wa shahada ya pili kunakuja ili kubaini kama nambari fulani ni masalio ya quadratic (kwa kutumia sheria ya usawa wa quadratic) na kisha kukokotoa modulo ya mzizi wa mraba.
Hadithi
Nadharia iliyobaki ya Kichina, iliyojulikana kwa karne nyingi, inasema (katika lugha ya kisasa ya hisabati) kwamba modulo ya pete iliyobaki ni bidhaa ya nambari kadhaa za coprime.
 Baadhi ya derivatives ya kazi ya vigeu vitatu
Baadhi ya derivatives ya kazi ya vigeu vitatu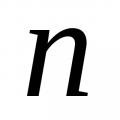 Chaguo za kukokotoa za usambazaji kwa kutumia sampuli hii, tengeneza kitendakazi cha usambaaji wa kimajaribio
Chaguo za kukokotoa za usambazaji kwa kutumia sampuli hii, tengeneza kitendakazi cha usambaaji wa kimajaribio Hakuna pesa, lakini unashikilia
Hakuna pesa, lakini unashikilia