Mfano

Kugawanya sehemu kwa nusu

Tatizo la sehemu mbili. Tumia dira na rula kugawanya sehemu hii AB katika sehemu mbili sawa. Moja ya suluhisho linaonyeshwa kwenye takwimu:

• Kwa kutumia dira tunachora miduara na vituo kwenye pointi A Na B eneo AB.
• Kutafuta pointi za makutano P Na Q miduara miwili iliyojengwa (arcs).
• Kwa kutumia rula, chora sehemu au mstari unaopitia pointi P Na Q.
• Kutafuta katikati inayotakiwa ya sehemu AB- hatua ya makutano AB Na PQ.

Ufafanuzi rasmi

Katika shida za ujenzi, seti ya vidokezo vyote vya ndege, seti ya mistari yote ya moja kwa moja ya ndege na seti ya duru zote za ndege huzingatiwa, ambayo shughuli zifuatazo zinaruhusiwa:

1. Chagua pointi kutoka kwa seti ya pointi zote:
   1. hatua ya kiholela
   2. hatua ya kiholela kwenye mstari fulani
   3. hatua ya kiholela kwenye duara fulani
   4. hatua ya makutano ya mistari miwili iliyotolewa
   5. hatua ya makutano/tangency ya mstari fulani na duara fulani
   6. pointi za makutano/tanjiti ya miduara miwili iliyotolewa
2. "Kwa kutumia watawala»chagua mstari kutoka kwa seti ya mistari yote:
   1. mstari wa moja kwa moja wa kiholela
   2. mstari wa moja kwa moja wa kiholela unaopita kwenye sehemu fulani
   3. mstari wa moja kwa moja unaopitia pointi mbili ulizopewa
3. "Kwa kutumia dira»chagua mduara kutoka kwa seti ya miduara yote:
   1. mduara wa kiholela
   2. mduara wa kiholela na kituo katika hatua fulani
   3. mduara wa kiholela na radius sawa na umbali kati ya pointi mbili zilizotolewa
   4. mduara ulio na kitovu katika sehemu fulani na yenye kipenyo sawa na umbali kati ya pointi mbili ulizopewa

Katika hali ya tatizo, seti fulani ya pointi imeelezwa. Inahitajika, kwa kutumia idadi maalum ya shughuli kutoka kati ya shughuli zinazokubalika zilizoorodheshwa hapo juu, kuunda seti nyingine ya pointi ambazo ziko katika uhusiano fulani na seti ya awali.

Suluhisho la shida ya ujenzi lina sehemu tatu muhimu:

1. Maelezo ya njia ya kuunda seti fulani.
2. Uthibitisho kwamba seti iliyojengwa kwa njia iliyoelezewa ni kweli iko katika uhusiano fulani na seti ya asili. Kawaida uthibitisho wa ujenzi unafanywa kama uthibitisho wa kawaida wa nadharia, kwa kuzingatia axioms na nadharia zingine zilizothibitishwa.
3. Uchambuzi wa njia iliyoelezwa ya ujenzi kwa matumizi yake kwa matoleo tofauti ya hali ya awali, na pia kwa pekee au isiyo ya pekee ya ufumbuzi uliopatikana kwa njia iliyoelezwa.

Masuala Yanayojulikana

• Tatizo la Apollonius la kuunda tanjenti ya duara hadi miduara mitatu iliyotolewa. Ikiwa hakuna duru zilizopewa ziko ndani ya nyingine, basi shida hii ina suluhisho 8 tofauti sana.
• Tatizo la Brahmagupta la kujenga sehemu ya pembe nne iliyoandikwa kwa kutumia pande zake nne.

Ujenzi wa poligoni za kawaida

Jiomita za kale zilijua jinsi ya kuunda kwa usahihi n-goni kwa , , na .

Miundo inayowezekana na isiyowezekana

Miundo yote sio zaidi ya suluhisho kwa equation fulani, na mgawo wa mlinganyo huu unahusiana na urefu wa sehemu zilizopewa. Kwa hivyo, ni rahisi kuzungumza juu ya kuunda nambari - suluhisho la picha kwa equation ya aina fulani. Ndani ya mfumo wa mahitaji hapo juu, ujenzi ufuatao unawezekana:

• Ujenzi wa suluhisho kwa milinganyo ya mstari.
• Kuunda suluhisho kwa milinganyo ya quadratic.

Kwa maneno mengine, inawezekana tu kuunda nambari sawa na maneno ya hesabu kwa kutumia mzizi wa mraba wa nambari za asili (urefu wa sehemu). Kwa mfano,

Tofauti na generalizations

• Ujenzi kwa kutumia dira moja. Kwa mujibu wa nadharia ya Mohr-Mascheroni, kwa msaada wa dira moja unaweza kujenga takwimu yoyote ambayo inaweza kujengwa kwa dira na mtawala. Katika kesi hii, mstari wa moja kwa moja unachukuliwa kuwa umejengwa ikiwa pointi mbili zinaelezwa juu yake.
• Ujenzi kwa kutumia rula moja. Ni rahisi kuona kwamba kwa msaada wa mtawala mmoja tu ujenzi wa projective-invariant unaweza kufanywa. Hasa, haiwezekani hata kugawanya sehemu katika sehemu mbili sawa, au kupata katikati ya mduara inayotolewa. Lakini ikiwa kuna mduara uliochorwa hapo awali kwenye ndege iliyo na kituo kilichowekwa alama, kwa kutumia mtawala, unaweza kufanya ujenzi sawa na dira na mtawala (Poncelet-Steiner theorem ( Kiingereza)), 1833. Ikiwa kuna noti mbili kwenye mtawala, basi ujenzi unaotumia ni sawa na ujenzi kwa kutumia dira na mtawala (Napoleon alichukua hatua muhimu katika kuthibitisha hili).
• Ujenzi kwa kutumia zana zenye uwezo mdogo. Katika matatizo ya aina hii, zana (kinyume na uundaji wa classical wa tatizo) huchukuliwa kuwa sio bora, lakini ni mdogo: mstari wa moja kwa moja kupitia pointi mbili unaweza kuteka kwa kutumia mtawala tu ikiwa umbali kati ya pointi hizi hauzidi kiwango fulani. thamani; eneo la miduara inayochorwa kwa kutumia dira inaweza kupunguzwa kutoka juu, chini, au zote mbili juu na chini.
• Ujenzi kwa kutumia origami ya gorofa. tazama sheria za Hujit

Angalia pia

• Mipango ya jiometri yenye nguvu inakuwezesha kufanya ujenzi kwa kutumia dira na mtawala kwenye kompyuta.

Vidokezo

Fasihi

• A. Adler Nadharia ya ujenzi wa kijiometri / Tafsiri kutoka kwa Kijerumani na G. M. Fikhtengolts. - Toleo la tatu. - L.: Uchpedgiz, 1940. - 232 p.
• I. I. Alexandrov Mkusanyiko wa matatizo ya ujenzi wa kijiometri. - Toleo la kumi na nane. - M.: Uchpedgiz, 1950. - 176 p.
• B. I. Argunov, M. B. Balk. - Toleo la pili. - M.: Uchpedgiz, 1957. - 268 p.
• A. M. Voronets Jiometri ya dira. - M.-L.: ONTI, 1934. - 40 p. - (Maktaba maarufu ya hisabati chini ya uhariri wa jumla wa L. A. Lyusternik).
• V. A. Geiler Shida za ujenzi zisizoweza kutatuliwa // baridi. - 1999. - Nambari 12. - P. 115-118.
• V. A. Kirichenko Ujenzi na dira na mtawala na nadharia ya Galois // Shule ya Majira ya joto "Hisabati ya Kisasa". -Dubna, 2005.
• Yu. I. Manin Kitabu IV. Jiometri // Encyclopedia ya hisabati ya msingi. - M.: Fizmatgiz, 1963. - 568 p.
• Y. Petersen Mbinu na nadharia za kutatua matatizo ya ujenzi wa kijiometri. - M.: Nyumba ya uchapishaji ya E. Lissner na Y. Roman, 1892. - 114 p.
• V. V. Prasolov Matatizo matatu ya ujenzi wa classic. Kuongeza mchemraba mara mbili, punguza pembe, piga mduara. - M.: Nauka, 1992. - 80 p. - (Mihadhara maarufu juu ya hisabati).
• J. Steiner Ujenzi wa kijiometri unaofanywa kwa kutumia mstari wa moja kwa moja na mduara uliowekwa. - M.: Uchpedgiz, 1939. - 80 p.
• Kozi ya hiari katika hisabati. 7-9 / Comp. I. L. Nikolskaya. - M.: Elimu, 1991. - P. 80. - 383 p. - ISBN 5-09-001287-3

Wikimedia Foundation. 2010.

Tazama "Ujenzi kwa kutumia dira na mtawala" ni nini katika kamusi zingine:

Watawala - pata kuponi ya kufanya kazi kwa punguzo la AllInstruments katika Akademika au ununue rula kwa faida na uwasilishaji bila malipo kwa mauzo katika AllInstruments

Tawi la jiometri ya Euclidean, inayojulikana tangu nyakati za zamani. Katika kazi za ujenzi, shughuli zifuatazo zinawezekana: Weka alama ya kiholela kwenye ndege, hatua kwenye moja ya mistari iliyojengwa, au sehemu ya makutano ya mistari miwili iliyojengwa. Kwa msaada wa ... ... Wikipedia

Ujenzi kwa kutumia dira na watawala ni tawi la jiometri ya Euclidean inayojulikana tangu nyakati za kale. Katika kazi za ujenzi, shughuli zifuatazo zinawezekana: Weka alama kwenye sehemu ya kiholela kwenye ndege, nukta kwenye moja ya mistari iliyojengwa, au nukta... ... Wikipedia.

Nomino, s., imetumika. kulinganisha mara nyingi Morphology: (hapana) nini? ujenzi, nini? ujenzi, (naona) nini? ujenzi, nini? ujenzi, kuhusu nini? kuhusu ujenzi; PL. Nini? ujenzi, (hapana) nini? ujenzi, nini? ujenzi, (naona) nini? ujenzi, na nini? ... Kamusi ya ufafanuzi ya Dmitriev

SHULE NDOGO YA SAYANSI YA WATOTO WA SHULE ZA UHALIFU

"MTAFUTA"

Sehemu "Hisabati"

UJENZI WA GEOMETRICAL KWA KUTUMIA KITAWALA CHENYE UPANDE MBILI

Nimefanya kazi A

_____________

Mwanafunzi wa darasa

Mkurugenzi wa kisayansi

UTANGULIZI…………………………………………………………………………………………..3.

I. UJENZI WA KIJIometri KWENYE NDEGE………………….4

I.1. Axioms ya jumla ya jiometri ya kujenga. Axioms ya zana za hisabati ………………………………………………………………………………..4

I.2. ……………………….....5

I.3. Miundo ya kijiometri yenye rula moja ……………………………..7

I.4. Kazi za msingi za kujenga kwa rula iliyo na pande mbili………………..8

I.5. Kutatua matatizo mbalimbali ya ujenzi ……………………………………12

I.6. Miundo yenye rula ya upande mmoja ………………………………………………………

I.7. Kubadilishana kwa rula yenye pande mbili yenye dira na rula....21

HITIMISHO…………………………………………………………….24

Orodha ya marejeleo………………………………………………….25

Utangulizi

Matatizo yanayohusu ujenzi usio na uwezo mdogo ni pamoja na matatizo yanayohusu ujenzi kwa kutumia dira na rula pekee, ambayo yanazingatiwa katika mtaala wa shule. Je, inawezekana kutatua matatizo ya ujenzi na mtawala mmoja tu? Mara nyingi huna dira karibu, lakini unaweza kupata mtawala kila wakati.

Matatizo juu ya ujenzi katika jiometri ni sehemu ya kuvutia. Kuvutiwa nayo ni kutokana na uzuri na unyenyekevu wa maudhui yake ya kijiometri. Umuhimu wa kuzingatia matatizo haya huongezeka kutokana na ukweli kwamba hutumiwa katika mazoezi. Uwezo wa kutumia mtawala mmoja kutatua matatizo yaliyozingatiwa katika kazi hii ni ya umuhimu mkubwa katika shughuli za vitendo, kwa sababu Mara kwa mara tunakabiliwa na matatizo ya kugawanya sehemu kwa nusu, mara mbili ya sehemu fulani, nk.

Karatasi hii inachunguza shida kuu za ujenzi ambazo hutumika kama msingi wa kutatua shida ngumu zaidi.

Kama uzoefu unavyoonyesha, kazi za ujenzi huamsha shauku na kuchangia uanzishaji wa shughuli za kiakili. Wakati wa kuzitatua, ujuzi juu ya mali ya takwimu hutumiwa kikamilifu, uwezo wa kufikiri hutengenezwa, na ujuzi wa ujenzi wa kijiometri unaboreshwa. Kama matokeo, uwezo wa kujenga hukua, ambayo ni moja ya malengo ya kusoma jiometri.

Hypothesis: matatizo yote ya ujenzi ambayo yanaweza kutatuliwa kwa kutumia dira na mtawala yanaweza kutatuliwa tu kwa kutumia mtawala wa pande mbili.

Kitu cha utafiti: kazi za ujenzi na mtawala wa pande mbili.

Malengo ya utafiti: kuthibitisha kwamba matatizo yote ya ujenzi yanaweza kutatuliwa tu kwa msaada wa mtawala wa pande mbili.

Malengo ya utafiti: kujifunza misingi ya kinadharia ya kutatua matatizo ya ujenzi; kutatua matatizo ya msingi ya ujenzi kwa kutumia mtawala wa pande mbili; toa mifano ya matatizo magumu zaidi ya ujenzi; panga nyenzo za kinadharia na vitendo.

I. UJENZI WA KIJIometri KWENYE NDEGE

I.1. Axioms ya jumla ya jiometri ya kujenga. Axioms ya zana za hisabati

Kwa jiometri ya kujenga ni muhimu kuwa na sahihi na, kwa madhumuni ya hisabati, maelezo kamili ya chombo fulani. Maelezo haya yametolewa kwa namna ya axioms. Axioms hizi katika fomu ya hisabati ya kufikirika huelezea sifa hizo za vyombo vya kuchora halisi ambavyo hutumiwa kwa ujenzi wa kijiometri.

Zana zinazotumika sana za ujenzi wa kijiometri ni:mtawala (upande mmoja) , dira, pande mbili mtawala (na kingo sambamba) na wengine wengine.

A. Axiom ya mtawala.

Mtawala hukuruhusu kufanya miundo ifuatayo ya kijiometri:
a) jenga sehemu inayounganisha pointi mbili zilizojengwa;

b) jenga mstari wa moja kwa moja unaopitia pointi mbili zilizojengwa;

c) tengeneza miale inayotoka kwenye sehemu iliyojengwa na kupitia sehemu nyingine iliyojengwa.

B. Axiom ya dira.

Dira hukuruhusu kufanya miundo ifuatayo ya kijiometri:
a) jenga mduara ikiwa katikati ya mduara na sehemu sawa na radius ya mduara (au mwisho wake) imejengwa;

B. Axiom ya mtawala wa pande mbili.

Mtawala wa pande mbili hukuruhusu:

a) kutekeleza ujenzi wowote ulioorodheshwa katika axiom A;

b) katika kila nusu ya ndege iliyofafanuliwa na mstari uliojengwa, tengeneza mstari sambamba na mstari huu na kupita kutoka kwa mbali.A, wapi A - sehemu iliyowekwa kwa mtawala aliyepewa (upana wa mtawala);

c) ikiwa alama mbili A na B zimeundwa, basi amua ikiwa AB itakuwa kubwa kuliko sehemu fulani iliyowekwa.A (upana wa mtawala), na ikiwa AB >A , kisha utengeneze jozi mbili za mistari sambamba inayopitia pointi A na B mtawalia na zitenganishwe kutoka kwa nyingine kwa umbali.A .

Mbali na zana zilizoorodheshwa, unaweza kutumia zana zingine za ujenzi wa kijiometri: pembe ya kiholela, mraba, mtawala na alama, jozi ya pembe za kulia, vifaa anuwai vya kuchora curves maalum, nk.

I.2. Kanuni za jumla za kutatua matatizo ya ujenzi

Kazi ya ujenzi inajumuisha ukweli kwamba inahitajika kujenga takwimu fulani na zana maalum ikiwa takwimu nyingine hutolewa na uhusiano fulani kati ya vipengele vya takwimu inayotaka na vipengele vya takwimu hii vinaonyeshwa.

Kila takwimu ambayo inakidhi masharti ya tatizo inaitwauamuzi kazi hii.

Tafuta suluhu kazi ya ujenzi ina maana ya kupunguza kwa idadi ya mwisho ya ujenzi wa msingi, yaani, kuonyesha mlolongo wa mwisho wa ujenzi wa msingi, baada ya hapo takwimu inayotaka itazingatiwa tayari kujengwa kwa mujibu wa axioms iliyokubalika ya jiometri ya kujenga. Orodha ya ujenzi wa msingi unaokubalika, na, kwa hiyo, maendeleo ya kutatua tatizo, kwa kiasi kikubwa inategemea zana gani maalum zinazotumiwa kwa ajili ya ujenzi.

Tatua tatizo la ujenzi - Maana, kupata ufumbuzi wake wote .

Ufafanuzi wa mwisho unahitaji ufafanuzi fulani. Takwimu zinazokidhi hali ya tatizo zinaweza kutofautiana katika sura au ukubwa, na nafasi kwenye ndege. Tofauti katika nafasi kwenye ndege huzingatiwa au hazizingatiwi kulingana na uundaji wa shida ya ujenzi yenyewe, ikiwa hali ya shida hutoa au haitoi eneo fulani la takwimu inayotaka kulingana na takwimu yoyote. .

Ikiwa suluhisho la tatizo linapatikana, basi katika siku zijazo inaruhusiwa kutumia suluhisho hili "kwa ujumla," yaani, bila kugawanya katika ujenzi kuu.

Kuna idadi ya shida rahisi za ujenzi wa kijiometri, ambazo mara nyingi hujumuishwa kama sehemu katika kutatua shida ngumu zaidi. Tutawaita matatizo ya msingi ya ujenzi wa kijiometri. Orodha ya kazi za kimsingi ni, bila shaka, masharti. Kazi za kimsingi kawaida ni pamoja na zifuatazo:

Gawanya sehemu hii kwa nusu.

Kugawanya pembe iliyopewa kwa nusu.

Kuunda kwenye mstari uliopewa sehemu sawa na ile iliyotolewa.

Kuunda pembe sawa na ile iliyotolewa.

Kuunda mstari unaopita kwenye sehemu fulani sambamba na mstari fulani.

Kuunda mstari unaopita kwenye ncha fulani na perpendicular kwa mstari fulani.

Mgawanyiko wa sehemu katika suala hili.

Kuunda pembetatu kwa kutumia pande tatu zilizopewa.

Kuunda pembetatu kwa kutumia upande na pembe mbili za karibu.

Kuunda pembetatu kwa kutumia pande mbili na pembe kati yao.

Wakati wa kutatua shida yoyote ngumu ya ujenzi, swali linatokea juu ya jinsi ya kufikiria ili kutafuta njia ya kutatua shida, kupata suluhisho zote za shida, kujua hali ya uwezekano wa kutatua shida, nk. , wakati wa kutatua shida za kujenga, hutumia mpango wa suluhisho, unaojumuisha hatua nne zifuatazo:

1) uchambuzi;
2) ujenzi;
3) ushahidi;
4) utafiti.

I.3. Ujenzi wa kijiometri na mtawala mmoja

Tutazingatia mtawala kutoka kwa maoni mawili: kama mtawala na mtawala wa pande mbili.

1. Mtawala wa pande mbili upana A tutaita mtawala na kingo zinazofanana ziko kwa mbali A kutoka kwa kila mmoja, na kuifanya iwezekane kujenga moja kwa moja:

a) mstari wa moja kwa moja wa kiholela;

b) mstari wa moja kwa moja unaopitia pointi mbili zilizotolewa au zilizopatikana katika mchakato wa kutatua tatizo;

c) mistari sambamba, ambayo kila mmoja hupitia moja ya pointi, umbali kati ya ambayo ni kubwa zaidiA (katika ujenzi huu, mtawala yuko katika nafasi ambayo kwa kila moja ya kando zake mbili za sambamba kuna moja ya pointi mbili zilizopewa; katika kesi hii, tutazungumzia kuhusu ujenzi wa moja kwa moja).

Upana wa mtawala katika ujenzi huu unazingatiwa mara kwa mara, na kwa hiyo, ikiwa katika mchakato wa kutatua tatizo fulani inakuwa muhimu kufanya ujenzi wa moja kwa moja kwa baadhi ya pointi zilizopatikana.A Na KATIKA , basi ni lazima kuthibitisha kwamba urefuAB tena A .

Tutazingatia hatua ya kujengwa ikiwa ni moja ya data au ni makutano ya mistari miwili iliyojengwa; kwa upande wake, tutazingatia mstari wa moja kwa moja wa kujengwa ikiwa unapita kupitia pointi zilizojengwa au zilizopewa.

Kwa kutumia mtawala wa pande mbili unaweza kuunda zifuatazo.

a) Kupitia pointi yoyote mbili unaweza kuchora mstari wa moja kwa moja, na moja tu.

b) Vyovyote vile mstari ulionyooka, kuna mistari miwili iliyonyooka kabisa kwenye ndege, sambamba nayo na kutengwa nayo kwa umbali.a .

c) Kupitia pointi mbili A na B katika AB A inawezekana kuteka jozi mbili za sambamba moja kwa moja; na AB = A unaweza kuchora jozi ya mistari sambamba, umbali kati ya ambayo ni sawaA .

Ikiwa pointi moja, mbili, tatu zimetolewa, basi hakuna pointi mpya zinazoweza kujengwa

(Kielelezo 1);

ikiwa pointi nne zinatolewa, baadhi ya tatu (au zote nne) ziko kwenye mstari huo huo, basi hakuna pointi nyingine zinaweza kujengwa (Mchoro 2);

Ikiwa umepewa pointi nne zilizo kwenye wima ya parallelogram, unaweza kujenga hatua moja tu - katikati yake. (Mchoro 3).

Baada ya kukubali yaliyo hapo juu, wacha tuzingatie kando shida zinazotatuliwa na mtawala wa pande mbili.

I.4. Kazi za msingi za kujenga na mtawala wa pande mbili

1
. Tengeneza kipenyo cha pili cha pembe ABC.

Suluhisho: (Kielelezo 4)

A  (IN C) Na b  (Bendi  b = D .

Tunapata B D- sehemu mbili  ABC.

Kwa kweli, iliyopatikana na

kujenga parallelogram ni

rhombus, kwani urefu wake ni sawa. KATIKAD –

diagonal ya rhombus ni bisector ABC. Mtini.4

2
. Mara mbili ya pembe iliyotolewa ABC

Suluhisho : (Mchoro 5) a) A  (AB),

A  (IN C)= D , kupitia pointi B na D

b moja kwa moja;

b) kupitia pointi B naD m  b

moja kwa moja,b Ç a = F .

Tunapata Ð AB F = 2 Ð ABC .

Mtini.5

3 . Kwa mstari uliopewa M N katika hili

chora kielelezo kwa uhakika A

Suluhisho : (Mtini.6)

1) (AA 1) || (BB 1) || (SS 1) -

moja kwa moja (B (M N),

NA Î (M N)); 2) kupitia A na B

m || n - moja kwa moja,

m Ç (SS 1) = D .

Tunapata (A D )  (M N ).

Mtini.6.

4
. Kupitia hatua fulani sio kulala

mstari uliopewa, kuchora perpendicular

Kwa mstari huu.

Suluhisho: Kupitia hatua hii O tunachora

mistari miwili inayokatiza iliyotolewa

mstari wa moja kwa moja AB, na mara mbili pembe za kusababisha

pembetatu zilizo karibu na hii

moja kwa moja.  OA N = 2  OAV na

OB N = 2  OVA (Mchoro 7).

Mtini.7

5. Tengeneza nukta linganifu kwa mstari uliopeanwa unaohusiana na mstari fulani.

Suluhisho: tazama tatizo la 4. (pointi O inalingana kwa kuashiriaN. Mtini.7)

6. Fanya mstari ulionyooka sambamba na hii

P
moja kwa moja M N , kupitia nukta A, sivyo

wa mstari wa M N .

Suluhisho la 1: (Kielelezo 8)

1) (AA 1) || (BB 1) || (SS 1) || (DD 1 ) || (KK 1) -

– moja kwa moja (SA)Ç (BB 1) = C 2;

2) (Na 2 K) Ç (DD 1 ) = F .

(A F ) ni mstari wa moja kwa moja unaotaka.

Kielelezo cha 8

Suluhisho la 2 . Katika Mchoro 8 1 imehesabiwa

mlolongo wa mistari iliyonyooka,

ambayo 1, 2 na 3 ni sambamba katika

ujenzi wa moja kwa moja;

(A F) || (M N).

Kielelezo 8 1

7
. Gawanya sehemu hii AB kwa nusu.

Suluhisho 1. (Mchoro 9) (tu kwa kesi wakati upana wa mtawala ni chini ya urefu wa sehemu hii). Chora moja kwa moja jozi mbili za mistari sambamba kupitia

mwisho wa sehemu hii, na kisha diagonal

rhombus inayosababisha. O - katikati AB.

Mchele. 9.

Suluhisho la 2. (Mchoro 9, a)

1) a || (Bendi b || (AB) - moja kwa moja;

2) (AR), (AR)Ç a = C, (AP) Ç b = D ;

3) (D NDANI) Ç a = M, (SV) Ç b = N ;

4) (M N ) Ç (AB) = K;

5) (D KWA) Ç (A N ) = F ;

6) (B F ) Ç b = D 1, (B F ) Ç a = C 1;

7) (D KATIKA ) Ç (A D 1) = X,

(AC 1) Ç (SV) = Z.

8) (X Z) Ç (AB) =O. Tunapata AO = OB.

Mtini.9, a

Suluhisho la 3 .( Mchele. 9, b)

Kama inavyojulikana , katikati ya trapezoid

besi, sehemu ya makutano

diagonals na hatua ya makutano

upanuzi wa pande

lala kwenye mstari ulionyooka.

1) m || (AB) - moja kwa moja;

2) C Î m , D Î m , (AS) Ç (IN D ) = KWA; Mtini.9,b

3) (NE) Ç (A D ) = F ; 4) (K F ) Ç (AB) =O. Tunapata AO = OB.

I.5. Kutatua matatizo mbalimbali ya ujenzi

Katika kutatua matatizo yafuatayo ya ujenzi kwa kutumia tu mtawala wa pande mbili, ujenzi wa moja kwa moja wa mistari ya sambamba na matatizo saba kuu yaliyotolewa hapo juu hutumiwa.

1. Chora mistari miwili ya pande zote kupitia hatua hii.

R suluhisho: tupitie hatua hii

mistari miwili ya kiholela,

na kisha - bisectors

pembe za karibu. (Mtini.10)

Mtini.10

2. Kwa kuzingatia sehemu A D urefu uliopewa a.

Unda sehemu ambayo urefu wake ni sawa na .

R
uamuzi : Hebu kutekeleza m  A Na h || m kupitia

uhakika A. f || (A D ) , k || (AD) moja kwa moja.

Hebu tuchore AB na AC, ambapo B =f  m ,

a C = m  k . Kwa njia inayojulikana

kugawanya AB na AC katika nusu na

wacha tuchore medians ya pembetatu

ABC. Kwa mali ya wapatanishi

pembetatu, O D = - inatafutwa

sehemu (Mchoro 11)

Mchele. kumi na moja

3. Tengeneza sehemu ambayo urefu wake ni

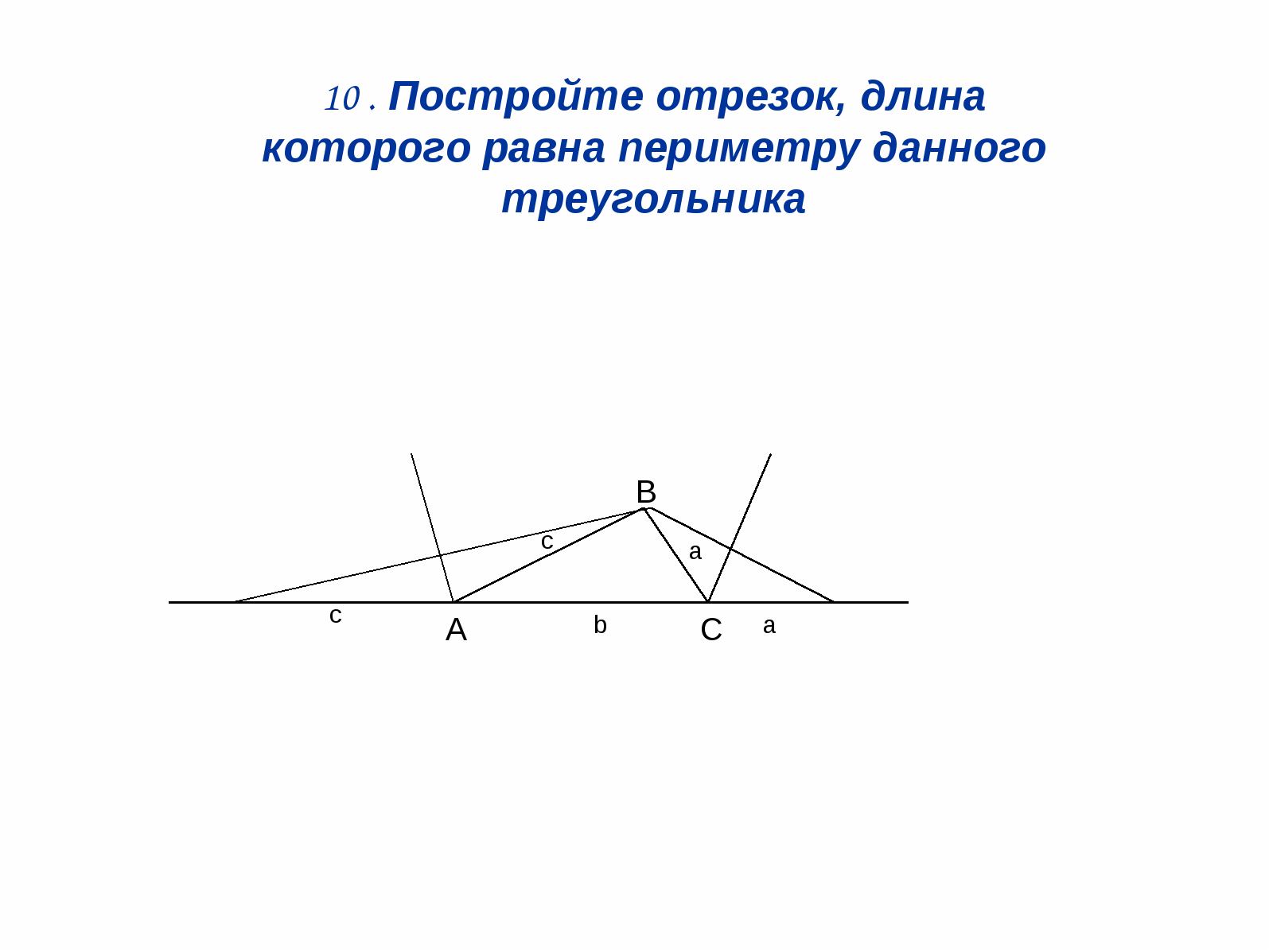sawa na mzunguko wa pembetatu iliyotolewa.

Suluhisho: (Mchoro 12). Wacha tutengeneze sehemu mbili

pembe mbili za nje za pembetatu, na kisha

3 vilele KATIKA hebu tuchore perpendiculars

kwa hawa wahusika wawili.

DE = a + b + s

Mtini.12

4. Kwa kuzingatia sehemu ya urefu a. Tengeneza sehemu za urefu 2a, 3a.

R suluhisho: (Kielelezo 13)

1M N) || (AB) na (M 1 N 1 ) || (M N) || (M 2 N 2 ) –

Moja kwa moja;

2) (CA) na (CB) kupitia A na B.

Sehemu A 1 B 1 na A 2 B 2 zinahitajika.

Suluhisho lingine la shida hii linaweza kuwa

kupatikana kutoka kwa suluhisho la shida 7.

Mchele. 13

5. Sehemu mbili hutolewa kwenye mstari wa moja kwa moja, urefu ambao ni na b . Tengeneza sehemu ambazo urefu wake ni sawa na + b , b - A, ( a + b )/2 na ( b - a )/2 .

Suluhisho: na kwa a + b(Mchoro 14, a)

Kielelezo 14, a

b) kwa ( a + b)/2 (Mchoro 14, b)

1) (A 1 B 1) || (A 2 B 2) || (AB) - moja kwa moja;

2) M Î (A 2 B 2), (MX) Ç (A 1 B 1 ) = N, (M H) Ç (A 1 B 1 ) = P;

3) (PY) Ç (A 2 B 2) = L, (LZ ) Ç (A 1 B 1 ) = O,

Tunapata: N O = NP + P.O. =
.

Mchele. 14, b

c) kwa b - A(Mchoro 14, c)

Mchele. 14, v

c) kwa ( b - a )/2 (Mchoro 14,d)

Mchele. 14, g

6
. Tengeneza katikati ya mduara huu.

Suluhisho : (Mchoro 15) Wacha tuchore mstari wa moja kwa moja AB,

kuingilia mduara kwa pointi A na B;

Jua  AB, ambapo C ni mahali pa makutano

na mduara.

Kupitia nukta C tunachora sambamba na AB

moja kwa moja C D; NADhukatiza mduara

kwa uhakikaD.

InaunganishaDna B ​​na A na C, tunapata

hatua inayotakiwa ni katikati ya duara. Mchele. 15

Suluhisho la 2: (Mchoro 16) Kwa kutumia mtawala wa pande mbili, jenga chords mbili zinazofananaAD NaB.C. . Tunapata trapezoid ya isoscelesABCD. HebuK NaP - pointi za makutano ya mistariA.C. NaBD , AB NaDC . Kisha moja kwa mojaP K hupitia katikati ya besi za trapezoid perpendicular kwao, ambayo ina maana inapita katikati ya mzunguko uliopewa. Kwa kuunda vile vile mstari mwingine sawa, tunapata katikati ya duara.

Mchele. 16

7. Arc ya mduara inatolewa. Tengeneza katikati ya duara

Suluhisho . (Kielelezo 17) Weka alama kwenye alama tatu A, B na C kwenye safu hii. Weka rula hadi mwisho wa sehemu ya AB na ufuatilie kingo zake. Tunapata mistari miwili inayofanana. Kubadilisha msimamo wa mtawala, tunachora mistari miwili zaidi inayofanana. Tunapata rhombus (parallelogram yenye urefu sawa). Moja ya diagonals ya rhombus ni bisector perpendicular kwa sehemuAB , kwa kuwa diagonal ya rhombus iko kwenye bisector perpendicular kwa diagonal nyingine. Vile vile, tunajenga bisector ya perpendicular kwa sehemuA.C. . Sehemu ya makutano ya bisectors iliyojengwa ni katikati ya mzunguko unaohitajika.

Mchele. 17

8. Kutokana na sehemu ya AB, mstari usio na sambamba l na uhakika M juu yake. Kwa kutumia rula moja ya pande mbili, jenga sehemu za makutano ya mstari wa moja kwa moja l na mduara wa radius AB na kituo cha M.

Suluhisho: (Mtini.18)

Hebu tumalize pembetatuA.B.M. kwa parallelogramABNM . Wacha tujenge sehemu mbili za MT naMSpembe katiMNna moja kwa mojal . Hebu kuchora kwa uhakikaN mistari sambamba na viambata viwili hivi:NQ || MS, NR || M.T.. MT│ MSkama sehemu mbili za pembe zilizo karibu. Ina maana,NQ │ MT, yaani, katika pembetatuNMQbisector ni urefu, kwa hivyo pembetatu ni isosceles:MQ = MN. Vile vile,BWANA. = MN. PointiQNaRinayotafutwa.

Mchele. 18

9. Imepewa mstari l na sehemu ya OA sambamba na l. Kwa kutumia rula moja ya pande mbili, jenga sehemu za makutano ya mstari wa moja kwa moja l na mduara wa radius OA na kituo O.

Suluhisho: (Mchoro 19, a)

Wacha tufanye moja kwa mojal 1 , sambamba na mstariO.A. na mbali nayo kwa mbalia . Wacha tuichukue kwenye mstari ulio sawal hatua ya kiholelaB . HebuB 1 - hatua ya makutano ya mistariO.B. Nal 1 . Hebu kuchora kwa uhakikaB 1 sawa, sambambaAB ; mstari huu unakatiza mstariO.A. kwa uhakikaA 1 . Wacha sasa tuchore kupitia pointiO NaA 1 jozi ya mistari sambamba, umbali kati yao nia (kunaweza kuwa na jozi mbili za mistari); basiX NaX 1 - pointi za makutano ya mstari unaopita kwenye hatuaO , yenye mistari iliyonyookal Nal 1 . Kwa sababuO.A. 1 = OX 1 na ∆O.A. 1 X 1 ∆ OAX , kisha OA = OX, uhakikaX inayotafutwa.

Vile vile, tunajenga hatua ya pili ya makutano ya mduara na mstari - uhakikaY(Mchoro 18, b).

Mchele. 18, a

Mchele. 18, b

I.6.Ujenzi na mtawala wa upande mmoja

Z
Hapa tunazingatia kesi maalum: wacha alama P zipewe,Q, R 1 NaQ 1 . nao hulala kwenye vipeo vya trapezoid.

1. Gawanya sehemu ya P Q katika nusu

Suluhisho inavyoonyeshwa katika Mchoro 19

Kwa kuzingatia pointi P,Q, R 1 NaQ 1 na mistari sambamba

RQ, R 1 Q 1 . Wacha tufanye RQ 1  QR 1 = B , RR 1  QQ 1 = A

Hebu tuunganishe pointi A na B. AB RQ = F- kati

sehemu ya PQ.

Mchele. 19

2. Sehemu mara mbili R 1 Q 1.

R
uamuzi inavyoonyeshwa kwenye Mchoro 20. Hebu tujenge

hatuaF- katikati ya sehemu ya PQna kuiunganisha

NaQ 1. R 1 Q FQ 1 = M. Wacha tufanye RM. RM R 1 Q 1 = R

usawaRQna P 1 Q 1 hufuata kutoka kwa kufanana

pembetatu RMFNa RMQ 1 ,

FMQNa R 1 MQ 1 , na usawa PFNaFQ.

Mchele. 20

3
. Tengeneza sehemu ya urefu n  R 1 Q 1 .

m – 1 sehemu sawa PQ 2 , Q 2 Q 3, … Q m -1 Q m

Kisha tunajenga (RR 1 ) NaQ m Q 1 na kuunganisha

sehemu yao ya makutano A yenye pointi

Q 2 , Q 3, … Q m Imepokelewam -1 moja kwa moja

kugawanyaR 1 Q 1 juum sawa sehemu.

Kwam = 4 suluhisho linaonyeshwa kwenye Mchoro 22

Mtini.22

I.7. Kubadilishana kwa mtawala wa pande mbili na dira na rula

Hebu tuthibitishe kwamba mtawala wa pande mbili anaweza kubadilishana na dira na mtawala. Ili kufanya hivyo, tunathibitisha kauli zifuatazo:

Taarifa ya 1: ujenzi wote unaoweza kufanywa na dira na mtawala unaweza kufanywa na mtawala wa pande mbili.

Kwa kuwa wakati wa kujenga na dira na mtawala, mtawala huchota mstari kupitia nukta mbili, na dira huunda mduara (hupata seti ya pointi sawa na ile iliyopewa), basi miundo yote iliyo na dira na mtawala hupunguzwa hadi. kujenga makutano ya mistari miwili ya moja kwa moja, miduara miwili na mduara na mstari wa moja kwa moja.

Makutano ya mistari miwili iliyonyooka inaweza kujengwa kwa kutumia mtawala.

Makutano ya duara na mstari wa moja kwa moja (Mchoro 23):

Ujenzi:Hebu sehemu ya AB itolewe - radius ya mduara, mstari wa moja kwa mojal , katikati ya duara O, kisha:

1) Tunafanya OS ||l , OS = AB.

2) Tunafanya OS ||kna kijijini kwa a.

3) TunatekelezaO.D., O.D. l = D; O.D. k) Kwa kufuatana na nadharia ya Thales

4) Kwa mujibu wa sheria ya transitivity ya usawa

5) FikiriaOMQE. OMQEni msambamba, tangu OM ||EQna OE ||M.C.(pande za mtawala ni sambamba). Hebu tuthibitishe kwamba hii ni rhombus.

5.1) MwenendoQZ O.C.NaQG WASHA, KishaQG = QZ = a.

5.2)  OMQ =  RQM(kulala kinyume);  OS =WASHA, ambayo ndiyo ilihitaji kuthibitishwa.

Makutano ya miduara miwili: sawa.

Taarifa ya 2: ujenzi wote unaoweza kufanywa na mtawala wa pande mbili unaweza kufanywa kwa dira na kunyoosha.

Ili kufanya hivyo, tutafanya kiwango cha ujenzi kwa mtawala wa pande mbili kwa kutumia dira na mtawala.

1) Mstari wa moja kwa moja kwa kutumia pointi mbili hujengwa kwa urahisi kwa kutumia mtawala.

2) Ujenzi wa mstari wa moja kwa moja unaofanana na uliopewa na kuondolewa kutoka kwake kwa umbali fulani:

2.1) Acha mstari ulionyooka upewekna sehemu ya urefua.

2.2) Tengeneza mstari wa moja kwa moja wa kiholelab k, basik b= B.

2.3) Imewashwabpande zote mbili za uhakikaBkwenye mstari wa moja kwa mojabweka kando kipande cha urefua, acha pointiCNaD.

2.4) Kupitia hatuaCjenga mstari ulionyookac k.

2.5) Kupitia hatuaDjenga mstari ulionyookad k.

2.6) Moja kwa mojacNad-inahitajika, kwa sababuB.C.NaBDsawaakwa ujenzi na ni sawa na umbali kati ya mstari wa moja kwa mojakna moja kwa moja

3) Ujenzi wa mistari ya moja kwa moja inayofanana kwa kila mmoja na kupitisha pointi mbili zilizopewa, na umbali kati yao ni sawa na sehemu iliyotolewa:

3.1) Wacha pointi zitoleweANaBna sehemu ya urefua.

3.2) Kuunda mduara na kituo kwa uhakikaAna radiusa.

3.3) Tengeneza tangent kwa duara fulani kupitia nuktaB; kuna tangents mbili kamaBiko nje ya duara (ikiwaAB> a), moja ikiwaBiko kwenye duara (ikiwaAB= a), hakuna kamaBiko ndani ya duara (AB< a) Tangent hii ni moja ya mistari tunayotafuta; inabaki kupitisha hatuaAmstari wa moja kwa moja sambamba nayo.

3.4) Kwa kuwa moja ya mistari ni ya kawaida kwa eneo la duara kama tangent, ya pili pia ni ya kawaida kwake (kwa kuwa ni sambamba), kwa hivyo, umbali kati yao ni sawa na radius, ambayo kwa ujenzi ni sawa na.a, ambayo ndiyo ilitakiwa kupatikana.

Kwa hivyo, tumethibitisha kubadilishana kwa mtawala wa pande mbili na dira na mtawala.

Hitimisho: Rula yenye pande mbili inaweza kubadilishana na dira na rula.

Hitimisho

Kwa hiyo, swali la uwezekano wa kutumia mtawala mmoja kutatua matatizo ya ujenzi wa classical kwa kutumia dira na mtawala imezingatiwa na kutatuliwa. Inatokea kwamba matatizo ya ujenzi yanaweza kutatuliwa kwa kutumia tu mtawala na edges sambamba. Wakati wa kutatua matatizo magumu zaidi, mtu anapaswa kutegemea zaidi kinachojulikana ujenzi wa msingi unaojadiliwa katika kazi hii.

Nyenzo zilizowasilishwa zinaweza kuwa na matumizi ya moja kwa moja sio tu katika masomo ya hisabati, katika madarasa ya mzunguko wa hisabati, lakini pia katika shughuli za vitendo.

Orodha ya fasihi iliyotumika

Aliev A.V. Miundo ya kijiometri. Hisabati shuleni. 1978 Nambari 3

Glazer G.I. Historia ya hisabati shuleni. M., Mwangaza. 1981.

Depman I.Ya. Nyuma ya kurasa za kitabu cha hisabati. M.. Mwangaza 1989.

Elensky Shch. Katika nyayo za Pythagoras. M., Detgiz. 1961.

Kamusi ya Encyclopedic ya mwanahisabati mchanga. M., Pedagogy. 1985

Katika kazi za ujenzi tutazingatia ujenzi wa takwimu ya kijiometri, ambayo inaweza kufanywa kwa kutumia mtawala na dira.

Kwa kutumia rula unaweza:

mstari wa moja kwa moja wa kiholela;

mstari wa moja kwa moja wa kiholela unaopitia hatua fulani;

mstari wa moja kwa moja unaopitia pointi mbili ulizopewa.

Kutumia dira, unaweza kuelezea mduara wa radius iliyotolewa kutoka kituo fulani.

Kutumia dira unaweza kupanga sehemu kwenye mstari uliopewa kutoka kwa hatua fulani.

Hebu fikiria kazi kuu za ujenzi.

Jukumu la 1. Jenga pembetatu na pande zilizopewa a, b, c (Mchoro 1).

Suluhisho. Kwa kutumia mtawala, chora mstari wa moja kwa moja wa kiholela na uchukue hatua ya kiholela B juu yake kwa kutumia ufunguzi wa dira sawa na a, tunaelezea mduara na kituo B na radius a. Acha C iwe mahali pa makutano yake na mstari. Kwa ufunguzi wa dira sawa na c, tunaelezea mduara kutoka katikati B, na kwa kufungua dira sawa na b, tunaelezea mduara kutoka katikati C. Hebu A iwe hatua ya makutano ya miduara hii. Pembetatu ABC ina pande sawa na a, b, c.

Maoni. Ili sehemu tatu zilizonyooka zitumike kama pande za pembetatu, ni muhimu kwamba kubwa kati yao iwe chini ya jumla ya zingine mbili (na< b + с).

Jukumu la 2.

Suluhisho. Pembe hii yenye kipeo A na OM ya miale imeonyeshwa kwenye Mchoro 2.

Wacha tuchore mduara wa kiholela na kituo chake kwenye vertex A ya pembe iliyotolewa. Hebu B na C kuwa pointi za makutano ya mduara na pande za pembe (Mchoro 3, a). Kwa radius AB tunatoa mduara na kituo kwenye hatua O - hatua ya mwanzo ya ray hii (Mchoro 3, b). Wacha tuonyeshe sehemu ya makutano ya duara hii na miale hii kama C 1 . Hebu tueleze mduara ulio na kituo C 1 na radius BC. Uhakika B 1 wa makutano ya miduara miwili iko upande wa pembe inayotaka. Hii inafuata kutoka kwa usawa Δ ABC = Δ OB 1 C 1 (ishara ya tatu ya usawa wa pembetatu).

Jukumu la 3. Jenga bisector ya pembe hii (Mchoro 4).

Suluhisho. Kutoka kwa vertex A ya pembe fulani, kama kutoka katikati, tunachora mduara wa radius ya kiholela. Hebu B na C ziwe pointi za makutano yake na pande za pembe. Kutoka kwa pointi B na C tunaelezea miduara yenye radius sawa. Acha D iwe sehemu yao ya makutano, tofauti na A. Ray AD ikitenganisha pembe A. Hii inafuatia kutoka kwa usawa Δ ABD = Δ ACD (kigezo cha tatu cha usawa wa pembetatu).

Jukumu la 4. Chora bisector perpendicular kwa sehemu hii (Mchoro 5).

Suluhisho. Kwa kutumia ufunguzi wa dira ya kiholela lakini sawa (kubwa kuliko 1/2 AB), tunaelezea arcs mbili na vituo kwenye pointi A na B, ambazo zitaingiliana kwa baadhi ya pointi C na D. CD ya mstari wa moja kwa moja itakuwa perpendicular inayotaka. Hakika, kama inavyoweza kuonekana kutoka kwa ujenzi, kila moja ya alama C na D iko mbali sawa na A na B; kwa hivyo, nukta hizi lazima ziwe kwenye kipenyo cha pembetatu hadi sehemu ya AB.

Jukumu la 5. Gawanya sehemu hii kwa nusu. Inatatuliwa kwa njia sawa na tatizo la 4 (tazama Mchoro 5).

Jukumu la 6. Kupitia hatua fulani chora mstari wa pembeni kwa mstari uliopewa.

Suluhisho. Kuna kesi mbili zinazowezekana:

1) hatua iliyopewa O iko kwenye mstari uliopewa moja kwa moja a (Mchoro 6).

Kutoka kwa hatua ya O tunachora mduara wa mstari wa kuingiliana wa radius ya kiholela a kwa pointi A na B. Kutoka kwa pointi A na B tunatoa miduara yenye radius sawa. Acha O 1 iwe mahali pa makutano yao, tofauti na O. Tunapata OO 1 ⊥ AB. Kwa kweli, pointi O na O 1 ni sawa kutoka mwisho wa sehemu ya AB na, kwa hiyo, ziko kwenye kipenyo cha pembetatu kwa sehemu hii.

Taasisi ya elimu ya bajeti ya manispaa

shule ya sekondari namba 34 na utafiti wa kina wa masomo ya mtu binafsi

MAN, fizikia na sehemu ya hisabati

"Miundo ya kijiometri kwa kutumia dira na rula"

Imekamilishwa na: mwanafunzi wa darasa la 7 "A"

Victoria Batishcheva

Mkuu: Koltovskaya V.V.

Voronezh, 2013

3. Kujenga angle sawa na iliyotolewa.

P Hebu tuchore mduara wa kiholela na kituo kwenye vertex A ya angle iliyotolewa (Mchoro 3). Wacha B na C ziwe alama za makutano ya duara na pande za pembe. Kwa radius AB tunachora mduara na kituo kwenye hatua O, mahali pa kuanzia la mstari huu wa nusu. Wacha tuonyeshe sehemu ya makutano ya duara hii na mstari huu wa nusu kama C 1 . Hebu tueleze mduara ulio na kituo C 1 na Mtini.3

radius ya ndege. Pointi B 1 makutano ya miduara iliyojengwa katika ndege ya nusu iliyoonyeshwa iko kwenye upande wa pembe inayotaka.

6. Ujenzi wa mistari ya perpendicular.

Tunachora mduara na radius ya kiholela r na kituo kwenye hatua O kwenye Mchoro 6. Mduara huvuka mstari kwa pointi A na B.Kutoka kwa pointi A na B tunachora miduara yenye radius AB. Acha melancholy C iwe mahali pa makutano ya miduara hii. Tulipata pointi A na B katika hatua ya kwanza, wakati wa kujenga mduara na radius ya kiholela.

Mstari wa moja kwa moja unaotaka hupitia alama C na O.

Mtini.6

Masuala Yanayojulikana

1.Tatizo la Brahmagupta

Tengeneza sehemu ya pembe nne iliyoandikwa kwa kutumia pande zake nne. Suluhisho moja linatumia mduara wa Apollonius.Wacha tusuluhishe shida ya Apollonius kwa kutumia mlinganisho kati ya mduara na pembetatu. Jinsi tunavyopata mduara ulioandikwa kwenye pembetatu: tunaunda sehemu ya makutano ya viboreshaji, tone perpendiculars kutoka kwake hadi pande za pembetatu, misingi ya perpendiculars (pointi za makutano ya perpendicular na upande ambao ni. imeshuka) na utupe pointi tatu zilizo kwenye mduara unaotaka. Chora mduara kupitia pointi hizi tatu - suluhisho ni tayari. Tutafanya vivyo hivyo na shida ya Apollonius.

2. Tatizo la Apollonius

Kwa kutumia dira na rula, jenga tanjiti ya duara kwa miduara mitatu uliyopewa. Kulingana na hadithi, shida iliundwa na Apollonius wa Perga karibu 220 BC. e. katika kitabu "Touch," ambacho kilipotea, lakini kilirejeshwa mnamo 1600 na François Viète, "Gallic Apollonius," kama watu wa wakati wake walivyomwita.

Ikiwa hakuna duru zilizopewa ziko ndani ya nyingine, basi shida hii ina suluhisho 8 tofauti sana.

Ujenzi wa poligoni za kawaida.

P

sahihi (au usawa ) pembetatu -Hii poligoni ya kawaidayenye pande tatu, ya kwanza ya poligoni za kawaida. Wote pande za pembetatu ya kawaida ni sawa kwa kila mmoja, na wote pembe ni 60 °. Ili kuunda pembetatu ya usawa, unahitaji kugawanya mduara katika sehemu 3 sawa. Ili kufanya hivyo, ni muhimu kuteka arc ya radius R ya mduara huu kutoka mwisho mmoja tu wa kipenyo, tunapata mgawanyiko wa kwanza na wa pili. Mgawanyiko wa tatu ni upande wa mwisho wa kipenyo. Kwa kuunganisha pointi hizi, tunapata pembetatu ya equilateral.

Hexagons ya kawaida Unawezajenga kwa kutumia dira na rula. Chininjia ya ujenzi imetolewakwa kugawanya duara katika sehemu 6. Tunatumia usawa wa pande za hexagons ya kawaida kwa radius ya mduara unaozunguka. Kutoka kwa ncha za kinyume za moja ya kipenyo cha mduara tunaelezea arcs ya radius R. Sehemu za makutano ya arcs hizi na mduara uliopewa zitagawanya katika sehemu 6 sawa. Kwa kuunganisha kwa sequentially pointi zilizopatikana, hexagon ya kawaida hupatikana.

Ujenzi wa pentagon ya kawaida.

P
pentagon ya kawaida inaweza kuwakujengwa kwa kutumia dira na rula, au kwa kukiweka kwenye kitu fulanimduara, au ujenzi kulingana na upande fulani. Utaratibu huu unaelezewa na Euclidkatika Mambo yake yapata 300 BC. e.

Hapa kuna njia moja ya kuunda pentagon ya kawaida kwenye duara fulani:

Tengeneza mduara ambamo pentagoni itaandikwa na uweke alama katikati yake kamaO . (Hii ni mduara wa kijani kwenye mchoro wa kulia).

Chagua pointi kwenye mduaraA , ambayo itakuwa moja ya wima ya pentagon. Tengeneza mstari wa moja kwa moja kupitiaO NaA .

Tengeneza mstari wa perpendicular kwa mstariO.A. , kupita kwa uhakikaO . Teua moja ya makutano yake na mduara kama hatuaB .

Panga hatuaC katikati katiO NaB .

C kupitia uhakikaA . Weka alama kwenye makutano yake na mstariO.B. (ndani ya duara asilia) kama nuktaD .

Chora duara na katikatiA kupitia nukta D, weka alama kwenye makutano ya mduara huu na asilia (mduara wa kijani) kama pointiE NaF .

Chora duara na katikatiE kupitia uhakikaA G .

Chora duara na katikatiF kupitia uhakikaA . Weka alama kwenye makutano yake mengine na mduara asilia kama nchaH .

Tengeneza pentagon ya kawaidaAEGHF .

Matatizo yasiyoweza kutatuliwa

Kazi tatu zifuatazo za ujenzi ziliwekwa zamani:

Trisection ya pembe - kugawanya angle ya kiholela katika sehemu tatu sawa.

Kwa maneno mengine, ni muhimu kujenga trisectors angle - rays kugawanya angle katika sehemu tatu sawa. P. L. Wanzel alithibitisha mwaka wa 1837 kwamba tatizo linaweza kutatuliwa tu wakati, kwa mfano, utatuzi unawezekana kwa pembe α = 360 °/n, mradi nambari kamili n haigawanyiki na 3. Hata hivyo, katika vyombo vya habari mara kwa mara (sio sahihi. ) njia za kukata pembe kwa dira na rula zinachapishwa.

Kuongeza mchemraba mara mbili - shida ya zamani ya kujenga na dira na mtawala makali ya mchemraba, kiasi ambacho ni mara mbili ya ujazo wa mchemraba uliopeanwa.

Katika nukuu ya kisasa, shida imepunguzwa ili kutatua equation. Yote inakuja kwa shida ya kuunda sehemu ya urefu. P. Wantzel alithibitisha mwaka wa 1837 kwamba tatizo hili haliwezi kutatuliwa kwa kutumia dira na makali ya moja kwa moja.

Kupiga mduara - kazi inayojumuisha kutafuta ujenzi kwa kutumia dira na mtawala wa mraba sawa na eneo la mduara uliopewa..

Kama unavyojua, kwa msaada wa dira na mtawala unaweza kufanya shughuli zote 4 za hesabu na kutoa mzizi wa mraba; inafuata kwamba squaring mduara inawezekana ikiwa na tu ikiwa, kwa kutumia idadi ya mwisho ya vitendo vile, inawezekana kujenga sehemu ya urefu π. Kwa hivyo, kutotatuliwa kwa tatizo hili kunafuata kutoka kwa asili isiyo ya algebraic (transcendence) ya nambari π, ambayo ilithibitishwa mwaka wa 1882 na Lindemann.

Tatizo jingine linalojulikana ambalo haliwezi kutatuliwa kwa kutumia dira na mtawala nikuunda pembetatu kwa kutumia urefu wa sehemu tatu ulizopewa .

Aidha, tatizo hili bado halijatatuliwa hata mbele ya trisector.

Ilikuwa tu katika karne ya 19 ambapo ilithibitishwa kwamba matatizo yote matatu hayakuweza kutatuliwa kwa kutumia tu dira na mwelekeo. Swali la uwezekano wa ujenzi linatatuliwa kabisa na mbinu za algebra kulingana na nadharia ya Galois.

JE, WAJUA KWAMBA...

(kutoka historia ya ujenzi wa kijiometri)

Hapo zamani za kale, maana ya fumbo iliwekezwa katika ujenzi wa poligoni za kawaida.

Kwa hivyo, Pythagoreans, wafuasi wa mafundisho ya kidini na ya kifalsafa yaliyoanzishwa na Pythagoras, na ambao waliishi katika Ugiriki ya kale.V I-I Vkarne nyingi BC BC), iliyopitishwa kama ishara ya muungano wao poligoni yenye umbo la nyota inayoundwa na vilaza vya pentagoni ya kawaida.

Sheria za ujenzi madhubuti wa kijiometri wa poligoni za kawaida zimewekwa katika kitabu "Elements" na mwanahisabati wa zamani wa Uigiriki Euclid, aliyeishi huko.IIIV. BC. Ili kutekeleza ujenzi huu, Euclid alipendekeza kutumia tu mtawala na dira, ambayo wakati huo haikuwa na kifaa cha bawaba cha kuunganisha miguu (kizuizi kama hicho katika vyombo kilikuwa hitaji lisiloweza kubadilika la hesabu ya zamani).

Polygons za kawaida zilitumiwa sana katika unajimu wa zamani. Ikiwa Euclid alipendezwa na ujenzi wa takwimu hizi kutoka kwa mtazamo wa hisabati, basi kwa mtaalam wa nyota wa zamani wa Uigiriki Claudius Ptolemy (karibu 90 - 160 BK) iligeuka kuwa muhimu kama zana ya msaidizi katika kutatua shida za unajimu. Kwa hivyo, katika kitabu cha 1 cha Almagests, sura nzima ya kumi imejitolea kwa ujenzi wa pentagoni za kawaida na decagons.

Walakini, pamoja na kazi za kisayansi tu, ujenzi wa poligoni za kawaida ulikuwa sehemu muhimu ya vitabu vya wajenzi, mafundi, na wasanii. Uwezo wa kuonyesha takwimu hizi umehitajika kwa muda mrefu katika usanifu, mapambo, na sanaa nzuri.

"Vitabu Kumi juu ya Usanifu" wa mbunifu wa Kirumi Vitruvius (aliyeishi takriban 63-14 KK) anasema kwamba kuta za jiji zinapaswa kuwa na muundo wa poligoni wa kawaida katika mpango, na minara ya ngome "inapaswa kufanywa pande zote au polygonal. , kwa ajili ya sehemu nne iliyoharibiwa na silaha za kuzingirwa.”

Mpangilio wa miji ulikuwa wa riba kubwa kwa Vitruvius, ambaye aliamini kwamba ilikuwa ni lazima kupanga mitaa ili upepo kuu usipige pamoja nao. Ilifikiriwa kuwa kulikuwa na pepo nane za aina hiyo na kwamba zilivuma kwa mwelekeo fulani.

Wakati wa Renaissance, ujenzi wa polygons za kawaida, na hasa pentagon, haikuwa mchezo rahisi wa hisabati, lakini ilikuwa sharti la lazima kwa ajili ya ujenzi wa ngome.

Heksagoni ya kawaida ilikuwa somo la uchunguzi wa pekee wa mwanaastronomia na mwanahisabati mkuu Mjerumani Johannes Kepler (1571-1630), ambalo anazungumzia katika kitabu chake “Zawadi ya Mwaka Mpya, au Matambara ya theluji ya Hexagonal.” Kujadili sababu kwa nini vipande vya theluji vina umbo la hexagonal, anabainisha, hasa, yafuatayo: "... ndege inaweza kufunikwa bila mapengo tu na takwimu zifuatazo: pembetatu za equilateral, mraba na hexagons za kawaida. Miongoni mwa takwimu hizi, hexagon ya kawaida inashughulikia eneo kubwa zaidi."

Mmoja wa wanasayansi mashuhuri waliohusika katika ujenzi wa kijiometri alikuwa msanii mkubwa wa Ujerumani na mwanahisabati Albrecht Durer (1471 -1528), ambaye alijitolea sehemu kubwa ya kitabu chake "Miongozo ..." kwao. Alipendekeza sheria za kuunda poligoni za kawaida zenye pande 3, 4, 5... 16. Mbinu za kugawanya mduara uliopendekezwa na Dürer sio zima; mbinu ya mtu binafsi hutumiwa katika kila kesi maalum.

Dürer alitumia mbinu za kuunda poligoni za kawaida katika mazoezi ya kisanii, kwa mfano, wakati wa kuunda aina mbalimbali za mapambo na mifumo ya parquet. Alichora mifumo hiyo wakati wa safari ya Uholanzi, ambapo sakafu za parquet zilipatikana katika nyumba nyingi.

Dürer alijumuisha mapambo kutoka kwa poligoni za kawaida, ambazo zimeunganishwa kwenye pete (pete za pembetatu sita za equilateral, quadrangles nne, hexagoni tatu au sita, heptagoni kumi na nne, octagons nne).

Hitimisho

Kwa hiyo,miundo ya kijiometri ni njia ya kutatua tatizo ambalo jibu linapatikana kwa mchoro. Ujenzi unafanywa kwa kutumia zana za kuchora kwa usahihi wa juu na usahihi wa kazi, kwani usahihi wa suluhisho inategemea hii.

Shukrani kwa kazi hii, nilifahamu historia ya asili ya dira, nilifahamu zaidi sheria za kufanya ujenzi wa kijiometri, nilipata ujuzi mpya na kuitumia kwa mazoezi.
Kutatua matatizo yanayohusisha ujenzi na dira na mtawala ni mchezo muhimu unaokuwezesha kuangalia upya mali inayojulikana ya takwimu za kijiometri na mambo yao.Karatasi hii inajadili shida kubwa zaidi zinazohusiana na ujenzi wa kijiometri kwa kutumia dira na watawala. Matatizo makuu yanazingatiwa na ufumbuzi wao hutolewa. Matatizo yaliyotolewa ni ya manufaa makubwa ya vitendo, kuunganisha ujuzi uliopatikana katika jiometri na inaweza kutumika kwa kazi ya vitendo.
Kwa hivyo, lengo la kazi limefikiwa, kazi zilizopewa zimekamilika.

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt=">Ujenzi kwa kutumia rula na dira Jiometria">!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="> Tengeneza sehemu sawa na Tatizo la A B lililopewa"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="> Kuunda pembe sawa na Pembetatu za Fikiria moja"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="> Kuunda sehemu-mbili ya tatizo la pembe Ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="> Ujenzi wa laini za pembeni Ú Tatizo la Given line"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="> Kuunda sehemu ya kati ya sehemu ya Muundo wa Jukumu la katikati kupewa"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}