Utegemezi wa mstari wa vekta mbili. Vekta zinazotegemea mstari na zinazojitegemea kwa mstari

Ili kuangalia ikiwa mfumo wa vekta unategemea mstari, ni muhimu kutunga mchanganyiko wa mstari wa vekta hizi, na uangalie ikiwa inaweza kuwa sifuri ikiwa angalau mgawo mmoja ni sawa na sifuri.

Kesi 1. Mfumo wa vectors hutolewa na vectors

Kufanya mchanganyiko wa mstari

Tumepata mfumo wa usawa wa milinganyo. Ikiwa ina ufumbuzi usio na sifuri, basi kiashiria lazima kiwe sawa na sifuri. Wacha tutunge kiambishi na tupate thamani yake.

Kiamuzi ni sifuri, kwa hivyo vekta zinategemea mstari.

Kesi 2. Mfumo wa vekta hufafanuliwa na kazi za uchambuzi:

a)
, ikiwa kitambulisho ni kweli, basi mfumo unategemea mstari.

Wacha tufanye mchanganyiko wa mstari.

Inahitajika kuangalia ikiwa kuna a, b, c (angalau moja ambayo si sawa na sifuri) ambayo usemi huu ni sawa na sifuri.

Hebu tuandike kazi za hyperbolic

,
, Kisha

basi mchanganyiko wa mstari wa vekta utachukua fomu:

Wapi
, chukua, kwa mfano, basi mchanganyiko wa mstari ni sifuri, kwa hiyo, mfumo unategemea mstari.

Jibu: mfumo unategemea mstari.

b)
, wacha tufanye mchanganyiko wa mstari

Mchanganyiko wa mstari wa vekta lazima uwe sawa na sifuri kwa thamani zozote za x.

Wacha tuangalie kesi maalum.

Mchanganyiko wa mstari wa vekta ni sawa na sifuri ikiwa tu migawo yote ni sawa na sifuri.

Kwa hiyo, mfumo ni linearly kujitegemea.

Jibu: mfumo ni linearly kujitegemea.

5.3. Tafuta msingi na uamua ukubwa wa nafasi ya suluhisho la mstari.

Wacha tuunda matrix iliyopanuliwa na tuipunguze kwa fomu ya trapezoid kwa kutumia njia ya Gaussian.

Ili kupata msingi fulani, wacha tubadilishe maadili ya kiholela:

Wacha tupate viwianishi vingine

Jibu:

5.4. Pata kuratibu za vector X kwa msingi, ikiwa imetolewa kwa msingi.

Kupata kuratibu za vekta kwa msingi mpya kunakuja kutatua mfumo wa equations

Mbinu 1. Kutafuta kwa kutumia matrix ya mpito

Wacha tuunde matrix ya mpito

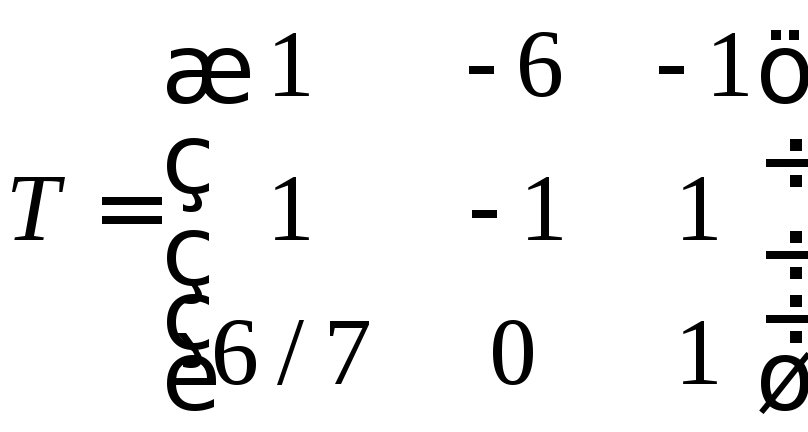
Wacha tupate vekta katika msingi mpya kwa kutumia fomula

Wacha tutafute matrix inverse na tufanye kuzidisha

,

Mbinu 2. Kupata kwa kutunga mfumo wa milinganyo.

Wacha tutunge veta za msingi kutoka kwa mgawo wa msingi

,
,

Kutafuta vekta katika msingi mpya kuna fomu

, Wapi d Hii vector iliyotolewa x.

Equation inayotokana inaweza kutatuliwa kwa njia yoyote, jibu litakuwa sawa.

Jibu: vekta katika msingi mpya
.

5.5. Acha x = (x 1 , x 2 , x 3 ) . Je, mabadiliko yafuatayo ni ya mstari?

Wacha tutunge matrices ya waendeshaji wa mstari kutoka kwa mgawo wa vekta zilizopewa.

Wacha tuangalie mali ya shughuli za mstari kwa kila matrix ya waendeshaji wa mstari.

Tunapata upande wa kushoto kwa kuzidisha matrix A kwa vekta

Tunapata upande wa kulia kwa kuzidisha vector iliyotolewa na scalar
.

Tunaona hilo
Hii ina maana kwamba mabadiliko si linear.

Wacha tuangalie vekta zingine.

, mabadiliko si ya mstari.

, mabadiliko ni ya mstari.

Jibu: Oh- Hapana mabadiliko ya mstari, Katika- sio mstari, Cx- mstari.

Kumbuka. Unaweza kukamilisha kazi hii kwa urahisi zaidi kwa kuangalia kwa uangalifu vekta zilizopewa. KATIKA Oh tunaona kwamba kuna maneno ambayo hayana vipengele X, ambayo haikuweza kupatikana kwa sababu ya operesheni ya mstari. KATIKA Katika kuna kipengele X kwa nguvu ya tatu, ambayo pia haikuweza kupatikana kwa kuzidisha na vector X.

5.6. Imetolewa x = { x 1 , x 2 , x 3 } , Shoka = { x 2 – x 3 , x 1 , x 1 + x 3 } , Bx = { x 2 , 2 x 3 , x 1 } . Fanya operesheni maalum: ( A ( B – A )) x .

Hebu tuandike matrices ya waendeshaji wa mstari.

Wacha tufanye operesheni kwenye matrices

Wakati wa kuzidisha matrix inayosababishwa na X, tunapata

Jibu:

Jukumu la 1. Jua ikiwa mfumo wa vekta ni huru kwa mstari. Mfumo wa vectors utaelezwa na tumbo la mfumo, nguzo ambazo zinajumuisha kuratibu za vectors.

.

Suluhisho. Acha mchanganyiko wa mstari sawa na sifuri. Baada ya kuandika usawa huu katika kuratibu, tunapata mfumo ufuatao wa equations:

.

Mfumo kama huo wa equations unaitwa triangular. Ana suluhisho moja tu . Kwa hiyo, vectors kujitegemea linearly.

Jukumu la 2. Jua ikiwa mfumo wa vekta ni huru kwa mstari.

.

Suluhisho. Vekta zinajitegemea kimstari (tazama Tatizo 1). Wacha tuthibitishe kuwa vekta ni mchanganyiko wa mstari wa vekta . Mgawo wa upanuzi wa Vekta imedhamiriwa kutoka kwa mfumo wa milinganyo

.

Mfumo huu, kama ule wa pembetatu, una suluhisho la kipekee.

Kwa hiyo, mfumo wa vectors tegemezi kwa mstari.

Maoni. Matrices ya aina sawa na katika Tatizo 1 huitwa pembetatu , na katika tatizo la 2 - kupitiwa pembetatu . Swali la utegemezi wa mstari wa mfumo wa vekta hutatuliwa kwa urahisi ikiwa matrix inayojumuisha kuratibu za vekta hizi ni hatua ya pembetatu. Ikiwa matrix haina aina maalum, kisha kutumia ubadilishaji wa kamba za msingi , kuhifadhi uhusiano wa mstari kati ya nguzo, inaweza kupunguzwa kwa fomu ya hatua ya triangular.

Mabadiliko ya msingi mistari matrices (EPS) shughuli zifuatazo kwenye tumbo huitwa:

1) upangaji upya wa mistari;

2) kuzidisha kamba kwa nambari isiyo ya sifuri;

3) kuongeza kamba nyingine kwenye kamba, ikizidishwa na nambari ya kiholela.

Jukumu la 3. Pata mfumo mdogo wa kiwango cha juu wa kujitegemea na uhesabu kiwango cha mfumo wa vekta

.

Suluhisho. Hebu tupunguze matrix ya mfumo kwa kutumia EPS kwa fomu ya hatua ya pembetatu. Ili kuelezea utaratibu, tunaashiria mstari na nambari ya tumbo inayobadilishwa na ishara. Safu baada ya mshale huonyesha vitendo kwenye safu mlalo za matrix zinazobadilishwa ambazo ni lazima zitekelezwe ili kupata safu mlalo za matrix mpya.

.

Kwa wazi, nguzo mbili za kwanza za matrix zinazosababisha zinajitegemea kwa mstari, safu ya tatu ni mchanganyiko wao wa mstari, na ya nne haitegemei mbili za kwanza. Vekta huitwa msingi. Wanaunda mfumo mdogo wa mfumo unaojitegemea wa kiwango cha juu zaidi , na cheo cha mfumo ni tatu.

Msingi, kuratibu

Jukumu la 4. Pata msingi na kuratibu za vekta katika msingi huu kwenye seti vectors za kijiometri, ambayo kuratibu zake zinakidhi hali hiyo .

Suluhisho. Seti ni ndege inayopitia asili. Msingi wa kiholela kwenye ndege unajumuisha vekta mbili zisizo za collinear. Kuratibu za vekta katika msingi uliochaguliwa imedhamiriwa kwa kutatua mfumo unaofanana wa equations za mstari.

Kuna njia nyingine ya kutatua tatizo hili, wakati unaweza kupata msingi kwa kutumia kuratibu.

Kuratibu nafasi sio kuratibu kwenye ndege, kwani zinahusiana na uhusiano , yaani hawajitegemei. Vigezo vya kujitegemea na (vinaitwa bure) hufafanua vekta ya pekee kwenye ndege na, kwa hiyo, zinaweza kuchaguliwa kama kuratibu katika . Kisha msingi inajumuisha vekta zilizolala ndani na zinazolingana na seti za vigeu vya bure Na , hiyo ni .

Jukumu la 5. Pata msingi na kuratibu za vectors katika msingi huu juu ya seti ya vectors wote katika nafasi ambao kuratibu isiyo ya kawaida ni sawa na kila mmoja.

Suluhisho. Wacha tuchague, kama katika shida iliyopita, kuratibu kwenye nafasi.

Kwa sababu , kisha vigeu vya bure kipekee kuamua vekta kutoka na hivyo ni kuratibu. Msingi unaofanana una vekta.

Jukumu la 6. Pata msingi na kuratibu za vectors katika msingi huu juu ya seti ya matrices yote ya fomu , Wapi - nambari za kiholela.

Suluhisho. Kila matrix kutoka inawakilishwa kipekee katika fomu:

Uhusiano huu ni upanuzi wa vector kutoka kwa heshima na msingi
na kuratibu .

Jukumu la 7. Pata mwelekeo na msingi wa safu ya mstari wa mfumo wa vekta

.

Suluhisho. Kwa kutumia EPS, tunabadilisha matrix kutoka kwa kuratibu za vekta za mfumo hadi fomu ya hatua ya pembetatu.

.

Safu matrices ya mwisho ni linearly huru, na nguzo linearly walionyesha kupitia kwao. Kwa hiyo, vectors kuunda msingi , Na .

Maoni. Msingi katika huchaguliwa kwa utata. Kwa mfano, vectors pia kuunda msingi .

a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.

Suluhisho. Wanatafuta uamuzi wa pamoja mifumo ya equations

a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

Njia ya Gauss. Ili kufanya hivyo, tunaandika mfumo huu wa homogeneous katika kuratibu:

Matrix ya Mfumo

Mfumo unaoruhusiwa una fomu: (r A = 2, n= 3). Mfumo huo ni wa ushirika na hauna uhakika. Suluhisho lake la jumla ( x 2 - tofauti ya bure): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o = . Uwepo wa suluhisho maalum isiyo ya sifuri, kwa mfano, inaonyesha kuwa vekta a 1 , a 2 , a 3 tegemezi kwa mstari.

Mfano 2.

Jua kama mfumo huu tegemezi la mstari au vekta zinazojitegemea kimstari:

1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.

Suluhisho. Fikiria mfumo wa usawa wa milinganyo a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ

au kwa namna iliyopanuliwa (kwa kuratibu)

Mfumo ni homogeneous. Ikiwa haijaharibika, basi ina suluhisho la pekee. Lini mfumo wa homogeneous– sifuri (kidogo) suluhisho. Hii ina maana kwamba katika kesi hii mfumo wa vectors ni huru. Ikiwa mfumo umepungua, basi una ufumbuzi usio na sifuri na, kwa hiyo, unategemea.

Tunaangalia mfumo kwa uharibifu:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Mfumo hauna uharibifu na, hivyo, vectors a 1 , a 2 , a 3 kujitegemea linearly.

Kazi. Jua ikiwa mfumo fulani wa vekta hutegemea mstari au huru kwa mstari:

1. a 1 = { -4, 2, 8 }, a 2 = { 14, -7, -28 }.

2. a 1 = { 2, -1, 3, 5 }, a 2 = { 6, -3, 3, 15 }.

3. a 1 = { -7, 5, 19 }, a 2 = { -5, 7 , -7 }, a 3 = { -8, 7, 14 }.

4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.

5. a 1 = { 1, 8 , -1 }, a 2 = { -2, 3, 3 }, a 3 = { 4, -11, 9 }.

6. a 1 = { 1, 2 , 3 }, a 2 = { 2, -1 , 1 }, a 3 = { 1, 3, 4 }.

7. a 1 = {0, 1, 1 , 0}, a 2 = {1, 1 , 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.

8. a 1 = {-1, 7, 1 , -2}, a 2 = {2, 3 , 2, 1}, a 3 = {4, 4, 4, -3}, a 4 = {1, 6, -11, 1}.

9. Thibitisha kuwa mfumo wa vekta utategemea mstari ikiwa una:

a) vekta mbili sawa;

b) vectors mbili za uwiano.

Vectors, mali zao na vitendo pamoja nao

Vekta, vitendo na vekta, nafasi ya vekta ya mstari.

Vekta ni mkusanyiko ulioagizwa wa idadi maalum ya nambari halisi.

Vitendo: 1.Kuzidisha vekta kwa nambari: lambda*vekta x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3.4, 0, 7)*3=(9, 12,0.21)

2. Ongezeko la vekta (ni ya nafasi sawa ya vekta) vekta x + vekta y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Vekta 0=(0,0…0)---n E n – n-dimensional (nafasi ya mstari) vekta x + vekta 0 = vekta x

Nadharia. Ili mfumo wa vekta n, nafasi ya mstari wa n-dimensional iwe tegemezi kwa mstari, ni muhimu na ya kutosha kwamba moja ya vectors iwe mchanganyiko wa mstari wa wengine.

Nadharia. Seti yoyote ya vekta za n+ 1 za nafasi ya mstari wa n-dimensional ya matukio. tegemezi kwa mstari.

Ongezeko la vekta, kuzidisha vekta kwa nambari. Utoaji wa vectors.

Jumla ya vectors mbili ni vector iliyoongozwa kutoka mwanzo wa vector hadi mwisho wa vector, mradi mwanzo unafanana na mwisho wa vector. Ikiwa vekta hutolewa na upanuzi wao katika vekta za kitengo cha msingi, basi wakati wa kuongeza vectors, kuratibu zao zinazofanana huongezwa.

Wacha tuzingatie hili kwa kutumia mfano wa mfumo wa kuratibu wa Cartesian. Hebu

Hebu tuonyeshe hilo

Kutoka Kielelezo 3 ni wazi kwamba

Kiasi cha yoyote nambari ya mwisho vekta zinaweza kupatikana kwa kutumia kanuni ya poligoni (Mchoro 4): kujenga jumla ya idadi ya vekta, inatosha kuchanganya mwanzo wa kila vekta inayofuata na mwisho wa uliopita na kujenga vector inayounganisha mwanzo. ya vekta ya kwanza na mwisho wa ya mwisho.

Sifa za operesheni ya kuongeza vekta:

Katika semi hizi m, n ni nambari.

Tofauti kati ya vekta inaitwa vekta.Muhula wa pili ni vector kinyume na vector katika mwelekeo, lakini sawa na urefu wake.

Kwa hivyo, uendeshaji wa vectors ya kuondoa hubadilishwa na operesheni ya kuongeza

Vekta ambayo mwanzo wake uko kwenye asili na mwisho katika hatua A (x1, y1, z1) inaitwa vekta ya radius ya uhakika A na inaonyeshwa kwa urahisi. Kwa kuwa kuratibu zake zinaendana na kuratibu za nukta A, upanuzi wake katika veta za kitengo una fomu.

Vekta inayoanzia kwa uhakika A(x1, y1, z1) na kuishia kwa uhakika B(x2, y2, z2) inaweza kuandikwa kama

ambapo r 2 ni vector ya radius ya uhakika B; r 1 - vekta ya radius ya uhakika A.

Kwa hiyo, upanuzi wa vector katika vectors kitengo ina fomu

Urefu wake ni sawa na umbali kati ya alama A na B

KUZIDISHA

Hivyo katika kesi tatizo la ndege bidhaa ya vekta kwa = (shoka; ay) kwa nambari b hupatikana kwa fomula

a b = (shoka b; ay b)

Mfano 1. Tafuta bidhaa ya vekta a = (1; 2) kwa 3.

3 a = (3 1; 3 2) = (3; 6)

Hivyo katika kesi tatizo la anga bidhaa ya vekta a = (shoka; ay; az) kwa nambari b hupatikana kwa fomula

a b = (shoka b; ay b; az b)

Mfano 1. Tafuta bidhaa ya vekta a = (1; 2; -5) kwa 2.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Bidhaa ya dot ya vekta na wapi angle kati ya vectors na; kama aidha, basi

Kutoka kwa ufafanuzi wa bidhaa ya scalar inafuata hiyo

ambapo, kwa mfano, ni ukubwa wa makadirio ya vector kwenye mwelekeo wa vector.

Vekta ya mraba ya scalar:

Tabia za bidhaa ya dot:

Bidhaa yenye nukta kwenye viwianishi

Kama Hiyo

Pembe kati ya vekta

Angle kati ya vectors - angle kati ya maelekezo ya vectors hizi (angle ndogo).

Bidhaa ya msalaba (Bidhaa ya msalaba ya vekta mbili.) - hii ni pseudovector, perpendicular kwa ndege, iliyojengwa kutokana na mambo mawili, ambayo ni matokeo ya operesheni ya binary "kuzidisha vekta" juu ya vekta katika nafasi ya Euclidean ya pande tatu. Bidhaa haibadilishi wala haishirikishi (ni anticommutative) na ni tofauti na bidhaa ya nukta ya vekta. Katika matatizo mengi ya uhandisi na fizikia, unahitaji kuwa na uwezo wa kujenga vector perpendicular kwa mbili zilizopo - bidhaa ya vector hutoa fursa hii. Bidhaa ya msalaba ni muhimu kwa "kupima" perpendicularity ya vectors - urefu wa bidhaa ya msalaba wa vectors mbili ni sawa na bidhaa ya urefu wao ikiwa ni perpendicular, na hupungua hadi sifuri ikiwa vectors ni sambamba au antiparallel.

Bidhaa ya msalaba inafafanuliwa tu katika nafasi tatu-dimensional na saba-dimensional. Matokeo ya bidhaa ya vekta, kama bidhaa ya scalar, inategemea kipimo cha nafasi ya Euclidean.

Tofauti na fomula ya kuhesabu kuratibu za vekta za bidhaa za dot katika mfumo wa kuratibu wa mstatili wa pande tatu, fomula ya bidhaa ya msalaba inategemea mwelekeo. mfumo wa mstatili kuratibu au, kwa maneno mengine, "ukatili" wake

Collinearity ya vekta.

Vekta mbili zisizo za sifuri (zisizo sawa na 0) huitwa collinear ikiwa zimelala kwenye mistari inayofanana au kwenye mstari mmoja. Sawe inayokubalika, lakini haipendekezwi ni vekta "sambamba". Vekta za Collinear inaweza kuelekezwa kwa kufanana ("mwelekeo-mwelekeo") au kuelekezwa kinyume (katika kesi ya mwisho wakati mwingine huitwa "anticollinear" au "antiparallel").

Mchanganyiko wa bidhaa za vekta ( a, b, c)- bidhaa ya scalar ya vekta a na bidhaa ya vekta ya vekta b na c:

(a,b,c)=a ⋅(b ×c)

wakati mwingine huitwa mara tatu bidhaa ya scalar vectors, uwezekano mkubwa kutokana na ukweli kwamba matokeo ni scalar (zaidi kwa usahihi, pseudoscalar).

Maana ya kijiometri: Moduli ya bidhaa iliyochanganywa ni sawa kiidadi na ujazo wa bomba la parallele linaloundwa na vekta. (a,b,c) .

Mali

Bidhaa iliyochanganywa ni skew-symmetric kwa heshima na hoja zake zote: i.e. e) kupanga upya vipengele vyovyote viwili hubadilisha ishara ya bidhaa. Inafuata kwamba bidhaa iliyochanganywa upande wa kulia Mfumo wa Cartesian kuratibu (katika msingi wa kawaida) ni sawa na kibainishi cha matriki inayojumuisha vekta na:

Bidhaa iliyochanganywa katika mfumo wa kuratibu wa Cartesian wa kushoto (katika msingi wa kawaida) ni sawa na kiashiria cha matrix inayojumuisha vekta na, ikichukuliwa na ishara ya minus:

Hasa,

Ikiwa vekta mbili zinafanana, basi kwa vector yoyote ya tatu huunda bidhaa iliyochanganywa sawa na sifuri.

Ikiwa vekta tatu zinategemea mstari (hiyo ni coplanar, amelala kwenye ndege moja), basi bidhaa zao zilizochanganywa ni sawa na sifuri.

Maana ya kijiometri - Bidhaa iliyochanganywa na thamani kamili sawa na kiasi cha parallelepiped (tazama takwimu) iliyoundwa na vectors na; ishara inategemea ikiwa hii mara tatu ya vekta ni ya mkono wa kulia au wa kushoto.

Coplanarity ya vectors.

Vekta tatu (au idadi kubwa zaidi) huitwa coplanar ikiwa wao, hupunguzwa hadi mwanzo wa jumla, lala kwenye ndege moja

Tabia za coplanarity

Ikiwa angalau moja ya vekta tatu- sifuri, basi vectors tatu pia huchukuliwa kuwa coplanar.

Mara tatu ya vekta zilizo na jozi ya vekta za collinear ni coplanar.

Bidhaa iliyochanganywa ya vekta za coplanar. Hiki ni kigezo cha uwiano wa vekta tatu.

Vekta za Coplanar zinategemea mstari. Hiki pia ni kigezo cha ushirikiano.

Katika nafasi ya 3-dimensional, vectors 3 zisizo za coplanar huunda msingi

Vekta zinazotegemea mstari na zinazojitegemea kwa mstari.

Mifumo ya vekta inayotegemea laini na inayojitegemea.Ufafanuzi. Mfumo wa vector unaitwa tegemezi kwa mstari, ikiwa kuna angalau mchanganyiko mmoja usio wa kawaida wa mstari wa vekta hizi sawa na vekta sifuri. Vinginevyo, i.e. ikiwa tu mchanganyiko mdogo wa mstari wa vekta uliyopewa ni sawa na vekta tupu, vekta huitwa. kujitegemea linearly.

Nadharia (kigezo cha utegemezi cha mstari). Ili mfumo wa vekta katika nafasi ya mstari kuwa tegemezi kwa mstari, ni muhimu na ya kutosha kwamba angalau moja ya vekta hizi ni mchanganyiko wa mstari wa wengine.

1) Ikiwa kati ya vectors kuna angalau vector moja ya sifuri, basi mfumo mzima wa vectors unategemea linearly.

Kwa kweli, kama, kwa mfano, , basi, tukichukulia , tuna mchanganyiko wa mstari usio na maana .▲

2) Ikiwa kati ya vekta zingine zinaunda mfumo tegemezi wa mstari, basi mfumo mzima unategemea mstari.

Kwa kweli, wacha vekta , , tegemezi kwa mstari. Hii ina maana kwamba kuna mchanganyiko usio wa kawaida wa mstari sawa na vekta ya sifuri. Lakini basi, kuchukua , pia tunapata mchanganyiko wa mstari usio wa kawaida sawa na vekta ya sifuri.

2. Msingi na mwelekeo. Ufafanuzi. Mfumo wa vekta zinazojitegemea zenye mstari nafasi ya vekta kuitwa msingi ya nafasi hii ikiwa vekta yoyote kutoka inaweza kuwakilishwa kama mchanganyiko wa mstari wa vekta za mfumo huu, i.e. kwa kila vekta kuna nambari za kweli Usawa huu unaitwa mtengano wa vekta kulingana na msingi, na nambari zinaitwa kuratibu za vector kuhusiana na msingi(au katika msingi) .

Theorem (juu ya upekee wa upanuzi kwa heshima na msingi). Kila vekta kwenye nafasi inaweza kupanuliwa kuwa msingi kwa njia pekee, i.e. kuratibu za kila vekta kwa msingi huamuliwa bila utata.

Mfumo wa vector unaitwa tegemezi kwa mstari, ikiwa kuna nambari ambazo angalau moja ni tofauti na sifuri, ili kwamba usawa https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src= > >.

Ikiwa usawa huu umeridhika tu katika kesi wakati wote , basi mfumo wa vekta unaitwa kujitegemea linearly.

Nadharia. Mfumo wa vector utafanya tegemezi kwa mstari ikiwa na tu ikiwa angalau moja ya vekta zake ni mchanganyiko wa mstari wa zingine.

Mfano 1. Polynomial ni muunganisho wa kimstari wa polimanomia https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24">. Ponomia huunda mfumo unaojitegemea kimstari, tangu polynomial https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.

Mfano 2. Mfumo wa matrix, , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> ni huru kimstari, kwa kuwa mchanganyiko wa mstari ni sawa na sifuri tumbo tu katika kesi wakati https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text /78/624 /images/image022_26.gif" width="40" height="21"> tegemezi kimstari.

Suluhisho.

Wacha tutengeneze mchanganyiko wa mstari wa vekta hizi https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" urefu=" 22">.

Kusawazisha kuratibu za jina moja vectors sawa, tunapata https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">

Hatimaye tunapata

Na

Mfumo una moja tu ufumbuzi usio na maana, kwa hivyo mchanganyiko wa mstari wa vekta hizi ni sawa na sifuri tu katika kesi wakati coefficients zote ni sawa na sifuri. Kwa hiyo, mfumo huu wa vectors ni linearly kujitegemea.

Mfano 4. Vekta zinajitegemea kwa mstari. Mifumo ya vekta itakuwaje?

a).;

b).?

Suluhisho.

a). Wacha tufanye mchanganyiko wa mstari na tufananishe na sifuri

Kwa kutumia mali ya utendakazi na vekta kwenye nafasi ya mstari, tunaandika tena usawa wa mwisho katika fomu.

Kwa kuwa vekta zinajitegemea kimstari, viweti lazima viwe sawa na sufuri, yaani.gif" width="12" height="23 src=">

Mfumo unaotokana wa equations una suluhisho la kipekee lisilo na maana .

Tangu usawa (*) inatekelezwa tu wakati https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> – huru kwa mstari;

b). Wacha tufanye usawa https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)

Kwa kutumia hoja sawa, tunapata

Kutatua mfumo wa equations kwa njia ya Gauss, tunapata

au

Mfumo wa mwisho una seti isiyo na mwisho suluhu https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. Kwa hivyo, kuna seti isiyo ya sufuri ya viambajengo ambavyo usawa anashikilia (**) . Kwa hiyo, mfumo wa vectors - tegemezi kwa mstari.

Mfano 5 Mfumo wa vekta unajitegemea kimstari, na mfumo wa vekta hutegemea kimstari..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)

Katika usawa (***) . Hakika, saa , mfumo ungekuwa tegemezi linearly.

Kutoka kwa uhusiano (***) tunapata au Hebu kuashiria .

Tunapata

Kazi za uamuzi wa kujitegemea(katika hadhira)

1. Mfumo ulio na vekta sifuri unategemea mstari.

2. Mfumo unaojumuisha vector moja A, inategemea kimstari ikiwa na tu ikiwa, a=0.

3. Mfumo unaojumuisha vekta mbili hutegemea mstari ikiwa na tu ikiwa vekta ni sawia (hiyo ni, moja yao hupatikana kutoka kwa nyingine kwa kuzidisha kwa nambari).

4. Ikiwa k ni ya mstari mfumo tegemezi ongeza vekta, unapata mfumo tegemezi wa mstari.

5. Ikiwa kutoka kwa mstari mfumo wa kujitegemea ondoa vekta, basi mfumo unaotokana wa vekta ni huru kwa mstari.

6. Ikiwa mfumo S inajitegemea kwa mstari, lakini inakuwa tegemezi kwa mstari wakati wa kuongeza vekta b, kisha vekta b imeonyeshwa kwa mstari kupitia vekta za mfumo S.

c). Mfumo wa matrices , , katika nafasi ya matrices ya pili.

10. Wacha mfumo wa veta a,b,c nafasi ya vekta inajitegemea kwa mstari. Thibitisha uhuru wa mstari mifumo ifuatayo vekta:

a).a+b, b, c.

b).a+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">– nambari ya kiholela

c).a+b, a+c, b+c.

11. Hebu a,b,c- vector tatu kwenye ndege ambayo pembetatu inaweza kuundwa. Je, vekta hizi zitakuwa tegemezi kwa mstari?

12. Vekta mbili zinatolewa a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Tafuta vekta mbili zaidi zenye sura nne a3 naa4 ili mfumo a1,a2,a3,a4 alikuwa anajitegemea kwa mstari .