Tafuta eigenvectors ya matrix. Mfumo wa milinganyo ya mstari wa homogeneous

Eigenvector ya matrix ya mraba ni ile ambayo, ikizidishwa na matrix fulani, husababisha vekta ya collinear. Kwa maneno rahisi, wakati wa kuzidisha matrix na eigenvector, mwisho hubakia sawa, lakini huongezeka kwa idadi fulani.

Ufafanuzi

Eigenvector ni vekta isiyo ya sifuri V, ambayo, ikizidishwa na matrix ya mraba M, inakuwa yenyewe kuongezeka kwa nambari fulani λ. Katika nukuu ya algebra inaonekana kama:

M × V = λ × V,

ambapo λ ni eigenvalue ya matrix M.

Hebu tuzingatie mfano wa nambari. Kwa urahisi wa kurekodi, nambari kwenye tumbo zitatenganishwa na semicolon. Wacha tuwe na matrix:

M = 0; 4;
6; 10.

Wacha tuizidishe kwa vekta ya safu:

V = -2;

Tunapozidisha matrix kwa vector ya safu, tunapata pia vector ya safu. Mkali lugha ya hisabati Njia ya kuzidisha matrix 2 × 2 na vekta ya safu inaweza kuonekana kama hii:

M × V = M11 × V11 + M12 × V21;
M21 × V11 + M22 × V21.

M11 ina maana ya kipengele cha matrix M kilicho katika safu ya kwanza na safu ya kwanza, na M22 inamaanisha kipengele kilicho katika safu ya pili na safu ya pili. Kwa matrix yetu, vipengele hivi ni sawa na M11 = 0, M12 = 4, M21 = 6, M22 10. Kwa vector ya safu, maadili haya ni sawa na V11 = -2, V21 = 1. Kulingana na fomula hii, tunapata matokeo yafuatayo ya bidhaa ya matrix ya mraba na vekta:

M × V = 0 × (-2) + (4) × (1) = 4;
6 × (-2) + 10 × (1) = -2.

Kwa urahisi, hebu tuandike vekta ya safu kwa safu. Kwa hivyo, tulizidisha matrix ya mraba na vekta (-2; 1), na kusababisha vekta (4; -2). Ni wazi, hii ni vekta sawa iliyozidishwa na λ = -2. Lambda ndani kwa kesi hii inaashiria eigenvalue ya matrix.

Eigenvector ya matrix ni vekta ya collinear, ambayo ni, kitu ambacho hakibadilishi msimamo wake katika nafasi wakati kinapozidishwa na tumbo. dhana ya collinearity katika algebra ya vekta sawa na neno usambamba katika jiometri. Katika tafsiri ya kijiometri vekta za collinear- Hizi ni sehemu zilizoelekezwa sambamba za urefu tofauti. Tangu wakati wa Euclid, tunajua kuwa mstari mmoja una idadi isiyo na kikomo ya mistari inayofanana, kwa hivyo ni busara kudhani kuwa kila matrix ina nambari isiyo na kikomo. eigenvectors.

Kutoka kwa mfano uliopita ni wazi kwamba eigenvectors inaweza kuwa (-8; 4), na (16; -8), na (32, -16). Hizi zote ni vekta za collinear zinazolingana na eigenvalue λ = -2. Wakati wa kuzidisha matrix ya asili na vekta hizi, bado tutaishia na vekta ambayo inatofautiana na asili kwa mara 2. Ndiyo sababu, wakati wa kutatua matatizo ya kutafuta eigenvector, ni muhimu kupata tu vitu vya vector vya kujitegemea vya mstari. Mara nyingi, kwa matrix ya n × n, kuna n idadi ya eigenvectors. Calculator yetu imeundwa kwa ajili ya uchambuzi wa matrices ya mraba ya pili, hivyo karibu kila mara matokeo yatapata eigenvectors mbili, isipokuwa kwa kesi wakati wao sanjari.

Katika mfano hapo juu, tulijua eigenvector ya matrix ya asili mapema na kuamua wazi nambari ya lambda. Walakini, katika mazoezi, kila kitu hufanyika kwa njia nyingine kote: eigenvalues hupatikana kwanza na kisha tu eigenveector.

Algorithm ya suluhisho

Wacha tuangalie matrix ya asili M tena na tujaribu kupata eigenveekta zake zote mbili. Kwa hivyo matrix inaonekana kama:

M = 0; 4;
6; 10.

Kwanza tunahitaji kuamua eigenvalue λ, ambayo inahitaji kuhesabu kibainishi cha matrix ifuatayo:

(0 − λ); 4;
6; (10 − λ).

Matrix hii kupatikana kwa kutoa isiyojulikana λ kutoka kwa vipengele kwenye diagonal kuu. Kiamuzi kimedhamiriwa kwa kutumia fomula ya kawaida:

detA = M11 × M21 - M12 × M22
detA = (0 − λ) × (10 − λ) − 24

Kwa kuwa vekta yetu lazima iwe isiyo sifuri, tunakubali mlinganyo unaotokana kuwa tegemezi kimstari na tunasawazisha kibainishi chetu cha detA hadi sufuri.

(0 − λ) × (10 − λ) − 24 = 0

Hebu tufungue mabano na tupate mlingano wa tabia matrices:

λ 2 − 10 − 24 = 0

Hii ni kiwango mlinganyo wa quadratic, ambayo inahitaji kutatuliwa kwa njia ya kibaguzi.

D = b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

Mzizi wa kibaguzi ni sqrt(D) = 14, kwa hivyo λ1 = -2, λ2 = 12. Sasa kwa kila thamani ya lambda tunahitaji kupata eigenvector. Hebu tueleze mgawo wa mfumo kwa λ = -2.

M - λ × E = 2; 4;
6; 12.

Katika fomula hii, E ni matrix ya utambulisho. Kulingana na matrix inayosababisha, tunaunda mfumo milinganyo ya mstari:

2x + 4y = 6x + 12y,

ambapo x na y ni vipengele vya eigenvector.

Wacha tukusanye X zote upande wa kushoto na Y zote upande wa kulia. Ni wazi - 4x = 8y. Gawanya usemi kwa - 4 na upate x = -2y. Sasa tunaweza kuamua eigenvector ya kwanza ya matrix, kwa kuchukua maadili yoyote ya haijulikani (kumbuka infinity ya eigenvectors tegemezi linearly). Hebu tuchukue y = 1, kisha x = -2. Kwa hivyo, eigenvector ya kwanza inaonekana kama V1 = (–2; 1). Rudi mwanzoni mwa makala. Ilikuwa ni kitu hiki cha vekta ambacho tulizidisha matrix kwa kuonyesha dhana ya eigenvector.

Sasa wacha tupate eigenvector ya λ = 12.

M - λ × E = -12; 4
6; -2.

Wacha tuunde mfumo sawa wa milinganyo ya mstari;

-12x + 4y = 6x - 2y
-18x = -6y
3x = y.

Sasa tunachukua x = 1, kwa hiyo y = 3. Kwa hiyo, eigenvector ya pili inaonekana kama V2 = (1; 3). Wakati wa kuzidisha matrix ya asili kwa vector iliyotolewa, matokeo yatakuwa daima vector sawa na 12. Hii inahitimisha algorithm ya ufumbuzi. Sasa unajua jinsi ya kuamua mwenyewe eigenvector ya matrix.

kibainishi;
kufuatilia, yaani, jumla ya vipengele kwenye diagonal kuu;
cheo, yaani kiasi cha juu safu mlalo/nguzo zinazojitegemea kwa mstari.

Mpango huo unafanya kazi kulingana na algorithm hapo juu, kufupisha mchakato wa ufumbuzi iwezekanavyo. Ni muhimu kusema kwamba katika mpango wa lambda huteuliwa na barua "c". Wacha tuangalie mfano wa nambari.

Mfano wa jinsi programu inavyofanya kazi

Wacha tujaribu kuamua eigenveekta kwa matrix ifuatayo:

M = 5; 13;
4; 14.

Wacha tuingize maadili haya kwenye seli za calculator na tupate jibu kwa fomu ifuatayo:

Kiwango cha Matrix: 2;
Kiamuzi cha Matrix: 18;
Ufuatiliaji wa Matrix: 19;
Mahesabu ya eigenvector: c 2 - 19.00c + 18.00 (equation ya tabia);
Hesabu ya Eigenvector: 18 (thamani ya kwanza ya lambda);
Hesabu ya Eigenvector: 1 (thamani ya pili ya lambda);
Mfumo wa equations kwa vector 1: -13x1 + 13y1 = 4x1 - 4y1;
Mfumo wa equations kwa vector 2: 4x1 + 13y1 = 4x1 + 13y1;
Eigenvector 1: (1; 1);
Eigenvector 2: (-3.25; 1).

Kwa hivyo, tulipata eigenveekta mbili huru za mstari.

Hitimisho

Aljebra ya mstari na jiometri ya uchanganuzi ni masomo ya kawaida kwa mwanafunzi yeyote wa kwanza utaalam wa kiufundi. Idadi kubwa ya vectors na matrices ni ya kutisha, na katika mahesabu hayo magumu ni rahisi kufanya makosa. Mpango wetu utawaruhusu wanafunzi kuangalia mahesabu yao au kutatua kiotomatiki tatizo la kutafuta eigenvector. Kuna vikokotoo vingine vya aljebra katika orodha yetu; vitumie katika masomo au kazi yako.

Jinsi ya kuingiza fomula za hisabati kwa tovuti?

Ikiwa utahitaji kuongeza fomula moja au mbili za hesabu kwenye ukurasa wa wavuti, basi njia rahisi zaidi ya kufanya hivyo ni kama ilivyoelezewa katika kifungu hicho: fomula za hesabu huingizwa kwa urahisi kwenye wavuti kwa njia ya picha zinazotolewa kiotomatiki na Wolfram Alpha. . Mbali na unyenyekevu, hii mbinu ya ulimwengu wote itasaidia kuboresha mwonekano wa tovuti injini za utafutaji. Imekuwa ikifanya kazi kwa muda mrefu (na, nadhani, itafanya kazi milele), lakini tayari imepitwa na wakati.

Ikiwa unatumia fomula za hesabu kila wakati kwenye wavuti yako, basi ninapendekeza utumie MathJax - maktaba maalum ya JavaScript inayoonyesha. nukuu ya hisabati katika vivinjari kwa kutumia MathML, LaTeX au ASCIIMAthML markup.

Kuna njia mbili za kuanza kutumia MathJax: (1) kwa kutumia msimbo rahisi, unaweza kuunganisha kwa haraka hati ya MathJax kwenye tovuti yako, ambayo wakati sahihi kupakia moja kwa moja kutoka kwa seva ya mbali (orodha ya seva); (2) pakua hati ya MathJax kutoka kwa seva ya mbali hadi kwenye seva yako na uiunganishe na kurasa zote za tovuti yako. Njia ya pili - ngumu zaidi na inayotumia wakati - itaharakisha upakiaji wa kurasa za tovuti yako, na ikiwa seva kuu ya MathJax haitapatikana kwa muda kwa sababu fulani, hii haitaathiri tovuti yako mwenyewe kwa njia yoyote. Licha ya faida hizi, nilichagua njia ya kwanza kwa kuwa ni rahisi, haraka na hauhitaji ujuzi wa kiufundi. Fuata mfano wangu, na kwa dakika 5 tu utaweza kutumia vipengele vyote vya MathJax kwenye tovuti yako.

Unaweza kuunganisha hati ya maktaba ya MathJax kutoka kwa seva ya mbali kwa kutumia chaguo mbili za msimbo zilizochukuliwa kutoka kwa tovuti kuu ya MathJax au kwenye ukurasa wa nyaraka:

Moja ya chaguo hizi za msimbo inahitaji kunakiliwa na kubandikwa kwenye msimbo wa ukurasa wako wa wavuti, ikiwezekana kati ya lebo na au mara baada ya lebo. Kulingana na chaguo la kwanza, MathJax hupakia haraka na kupunguza kasi ya ukurasa. Lakini chaguo la pili hufuatilia kiotomatiki na kupakia matoleo ya hivi karibuni ya MathJax. Ukiingiza msimbo wa kwanza, utahitaji kusasishwa mara kwa mara. Ukiingiza msimbo wa pili, kurasa zitapakia polepole zaidi, lakini hutahitaji kufuatilia mara kwa mara masasisho ya MathJax.

Njia rahisi zaidi ya kuunganisha MathJax ni katika Blogger au WordPress: kwenye paneli dhibiti ya tovuti, ongeza wijeti iliyoundwa ili kuingiza msimbo wa JavaScript wa kampuni nyingine, nakili toleo la kwanza au la pili la msimbo wa upakuaji uliowasilishwa hapo juu ndani yake, na uweke wijeti karibu. hadi mwanzo wa template (kwa njia, hii sio lazima kabisa , kwani maandishi ya MathJax yanapakiwa asynchronously). Ni hayo tu. Sasa jifunze sintaksia ya ghafi ya MathML, LaTeX, na ASCIIMAthML, na uko tayari kuingiza fomula za hisabati kwenye kurasa za wavuti za tovuti yako.

Fractal yoyote inajengwa kulingana na sheria fulani, ambayo hutumiwa mara kwa mara idadi isiyo na kikomo ya nyakati. Kila wakati kama huo huitwa kurudia.

Algorithm ya kurudia ya kuunda sifongo cha Menger ni rahisi sana: mchemraba wa asili ulio na upande wa 1 umegawanywa na ndege sambamba na nyuso zake katika cubes 27 sawa. Mchemraba mmoja wa kati na cubes 6 karibu nayo kando ya nyuso huondolewa kutoka kwake. Matokeo yake ni seti inayojumuisha cubes 20 ndogo iliyobaki. Kufanya vivyo hivyo na kila moja ya cubes hizi, tunapata seti inayojumuisha cubes 400 ndogo. Kuendeleza mchakato huu bila mwisho, tunapata sifongo cha Menger.

www.site hukuruhusu kupata. Tovuti hufanya hesabu. Katika sekunde chache seva itatoa suluhisho sahihi. Equation ya tabia kwa matrix itakuwa usemi wa algebra, iliyopatikana na sheria ya kuhesabu kiamua cha matrix ya tumbo, wakati kando ya diagonal kuu kutakuwa na tofauti katika maadili ya vipengele vya diagonal na kutofautiana. Wakati wa kukokotoa mlingano wa sifa kwa matriki mtandaoni, kila kipengele cha matriki kitazidishwa na vipengele vingine vinavyolingana vya matriki. Unaweza kuipata mtandaoni kwa matrix ya mraba pekee. Uendeshaji wa kutafuta equation ya tabia kwa matrix ya mtandaoni hupunguzwa kwa kuhesabu jumla ya algebra bidhaa ya vipengele vya matrix kama matokeo ya kupata kibainishi cha matriki, kwa madhumuni ya kubainisha mlingano wa sifa wa matriki mtandaoni. Operesheni hii inachukua mahali maalum katika nadharia ya matrix, inaruhusu mtu kupata eigenvalues na vekta kwa kutumia mizizi. Kazi ya kutafuta mlingano wa tabia ya matrix mtandaoni ni kuzidisha vipengele vya tumbo na kisha kujumlisha bidhaa hizi kulingana na sheria fulani. www.site hupata mlingano wa sifa kwa matriki ya kipimo fulani mtandaoni. Kukokotoa mlinganyo wa tabia wa matriki mtandaoni kwa kipimo fulani ni kutafuta polinomia yenye viambatanisho vya nambari au ishara, vinavyopatikana kulingana na kanuni ya kukokotoa kiambishi cha matrix - kama jumla ya bidhaa za vipengele vinavyolingana vya matrix, kwa madhumuni ya kubainisha mlingano wa tabia kwa matrix mtandaoni. Kupata polinomia kwa heshima na kigezo cha matriki ya mraba, kama ufafanuzi wa mlingano wa sifa wa matriki, ni jambo la kawaida katika nadharia ya matriki. Thamani ya mizizi ya polynomial ya equation ya tabia kwa matrix ya mtandaoni hutumiwa kuamua eigenvectors na. eigenvalues kwa matrix. Kwa kuongezea, ikiwa kiashiria cha matrix ni sawa na sifuri, basi equation ya tabia ya matrix bado itakuwepo, tofauti na matrix ya kinyume. Ili kuhesabu equation ya tabia kwa matrix au kupata milinganyo ya tabia kwa matrices kadhaa mara moja, unahitaji kutumia muda mwingi na jitihada, wakati seva yetu itapata equation ya tabia ya matrix mtandaoni katika suala la sekunde. Katika kesi hii, jibu la kutafuta equation ya tabia ya matrix ya mtandaoni itakuwa sahihi na kwa usahihi wa kutosha, hata kama nambari wakati wa kupata equation ya tabia ya matrix ya mtandaoni itakuwa isiyo na maana. Kwenye tovuti www.site, maingizo ya ishara katika vipengele vya matrix yanaruhusiwa, yaani, equation ya tabia ya matrix ya mtandaoni inaweza kuwakilishwa kwa fomu ya jumla ya ishara wakati wa kuhesabu equation ya tabia ya matrix ya mtandaoni. Ni muhimu kuangalia jibu lililopatikana wakati wa kusuluhisha shida ya kupata mlingano wa tabia kwa matrix mkondoni kwa kutumia tovuti www.site. Wakati wa kufanya operesheni ya kuhesabu polynomial - equation ya tabia ya matrix, lazima uwe mwangalifu na umakini sana wakati wa kutatua shida hii. Kwa upande mwingine, tovuti yetu itakusaidia kuangalia suluhisho lako juu ya mada ya equation ya tabia ya matrix mkondoni. Ikiwa huna muda wa kuangalia kwa muda mrefu matatizo yaliyotatuliwa, basi www.site hakika itakuwa chombo rahisi cha kuangalia wakati wa kutafuta na kuhesabu equation ya tabia ya matrix mtandaoni.

". Sehemu ya kwanza inaweka masharti ambayo ni muhimu kidogo kwa kuelewa kemia, na sehemu ya pili ina ukweli ambao unahitaji kujua kwa uelewa wa kina wa mbinu. uchambuzi wa multivariate. Wasilisho linaonyeshwa kwa mifano iliyofanywa katika kitabu cha kazi cha Excel Matrix.xls, ambayo inaambatana na hati hii.

Viungo vya mifano vimewekwa kwenye maandishi kama vitu vya Excel. Mifano hii ni ya kufikirika kwa asili, haijafungwa kwa njia yoyote na kazi kemia ya uchambuzi. Mifano halisi Matumizi ya aljebra ya matriki katika kemia yanajadiliwa katika maandishi mengine yanayohusu aina mbalimbali za matumizi ya kemia.

Vipimo vingi vilivyofanywa katika kemia ya uchambuzi sio moja kwa moja, lakini isiyo ya moja kwa moja. Hii ina maana kwamba katika jaribio, badala ya thamani ya mchambuzi C (mkusanyiko), thamani nyingine inapatikana. x(signal), kuhusiana lakini si sawa na C, i.e. x(C) ≠ C. Kama sheria, aina ya utegemezi x(C) haijulikani, lakini kwa bahati nzuri katika kemia ya uchanganuzi vipimo vingi ni sawia. Hii inamaanisha kuwa kwa kuongezeka kwa mkusanyiko wa C ndani a nyakati, ishara X itaongezeka kwa kiasi sawa, i.e. x(a C) = a x(C). Kwa kuongezea, ishara pia ni nyongeza, kwa hivyo ishara kutoka kwa sampuli ambayo vitu viwili vilivyo na viwango C 1 na C 2 vitakuwapo. sawa na jumla ishara kutoka kwa kila sehemu, i.e. x(C 1 + C 2) = x(C 1)+ x(C 2). Uwiano na nyongeza pamoja toa mstari. Mifano mingi inaweza kutolewa ili kuonyesha kanuni ya mstari, lakini inatosha kutaja hizo mbili zaidi mifano inayong'aa- chromatography na spectroscopy. Kipengele cha pili kilichopo katika jaribio la kemia ya uchanganuzi ni njia nyingi. Vifaa vya kisasa vya uchambuzi wakati huo huo hupima ishara kwa njia nyingi. Kwa mfano, ukubwa wa maambukizi ya mwanga hupimwa kwa urefu wa wavelengths kadhaa mara moja, i.e. mbalimbali. Kwa hiyo, katika jaribio tunashughulika na ishara nyingi x 1 , x 2 ,...., x n, sifa ya seti ya viwango C 1, C 2, ..., C m ya vitu vilivyopo katika mfumo unaojifunza.

Mchele. 1 Spectra

Kwa hivyo, majaribio ya uchanganuzi yana sifa ya mstari na multidimensionality. Kwa hivyo, ni rahisi kuzingatia data ya majaribio kama vekta na matiti na kuibadilisha kwa kutumia vifaa vya aljebra ya matrix. Ufanisi wa mbinu hii unaonyeshwa na mfano ulioonyeshwa, ambao unawasilisha spectra tatu zilizochukuliwa kwa urefu wa mawimbi 200 kutoka 4000 hadi 4796 cm -1. Mwonekano wa kwanza (x 1) na wa pili (x 2) ulipatikana kwa sampuli za kawaida ambapo viwango vya vitu viwili A na B vinajulikana: katika sampuli ya kwanza [A] = 0.5, [B] = 0.1, na katika sampuli ya pili [A] = 0.2, [B] = 0.6. Ni nini kinachoweza kusema juu ya sampuli mpya, isiyojulikana, wigo ambao umeteuliwa x 3?

Hebu tuchunguze vielelezo vitatu vya majaribio x 1, x 2 na x 3 kama vivekta vitatu vya mwelekeo wa 200. Kwa kutumia aljebra ya mstari, tunaweza kuonyesha kwa urahisi kwamba x 3 = 0.1 x 1 +0.3 x 2, kwa hiyo, katika sampuli ya tatu, vitu A pekee. na B ni wazi kuwepo katika viwango [A] = 0.5×0.1 + 0.2×0.3 = 0.11 na [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Taarifa za msingi 1.1 Matrices

Matrix inayoitwa meza ya mstatili ya nambari, kwa mfano

Mchele. 2 Matrix

Matrices yanaonyeshwa kwa herufi kubwa kubwa (A) na mambo yao kwa sambamba herufi ndogo na fahirisi, i.e. a ij. Fahirisi ya kwanza inahesabu safu, na ya pili - safu. Katika kemia ni desturi kuashiria thamani ya juu faharasa yenye herufi sawa na faharasa yenyewe, lakini yenye herufi kubwa. Kwa hivyo, matrix A inaweza pia kuandikwa kama ( a ij , i = 1,..., I; j = 1,..., J) Kwa mfano matrix I = 4, J= 3 na a 23 = −7.5.

Jozi ya nambari I Na J inaitwa mwelekeo wa matrix na inaonyeshwa kama I× J. Mfano wa matrix katika kemia ni seti ya spectra iliyopatikana kwa I sampuli kwa J urefu wa mawimbi.

1.2. Shughuli rahisi zaidi na matrices

Matrices inaweza kuwa zidisha kwa nambari. Katika kesi hii, kila kipengele kinazidishwa na nambari hii. Kwa mfano -

Mchele. 3 Kuzidisha matrix kwa nambari

Matrices mawili ya mwelekeo sawa yanaweza kuwa kipengele kwa kipengele kunja Na ondoa. Kwa mfano,

Mchele. 4 Nyongeza ya Matrix

Kama matokeo ya kuzidisha kwa nambari na kuongeza, matrix ya kipimo sawa hupatikana.

Matrix ya sifuri ni matrix inayojumuisha sifuri. Inaashiria O. Ni wazi, A +O = A, A −A = O na 0A = O.

Matrix inaweza kuwa transpose. Wakati wa operesheni hii, matrix hupinduliwa, i.e. safu na nguzo hubadilishwa. Ubadilishaji unaonyeshwa kwa msingi, A" au hati ndogo A t. Kwa hivyo, ikiwa A = ( a ij , i = 1,..., I; j = 1,...,J), kisha A t = ( a ji , j = 1,...,J; i = 1,..., I) Kwa mfano

Mchele. 5 Ubadilishaji wa Matrix

Ni dhahiri kwamba (A t) t = A, (A + B) t = A t + B t.

1.3. Kuzidisha kwa tumbo

Matrices inaweza kuwa zidisha, lakini tu ikiwa wana vipimo vinavyofaa. Kwa nini hii ni hivyo itakuwa wazi kutoka kwa ufafanuzi. Bidhaa ya tumbo A, mwelekeo I× K, na tumbo B, mwelekeo K× J, inayoitwa tumbo C, mwelekeo I× J, ambao vipengele vyake ni namba

Kwa hivyo, kwa bidhaa AB ni muhimu kwamba idadi ya safu wima katika matrix ya kushoto A iwe sawa na idadi ya safu katika matrix B ya kulia. Mfano wa bidhaa ya matrix -

Mtini.6 Bidhaa ya matrices

Kanuni ya kuzidisha matrix inaweza kutengenezwa kama ifuatavyo. Ili kupata kipengele cha matrix C kwenye makutano i- mstari na j safu ya th ( c ij) lazima izidishwe kipengele kwa kipengele i safu mlalo ya matrix ya kwanza A imewashwa j th safu ya matrix ya pili B na ongeza matokeo yote. Kwa hivyo katika mfano ulioonyeshwa, kipengee kutoka safu ya tatu na safu ya pili hupatikana kama jumla ya bidhaa za busara za safu ya tatu A na safu ya pili B.

Mtini.7 Kipengele cha bidhaa ya matrices

Bidhaa ya matrices inategemea utaratibu, i.e. AB ≠ BA, angalau kwa sababu za kimaumbile. Wanasema kuwa sio ya kubadilisha. Hata hivyo, bidhaa ya matrices ni associative. Hii ina maana kwamba ABC = (AB)C = A(BC). Kwa kuongeza, pia ni kusambaza, i.e. A (B +C) = AB +AC. Ni wazi AO = O.

1.4. Matrices ya mraba

Ikiwa idadi ya safu wima ni sawa na idadi ya safu mlalo zake ( I = J=N), basi matrix kama hiyo inaitwa mraba. Katika sehemu hii tutazingatia matrices vile tu. Kati ya matrices haya, matrices yenye mali maalum yanaweza kutofautishwa.

Mtu mmoja matrix (iliyoashiria I, na wakati mwingine E) ni matrix ambayo vipengele vyote ni sawa na sifuri, isipokuwa ya diagonal, ambayo ni sawa na 1, i.e.

Ni wazi AI = IA = A.

Matrix inaitwa diagonal, ikiwa vipengele vyake vyote isipokuwa vile vya diagonal ( a ii) ni sawa na sifuri. Kwa mfano

Mchele. 8 tumbo la diagonal

Matrix A inaitwa juu pembetatu, ikiwa vipengele vyake vyote vilivyo chini ya diagonal ni sawa na sifuri, i.e. a ij= 0, saa i>j. Kwa mfano

Mchele. 9 Juu matrix ya pembe tatu

Matrix ya pembetatu ya chini imefafanuliwa vile vile.

Matrix A inaitwa ulinganifu, ikiwa A t = A . Kwa maneno mengine a ij = a ji. Kwa mfano

Mchele. 10 matrix ya ulinganifu

Matrix A inaitwa ya orthogonal, Kama

A t A = AA t = mimi.

Matrix inaitwa kawaida Kama

1.5. Kufuatilia na kuamua

Inayofuata matrix ya mraba A (inayoonyeshwa na Tr(A) au Sp(A)) ni jumla ya vipengele vyake vya mshazari,

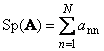
Kwa mfano,

Mchele. 11 Ufuatiliaji wa Matrix

Ni dhahiri kwamba

Sp(α A ) = α Sp(A) na

Sp(A +B) = Sp(A)+ Sp(B).

Inaweza kuonyeshwa hivyo

Sp(A) = Sp(A t), Sp(I) = N,

na pia kwamba

Sp(AB) = Sp(BA).

Mwingine sifa muhimu matrix ya mraba ni yake kibainishi(iliyoashiria det(A )). Ufafanuzi wa kibainishi katika kesi ya jumla ngumu kabisa, kwa hiyo tutaanza na chaguo rahisi zaidi - matrix A ya mwelekeo (2x2). Kisha

Kwa matrix ya (3×3) kibainishi kitakuwa sawa na

Katika kesi ya matrix ( N× N) kiambishi kinakokotolewa kama jumla 1·2·3· ... · N= N! masharti, ambayo kila moja ni sawa

Fahirisi k 1 , k 2 ,..., k N hufafanuliwa kama vibali vyote vinavyowezekana vilivyoagizwa r nambari katika seti (1, 2, ..., N) Kuhesabu kiashiria cha tumbo ni utaratibu mgumu, ambao kwa mazoezi unafanywa kwa kutumia programu maalum. Kwa mfano,

Mchele. 12 Kiamuzi cha Matrix

Wacha tuangalie mali dhahiri tu:

det(I) = 1, det(A ) = det(A t),

det(AB) = det(A)det(B).

1.6. Vekta

Ikiwa tumbo lina safu moja tu ( J= 1), basi kitu kama hicho kinaitwa vekta. Kwa usahihi, vekta ya safu. Kwa mfano

Mtu anaweza pia kuzingatia matrices yenye safu moja, kwa mfano

Kitu hiki pia ni vector, lakini vekta ya safu. Wakati wa kuchambua data, ni muhimu kuelewa ni vekta gani tunashughulikia - safu au safu. Kwa hivyo wigo uliochukuliwa kwa sampuli moja unaweza kuzingatiwa kama vekta ya safu. Kisha seti ya nguvu za spectral katika urefu fulani wa wimbi kwa sampuli zote inapaswa kutibiwa kama vekta ya safu.

Kipimo cha vector ni idadi ya vipengele vyake.

Ni wazi kwamba vector yoyote ya safu inaweza kugeuka kuwa vector ya mstari kwa uhamisho, i.e.

Katika hali ambapo sura ya vector haijainishwa hasa, lakini inasemekana tu kuwa vector, basi wanamaanisha vector ya safu. Pia tutazingatia kanuni hii. Vekta inaonyeshwa na herufi ndogo, iliyo wima, na ya ujasiri. Vekta ya sifuri ni vekta ambayo vipengele vyote ni sifuri. Imeteuliwa 0.

1.7. Shughuli rahisi zaidi na vekta

Vekta zinaweza kuongezwa na kuzidishwa na nambari kwa njia sawa na matrices. Kwa mfano,

Mchele. 13 Uendeshaji na vekta

Vekta mbili x na y zinaitwa colinear, ikiwa kuna nambari α kama hiyo

1.8. Bidhaa za vekta

Vekta mbili za kipimo sawa N inaweza kuzidishwa. Wacha kuwe na vekta mbili x = ( x 1 , x 2 ,...,x N) t na y = ( y 1 , y 2 ,...,y N) t. Kwa kuongozwa na sheria ya kuzidisha safu-kwa-safu, tunaweza kutunga bidhaa mbili kutoka kwao: x t y na xy t. Kazi ya kwanza

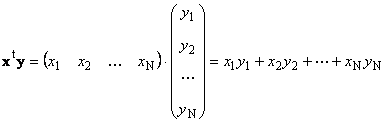
kuitwa scalar au ndani. Matokeo yake ni nambari. Alama (x ,y )= x t y pia inatumika kwa ajili yake. Kwa mfano,

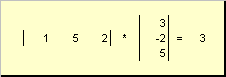
Mchele. 14 Bidhaa ya ndani (scalar).

Kipande cha pili

kuitwa ya nje. Matokeo yake ni matrix ya mwelekeo ( N× N) Kwa mfano,

Mchele. 15 Kazi ya nje

Vekta, bidhaa ya scalar ambayo ni sawa na sifuri huitwa ya orthogonal.

1.9. Vector kawaida

Bidhaa ya scalar ya vector yenyewe inaitwa mraba wa scalar. Thamani hii

inafafanua mraba urefu vekta x. Ili kuonyesha urefu (pia inaitwa kawaida vekta) nukuu inatumika

Kwa mfano,

Mchele. 16 Vector kawaida

Vekta ya urefu wa kitengo (||x || = 1) inaitwa kawaida. Vector isiyo ya sifuri (x ≠ 0) inaweza kuwa ya kawaida kwa kuigawanya kwa urefu wake, i.e. x = ||x || (x/ ||x ||) = ||x || e. Hapa e = x/ ||x || - vector ya kawaida.

Vekta huitwa orthonormal ikiwa zote ni za kawaida na za jozi za orthogonal.

1.10. Pembe kati ya vekta

Bidhaa ya scalar huamua na konaφ kati ya vekta mbili x na y

Ikiwa vectors ni orthogonal, basi cosφ = 0 na φ = π/2, na ikiwa ni colinear, basi cosφ = 1 na φ = 0.

1.11. Uwakilishi wa Vekta ya tumbo

Kila matrix A ya ukubwa I× J inaweza kuwakilishwa kama seti ya vekta

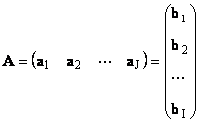
Hapa kila vekta a j ni j safu wima, na vekta ya safu b i ni i safu ya th ya matrix A

1.12. Vekta zinazotegemea mstari

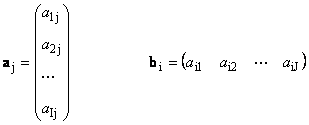
Vekta za ukubwa sawa ( N) inaweza kuongezwa na kuzidishwa na nambari, kama matrices. Matokeo yake yatakuwa vector ya mwelekeo sawa. Acha kuwe na vekta kadhaa za kipimo sawa x 1, x 2,..., x K na idadi sawa ya nambari α α 1, α 2,..., α K. Vekta

y = α 1 x 1 + α 2 x 2 +...+ α K x K

kuitwa mchanganyiko wa mstari vekta x k .

Ikiwa kuna nambari zisizo za sifuri α k ≠ 0, k = 1,..., K kwamba y = 0, basi seti kama hiyo ya vekta x k kuitwa tegemezi kwa mstari. Vinginevyo, vekta zinasemekana kuwa huru kwa mstari. Kwa mfano, vekta x 1 = (2, 2) t na x 2 = (-1, −1) t zinategemeana, kwa sababu. x 1 +2x 2 = 0

1.13. Kiwango cha Matrix

Fikiria seti ya K vekta x 1 , x 2 ,...,x K vipimo N. Kiwango cha mfumo huu wa vekta ni idadi ya juu ya vekta zinazojitegemea zenye mstari. Kwa mfano katika seti

kuna vekta mbili tu zinazojitegemea kwa mstari, kwa mfano x 1 na x 2, kwa hivyo kiwango chake ni 2.

Ni wazi, ikiwa kuna vekta zaidi kwenye seti kuliko kipimo chao ( K>N), basi zinategemeana kwa mstari.

Kiwango cha Matrix(iliyoonyeshwa na cheo(A)) ni cheo cha mfumo wa vekta ambayo inajumuisha. Ingawa matrix yoyote inaweza kuwakilishwa kwa njia mbili (safu wima au vekta za safu), hii haiathiri thamani ya kiwango, kwa sababu.

1.14. matrix ya kinyume

Matrix ya mraba A inaitwa isiyo ya umoja ikiwa ina kipekee kinyume matrix A -1 imedhamiriwa na masharti

AA −1 = A −1 A = I .

Matrix inverse haipo kwa matrices yote. Hali ya lazima na ya kutosha kwa kutoharibika ni

det(A) ≠ 0 au cheo(A) = N.

Inversion ya matrix ni utaratibu mgumu ambao kuna programu maalum. Kwa mfano,

Mchele. 17 Ubadilishaji wa Matrix

Wacha tuwasilishe fomula za kesi rahisi - matrix 2x2

Ikiwa matrices A na B sio umoja, basi

(AB ) −1 = B −1 A −1 .

1.15. Matrix ya pseudoinverse

Ikiwa matrix A ni ya umoja na matrix inverse haipo, basi katika baadhi ya matukio unaweza kutumia pseudoinverse matrix, ambayo inafafanuliwa kama matrix A+ kama hiyo

AA + A = A.

Matrix ya pseudoinverse sio pekee na fomu yake inategemea njia ya ujenzi. Kwa mfano kwa tumbo la mstatili Njia ya Moore-Penrose inaweza kutumika.

Ikiwa idadi ya safu idadi ndogo mistari basi

A + =(A t A ) −1 A t

Kwa mfano,

Mchele. 17a Ugeuzaji-uongo wa tumbo

Ikiwa idadi ya safu nambari zaidi mistari basi

A + =A t (AA t) −1

1.16. Kuzidisha vekta kwa matrix

Vekta x inaweza kuzidishwa na matrix A ya mwelekeo unaofaa. Katika kesi hii, vekta ya safu huzidishwa kwenye Ax ya kulia, na vekta ya safu huzidishwa upande wa kushoto x t A. Ikiwa mwelekeo wa vector J, na mwelekeo wa matrix I× J basi matokeo yatakuwa vector ya mwelekeo I. Kwa mfano,

Mchele. 18 Kuzidisha vekta kwa tumbo

Ikiwa matrix A ni mraba ( I× I), kisha vekta y = Ax ina mwelekeo sawa na x. Ni dhahiri kwamba

A (α 1 x 1 + α 2 x 2) = α 1 Shoka 1 + α 2 Shoka 2 .

Kwa hivyo, matrices yanaweza kuzingatiwa kama mabadiliko ya mstari wa vekta. Hasa, Ix = x, Ox = 0.

2. Maelezo ya ziada 2.1. Mifumo ya milinganyo ya mstari

Acha A iwe matrix ya saizi I× J, na b ni vekta ya mwelekeo J. Fikiria mlinganyo

Shoka = b

kuhusiana na vector x, mwelekeo I. Kimsingi, ni mfumo wa I milinganyo ya mstari na J haijulikani x 1 ,...,x J. Suluhisho lipo ikiwa na tu ikiwa

cheo(A) = cheo(B) = R,

ambapo B ni matriki ya mwelekeo ulioongezwa I×( J+1), inayojumuisha matrix A inayokamilishwa na safu b, B = (A b). Vinginevyo, equations haziendani.

Kama R = I = J, basi suluhisho ni la kipekee

x = A -1 b .

Kama R < I, basi wapo wengi ufumbuzi mbalimbali, ambayo inaweza kuonyeshwa kupitia mchanganyiko wa mstari J−R vekta. Mfumo milinganyo ya homogeneous Ax = 0 na matrix ya mraba A ( N× N) haina ufumbuzi usio na maana(x ≠ 0) ikiwa na tu ikiwa det(A) = 0. Ikiwa R= cheo(A) 0.

Vile vile hufafanuliwa hasi(x t Ax< 0), zisizo hasi(x t Ax ≥ 0) na hasi(x t Ax ≤ 0) matrices fulani.

2.4. Mtengano wa Cholesky

Ikiwa matriki ya ulinganifu A ni chanya dhahiri, basi kuna matriki ya kipekee ya pembe tatu U yenye vitu vyema ambavyo kwayo

A = U t U .

Kwa mfano,

Mchele. 19 Mtengano wa Cholesky

2.5. Mtengano wa polar

Wacha A awe asiyeharibika matrix ya mraba vipimo N× N. Kisha kuna kipekee polar utendaji

A = SR,

ambapo S ni matrix ya ulinganifu isiyo hasi na R ni matriki ya othogonal. Matrices S na R yanaweza kufafanuliwa kwa uwazi:

S 2 = AA t au S = (AA t) ½ na R = S −1 A = (AA t) −½ A .

Kwa mfano,

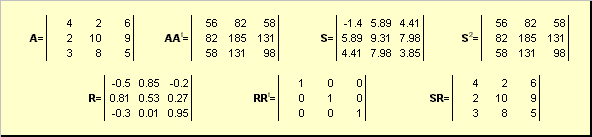
Mchele. 20 Mtengano wa polar

Ikiwa matrix A ni ya umoja, basi mtengano sio wa kipekee - ambayo ni: S bado ni moja, lakini kunaweza kuwa na R. Mtengano wa polar unawakilisha matriki A kama mchanganyiko wa mbano/kiendelezi S na mzunguko R .

2.6. Eigenvectors na eigenvalues

Acha A iwe tumbo la mraba. Vekta v inaitwa eigenvector matrix A ikiwa

Av = λv,

ambapo nambari λ inaitwa thamani ya eigen matrices A. Kwa hivyo, mabadiliko ambayo matrix A hufanya kwenye vector v hupunguzwa kwa kunyoosha rahisi au ukandamizaji na mgawo λ. Eigenvector imedhamiriwa hadi kuzidisha kwa mara kwa mara α ≠ 0, i.e. ikiwa v ni eigenvector, basi αv pia ni eigenvector.

2.7. Maadili ya Eigen

Matrix A ina mwelekeo ( N× N) haiwezi kuwa zaidi ya N eigenvalues. Wanatosheleza mlingano wa tabia

det(A − λI ) = 0,

kuwa mlinganyo wa algebra N- utaratibu. Hasa, kwa tumbo 2 × 2 equation ya tabia ina fomu

Kwa mfano,

Mchele. 21 Eigenvalues

Seti ya maadili eigen \ λ 1 ,..., λ N matrix A inaitwa wigo A.

Wigo una sifa mbalimbali. Hasa

det(A ) = λ 1 ×...×λ N, Sp(A ) = λ 1 +...+λ N.

Eigenvalues ya matrix ya kiholela inaweza kuwa nambari ngumu, lakini ikiwa matrix ni linganifu (A t = A), basi maadili yake ni ya kweli.

2.8. Eigenvectors

Matrix A ina mwelekeo ( N× N) haiwezi kuwa zaidi ya N eigenvectors, ambayo kila moja inalingana na eigenvalue yake. Kuamua eigenvector v n haja ya kutatua mfumo wa equations homogeneous

(A − λ n I) v n = 0 .

Inayo suluhisho isiyo ya kawaida, kwani det(A - λ n I) = 0.

Kwa mfano,

Mchele. 22 Eigenvectors

Eigenveekta za matrix ya ulinganifu ni ya orthogonal.

Eigenvalues (nambari) na eigenvectors.
Mifano ya ufumbuzi

Kuwa wewe mwenyewe

Kutoka kwa equations zote mbili inafuata hiyo.

Hebu tuweke basi: .

Matokeo yake: - eigenvector ya pili.

Hebu kurudia pointi muhimu ufumbuzi:

- mfumo unaosababisha hakika una uamuzi wa pamoja(equations zinategemea mstari);

- tunachagua "y" kwa njia ambayo ni kamili na ya kwanza "x" ya kuratibu ni integer, chanya na ndogo iwezekanavyo.

- tunaangalia kuwa suluhisho mahususi linakidhi kila mlinganyo wa mfumo.

Jibu .

Kulikuwa na "vituo vya ukaguzi" vya kutosha vya kati, kwa hivyo kuangalia usawa, kimsingi, sio lazima.

Katika vyanzo anuwai vya habari, kuratibu za eigenveekta mara nyingi huandikwa sio kwenye safu, lakini kwa safu, kwa mfano: (na, kuwa mkweli, mimi mwenyewe nimezoea kuziandika kwenye mistari). Chaguo hili linakubalika, lakini kwa kuzingatia mada ya mabadiliko ya mstari ni rahisi zaidi kutumia kitaalam vekta za safu.

Labda suluhisho lilionekana kuwa refu sana kwako, lakini hii ni kwa sababu nilitoa maoni juu ya mfano wa kwanza kwa undani sana.

Mfano 2

Matrices

Wacha tufanye mazoezi peke yetu! Mfano wa takriban wa kazi ya mwisho mwishoni mwa somo.

Wakati mwingine unahitaji kufanya kazi ya ziada, yaani:

andika mtengano wa matrix ya kisheria

Ni nini?

Ikiwa eigenvectors ya fomu ya matrix msingi, basi inaweza kuwakilishwa kama:

Ambapo ni matrix inayojumuisha kuratibu za eigenveekta, - diagonal matrix yenye eigenvalues zinazolingana.

Mtengano huu wa matrix unaitwa kisheria au diagonal.

Wacha tuangalie matrix ya mfano wa kwanza. Eigenvectors zake kujitegemea linearly(isiyo ya collinear) na kuunda msingi. Wacha tuunda matrix ya kuratibu zao:

Washa diagonal kuu matrices kwa utaratibu ufaao eigenvalues ziko, na vitu vilivyobaki ni sawa na sifuri:
- Ninasisitiza tena umuhimu wa utaratibu: "mbili" inafanana na vector ya 1 na kwa hiyo iko kwenye safu ya 1, "tatu" - kwa vector ya 2.

Kutumia algorithm ya kawaida ya kupata matrix inverse au njia ya Gauss-Jordan, tunapata . Hapana, hiyo si typo! - kabla ya wewe ni nadra, kama kupatwa kwa jua tukio wakati kinyume kinalingana na matriki asilia.

Inabakia kuandika mtengano wa kisheria wa matrix:

Mfumo unaweza kutatuliwa kwa kutumia mabadiliko ya msingi na katika mifano ifuatayo tutakimbilia njia hii. Lakini hapa njia ya "shule" inafanya kazi kwa kasi zaidi. Kutoka kwa mlingano wa 3 tunaeleza: - badala ya mlingano wa pili:

Kwa kuwa uratibu wa kwanza ni sifuri, tunapata mfumo, kutoka kwa kila equation ambayo inafuata kwamba .

Tena, makini na uwepo wa lazima wa uhusiano wa mstari. Ikiwa tu suluhisho lisilo na maana linapatikana , basi ama eigenvalue ilipatikana kimakosa, au mfumo ulikusanywa/kutatuliwa kwa hitilafu.

Viwianishi vya kompakt hutoa thamani

Eigenvector:

Na mara nyingine tena, tunaangalia kwamba suluhisho limepatikana inakidhi kila equation ya mfumo. Katika aya zinazofuata na katika kazi zinazofuata, ninapendekeza kuchukua matakwa haya kama sheria ya lazima.

2) Kwa eigenvalue, kwa kutumia kanuni hiyo hiyo, tunapata mfumo ufuatao:

Kutoka kwa mlingano wa 2 wa mfumo tunaeleza: - badala ya mlinganyo wa tatu:

Kwa kuwa uratibu wa "zeta" ni sawa na sifuri, tunapata mfumo kutoka kwa kila mlinganyo unaofuata. utegemezi wa mstari.

Hebu

Kuangalia kwamba suluhisho inakidhi kila equation ya mfumo.

Kwa hivyo, eigenvector ni:.

3) Na mwishowe, mfumo unalingana na eigenvalue:

Mlinganyo wa pili unaonekana rahisi zaidi, kwa hivyo wacha tuielezee na tuibadilishe katika milinganyo ya 1 na ya 3:

Kila kitu kiko sawa - uhusiano wa mstari umeibuka, ambao tunabadilisha kwa usemi:

Kama matokeo, "x" na "y" zilionyeshwa kupitia "z": . Kwa mazoezi, sio lazima kufikia uhusiano kama huo; katika hali zingine ni rahisi zaidi kuelezea kupitia au na kupitia . Au hata "treni" - kwa mfano, "X" hadi "mimi", na "mimi" hadi "Z"

Hebu tuweke basi:

Tunaangalia kuwa suluhisho limepatikana inakidhi kila equation ya mfumo na inaandika eigenvector ya tatu

Jibu: eigenvectors:

Kijiometri, vekta hizi hufafanua mwelekeo tatu tofauti wa anga ("Huko na kurudi tena"), ambapo mabadiliko ya mstari hubadilisha vekta zisizo za sifuri (eigenveeta) kuwa vekta za collinear.

Ikiwa hali ilihitaji kupata mtengano wa kisheria, basi hii inawezekana hapa, kwa sababu eigenvalues tofauti hulingana na eigenveekta tofauti zinazojitegemea. Kutengeneza matrix kutoka kwa kuratibu zao, tumbo la diagonal kutoka husika eigenvalues na kupata matrix inverse.

Ikiwa, kwa hali, unahitaji kuandika tumbo mabadiliko ya mstari kwa msingi wa eigenvectors, kisha tunatoa jibu katika fomu. Kuna tofauti, na tofauti ni muhimu! Kwa sababu matrix hii ni matrix ya "de".

Tatizo na zaidi mahesabu rahisi Kwa uamuzi wa kujitegemea:

Mfano 5

Pata eigenveekta za ubadilishaji wa mstari uliotolewa na matrix

Unapotafuta nambari zako mwenyewe, jaribu kutokwenda hadi digrii ya 3 ya polynomial. Kwa kuongeza, ufumbuzi wa mfumo wako unaweza kutofautiana na ufumbuzi wangu - hakuna uhakika hapa; na vekta unazopata zinaweza kutofautiana kutoka kwa vekta za sampuli hadi usawa wa kuratibu zao. Kwa mfano, na. Inapendeza zaidi kuwasilisha jibu katika fomu, lakini ni sawa ikiwa utaacha chaguo la pili. Hata hivyo, kuna kila kitu mipaka inayofaa, toleo halionekani zuri sana tena.

Takriban sampuli ya mwisho ya mgawo mwishoni mwa somo.

Jinsi ya kutatua shida katika kesi ya eigenvalues nyingi?

Algorithm ya jumla inabakia sawa, lakini ina sifa zake, na inashauriwa kuweka baadhi ya sehemu za suluhisho kwa mtindo mkali zaidi wa kitaaluma:

Mfano 6

Tafuta eigenvalues na eigenveekta

Suluhisho

Bila shaka, hebu tuweke herufi kubwa safu ya kwanza nzuri:

Na, baada ya kuharibika quadratic trinomial na vizidishi:

Kama matokeo, eigenvalues hupatikana, mbili ambazo ni nyingi.

Tutafute yetu vekta:

1) Wacha tushughulike na askari pekee kulingana na mpango "uliorahisishwa":

Kutoka kwa milinganyo miwili ya mwisho, usawa unaonekana wazi, ambao, kwa hakika, unapaswa kubadilishwa kuwa mlingano wa 1 wa mfumo:

Hutapata mchanganyiko bora:
Eigenvector:

2-3) Sasa tunaondoa walinzi kadhaa. Katika kesi hii, unaweza kupata eigenvector mbili au moja. Bila kujali wingi wa mizizi, tunabadilisha thamani kwenye kibainishi , ambayo hutuletea mfumo ufuatao wa homogeneous wa milinganyo ya mstari:

Eigenvectors ni vekta haswa
mfumo wa msingi wa suluhisho

Kwa kweli, katika somo lote hatukufanya chochote isipokuwa kupata vekta za mfumo wa kimsingi. Kwa muda tu muda huu sikuihitaji sana. Kwa njia, wale wanafunzi wajanja ambao waliruka mada ya equations homogeneous katika suti za kuficha watalazimika kujaribu sasa.

Kitendo pekee kilikuwa kuondoa mistari ya ziada. Matokeo yake ni matrix moja kwa tatu na "hatua" rasmi katikati.
– tofauti za kimsingi, – vigeu vya bure. Kuna vigezo viwili vya bure, kwa hiyo, pia kuna vectors mbili za mfumo wa msingi.

Wacha tuonyeshe utofauti wa kimsingi katika suala la anuwai za bure: . Kizidishi cha sifuri mbele ya "X" kinairuhusu kuchukua maadili yoyote (ambayo yanaonekana wazi kutoka kwa mfumo wa equations).

Katika muktadha wa shida hii, ni rahisi zaidi kuandika suluhisho la jumla sio safu, lakini kwa safu:

Jozi hiyo inalingana na eigenvector:
Jozi hiyo inalingana na eigenvector:

Kumbuka : wasomaji wa hali ya juu wanaweza kuchagua vekta hizi kwa mdomo - kwa kuchambua tu mfumo , lakini ujuzi fulani unahitajika hapa: kuna vigezo vitatu, kiwango cha matrix ya mfumo ni moja, ambayo ina maana kwamba mfumo wa msingi wa ufumbuzi una 3 - 1 = 2 vectors. Walakini, vekta zilizopatikana zinaonekana wazi hata bila ujuzi huu, kwa kiwango cha angavu. Katika kesi hii, vector ya tatu itaandikwa hata zaidi "kwa uzuri":. Hata hivyo, ninatahadharisha hilo katika mfano mwingine uteuzi rahisi Inaweza isiwe hivyo, ndiyo sababu kifungu hicho kinakusudiwa watu wenye uzoefu. Kwa kuongeza, kwa nini usichukue, sema, kama vekta ya tatu? Baada ya yote, kuratibu zake pia kukidhi kila equation ya mfumo, na vectors kujitegemea linearly. Chaguo hili, kimsingi, linafaa, lakini "lililopotoka", kwani vekta "nyingine" ni mchanganyiko wa mstari wa veta za mfumo wa kimsingi.

Jibu: eigenvalues: , eigenvectors:

Mfano sawa wa suluhisho la kujitegemea:

Mfano 7

Tafuta eigenvalues na eigenveekta

Sampuli ya takriban ya muundo wa mwisho mwishoni mwa somo.

Ikumbukwe kwamba katika mifano ya 6 na 7 tunapata mara tatu ya eigenveekta huru, na kwa hivyo matrix ya asili inawakilishwa. upanuzi wa kanuni. Lakini raspberries kama hizo hazifanyiki katika hali zote:

Mfano 8