ตัวเลขเทียบเคียงโมดูโล 7 เปรียบเทียบโมดูโลกับจำนวนธรรมชาติ
เปรียบเทียบกับอันที่ไม่รู้จัก xดูเหมือน
ที่ไหน . ถ้า ก n หารด้วยไม่ได้ มนั่นคือสิ่งที่เรียกว่า ระดับการเปรียบเทียบ
โดยการตัดสินใจการเปรียบเทียบคือจำนวนเต็มใดๆ x 0 , ซึ่ง
ถ้า เอ็กซ์ 0 เป็นไปตามการเปรียบเทียบ ดังนั้น ตามคุณสมบัติของการเปรียบเทียบทั้ง 9 รายการ จำนวนเต็มทั้งหมดที่เทียบเคียงได้ x 0 โมดูโล่ ม. ดังนั้น สารละลายเปรียบเทียบทั้งหมดจึงอยู่ในโมดูโลคลาสสารตกค้างเดียวกัน ตเราจะถือว่ามันเป็นทางออกหนึ่ง ดังนั้นการเปรียบเทียบจึงมีวิธีแก้ปัญหามากพอๆ กับองค์ประกอบของระบบสารตกค้างที่สมบูรณ์ที่ตอบสนองความต้องการดังกล่าว
การเปรียบเทียบที่มีชุดโซลูชันตรงกันเรียกว่า เทียบเท่า.
2.2.1 การเปรียบเทียบระดับแรก
การเปรียบเทียบระดับแรกกับอันที่ไม่รู้จัก เอ็กซ์ดูเหมือน
![]() (2.2)
(2.2)
ทฤษฎีบท 2.4 การที่จะเปรียบเทียบได้อย่างน้อยหนึ่งวิธีก็จำเป็นและเพียงพอกับจำนวนนั้น ข หารด้วย GCD( ก, ม).
การพิสูจน์.ก่อนอื่นเราพิสูจน์ความจำเป็น อนุญาต ง
=
จีซีดี( ก,
ม)
และ เอ็กซ์ 0
- โซลูชันการเปรียบเทียบ แล้ว ![]() นั่นคือความแตกต่าง โอ้ 0
−
ข
หารด้วย ต.มันจึงมีจำนวนเต็มแบบนั้น ถาม,
อะไร โอ้ 0
−
ข
=
คิวเอ็ม.
จากที่นี่ ข= อา 0
−
คิวเอ็ม.
และตั้งแต่นั้นเป็นต้นมา ง,
เป็นตัวหารร่วม, หารตัวเลข กและ ที,จากนั้น minuend และ subtrahend จะถูกหารด้วย ง,
และดังนั้นจึง ข
หารด้วย ง.
นั่นคือความแตกต่าง โอ้ 0
−
ข
หารด้วย ต.มันจึงมีจำนวนเต็มแบบนั้น ถาม,
อะไร โอ้ 0
−
ข
=
คิวเอ็ม.
จากที่นี่ ข= อา 0
−
คิวเอ็ม.
และตั้งแต่นั้นเป็นต้นมา ง,
เป็นตัวหารร่วม, หารตัวเลข กและ ที,จากนั้น minuend และ subtrahend จะถูกหารด้วย ง,
และดังนั้นจึง ข
หารด้วย ง.
ทีนี้เรามาพิสูจน์ความเพียงพอกันดีกว่า อนุญาต ง- ตัวหารร่วมมากของตัวเลข กและ ที,และ ข หารด้วย ง. จากนั้นตามคำจำกัดความของการหารลงตัว จะได้จำนวนเต็มดังต่อไปนี้ ก 1 , ข 1 ,ท 1 , อะไร .
เมื่อใช้อัลกอริธึมยุคลิดแบบขยาย เราจะพบการแสดงเชิงเส้นของจำนวน 1 = gcd( ก 1 , ม 1 ):
![]()
สำหรับบางคน x 0 , ย 0 . ลองคูณทั้งสองข้างของความเสมอภาคสุดท้ายด้วย ข 1 ง:
หรือสิ่งที่เหมือนกัน
,
นั่นคือและเป็นวิธีแก้ปัญหาการเปรียบเทียบ □
ตัวอย่าง 2.10. การเปรียบเทียบ 9 เอ็กซ์= 6 (mod 12) มีวิธีแก้ปัญหาเนื่องจาก gcd(9, 12) = 3 และ 6 หารด้วย 3 ลงตัว □
ตัวอย่าง 2.11. การเปรียบเทียบ 6x= 9 (mod 12) ไม่มีคำตอบ เนื่องจาก gcd(6, 12) = 6 และ 9 หารด้วย 6 ไม่ลงตัว □
ทฤษฎีบท 2.5 ให้การเปรียบเทียบ (2.2) สามารถแก้ไขได้และ ง = จีซีดี( ก, ม). จากนั้นชุดโซลูชั่นการเปรียบเทียบ (2.2) ประกอบด้วย ง คลาสสารตกค้างแบบโมดูโล ที,กล่าวคือถ้า เอ็กซ์ 0 - หนึ่งในวิธีแก้ปัญหา จากนั้นวิธีแก้ปัญหาอื่นๆ ทั้งหมดก็คือ
การพิสูจน์.อนุญาต เอ็กซ์ 0
- คำตอบของการเปรียบเทียบ (2.2) นั่นคือ ![]() และ ,
.
จึงมีเรื่องเช่นนี้ ถาม, อะไร โอ้ 0
−
ข
=
คิวเอ็ม.
ตอนนี้แทนที่เป็นความเสมอภาคสุดท้ายแทน เอ็กซ์ 0
วิธีแก้ปัญหาตามอำเภอใจของแบบฟอร์มโดยที่เราได้รับนิพจน์
และ ,
.
จึงมีเรื่องเช่นนี้ ถาม, อะไร โอ้ 0
−
ข
=
คิวเอ็ม.
ตอนนี้แทนที่เป็นความเสมอภาคสุดท้ายแทน เอ็กซ์ 0
วิธีแก้ปัญหาตามอำเภอใจของแบบฟอร์มโดยที่เราได้รับนิพจน์
, หารด้วย ม. □
ตัวอย่าง 2.12. การเปรียบเทียบ 9 เอ็กซ์=6 (mod 12) มีสามวิธีแก้ปัญหาตั้งแต่ gcd(9, 12)=3 โซลูชั่นเหล่านี้: เอ็กซ์ 0 = 2, x 0 + 4 = 6, เอ็กซ์ 0 + 2∙4=10.□
ตัวอย่าง 2.13. การเปรียบเทียบ 11 เอ็กซ์=2 (mod 15) มีวิธีแก้ปัญหาที่ไม่เหมือนใคร เอ็กซ์ 0 = 7 เนื่องจาก GCD(11,15)=1.□
เราจะแสดงวิธีแก้ปัญหาการเปรียบเทียบระดับแรกให้คุณ โดยไม่สูญเสียลักษณะทั่วไป เราจะถือว่า GCD( ก, เสื้อ) = 1. จากนั้นสามารถหาคำตอบของการเปรียบเทียบ (2.2) ได้ เช่น โดยใช้อัลกอริธึมแบบยุคลิด แท้จริงแล้ว การใช้อัลกอริธึมแบบยุคลิดแบบขยายทำให้เราแทนเลข 1 ในรูปผลรวมเชิงเส้นของตัวเลข กและ ต:
ลองคูณทั้งสองข้างของความเท่าเทียมกันนี้ด้วย ข, เราได้รับ: ข = ABQ + นาย, ที่ไหน ABQ - ข = - นาย, นั่นคือ ก ∙ (บาร์บีคิว) = ข(รุ่น ม) และ บาร์บีคิว- วิธีแก้ปัญหาการเปรียบเทียบ (2.2)
วิธีแก้อีกอย่างหนึ่งคือใช้ทฤษฎีบทของออยเลอร์ เราเชื่ออีกครั้งว่า GCD(a, ที)= 1. เราใช้ทฤษฎีบทของออยเลอร์: ![]() . คูณทั้งสองข้างของการเปรียบเทียบด้วย ข:
. คูณทั้งสองข้างของการเปรียบเทียบด้วย ข:
![]() .
เขียนนิพจน์สุดท้ายใหม่เป็น
.
เขียนนิพจน์สุดท้ายใหม่เป็น  เราพบว่านั่นเป็นวิธีแก้ปัญหาการเปรียบเทียบ (2.2)
เราพบว่านั่นเป็นวิธีแก้ปัญหาการเปรียบเทียบ (2.2)
ตอนนี้ให้ GCD( ก, ม) = ง>1. แล้ว ก = กทีง, ม = มทีง, โดยที่ GCD( ก 1 , ม 1) = 1 นอกจากนี้ก็จำเป็น ข = ข 1 ง, เพื่อให้การเปรียบเทียบสามารถแก้ไขได้ ถ้า เอ็กซ์ 0 - โซลูชันการเปรียบเทียบ ก 1 x = ข 1 (รุ่น ม 1) และเป็นอันเดียว เนื่องจาก GCD( ก 1 , ม 1) = 1 แล้ว เอ็กซ์ 0 จะเป็นแนวทางแก้ไขและเปรียบเทียบ ก 1 xd = ฐานข้อมูล 1 (รุ่น ม 1), นั่นคือการเปรียบเทียบเดิม (2.2) พักผ่อน ง- พบคำตอบ 1 ข้อโดยทฤษฎีบท 2.5
โครงการคณิตศาสตร์ในหัวข้อ
"การเปรียบเทียบแบบโมดูโล"
ซาริโปวา ไอซีลู
เขต Sovetsky ของคาซาน
MBOU "โรงเรียนมัธยมหมายเลข 166" เกรด 7a
หัวหน้างานด้านวิทยาศาสตร์: Antonova N.A.
สารบัญ
บทนำ__________________________________________________________3
การเปรียบเทียบคืออะไร_____________________________________________4
แนวคิดของการเปรียบเทียบแบบโมดูโล__________________________4
ประวัติความเป็นมาของแนวคิดการเปรียบเทียบแบบโมดูโล_____4
คุณสมบัติของการเปรียบเทียบ_________________________________________4
การใช้การเปรียบเทียบแบบโมดูโลที่ง่ายที่สุดคือการกำหนดความสามารถในการหารของตัวเลข___________________________6
งานเปรียบเทียบหนึ่งงาน_______________________________8
การใช้การเปรียบเทียบแบบโมดูโลในกิจกรรมระดับมืออาชีพ________________________________________________9
การใช้การเปรียบเทียบในการแก้ปัญหา__________________________6
บทสรุป_________________________________________________10
รายการวรรณกรรมที่ใช้แล้ว_______________________________________11
การแนะนำ.
หัวข้อ: การเปรียบเทียบแบบโมดูโล่
ปัญหา: นักเรียนหลายคนประสบปัญหาในการเตรียมตัวสำหรับการแข่งขันกีฬาโอลิมปิก ซึ่งวิธีแก้ปัญหานี้ขึ้นอยู่กับความรู้เรื่องเศษจากการหารจำนวนเต็มด้วยจำนวนธรรมชาติ เราสนใจปัญหาประเภทนี้และวิธีการแก้ไขที่เป็นไปได้ ปรากฎว่าพวกเขาสามารถแก้ไขได้โดยใช้การเปรียบเทียบแบบโมดูโล
เป้าหมาย: ค้นหาสาระสำคัญของการเปรียบเทียบแบบโมดูโล ซึ่งเป็นวิธีการหลักในการทำงานกับการเปรียบเทียบแบบโมดูโล
วัตถุประสงค์: ค้นหาเนื้อหาทางทฤษฎีในหัวข้อนี้ พิจารณาปัญหาที่แก้ไขได้โดยใช้การเปรียบเทียบแบบโมดูโล แสดงวิธีการทั่วไปในการแก้ปัญหาดังกล่าว สรุปผล
วัตถุประสงค์การศึกษา: ทฤษฎีจำนวน
หัวข้อวิจัย: ทฤษฎีการเปรียบเทียบแบบโมดูโล
ผลงานนี้เป็นงานวิจัยเชิงทฤษฎีและสามารถนำไปใช้ในการเตรียมการแข่งขันคณิตศาสตร์โอลิมปิกได้ เนื้อหาเปิดเผยแนวคิดพื้นฐานของการเปรียบเทียบแบบโมดูโลและคุณสมบัติหลัก และให้ตัวอย่างการแก้ปัญหาในหัวข้อนี้
ฉัน . การเปรียบเทียบคืออะไร?
แนวคิดของการเปรียบเทียบแบบโมดูโล
ตัวเลขที่กล่าวกันว่าเทียบเคียงได้เป็นโมดูลัสถ้าหารด้วยหรืออีกนัยหนึ่งคือ a และ b จะมีเศษเท่ากันเมื่อหารด้วย.
การกำหนด
ตัวอย่าง:
12 และ 32 เทียบเคียงได้กับโมดูโล 5 เนื่องจาก 12 เมื่อหารด้วย 5 จะมีเศษเป็น 2 และ 32 เมื่อหารด้วย 2 จะมีเศษเป็น 2 เขียนไว้ว่า12 ;
101 และ 17 เทียบได้กับโมดูโล 21;
ประวัติความเป็นมาของแนวคิดการเปรียบเทียบแบบโมดูโล
ทฤษฎีการแบ่งแยกส่วนใหญ่สร้างขึ้นโดยออยเลอร์ คำจำกัดความของการเปรียบเทียบกำหนดไว้ในหนังสือของ K.F. Gauss “Arithmetic Studies” งานนี้เขียนเป็นภาษาละตินเริ่มพิมพ์ในปี พ.ศ. 2340 แต่หนังสือเล่มนี้ได้รับการตีพิมพ์ในปี พ.ศ. 2344 เท่านั้นเนื่องจากกระบวนการพิมพ์ในเวลานั้นต้องใช้แรงงานมากและใช้เวลานานมาก ส่วนแรกของหนังสือของเกาส์มีชื่อว่า "ในการเปรียบเทียบตัวเลข" Gauss เป็นผู้ที่เสนอสัญลักษณ์ของการเปรียบเทียบแบบโมดูโลที่เป็นที่ยอมรับในวิชาคณิตศาสตร์
คุณสมบัติของการเปรียบเทียบ
ถ้า
การพิสูจน์:
ถ้าเราบวกวินาทีเข้ากับความเท่าเทียมกันแรก เราจะได้
คือผลรวมของจำนวนเต็มสองตัว ดังนั้น จึงเป็นจำนวนเต็ม ดังนั้น
ถ้าเราลบอันที่สองจากความเท่าเทียมกันอันแรก เราจะได้
นี่คือผลต่างของจำนวนเต็มสองตัว ซึ่งหมายความว่ามันเป็นจำนวนเต็ม
พิจารณาการแสดงออก:
นี่คือผลต่างของผลิตภัณฑ์ของจำนวนเต็ม ซึ่งหมายความว่ามันเป็นจำนวนเต็ม
นี่เป็นผลมาจากคุณสมบัติที่สามของการเปรียบเทียบ
Q.E.D.
5) ถ้า.
การพิสูจน์: ลองหาผลรวมของสองนิพจน์นี้:
คือผลรวมของจำนวนเต็มสองตัว จึงเป็นจำนวนเต็ม ดังนั้น
Q.E.D.
6) ถ้าเป็นจำนวนเต็มแล้ว
หลักฐาน: , ที่ไหนพี– จำนวนเต็ม คูณความเท่าเทียมกันนี้ด้วย เราจะได้: . เนื่องจากเป็นผลคูณของจำนวนเต็ม นั่นคือสิ่งที่จำเป็นต้องพิสูจน์
7) ถ้า
การพิสูจน์: การให้เหตุผลคล้ายกับการพิสูจน์ทรัพย์สิน 6
8) ถ้า - เลขโคไพรม์แล้ว
การพิสูจน์: หารนิพจน์นี้ด้วย เราจะได้: - ตัวเลขโคไพรม์ ซึ่งหมายความว่าหารด้วยจำนวนเต็มลงตัว เช่น =. และนี่หมายความว่าสิ่งที่จำเป็นต้องได้รับการพิสูจน์
ครั้งที่สอง . การใช้การเปรียบเทียบในการแก้ปัญหา
2.1. การใช้การเปรียบเทียบแบบโมดูโลที่ง่ายที่สุดคือการกำหนดความสามารถในการหารของตัวเลข
ตัวอย่าง. หาเศษของ 2 2009 เวลา 7.
วิธีแก้ปัญหา: พิจารณากำลังของ 2:
เพิ่มการเปรียบเทียบยกกำลัง 668 แล้วคูณด้วย เราจะได้:
คำตอบ: 4.
ตัวอย่าง. พิสูจน์ว่า 7+7 2 +7 3 +…+7 4 n หารด้วย 100 สำหรับค่าใดๆ ก็ได้nจากเซตของจำนวนเต็ม
วิธีแก้ไข: พิจารณาการเปรียบเทียบ
ฯลฯ ลักษณะวัฏจักรของเศษจะอธิบายได้โดยใช้กฎสำหรับการคูณตัวเลขในคอลัมน์ เมื่อรวมการเปรียบเทียบสี่รายการแรกเข้าด้วยกัน เราจะได้:
ซึ่งหมายความว่าจำนวนเงินนี้หารด้วย 100 โดยไม่มีเศษเหลือ ในทำนองเดียวกัน เมื่อบวกการเปรียบเทียบต่อไปนี้ประมาณสี่ เราจะพบว่าผลรวมแต่ละผลหารด้วย 100 ลงตัวโดยไม่มีเศษ หมายความว่าผลรวมทั้งหมดประกอบด้วย 4nเทอมจะหารด้วย 100 ลงตัวโดยไม่มีเศษ Q.E.D.
ตัวอย่าง. กำหนดว่ามีค่าเท่าใดnนิพจน์นี้หารด้วย 19 ลงตัวโดยไม่มีเศษเหลือ
สารละลาย: .
ลองคูณการเปรียบเทียบนี้ด้วย 20 เราได้
เรามารวมการเปรียบเทียบกัน . ดังนั้น ด้านขวาของการเปรียบเทียบจะหารด้วย 19 ลงตัวเสมอสำหรับจำนวนธรรมชาติใดๆnซึ่งหมายความว่านิพจน์ดั้งเดิมหารด้วย 19 ลงตัวด้วยธรรมชาติn.
คำตอบ n – จำนวนธรรมชาติใดๆ
ตัวอย่าง. ตัวเลขลงท้ายด้วยเลขอะไร?
สารละลาย. เพื่อแก้ไขปัญหานี้ เราจะตรวจสอบเฉพาะตัวเลขสุดท้ายเท่านั้น พิจารณาพลังของหมายเลข 14:
คุณจะสังเกตได้ว่าหากเลขชี้กำลังเป็นเลขคี่ ค่าของดีกรีจะสิ้นสุดด้วย 4 และหากเลขชี้กำลังเป็นเลขคู่ ก็จะสิ้นสุดด้วย 6 จากนั้นจะสิ้นสุดด้วย 6 กล่าวคือ เป็นจำนวนคู่ ดังนั้นจะสิ้นสุดใน 6
ตอบ 6.
2.2. งานเปรียบเทียบหนึ่งงาน
บทความโดย N. Vilenkin "การเปรียบเทียบและประเภทของสารตกค้าง" นำเสนอปัญหาที่ Dirac นักฟิสิกส์ชาวอังกฤษผู้โด่งดังแก้ไขได้ในช่วงที่เขาเรียนอยู่
นอกจากนี้ยังมีวิธีแก้ปัญหาโดยย่อสำหรับปัญหานี้โดยใช้การเปรียบเทียบแบบโมดูโล แต่เราพบปัญหาที่คล้ายกันหลายประการ ตัวอย่างเช่น.
ผู้สัญจรไปมาคนหนึ่งพบกองแอปเปิ้ลใกล้ต้นไม้ซึ่งมีลิงตัวหนึ่งนั่งอยู่ หลังจากนับแล้ว เขาก็ตระหนักว่าถ้าให้ลิง 1 ผล จำนวนแอปเปิ้ลที่เหลือจะถูกแบ่งออกเป็น n ไร้ร่องรอย เมื่อให้แอปเปิ้ลที่เหลือแก่ลิงแล้ว เขาก็รับไป 1/ n แอปเปิ้ลที่เหลือและจากไป ต่อมาผู้สัญจรรายต่อไปเข้ามาใกล้กองแล้วรายต่อไปเป็นต้น ผู้ที่สัญจรผ่านไปมาแต่ละคนเมื่อนับผลแอปเปิ้ลแล้ว สังเกตว่าเมื่อหารด้วยจำนวนแล้ว n ให้ส่วนที่เหลือ 1 ผล และเมื่อให้แอปเปิ้ลเพิ่มอีกผลหนึ่งแก่ลิงแล้ว เขาก็หยิบอีก 1 ผลเป็นของตัวเอง n แอปเปิ้ลที่เหลือและเดินหน้าต่อไป หลังจากคนสุดท้ายออกไป n คนที่เดินผ่านไป จำนวนแอปเปิ้ลที่เหลืออยู่ในกองหารด้วย n ไร้ร่องรอย ตอนแรกมีแอปเปิ้ลกี่ลูก?
เมื่อใช้เหตุผลเดียวกันกับ Dirac เราได้รับสูตรทั่วไปสำหรับการแก้ปัญหาประเภทเดียวกัน: , โดยที่n- จำนวนธรรมชาติ
2.3. การประยุกต์การเปรียบเทียบโมดูลในกิจกรรมทางวิชาชีพ
ทฤษฎีเปรียบเทียบใช้กับทฤษฎีการเข้ารหัส ดังนั้นทุกคนที่เลือกอาชีพที่เกี่ยวข้องกับคอมพิวเตอร์จะได้ศึกษา และอาจนำการเปรียบเทียบไปใช้ในกิจกรรมทางวิชาชีพของตน ตัวอย่างเช่น แนวคิดทฤษฎีจำนวนจำนวนหนึ่ง รวมถึงการเปรียบเทียบแบบโมดูโล ถูกนำมาใช้เพื่อพัฒนาอัลกอริธึมการเข้ารหัสคีย์สาธารณะ
บทสรุป.
งานนี้สรุปแนวคิดพื้นฐานและคุณสมบัติของการเปรียบเทียบแบบโมดูโล และแสดงให้เห็นการใช้การเปรียบเทียบแบบโมดูโลพร้อมตัวอย่าง วัสดุนี้สามารถนำไปใช้ในการเตรียมการสำหรับการแข่งขันกีฬาโอลิมปิกในวิชาคณิตศาสตร์และการสอบ Unified State
รายการข้อมูลอ้างอิงที่ให้ไว้ หากจำเป็น สามารถพิจารณาแง่มุมที่ซับซ้อนมากขึ้นของทฤษฎีการเปรียบเทียบแบบโมดูโลและการประยุกต์ได้
รายชื่อวรรณกรรมที่ใช้แล้ว
อัลฟูโตวา เอ็น.บี. พีชคณิตและทฤษฎีจำนวน/N.B.Alfutova, A.V.Ustinov อ.:MCNMO, 2545, 466 หน้า
บุคชตาบ เอ.เอ. ทฤษฎีจำนวน /A.A.บุคห์ทับ. อ.: การศึกษา, 2503.
Vilenkin N. การเปรียบเทียบและประเภทของสารตกค้าง/N. Vilenkin.//ควอนตัม – 1978.- 10.
Fedorova N.E. ศึกษาพีชคณิตและการวิเคราะห์ทางคณิตศาสตร์ ชั้นประถมศึกษาปีที่ 10http:// www. ข้อดี. รุ/ ebooks/ เฟโดโรวา_ พีชคณิต_10 กิโล/1/ xht
รุ. วิกิพีเดีย. องค์กร/ วิกิ/Comparison_modulo.
คำนิยาม 1. หากตัวเลขสองตัวคือ 1) กและ ขเมื่อแบ่งตาม พีให้ส่วนที่เหลือเท่ากัน รแล้วตัวเลขดังกล่าวเรียกว่า equiremainder หรือ เทียบเคียงได้ในโมดูลัส พี.
คำแถลง 1. อนุญาต พีจำนวนบวกจำนวนหนึ่ง แล้วทุกเลข. กเสมอ และยิ่งกว่านั้น ด้วยวิธีเดียวที่สามารถแสดงในรูปแบบได้
แต่ตัวเลขเหล่านี้สามารถรับได้โดยการตั้งค่า รเท่ากับ 0, 1, 2,..., พี−1. เพราะฉะนั้น เอสพี+อาร์=กจะได้รับค่าจำนวนเต็มที่เป็นไปได้ทั้งหมด
ให้เราแสดงให้เห็นว่าการเป็นตัวแทนนี้มีเอกลักษณ์เฉพาะตัว สมมุติว่า พีสามารถแสดงได้สองวิธี ก=sp+rและ ก=ส 1 พี+ร 1. แล้ว
| (2) |
เพราะ ร 1 ยอมรับหนึ่งในตัวเลข 0,1, ..., พี−1 แล้วจึงเป็นค่าสัมบูรณ์ ร 1 −รน้อย พี. แต่จาก (2) เป็นไปตามนั้น ร 1 −รหลายรายการ พี. เพราะฉะนั้น ร 1 =รและ ส 1 =ส.
ตัวเลข รเรียกว่า ลบตัวเลข กโมดูโล่ พี(หรืออีกนัยหนึ่งคือจำนวน รเรียกว่าเศษของตัวเลข กบน พี).
คำแถลง 2. ถ้าเป็นเลขสองตัว กและ ขเทียบเคียงได้ในโมดูลัส พี, ที่ ก-ขหารด้วย พี.
จริงหรือ. ถ้าเป็นเลขสองตัว กและ ขเทียบเคียงได้ในโมดูลัส พีแล้วเมื่อหารด้วย พีมียอดคงเหลือเท่ากัน พี. แล้ว
หารด้วย พี, เพราะ ทางด้านขวาของสมการ (3) หารด้วย พี.
คำแถลง 3. หากผลต่างของตัวเลขสองตัวหารด้วย พีแล้วตัวเลขเหล่านี้เทียบเคียงได้ในโมดูลัส พี.
การพิสูจน์. ให้เราแสดงโดย รและ รเหลืออีก 1 ดิวิชั่น กและ ขบน พี. แล้ว
ตัวอย่าง 25≡39 (รุ่น 7), −18≡14 (รุ่น 4)
จากตัวอย่างแรก 25 เมื่อหารด้วย 7 จะได้เศษเท่ากับ 39 ซึ่งจริงๆ แล้ว 25 = 3·7+4 (เศษ 4) 39=3·7+4 (เหลือ 4) เมื่อพิจารณาตัวอย่างที่สอง คุณต้องคำนึงว่าส่วนที่เหลือต้องเป็นจำนวนที่ไม่เป็นลบซึ่งน้อยกว่าโมดูลัส (เช่น 4) จากนั้นเราสามารถเขียนได้: −18=−5·4+2 (ส่วนที่เหลือ 2), 14=3·4+2 (ส่วนที่เหลือ 2) ดังนั้น −18 เมื่อหารด้วย 4 จะเหลือเศษ 2 และ 14 เมื่อหารด้วย 4 จะเหลือเศษ 2
คุณสมบัติของการเปรียบเทียบแบบโมดูโล
คุณสมบัติ 1. สำหรับใครก็ตาม กและ พีเสมอ
ไม่มีการเปรียบเทียบเสมอไป
ที่ไหน λ เป็นตัวหารร่วมมากของตัวเลข มและ พี.
การพิสูจน์. อนุญาต λ ตัวหารร่วมมากของตัวเลข มและ พี. แล้ว
เพราะ ม(ก-ข)หารด้วย เค, ที่
เพราะฉะนั้น
และ มเป็นหนึ่งในตัวหารของจำนวน พี, ที่
ที่ไหน h=pqs.
โปรดทราบว่าเราสามารถอนุญาตให้มีการเปรียบเทียบตามโมดูลเชิงลบได้ เช่น การเปรียบเทียบ ก≡ขม็อด( พี) ในกรณีนี้หมายถึงความแตกต่าง ก-ขหารด้วย พี. คุณสมบัติทั้งหมดของการเปรียบเทียบยังคงมีผลบังคับใช้สำหรับโมดูลเชิงลบ
การเปรียบเทียบระดับแรกกับสิ่งที่ไม่รู้จักมีรูปแบบ:
ฉ(x) 0 (รุ่น ม); ฉ(เอ็กซ์) = โอ้ + และ n. (1)
แก้การเปรียบเทียบ- หมายถึงการค้นหาค่าทั้งหมดของ x ที่เป็นไปตามนั้น เรียกว่าการเปรียบเทียบสองครั้งที่ตรงกับค่า x เดียวกัน เทียบเท่า.
หากการเปรียบเทียบ (1) เป็นที่พอใจใดๆ x = x 1 แล้ว (ตามข้อ 49) ตัวเลขทั้งหมดที่สามารถเทียบเคียงได้ x 1, โมดูโล ม: x x 1 (รุ่น ม). ตัวเลขทั้งคลาสนี้ถือเป็น ทางออกหนึ่ง. ด้วยข้อตกลงดังกล่าวสามารถสรุปได้ดังต่อไปนี้
66.ค การจัดตำแหน่ง (1) จะมีวิธีแก้ปัญหามากเท่ากับจำนวนสารตกค้างของระบบที่สมบูรณ์ที่ตอบสนองได้.
ตัวอย่าง. การเปรียบเทียบ
6x– 4 0 (รุ่น 8)
ในบรรดาตัวเลข 0, 1,2, 3, 4, 5, 6, 7 ตัวเลขสองตัวเป็นไปตามระบบที่สมบูรณ์ของสารตกค้างแบบโมดูโล 8: เอ็กซ์= 2 และ เอ็กซ์= 6 ดังนั้น การเปรียบเทียบนี้จึงมีคำตอบสองวิธี:
x 2 (รุ่น 8) เอ็กซ์ 6 (รุ่น 8)
การเปรียบเทียบดีกรีแรกโดยการย้ายเทอมอิสระ (ที่มีเครื่องหมายตรงข้าม) ไปทางด้านขวาสามารถลดขนาดลงได้
ขวาน ข(รุ่น ม). (2)
พิจารณาการเปรียบเทียบที่ตรงตามเงื่อนไข ( ก, ม) = 1.
จากข้อมูลของ 66 การเปรียบเทียบของเรามีวิธีแก้ปัญหามากพอๆ กับที่ระบบทั้งหมดยังเหลืออยู่ซึ่งเป็นไปตามนั้น แต่เมื่อ xไหลผ่านสารตกค้างโมดูโลทั้งระบบ ที,ที่ โอ้ดำเนินการผ่านระบบการหักเงินทั้งหมด (เต็ม 60) ดังนั้นเพื่อค่าเดียวเท่านั้น เอ็กซ์,นำมาจากระบบที่สมบูรณ์ โอ้จะเทียบเคียงได้กับ ข.ดังนั้น,
67. เมื่อ (a, m) = 1 ขวานเปรียบเทียบ ข(รุ่น ม)มีทางออกเดียว
ให้ตอนนี้ ( ก, ม) = ง> 1. จากนั้น การเปรียบเทียบ (2) ถึงจะมีคำตอบ จำเป็น (เต็ม 55) ขหารด้วย ง,มิฉะนั้นการเปรียบเทียบ (2) จะเป็นไปไม่ได้สำหรับจำนวนเต็ม x ใดๆ . สมมุติดังนั้น ขทวีคูณ ง,เอาล่ะ ก = ก 1 ง, ข = ข 1 ง, ม = ม 1 ง.จากนั้นการเปรียบเทียบ (2) จะเทียบเท่ากับสิ่งนี้ (ย่อโดย ง): ก 1 x ข 1 (รุ่น ม), ซึ่งแล้ว ( ก 1 , ม 1) = 1, ดังนั้นมันจึงจะมีวิธีแก้ปัญหาแบบโมดูโลเดียว ม 1. อนุญาต เอ็กซ์ 1 – สารตกค้างที่ไม่เป็นลบที่เล็กที่สุดของสารละลายนี้แบบโมดูโล ม. 1 , แล้วตัวเลขทั้งหมดคือ x , การขึ้นรูปสารละลายนี้จะพบได้ในรูปแบบ
x x 1 (รุ่น ม 1). (3)
โมดูโล m ตัวเลข (3) ไม่ใช่คำตอบเดียว แต่มากกว่านั้น คือจำนวนคำตอบทั้งหมดที่มี (3) ในอนุกรม 0, 1, 2 ..., ม – 1 โมดูโลตกค้างที่ไม่เป็นลบน้อยที่สุด ม.แต่ตัวเลข (3) ต่อไปนี้จะอยู่ที่นี่:
x 1 , x 1 + ม 1 , x 1 + 2ม 1 , ..., x 1 + (ง – 1) ม 1 ,
เหล่านั้น. ทั้งหมด งตัวเลข (3); ดังนั้นการเปรียบเทียบ (2) จึงมี งการตัดสินใจ
เราได้รับทฤษฎีบท:
68. ให้ (a, m) = d ขวานเปรียบเทียบ ข (ม็อด m) เป็นไปไม่ได้ถ้า b หารด้วย d ไม่ลงตัว เมื่อ b เป็นผลคูณของ d การเปรียบเทียบจะมีคำตอบเป็น d
69. วิธีการแก้การเปรียบเทียบระดับแรกตามทฤษฎีเศษส่วนต่อเนื่อง:
ขยายความสัมพันธ์ออกเป็นเศษส่วนต่อเนื่อง ม:ก,

และดูเศษส่วนที่ตรงกันสองตัวสุดท้าย:

ตามคุณสมบัติของเศษส่วนต่อเนื่อง (ตาม 30 ) เรามี

ดังนั้นการเปรียบเทียบจึงมีทางออก
เพื่อหาซึ่งก็เพียงพอที่จะคำนวณได้ พีเอ็น– 1 ตามวิธีที่กำหนดในข้อ 30
ตัวอย่าง. มาแก้การเปรียบเทียบกัน
111x= 75 (รุ่น 321) (4)
โดยที่ (111, 321) = 3 และ 75 เป็นผลคูณของ 3 ดังนั้น การเปรียบเทียบจึงมีวิธีแก้ปัญหา 3 วิธี
เมื่อหารทั้งสองข้างของการเปรียบเทียบและโมดูลัสด้วย 3 เราจะได้การเปรียบเทียบ
37x= 25 (ม็อด 107), (5)
ซึ่งเราต้องแก้ก่อน เรามี
| ถาม | |||||
| ป 3 |

ดังนั้นในกรณีนี้ n = 4, พี เอ็น – 1 = 26, ข= 25 และเรามีคำตอบสำหรับการเปรียบเทียบ (5) ในรูปแบบ
x–26 ∙ 25 99 (รุ่น 107)
ดังนั้น แนวทางแก้ไขสำหรับการเปรียบเทียบ (4) จึงนำเสนอได้ดังนี้
เอ็กซ์ 99; 99 + 107; 99 + 2 ∙ 107 (รุ่น 321)
เอ็กซ์º99; 206; 313 (รุ่น 321)
การคำนวณองค์ประกอบผกผันโดยโมดูโลที่กำหนด
70.ถ้าตัวเลขเป็นจำนวนเต็ม กและ nเป็นไพรม์ก็จะมีตัวเลข อา'พอใจในการเปรียบเทียบ ก ∙ a′ ≡ 1(สมัย n). ตัวเลข อา'เรียกว่า การผกผันการคูณของโมดูโล nและสัญกรณ์ที่ใช้คือ ก- 1 (รุ่น n).
การคำนวณปริมาณซึ่งกันและกันแบบโมดูโลค่าหนึ่งสามารถทำได้โดยการแก้การเปรียบเทียบระดับแรกกับค่าที่ไม่รู้จักซึ่ง xยอมรับหมายเลขแล้ว อา'.
เพื่อหาแนวทางเปรียบเทียบ
ก∙x≡ 1(ดัดแปลง ม),
ที่ไหน ( เช้า)= 1,
คุณสามารถใช้อัลกอริทึมยุคลิด (69) หรือทฤษฎีบทแฟร์มาต์-ออยเลอร์ ซึ่งระบุว่าถ้า ( เช้า) = 1 แล้ว
ก φ( ม) ≡ 1(ม็อด ม).
x ≡ ก φ( ม)–1 (รุ่น ม).
กลุ่มและคุณสมบัติของพวกเขา
กลุ่มเป็นหนึ่งในชั้นเรียนอนุกรมวิธานที่ใช้ในการจำแนกโครงสร้างทางคณิตศาสตร์ที่มีคุณสมบัติลักษณะทั่วไป กลุ่มมีสององค์ประกอบ: พวงของ (ช) และ การดำเนินงาน() ที่กำหนดไว้ในชุดนี้
แนวคิดเรื่องเซต องค์ประกอบ และสมาชิกภาพเป็นแนวคิดพื้นฐานของคณิตศาสตร์สมัยใหม่ที่ไม่ได้นิยามไว้ ชุดใดๆ จะถูกกำหนดโดยองค์ประกอบที่รวมอยู่ในชุดนั้น (ซึ่งในทางกลับกัน ก็สามารถตั้งค่าได้เช่นกัน) ดังนั้นเราจึงกล่าวว่าเซตถูกกำหนดหรือกำหนดว่าสำหรับองค์ประกอบใดๆ เราสามารถบอกได้ว่ามันเป็นของเซตนี้หรือไม่
สำหรับสองชุด เอ, บีบันทึก บี ก, บี ก, บี∩ ก, บี ก, บี \ ก, ก × บีตามลำดับหมายความว่าอย่างนั้น บีเป็นสับเซตของเซต ก(เช่น องค์ประกอบใดๆ จาก บีมีอยู่ใน กตัวอย่างเช่น เซตของจำนวนธรรมชาติมีอยู่ในเซตของจำนวนจริง นอกจากนี้เสมอ ก ก), บีเป็นสับเซตแท้ของเซต ก(เหล่านั้น. บี กและ บี ≠ ก) จุดตัดของหลาย ๆ คน บีและ ก(นั่นคือองค์ประกอบทั้งหมดที่อยู่พร้อมกัน ก, และใน บีเช่น จุดตัดกันของจำนวนเต็มและจำนวนจริงบวกคือเซตของจำนวนธรรมชาติ) การรวมกันของเซต บีและ ก(เช่น เซตที่ประกอบด้วยธาตุที่อยู่อย่างใดอย่างหนึ่ง กไม่ว่าจะเข้า บี) กำหนดความแตกต่าง บีและ ก(เช่น เซตของธาตุที่อยู่ในนั้น บีแต่อย่าโกหก ก) ผลคูณคาร์ทีเซียนของเซต กและ บี(เช่น ชุดคู่ของแบบฟอร์ม ( ก, ข), ที่ไหน ก ก, ข บี). ผ่าน | ก| พลังของชุดจะแสดงเสมอ ก, เช่น. จำนวนองค์ประกอบในชุด ก.
การดำเนินการเป็นกฎที่องค์ประกอบสององค์ประกอบของเซต ช(กและ ข) จับคู่กับองค์ประกอบที่สามจาก G: ข
องค์ประกอบมากมาย ชด้วยการดำเนินการที่เรียกว่า กลุ่มหากตรงตามเงื่อนไขต่อไปนี้
ที่ n พวกมันให้เศษเท่ากัน
สูตรที่เทียบเท่า: a และ b เทียบเคียงได้ในโมดูลัสถ้าความแตกต่างของพวกเขา ก - ขหารด้วย n ลงตัว หรือถ้า a เขียนแทนเป็นได้ ก = ข + เคn , ที่ไหน เค- จำนวนเต็มบางส่วน ตัวอย่างเช่น: 32 และ −10 เทียบเคียงได้กับโมดูโล 7 เนื่องจาก
ข้อความ “a และ b เทียบเคียงได้กับโมดูโล n” เขียนเป็น:
คุณสมบัติความเท่าเทียมกันของโมดูโล่
ความสัมพันธ์การเปรียบเทียบแบบโมดูโลมีคุณสมบัติ
จำนวนเต็มสองตัวใดๆ กและ ขโมดูโลที่เทียบเคียงได้ 1
เพื่อให้เป็นตัวเลข กและ ขเทียบเคียงได้ในโมดูลัส nจำเป็นและเพียงพอที่จะหารผลต่างของมันให้ลงตัว n.
ถ้าตัวเลขและมีค่าเทียบเคียงเป็นโมดูลัส nจากนั้นผลรวมของพวกเขา และ เช่นเดียวกับผลคูณและยังเทียบเคียงได้ในโมดูลัสด้วย n.
ถ้าเป็นตัวเลข กและ ขเทียบเคียงได้ในโมดูลัส nแล้วองศาของพวกเขา ก เคและ ข เคก็เทียบเคียงได้ในโมดูลัสเช่นกัน nภายใต้ธรรมชาติใดๆ เค.
ถ้าเป็นตัวเลข กและ ขเทียบเคียงได้ในโมดูลัส n, และ nหารด้วย ม, ที่ กและ ขเทียบเคียงได้ในโมดูลัส ม.
เพื่อให้เป็นตัวเลข กและ ขเทียบเคียงได้ในโมดูลัส nนำเสนอในรูปแบบของการสลายตัวตามบัญญัติเป็นปัจจัยง่ายๆ พี ฉัน
จำเป็นและเพียงพอต่อการ
ความสัมพันธ์เชิงเปรียบเทียบเป็นความสัมพันธ์ที่เท่าเทียมกันและมีคุณสมบัติหลายประการของความเสมอภาคสามัญ ตัวอย่างเช่น สามารถเพิ่มและคูณได้: ถ้า
อย่างไรก็ตาม การเปรียบเทียบโดยทั่วไปไม่สามารถหารกันหรือหารด้วยตัวเลขอื่นได้ ตัวอย่าง: อย่างไรก็ตาม เมื่อลดลง 2 เราจะได้การเปรียบเทียบที่ผิดพลาด: กฎการใช้อักษรย่อสำหรับการเปรียบเทียบมีดังนี้
คุณยังไม่สามารถดำเนินการเปรียบเทียบได้หากโมดูลไม่ตรงกัน
คุณสมบัติอื่นๆ:
คำจำกัดความที่เกี่ยวข้อง
ชั้นเรียนการหักเงิน
เซตของตัวเลขทุกตัวเทียบเคียงได้ กโมดูโล่ nเรียกว่า ชั้นหัก กโมดูโล่ n และมักจะแสดงแทน [ ก] nหรือ . ดังนั้นการเปรียบเทียบจึงเทียบเท่ากับความเท่าเทียมกันของคลาสสารตกค้าง [ก] n = [ข] n .
ตั้งแต่การเปรียบเทียบแบบโมดูโล่ nคือความสัมพันธ์ที่เท่ากันของเซตของจำนวนเต็ม จากนั้นจึงเป็นคลาสโมดูโลของเรซิดิว nเป็นตัวแทนของคลาสที่เท่าเทียมกัน จำนวนของพวกเขาเท่ากัน n. ชุดของคลาสโมดูโลที่เหลือทั้งหมด nแสดงโดยหรือ
การดำเนินการของการบวกและการคูณโดยเหนี่ยวนำการดำเนินการที่สอดคล้องกันบนเซต:
[ก] n + [ข] n = [ก + ข] nสำหรับการดำเนินการเหล่านี้ เซตจะเป็นวงแหวนจำกัด และถ้า nง่าย - ฟิลด์จำกัด
ระบบการหักเงิน
ระบบส่วนที่เหลือช่วยให้คุณสามารถดำเนินการทางคณิตศาสตร์กับชุดตัวเลขที่มีจำกัดโดยไม่เกินขีดจำกัด หักเงินเต็มระบบโมดูโล n คือเซตของจำนวนเต็ม n ใดๆ ที่เป็นโมดูโล n ที่หาตัวจับยาก โดยปกติแล้ว สารตกค้างที่ไม่เป็นลบที่เล็กที่สุดจะถูกถือเป็นระบบที่สมบูรณ์ของสารตกค้างแบบโมดูโล n
0,1,...,n − 1หรือการหักเงินที่น้อยที่สุดที่ประกอบด้วยตัวเลข
,ในกรณีที่แปลก nและตัวเลข
ในกรณีที่เท่ากัน n .
การแก้ปัญหาการเปรียบเทียบ
การเปรียบเทียบระดับแรก
ในทฤษฎีจำนวน วิทยาการเข้ารหัสลับ และสาขาวิทยาศาสตร์อื่นๆ ปัญหาในการค้นหาวิธีแก้ไขการเปรียบเทียบรูปแบบระดับแรกมักเกิดขึ้น:
การแก้ไขการเปรียบเทียบดังกล่าวเริ่มต้นด้วยการคำนวณ gcd (ก, ม.)=ง. ในกรณีนี้เป็นไปได้ 2 กรณี คือ
- ถ้า ขไม่ใช่หลายรายการ งแล้วการเปรียบเทียบก็ไม่มีวิธีแก้ปัญหา
- ถ้า ขหลายรายการ งจากนั้นการเปรียบเทียบจะมีโซลูชันแบบโมดูโลที่เป็นเอกลักษณ์ ม / งหรือสิ่งที่เหมือนกัน งโซลูชั่นแบบโมดูโล่ ม. ในกรณีนี้เป็นผลจากการลดการเปรียบเทียบเดิมลงด้วย งการเปรียบเทียบคือ:
ที่ไหน ก 1 = ก / ง , ข 1 = ข / ง และ ม 1 = ม / ง เป็นจำนวนเต็ม และ ก 1 และ ม 1 ค่อนข้างเป็นจำนวนเฉพาะ ดังนั้นจำนวน ก 1 สามารถกลับหัวแบบโมดูโลได้ ม 1 นั่นคือหาตัวเลขดังกล่าว คนั่น (กล่าวอีกนัยหนึ่ง ) ตอนนี้หาวิธีแก้ปัญหาได้โดยการคูณผลการเปรียบเทียบด้วย ค:
การคำนวณมูลค่าในทางปฏิบัติ คสามารถนำไปใช้ได้หลายวิธี: การใช้ทฤษฎีบทของออยเลอร์, อัลกอริทึมของ Euclid, ทฤษฎีเศษส่วนต่อเนื่อง (ดูอัลกอริทึม) ฯลฯ โดยเฉพาะอย่างยิ่ง ทฤษฎีบทของออยเลอร์ช่วยให้คุณสามารถเขียนค่าได้ คเช่น:
ตัวอย่าง
สำหรับการเปรียบเทียบที่เรามี ง= 2 ดังนั้นการเปรียบเทียบแบบโมดูโล 22 จึงมีคำตอบสองวิธี ลองแทนที่ 26 ด้วย 4 เทียบได้กับ modulo 22 แล้วลดตัวเลขทั้ง 3 ตัวลง 2:
เนื่องจาก 2 เป็น coprime ของโมดูโล 11 เราจึงสามารถลดด้านซ้ายและขวาลง 2 ได้ ด้วยเหตุนี้ เราจึงได้โซลูชันโมดูโล 11: เพียงหนึ่งโซลูชัน เทียบเท่ากับสองโซลูชันโมดูโล 22:
การเปรียบเทียบระดับที่สอง
การแก้การเปรียบเทียบระดับที่สองนั้นเกิดขึ้นเพื่อค้นหาว่าจำนวนที่กำหนดนั้นเป็นค่าตกค้างกำลังสองหรือไม่ (โดยใช้กฎการกลับกันกำลังสอง) แล้วจึงคำนวณโมดูโลรากที่สอง
เรื่องราว
ทฤษฎีบทเศษที่เหลือของจีน ซึ่งเป็นที่รู้จักมานานหลายศตวรรษ กล่าวไว้ (ในภาษาคณิตศาสตร์สมัยใหม่) ว่าวงแหวนตกค้างแบบโมดูโลเป็นผลคูณของจำนวนโคไพรม์หลายจำนวนคือ
 อนุพันธ์บางส่วนของฟังก์ชันของตัวแปร 3 ตัว
อนุพันธ์บางส่วนของฟังก์ชันของตัวแปร 3 ตัว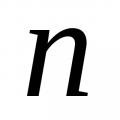 ฟังก์ชันการแจกแจงเชิงประจักษ์ ใช้ตัวอย่างนี้เพื่อสร้างฟังก์ชันการแจกแจงเชิงประจักษ์
ฟังก์ชันการแจกแจงเชิงประจักษ์ ใช้ตัวอย่างนี้เพื่อสร้างฟังก์ชันการแจกแจงเชิงประจักษ์ ไม่มีเงินแต่คุณรออยู่
ไม่มีเงินแต่คุณรออยู่