ตัวอย่าง

แบ่งส่วนออกครึ่งหนึ่ง

ปัญหาการแบ่งแยก- ใช้เข็มทิศและไม้บรรทัดเพื่อแบ่งส่วนนี้ เอบีออกเป็นสองส่วนเท่าๆ กัน หนึ่งในวิธีแก้ปัญหาแสดงในรูป:

• ใช้เข็มทิศวาดวงกลมโดยมีจุดศูนย์กลางอยู่ที่จุดต่างๆ กและ บีรัศมี เอบี.
• การหาจุดตัดกัน ปและ ถามวงกลมที่สร้างขึ้นสองวง (ส่วนโค้ง)
• ใช้ไม้บรรทัดวาดส่วนหรือเส้นที่ผ่านจุดต่างๆ ปและ ถาม.
• ค้นหาจุดกึ่งกลางของส่วนที่ต้องการ เอบี- จุดตัด เอบีและ PQ.

คำนิยามที่เป็นทางการ

ในปัญหาการก่อสร้าง ให้พิจารณาเซตของจุดทุกจุดของระนาบ เซตของเส้นตรงทั้งหมดของระนาบ และเซตของวงกลมทั้งหมดของระนาบ ซึ่งอนุญาตให้ดำเนินการดังต่อไปนี้:

1. เลือกจุดจากชุดของจุดทั้งหมด:
   1. จุดใดก็ได้
   2. จุดใดก็ได้บนเส้นที่กำหนด
   3. จุดใดก็ได้บนวงกลมที่กำหนด
   4. จุดตัดของเส้นตรงสองเส้นที่กำหนด
   5. จุดตัด/สัมผัสกันของเส้นตรงและวงกลมที่กำหนด
   6. จุดตัด/สัมผัสกันของวงกลมสองวงที่กำหนด
2. "โดยใช้ ผู้ปกครอง» เลือกบรรทัดจากชุดของบรรทัดทั้งหมด:
   1. เส้นตรงโดยพลการ
   2. เส้นตรงใดๆ ที่ผ่านจุดที่กำหนด
   3. เส้นตรงที่ผ่านจุดที่กำหนดสองจุด
3. "โดยใช้ เข็มทิศ» เลือกวงกลมจากชุดวงกลมทั้งหมด:
   1. วงกลมตามอำเภอใจ
   2. วงกลมใดๆ ที่มีจุดศูนย์กลางอยู่ที่จุดที่กำหนด
   3. วงกลมใดๆ ที่มีรัศมีเท่ากับระยะห่างระหว่างจุดสองจุดที่กำหนด
   4. วงกลมที่มีจุดศูนย์กลางอยู่ที่จุดที่กำหนดและมีรัศมีเท่ากับระยะห่างระหว่างจุดที่กำหนดสองจุด

ในเงื่อนไขของปัญหา จะมีการระบุชุดคะแนนที่แน่นอน จำเป็นต้องใช้การดำเนินการจำนวนจำกัดจากการดำเนินการที่ยอมรับได้ที่ระบุไว้ข้างต้น เพื่อสร้างชุดจุดอื่นที่อยู่ในความสัมพันธ์ที่กำหนดกับชุดดั้งเดิม

การแก้ปัญหาการก่อสร้างประกอบด้วยสามส่วนสำคัญ:

1. คำอธิบายวิธีการสร้างชุดที่กำหนด
2. พิสูจน์ว่าฉากที่สร้างขึ้นในลักษณะที่อธิบายไว้นั้นมีความสัมพันธ์ที่กำหนดกับฉากดั้งเดิมจริงๆ โดยปกติแล้ว การพิสูจน์การก่อสร้างจะดำเนินการเป็นการพิสูจน์ทฤษฎีบทเป็นประจำ โดยยึดตามสัจพจน์และทฤษฎีบทที่พิสูจน์แล้วอื่นๆ
3. การวิเคราะห์วิธีการก่อสร้างที่อธิบายไว้สำหรับการนำไปใช้กับเงื่อนไขเริ่มต้นรุ่นต่างๆ รวมถึงความเป็นเอกลักษณ์หรือไม่ซ้ำกันของโซลูชันที่ได้รับจากวิธีที่อธิบายไว้

ปัญหาที่ทราบ

• ปัญหาของ Apollonius ในการสร้างวงกลมแทนเจนต์กับวงกลมที่กำหนดสามวง หากไม่มีวงกลมใดวงกลมหนึ่งอยู่ภายในอีกวงกลมหนึ่ง แสดงว่าปัญหานี้มีวิธีแก้ไขที่แตกต่างกันอย่างมาก 8 วิธี
• ปัญหาของพรหมคุปต์ในการสร้างรูปสี่เหลี่ยมที่จารึกไว้โดยใช้ด้านทั้งสี่ของมัน

การสร้างรูปหลายเหลี่ยมปกติ

เรขาคณิตโบราณรู้วิธีสร้างที่ถูกต้อง n-gons สำหรับ , , และ .

สิ่งก่อสร้างที่เป็นไปได้และเป็นไปไม่ได้

โครงสร้างทั้งหมดไม่มีอะไรมากไปกว่าการแก้สมการบางสมการ และค่าสัมประสิทธิ์ของสมการนี้สัมพันธ์กับความยาวของส่วนที่กำหนด ดังนั้นจึงสะดวกที่จะพูดถึงการสร้างตัวเลขซึ่งเป็นวิธีแก้ปัญหาแบบกราฟิกของสมการบางประเภท ภายในกรอบของข้อกำหนดข้างต้น การก่อสร้างต่อไปนี้เป็นไปได้:

• การสร้างคำตอบของสมการเชิงเส้น
• การสร้างคำตอบของสมการกำลังสอง

กล่าวอีกนัยหนึ่ง เป็นไปได้ที่จะสร้างตัวเลขเท่ากับนิพจน์ทางคณิตศาสตร์โดยใช้รากที่สองของตัวเลขเดิมเท่านั้น (ความยาวของส่วน) ตัวอย่างเช่น,

รูปแบบและลักษณะทั่วไป

• การก่อสร้างโดยใช้เข็มทิศเดียวตามทฤษฎีบท Mohr-Mascheroni ด้วยความช่วยเหลือของเข็มทิศหนึ่งวงคุณสามารถสร้างรูปใดก็ได้ที่สามารถสร้างด้วยเข็มทิศและไม้บรรทัดได้ ในกรณีนี้ จะถือว่าสร้างเส้นตรงหากมีการระบุจุดสองจุดไว้
• ก่อสร้างโดยใช้ไม้บรรทัดเดียวเป็นเรื่องง่ายที่จะเห็นว่าด้วยความช่วยเหลือของผู้ปกครองเพียงคนเดียวเท่านั้นที่สามารถดำเนินการก่อสร้างที่ไม่แปรเปลี่ยนได้ โดยเฉพาะอย่างยิ่ง เป็นไปไม่ได้เลยที่จะแบ่งส่วนออกเป็นสองส่วนเท่าๆ กัน หรือหาจุดศูนย์กลางของวงกลมที่วาดไว้ แต่หากมีวงกลมที่วาดไว้ล่วงหน้าบนเครื่องบินโดยมีจุดศูนย์กลางที่ทำเครื่องหมายไว้ โดยใช้ไม้บรรทัด คุณสามารถดำเนินการก่อสร้างแบบเดียวกันกับวงเวียนและไม้บรรทัดได้ (ทฤษฎีบท Poncelet-Steiner ( ภาษาอังกฤษ)), พ.ศ. 2376 (ค.ศ. 1833) ถ้าไม้บรรทัดมีรอยบากสองรอย สิ่งก่อสร้างที่ใช้ก็เทียบเท่ากับการก่อสร้างโดยใช้วงเวียนและไม้บรรทัด (นโปเลียนใช้ขั้นตอนสำคัญในการพิสูจน์สิ่งนี้)
• การก่อสร้างโดยใช้เครื่องมือที่มีความสามารถจำกัดในปัญหาประเภทนี้ เครื่องมือ (ซึ่งตรงกันข้ามกับการกำหนดปัญหาแบบคลาสสิก) ถือว่าไม่เหมาะ แต่มีข้อ จำกัด: สามารถลากเส้นตรงผ่านจุดสองจุดได้โดยใช้ไม้บรรทัดก็ต่อเมื่อระยะห่างระหว่างจุดเหล่านี้ไม่เกินค่าที่กำหนด ค่า; รัศมีของวงกลมที่วาดโดยใช้เข็มทิศสามารถจำกัดได้จากด้านบน ด้านล่าง หรือทั้งด้านบนและด้านล่าง
• การก่อสร้างโดยใช้ origami แบบแบนดูกฎของ Hujit

ดูสิ่งนี้ด้วย

• โปรแกรมเรขาคณิตแบบไดนามิกช่วยให้คุณสามารถก่อสร้างโดยใช้เข็มทิศและไม้บรรทัดบนคอมพิวเตอร์

หมายเหตุ

วรรณกรรม

• อ. แอดเลอร์ทฤษฎีการก่อสร้างทางเรขาคณิต / การแปลจากภาษาเยอรมัน โดย G. M. Fikhtengolts - ฉบับที่สาม - ล.: อุชเพ็ดกิซ, 2483. - 232 น.
• I.I. อเล็กซานดรอฟการรวบรวมปัญหาการก่อสร้างทางเรขาคณิต - ฉบับที่สิบแปด. - อ.: อุชเพ็ดกิซ, 2493. - 176 น.
• บี.ไอ. อาร์กูนอฟ, เอ็ม.บี. บัลค์- - ฉบับที่สอง. - อ.: อุชเพ็ดกิซ, 2500. - 268 หน้า
• อ. เอ็ม. โวโรเนตส์เรขาคณิตของเข็มทิศ - ม.-ล.: ONTI, 2477. - 40 น. - (ห้องสมุดยอดนิยมด้านคณิตศาสตร์ภายใต้บรรณาธิการทั่วไปของ L. A. Lyusternik)
• วี.เอ. ไกเลอร์ปัญหาการก่อสร้างที่แก้ไม่ได้ // สารหล่อเย็น- - พ.ศ. 2542. - ฉบับที่ 12. - หน้า 115-118.
• วี.เอ. คิริเชนโกะโครงสร้างด้วยเข็มทิศและไม้บรรทัด และทฤษฎีกาลัวส์ // โรงเรียนภาคฤดูร้อน “คณิตศาสตร์สมัยใหม่”- - ดุบนา, 2548.
• ยู.ไอ.มินทร์เล่มที่ 4 เรขาคณิต // สารานุกรมคณิตศาสตร์ระดับประถมศึกษา - ม.: Fizmatgiz, 2506. - 568 หน้า
• วาย. ปีเตอร์เซ่นวิธีการและทฤษฎีในการแก้ปัญหาการก่อสร้างทางเรขาคณิต - M.: โรงพิมพ์ของ E. Lissner และ Y. Roman, 1892. - 114 น.
• V. V. Prasolovปัญหาการก่อสร้างแบบคลาสสิกสามประการ เพิ่มลูกบาศก์เป็นสองเท่า, แบ่งมุมเป็นสามส่วน, ยกกำลังสองเป็นวงกลม - อ.: Nauka, 1992. - 80 น. - (บรรยายยอดนิยมวิชาคณิตศาสตร์)
• เจ. สไตเนอร์โครงสร้างทางเรขาคณิตดำเนินการโดยใช้เส้นตรงและวงกลมคงที่ - อ.: อุชเพ็ดกิซ, 2482. - 80 น.
• หลักสูตรเสริมในวิชาคณิตศาสตร์ 7-9 / คอมพ์ ไอ. แอล. นิโคลสกายา - อ.: การศึกษา, 2534. - น. 80. - 383 น. - ไอ 5-09-001287-3

มูลนิธิวิกิมีเดีย 2010.

ดูว่า "การก่อสร้างโดยใช้เข็มทิศและไม้บรรทัด" ในพจนานุกรมอื่น ๆ คืออะไร:

ไม้บรรทัด - รับคูปองใช้งานได้เพื่อรับส่วนลดจาก AllInstruments ที่ Akademika หรือซื้อไม้บรรทัดที่มีกำไรพร้อมจัดส่งฟรีที่ AllInstruments

สาขาหนึ่งของเรขาคณิตแบบยุคลิดที่รู้จักกันมาตั้งแต่สมัยโบราณ ในงานก่อสร้าง การดำเนินการต่อไปนี้เป็นไปได้: ทำเครื่องหมายจุดใดก็ได้บนเครื่องบิน จุดที่หนึ่งในเส้นที่สร้างขึ้น หรือจุดตัดของเส้นที่สร้างขึ้นสองเส้น ด้วยความช่วยเหลือจาก... ... วิกิพีเดีย

สิ่งก่อสร้างที่ใช้วงเวียนและไม้บรรทัดเป็นสาขาหนึ่งของเรขาคณิตแบบยุคลิดที่รู้จักกันมาตั้งแต่สมัยโบราณ ในงานก่อสร้าง การดำเนินการต่อไปนี้เป็นไปได้: ทำเครื่องหมายจุดใดๆ บนเครื่องบิน, จุดบนเส้นใดเส้นหนึ่งที่สร้างขึ้น หรือจุด... ... Wikipedia

คำนาม, ส., ใช้แล้ว. เปรียบเทียบ บ่อยครั้ง สัณฐานวิทยา: (ไม่) อะไร? การก่อสร้าง อะไรนะ? การก่อสร้าง (ฉันเห็น) อะไร? การก่อสร้าง อะไรนะ? การก่อสร้างเกี่ยวกับอะไร? เกี่ยวกับการก่อสร้าง กรุณา อะไร การก่อสร้าง (ไม่) อะไร? การก่อสร้างอะไรนะ? การก่อสร้าง (ฉันเห็น) อะไร? ก่อสร้างด้วยอะไร?... ... พจนานุกรมอธิบายของ Dmitriev

สถาบันการศึกษาขนาดเล็กแห่งวิทยาศาสตร์ของเด็กนักเรียนแห่งอาชญากรรม

"ซีกเกอร์"

หมวด "คณิตศาสตร์"

โครงสร้างทางเรขาคณิตโดยใช้ไม้บรรทัดสองด้าน

ฉันทำงานเสร็จแล้ว ก

_____________

นักเรียนชั้น

ผู้อำนวยการด้านวิทยาศาสตร์

บทนำ……………………………………………………………………..…..3

I. โครงสร้างทางเรขาคณิตบนเครื่องบิน………………...4

I.1. สัจพจน์ทั่วไปของเรขาคณิตเชิงสร้างสรรค์ สัจพจน์ของเครื่องมือทางคณิตศาสตร์……………………………………………………………………..4

I.2. ……………………….....5

I.3. โครงสร้างทางเรขาคณิตด้วยไม้บรรทัดหนึ่งอัน……………………………..7

ฉัน.4. งานพื้นฐานการก่อสร้างด้วยไม้บรรทัดสองด้าน………..8

I.5. การแก้ปัญหาการก่อสร้างต่างๆ ………………………………12

I.6. โครงสร้างโดยใช้ไม้บรรทัดด้านเดียว………………………………….....20

I.7. ความสามารถในการเปลี่ยนไม้บรรทัดสองด้านกับเข็มทิศและไม้บรรทัด....21

สรุป…………………………………………………………….24

รายการอ้างอิง……………………………..………….25

การแนะนำ

ปัญหาการก่อสร้างด้วยวิธีการอันจำกัด ได้แก่ ปัญหาการก่อสร้างโดยใช้เพียงวงเวียนและไม้บรรทัด ซึ่งถือเป็นหลักสูตรของโรงเรียน เป็นไปได้ไหมที่จะแก้ปัญหาการก่อสร้างด้วยไม้บรรทัดเพียงอันเดียว? บ่อยครั้งที่คุณไม่มีเข็มทิศอยู่ในมือ แต่คุณสามารถหาไม้บรรทัดได้ตลอดเวลา

ปัญหาเกี่ยวกับการก่อสร้างทางเรขาคณิตเป็นส่วนที่น่าสนใจ ความสนใจนั้นเกิดจากความสวยงามและความเรียบง่ายของเนื้อหาทางเรขาคณิต ความเกี่ยวข้องในการพิจารณาปัญหาเหล่านี้เพิ่มขึ้นเนื่องจากมีการใช้ในทางปฏิบัติ ความสามารถในการใช้ไม้บรรทัดหนึ่งอันในการแก้ปัญหาที่พิจารณาในงานนี้มีความสำคัญอย่างยิ่งในกิจกรรมภาคปฏิบัติเพราะว่า เราต้องเผชิญกับปัญหาอย่างต่อเนื่องในการแบ่งส่วนครึ่งหนึ่ง เพิ่มส่วนที่กำหนดเป็นสองเท่า ฯลฯ

บทความนี้จะตรวจสอบงานก่อสร้างหลักที่ใช้เป็นพื้นฐานในการแก้ปัญหาที่ซับซ้อนมากขึ้น

ตามประสบการณ์แสดงให้เห็นว่างานก่อสร้างกระตุ้นความสนใจและมีส่วนช่วยในการกระตุ้นกิจกรรมทางจิต เมื่อทำการแก้ไขความรู้เกี่ยวกับคุณสมบัติของตัวเลขจะถูกนำมาใช้อย่างแข็งขันความสามารถในการให้เหตุผลได้รับการพัฒนาและปรับปรุงทักษะของการสร้างทางเรขาคณิต เป็นผลให้ความสามารถเชิงสร้างสรรค์พัฒนาขึ้นซึ่งเป็นหนึ่งในเป้าหมายของการศึกษาเรขาคณิต

สมมติฐาน: ปัญหาการก่อสร้างทั้งหมดที่สามารถแก้ไขได้โดยใช้เข็มทิศและไม้บรรทัดสามารถแก้ไขได้โดยใช้ไม้บรรทัดสองด้านเท่านั้น

วัตถุประสงค์การศึกษา: งานก่อสร้างและไม้บรรทัดสองด้าน

วัตถุประสงค์การวิจัย: เพื่อพิสูจน์ว่าปัญหาการก่อสร้างทั้งหมดสามารถแก้ไขได้ด้วยความช่วยเหลือของไม้บรรทัดสองด้านเท่านั้น.

วัตถุประสงค์การวิจัย: เพื่อศึกษารากฐานทางทฤษฎีในการแก้ปัญหาการก่อสร้าง แก้ปัญหาการก่อสร้างขั้นพื้นฐานโดยใช้ไม้บรรทัดสองด้าน ยกตัวอย่างงานก่อสร้างที่ซับซ้อนมากขึ้น จัดระบบเนื้อหาทางทฤษฎีและปฏิบัติ

I. โครงสร้างทางเรขาคณิตบนเครื่องบิน

I.1. สัจพจน์ทั่วไปของเรขาคณิตเชิงสร้างสรรค์ สัจพจน์ของเครื่องมือทางคณิตศาสตร์

สำหรับเรขาคณิตเชิงสร้างสรรค์ จำเป็นต้องมีคำอธิบายที่สมบูรณ์ของเครื่องมือเฉพาะอย่างแม่นยำและเพื่อวัตถุประสงค์ทางคณิตศาสตร์ คำอธิบายนี้ให้ไว้ในรูปแบบของสัจพจน์ สัจพจน์เหล่านี้ในรูปแบบทางคณิตศาสตร์เชิงนามธรรมแสดงถึงคุณสมบัติของเครื่องมือวาดภาพจริงที่ใช้สำหรับการสร้างทางเรขาคณิต

เครื่องมือก่อสร้างทางเรขาคณิตที่ใช้กันมากที่สุดคือ:ไม้บรรทัด (ด้านเดียว) , เข็มทิศ, สองด้าน ไม้บรรทัด (มีขอบขนาน) และคนอื่นๆ บ้าง

ก. สัจพจน์ของผู้ปกครอง

ไม้บรรทัดอนุญาตให้คุณสร้างโครงสร้างทางเรขาคณิตต่อไปนี้:
ก) สร้างส่วนที่เชื่อมต่อสองจุดที่สร้างขึ้น

b) สร้างเส้นตรงผ่านจุดที่สร้างขึ้นสองจุด

c) สร้างรังสีที่เล็ดลอดออกมาจากจุดที่สร้างขึ้นและผ่านจุดที่สร้างขึ้นอีกจุดหนึ่ง

ข. สัจพจน์ของเข็มทิศ

เข็มทิศช่วยให้คุณสร้างโครงสร้างทางเรขาคณิตต่อไปนี้:
ก) สร้างวงกลมถ้ามีการสร้างจุดศูนย์กลางของวงกลมและส่วนที่เท่ากับรัศมีของวงกลม (หรือส่วนปลายของวงกลม)

ข. สัจพจน์ของไม้บรรทัดสองด้าน

ไม้บรรทัดสองด้านช่วยให้คุณ:

ก) ดำเนินการก่อสร้างใด ๆ ที่ระบุไว้ในสัจพจน์ A;

b) ในแต่ละระนาบครึ่งที่กำหนดโดยเส้นที่สร้างขึ้น สร้างเส้นขนานกับเส้นนี้และผ่านจากมันในระยะไกลก, ที่ไหน ก - ส่วนที่กำหนดไว้สำหรับไม้บรรทัดที่กำหนด (ความกว้างของไม้บรรทัด)

c) หากมีการสร้างจุด A และ B สองจุด ให้พิจารณาว่า AB จะมากกว่าส่วนคงที่ที่กำหนดหรือไม่ก (ความกว้างของไม้บรรทัด) และถ้า AB >ก จากนั้นสร้างเส้นคู่ขนานสองคู่ที่ผ่านจุด A และ B ตามลำดับ และเว้นระยะห่างจากกันก .

นอกจากเครื่องมือที่ระบุไว้แล้ว คุณสามารถใช้เครื่องมืออื่นๆ สำหรับการก่อสร้างทางเรขาคณิตได้: มุมที่กำหนดเอง, สี่เหลี่ยมจัตุรัส, ไม้บรรทัดพร้อมเครื่องหมาย, มุมฉากคู่หนึ่ง, อุปกรณ์ต่างๆ สำหรับการวาดเส้นโค้งพิเศษ ฯลฯ

I.2. หลักการทั่วไปในการแก้ปัญหาการก่อสร้าง

งานก่อสร้าง ประกอบด้วยความจริงที่ว่าจำเป็นต้องสร้างตัวเลขบางอย่างด้วยเครื่องมือที่ระบุหากได้รับตัวเลขอื่นและมีการระบุความสัมพันธ์บางอย่างระหว่างองค์ประกอบของตัวเลขที่ต้องการและองค์ประกอบของตัวเลขนี้

แต่ละตัวเลขที่ตรงตามเงื่อนไขของปัญหาเรียกว่าการตัดสินใจงานนี้

ค้นหาวิธีแก้ปัญหา งานก่อสร้างหมายถึงการลดการก่อสร้างพื้นฐานให้เหลือจำนวนจำกัด เช่น ระบุลำดับที่จำกัดของการก่อสร้างพื้นฐาน หลังจากนั้นร่างที่ต้องการจะได้รับการพิจารณาให้สร้างขึ้นโดยอาศัยสัจพจน์ที่ยอมรับของเรขาคณิตเชิงสร้างสรรค์ รายการการก่อสร้างพื้นฐานที่ยอมรับได้ และผลที่ตามมาคือความคืบหน้าในการแก้ปัญหา ขึ้นอยู่กับว่าใช้เครื่องมือเฉพาะใดในการก่อสร้าง

แก้ไขปัญหาการก่อสร้าง - วิธี, ค้นหาวิธีแก้ปัญหาทั้งหมด .

คำจำกัดความสุดท้ายต้องมีการชี้แจงบางอย่าง ตัวเลขที่ตรงตามเงื่อนไขของปัญหาอาจแตกต่างกันทั้งรูปร่างหรือขนาด และตำแหน่งบนระนาบ ความแตกต่างในตำแหน่งบนเครื่องบินจะถูกนำมาพิจารณาหรือไม่นำมาพิจารณา ขึ้นอยู่กับการกำหนดของปัญหาการก่อสร้างนั้นเอง โดยขึ้นอยู่กับว่าสภาพของปัญหานั้นให้หรือไม่ได้ระบุตำแหน่งที่แน่นอนของตัวเลขที่ต้องการเทียบกับตัวเลขที่กำหนดใดๆ .

หากพบวิธีแก้ไขปัญหาในอนาคตจะได้รับอนุญาตให้ใช้วิธีแก้ปัญหานี้ "โดยรวม" นั่นคือโดยไม่ต้องแบ่งออกเป็นโครงสร้างหลัก

มีปัญหาการก่อสร้างทางเรขาคณิตง่ายๆ หลายประการ ซึ่งมักรวมไว้เป็นองค์ประกอบในการแก้ปัญหาที่ซับซ้อนมากขึ้น เราจะเรียกพวกเขาว่าปัญหาการก่อสร้างทางเรขาคณิตเบื้องต้น แน่นอนว่ารายการงานเบื้องต้นนั้นมีเงื่อนไข งานพื้นฐานมักมีดังต่อไปนี้:

แบ่งส่วนนี้ออกครึ่งหนึ่ง

การแบ่งมุมที่กำหนดออกเป็นสองส่วน

การสร้างเซ็กเมนต์บนบรรทัดที่กำหนดจะเท่ากับส่วนที่กำหนด

การสร้างมุมเท่ากับมุมที่กำหนด

การสร้างเส้นที่ผ่านจุดที่กำหนดขนานกับเส้นที่กำหนด

การสร้างเส้นที่ผ่านจุดที่กำหนดและตั้งฉากกับเส้นที่กำหนด

การแบ่งส่วนในส่วนนี้

การสร้างรูปสามเหลี่ยมโดยใช้ด้านที่กำหนดสามด้าน

การสร้างรูปสามเหลี่ยมโดยใช้ด้านหนึ่งและมุมสองมุมที่อยู่ติดกัน

การสร้างรูปสามเหลี่ยมโดยใช้สองด้านและมุมระหว่างสองด้าน

ในการแก้ปัญหาการก่อสร้างที่ค่อนข้างซับซ้อนจะเกิดคำถามว่า จะหาเหตุผลอย่างไร เพื่อหาทางแก้ไขปัญหา เพื่อให้ได้ทางแก้ไขปัญหาทั้งหมด เพื่อหาเงื่อนไขความเป็นไปได้ในการแก้ปัญหา เป็นต้น ดังนั้น เมื่อแก้ไขปัญหาเชิงสร้างสรรค์ พวกเขาใช้โครงร่างการแก้ปัญหา ประกอบด้วยสี่ขั้นตอนต่อไปนี้:

1) การวิเคราะห์;
2) การก่อสร้าง;
3) หลักฐาน;
4) การวิจัย

I.3. โครงสร้างทางเรขาคณิตด้วยไม้บรรทัดเดียว

เราจะพิจารณาไม้บรรทัดจากสองมุมมอง: ในฐานะไม้บรรทัดและไม้บรรทัดสองด้าน

1. ไม้บรรทัดสองด้านความกว้าง ก เราจะเรียกไม้บรรทัดที่มีขอบขนานกันซึ่งอยู่ในระยะไกล ก จากกันทำให้สามารถสร้างได้โดยตรง:

ก) เส้นตรงโดยพลการ;

b) เส้นตรงที่ผ่านจุดสองจุดที่ให้หรือได้รับในกระบวนการแก้ไขปัญหา

c) เส้นขนานซึ่งแต่ละเส้นผ่านจุดใดจุดหนึ่งซึ่งมีระยะห่างระหว่างกันมากกว่าก (ในการก่อสร้างนี้ ไม้บรรทัดอยู่ในตำแหน่งที่แต่ละขอบขนานกันทั้งสองมีจุดที่กำหนด ในกรณีนี้ เราจะพูดถึงการก่อสร้างโดยตรง)

ความกว้างของไม้บรรทัดในการก่อสร้างนี้ถือว่าคงที่ดังนั้นหากในกระบวนการแก้ไขปัญหาเฉพาะเจาะจงจำเป็นต้องทำการก่อสร้างโดยตรงโดยสัมพันธ์กับบางจุดที่ได้รับกและ ใน แล้วเราต้องพิสูจน์ความยาวเอบีอีกต่อไป ก .

เราจะพิจารณาจุดที่จะสร้างหากเป็นจุดหนึ่งในข้อมูลหรือเป็นจุดตัดของเส้นสองเส้นที่สร้างขึ้น ในทางกลับกันเราจะพิจารณาสร้างเส้นตรงหากผ่านจุดที่สร้างหรือกำหนดไว้

การใช้ไม้บรรทัดสองด้านคุณสามารถสร้างสิ่งต่อไปนี้ได้

ก) คุณสามารถวาดเส้นตรงผ่านจุดสองจุดใดก็ได้และมีเพียงจุดเดียวเท่านั้น

b) ไม่ว่าเส้นตรงจะเป็นเส้นตรงก็ตาม จะมีเส้นตรงสองเส้นอยู่ในระนาบขนานกับเส้นนั้นและแยกออกจากระนาบนั้นด้วยระยะห่างก .

c) ผ่านสองจุด A และ B ที่ AB ก เป็นไปได้ที่จะวาดเส้นขนานสองคู่ตรง; โดยมีเอบี = ก คุณสามารถวาดเส้นคู่ขนานได้โดยมีระยะห่างระหว่างกันเท่ากันก .

ถ้าให้หนึ่ง สอง สามคะแนน ก็ไม่สามารถสร้างคะแนนใหม่ได้

(รูปที่ 1);

ถ้าให้สี่คะแนน โดยสามจุด (หรือทั้งสี่) อยู่บนเส้นเดียวกัน ก็ไม่สามารถสร้างจุดอื่นได้ (รูปที่ 2)

หากคุณได้รับจุดสี่จุดที่วางอยู่บนจุดยอดของสี่เหลี่ยมด้านขนาน คุณสามารถสร้างจุดศูนย์กลางได้เพียงจุดเดียวเท่านั้น (รูปที่ 3)

เมื่อยอมรับสิ่งที่กล่าวมาข้างต้นแล้ว ให้เราพิจารณาแยกปัญหาที่แก้ไขได้ด้วยไม้บรรทัดสองด้าน

ฉัน.4. งานพื้นฐานในการสร้างด้วยไม้บรรทัดสองด้าน

1
. สร้างเส้นแบ่งครึ่งของมุม ABC

สารละลาย: (รูปที่ 4)

ก  (ใน ค) และ ข  (วงดนตรี  ข = ดี .

เราได้รับบี ดี– แบ่งครึ่ง  เอบีซี

แท้จริงแล้วได้รับจาก

การสร้างสี่เหลี่ยมด้านขนานคือ

รูปสี่เหลี่ยมขนมเปียกปูน เนื่องจากส่วนสูงเท่ากัน ในดี –

เส้นทแยงมุมของสี่เหลี่ยมขนมเปียกปูนคือเส้นแบ่งครึ่ง เอบีซี รูปที่ 4

2
. เพิ่มมุม ABC เป็นสองเท่า

สารละลาย : (รูปที่ 5) ก) ก  (เอบี)

ก  (ใน ค)= ดี , ผ่านจุด B และ ดี

ข โดยตรง;

b) ผ่านจุด B และดี ม  ข

โดยตรง,ข Ç ก = เอฟ .

เราได้รับ Ð เอบี เอฟ = 2 Ð เอบีซี .

รูปที่ 5

3 - ถึงเส้นตรงที่กำหนด M เอ็น ในเรื่องนี้

วาดเส้นตั้งฉากกับจุด A

สารละลาย : (รูปที่ 6)

1) (เอเอ 1) || (บีบี 1) || (อส.1) –

โดยตรง (บี (ม เอ็น),

กับ Î (ม เอ็น- 2) ผ่าน A และ B

ม || n - โดยตรง,

ม Ç (อส.1) = ดี .

เราได้รับ (ก ดี )  (ม เอ็น ).

รูปที่ 6.

4
. ผ่านจุดที่กำหนดไม่โกหก

เส้นที่กำหนด วาดเส้นตั้งฉาก

ถึง บรรทัดนี้

สารละลาย: ผ่านจุดนี้ O เราวาด

เส้นสองเส้นตัดกันที่กำหนด

เส้นตรง AB และเพิ่มมุมของผลลัพธ์เป็นสองเท่า

สามเหลี่ยมที่อยู่ติดกันนี้

ตรง.  โอเอ เอ็น = 2  โอเอวีและ

อ.บ เอ็น = 2  OVA (รูปที่ 7)

รูปที่ 7

5. สร้างจุดที่สมมาตรกับเส้นที่กำหนดโดยสัมพันธ์กับเส้นที่กำหนด

สารละลาย: ดูปัญหาที่ 4 (จุด O มีความสมมาตรต่อจุดเอ็น- รูปที่ 7)

6. ดำเนินการเป็นเส้นตรง ขนานไปกับสิ่งนี้

ป
ตรงเอ็ม เอ็น ผ่านจุด A ไม่ใช่

อยู่ในสาย M เอ็น .

โซลูชันที่ 1: (รูปที่ 8)

1)(เอเอ 1) || (บีบี 1) || (อส.1) || (วว 1 ) || (เคเค 1) -

– โดยตรง (SA)Ç (บีบี 1) = ค 2;

2) (ด้วย 2 K) Ç (วว 1 ) = เอฟ .

(ก เอฟ ) คือเส้นตรงที่ต้องการ

รูปที่ 8

โซลูชันที่ 2 . ในรูปที่ 8 1 มีหมายเลขกำกับอยู่

ลำดับของเส้นตรง

โดยที่ 1, 2 และ 3 ขนานกัน

การก่อสร้างโดยตรง

(ก เอฟ) || (ม เอ็น).

รูปที่ 8 1

7
. แบ่ง AB ส่วนนี้ออกเป็นสองส่วน

โซลูชันที่ 1 (รูปที่ 9) (เฉพาะกรณีที่ความกว้างของไม้บรรทัดน้อยกว่าความยาวของส่วนนี้เท่านั้น) ลากเส้นคู่ขนานสองคู่ผ่านโดยตรง

ส่วนปลายของส่วนนี้แล้วจึงเป็นเส้นทแยงมุม

รูปสี่เหลี่ยมขนมเปียกปูนที่เกิดขึ้น O – AB กลาง

ข้าว. 9.

โซลูชันที่ 2 (รูปที่ 9 ก)

1) ก || (วงดนตรี ข || (AB) – โดยตรง;

2) (อาร์), (อาร์)Ç ก = C, (เอพี) Ç ข = ดี ;

3) (ดี ใน) Ç ก = ม, (SV) Ç ข = เอ็น ;

4) (ม เอ็น ) Ç (AB) = K;

5) (ดี ถึง) Ç (ก เอ็น ) = เอฟ ;

6) (บี เอฟ ) Ç ข = ดี 1, (บ เอฟ ) Ç ก = ค 1;

7) (ดี ใน ) Ç (ก ดี 1 ) = X,

(เอซี 1) Ç (สวี) = ซี.

8) (เอ็กซ์ ซี) Ç (เอบี) =อ. เราได้ AO = OB

รูปที่ 9,ก

โซลูชันที่ 3 .(ข้าว. 9, ข)

ตามที่ทราบกันดีอยู่แล้ว , ตรงกลางสี่เหลี่ยมคางหมู

ฐาน, จุดตัดกัน

เส้นทแยงมุมและจุดตัด

ส่วนขยายของด้านข้าง

นอนอยู่บนเส้นตรงเดียวกัน

1) ม || (AB) – โดยตรง;

2) ค Î ม , ดี Î ม , (เช่น) Ç (ใน ดี ) = ถึง; รูปที่ 9,ข

3) (ตะวันออกเฉียงเหนือ) Ç (ก ดี ) = เอฟ ; 4) (เค เอฟ ) Ç (เอบี) =อ. เราได้ AO = OB

I.5. แก้ไขปัญหาการก่อสร้างต่างๆ

ในการแก้ปัญหาการก่อสร้างต่อไปนี้โดยใช้เพียงไม้บรรทัดสองด้าน จะใช้การสร้างเส้นคู่ขนานโดยตรงและปัญหาหลักเจ็ดประการข้างต้น

1. ลากเส้นตั้งฉากสองเส้นผ่านจุดนี้

ร สารละลาย: ผ่านจุดนี้ไปเถอะ

สองบรรทัดโดยพลการ

แล้ว - แบ่งครึ่ง

มุมที่อยู่ติดกัน (รูปที่ 10)

รูปที่ 10

2. เมื่อพิจารณาจากส่วน A ดี เมื่อกำหนดความยาว

สร้างส่วนที่มีความยาวเท่ากับ

ร
การตัดสินใจ : มาดำเนินการกัน ม  กและ ชม. || ม ผ่าน

จุดก ฉ || (ก ดี ) , เค || (ค.ศ) โดยตรง.

ลองวาด AB และ AC โดยที่ B =ฉ  ม ,

ค = ม  เค - ในลักษณะที่ทราบแล้ว

แบ่ง AB และ AC ออกเป็นสองส่วนและ

ลองวาดค่ามัธยฐานของสามเหลี่ยมกัน

เอบีซี โดยทรัพย์สินของมัธยฐาน

สามเหลี่ยม, O ดี = - แสวง

ส่วน (รูปที่ 11)

ข้าว. สิบเอ็ด

3. สร้างส่วนที่มีความยาว

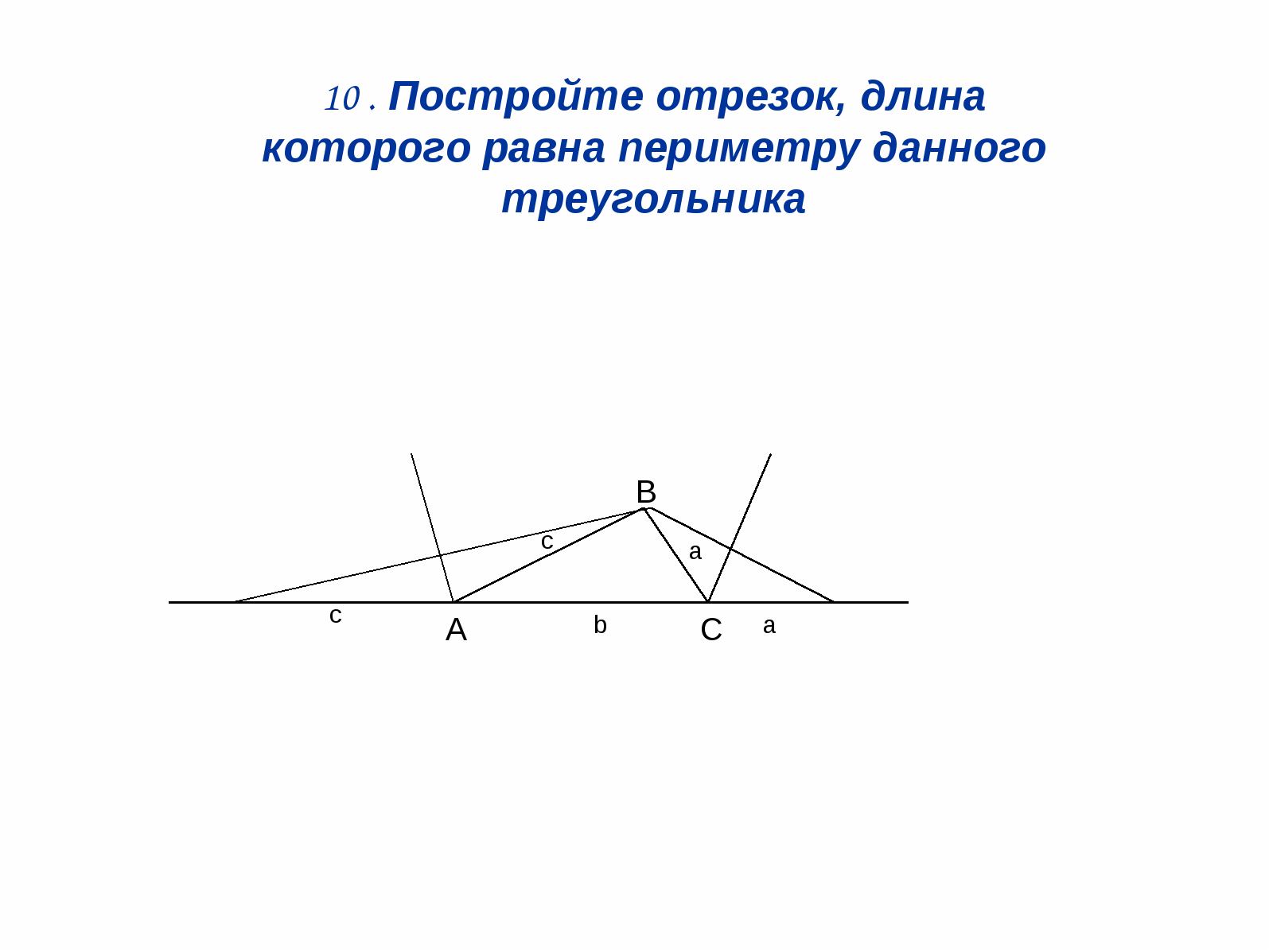เท่ากับเส้นรอบรูปของสามเหลี่ยมที่กำหนด

สารละลาย: (รูปที่ 12) มาสร้างเส้นแบ่งครึ่งกัน

มุมด้านนอกสองมุมของรูปสามเหลี่ยม จากนั้น

3 ยอด ใน มาวาดตั้งฉากกันดีกว่า

ถึงเส้นแบ่งครึ่งเหล่านี้

เด = ก + ข + ส

รูปที่ 12

4. เมื่อพิจารณาส่วนของความยาว a สร้างส่วนความยาว 2ก, 3ก

ร สารละลาย: (รูปที่ 13)

1ม เอ็น) || (AB) และ (ม 1 เอ็น 1 ) || (ม เอ็น) || (ม2 เอ็น 2 ) –

โดยตรง;

2) (CA) และ (CB) ถึง A และ B

จำเป็นต้องมีเซ็กเมนต์ A 1 B 1 และ A 2 B 2

วิธีแก้ไขปัญหานี้ก็คือ

ที่ได้จากการแก้ปัญหาข้อที่ 7

ข้าว. 13

5. เส้นตรงจะมีสองส่วน โดยมีความยาว a และ ข - สร้างส่วนที่มีความยาวเท่ากับ + ข , ข - ก, ( ก + ข )/2 และ ( ข - ก )/2 .

สารละลาย: และสำหรับ ก + ข(รูปที่ 14 ก)

รูปที่ 14a

ข) สำหรับ ( ก + ข)/2 (รูปที่ 14, b)

1) (ก 1 ข 1) || (ก 2 บี 2) || (AB) – โดยตรง;

2) ม Î (ก 2 บี 2), (เอ็มเอ็กซ์) Ç (ก 1 ข 1 ) = เอ็น, (ม ชม) Ç (ก 1 ข 1 ) = ป;

3) (พี) Ç (ก 2 ข 2) = ล, (แอลแซด ) Ç (ก 1 ข 1 ) = โอ้

เราได้รับ: เอ็น โอ = เอ็นพี + ปณ. =
.

ข้าว. 14 บี

ค) สำหรับ ข - ก(รูปที่ 14 ค)

ข้าว. 14,ว

ค) สำหรับ ( ข - ก )/2 (รูปที่ 14,ง)

ข้าว. 14,ก

6
. สร้างศูนย์กลางของวงกลมนี้

สารละลาย : (รูปที่ 15) ลองวาดเส้นตรง AB

ตัดวงกลมที่จุด A และ B;

ดวงอาทิตย์  AB โดยที่ C คือจุดตัด

มีวงกลม

ผ่านจุด C เราวาดขนานกับ AB

ตรงซี ดี- กับดีตัดกันเป็นวงกลม

ตรงจุดดี.

กำลังเชื่อมต่อดีด้วย B และ A กับ C เราได้

จุดที่ต้องการคือจุดศูนย์กลางของวงกลม ข้าว. 15

โซลูชันที่ 2: (รูปที่ 16) ใช้ไม้บรรทัดสองด้านสร้างคอร์ดขนานกันสองคอร์ดค.ศ และบี.ซี. - เราได้สี่เหลี่ยมคางหมูหน้าจั่วเอบีซีดี- อนุญาตเค และป - จุดตัดกันของเส้นเอ.ซี. และบีดี , เอบี และกระแสตรง - แล้วตรงป เค ผ่านจุดกึ่งกลางของฐานของสี่เหลี่ยมคางหมูที่ตั้งฉากกับพวกมัน ซึ่งหมายความว่ามันผ่านจุดศูนย์กลางของวงกลมที่กำหนด ในทำนองเดียวกัน การสร้างเส้นตรงอีกเส้นหนึ่ง เราจะพบจุดศูนย์กลางของวงกลม

ข้าว. 16

7. ให้ค่าส่วนโค้งของวงกลม สร้างจุดศูนย์กลางของวงกลม

สารละลาย . (รูปที่ 17) ทำเครื่องหมายสามจุด A, B และ C บนส่วนโค้งนี้ ใช้ไม้บรรทัดที่ส่วนท้ายของส่วน AB แล้วลากตามขอบ เราได้เส้นขนานสองเส้น การเปลี่ยนตำแหน่งของไม้บรรทัดเราวาดเส้นคู่ขนานอีกสองเส้น เราได้สี่เหลี่ยมขนมเปียกปูน (สี่เหลี่ยมด้านขนานที่มีความสูงเท่ากัน) เส้นทแยงมุมด้านหนึ่งของสี่เหลี่ยมขนมเปียกปูนคือเส้นแบ่งครึ่งตั้งฉากกับส่วนนั้นเอบี เนื่องจากเส้นทแยงมุมของสี่เหลี่ยมขนมเปียกปูนอยู่บนเส้นแบ่งครึ่งตั้งฉากกับเส้นทแยงมุมอีกเส้นหนึ่ง ในทำนองเดียวกัน เราสร้างเส้นแบ่งครึ่งตั้งฉากกับเซ็กเมนต์เอ.ซี. - จุดตัดของเส้นแบ่งครึ่งที่สร้างขึ้นคือจุดศูนย์กลางของวงกลมที่ต้องการ

ข้าว. 17

8. เมื่อกำหนดเซ็กเมนต์ AB ซึ่งเป็นเส้นไม่ขนาน l และมีจุด M อยู่บนนั้น ใช้ไม้บรรทัดสองด้านสร้างจุดตัดของเส้นตรง l โดยมีวงกลมรัศมี AB กับจุดศูนย์กลาง M

สารละลาย: (รูปที่ 18)

มาทำสามเหลี่ยมให้สมบูรณ์กันเถอะเอ.บี.เอ็ม. ถึงสี่เหลี่ยมด้านขนานเอบีเอ็นเอ็ม - ให้เราสร้างเส้นแบ่งครึ่ง MT และนางสาวมุมระหว่างมนและตรงล . มาวาดจุดกันเอ็น เส้นขนานกับเส้นแบ่งครึ่งเหล่านี้:เอ็นคิว || นางสาว, NR || เอ็ม.ที.- มท│ นางสาวเป็นเส้นแบ่งครึ่งของมุมที่อยู่ติดกัน วิธี,เอ็นคิว │ MT นั่นคือในรูปสามเหลี่ยมเอ็นเอ็มคิวเส้นแบ่งครึ่งคือความสูง ดังนั้นสามเหลี่ยมจึงเป็นหน้าจั่ว:ตรม = มน- เช่นเดียวกัน,นาย. = มน- คะแนนถามและรแสวง.

ข้าว. 18

9. ให้เส้นตรง l และส่วน OA ขนานกับ l ใช้ไม้บรรทัดสองด้านสร้างจุดตัดของเส้นตรง l โดยมีวงกลมรัศมี OA กับจุดศูนย์กลาง O

สารละลาย: (รูปที่ 19 ก)

มาทำไดเร็กกันเถอะล 1 ขนานไปกับเส้นโอเอ และห่างไกลจากมันก - ลองเอามันไปเป็นเส้นตรงดูล จุดใดก็ได้บี - อนุญาตบี 1 - จุดตัดของเส้นโอ.บี. และล 1 - มาวาดจุดกันบี 1 ตรง, ขนานเอบี - เส้นนี้ตัดกันเส้นนี้โอเอ ตรงจุดก 1 - ให้เราวาดผ่านจุดต่างๆโอ และก 1 เส้นขนานคู่หนึ่งซึ่งมีระยะห่างระหว่างพวกมันคือก (สามารถมีได้สองคู่ของเส้นดังกล่าว); อนุญาตเอ็กซ์ และเอ็กซ์ 1 - จุดตัดของเส้นที่ผ่านจุดหนึ่งโอ โดยมีเส้นตรงล และล 1 - เพราะโอเอ 1 = วัว 1 และ ∆โอเอ 1 เอ็กซ์ 1 ∆ โอเอเอ็กซ์ จากนั้น OA = OX ชี้เอ็กซ์ ตามหา

ในทำนองเดียวกัน เราสร้างจุดตัดที่สองของวงกลมและเส้น - จุดย(รูปที่ 18 ข)

ข้าว. 18,ก

ข้าว. 18 บี

I.6.โครงสร้างโดยใช้ไม้บรรทัดด้านเดียว

ซี
ที่นี่เราพิจารณากรณีพิเศษ: ให้คะแนน Pถาม, อาร์ 1 และถาม 1 - และพวกมันนอนอยู่ที่จุดยอดของสี่เหลี่ยมคางหมู

1. แบ่งส่วน P ถาม ครึ่งหนึ่ง

สารละลาย แสดงในรูปที่ 19

ให้คะแนน Pถาม, อาร์ 1 และถาม 1 และเส้นคู่ขนาน

รถาม, อาร์ 1 ถาม 1 - มาดำเนินการ Rถาม 1  ถามร 1 = บี , ร.ร 1  คิวคิว 1 = ก

มาเชื่อมต่อจุด A และ B. AB กัน รถาม = เอฟ- กลาง

ส่วนพีถาม.

ข้าว. 19

2. เพิ่มส่วนเป็นสองเท่า ร 1 ถาม 1.

ร
การตัดสินใจ แสดงในรูปที่ 20 มาสร้างกัน

จุดเอฟ– ตรงกลางของส่วน Pถามและเชื่อมต่อมัน

กับถาม 1. ร 1 ถาม FQ 1 = M. มาดำเนินการ RM กันเถอะ RM ร 1 ถาม 1 = ร

ความเท่าเทียมกันอาร์คิวและป 1 ถาม 1 ตามมาจากความคล้ายคลึงกัน

สามเหลี่ยม RMเอฟและ รมถาม 1 ,

เอฟมถามและ ร 1 มถาม 1 และความเท่าเทียมกัน PเอฟและFQ.

ข้าว. 20

3
. สร้างส่วนความยาว n  ร 1 ถาม 1 .

ม – 1 ส่วนเท่ากัน Pถาม 2 , ถาม 2 ถาม 3, … ถาม ม -1 ถาม ม

จากนั้นเราสร้าง (ร.ร 1 ) และถาม ม ถาม 1 และเชื่อมต่อ

จุดตัด A กับจุด

ถาม 2 , ถาม 3, … ถาม ม ได้รับม -1 โดยตรง

แบ่งร 1 ถาม 1 บนม เท่ากัน ชิ้นส่วน

สำหรับม = 4 วิธีแก้ไขจะแสดงในรูปที่ 22

รูปที่.22

I.7. ความสามารถในการเปลี่ยนไม้บรรทัดสองด้านด้วยเข็มทิศและไม้บรรทัด

ให้เราพิสูจน์ว่าไม้บรรทัดสองด้านสามารถใช้แทนกันได้กับเข็มทิศและไม้บรรทัด เมื่อต้องการทำเช่นนี้ เราพิสูจน์ข้อความต่อไปนี้:

ข้อความที่ 1: การสร้างทั้งหมดที่สามารถทำได้ด้วยเข็มทิศและไม้บรรทัดสามารถทำได้ด้วยไม้บรรทัดสองด้าน

เนื่องจากเมื่อสร้างด้วยเข็มทิศและไม้บรรทัด ไม้บรรทัดจะลากเส้นผ่านจุดสองจุด และเข็มทิศจะสร้างวงกลม (ค้นหาชุดของจุดที่อยู่ห่างจากจุดที่กำหนดให้เท่ากัน) จากนั้นสิ่งก่อสร้างทั้งหมดที่มีเข็มทิศและไม้บรรทัดจะลดลงเหลือ การสร้างจุดตัดกันของเส้นตรงสองเส้น วงกลมสองวง และวงกลมที่มีเส้นตรง

จุดตัดของเส้นตรงสองเส้นสามารถสร้างขึ้นได้โดยใช้ไม้บรรทัด

จุดตัดของวงกลมและเส้นตรง (รูปที่ 23):

การก่อสร้าง:ให้กำหนดส่วน AB - รัศมีของวงกลมเป็นเส้นตรงล , จุดศูนย์กลางของวงกลม O แล้ว:

1) เราดำเนินการ OS ||ล , ระบบปฏิบัติการ = AB

2) เราดำเนินการ OS ||เคและห่างไกลจากก.

3) เราดำเนินการโอ.ดี., โอ.ดี. ล = ดี; โอ.ดี. k) ตามข้อพิสูจน์ของทฤษฎีบทของทาเลส

4) ตามกฎแห่งการผ่านของความเท่าเทียมกัน

5) พิจารณาออมคิวอี. ออมคิวอีเป็นสี่เหลี่ยมด้านขนาน เนื่องจาก OM ||อีคิวและ OE ||เอ็ม.ซี.(ด้านของไม้บรรทัดขนานกัน) ลองพิสูจน์ว่านี่คือสี่เหลี่ยมขนมเปียกปูน

5.1) ความประพฤติคิวแซด โอ.ซี.และคิวจี บน, แล้วคิวจี = คิวแซด = ก.

5.2)  โอมคิว =  รม(นอนขวาง);  ระบบปฏิบัติการ =บนซึ่งเป็นสิ่งที่จำเป็นต้องได้รับการพิสูจน์

จุดตัดของวงกลมสองวง: คล้ายกัน

ข้อความที่ 2: โครงสร้างทั้งหมดที่สามารถทำได้ด้วยไม้บรรทัดสองด้านสามารถทำได้โดยใช้เข็มทิศและเส้นตรง

ในการดำเนินการนี้ เราจะดำเนินการตามมาตรฐานการก่อสร้างสำหรับไม้บรรทัดสองด้านโดยใช้เข็มทิศและไม้บรรทัด

1) เส้นตรงที่ใช้สองจุดสร้างได้ง่ายโดยใช้ไม้บรรทัด

2) การสร้างเส้นตรงขนานกับเส้นที่กำหนดและนำออกจากระยะที่กำหนด:

2.1) ให้กำหนดเส้นตรงเคและส่วนความยาวก.

2.2) สร้างเส้นตรงตามอำเภอใจข เค, อนุญาตเค ข= บี.

2.3) เปิดขทั้งสองด้านของจุดบีบนเส้นตรงขกันชิ้นส่วนที่มีความยาวไว้กปล่อยให้จุดคและดี.

2.4) ผ่านจุดคสร้างเส้นตรงค เค.

2.5) ผ่านจุดดีสร้างเส้นตรงง เค.

2.6) ทางตรงคและง-จำเป็นเพราะว่าบี.ซี.และบีดีเท่ากันกโดยการก่อสร้างและมีระยะเท่ากับระยะห่างระหว่างเส้นตรงเคและตรง

3) การสร้างเส้นขนานกันและผ่านจุดที่กำหนดสองจุด และระยะห่างระหว่างจุดเหล่านั้นเท่ากับส่วนที่กำหนด:

3.1) ปล่อยให้คะแนนได้รับกและบีและส่วนความยาวก.

3.2) การสร้างวงกลมโดยมีจุดศูนย์กลางอยู่ที่จุดหนึ่งกและรัศมีก.

3.3) สร้างเส้นสัมผัสกันของวงกลมที่กำหนดผ่านจุดหนึ่งบี- มีสองแทนเจนต์ดังกล่าวถ้าบีอยู่นอกวงกลม (ถ้าเอบี> ก) หนึ่งถ้าบีอยู่บนวงกลม (ถ้าเอบี= ก) ไม่มีถ้าบีอยู่ภายในวงกลม (เอบี< ก- แทนเจนต์นี้เป็นหนึ่งในเส้นที่เรากำลังมองหา มันยังคงผ่านจุดนั้นไปกเส้นตรงขนานไปกับมัน

3.4) เนื่องจากเส้นหนึ่งตั้งฉากกับรัศมีของวงกลมในรูปแทนเจนต์ เส้นที่สองจึงตั้งฉากกับเส้นนั้นด้วย (เนื่องจากเส้นขนานกัน) ดังนั้น ระยะห่างระหว่างเส้นทั้งสองจึงเท่ากับรัศมี ซึ่งโดยการก่อสร้างจะเท่ากับกซึ่งเป็นสิ่งที่จำเป็นต้องได้รับ

ดังนั้นเราจึงได้พิสูจน์ความสามารถในการใช้แทนกันได้ของไม้บรรทัดสองด้านกับเข็มทิศและไม้บรรทัด

สรุป: ไม้บรรทัดสองด้านสามารถใช้แทนกันได้กับเข็มทิศและไม้บรรทัด

บทสรุป

ดังนั้นคำถามเกี่ยวกับความเป็นไปได้ในการใช้ไม้บรรทัดหนึ่งอันในการแก้ปัญหาการก่อสร้างแบบคลาสสิกโดยใช้เข็มทิศและไม้บรรทัดจึงได้รับการพิจารณาและแก้ไข ปรากฎว่าปัญหาการก่อสร้างสามารถแก้ไขได้โดยใช้เพียงไม้บรรทัดที่มีขอบขนานกัน เมื่อแก้ไขปัญหาที่ซับซ้อนมากขึ้น เราควรพึ่งพาสิ่งก่อสร้างพื้นฐานที่เรียกว่าโครงสร้างพื้นฐานที่กล่าวถึงในงานนี้เพิ่มเติม

เนื้อหาที่นำเสนอสามารถนำไปใช้ได้โดยตรงไม่เพียงแต่ในบทเรียนคณิตศาสตร์ ในชั้นเรียนคณิตศาสตร์เท่านั้น แต่ยังรวมถึงกิจกรรมภาคปฏิบัติด้วย

รายชื่อวรรณกรรมที่ใช้แล้ว

อาลีฟ เอ.วี. โครงสร้างทางเรขาคณิต คณิตศาสตร์ที่โรงเรียน 2521 ฉบับที่ 3

เกลเซอร์ จี.ไอ. ประวัติคณิตศาสตร์ที่โรงเรียน ม. การตรัสรู้. 1981.

เดปแมน ไอ.ยา. ด้านหลังหน้าหนังสือเรียนคณิตศาสตร์ ม.. ตรัสรู้. 2532.

Elensky Shch ตามรอยพีทาโกรัส ม., เดตกิซ. 1961.

พจนานุกรมสารานุกรมของนักคณิตศาสตร์รุ่นเยาว์ ม., การสอน. 1985

ในงานก่อสร้างเราจะพิจารณาการสร้างรูปทรงเรขาคณิตซึ่งสามารถทำได้โดยใช้ไม้บรรทัดและเข็มทิศ

การใช้ไม้บรรทัดทำให้คุณสามารถ:

เส้นตรงโดยพลการ

เส้นตรงที่ผ่านจุดที่กำหนด

เส้นตรงที่ผ่านจุดที่กำหนดสองจุด

เมื่อใช้เข็มทิศ คุณสามารถอธิบายวงกลมที่มีรัศมีที่กำหนดจากจุดศูนย์กลางที่กำหนดได้

การใช้เข็มทิศทำให้คุณสามารถวาดส่วนบนเส้นที่กำหนดจากจุดที่กำหนดได้

พิจารณางานก่อสร้างหลัก

ภารกิจที่ 1สร้างสามเหลี่ยมโดยให้ด้าน a, b, c (รูปที่ 1)

สารละลาย. ใช้ไม้บรรทัดวาดเส้นตรงใดๆ แล้วกำหนดจุด B บนเส้นนั้น โดยการใช้ช่องเข็มทิศเท่ากับ a เราจะอธิบายวงกลมที่มีจุดศูนย์กลาง B และรัศมี a ให้ C เป็นจุดตัดกับเส้นตรง เมื่อเข็มทิศเปิดเท่ากับ c เราจะอธิบายวงกลมจากศูนย์กลาง B และเมื่อเข็มทิศเปิดเท่ากับ b เราจะอธิบายวงกลมจากศูนย์กลาง C โดยให้ A เป็นจุดตัดของวงกลมเหล่านี้ สามเหลี่ยม ABC มีด้านเท่ากับ a, b, c

ความคิดเห็น เพื่อให้ส่วนของเส้นตรงสามเส้นทำหน้าที่เป็นด้านของสามเหลี่ยม จำเป็นที่เส้นที่ใหญ่ที่สุดจะต้องน้อยกว่าผลรวมของอีกสองเส้นที่เหลือ (และ< b + с).

ภารกิจที่ 2

สารละลาย. มุมที่มีจุดยอด A และรังสี OM แสดงในรูปที่ 2

ให้เราวาดวงกลมตามใจชอบโดยมีจุดศูนย์กลางอยู่ที่จุดยอด A ของมุมที่กำหนด ให้ B และ C เป็นจุดตัดของวงกลมกับด้านข้างของมุม (รูปที่ 3, a) ด้วยรัศมี AB เราวาดวงกลมโดยมีศูนย์กลางอยู่ที่จุด O - จุดเริ่มต้นของรังสีนี้ (รูปที่ 3, b) ให้เราแสดงจุดตัดของวงกลมนี้ด้วยรังสีนี้เป็น C 1 . ให้เราอธิบายวงกลมที่มีศูนย์กลาง C 1 และรัศมี BC จุด B 1 ของจุดตัดของวงกลมสองวงอยู่ที่ด้านข้างของมุมที่ต้องการ สิ่งนี้ตามมาจากความเท่าเทียมกัน Δ ABC = Δ OB 1 C 1 (เครื่องหมายที่สามของความเท่าเทียมกันของรูปสามเหลี่ยม)

ภารกิจที่ 3สร้างเส้นแบ่งครึ่งของมุมนี้ (รูปที่ 4)

สารละลาย. จากจุดยอด A ของมุมที่กำหนด เช่นเดียวกับจากจุดศูนย์กลาง เราวาดวงกลมที่มีรัศมีตามใจชอบ ให้ B และ C เป็นจุดตัดกับด้านข้างของมุม จากจุด B และ C เราอธิบายวงกลมที่มีรัศมีเท่ากัน ให้ D เป็นจุดตัดกัน แตกต่างจาก A. เรย์ AD ตัดมุม A ตามมาจากความเท่าเทียมกัน Δ ABD = Δ ACD (เกณฑ์ที่สามสำหรับความเท่าเทียมกันของรูปสามเหลี่ยม)

ภารกิจที่ 4วาดเส้นแบ่งครึ่งตั้งฉากกับส่วนนี้ (รูปที่ 5)

สารละลาย. ด้วยการใช้การเปิดเข็มทิศแบบอิสระแต่เหมือนกัน (ขนาดใหญ่กว่า 1/2 AB) เราจะอธิบายส่วนโค้งสองส่วนที่มีจุดศูนย์กลางอยู่ที่จุด A และ B ซึ่งจะตัดกันที่จุด C และ D บางจุด เส้น CD เส้นตรงจะเป็นเส้นตั้งฉากที่ต้องการ จริงๆ แล้ว ดังที่เห็นได้จากการก่อสร้าง แต่ละจุด C และ D อยู่ห่างจาก A และ B เท่าๆ กัน ดังนั้นจุดเหล่านี้จึงต้องอยู่บนเส้นแบ่งครึ่งตั้งฉากกับส่วน AB

ภารกิจที่ 5แบ่งส่วนนี้ออกครึ่งหนึ่ง แก้ไขได้ในลักษณะเดียวกับปัญหาที่ 4 (ดูรูปที่ 5)

ภารกิจที่ 6ผ่านจุดที่กำหนด ให้ลากเส้นตั้งฉากกับเส้นที่กำหนด

สารละลาย. มีสองกรณีที่เป็นไปได้:

1) จุดที่กำหนด O อยู่บนเส้นตรงที่กำหนด a (รูปที่ 6)

จากจุด O เราวาดวงกลมโดยมีรัศมีใดก็ได้ตัดกับเส้น a ที่จุด A และ B จากจุด A และ B เราวาดวงกลมที่มีรัศมีเท่ากัน ให้ O 1 เป็นจุดตัดกัน แตกต่างจาก O เราจะได้ OO 1 ⊥ AB ที่จริงแล้ว จุด O และ O 1 นั้นมีระยะห่างเท่ากันจากปลายส่วน AB ดังนั้นจึงอยู่บนเส้นแบ่งครึ่งตั้งฉากกับส่วนนี้

สถาบันการศึกษางบประมาณเทศบาล

มัธยมศึกษาปีที่ 34 มีการศึกษารายวิชาเชิงลึกรายวิชา

ส่วน MAN ฟิสิกส์และคณิตศาสตร์

“การก่อสร้างทางเรขาคณิตโดยใช้เข็มทิศและไม้บรรทัด”

เสร็จสิ้นโดย: นักเรียนชั้นประถมศึกษาปีที่ 7 “A”

บาติชเชวา วิกตอเรีย

หัวหน้า: Koltovskaya V.V.

โวโรเนซ, 2013

3. การสร้างมุมให้เท่ากับมุมที่กำหนด

ป ลองวาดวงกลมตามใจชอบโดยมีจุดศูนย์กลางอยู่ที่จุดยอด A ของมุมที่กำหนด (รูปที่ 3) ให้ B และ C เป็นจุดตัดของวงกลมกับด้านข้างของมุม ด้วยรัศมี AB เราวาดวงกลมโดยมีจุดศูนย์กลางอยู่ที่จุด O ซึ่งเป็นจุดเริ่มต้นของครึ่งเส้นนี้ ให้เราแสดงจุดตัดของวงกลมนี้ด้วยเส้นครึ่งเส้นนี้เป็น C 1 - ให้เราอธิบายวงกลมที่มีจุดศูนย์กลาง C 1 และรูปที่ 3

รัศมีของเครื่องบิน จุด ข 1 จุดตัดของวงกลมที่สร้างขึ้นในระนาบครึ่งที่ระบุนั้นอยู่ที่ด้านข้างของมุมที่ต้องการ

6. การสร้างเส้นตั้งฉาก

เราวาดวงกลมโดยมีรัศมีใดก็ได้ r โดยมีจุดศูนย์กลางอยู่ที่จุด O ในรูปที่ 6 วงกลมตัดเส้นที่จุด A และ Bจากจุด A และ B เราวาดวงกลมที่มีรัศมี AB ให้ความโศกเศร้า C เป็นจุดตัดของวงกลมเหล่านี้ เราได้รับคะแนน A และ B ในขั้นตอนแรก เมื่อสร้างวงกลมที่มีรัศมีตามใจชอบ

เส้นตรงที่ต้องการผ่านจุด C และ O

รูปที่ 6

ปัญหาที่ทราบ

1.ปัญหาของพรหมคุปต์

สร้างรูปสี่เหลี่ยมที่จารึกไว้โดยใช้ด้านทั้งสี่ แนวทางหนึ่งใช้วงกลมอะพอลโลเนียสมาแก้ปัญหาของ Apollonius โดยใช้การเปรียบเทียบระหว่างสามเหลี่ยมสามวงกลมกับสามเหลี่ยมกัน วิธีที่เราค้นหาวงกลมที่ถูกจารึกไว้ในรูปสามเหลี่ยม: เราสร้างจุดตัดของเส้นแบ่งครึ่ง, วางเส้นตั้งฉากจากนั้นไปที่ด้านข้างของสามเหลี่ยม, ฐานของเส้นตั้งฉาก (จุดตัดของเส้นตั้งฉากกับด้านที่มัน หล่นลงมา) และให้สามแต้มแก่เรานอนอยู่บนวงกลมที่ต้องการ วาดวงกลมผ่านจุดทั้งสามนี้ - วิธีแก้ปัญหาพร้อมแล้ว เราจะทำเช่นเดียวกันกับปัญหาของอพอลโลเนียส

2. ปัญหาของอพอลโลเนียส

ใช้เข็มทิศและไม้บรรทัด สร้างวงกลมแทนวงกลมทั้งสามวงที่กำหนด ตามตำนาน ปัญหาดังกล่าวถูกกำหนดโดย Apollonius แห่ง Perga ประมาณ 220 ปีก่อนคริสตกาล จ. ในหนังสือ "Touches" ซึ่งสูญหายไป แต่ได้รับการบูรณะในปี 1600 โดย François Viète "Gallic Apollonius" ตามที่คนรุ่นเดียวกันเรียกเขาว่า

หากไม่มีวงกลมใดวงกลมหนึ่งอยู่ภายในอีกวงกลมหนึ่ง แสดงว่าปัญหานี้มีวิธีแก้ไขที่แตกต่างกันอย่างมาก 8 วิธี

การสร้างรูปหลายเหลี่ยมปกติ

ป

ถูกต้อง (หรือ ด้านเท่ากันหมด ) สามเหลี่ยม - นี้ รูปหลายเหลี่ยมปกติมีสามด้าน ซึ่งเป็นด้านแรกของรูปหลายเหลี่ยมปกติ ทั้งหมดด้านของสามเหลี่ยมปกติ เท่าเทียมกันและทั้งหมดมุมคือ 60° ในการสร้างสามเหลี่ยมด้านเท่า คุณต้องแบ่งวงกลมออกเป็น 3 ส่วนเท่าๆ กัน ในการทำเช่นนี้จำเป็นต้องวาดส่วนโค้งรัศมี R ของวงกลมนี้จากปลายด้านหนึ่งของเส้นผ่านศูนย์กลางเพียงด้านเดียวเราจะได้ส่วนที่หนึ่งและสอง ส่วนที่สามอยู่ที่ปลายด้านตรงข้ามของเส้นผ่านศูนย์กลาง เมื่อเชื่อมต่อจุดเหล่านี้ เราจะได้สามเหลี่ยมด้านเท่า

หกเหลี่ยมปกติ สามารถสร้างโดยใช้เข็มทิศและไม้บรรทัด ด้านล่างมีการกำหนดวิธีการก่อสร้างโดยการแบ่งวงกลมออกเป็น 6 ส่วน เราใช้ความเท่ากันของด้านของรูปหกเหลี่ยมปกติกับรัศมีของวงกลมที่ล้อมกรอบไว้ จากปลายด้านตรงข้ามของเส้นผ่านศูนย์กลางด้านใดด้านหนึ่งของวงกลม เราจะอธิบายส่วนโค้งของรัศมี R จุดตัดกันของส่วนโค้งเหล่านี้กับวงกลมที่กำหนดจะแบ่งออกเป็น 6 ส่วนเท่าๆ กัน โดยการเชื่อมต่อจุดที่พบตามลำดับจะได้รูปหกเหลี่ยมปกติ

การก่อสร้างรูปห้าเหลี่ยมปกติ

ป
รูปห้าเหลี่ยมปกติสามารถเป็นได้สร้างขึ้นโดยใช้วงเวียนและไม้บรรทัด หรือโดยการต่อให้เข้ากับที่กำหนดวงกลมหรือการก่อสร้างตามด้านที่กำหนด กระบวนการนี้อธิบายโดย Euclidในองค์ประกอบของเขาประมาณ 300 ปีก่อนคริสตกาล จ.

ต่อไปนี้เป็นวิธีหนึ่งในการสร้างรูปห้าเหลี่ยมปกติในวงกลมที่กำหนด:

สร้างวงกลมที่จะจารึกรูปห้าเหลี่ยมไว้และทำเครื่องหมายตรงกลางเป็นโอ - (นี่คือวงกลมสีเขียวในแผนภาพด้านขวา)

เลือกจุดบนวงกลมก ซึ่งจะเป็นหนึ่งในจุดยอดของรูปห้าเหลี่ยม สร้างเส้นตรงผ่านโอ และก .

สร้างเส้นตั้งฉากกับเส้นโอเอ ,ผ่านจุดโอ - กำหนดทางแยกด้านใดด้านหนึ่งโดยให้วงกลมเป็นจุดบี .

พล็อตจุดค อยู่ตรงกลางระหว่างโอ และบี .

ค ผ่านจุดก - ทำเครื่องหมายจุดตัดด้วยเส้นโอ.บี. (ภายในวงกลมเดิม) เป็นจุดดี .

วาดวงกลมโดยให้จุดศูนย์กลางอยู่ที่ก ผ่านจุด D ทำเครื่องหมายจุดตัดของวงกลมนี้โดยมีจุดเดิม (วงกลมสีเขียว) เป็นจุดอี และเอฟ .

วาดวงกลมโดยให้จุดศูนย์กลางอยู่ที่อี ผ่านจุดก ช .

วาดวงกลมโดยให้จุดศูนย์กลางอยู่ที่เอฟ ผ่านจุดก - กำหนดจุดตัดอีกจุดหนึ่งโดยให้วงกลมเดิมเป็นจุดชม .

สร้างรูปห้าเหลี่ยมปกติเออีจีเอฟ .

ปัญหาที่แก้ไขไม่ได้

งานก่อสร้างสามประการต่อไปนี้ถูกกำหนดไว้ในสมัยโบราณ:

การแยกมุม - แบ่งมุมตามใจชอบออกเป็นสามส่วนเท่า ๆ กัน

กล่าวอีกนัยหนึ่ง จำเป็นต้องสร้างมุมไตรเซกเตอร์ - รังสีแบ่งมุมออกเป็นสามส่วนเท่า ๆ กัน P. L. Wanzel พิสูจน์ในปี 1837 ว่าปัญหาจะแก้ได้ก็ต่อเมื่อ ตัวอย่างเช่น การแยกสามส่วนสามารถทำได้สำหรับมุม α = 360°/n โดยมีเงื่อนไขว่าจำนวนเต็ม n ไม่สามารถหารด้วย 3 ลงตัวได้ อย่างไรก็ตาม ในสื่อเป็นครั้งคราว (ไม่ถูกต้อง ) มีการเผยแพร่วิธีการไตรภาคมุมด้วยเข็มทิศและไม้บรรทัด

เพิ่มลูกบาศก์เป็นสองเท่า - ปัญหาคลาสสิกโบราณของการก่อสร้างด้วยเข็มทิศและไม้บรรทัดที่ขอบของลูกบาศก์ ซึ่งมีปริมาตรเป็นสองเท่าของปริมาตรของลูกบาศก์ที่กำหนด

ในสัญกรณ์สมัยใหม่ ปัญหาจะลดลงเหลือเพียงการแก้สมการเท่านั้น. ทั้งหมดนี้มาจากปัญหาในการสร้างส่วนที่มีความยาว- P. Wantzel พิสูจน์ในปี 1837 ว่าปัญหานี้ไม่สามารถแก้ไขได้โดยใช้วงเวียนและไม้บรรทัด

กำลังสองวงกลม - งานที่ประกอบด้วยการหาสิ่งก่อสร้างโดยใช้เข็มทิศและไม้บรรทัดของสี่เหลี่ยมจัตุรัสซึ่งมีพื้นที่เท่ากับวงกลมที่กำหนด.

ดังที่คุณทราบ ด้วยความช่วยเหลือของเข็มทิศและไม้บรรทัด คุณสามารถดำเนินการทางคณิตศาสตร์ทั้ง 4 รายการและแยกรากที่สองได้ ตามมาว่าการยกกำลังสองของวงกลมเป็นไปได้ก็ต่อเมื่อสามารถสร้างส่วนของความยาว π ได้โดยใช้การกระทำดังกล่าวในจำนวนจำกัด ดังนั้น ความไม่สามารถแก้ปัญหานี้ได้จึงเป็นไปตามธรรมชาติที่ไม่ใช่พีชคณิต (ความเหนือกว่า) ของจำนวน π ซึ่งได้รับการพิสูจน์โดยลินเดมันน์ในปี พ.ศ. 2425

ปัญหาที่รู้จักกันดีอีกประการหนึ่งที่ไม่สามารถแก้ไขได้โดยใช้เข็มทิศและไม้บรรทัดก็คือการสร้างรูปสามเหลี่ยมโดยใช้ความยาวเส้นแบ่งครึ่งที่กำหนดสามเส้น .

ยิ่งไปกว่านั้น ปัญหานี้ยังคงไม่สามารถแก้ไขได้แม้ว่าจะมีไตรเซกเตอร์ก็ตาม

เฉพาะในศตวรรษที่ 19 เท่านั้นที่ได้รับการพิสูจน์แล้วว่าปัญหาทั้งสามนั้นไม่สามารถแก้ไขได้โดยใช้เพียงเข็มทิศและเส้นตรง คำถามเกี่ยวกับความเป็นไปได้ของการก่อสร้างได้รับการแก้ไขอย่างสมบูรณ์โดยวิธีพีชคณิตตามทฤษฎี Galois

คุณรู้หรือเปล่าว่า...

(จากประวัติความเป็นมาของการก่อสร้างทางเรขาคณิต)

กาลครั้งหนึ่งมีการลงทุนความหมายลึกลับในการสร้างรูปหลายเหลี่ยมปกติ

ดังนั้นชาวพีทาโกรัสซึ่งเป็นสาวกของคำสอนทางศาสนาและปรัชญาที่ก่อตั้งโดยพีทาโกรัสและอาศัยอยู่ในสมัยกรีกโบราณ (วีฉัน-ฉัน วีศตวรรษ พ.ศ ก่อนคริสต์ศักราช) ใช้รูปหลายเหลี่ยมรูปดาวที่เกิดจากเส้นทแยงมุมของรูปห้าเหลี่ยมปกติเป็นสัญลักษณ์ของการรวมตัวของพวกเขา

กฎสำหรับการสร้างทางเรขาคณิตที่เข้มงวดของรูปหลายเหลี่ยมปกติกำหนดไว้ในหนังสือ "องค์ประกอบ" โดยนักคณิตศาสตร์ชาวกรีกโบราณ Euclid ซึ่งอาศัยอยู่ในสามวี. พ.ศ. เพื่อดำเนินการก่อสร้างเหล่านี้ Euclid เสนอให้ใช้เพียงไม้บรรทัดและเข็มทิศ ซึ่งในเวลานั้นไม่มีอุปกรณ์บานพับสำหรับเชื่อมต่อขา (ข้อจำกัดดังกล่าวในเครื่องมือเป็นข้อกำหนดที่ไม่เปลี่ยนรูปของคณิตศาสตร์โบราณ)

รูปหลายเหลี่ยมปกติถูกนำมาใช้กันอย่างแพร่หลายในดาราศาสตร์โบราณ หาก Euclid สนใจในการสร้างตัวเลขเหล่านี้จากมุมมองของคณิตศาสตร์ดังนั้นสำหรับนักดาราศาสตร์ชาวกรีกโบราณ Claudius Ptolemy (ประมาณ 90 - 160 AD) ก็กลายเป็นสิ่งจำเป็นในฐานะเครื่องมือเสริมในการแก้ปัญหาทางดาราศาสตร์ ดังนั้นในหนังสือเล่มที่ 1 ของ Almagests บทที่สิบทั้งหมดจึงอุทิศให้กับการสร้างรูปห้าเหลี่ยมและรูปสิบเหลี่ยมปกติ

อย่างไรก็ตาม นอกเหนือจากงานทางวิทยาศาสตร์ล้วนๆ แล้ว การสร้างรูปหลายเหลี่ยมปกติยังเป็นส่วนสำคัญของหนังสือสำหรับช่างก่อสร้าง ช่างฝีมือ และศิลปิน ความสามารถในการแสดงภาพบุคคลเหล่านี้เป็นที่ต้องการมานานแล้วในสถาปัตยกรรม เครื่องประดับ และวิจิตรศิลป์

“หนังสือสิบเล่มเกี่ยวกับสถาปัตยกรรม” ของสถาปนิกชาวโรมัน Vitruvius (ผู้มีชีวิตอยู่ประมาณ 63-14 ปีก่อนคริสตกาล) กล่าวว่ากำแพงเมืองควรมีรูปแบบของรูปหลายเหลี่ยมปกติในแผน และหอคอยของป้อมปราการ “ควรทำทรงกลมหรือเหลี่ยม สำหรับจตุรัสที่ค่อนข้างจะถูกทำลายด้วยอาวุธปิดล้อม”

แผนผังของเมืองเป็นที่สนใจอย่างมากสำหรับ Vitruvius ซึ่งเชื่อว่าจำเป็นต้องวางแผนถนนเพื่อไม่ให้ลมหลักพัดมา สันนิษฐานว่ามีลมเช่นนี้อยู่แปดแบบและพัดไปในทิศทางใดทิศทางหนึ่ง

ในช่วงยุคเรอเนซองส์ การสร้างรูปหลายเหลี่ยมปกติ และโดยเฉพาะรูปห้าเหลี่ยม ไม่ใช่เกมคณิตศาสตร์ง่ายๆ แต่เป็นข้อกำหนดเบื้องต้นที่จำเป็นสำหรับการสร้างป้อมปราการ

รูปหกเหลี่ยมปกติเป็นเรื่องของการศึกษาพิเศษโดยนักดาราศาสตร์และนักคณิตศาสตร์ชาวเยอรมันผู้ยิ่งใหญ่ โยฮันเนส เคปเลอร์ (ค.ศ. 1571-1630) ซึ่งเขาพูดถึงในหนังสือ "ของขวัญปีใหม่หรือเกล็ดหิมะหกเหลี่ยม" เมื่อกล่าวถึงสาเหตุที่เกล็ดหิมะมีรูปทรงหกเหลี่ยม เขาตั้งข้อสังเกตเป็นพิเศษดังต่อไปนี้: “... เครื่องบินสามารถถูกปกคลุมได้โดยไม่มีช่องว่างด้วยตัวเลขต่อไปนี้เท่านั้น: สามเหลี่ยมด้านเท่า, สี่เหลี่ยมจัตุรัสและรูปหกเหลี่ยมปกติ ในบรรดาตัวเลขเหล่านี้ รูปหกเหลี่ยมปกติครอบคลุมพื้นที่ที่ใหญ่ที่สุด"

นักวิทยาศาสตร์ที่มีชื่อเสียงที่สุดคนหนึ่งที่เกี่ยวข้องกับการก่อสร้างทางเรขาคณิตคือศิลปินและนักคณิตศาสตร์ชาวเยอรมันผู้ยิ่งใหญ่ Albrecht Durer (1471 - 1528) ซึ่งอุทิศส่วนสำคัญของหนังสือ "Manuals..." ของเขาให้กับพวกเขา เขาเสนอกฎสำหรับการสร้างรูปหลายเหลี่ยมปกติที่มีด้าน 3, 4, 5... 16 ด้าน วิธีการแบ่งวงกลมที่ Dürer เสนอนั้นไม่เป็นสากล แต่จะใช้เทคนิคเฉพาะในแต่ละกรณี

Dürer ใช้วิธีการสร้างรูปหลายเหลี่ยมปกติในการปฏิบัติงานทางศิลปะ เช่น เมื่อสร้างเครื่องประดับและลวดลายต่างๆ สำหรับไม้ปาร์เก้ เขาร่างรูปแบบดังกล่าวระหว่างเดินทางไปเนเธอร์แลนด์ ซึ่งพบพื้นปาร์เกต์ในบ้านหลายหลัง

ดูเรอร์แต่งเครื่องประดับจากรูปหลายเหลี่ยมปกติซึ่งเชื่อมต่อกันเป็นวงแหวน (วงแหวนที่มีรูปสามเหลี่ยมด้านเท่าหกรูป รูปสี่เหลี่ยมจัตุรัสสี่รูป รูปหกเหลี่ยมสามหรือหกรูป รูปเจ็ดเหลี่ยมสิบสี่รูปแปดเหลี่ยมสี่รูป)

บทสรุป

ดังนั้น,โครงสร้างทางเรขาคณิต เป็นวิธีการแก้ปัญหาที่ได้คำตอบเป็นภาพกราฟิก การก่อสร้างดำเนินการโดยใช้เครื่องมือวาดภาพที่มีความแม่นยำและความแม่นยำสูงสุดในการทำงานเนื่องจากความถูกต้องของการแก้ปัญหาขึ้นอยู่กับสิ่งนี้

ต้องขอบคุณงานนี้ ฉันจึงได้คุ้นเคยกับประวัติความเป็นมาของเข็มทิศ คุ้นเคยกับกฎเกณฑ์ในการก่อสร้างทางเรขาคณิตมากขึ้น ได้รับความรู้ใหม่ ๆ และนำไปประยุกต์ใช้ในทางปฏิบัติ
การแก้ปัญหาที่เกี่ยวข้องกับการก่อสร้างด้วยวงเวียนและไม้บรรทัดเป็นงานอดิเรกที่มีประโยชน์ซึ่งช่วยให้คุณสามารถดูคุณสมบัติที่ทราบของรูปทรงเรขาคณิตและองค์ประกอบของรูปทรงเรขาคณิตได้ใหม่บทความนี้จะกล่าวถึงปัญหาเร่งด่วนที่สุดที่เกี่ยวข้องกับการสร้างทางเรขาคณิตโดยใช้วงเวียนและไม้บรรทัด มีการพิจารณาปัญหาหลักและเสนอแนวทางแก้ไข ปัญหาที่กำหนดเป็นประเด็นที่สนใจในทางปฏิบัติอย่างมาก รวบรวมความรู้ที่ได้รับในเรขาคณิต และสามารถนำไปใช้งานภาคปฏิบัติได้
ดังนั้นงานจึงบรรลุตามเป้าหมาย งานที่ได้รับมอบหมายจึงสำเร็จลุล่วง

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt=">การก่อสร้างโดยใช้ไม้บรรทัดและเข็มทิศ เรขาคณิต">!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="> สร้างเซ็กเมนต์เท่ากับ Ú ปัญหา A B ที่กำหนด"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="> การสร้างมุมเท่ากับมุมที่กำหนด พิจารณารูปสามเหลี่ยม"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="> การสร้างเส้นแบ่งครึ่งของปัญหามุม Ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="> การสร้างเส้นตั้งฉาก Ú ปัญหาการกำหนดเส้น"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="> การสร้างจุดกึ่งกลางของงานส่วน Ú สร้างจุดกึ่งกลางของ ที่ให้ไว้"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}