Ví dụ

Chia một đoạn làm đôi

Bài toán chia đôi. Dùng compa và thước kẻ để chia đoạn thẳng này AB thành hai phần bằng nhau. Một trong những giải pháp được thể hiện trong hình:

• Dùng compa vẽ đường tròn tâm tại các điểm MỘT Và B bán kính AB.
• Tìm giao điểm P Và Q hai vòng tròn được xây dựng (cung).
• Dùng thước vẽ đoạn thẳng đi qua các điểm P Và Q.
• Tìm điểm giữa mong muốn của đoạn AB- điểm giao nhau AB Và PQ.

định nghĩa chính thức

Trong các bài toán dựng hình, xét tập hợp tất cả các điểm trên mặt phẳng, tập hợp tất cả các đường thẳng của mặt phẳng và tập hợp tất cả các đường tròn của mặt phẳng, trên đó cho phép thực hiện các phép toán sau:

1. Chọn một điểm trong tập hợp tất cả các điểm:
   1. điểm tùy ý
   2. điểm tùy ý trên một dòng nhất định
   3. điểm tùy ý trên một vòng tròn nhất định
   4. giao điểm của hai đường thẳng cho trước
   5. điểm giao nhau/tiếp tuyến của một đường thẳng và một đường tròn cho trước
   6. điểm giao nhau/tiếp tuyến của hai đường tròn cho trước
2. "Bằng cách sử dụng những cây thước» chọn một dòng từ tập hợp tất cả các dòng:
   1. đường thẳng tùy ý
   2. một đường thẳng tùy ý đi qua một điểm cho trước
   3. một đường thẳng đi qua hai điểm cho trước
3. "Bằng cách sử dụng la bàn» chọn một vòng tròn từ tập hợp tất cả các vòng tròn:
   1. vòng tròn tùy ý
   2. một đường tròn tùy ý có tâm tại một điểm cho trước
   3. một đường tròn tùy ý có bán kính bằng khoảng cách giữa hai điểm đã cho
   4. một đường tròn có tâm tại một điểm cho trước và có bán kính bằng khoảng cách giữa hai điểm cho trước

Trong các điều kiện của bài toán, một tập hợp các điểm nhất định được chỉ định. Cần phải sử dụng một số hữu hạn các phép toán trong số các phép toán có thể chấp nhận được liệt kê ở trên để xây dựng một tập hợp điểm khác có mối quan hệ cho trước với tập hợp ban đầu.

Giải pháp cho vấn đề xây dựng bao gồm ba phần thiết yếu:

1. Mô tả phương pháp xây dựng một tập hợp nhất định.
2. Chứng minh rằng tập hợp được xây dựng theo cách được mô tả thực sự có mối quan hệ nhất định với tập hợp ban đầu. Thông thường việc chứng minh việc xây dựng được tiến hành như một chứng minh thông thường của định lý, dựa trên các tiên đề và các định lý đã được chứng minh khác.
3. Phân tích phương pháp xây dựng được mô tả về khả năng áp dụng của nó cho các phiên bản khác nhau của các điều kiện ban đầu, cũng như tính duy nhất hoặc không duy nhất của giải pháp thu được bằng phương pháp được mô tả.

Sự cố đã biết

• Bài toán xây dựng đường tròn tiếp xúc với ba đường tròn cho trước của Apollonius. Nếu không có đường tròn nào nằm bên trong đường tròn kia thì bài toán này có 8 nghiệm khác nhau đáng kể.
• Bài toán Brahmagupta dựng một tứ giác nội tiếp bằng bốn cạnh của nó.

Xây dựng đa giác đều

Các nhà hình học cổ đại đã biết cách xây dựng chính xác N-giác cho , , và .

Công trình có thể và không thể

Tất cả các cách xây dựng không gì khác hơn là nghiệm của một phương trình nào đó, và các hệ số của phương trình này có liên quan đến độ dài của các đoạn đã cho. Vì vậy, thật thuận tiện khi nói về việc xây dựng một số - một nghiệm đồ họa cho một phương trình thuộc một loại nhất định. Trong khuôn khổ các yêu cầu trên, có thể thực hiện các công trình sau:

• Xây dựng nghiệm của phương trình tuyến tính.
• Xây dựng giải pháp cho phương trình bậc hai.

Nói cách khác, chỉ có thể xây dựng các số bằng biểu thức số học bằng cách sử dụng căn bậc hai của các số ban đầu (độ dài của các đoạn). Ví dụ,

Các biến thể và khái quát

• Công trình sử dụng một la bàn. Theo định lý Mohr-Mascheroni, với sự trợ giúp của một la bàn, bạn có thể dựng bất kỳ hình nào có thể dựng được bằng la bàn và thước kẻ. Trong trường hợp này, một đường thẳng được coi là được xây dựng nếu có hai điểm được chỉ định trên đó.
• Công trình sử dụng một thước kẻ. Dễ dàng nhận thấy rằng với sự trợ giúp của một thước kẻ, chỉ có thể thực hiện được các phép dựng hình ảnh bất biến. Đặc biệt, thậm chí không thể chia một đoạn thành hai phần bằng nhau hoặc tìm tâm của một đường tròn đã vẽ. Nhưng nếu có một đường tròn được vẽ sẵn trên mặt phẳng với tâm được đánh dấu, bằng cách sử dụng thước, bạn có thể thực hiện các phép dựng tương tự như với compa và thước (định lý Poncelet-Steiner (định lý Poncelet-Steiner (định lý Poncelet-Steiner) Tiếng Anh)), 1833. Nếu có hai khía trên thước thì các công trình xây dựng sử dụng nó tương đương với các công trình sử dụng la bàn và thước kẻ (Napoléon đã thực hiện một bước quan trọng trong việc chứng minh điều này).
• Công trình sử dụng các công cụ có khả năng hạn chế. Trong các bài toán thuộc loại này, các công cụ (ngược lại với công thức cổ điển của bài toán) được coi là không lý tưởng nhưng bị hạn chế: một đường thẳng đi qua hai điểm chỉ có thể được vẽ bằng thước nếu khoảng cách giữa các điểm này không vượt quá một giá trị nhất định. giá trị; bán kính của các vòng tròn được vẽ bằng la bàn có thể được giới hạn từ phía trên, phía dưới hoặc cả phía trên và phía dưới.
• Công trình sử dụng origami phẳng. xem quy tắc Hujit

Xem thêm

• Các chương trình hình học động cho phép bạn thực hiện các công trình bằng la bàn và thước kẻ trên máy tính.

Ghi chú

Văn học

• A. Adler Lý thuyết về công trình hình học / Bản dịch từ tiếng Đức của G. M. Fikhtengolts. - Ấn bản thứ ba. - L.: Uchpedgiz, 1940. - 232 tr.
• I. I. Alexandrov Tuyển tập các bài toán xây dựng hình học. - Ấn bản thứ mười tám. - M.: Uchpedgiz, 1950. - 176 tr.
• B. I. Argunov, M. B. Balk. - Phiên bản thứ hai. - M.: Uchpedgiz, 1957. - 268 tr.
• A. M. Voronets Hình học của la bàn. - M.-L.: ONTI, 1934. - 40 tr. - (Thư viện phổ biến về toán học dưới sự tổng biên tập của L. A. Lyusternik).
• V. A. Geiler Những vấn đề xây dựng không thể giải quyết // chất làm mát. - 1999. - Số 12. - Tr. 115-118.
• V. A. Kirichenko Các công trình bằng la bàn và thước kẻ và lý thuyết Galois // Trường hè “Toán học hiện đại”. -Dubna, 2005.
• Yu. I. Manin Quyển IV. Hình học // Bách khoa toàn thư toán tiểu học. - M.: Fizmatgiz, 1963. - 568 tr.
• Y. Petersen Các phương pháp và lý thuyết giải các bài toán xây dựng hình học. - M.: Nhà in của E. Lissner và Y. Roman, 1892. - 114 tr.
• V. V. Prasolov Ba vấn đề xây dựng cổ điển. Nhân đôi một hình lập phương, chia một góc, bình phương một hình tròn. - M.: Nauka, 1992. - 80 tr. - (Bài giảng phổ biến về toán học).
• J. Steiner Các công trình hình học được thực hiện bằng đường thẳng và đường tròn cố định. - M.: Uchpedgiz, 1939. - 80 tr.
• Khóa học tùy chọn về toán học. 7-9 / Comp. I. L. Nikolskaya. - M.: Giáo dục, 1991. - Tr. 80. - 383 tr. - ISBN 5-09-001287-3

Quỹ Wikimedia. 2010.

Xem thêm “Xây dựng bằng compa và thước kẻ” trong các từ điển khác:

Thước kẻ - nhận phiếu giảm giá đang hoạt động cho AllInstruments tại Akademika hoặc mua thước kẻ để kiếm lời và giao hàng miễn phí khi bán tại AllInstruments

Một nhánh của hình học Euclide, được biết đến từ thời cổ đại. Trong các nhiệm vụ xây dựng, có thể thực hiện các thao tác sau: Đánh dấu một điểm tùy ý trên mặt phẳng, một điểm trên một trong các đường đã dựng hoặc điểm giao nhau của hai đường đã dựng. Với sự giúp đỡ của... ... Wikipedia

Công trình xây dựng sử dụng la bàn và thước kẻ là một nhánh của hình học Euclide được biết đến từ thời cổ đại. Trong các nhiệm vụ xây dựng, có thể thực hiện các thao tác sau: Đánh dấu một điểm tùy ý trên mặt phẳng, một điểm trên một trong các đường được xây dựng hoặc một điểm... ... Wikipedia

Danh từ, s., được sử dụng. so sánh thường Hình thái: (không) cái gì? xây dựng, cái gì? xây dựng, (tôi hiểu) cái gì? xây dựng, cái gì? xây dựng, về cái gì? về xây dựng; làm ơn. Cái gì? xây dựng, (không) cái gì? công trình xây dựng, cái gì? công trình xây dựng, (tôi hiểu) cái gì? xây dựng, bằng cái gì?... ... Từ điển giải thích của Dmitriev

HỌC VIỆN KHOA HỌC NHỎ CỦA HỌC SINH CRIMEA

"Người TÌM KIẾM"

Phần "Toán học"

CÔNG TRÌNH HÌNH HỌC SỬ DỤNG THƯỚC ĐÔI MẶT

Tôi đã hoàn thành công việc MỘT

_____________

học sinh lớp

Giám đốc khoa học

GIỚI THIỆU………………………………..…..3

I. CÔNG CỤ HÌNH HỌC TRÊN MẶT BAY………….4

I.1. Các tiên đề chung của hình học kiến ​​tạo. Tiên đề của các công cụ toán học………………………………..4

I.2. ……………………….....5

I.3. Các công trình hình học bằng một thước đo………………………..7

TÔI.4. Các thao tác cơ bản khi dựng hình bằng thước hai mặt…………..8

I.5. Giải quyết các vấn đề khác nhau trong xây dựng …………………….12

I.6. Công trình bằng thước kẻ một phía……………………….20

I.7. Khả năng hoán đổi của thước hai mặt với compa và thước kẻ....21

KẾT LUẬN…………………………………………………….24

Danh sách tài liệu tham khảo…………..………….25

Giới thiệu

Các bài toán liên quan đến việc xây dựng với phương tiện hạn chế bao gồm các bài toán liên quan đến việc xây dựng chỉ sử dụng la bàn và thước kẻ, được đưa vào chương trình giảng dạy ở trường. Có thể giải quyết vấn đề xây dựng chỉ với một cây thước? Thường thì bạn không có la bàn trong tay, nhưng bạn luôn có thể tìm thấy một chiếc thước kẻ.

Các bài toán về công trình trong hình học là một phần hấp dẫn. Sự quan tâm đến nó là do vẻ đẹp và sự đơn giản của nội dung hình học của nó. Sự liên quan của việc xem xét những vấn đề này tăng lên do chúng được sử dụng trong thực tế. Khả năng sử dụng một cây thước để giải các bài toán nêu trong luận văn này có ý nghĩa rất quan trọng trong hoạt động thực tiễn, bởi vì Chúng ta liên tục phải đối mặt với các vấn đề về chia một phân khúc làm đôi, nhân đôi một phân khúc nhất định, v.v.

Bài viết này xem xét các vấn đề xây dựng chính làm cơ sở để giải quyết các vấn đề phức tạp hơn.

Kinh nghiệm cho thấy, nhiệm vụ xây dựng khơi dậy sự hứng thú và góp phần kích hoạt hoạt động trí óc. Khi giải chúng, kiến ​​​​thức về tính chất của các hình được sử dụng tích cực, khả năng suy luận được phát triển và kỹ năng xây dựng hình học được cải thiện. Kết quả là khả năng xây dựng phát triển, đó là một trong những mục tiêu của việc nghiên cứu hình học.

Giả thuyết: tất cả các bài toán xây dựng có thể giải được bằng compa và thước chỉ có thể giải được bằng thước hai mặt.

Đối tượng nghiên cứu: Nhiệm vụ thi công và thước kẻ hai mặt.

Mục tiêu nghiên cứu: chứng minh rằng mọi bài toán xây dựng chỉ có thể giải được khi có sự trợ giúp của thước hai mặt.

Mục tiêu nghiên cứu: nghiên cứu cơ sở lý luận của việc giải quyết các vấn đề xây dựng; giải các bài toán xây dựng cơ bản bằng thước hai mặt; đưa ra ví dụ về các nhiệm vụ xây dựng phức tạp hơn; hệ thống hóa tài liệu lý luận và thực tiễn.

I. CÔNG CỤ HÌNH HỌC TRÊN MÁY BAY

I.1. Các tiên đề chung của hình học kiến ​​tạo. Tiên đề của các công cụ toán học

Đối với hình học xây dựng, cần phải có một bản mô tả chính xác và đầy đủ về một công cụ cụ thể cho mục đích toán học. Mô tả này được đưa ra dưới dạng tiên đề. Những tiên đề này ở dạng toán học trừu tượng thể hiện những tính chất của các công cụ vẽ thực tế được sử dụng trong các công trình hình học.

Các công cụ xây dựng hình học được sử dụng phổ biến nhất là:thước kẻ (một mặt) , la bàn, hai mặt thước kẻ (có các cạnh song song) và một số người khác.

A. Tiên đề người cai trị.

Thước cho phép bạn thực hiện các công trình hình học sau:
a) dựng đoạn nối hai điểm đã dựng;

b) dựng đường thẳng đi qua hai điểm đã dựng;

c) dựng tia sáng phát ra từ một điểm đã dựng và đi qua một điểm dựng sẵn khác.

B. Tiên đề la bàn.

La bàn cho phép bạn thực hiện các công trình hình học sau:
a) dựng đường tròn nếu tâm của đường tròn và một đoạn bằng bán kính của đường tròn (hoặc các đầu của nó) đã được dựng;

B. Tiên đề thước kẻ hai mặt.

Thước hai mặt cho phép bạn:

a) thực hiện bất kỳ cách xây dựng nào được liệt kê trong tiên đề A;

b) Trong mỗi nửa mặt phẳng được xác định bởi đường dựng sẵn, dựng một đường thẳng song song với đường thẳng này và đi qua nó một khoảngMỘT, Ở đâu MỘT - một đoạn cố định cho một thước đo nhất định (chiều rộng của thước);

c) Nếu dựng hai điểm A và B thì xác định xem AB có lớn hơn một đoạn cố định nào đó khôngMỘT (chiều rộng thước) và nếu AB >MỘT , khi đó dựng hai cặp đường thẳng song song lần lượt đi qua các điểm A và B và cách nhau một khoảngMỘT .

Ngoài các công cụ được liệt kê, bạn có thể sử dụng các công cụ khác để xây dựng hình học: góc tùy ý, hình vuông, thước kẻ có dấu, một cặp góc vuông, các thiết bị khác nhau để vẽ các đường cong đặc biệt, v.v.

I.2. Nguyên tắc chung giải quyết vấn đề xây dựng

Nhiệm vụ xây dựng bao gồm thực tế là cần phải xây dựng một hình nhất định bằng các công cụ được chỉ định nếu một số hình khác được đưa ra và các mối quan hệ nhất định giữa các phần tử của hình mong muốn và các phần tử của hình này được chỉ ra.

Mỗi hình thỏa mãn điều kiện của bài toán được gọi làphán quyết nhiệm vụ này.

Tìm một giải pháp Nhiệm vụ xây dựng có nghĩa là giảm nó xuống một số hữu hạn các công trình cơ bản, tức là chỉ ra một chuỗi hữu hạn các công trình cơ bản, sau đó hình mong muốn sẽ được xem xét xây dựng nhờ các tiên đề được chấp nhận của hình học xây dựng. Danh sách các công trình xây dựng cơ bản có thể chấp nhận được, và do đó, tiến độ giải quyết vấn đề, phụ thuộc đáng kể vào những công cụ cụ thể nào được sử dụng cho công trình xây dựng.

Giải quyết bài toán xây dựng - Có nghĩa, tìm tất cả các giải pháp của nó .

Định nghĩa cuối cùng yêu cầu một số làm rõ. Các hình thỏa mãn điều kiện của bài toán có thể khác nhau cả về hình dạng, kích thước và vị trí trên mặt phẳng. Sự khác biệt về vị trí trên mặt phẳng được tính đến hoặc không được tính đến tùy thuộc vào việc xây dựng bài toán xây dựng, vào việc điều kiện của bài toán cung cấp hay không cung cấp một vị trí nhất định của hình mong muốn so với bất kỳ hình nào đã cho. .

Nếu tìm ra giải pháp cho một vấn đề, thì trong tương lai người ta được phép sử dụng giải pháp này “một cách tổng thể”, tức là không chia nó thành các công trình chính.

Có một số bài toán xây dựng hình học đơn giản, đặc biệt thường được đưa vào như các thành phần để giải các bài toán phức tạp hơn. Chúng ta sẽ gọi chúng là những bài toán xây dựng hình học cơ bản. Tất nhiên, danh sách các nhiệm vụ cơ bản có điều kiện. Các công việc cơ bản thường bao gồm những việc sau:

Chia đoạn này làm đôi.

Chia một góc đã cho làm đôi.

Xây dựng trên một đường thẳng cho trước một đoạn bằng đoạn đã cho.

Dựng một góc bằng một góc cho trước.

Dựng đường thẳng đi qua một điểm và song song với một đường thẳng cho trước.

Dựng đường thẳng đi qua một điểm và vuông góc với một đường thẳng cho trước.

Phân chia một phân khúc về mặt này.

Xây dựng một tam giác bằng cách sử dụng ba cạnh cho trước.

Vẽ một tam giác có một cạnh và hai góc kề nhau.

Vẽ một tam giác bằng cách sử dụng hai cạnh và góc xen giữa chúng.

Khi giải một bài toán xây dựng có phần phức tạp nào đó, câu hỏi đặt ra là phải suy luận như thế nào để tìm ra cách giải bài toán, tìm ra mọi giải pháp cho bài toán, tìm ra các điều kiện để có khả năng giải bài toán đó, v.v. , khi giải quyết các vấn đề mang tính xây dựng, họ sử dụng sơ đồ giải pháp, bao gồm bốn giai đoạn sau:

1) phân tích;
2) xây dựng;
3) bằng chứng;
4) nghiên cứu.

I.3. Công trình hình học với một thước kẻ

Chúng ta sẽ xem xét cây thước từ hai quan điểm: như một cây thước và như một cây thước hai mặt.

1. Thước kẻ hai mặt chiều rộng MỘT chúng ta sẽ gọi một thước kẻ có các cạnh song song nằm ở khoảng cách MỘT với nhau, giúp có thể trực tiếp xây dựng:

a) một đường thẳng tùy ý;

b) Đường thẳng đi qua hai điểm đã cho hoặc có được trong quá trình giải bài toán;

c) các đường thẳng song song, mỗi đường đi qua một trong các điểm có khoảng cách giữa chúng lớn hơnMỘT (trong cách xây dựng này, thước ở vị trí sao cho trên mỗi cạnh song song của nó có một trong hai điểm đã cho; trong trường hợp này, chúng ta sẽ nói về cách dựng trực tiếp).

Chiều rộng của thước trong cách xây dựng này được coi là không đổi, và do đó, nếu trong quá trình giải một bài toán cụ thể, cần phải thực hiện việc xây dựng trực tiếp so với một số điểm thu đượcMỘT Và TRONG , thì ta phải chứng minh rằng độ dàiAB lâu hơn MỘT .

Chúng ta sẽ xem xét một điểm được xây dựng nếu nó là một trong các dữ liệu hoặc là giao điểm của hai đường được xây dựng; lần lượt, chúng ta sẽ coi một đường thẳng được dựng nếu nó đi qua các điểm đã cho hoặc đã dựng.

Bằng cách sử dụng thước kẻ hai mặt, bạn có thể xây dựng như sau.

a) Qua hai điểm bất kỳ vẽ được một đường thẳng và chỉ có một đường thẳng.

b) Dù là đường thẳng nào thì trong mặt phẳng có đúng hai đường thẳng song song với nó và cách nhau một khoảngMột .

c) Qua hai điểm A, B tại AB MỘT có thể vẽ hai cặp đường thẳng song song thẳng; với AB = MỘT bạn có thể vẽ một cặp đường thẳng song song, khoảng cách giữa chúng bằng nhauMỘT .

Nếu cho trước một, hai, ba điểm thì không thể xây dựng được điểm mới

(Hình 1);

nếu bốn điểm được cho, trong đó có ba (hoặc cả bốn) điểm nằm trên cùng một đường thẳng thì không thể dựng được điểm nào khác (Hình 2);

Nếu bạn có bốn điểm nằm ở các đỉnh của hình bình hành, bạn chỉ có thể dựng được một điểm - tâm của nó. (Hình 3).

Sau khi chấp nhận những điều trên, chúng ta hãy xem xét riêng các vấn đề được giải quyết bằng thước hai mặt.

TÔI.4. Các thao tác cơ bản khi dựng hình bằng thước hai mặt

1
. Vẽ tia phân giác của góc ABC.

Giải pháp: (Hình 4)

MỘT  (TRONG C) Và b  (AB) và  b = D .

Chúng tôi nhận được B D– đường phân giác  ABC.

Thật vậy, thu được bằng

dựng hình bình hành là

hình thoi vì chiều cao của nó bằng nhau. TRONGD –

đường chéo của hình thoi là đường phân giác ABC. Hình 4

2
. Nhân đôi góc ABC đã cho

Giải pháp : (Hình 5) a) MỘT  (AB),

MỘT  (TRONG C)= D , qua điểm B và D

b trực tiếp;

b) qua điểm B vàD tôi  b

trực tiếp,b Ç một = F .

Chúng tôi nhận được Ð AB F = 2 Ð ABC .

Hình 5

3 . Đối với một đường thẳng M N trong này

vẽ đường vuông góc với điểm A

Giải pháp : (Hình 6)

1) (AA 1) || (BB 1) || (SS 1) –

trực tiếp (B (M N),

VỚI Î (M N)); 2) qua A và B

tôi || N - trực tiếp,

tôi Ç (SS 1) = D .

Chúng tôi nhận được (A D )  (M N ).

Hình 6.

4
. Qua một điểm cho trước không nằm trên

dòng đã cho, vẽ đường vuông góc

ĐẾN đường thẳng này.

Giải pháp: Qua điểm này O ta vẽ

hai đường thẳng cắt nhau cho trước

đường thẳng AB và nhân đôi góc của kết quả

tam giác liền kề này

thẳng.  viêm khớp N = 2  OAV và

OB N = 2  OVA (Hình 7).

Hình 7

5. Xây dựng một điểm đối xứng với một đường thẳng cho trước so với một đường thẳng cho trước.

Giải pháp: xem bài 4. (điểm O đối xứng với điểmN. Hình 7)

6. Thực hiện một đường thẳng song song với cái này

P
thẳng M N , qua điểm A, không

thuộc đường thẳng M N .

Giải pháp 1: (Hình 8)

1)(AA 1) || (BB 1) || (SS 1) || (ĐĐ 1 ) || (KК 1) -

– trực tiếp, (SA)Ç (BB 1) = C 2;

2) (Với 2K) Ç (ĐĐ 1 ) = F .

(MỘT F ) là đường thẳng mong muốn.

Hình 8

Giải pháp 2 . Trong hình 8 1 được đánh số

chuỗi các đường thẳng,

trong đó 1, 2 và 3 song song

trực tiếp xây dựng;

(MỘT F) || (M N).

Hình 8 1

7
. Chia đoạn AB này làm đôi.

Giải pháp 1. (Hình 9) (chỉ dành cho trường hợp chiều rộng của thước nhỏ hơn chiều dài của đoạn này). Vẽ hai cặp đường thẳng song song đi qua

các đầu của đoạn này và sau đó là đường chéo

kết quả là hình thoi. O – AB giữa.

Cơm. 9.

Giải pháp 2. (Hình 9,a)

1) một || (AB) và b || (AB) – trực tiếp;

2) (AR), (AR)Ç a = C, (AP) Ç b = D ;

3) (D TRONG) Ç a = M, (SV) Ç b = N ;

4) (M N ) Ç (AB) = K;

5) (D ĐẾN) Ç (MỘT N ) = F ;

6) (B F ) Ç b = D 1, (B F ) Ç a = C 1;

7) (D TRONG ) Ç (MỘT D 1 ) = X,

(AC 1) Ç (SV) = Z.

8) (X Z) Ç (AB) =O. Ta được AO = OB.

Hình 9, a

Giải pháp 3 .( Cơm. 9,b)

Như đã biết , ở giữa hình thang

căn cứ, điểm giao nhau

đường chéo và điểm giao nhau

phần mở rộng của các bên

nằm trên cùng một đường thẳng.

1) tôi || (AB) – trực tiếp;

2) C Î tôi , D Î tôi , (BẰNG) Ç (TRONG D ) = ĐẾN; Hình 9, b

3) (ĐB) Ç (MỘT D ) = F ; 4) (K F ) Ç (AB) =O. Ta được AO = OB.

I.5. Giải quyết các vấn đề xây dựng khác nhau

Để giải các bài toán dựng hình sau chỉ dùng thước hai mặt, người ta sử dụng cách dựng trực tiếp các đường thẳng song song và bảy bài toán chính nêu trên.

1. Vẽ hai đường thẳng vuông góc với nhau đi qua điểm này.

R giải pháp: chúng ta hãy đi qua điểm này

hai đường tùy ý,

và sau đó - phân giác

các góc liền kề. (Hình 10)

Hình 10

2. Cho đoạn A D độ dài đã cho a.

Xây dựng một đoạn có độ dài bằng .

R
phán quyết : Hãy thực hiện tôi  MỘT Và h || tôi bởi vì

điểm A f || (MỘT D ) , k || (QUẢNG CÁO) trực tiếp.

Vẽ AB và AC sao cho B =f  tôi ,

một C = tôi  k . Theo một cách đã biết

chia AB và AC làm đôi và

hãy vẽ các đường trung tuyến của tam giác

ABC. Theo tính chất trung vị

tam giác, O D = – tìm kiếm

đoạn (Hình 11)

Cơm. mười một

3. Xây dựng một đoạn có độ dài là

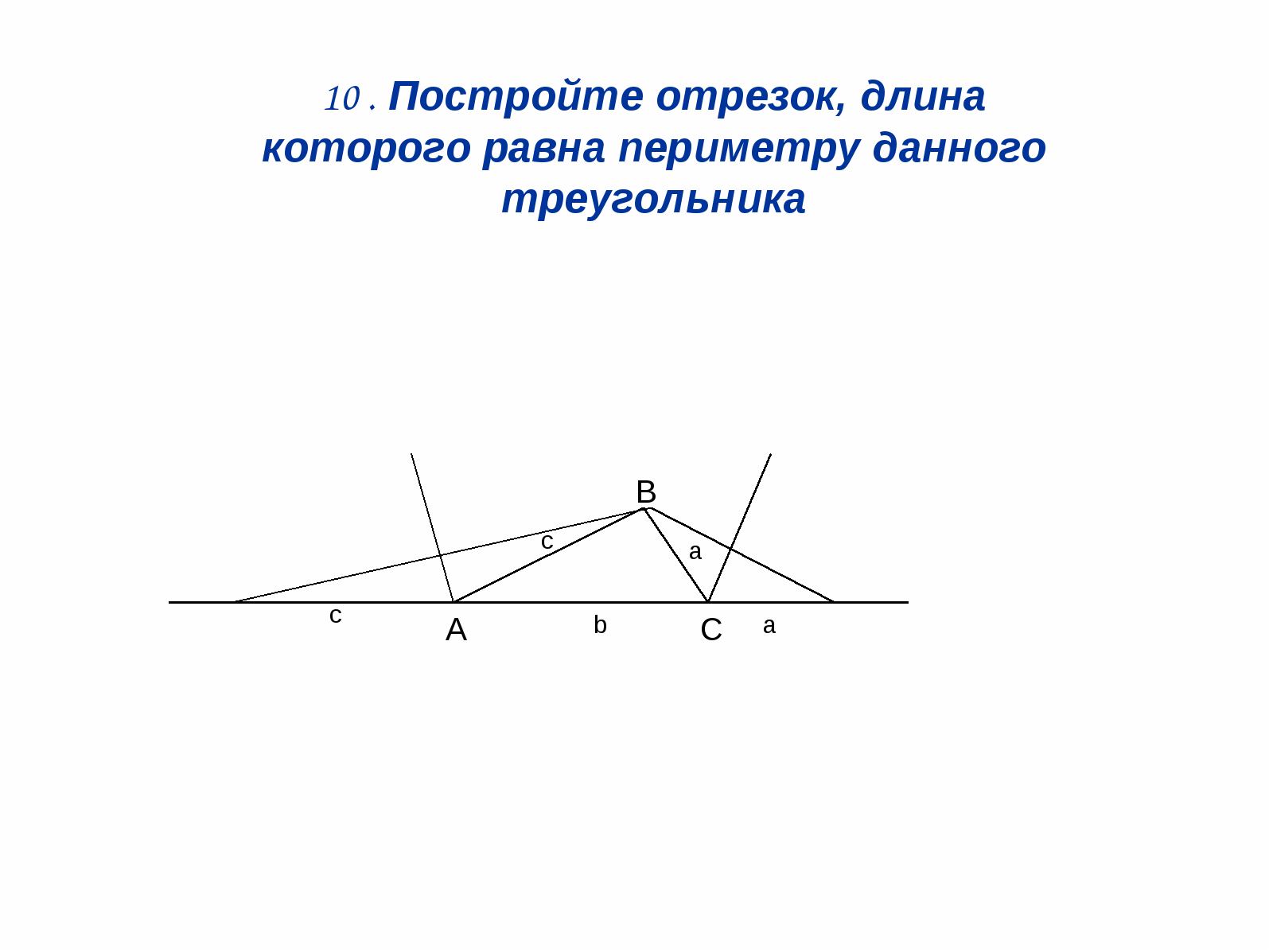bằng chu vi của tam giác đã cho.

Giải pháp: (Hình 12). Hãy dựng các đường phân giác

hai góc ngoài của tam giác, sau đó

3 đỉnh TRONG hãy vẽ các đường vuông góc

tới các đường phân giác này.

DE = một + b + s

Hình 12

4. Cho một đoạn có độ dài a. Xây dựng các đoạn có chiều dài 2a, 3a.

R giải pháp: (Hình 13)

1 triệu N) || (AB) và (M 1 N 1 ) || (M N) || (M 2 N 2 ) –

Trực tiếp;

2) (CA) và (CB) qua A và B.

Các phân đoạn A 1 B 1 và A 2 B 2 là bắt buộc.

Một giải pháp khác cho vấn đề này có thể là

thu được từ lời giải của bài toán 7.

Cơm. 13

5. Cho hai đoạn thẳng có độ dài là a và b . Xây dựng các đoạn có độ dài bằng a + b , b - MỘT, ( Một + b )/2 và ( b - Một )/2 .

Giải pháp: va cho Một + b(Hình 14, a)

Hình 14, a

b) cho ( Một + b)/2 (Hình 14, b)

1) (A 1 B 1) || (A 2 B 2) || (AB) – trực tiếp;

2) M Î (A 2 B 2), (MX) Ç (A 1 B 1 ) = N, (M H) Ç (A 1 B 1 ) = P;

3) (PY) Ç (A 2 B 2) = L, (bãi đáp ) Ç (A 1 B 1 ) = ồ,

Chúng tôi nhận được: N ồ = NP + P.O. =
.

Cơm. 14, b

c) cho b - MỘT(Hình 14, c)

Cơm. 14, v

c) cho ( b - Một )/2 (Hình 14, d)

Cơm. 14,g

6
. Xây dựng tâm của vòng tròn này.

Giải pháp : (Hình 15) Vẽ đường thẳng AB,

cắt đường tròn tại điểm A và B;

Mặt trời  AB, trong đó C là giao điểm

với một vòng tròn.

Qua điểm C vẽ song song với AB

thẳng C D; VỚIDcắt một vòng tròn

tại điểmD.

Đang kết nốiDvới B và A với C, ta có

điểm mong muốn là tâm của vòng tròn. Cơm. 15

Giải pháp 2: (Hình 16) Dùng thước kẻ hai mặt dựng hai dây cung song songQUẢNG CÁO VàBC . Ta được một hình thang cânA B C D. Cho phépK VàP - điểm giao nhau của đườngAC. VàBD , AB VàDC . Sau đó thẳngP K đi qua trung điểm các đáy của hình thang vuông góc với chúng, nghĩa là nó đi qua tâm của đường tròn đã cho. Bằng cách xây dựng tương tự một đường thẳng khác như vậy, chúng ta tìm được tâm của đường tròn.

Cơm. 16

7. Cho một cung tròn. Xây dựng tâm của đường tròn

Giải pháp . (Hình 17) Đánh dấu ba điểm A, B và C trên cung này. Dùng thước đo vào hai đầu đoạn AB và vẽ các cạnh của nó. Chúng ta có được hai đường thẳng song song. Thay đổi vị trí của thước kẻ, chúng ta vẽ thêm hai đường thẳng song song. Chúng ta có một hình thoi (hình bình hành có chiều cao bằng nhau). Một trong các đường chéo của hình thoi là đường phân giác vuông góc của đoạnAB , vì đường chéo của hình thoi nằm trên đường phân giác vuông góc với đường chéo kia. Tương tự ta dựng đường phân giác vuông góc của đoạnAC. . Điểm giao nhau của các đường phân giác được dựng là tâm của đường tròn mong muốn.

Cơm. 17

8. Cho đoạn thẳng AB, đường thẳng l không song song và điểm M trên đó. Dùng thước hai mặt dựng các giao điểm của đường thẳng l với đường tròn bán kính AB tâm M.

Giải pháp: (Hình 18)

Hãy hoàn thành hình tam giácA.B.M. thành hình bình hànhABNM . Hãy dựng các đường phân giác MT vàbệnh đa xơ cứnggóc giữaMNvà thẳngtôi . Hãy vẽ qua điểmN các đường thẳng song song với các đường phân giác đó:NQ || bệnh đa xơ cứng, NR || M.T.. MT│ bệnh đa xơ cứngnhư phân giác của các góc kề nhau. Có nghĩa,NQ │ MT, nghĩa là trong một tam giácNMQđường phân giác là đường cao nên tam giác là cân:MQ = MN. Tương tự như vậy,ÔNG. = MN. ĐiểmQVàRđã tìm kiếm.

Cơm. 18

9. Cho đường thẳng l và đoạn OA song song với l. Dùng thước hai mặt dựng các giao điểm của đường thẳng l với đường tròn bán kính OA tâm O.

Giải pháp: (Hình 19,a)

Hãy trực tiếp thực hiệntôi 1 , song song với đường thẳngO.A. và cách xa nó ở một khoảng cáchMột . Hãy đưa nó đi theo một đường thẳngtôi điểm tùy ýB . Cho phépB 1 - giao điểm của đườngO.B. Vàtôi 1 . Hãy vẽ qua điểmB 1 thẳng, song songAB ; đường này cắt đườngO.A. tại điểmMỘT 1 . Bây giờ chúng ta hãy vẽ qua các điểmồ VàMỘT 1 một cặp đường thẳng song song, khoảng cách giữa chúng làMột (có thể có hai cặp đường thẳng như vậy); cho phépX VàX 1 - Giao điểm của đường thẳng đi qua một điểmồ , với các đường thẳngtôi Vàtôi 1 . Bởi vìO.A. 1 = CON BÒ ĐỰC 1 và ∆O.A. 1 X 1 ∆ OAX , thì OA = OX, điểmX được săn đón.

Tương tự, ta dựng giao điểm thứ hai của đường tròn và đường thẳng - điểmY(Hình 18, b).

Cơm. 18, một

Cơm. 18, b

I.6.Công trình có thước kẻ một mặt

Z
Ở đây chúng ta xét một trường hợp đặc biệt: cho điểm P,Q, R 1 VàQ 1 . và chúng nằm ở các đỉnh của hình thang.

1. Chia đoạn P Q Trong một nửa

Giải pháp thể hiện trong hình 19

Cho điểm P,Q, R 1 VàQ 1 và đường thẳng song song

RQ, R 1 Q 1 . Hãy thực hiện RQ 1  QR 1 = B , RR 1  QQ 1 = A

Hãy nối điểm A và B. AB RQ = F- ở giữa

đoạn PQ.

Cơm. 19

2. Nhân đôi phân khúc R 1 Q 1.

R
phán quyết thể hiện trong Hình 20. Hãy xây dựng

điểmF- chính giữa đoạn PQvà kết nối nó

VớiQ 1. R 1 Q Câu hỏi thường gặp 1 = M. Hãy thực hiện RM. RM R 1 Q 1 = R

bình đẳngRQvà P 1 Q 1 suy ra từ sự giống nhau

Hình tam giác RMFVà RMQ 1 ,

FMQVà R 1 MQ 1 , và đẳng thức PFVàCâu hỏi thường gặp.

Cơm. 20

3
. Xây dựng một đoạn có chiều dài N  R 1 Q 1 .

tôi – 1 các đoạn bằng nhau PQ 2 , Q 2 Q 3, … Q tôi -1 Q tôi

Sau đó, chúng tôi xây dựng (RR 1 ) VàQ tôi Q 1 và kết nối

giao điểm của chúng là A với các điểm

Q 2 , Q 3, … Q tôi Đã nhậntôi -1 trực tiếp

chiaR 1 Q 1 TRÊNtôi bình đẳng các bộ phận.

Vìtôi = 4 giải pháp được thể hiện trong Hình 22

Hình 22

I.7. Khả năng hoán đổi của thước kẻ hai mặt với la bàn và thước kẻ

Hãy chứng minh rằng thước hai mặt có thể hoán đổi cho nhau bằng compa và thước kẻ. Để làm điều này, chúng tôi chứng minh các tuyên bố sau:

Phát biểu 1: tất cả các công việc xây dựng có thể thực hiện được bằng compa và thước kẻ đều có thể thực hiện được bằng thước kẻ hai mặt.

Vì khi dựng hình bằng compa và thước, thước vẽ một đường thẳng đi qua hai điểm, còn compa dựng một đường tròn (tìm tập hợp các điểm cách đều một điểm đã cho), nên mọi cách dựng bằng compa và thước đều quy về dựng giao điểm của hai đường thẳng, hai đường tròn và một đường tròn với một đường thẳng.

Giao điểm của hai đường thẳng có thể được dựng bằng thước kẻ.

Giao điểm của đường tròn và đường thẳng (Hình 23):

Sự thi công:Cho đoạn AB - bán kính đường tròn, đường thẳngtôi , tâm đường tròn O thì:

1) Chúng tôi thực hiện hệ điều hành ||tôi , OS = AB.

2) Chúng tôi thực hiện hệ điều hành ||kvà từ xa đến a.

3) Chúng tôi thực hiệnOD, OD tôi = D; OD k) Theo hệ quả của định lý Thales

4) Theo định luật đẳng thức đẳng thức

5) Hãy xem xétOMQE. OMQElà hình bình hành vì OM ||EQvà OE ||MC(các cạnh của thước song song). Hãy chứng minh đây là hình thoi.

5.1) Ứng xửQZ OCVàQG TRÊN, Sau đóQG = QZ = Một.

5.2)  OMQ =  RQM(nằm ngang);  hệ điều hành =TRÊN, đó là điều cần chứng minh.

Giao điểm của hai đường tròn: bằng nhau.

Phát biểu 2: mọi phép dựng có thể thực hiện được bằng thước hai mặt đều có thể thực hiện được bằng compa và thước thẳng.

Để làm điều này, chúng ta sẽ thực hiện tiêu chuẩn xây dựng thước kẻ hai mặt bằng compa và thước kẻ.

1) Một đường thẳng có hai điểm có thể dễ dàng vẽ bằng thước.

2) Dựng đường thẳng song song với một đường thẳng cho trước và cách xa nó một khoảng cho trước:

2.1) Cho một đường thẳngkvà đoạn có độ dàiMột.

2.2) Vẽ đoạn thẳng tùy ýb k, cho phépk b= B.

2.3) Bậtbở cả hai phía của điểmBtrên một đường thẳngbdành một đoạn dàiMột, cho điểmCVàD.

2.4) Qua một điểmCxây dựng một đường thẳngc k.

2.5) Qua một điểmDxây dựng một đường thẳngd k.

2.6) Trực tiếpcVàd-bắt buộc, bởi vìBCVàBDbình đẳngMộttheo cách xây dựng và bằng khoảng cách giữa đường thẳngkvà thẳng

3) Dựng các đường thẳng song song nhau và đi qua hai điểm cho trước và khoảng cách giữa chúng bằng đoạn thẳng cho trước:

3.1) Hãy cho điểmMỘTVàBvà đoạn có độ dàiMột.

3.2) Dựng đường tròn có tâm tại một điểmMỘTvà bán kínhMột.

3.3) Vẽ tiếp tuyến của đường tròn cho trước qua một điểmB; có hai tiếp tuyến như vậy nếuBnằm ngoài đường tròn (nếuAB> Một), một nếuBnằm trên đường tròn (nếuAB= Một), không có nếuBnằm trong đường tròn (AB< Một). Tiếp tuyến này là một trong những đường chúng ta đang tìm kiếm; nó vẫn đi qua điểmMỘTđường thẳng song song với nó.

3.4) Vì một trong các đường thẳng vuông góc với bán kính của đường tròn là tiếp tuyến nên đường thẳng thứ hai cũng vuông góc với nó (vì chúng song song), do đó, khoảng cách giữa chúng bằng bán kính, theo cách xây dựng bằngMột, đó là những gì cần thiết để có được.

Như vậy, chúng ta đã chứng minh được khả năng thay thế lẫn nhau của thước hai mặt với la bàn và thước kẻ.

Kết luận: Thước hai mặt có thể hoán đổi cho nhau bằng compa và thước kẻ.

Phần kết luận

Vì vậy, câu hỏi về khả năng sử dụng một thước để giải các bài toán xây dựng cổ điển bằng compa và thước đã được xem xét và giải quyết. Hóa ra các vấn đề về xây dựng có thể được giải quyết chỉ bằng cách sử dụng thước kẻ có các cạnh song song. Khi giải các bài toán phức tạp hơn, người ta nên dựa nhiều hơn vào cái gọi là các cấu trúc cơ bản được thảo luận trong bài viết này.

Tài liệu được trình bày có thể được áp dụng trực tiếp không chỉ trong các bài học toán, trong các lớp học vòng tròn toán mà còn trong các hoạt động thực tiễn.

Danh sách tài liệu được sử dụng

Aliev A.V. Các công trình hình học. Toán ở trường. 1978 số 3

Glazer G.I. Lịch sử toán học ở trường. M., Sự giác ngộ. 1981.

Depman I.Ya. Đằng sau những trang sách giáo khoa toán học M.. Khai sáng, 1989.

Elensky Shch Theo bước chân của Pythagoras. M., Detgiz. 1961.

Từ điển bách khoa của một nhà toán học trẻ. M., Sư phạm. 1985

Trong các nhiệm vụ xây dựng, chúng ta sẽ xem xét việc xây dựng một hình hình học, có thể được thực hiện bằng thước kẻ và la bàn.

Sử dụng thước kẻ bạn có thể:

đường thẳng tùy ý;

một đường thẳng tùy ý đi qua một điểm cho trước;

đường thẳng đi qua hai điểm cho trước.

Sử dụng la bàn, bạn có thể mô tả một đường tròn có bán kính nhất định tính từ một tâm nhất định.

Sử dụng la bàn, bạn có thể vẽ một đoạn trên một đường nhất định từ một điểm nhất định.

Hãy xem xét các nhiệm vụ xây dựng chính.

Nhiệm vụ 1. Vẽ một tam giác có các cạnh a, b, c (Hình 1).

Giải pháp. Dùng thước vẽ một đường thẳng tùy ý và lấy một điểm B tùy ý trên đó.Dùng thước mở la bàn bằng a, ta vẽ một đường tròn có tâm B và bán kính a. Gọi C là giao điểm của nó với đường thẳng. Với độ mở la bàn bằng c, chúng ta mô tả một đường tròn từ tâm B, và với độ mở la bàn bằng b, chúng ta mô tả một đường tròn từ tâm C. Gọi A là giao điểm của các đường tròn này. Tam giác ABC có các cạnh bằng a, b, c.

Bình luận. Để ba đoạn thẳng đóng vai trò là các cạnh của một tam giác, điều cần thiết là đoạn thẳng lớn nhất phải nhỏ hơn tổng của hai đoạn còn lại (và< b + с).

Nhiệm vụ 2.

Giải pháp. Góc này với đỉnh A và tia OM được thể hiện trên Hình 2.

Chúng ta vẽ một đường tròn tùy ý có tâm ở đỉnh A của một góc đã cho. Gọi B và C là giao điểm của đường tròn với các cạnh của góc (Hình 3, a). Với bán kính AB ta vẽ đường tròn có tâm tại điểm O - điểm bắt đầu của tia này (Hình 3, b). Chúng ta hãy biểu thị giao điểm của đường tròn này với tia này là C 1 . Hãy vẽ đường tròn tâm C1, bán kính BC. Điểm B 1 của giao điểm của hai đường tròn nằm trên cạnh của góc mong muốn. Điều này suy ra từ đẳng thức Δ ABC = Δ OB 1 C 1 (dấu thứ ba của đẳng thức tam giác).

Nhiệm vụ 3. Dựng đường phân giác của góc này (Hình 4).

Giải pháp. Từ đỉnh A của một góc cho trước, cũng như từ tâm, vẽ một đường tròn có bán kính tùy ý. Gọi B và C là giao điểm của nó với các cạnh của góc. Từ điểm B và C chúng ta mô tả các đường tròn có cùng bán kính. Gọi D là giao điểm của chúng, khác A. Tia AD chia đôi góc A. Điều này suy ra từ đẳng thức Δ ABD = Δ ACD (tiêu chí thứ ba về đẳng thức của các tam giác).

Nhiệm vụ 4. Vẽ một đường phân giác vuông góc với đoạn này (Hình 5).

Giải pháp. Sử dụng độ mở la bàn tùy ý nhưng giống hệt nhau (lớn hơn 1/2 AB), chúng ta mô tả hai cung có tâm tại các điểm A và B, sẽ cắt nhau tại một số điểm C và D. Đường thẳng CD sẽ vuông góc như mong muốn. Thật vậy, như có thể thấy từ cách xây dựng, mỗi điểm C và D cách xa A và B như nhau; do đó các điểm này phải nằm trên đường trung trực của đoạn AB.

Nhiệm vụ 5. Chia đoạn này làm đôi. Nó được giải theo cách tương tự như vấn đề 4 (xem Hình 5).

Nhiệm vụ 6. Qua một điểm cho trước vẽ đường thẳng vuông góc với đường thẳng đã cho.

Giải pháp. Có hai trường hợp có thể xảy ra:

1) điểm O cho trước nằm trên đường thẳng a cho trước (Hình 6).

Từ điểm O vẽ đường tròn có bán kính tùy ý cắt đường a tại các điểm A và B. Từ điểm A và B vẽ đường tròn có cùng bán kính. Gọi O 1 là giao điểm của chúng, khác với O. Ta thu được OO 1 ⊥ AB. Trong thực tế, các điểm O và O 1 cách đều hai đầu đoạn AB và do đó nằm trên đường trung trực của đoạn này.

Cơ sở giáo dục ngân sách thành phố

Trường THCS số 34 chuyên sâu từng môn học

MAN, phần vật lý và toán học

“Dựng hình học bằng compa và thước”

Người hoàn thành: Học sinh lớp 7 “A”

Batishcheva Victoria

Người đứng đầu: Koltovskaya V.V.

Voronezh, 2013

3. Dựng một góc bằng góc đã cho.

P Hãy vẽ một đường tròn tùy ý có tâm ở đỉnh A và một góc cho trước (Hình 3). Gọi B và C là giao điểm của đường tròn với các cạnh của góc. Với bán kính AB ta vẽ đường tròn có tâm tại điểm O, điểm bắt đầu của nửa đường thẳng này. Chúng ta hãy biểu thị giao điểm của đường tròn này với nửa đường thẳng này là C 1 . Hãy vẽ đường tròn tâm C 1 và Hình 3

bán kính của máy bay. Điểm B 1 giao điểm của các đường tròn dựng nên trong nửa mặt phẳng được chỉ định nằm ở phía của góc mong muốn.

6. Thi công đường vuông góc.

Chúng ta vẽ một đường tròn có bán kính r tùy ý có tâm tại điểm O trong Hình 6. Đường tròn cắt đường thẳng tại hai điểm A và B.Từ hai điểm A và B vẽ đường tròn bán kính AB. Gọi u sầu C là giao điểm của các đường tròn này. Chúng ta đã thu được điểm A và B ở bước đầu tiên khi dựng đường tròn có bán kính tùy ý.

Đường thẳng mong muốn đi qua các điểm C và O.

Hình 6

Sự cố đã biết

1.Vấn đề của Brahmagupta

Xây dựng một tứ giác nội tiếp bằng cách sử dụng bốn cạnh của nó. Một giải pháp sử dụng vòng tròn Apollonius.Hãy giải bài toán Apollonius bằng cách sử dụng phép so sánh giữa hình tam giác và hình tam giác. Cách tìm đường tròn nội tiếp một tam giác: dựng giao điểm của các đường phân giác, thả các đường vuông góc từ nó đến các cạnh của tam giác, các đáy của các đường vuông góc (điểm giao nhau của đường vuông góc với cạnh mà nó bị bỏ đi) và cho chúng ta ba điểm nằm trên đường tròn mong muốn. Vẽ một vòng tròn qua ba điểm này - giải pháp đã sẵn sàng. Chúng ta sẽ làm tương tự với bài toán Apollonius.

2. Vấn đề của Apollonius

Dùng compa và thước kẻ vẽ đường tròn tiếp xúc với ba đường tròn đã cho. Theo truyền thuyết, bài toán này được Apollonius xứ Perga đưa ra vào khoảng năm 220 trước Công nguyên. đ. trong cuốn sách "Touch", đã bị thất lạc nhưng được François Viète, "Gallic Apollonius" khôi phục vào năm 1600, như những người cùng thời gọi ông.

Nếu không có đường tròn nào nằm bên trong đường tròn kia thì bài toán này có 8 nghiệm khác nhau đáng kể.

Xây dựng đa giác thường xuyên.

P

Chính xác (hoặc đều ) Tam giác - Cái này đa giác đềucó ba cạnh, là đa giác đều đầu tiên. Tất cả các cạnh của một tam giác đều đều bình đẳng với nhau và tất cả các góc là 60°. Để dựng một tam giác đều, bạn cần chia hình tròn thành 3 phần bằng nhau. Để làm được điều này, chỉ cần vẽ một cung có bán kính R của đường tròn này chỉ từ một đầu của đường kính, ta được phép chia thứ nhất và thứ hai. Vạch thứ ba nằm ở đầu đối diện của đường kính. Bằng cách kết nối những điểm này, chúng ta sẽ có được một tam giác đều.

Hình lục giác đều Có thểdựng bằng compa và thước. Dướiphương pháp xây dựng được đưa rabằng cách chia hình tròn thành 6 phần. Chúng ta sử dụng sự bằng nhau của các cạnh của một hình lục giác đều với bán kính của hình tròn ngoại tiếp. Từ các đầu đối diện của một trong các đường kính của hình tròn, chúng ta mô tả các cung có bán kính R. Giao điểm của các cung này với một đường tròn cho trước sẽ chia nó thành 6 phần bằng nhau. Bằng cách kết nối tuần tự các điểm tìm thấy, sẽ thu được một hình lục giác đều.

Xây dựng một hình ngũ giác đều.

P
một hình ngũ giác đều có thểđược xây dựng bằng compa và thước kẻ, hoặc bằng cách lắp nó vào một khuôn mẫu nhất địnhvòng tròn, hoặc xây dựng dựa trên một mặt nhất định. Quá trình này được Euclid mô tảtrong cuốn Elements của ông vào khoảng năm 300 trước Công Nguyên. đ.

Đây là một phương pháp để dựng một hình ngũ giác đều trong một đường tròn cho trước:

Xây dựng một vòng tròn trong đó hình ngũ giác sẽ được ghi vào đó và đánh dấu tâm của nó làồ . (Đây là vòng tròn màu xanh lá cây trong sơ đồ bên phải).

Chọn một điểm trên đường trònMỘT , đây sẽ là một trong các đỉnh của hình ngũ giác. Dựng đường thẳng đi quaồ VàMỘT .

Dựng đường thẳng vuông góc với đường thẳngO.A. , đi qua điểmồ . Chỉ định một trong các giao điểm của nó với đường tròn làm điểmB .

Vẽ một điểmC ở giữaồ VàB .

C qua điểmMỘT . Đánh dấu giao điểm của nó với đườngO.B. (bên trong vòng tròn ban đầu) là một điểmD .

Vẽ đường tròn có tâm tạiMỘT qua điểm D, đánh dấu giao điểm của đường tròn này với đường tròn ban đầu (vòng tròn màu xanh lá cây) là điểmE VàF .

Vẽ đường tròn có tâm tạiE qua điểmMỘT G .

Vẽ đường tròn có tâm tạiF qua điểmMỘT . Dán nhãn giao điểm khác của nó bằng đường tròn ban đầu là một điểmH .

Xây dựng một hình ngũ giác đềuAEGHF .

Những vấn đề không thể giải quyết

Ba nhiệm vụ xây dựng sau đây đã được đặt ra vào thời cổ đại:

Phép chia một góc - chia một góc tùy ý thành ba phần bằng nhau.

Nói cách khác, cần dựng các tia phân giác góc - các tia chia góc thành ba phần bằng nhau. P. L. Wanzel đã chứng minh vào năm 1837 rằng bài toán chỉ có thể giải được khi, ví dụ, phép chia ba có thể thực hiện được đối với các góc α = 360°/n, với điều kiện là số nguyên n không chia hết cho 3. Tuy nhiên, trên báo chí thỉnh thoảng (không chính xác) ) phương pháp chia một góc bằng compa và thước đã được công bố.

Nhân đôi khối lập phương - bài toán cổ điển về việc dùng thước và compa dựng cạnh của một hình lập phương có thể tích gấp đôi thể tích của hình lập phương đã cho.

Trong ký hiệu hiện đại, bài toán được rút gọn thành việc giải phương trình. Tất cả đều bắt nguồn từ vấn đề xây dựng một đoạn có độ dài. P. Wantzel đã chứng minh vào năm 1837 rằng bài toán này không thể giải được bằng compa và thước thẳng.

Bình phương một hình tròn - một nhiệm vụ bao gồm việc tìm một công trình bằng cách sử dụng la bàn và thước kẻ của một hình vuông có diện tích bằng hình tròn đã cho.

Như bạn đã biết, với sự trợ giúp của la bàn và thước kẻ, bạn có thể thực hiện cả 4 phép tính số học và trích căn bậc hai; Theo đó, việc bình phương đường tròn là có thể thực hiện được khi và chỉ khi, bằng cách sử dụng một số hữu hạn các hành động như vậy, có thể xây dựng được một đoạn có độ dài π. Do đó, tính không giải được của bài toán này xuất phát từ bản chất phi đại số (siêu việt) của số π, được chứng minh vào năm 1882 bởi Lindemann.

Một bài toán nổi tiếng khác không thể giải bằng compa và thước làdựng tam giác bằng ba độ dài phân giác cho trước .

Hơn nữa, vấn đề này vẫn không thể giải quyết được ngay cả khi có trisector.

Chỉ đến thế kỷ 19, người ta mới chứng minh được rằng cả ba bài toán đều không thể giải được chỉ bằng compa và thước thẳng. Câu hỏi về khả năng xây dựng được giải quyết hoàn toàn bằng phương pháp đại số dựa trên lý thuyết Galois.

BẠN CÓ BIẾT RẰNG...

(từ lịch sử của các công trình hình học)

Ngày xửa ngày xưa, một ý nghĩa thần bí đã được đầu tư vào việc xây dựng các đa giác đều.

Do đó, người Pythagore, những người theo giáo lý tôn giáo và triết học do Pythagoras sáng lập, và sống ở Hy Lạp cổ đại (V. tôi-tôi V.thế kỉ BC BC), được coi là dấu hiệu của sự kết hợp của họ, một đa giác hình ngôi sao được hình thành bởi các đường chéo của một hình ngũ giác đều.

Các quy tắc xây dựng hình học chặt chẽ của một số đa giác đều được nêu trong cuốn sách “Các phần tử” của nhà toán học Hy Lạp cổ đại Euclid, người sống ởIIIV. BC. Để thực hiện những công trình này, Euclid đề xuất chỉ sử dụng thước kẻ và la bàn, vào thời điểm đó chưa có thiết bị bản lề để nối các chân (hạn chế về dụng cụ như vậy là một yêu cầu bất di bất dịch của toán học cổ đại).

Đa giác đều được sử dụng rộng rãi trong thiên văn học cổ đại. Nếu Euclid quan tâm đến việc xây dựng những hình vẽ này theo quan điểm toán học, thì đối với nhà thiên văn học Hy Lạp cổ đại Claudius Ptolemy (khoảng 90 - 160 sau Công Nguyên), nó hóa ra cần thiết như một công cụ phụ trợ trong việc giải quyết các vấn đề thiên văn. Vì vậy, trong cuốn sách đầu tiên của Almagests, toàn bộ chương thứ mười được dành cho việc xây dựng các hình ngũ giác và hình thập giác đều.

Tuy nhiên, ngoài những công trình khoa học thuần túy, việc xây dựng các đa giác đều là một phần không thể thiếu trong sách dành cho các nhà xây dựng, thợ thủ công và nghệ sĩ. Khả năng khắc họa những hình tượng này từ lâu đã được yêu cầu trong kiến ​​trúc, đồ trang sức và mỹ thuật.

“Mười cuốn sách về kiến ​​trúc” của kiến ​​trúc sư La Mã Vitruvius (sống khoảng 63-14 trước Công nguyên) nói rằng các bức tường thành phải có dạng đa giác đều trong sơ đồ, và các tháp của pháo đài “nên được làm hình tròn hoặc đa giác”. , cho một tứ giác bị phá hủy bởi vũ khí công thành.”

Cách bố trí của các thành phố rất được Vitruvius quan tâm, người tin rằng cần phải quy hoạch các đường phố để gió chính không thổi dọc theo chúng. Người ta cho rằng có tám cơn gió như vậy và chúng thổi theo những hướng nhất định.

Trong thời kỳ Phục hưng, việc xây dựng các đa giác đều, và đặc biệt là hình ngũ giác, không phải là một trò chơi toán học đơn giản mà là điều kiện tiên quyết cần thiết để xây dựng các pháo đài.

Hình lục giác đều là chủ đề của một nghiên cứu đặc biệt của nhà thiên văn học và toán học vĩ đại người Đức Johannes Kepler (1571-1630), mà ông đã nói đến trong cuốn sách “Món quà năm mới, hay những bông tuyết hình lục giác”. Thảo luận về lý do tại sao bông tuyết có hình lục giác, ông đặc biệt lưu ý như sau: “... một mặt phẳng có thể được bao phủ mà không có khoảng trống chỉ bằng các hình sau: hình tam giác đều, hình vuông và hình lục giác đều. Trong số những hình này, hình lục giác đều có diện tích lớn nhất."

Một trong những nhà khoa học nổi tiếng nhất liên quan đến các công trình hình học là nghệ sĩ và nhà toán học vĩ đại người Đức Albrecht Durer (1471 -1528), người đã dành một phần quan trọng trong cuốn sách “Sổ tay…” cho họ. Ông đề xuất quy tắc dựng các đa giác đều có 3, 4, 5... 16 cạnh. Các phương pháp chia vòng tròn do Dürer đề xuất không phổ biến, mỗi trường hợp cụ thể sẽ sử dụng một kỹ thuật riêng.

Dürer đã sử dụng các phương pháp xây dựng đa giác đều trong thực hành nghệ thuật, chẳng hạn như khi tạo ra các loại đồ trang trí và hoa văn khác nhau cho sàn gỗ. Ông đã phác thảo những mẫu như vậy trong một chuyến đi đến Hà Lan, nơi có nhiều ngôi nhà lát sàn gỗ.

Dürer đã sáng tác các đồ trang trí từ các đa giác đều, được kết nối thành các vòng (vòng gồm sáu hình tam giác đều, bốn hình tứ giác, ba hoặc sáu hình lục giác, mười bốn hình bảy cạnh, bốn hình bát giác).

Phần kết luận

Vì thế,công trình hình học là một phương pháp giải một bài toán trong đó lời giải được đưa ra bằng đồ họa. Việc xây dựng được thực hiện bằng cách sử dụng các công cụ vẽ với độ chính xác và độ chính xác tối đa của công việc, vì tính chính xác của giải pháp phụ thuộc vào điều này.

Nhờ tác phẩm này, tôi được làm quen với lịch sử nguồn gốc của la bàn, biết thêm các quy tắc thực hiện các phép dựng hình học, thu được những kiến ​​thức mới và áp dụng được vào thực tế.
Giải các bài toán liên quan đến việc xây dựng bằng la bàn và thước kẻ là một trò tiêu khiển hữu ích cho phép bạn có cái nhìn mới về các tính chất đã biết của các hình hình học và các phần tử của chúng.Bài viết này thảo luận về những vấn đề cấp bách nhất liên quan đến việc xây dựng hình học bằng cách sử dụng la bàn và thước kẻ. Các vấn đề chính được xem xét và giải pháp của họ được đưa ra. Các bài toán đã cho có ý nghĩa quan trọng trong thực tiễn, củng cố kiến ​​thức đã học về hình học và có thể sử dụng vào công việc thực tế.
Như vậy, mục tiêu của công việc đã đạt được, nhiệm vụ được giao đã hoàn thành.

Src="https://hiện5.com/trình bày/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt=">Xây dựng bằng thước kẻ và la bàn Hình học">!}

Src="https://hiện tại5.com/trình bày/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="> Xây dựng một đoạn bằng Ú Bài toán A B đã cho"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

Src="https://hiện tại5.com/trình bày/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="> Dựng một góc bằng một góc cho trước Xét tam giác"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

Src="https://hiện tại5.com/trình bày/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="> Dựng đường phân giác của một góc Bài toán Ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

Src="https://hiện5.com/trình bày/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="> Dựng đường thẳng vuông góc Ú Bài toán Cho một đường thẳng"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}

Src="https://hiện tại5.com/trình bày/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="> Xây dựng trung điểm của một đoạn Bài tập Ú Xây dựng trung điểm của một được cho"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}