Bài đại số "Biến cố ngẫu nhiên. Xác suất của biến cố ngẫu nhiên."
Ban đầu, chỉ là một tập hợp thông tin và quan sát thực nghiệm về trò chơi súc sắc, lý thuyết xác suất đã trở thành một khoa học vững chắc. Fermat và Pascal là những người đầu tiên cung cấp cho nó một khung toán học.
Từ những suy ngẫm về cái vĩnh cửu đến lý thuyết xác suất
Hai cá nhân mà lý thuyết xác suất mắc nợ nhiều công thức cơ bản, Blaise Pascal và Thomas Bayes, được biết đến như những người sùng đạo sâu sắc, người sau là một mục sư Trưởng lão. Rõ ràng, mong muốn của hai nhà khoa học này là chứng minh sự sai lầm của quan điểm về một Vận may nào đó, mang lại may mắn cho những người yêu thích của cô ấy, đã thúc đẩy nghiên cứu trong lĩnh vực này. Xét cho cùng, trên thực tế, bất kỳ trò chơi may rủi nào, với thắng thua, chỉ là một bản giao hưởng của các nguyên tắc toán học.
Nhờ sự kích động của Chevalier de Mere, một tay cờ bạc không kém và cũng là một người không thờ ơ với khoa học, Pascal buộc phải tìm cách tính xác suất. De Mere quan tâm đến câu hỏi này: "Bạn cần tung hai con xúc xắc theo cặp bao nhiêu lần để xác suất được 12 điểm vượt quá 50%?". Câu hỏi thứ hai khiến quý ông vô cùng quan tâm: "Làm thế nào để chia tiền cược giữa những người tham gia trò chơi chưa hoàn thành?" Tất nhiên, Pascal đã trả lời thành công cả hai câu hỏi của de Mere, người vô tình trở thành người khởi xướng sự phát triển của lý thuyết xác suất. Điều thú vị là con người của de Mere vẫn được biết đến trong lĩnh vực này chứ không phải trong văn học.
Trước đây, chưa có nhà toán học nào cố gắng tính xác suất của các sự kiện, vì người ta tin rằng đây chỉ là một giải pháp phỏng đoán. Blaise Pascal đã đưa ra định nghĩa đầu tiên về xác suất của một sự kiện và chỉ ra rằng đây là một con số cụ thể có thể chứng minh bằng toán học. Lý thuyết xác suất đã trở thành cơ sở cho thống kê và được sử dụng rộng rãi trong khoa học hiện đại.
ngẫu nhiên là gì
Nếu chúng ta xem xét một phép thử có thể được lặp lại vô số lần, thì chúng ta có thể định nghĩa một biến cố ngẫu nhiên. Đây là một trong những kết quả có thể xảy ra của trải nghiệm.
Kinh nghiệm là việc thực hiện các hành động cụ thể trong điều kiện không đổi.

Để có thể làm việc với kết quả của kinh nghiệm, các sự kiện thường được ký hiệu bằng các chữ cái A, B, C, D, E ...
Xác suất của một sự kiện ngẫu nhiên
Để có thể tiến hành phần toán học của xác suất, cần phải xác định tất cả các thành phần của nó.
Xác suất của một sự kiện là thước đo bằng số về khả năng xảy ra một số sự kiện (A hoặc B) do trải nghiệm. Xác suất được ký hiệu là P(A) hoặc P(B).
Lý thuyết xác suất là:
- đáng tin cậy sự kiện chắc chắn sẽ xảy ra do kết quả của thí nghiệm Р(Ω) = 1;
- không thể nào sự kiện không bao giờ có thể xảy ra Р(Ø) = 0;
- ngẫu nhiên biến cố nằm giữa chắc chắn và không thể xảy ra, tức là xác suất xảy ra của nó là có thể xảy ra nhưng không đảm bảo (xác suất của biến cố ngẫu nhiên luôn nằm trong khoảng 0≤P(A)≤1).
Mối quan hệ giữa các sự kiện
Cả một và tổng các sự kiện A + B đều được xem xét khi sự kiện được tính trong quá trình triển khai ít nhất một trong các thành phần A hoặc B hoặc cả hai - A và B.
Trong mối quan hệ với nhau, các sự kiện có thể là:
- Như nhau có thể.
- tương thích.
- không tương thích.
- Ngược lại (loại trừ lẫn nhau).
- Sự phụ thuộc.
Nếu hai biến cố có thể xảy ra với xác suất bằng nhau thì chúng đều có thể.
Nếu sự xuất hiện của biến cố A không triệt tiêu xác suất xuất hiện của biến cố B, thì chúng tương thích.
Nếu các biến cố A và B không bao giờ xảy ra đồng thời trong cùng một thí nghiệm thì chúng được gọi là không tương thích. Tung đồng xu là một ví dụ điển hình: mặt sấp sẽ tự động không xuất hiện mặt ngửa.

Xác suất của tổng các sự kiện không tương thích như vậy bao gồm tổng các xác suất của từng sự kiện:
P(A+B)=P(A)+P(B)
Nếu sự xuất hiện của một sự kiện làm cho sự xuất hiện của sự kiện khác không thể xảy ra, thì chúng được gọi là ngược lại. Sau đó, một trong số chúng được chỉ định là A và cái còn lại - Ā (đọc là "không phải A"). Sự kiện A xảy ra có nghĩa là Ā không xảy ra. Hai sự kiện này tạo thành một nhóm hoàn chỉnh với tổng xác suất bằng 1.

Các sự kiện phụ thuộc có ảnh hưởng lẫn nhau, làm giảm hoặc tăng xác suất của nhau.
Mối quan hệ giữa các sự kiện. ví dụ
Việc hiểu các nguyên tắc của lý thuyết xác suất và sự kết hợp của các sự kiện bằng cách sử dụng các ví dụ sẽ dễ dàng hơn nhiều.
Thí nghiệm sẽ được thực hiện là kéo các quả bóng ra khỏi hộp và kết quả của mỗi thí nghiệm là một kết quả cơ bản.
Một sự kiện là một trong những kết quả có thể xảy ra của một trải nghiệm - một quả bóng đỏ, một quả bóng xanh, một quả bóng có số sáu, v.v.
Bài kiểm tra số 1. Có 6 quả bóng, trong đó có 3 quả màu xanh đánh số lẻ, 3 quả màu đỏ đánh số chẵn.

Bài kiểm tra số 2. Có 6 quả bóng màu xanh đánh số từ 1 đến 6.

Dựa trên ví dụ này, chúng ta có thể đặt tên cho các kết hợp:
- Sự kiện đáng tin cậy. bằng tiếng Tây Ban Nha Thứ 2, sự kiện "lấy được quả bóng màu xanh" là đáng tin cậy, vì xác suất xảy ra của nó là 1, vì tất cả các quả bóng đều màu xanh và không thể bỏ lỡ. Trong khi đó, sự kiện "lấy được quả bóng với số 1" là ngẫu nhiên.
- Sự kiện bất khả thi. bằng tiếng Tây Ban Nha Số 1 với các quả bóng màu xanh và đỏ, sự kiện "lấy được quả bóng màu tím" là không thể xảy ra vì xác suất xảy ra của nó bằng 0.
- Sự kiện tương đương bằng tiếng Tây Ban Nha 1 thì các biến cố “lấy được bi số 2” và “lấy được bi số 3” có xác suất xảy ra bằng nhau, các biến cố “lấy được bi số chẵn” và “lấy được bi số 2 ” có xác suất khác nhau.
- Các sự kiện tương thích Nhận được sáu trong quá trình tung xúc xắc hai lần liên tiếp là các sự kiện tương thích.
- Các sự kiện không tương thích Trong cùng một tiếng Tây Ban Nha Sự kiện số 1 "lấy bóng đỏ" và "lấy bóng số lẻ" không thể kết hợp trong cùng một trải nghiệm.
- sự kiện ngược lại. Ví dụ nổi bật nhất của việc này là tung đồng xu, trong đó việc rút mặt ngửa cũng giống như không rút mặt sấp và tổng xác suất của chúng luôn là 1 (nhóm đầy đủ).
- sự kiện phụ thuộc. Vì vậy, trong tiếng Tây Ban Nha Số 1, bạn có thể đặt cho mình mục tiêu lấy được quả bóng đỏ hai lần liên tiếp. Trích xuất hay không trích xuất lần đầu tiên ảnh hưởng đến xác suất trích xuất lần thứ hai.

Có thể thấy rằng sự kiện đầu tiên ảnh hưởng đáng kể đến xác suất của sự kiện thứ hai (40% và 60%).
Công thức xác suất sự kiện
Quá trình chuyển đổi từ bói toán sang dữ liệu chính xác xảy ra bằng cách chuyển chủ đề sang mặt phẳng toán học. Nghĩa là, các phán đoán về một sự kiện ngẫu nhiên như "xác suất cao" hoặc "xác suất tối thiểu" có thể được chuyển thành dữ liệu số cụ thể. Đã được phép đánh giá, so sánh và đưa tài liệu đó vào các tính toán phức tạp hơn.
Từ quan điểm tính toán, định nghĩa xác suất của một sự kiện là tỷ lệ giữa số lượng kết quả tích cực cơ bản với số lượng tất cả các kết quả có thể có của kinh nghiệm đối với một sự kiện cụ thể. Xác suất được ký hiệu là P (A), trong đó P có nghĩa là từ "xác suất", được dịch từ tiếng Pháp là "xác suất".
Vì vậy, công thức cho xác suất của một sự kiện là:
Trong đó m là số kết quả thuận lợi cho sự kiện A, n là tổng của tất cả các kết quả có thể xảy ra cho trải nghiệm này. Xác suất của một sự kiện luôn nằm trong khoảng từ 0 đến 1:
0 ≤ P(A) ≤ 1.
Tính toán xác suất của một sự kiện. Ví dụ
Hãy học tiếng Tây Ban Nha. Số 1 với các quả bóng, được mô tả trước đó: 3 quả bóng màu xanh có số 1/3/5 và 3 quả bóng màu đỏ có số 2/4/6.

Dựa trên thử nghiệm này, một số nhiệm vụ khác nhau có thể được xem xét:
- A - bóng đỏ rơi. Có 3 quả bóng đỏ và tổng cộng có 6 biến thể. Đây là ví dụ đơn giản nhất, trong đó xác suất của một biến cố là P(A)=3/6=0,5.
- B - giảm một số chẵn. Có tổng cộng 3 (2,4,6) số chẵn và tổng số các tùy chọn số có thể có là 6. Xác suất của sự kiện này là P(B)=3/6=0,5.
- C - mất một số lớn hơn 2. Có 4 phương án như vậy (3,4,5,6) trong tổng số các kết quả có thể xảy ra là 6. Xác suất của biến cố C là P(C)=4/6= 0,67.
Như có thể thấy từ các tính toán, sự kiện C có xác suất cao hơn, vì số lượng kết quả tích cực có thể xảy ra cao hơn ở A và B.
sự kiện không tương thích
Những sự kiện như vậy không thể xuất hiện đồng thời trong cùng một trải nghiệm. Như trong tiếng Tây Ban Nha Số 1, không thể có được một quả bóng màu xanh và màu đỏ cùng một lúc. Đó là, bạn có thể nhận được một quả bóng màu xanh hoặc màu đỏ. Tương tự như vậy, một số chẵn và một số lẻ không thể xuất hiện đồng thời trong một con súc sắc.
Xác suất của hai biến cố được coi là xác suất của tổng hoặc tích của chúng. Tổng của các sự kiện như vậy A + B được coi là một sự kiện bao gồm sự xuất hiện của một sự kiện A hoặc B và tích của AB của chúng - trong sự xuất hiện của cả hai. Ví dụ, sự xuất hiện của hai con sáu cùng một lúc trên mặt của hai con xúc xắc trong một lần ném.

Tổng của một số sự kiện là một sự kiện ngụ ý sự xuất hiện của ít nhất một trong số chúng. Sản phẩm của một số sự kiện là sự xuất hiện chung của tất cả chúng.
Trong lý thuyết xác suất, theo quy luật, việc sử dụng phép hợp "và" biểu thị tổng, phép hợp "hoặc" - phép nhân. Các công thức có ví dụ sẽ giúp bạn hiểu logic của phép cộng và phép nhân trong lý thuyết xác suất.
Xác suất của tổng các sự kiện không tương thích
Nếu xác suất của các sự kiện không tương thích được xem xét, thì xác suất của tổng các sự kiện bằng tổng xác suất của chúng:
P(A+B)=P(A)+P(B)
Ví dụ: chúng tôi tính xác suất bằng tiếng Tây Ban Nha. Số 1 với các quả bóng màu xanh và đỏ sẽ đánh rơi một số từ 1 đến 4. Chúng tôi sẽ tính toán không phải bằng một hành động mà bằng tổng xác suất của các thành phần cơ bản. Vì vậy, trong một thí nghiệm như vậy chỉ có 6 quả bóng hoặc 6 trong số tất cả các kết quả có thể xảy ra. Các số thỏa mãn điều kiện là 2 và 3. Xác suất ra được số 2 là 1/6, xác suất ra được số 3 cũng là 1/6. Xác suất để được số từ 1 đến 4 là:
Xác suất của tổng các sự kiện không tương thích của một nhóm hoàn chỉnh là 1.
Vì vậy, nếu trong thí nghiệm với một khối lập phương, chúng ta cộng các xác suất để nhận được tất cả các số, thì kết quả là chúng ta sẽ nhận được một.
Điều này cũng đúng đối với các biến cố ngược chiều, ví dụ, trong thí nghiệm với một đồng xu, trong đó một trong các mặt của nó là biến cố A và mặt kia là biến cố ngược lại Ā, như đã biết,
Р(А) + Р(Ā) = 1
Xác suất tạo ra các sự kiện không tương thích
Phép nhân xác suất được sử dụng khi xem xét sự xuất hiện của hai hoặc nhiều sự kiện xung khắc trong một lần quan sát. Xác suất để các sự kiện A và B xuất hiện trong đó cùng một lúc bằng tích các xác suất của chúng, hoặc:
P(A*B)=P(A)*P(B)
Ví dụ, xác suất mà trong Số 1 là kết quả của hai lần thử, một quả bóng màu xanh sẽ xuất hiện hai lần, bằng
Nghĩa là, xác suất của một sự kiện xảy ra khi, do kết quả của hai lần thử lấy các quả bóng, chỉ các quả bóng màu xanh sẽ được lấy ra, là 25%. Rất dễ dàng để thực hiện các thí nghiệm thực tế về vấn đề này và xem liệu đây có phải là trường hợp thực tế hay không.
sự kiện chung
Các sự kiện được coi là chung khi sự xuất hiện của một trong số chúng có thể trùng với sự xuất hiện của sự kiện kia. Mặc dù thực tế là chúng liên kết với nhau, xác suất của các sự kiện độc lập vẫn được xem xét. Ví dụ: tung hai con xúc xắc có thể cho kết quả khi cả hai con đều có số 6. Mặc dù các sự kiện trùng khớp và xuất hiện đồng thời nhưng chúng độc lập với nhau - chỉ một con sáu có thể rơi ra, con xúc xắc thứ hai không có. ảnh hưởng lên nó.

Xác suất của các sự kiện chung được coi là xác suất của tổng của chúng.
Xác suất của tổng các sự kiện chung. Ví dụ
Xác suất của tổng các sự kiện A và B, liên quan đến nhau trong mối quan hệ với nhau, bằng tổng xác suất của sự kiện trừ đi xác suất của sản phẩm của chúng (nghĩa là sự thực hiện chung của chúng):
khớp R. (A + B) \u003d P (A) + P (B) - P (AB)
Giả sử rằng xác suất bắn trúng mục tiêu bằng một lần bắn là 0,4. Sau đó, sự kiện A - bắn trúng mục tiêu trong lần thử đầu tiên, B - trong lần thứ hai. Những sự kiện này là chung, vì có thể bắn trúng mục tiêu cả từ phát thứ nhất và từ phát thứ hai. Nhưng các sự kiện không phụ thuộc. Xác suất của sự kiện bắn trúng mục tiêu bằng hai phát (ít nhất một) là bao nhiêu? Theo công thức:
0,4+0,4-0,4*0,4=0,64
Đáp án cho câu hỏi là: "Xác suất bắn trúng mục tiêu bằng hai lần bắn là 64%".
Công thức tính xác suất của một biến cố này cũng có thể được áp dụng cho các biến cố xung khắc, trong đó xác suất xảy ra đồng thời của một biến cố P(AB) = 0. Điều này có nghĩa là xác suất của tổng các biến cố xung khắc có thể được coi là một trường hợp đặc biệt của công thức đề xuất.
Hình học xác suất cho rõ ràng
Thật thú vị, xác suất của tổng các sự kiện chung có thể được biểu diễn dưới dạng hai khu vực A và B giao nhau. Như bạn có thể thấy từ hình ảnh, diện tích liên kết của chúng bằng tổng diện tích trừ đi diện tích giao điểm của chúng. Giải thích hình học này làm cho công thức có vẻ phi logic trở nên dễ hiểu hơn. Lưu ý rằng các giải pháp hình học không phải là hiếm trong lý thuyết xác suất.

Định nghĩa về xác suất của tổng của một tập hợp (hơn hai) sự kiện chung là khá rườm rà. Để tính toán nó, bạn cần sử dụng các công thức được cung cấp cho những trường hợp này.
sự kiện phụ thuộc
Các sự kiện phụ thuộc được gọi nếu sự xuất hiện của một (A) trong số chúng ảnh hưởng đến xác suất xảy ra của (B) kia. Hơn nữa, ảnh hưởng của cả việc xảy ra và không xảy ra sự kiện A đều được tính đến. Mặc dù các sự kiện được gọi là phụ thuộc theo định nghĩa, nhưng chỉ một trong số chúng là phụ thuộc (B). Xác suất thông thường được ký hiệu là P(B) hoặc xác suất của các sự kiện độc lập. Trong trường hợp người phụ thuộc, một khái niệm mới được đưa ra - xác suất có điều kiện P A (B), là xác suất của sự kiện phụ thuộc B với điều kiện là sự kiện A (giả thuyết) đã xảy ra mà nó phụ thuộc vào.
Nhưng sự kiện A cũng là ngẫu nhiên nên nó cũng có xác suất phải và có thể tính đến trong các phép tính. Ví dụ sau sẽ chỉ ra cách làm việc với các sự kiện phụ thuộc và một giả thuyết.
Ví dụ về tính xác suất của các sự kiện phụ thuộc
Một ví dụ điển hình để tính các sự kiện phụ thuộc là một cỗ bài tiêu chuẩn.

Trong ví dụ về bộ bài 36 lá, hãy xem xét các sự kiện phụ thuộc. Cần xác định xác suất để lá bài thứ hai được rút ra từ bộ bài sẽ là bộ kim cương, nếu lá bài đầu tiên được rút ra là:
- Lục lạc.
- Một bộ đồ khác.
Rõ ràng, xác suất của sự kiện B thứ hai phụ thuộc vào sự kiện A đầu tiên. Vì vậy, nếu lựa chọn đầu tiên là đúng, đó là 1 thẻ (35) và 1 viên kim cương (8) ít hơn trong bộ bài, thì xác suất của sự kiện B:
P A (B) \u003d 8 / 35 \u003d 0,23
Nếu phương án thứ hai là đúng, thì có 35 lá bài trong bộ bài và tổng số trống lục lạc (9) vẫn được giữ nguyên, thì xác suất của biến cố sau là B:
P A (B) \u003d 9/35 \u003d 0,26.
Có thể thấy rằng nếu sự kiện A có điều kiện là quân bài đầu tiên là một viên kim cương, thì xác suất của sự kiện B sẽ giảm và ngược lại.
Nhân các sự kiện phụ thuộc
Dựa vào chương trước, chúng ta chấp nhận sự kiện đầu tiên (A) là một sự thật, nhưng về bản chất, nó có tính chất ngẫu nhiên. Xác suất của sự kiện này, cụ thể là lấy được một trống lục lạc từ một cỗ bài, bằng:
P(A) = 9/36=1/4
Vì lý thuyết không tự tồn tại mà được kêu gọi để phục vụ các mục đích thực tế, nên công bằng mà nói, hầu hết các trường hợp đều cần đến xác suất tạo ra các sự kiện phụ thuộc.
Theo định lý về tích xác suất của các sự kiện phụ thuộc, xác suất xảy ra các sự kiện phụ thuộc chung A và B bằng xác suất của một sự kiện A, nhân với xác suất có điều kiện của sự kiện B (tùy thuộc vào A):
P (AB) \u003d P (A) * P A (B)
Sau đó, trong ví dụ với một cỗ bài, xác suất rút được hai lá bài có bộ kim cương là:
9/36*8/35=0,0571 hay 5,7%
Và xác suất lấy ra không phải kim cương lúc đầu, rồi sau đó là kim cương, bằng:
27/36*9/35=0,19 hoặc 19%
Có thể thấy rằng xác suất xảy ra sự kiện B lớn hơn, với điều kiện là một quân bài của một bộ đồ không phải là một viên kim cương được rút trước. Kết quả này khá logic và dễ hiểu.
Tổng xác suất của một sự kiện
Khi một vấn đề với xác suất có điều kiện trở nên nhiều mặt, nó không thể được tính toán bằng các phương pháp thông thường. Khi có nhiều hơn hai giả thuyết, cụ thể là A1, A2, ..., A n, .. tạo thành một nhóm đầy đủ các biến cố với điều kiện:
- P(A i)>0, i=1,2,…
- A i ∩ A j =Ø,i≠j.
- Σ k A k =Ω.
Vậy công thức tính tổng xác suất của biến cố B với nhóm đầy đủ các biến cố ngẫu nhiên A1, A2, ..., A n là:

Một cái nhìn về tương lai
Xác suất của một sự kiện ngẫu nhiên là cần thiết trong nhiều lĩnh vực khoa học: kinh tế lượng, thống kê, vật lý, v.v. Vì một số quy trình không thể được mô tả một cách xác định, vì bản thân chúng là xác suất, nên cần có các phương pháp làm việc đặc biệt. Xác suất của một lý thuyết sự kiện có thể được sử dụng trong bất kỳ lĩnh vực công nghệ nào như một cách để xác định khả năng xảy ra lỗi hoặc trục trặc.
Có thể nói rằng, bằng cách thừa nhận xác suất, chúng ta phần nào tiến một bước về mặt lý thuyết vào tương lai, nhìn nó qua lăng kính của các công thức.
Hướng dẫn xác suất: Nội dung
Chương 1. Biến cố ngẫu nhiên. tính xác suất
1.1. Các yếu tố của tổ hợp
1.2. Định nghĩa cổ điển về xác suất
1.3. Định nghĩa hình học của xác suất
1.4. Cộng và nhân xác suất
1.5. xác suất có điều kiện
1.6. Công thức xác suất tổng và công thức Bayes
1.7. Các bài kiểm tra độc lập. công thức Bernoulli
1.8. Số lần thành công nhiều khả năng
1.9. công thức độc
1.10. Định lý De Moivre-Laplace
1.1. Các yếu tố của tổ hợp
Xét một số tập hợp X, bao gồm N phần tử . Chúng tôi sẽ chọn từ tập hợp này các tập hợp con được sắp xếp khác nhau từ k phần tử.
Chỗ ở từ N thiết lập các yếu tố X Qua k các phần tử, chúng tôi muốn nói đến bất kỳ tập hợp có thứ tự nào của các phần tử của tập hợp X.
Nếu việc chọn các phần tử của tập hợp từ X xảy ra với sự trở lại, tức là mỗi phần tử của tập hợp X có thể được chọn nhiều lần, sau đó số lượng vị trí từ N Qua kđược tìm bởi công thức ( vị trí với sự lặp lại ).
Nếu sự lựa chọn được thực hiện mà không có sự trở lại, tức là mỗi phần tử của tập hợp X chỉ có thể được chọn một lần, sau đó số lượng vị trí từ N Qua kđược biểu thị và định nghĩa bởi đẳng thức
(vị trí không lặp lại ).
Ví dụ. Cho sáu chữ số đã cho: 1; 2; 3; 4; 5; 6. Từ các số này lập được bao nhiêu số có ba chữ số.
Giải pháp. Nếu các chữ số có thể được lặp lại thì số các số có ba chữ số sẽ là ![]() . Nếu các số không lặp lại, thì
. Nếu các số không lặp lại, thì ![]() .
.
Ví dụ. Sinh viên của viện học mười môn học trong mỗi học kỳ. Lịch học bao gồm 3 môn mỗi ngày. Phòng điều khiển có thể lập bao nhiêu lịch trình khác nhau?
Giải pháp. Lịch trình cho mỗi ngày có thể khác nhau về mặt hàng hoặc thứ tự đặt các mặt hàng này, vì vậy chúng tôi có các vị trí sau: ![]()
Một trường hợp đặc biệt của vị trí tại N=k gọi điện hoán vị
từ N phần tử. Số lượng tất cả các hoán vị từ N yếu tố bằng
.
Ví dụ. Trên giá sách có 30 cuốn sách, trong đó có 27 cuốn khác loại và 3 cuốn của cùng một tác giả. Có bao nhiêu cách sắp xếp những cuốn sách này trên giá sách sao cho các cuốn sách của cùng một tác giả nằm cạnh nhau?
Giải pháp. Ta sẽ coi ba cuốn sách của một tác giả là một cuốn sách thì số hoán vị sẽ là . Và ba cuốn sách có thể được sắp xếp lại với nhau theo các cách, khi đó theo quy tắc tích ta có số cách cần thiết bằng: *=3!*28!
Hãy để bây giờ từ bộ X một tập hợp con không có thứ tự được chọn (thứ tự của các phần tử trong tập hợp con không quan trọng). kết hợp
từ N yếu tố bởi k gọi là tập con của k các phần tử khác nhau ít nhất một phần tử. Tổng số tất cả các kết hợp của N Qua k biểu thị và bằng nhau ![]() .
.
Đẳng thức có giá trị: , , .
Ví dụ. Trong một nhóm 27 sinh viên, phải chọn ba người phục vụ. Trong bao nhiêu cách có thể được thực hiện?
Giải pháp. Vì thứ tự của học sinh không quan trọng, chúng tôi sử dụng công thức cho số lượng kết hợp: ![]() .
.
Khi giải các bài toán tổ hợp sử dụng các quy tắc sau:
Quy tắc cộng. Nếu một đối tượng A có thể được chọn từ một tập hợp các đối tượng theo m cách và một đối tượng B khác có thể được chọn theo n cách, thì A hoặc B có thể được chọn theo m + n cách.
Quy tắc nhân. Nếu đối tượng A có thể được chọn từ một tập hợp các đối tượng theo m cách và sau mỗi cách chọn như vậy, đối tượng B có thể được chọn theo n cách, thì cặp đối tượng (A, B) theo thứ tự đã chỉ định có thể được chọn trong m * n cách.
Ví dụ. Trang phục của học sinh bao gồm áo cánh, váy và giày. Cô gái có bốn chiếc áo cánh, năm chiếc váy và ba đôi giày trong tủ quần áo của mình. Học sinh có thể có bao nhiêu bộ quần áo?
Giải pháp. Cho học sinh chọn áo trước. Sự lựa chọn này có thể được thực hiện theo bốn cách, vì học sinh có bốn chiếc áo cánh, nên trong năm cách sẽ có một sự lựa chọn về váy và trong ba cách sẽ có một sự lựa chọn về giày. Theo nguyên tắc nhân, thu được 4 * 5 * 3 = 60 trang phục (kết hợp).
1.2. Định nghĩa cổ điển về xác suất
Khái niệm cơ bản của lý thuyết xác suất là khái niệm về biến cố ngẫu nhiên. sự kiện ngẫu nhiên Một biến cố được gọi là biến cố mà trong những điều kiện nhất định, nó có thể xảy ra hoặc không xảy ra. Ví dụ: bắn trúng hoặc bỏ sót một đối tượng khi bắn vào đối tượng này bằng vũ khí đã cho là một sự kiện ngẫu nhiên.
Sự kiện được gọi là thật nếu, do kết quả của thử nghiệm, nó nhất thiết phải xảy ra. Không thể nào Một biến cố được gọi là biến cố không thể xảy ra do phép thử.
Biến cố ngẫu nhiên được gọi là không tương thích trong một thử nghiệm nhất định nếu không có hai trong số họ có thể xuất hiện cùng nhau.
Mẫu sự kiện ngẫu nhiên nhóm đầy đủ , nếu tại mỗi lần thử, bất kỳ sự kiện nào trong số chúng có thể xuất hiện và không có sự kiện nào khác không tương thích với chúng có thể xuất hiện.
Hãy xem xét nhóm đầy đủ các sự kiện ngẫu nhiên không tương thích có thể xảy ra như nhau. Những sự kiện như vậy sẽ được gọi là kết quả. Exodus được gọi là thuận lợi sự xuất hiện của một sự kiện MỘT nếu sự xuất hiện của sự kiện này kéo theo sự xuất hiện của sự kiện MỘT.
Ví dụ. Một hộp chứa 8 quả cầu được đánh số (mỗi quả cầu có một số từ 1 đến 8). Bi có số 1, 2, 3 có màu đỏ, các bi còn lại có màu đen. Sự xuất hiện của bi mang số 1 (hoặc số 2 hoặc số 3) là biến cố thuận lợi cho sự xuất hiện của bi đỏ. Bi có số 4 (hoặc 5, 6, 7, 8) là biến cố xuất hiện bi đen.
Xác suất của một sự kiện
MỘT là tỷ lệ giữa số m kết quả thuận lợi cho sự kiện này với tổng số n của tất cả các kết quả cơ bản không tương thích có thể xảy ra như nhau tạo thành một nhóm hoàn chỉnh
Tài sản 1. Xác suất của một biến cố nào đó bằng một
Tài sản 2. Xác suất của một sự kiện không thể xảy ra là bằng không.
Tài sản 3. Xác suất của một biến cố ngẫu nhiên là một số dương nằm trong khoảng từ 0 đến 1.
Vì vậy, xác suất của bất kỳ sự kiện nào thỏa mãn bất đẳng thức kép.
Ví dụ. Trong hũ có 10 viên bi được đánh số thứ tự từ 1 đến 10. Lấy ra 1 viên bi. Xác suất để số quả bóng rút được không vượt quá 10 là bao nhiêu?
Giải pháp. Hãy để sự kiện MỘT= (Số bi được rút không vượt quá 10). Số lần xuất hiện của các sự kiện thuận lợi MỘT bằng số tất cả các trường hợp có thể tôi=N=10. Kể từ đây, r(MỘT)=1. Sự kiện một đáng tin cậy.
Ví dụ. Có 10 quả bóng trong một cái hộp: 6 trắng và 4 đen. Kéo ra hai quả bóng. Xác suất mà cả hai quả bóng là màu trắng là gì?
Giải pháp. Hai trong số mười quả bóng có thể được rút ra theo một số cách sau: ![]() .
.
Số lần trong hai quả cầu đó có hai quả cầu trắng là ![]() .
.
xác suất mong muốn ![]() .
.
Ví dụ. Có 15 quả bóng trong một cái bình: 5 trắng và 10 đen. Xác suất để lấy được một quả bóng màu xanh từ chiếc bình là bao nhiêu?
Giải pháp. Vì không có quả bóng màu xanh trong bình, tôi=0, N=15. Do đó, xác suất mong muốn r=0. Sự kiện vẽ một quả bóng màu xanh không thể nào.
Ví dụ. Một lá bài được rút từ bộ bài 36 lá. Xác suất của một thẻ trái tim xuất hiện là gì?
Giải pháp. Số kết quả cơ bản (số thẻ) N=36. Sự kiện MỘT= (Xuất hiện thẻ phù hợp với trái tim). Số lần thuận lợi cho sự kiện xảy ra MỘT, tôi=9. Kể từ đây, ![]() .
.
Ví dụ. Có 6 nam và 4 nữ trong văn phòng. 7 người được chọn ngẫu nhiên cho việc di chuyển. Tính xác suất để trong số những người được chọn có 3 nữ.
Giải pháp. Tổng số kết quả có thể xảy ra bằng số cách chọn 7 người trong số 10 người, tức là ![]() .
.
Hãy tìm số kết quả có lợi cho sự kiện mà chúng ta quan tâm: ba phụ nữ có thể được chọn từ bốn cách; trong khi bốn người còn lại phải là nam giới, họ có thể được chọn theo nhiều cách. Do đó, số lượng kết quả thuận lợi bằng ![]() .
.
xác suất mong muốn  .
.
1.3. Định nghĩa hình học của xác suất
Hãy coi phép thử ngẫu nhiên là ném ngẫu nhiên một điểm vào một vùng hình học G nào đó (trên một đường thẳng, mặt phẳng hoặc không gian). Kết quả sơ cấp là các điểm riêng lẻ G, bất kỳ biến cố nào cũng là tập con của miền này, không gian của các kết quả sơ cấp G. Chúng ta có thể giả sử rằng tất cả các điểm G đều “bằng nhau” và khi đó xác suất của một điểm rơi vào một tập con nào đó tỷ lệ thuận với đo lường (chiều dài, diện tích, thể tích) và không phụ thuộc vào vị trí và hình dạng của nó.
xác suất hình học
biến cố A được xác định bởi quan hệ:
,
trong đó m(G), m(A) là các số đo hình học (độ dài, diện tích hoặc thể tích) của toàn bộ không gian của các kết quả cơ bản và biến cố A.
Ví dụ. Một vòng tròn bán kính r () được ném ngẫu nhiên lên một mặt phẳng được chia bởi các dải song song có chiều rộng 2d, khoảng cách giữa các đường trục bằng 2D. Tìm xác suất để đường tròn cắt một số dải.
Giải pháp. Như một kết quả cơ bản của thử nghiệm này, chúng tôi sẽ xem xét khoảng cách x từ tâm của vòng tròn đến đường trung tâm của dải gần vòng tròn nhất. Khi đó toàn bộ không gian các kết cục sơ cấp là một đoạn ![]() . Giao điểm của vòng tròn với dải sẽ xảy ra nếu tâm của nó rơi vào dải, tức là , hoặc sẽ được đặt từ mép của dải ở khoảng cách nhỏ hơn bán kính, tức là .
. Giao điểm của vòng tròn với dải sẽ xảy ra nếu tâm của nó rơi vào dải, tức là , hoặc sẽ được đặt từ mép của dải ở khoảng cách nhỏ hơn bán kính, tức là .
Đối với xác suất mong muốn, chúng tôi có được: .
1.4. Cộng và nhân xác suất
Sự kiện MỘT gọi điện trương hợp đặc biệt sự kiện TRONG, nếu khi xảy ra MỘTđến và TRONG. Cái gì MỘT là một trường hợp đặc biệt TRONG, viết ra .
Sự kiện MỘT Và TRONG gọi điện bình đẳng, nếu cái này là trường hợp đặc biệt của cái kia. Sự bình đẳng của các sự kiện MỘT Và TRONG viết ra A = B.
Tổng sự kiện MỘT Và TRONGđược gọi là một sự kiện A+B, xảy ra khi và chỉ khi ít nhất một trong các sự kiện xảy ra: MỘT hoặc TRONG.
Định lý về phép cộng xác suất. Xác suất của một trong hai không tương thích biến cố bằng tổng xác suất của các biến cố này.
Lưu ý rằng định lý được xây dựng có giá trị đối với bất kỳ số lượng sự kiện xung khắc nào:
![]() .
.
Nếu các biến cố ngẫu nhiên tạo thành một nhóm đầy đủ các biến cố xung khắc thì đẳng thức
công việc sự kiện MỘT Và TRONGđược gọi là một sự kiện AB, xảy ra khi và chỉ khi cả hai sự kiện xảy ra: MỘT Và TRONGđồng thời. Những sự kiện ngẫu nhiên MỘT Và b gọi điện chung nếu cả hai sự kiện này có thể xảy ra trong một thử nghiệm nhất định.
Định lý xác suất bổ sung 2. xác suất tổng chung sự kiện được tính theo công thức
sự kiện sự kiện MỘT Và TRONG gọi điện độc lập nếu sự xuất hiện của một trong số chúng không làm thay đổi xác suất xảy ra của cái kia. Sự kiện MỘT gọi điện sự phụ thuộc từ sự kiện TRONG nếu xác suất của biến cố MỘT thay đổi tùy theo sự kiện TRONG hay không.
Định lý về phép nhân xác suất. Xác suất tạo ra các sự kiện độc lập MỘT Và TRONG tính theo công thức:
Xác suất của tích các sự kiện phụ thuộc được tính bằng công thức xác suất có điều kiện (xem phần tiếp theo).
Ví dụ. Hộp thứ nhất chứa 1 bi trắng và 5 bi đen, hộp thứ hai chứa 8 bi trắng và 4 bi đen. Một quả bóng đã được lấy từ mỗi hộp. Tìm xác suất để một trong các quả bóng được lấy ra là màu trắng và quả bóng còn lại là màu đen.
Giải pháp. Hãy biểu thị các sự kiện: MỘT- họ lấy ra một quả bóng trắng từ hộp đầu tiên,
;
Họ lấy ra một quả bóng đen từ hộp đầu tiên,
;
TRONG- một quả bóng trắng từ hộp thứ hai,
;
Quả bóng đen từ hộp thứ hai,
.
Chúng tôi cần một trong các sự kiện hoặc . Theo định lý nhân xác suất
, .
Sau đó, xác suất mong muốn theo định lý bổ sung sẽ là
.
Ví dụ. Xác suất bắn trúng mục tiêu của người bắn đầu tiên là 0,8, của người thứ hai - 0,9. Mũi tên thực hiện một phát bắn. Tìm xác suất để: a) bắn trúng hai lần; b) ít nhất một lần trúng đích; d) một cú đánh.
Giải pháp.
Cho phép MỘT– cú đánh của người bắn đầu tiên, ;
TRONG- người bắn thứ hai trúng đích, .
Sau đó - bỏ lỡ lần đầu tiên, ![]() ;
;
Thiếu cái thứ hai ![]() .
.
Hãy tìm các xác suất cần thiết.
MỘT) AB- đánh đôi
b) - bỏ lỡ kép, .
V) MỘT+TRONG- ít nhất một cú đánh
d) một cú đánh
Ví dụ. Học sinh tìm kiếm công thức mình cần trong ba cuốn sách tham khảo. Xác suất mà công thức được chứa trong thư mục thứ nhất, thứ hai và thứ ba là 0,6; 0,7 và 0,8. Tìm xác suất mà công thức được chứa 1) chỉ trong một thư mục; 2) chỉ trong hai thư mục; 3) trong cả ba thư mục.
Giải pháp.
MỘT- công thức được chứa trong thư mục đầu tiên;
TRONG- công thức được chứa trong thư mục thứ hai;
VỚI- công thức được chứa trong thư mục thứ ba.
Hãy sử dụng các định lý cộng và nhân xác suất.
Giả sử kết quả của phép thử n sự kiện, độc lập trong tổng thể hoặc một số trong số chúng (cụ thể là chỉ một hoặc không có sự kiện nào) có thể xuất hiện và xác suất xảy ra của từng sự kiện được biết đến. Làm thế nào để tìm xác suất mà ít nhất một trong những sự kiện này sẽ xảy ra? Ví dụ: nếu ba sự kiện có thể xuất hiện do một phép thử, thì sự xuất hiện của ít nhất một trong các sự kiện này có nghĩa là sự xuất hiện của một hoặc hai hoặc ba sự kiện. Câu trả lời cho câu hỏi này được đưa ra bởi định lý sau.
định lý. xác suất sự xuất hiện của ít nhất một trong các sự kiện , độc lập trong tổng thể, bằng hiệu giữa đơn vị và tích xác suất của các sự kiện ngược lại
Nếu các sự kiện có cùng xác suất, thì công thức có dạng đơn giản:
![]() .
.
Ví dụ. Xác suất bắn trúng mục tiêu khi bắn từ ba khẩu súng như sau: P 1 = 0,8;P 2 = 0,7; P 3 = 0,9. Tìm xác suất để ít nhất một phát trúng (sự kiện A) bằng một phát từ tất cả các súng.
Giải pháp. Xác suất bắn trúng mục tiêu của mỗi khẩu súng không phụ thuộc vào kết quả bắn của các khẩu súng khác, vì vậy các sự kiện đang xét (trúng bởi khẩu thứ nhất), (trúng bởi khẩu thứ hai) và (trúng bởi khẩu thứ ba) súng) là độc lập trong tổng hợp.
Xác suất của các sự kiện ngược lại với các sự kiện và (nghĩa là xác suất bỏ lỡ) tương ứng là:
![]() ,
, ![]() ,
, ![]()
Xác suất mong muốn.
Ví dụ. Nhà in có 4 máy in phẳng. Đối với mỗi máy, xác suất để nó hiện đang chạy là 0,9. Tìm xác suất để có ít nhất một máy đang chạy (sự kiện A).
Giải pháp. Các sự kiện "máy đang chạy" và "máy không chạy" (tại thời điểm này) trái ngược nhau, vì vậy tổng xác suất của chúng bằng một:
Do đó xác suất máy hiện không chạy bằng
xác suất mong muốn
Vì xác suất thu được rất gần với 1, nên trên cơ sở hệ quả từ nguyên tắc không thể xảy ra trong thực tế của các sự kiện khó xảy ra, chúng ta có quyền kết luận rằng ít nhất một trong các máy đang hoạt động vào lúc này.
Ví dụ. Xác suất để trong một lần bắn trúng mục tiêu là 0,4. Người bắn phải bắn bao nhiêu phát để xác suất bắn trúng mục tiêu ít nhất là 0,9?
Giải pháp. Kí hiệu A là biến cố "có n lần bắn, người bắn trúng mục tiêu ít nhất một lần". Các sự kiện bắn trúng mục tiêu ở lần bắn đầu tiên, lần bắn thứ hai, v.v., là độc lập chung, vì vậy công thức được áp dụng.
Có tính đến điều đó, theo điều kiện, ![]() (do đó, ), chúng tôi nhận được
(do đó, ), chúng tôi nhận được
Chúng ta lấy logarit của bất đẳng thức này trong cơ số 10:

Vì vậy, tức là Người bắn phải bắn ít nhất 5 phát.
1.5. xác suất có điều kiện
Biến cố ngẫu nhiên được định nghĩa là biến cố mà dưới sự thực hiện của một tập hợp các điều kiện thí nghiệm, nó có thể xảy ra hoặc không. Nếu khi tính xác suất của một sự kiện, không có giới hạn nào khác được áp đặt, ngoại trừ các điều kiện của thí nghiệm, thì xác suất đó được gọi là vô điều kiện ; nếu các điều kiện bổ sung khác được áp đặt, thì xác suất của một sự kiện được gọi là có điều kiện . Ví dụ, người ta thường tính xác suất của một biến cố TRONG với điều kiện bổ sung là một sự kiện đã xảy ra MỘT.
xác suất có điều kiện
![]() (hai ký hiệu) được gọi là xác suất của biến cố TRONG, được tính theo giả định rằng sự kiện MỘTđã đến rồi.
(hai ký hiệu) được gọi là xác suất của biến cố TRONG, được tính theo giả định rằng sự kiện MỘTđã đến rồi.
xác suất sự xuất hiện chung của hai sự kiện phụ thuộc bằng tích xác suất của một trong số chúng với xác suất có điều kiện của lần thứ hai, được tính với điều kiện là sự kiện đầu tiên xảy ra, tức là
Đặc biệt, từ đây ta có được ![]() .
.
Ví dụ. Một hộp đựng 3 quả cầu trắng và 2 quả cầu đen. Một quả bóng được rút ra từ chiếc bình, và sau đó là quả bóng thứ hai. Sự kiện TRONG- sự xuất hiện của một quả bóng trắng ở lần loại bỏ đầu tiên. Sự kiện MỘT- sự xuất hiện của một quả bóng trắng ở lần loại bỏ thứ hai.
Giải pháp. Rõ ràng là xác suất của một sự kiện MỘT nếu sự kiện TRONGđã xảy ra, sẽ ![]() .
.
xác suất sự kiện MỘT miễn là sự kiện TRONGđã không xảy ra, sẽ
.
Ví dụ. Một hộp đựng 3 quả cầu trắng và 3 quả cầu đen. Một quả bóng được lấy ra khỏi bình hai lần mà không trả lại chúng. Tìm xác suất để bi trắng xuất hiện trong lần thử thứ hai (biến cố B) nếu trong lần thử đầu tiên (biến cố A) rút được bi đen.
Giải pháp. Sau lần thử thứ nhất, trong hộp còn lại 5 viên bi, trong đó có 3 viên màu trắng. Xác suất có điều kiện mong muốn .
Kết quả tương tự có thể thu được từ công thức
.
Thật vậy, xác suất để bi trắng xuất hiện ở lần thử đầu tiên
.
Tính xác suất để lần thứ nhất xuất hiện bi đen, lần thứ hai xuất hiện bi trắng. Tổng số kết quả - sự xuất hiện chung của hai quả bóng, bất kể màu gì, bằng với số lượng vị trí. Trong số các kết quả này, sự kiện được ủng hộ bởi các kết quả. Kể từ đây, ![]() .
.
Xác suất có điều kiện bắt buộc ![]()
Các kết quả phù hợp.
Ví dụ.Đội tàu điện có 15 xe điện tuyến số 1 và 10 xe điện tuyến số 2. Xác suất mà xe điện thứ hai trên tuyến sẽ là tuyến 1 là gì?
Giải pháp. Cho phép MỘT- một sự kiện bao gồm việc tuyến xe điện số 1 vào tuyến, TRONG- tuyến đường số 2.
Xem xét tất cả các sự kiện có thể xảy ra trong trường hợp này (trong các điều kiện của vấn đề của chúng tôi): ![]() . Trong số này, chúng ta sẽ chỉ quan tâm đến tuyến thứ nhất và thứ ba, khi tuyến xe điện số 1 xuất hiện ở vị trí thứ hai.
. Trong số này, chúng ta sẽ chỉ quan tâm đến tuyến thứ nhất và thứ ba, khi tuyến xe điện số 1 xuất hiện ở vị trí thứ hai.
Vì tất cả các sự kiện này là chung, sau đó:
![]() ;
;
![]() ;
;
do đó xác suất mong muốn
Ví dụ. Xác suất để 2 lá bài rút ra từ bộ bài 36 lá cùng chất là bao nhiêu?
Giải pháp. Đầu tiên, chúng tôi tính xác suất để hai quân bài cùng chất cụ thể (ví dụ: quân bích chẳng hạn). Cho phép MỘT- sự xuất hiện của thẻ đầu tiên của bộ đồ này, TRONG- sự xuất hiện của thẻ thứ hai của cùng một bộ đồ. Sự kiện TRONG sự kiện phụ thuộc MỘT, bởi vì xác suất của nó thay đổi tùy thuộc vào việc sự kiện có xảy ra hay không MỘT. Do đó, chúng ta sẽ phải sử dụng định lý nhân ở dạng tổng quát:
![]() ,
,
Ở đâu ![]() (sau khi rút quân bài đầu tiên còn lại 35 quân bài, trong đó có 8 quân bài cùng chất với quân bài đầu tiên).
(sau khi rút quân bài đầu tiên còn lại 35 quân bài, trong đó có 8 quân bài cùng chất với quân bài đầu tiên).
Chúng tôi nhận được
.
Các sự kiện bao gồm thực tế là hai lá bài của bộ bích, bộ gậy, v.v. sẽ được rút ra là không tương thích với nhau. Do đó, để tìm xác suất kết hợp của chúng, chúng tôi sử dụng định lý bổ sung: ![]() .
.
1.6. Công thức xác suất tổng và công thức Bayes
Nếu sự kiện MỘT chỉ có thể xảy ra khi một trong các sự kiện hình thành nhóm đầy đủ các sự kiện không tương thích , thì xác suất của biến cố MỘT tính theo công thức
Công thức này được gọi là tổng công thức xác suất .
Xem xét lại nhóm đầy đủ các sự kiện không tương thích, xác suất của chúng là . Sự kiện MỘT chỉ có thể xảy ra cùng với bất kỳ sự kiện nào mà chúng ta sẽ gọi giả thuyết . Khi đó theo công thức xác suất tổng
Nếu sự kiện MỘT xảy ra, nó có thể làm thay đổi xác suất của các giả thuyết.
Theo định lý nhân xác suất
![]() .
.
Tương tự, đối với các giả thuyết khác
![]()
Công thức kết quả được gọi là công thức bayes (công thức bayes ). Xác suất của các giả thuyết được gọi là xác suất sau , trong khi - xác suất trước .
Ví dụ. Cửa hàng nhận sản phẩm mới từ 3 doanh nghiệp 20% - sản phẩm của doanh nghiệp thứ nhất, 30% - sản phẩm của doanh nghiệp thứ hai, 50% - sản phẩm của doanh nghiệp thứ ba; hơn nữa, 10% sản phẩm của doanh nghiệp thứ nhất có cấp cao nhất, doanh nghiệp thứ hai - 5% và doanh nghiệp thứ ba - 20% sản phẩm cấp cao nhất. Tìm xác suất để một sản phẩm mới được mua ngẫu nhiên sẽ có chất lượng cao nhất.
Giải pháp. Biểu thị bởi TRONG sự kiện bao gồm việc sản phẩm cao cấp sẽ được mua, chúng ta hãy biểu thị các sự kiện bao gồm việc mua sản phẩm của doanh nghiệp thứ nhất, thứ hai và thứ ba, tương ứng.
Chúng ta có thể áp dụng công thức tổng xác suất và trong ký hiệu của chúng ta:
Thay thế các giá trị này vào công thức xác suất tổng, chúng tôi thu được xác suất mong muốn:
Ví dụ. Một trong ba xạ thủ được gọi đến tuyến lửa và bắn hai phát. Xác suất bắn trúng mục tiêu trong một phát của người bắn thứ nhất là 0,3, của người thứ hai là 0,5; cho thứ ba - 0,8. Mục tiêu không trúng. Tìm xác suất để người bắn thứ nhất bắn trúng.
Giải pháp. Ba giả thuyết có thể xảy ra:
A 1 - người bắn đầu tiên được gọi vào tuyến lửa,
A 2 - người bắn thứ hai được gọi đến tuyến lửa,
A 1 - người bắn thứ ba được gọi đến tuyến lửa.
Vì việc gọi bất kỳ người bắn nào vào tuyến lửa đều có thể xảy ra như nhau, nên ![]()
Kết quả của thí nghiệm, sự kiện B đã được quan sát - sau khi các phát súng được bắn, mục tiêu không bị bắn trúng. Các xác suất có điều kiện của sự kiện này theo các giả thuyết được đưa ra là:

sử dụng công thức Bayes, chúng tôi tìm thấy xác suất của giả thuyết sau thí nghiệm:
Ví dụ. Trên ba máy tự động, các bộ phận cùng loại được xử lý, các bộ phận này sẽ đến sau khi xử lý trên một băng tải chung. Máy đầu tiên cho 2% từ chối, máy thứ hai - 7%, máy thứ ba - 10%. Năng suất của máy thứ nhất gấp 3 lần năng suất của máy thứ hai, năng suất của máy thứ ba kém năng suất của máy thứ hai 2 lần.
a) Tỷ lệ lỗi trên dây chuyền lắp ráp là bao nhiêu?
b) Tỉ lệ các bộ phận của từng máy trong số các bộ phận hỏng trên băng tải là bao nhiêu?
Giải pháp. Hãy lấy ngẫu nhiên một bộ phận từ dây chuyền lắp ráp và xét biến cố A - bộ phận đó bị lỗi. Nó liên quan đến các giả thuyết về nơi bộ phận này được gia công: – một bộ phận được chọn ngẫu nhiên được gia công trên máy thứ -, .
Xác suất có điều kiện (trong điều kiện của bài toán, chúng được đưa ra dưới dạng tỷ lệ phần trăm):
Sự phụ thuộc giữa hiệu suất của máy có nghĩa như sau:
Và vì các giả thuyết tạo thành một nhóm hoàn chỉnh, nên .
Sau khi giải hệ phương trình kết quả, chúng tôi tìm thấy: .
a) Tổng xác suất để một bộ phận được lấy ngẫu nhiên từ dây chuyền lắp ráp bị lỗi:
Nói cách khác, trong khối lượng các bộ phận ra khỏi dây chuyền lắp ráp, lỗi là 4%.
b) Biết rằng một chi tiết lấy ngẫu nhiên bị hỏng. Sử dụng công thức Bayes, chúng tôi tìm thấy xác suất có điều kiện của các giả thuyết:
Do đó, trong tổng khối lượng các bộ phận bị lỗi trên băng tải, tỷ lệ của máy thứ nhất là 33%, máy thứ hai - 39%, máy thứ ba - 28%.
1.7. Các bài kiểm tra độc lập. công thức Bernoulli
Khi giải các bài toán xác suất, người ta thường gặp các tình huống trong đó cùng một phép thử được lặp lại nhiều lần và kết quả của mỗi phép thử độc lập với kết quả của các phép thử khác. Thí nghiệm này còn được gọi là sơ đồ thử nghiệm độc lập lặp đi lặp lại hoặc sơ đồ Bernoulli .
Ví dụ về kiểm tra lại:
1) nhiều lần lấy một quả bóng ra khỏi bình, với điều kiện là quả bóng lấy ra sau khi đăng ký màu của nó được đặt trở lại bình;
2) một người bắn lặp lại các phát bắn vào cùng một mục tiêu, với điều kiện là xác suất bắn trúng mục tiêu của mỗi lần bắn được coi là như nhau (không tính đến vai trò của điểm không).
Vì vậy, hãy để kết quả của bài kiểm tra có thể hai kết quả
: hoặc một sự kiện sẽ xuất hiện MỘT, hoặc sự kiện ngược lại của nó. Hãy thực hiện n phép thử Bernoulli. Điều này có nghĩa là tất cả n phép thử đều độc lập; xác suất của một sự kiện xảy ra MỘT trong mỗi bài kiểm tra riêng lẻ hoặc đơn lẻ là không đổi và không thay đổi từ bài kiểm tra này sang bài kiểm tra khác (nghĩa là các bài kiểm tra được thực hiện trong cùng điều kiện). Biểu thị xác suất xảy ra của một sự kiện MỘT trong một bài kiểm tra duy nhất với chữ p, i.e. , và xác suất của biến cố ngược lại (biến cố MỘTđã không đến) - thư ![]() .
.
Khi đó xác suất để biến cố MỘT sẽ xuất hiện trong này N kiểm tra chính xác k lần, thể hiện công thức Bernoulli
Phân phối số lần thành công (lần xuất hiện của một sự kiện) được gọi là phân phối nhị thức .
Ví dụ. Một hộp đựng 20 quả cầu trắng và 10 quả cầu đen. 4 quả bóng được lấy ra, và mỗi quả bóng được lấy ra sẽ được trả lại bình trước khi quả tiếp theo được rút ra và các quả bóng trong bình được trộn lẫn. Tính xác suất để trong 4 quả lấy ra có 2 quả trắng.
Giải pháp. Sự kiện MỘT- có một quả bóng trắng. Khi đó xác suất
, .
Theo công thức Bernoulli, xác suất cần thiết là ![]() .
.
Ví dụ. Tính xác suất để trong một gia đình có 5 người sẽ có không quá 3 người con gái. Xác suất sinh con trai và con gái được giả định là như nhau.
Giải pháp. Xác suất sinh con gái
, Sau đó .
Hãy tính xác suất để trong gia đình không có con gái, có một, hai hoặc ba con gái được sinh ra:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Do đó, xác suất mong muốn
![]() .
.
Ví dụ. Trong số các bộ phận được xử lý bởi công nhân, trung bình có 4% không đạt tiêu chuẩn. Tìm xác suất để hai trong số 30 bộ phận được lấy để thử nghiệm không đạt tiêu chuẩn.
Giải pháp.Ở đây, kinh nghiệm nằm ở việc kiểm tra chất lượng của từng bộ phận trong số 30 bộ phận. Biến cố A là “sự xuất hiện của một bộ phận không chuẩn”, xác suất của nó là , khi đó . Từ đây, theo công thức Bernoulli, ta tìm được
.
Ví dụ.Đối với mỗi phát bắn riêng lẻ từ súng, xác suất bắn trúng mục tiêu là 0,9. Tìm xác suất để trong 20 lần bắn, số lần bắn thành công ít nhất là 16 và nhiều nhất là 19.
Giải pháp. Chúng tôi tính toán theo công thức Bernoulli:

Ví dụ. Thử nghiệm độc lập tiếp tục cho đến khi sự kiện MỘT sẽ không xảy ra k một lần. Tìm xác suất mà nó sẽ mất N phép thử (n ³ k), nếu trong mỗi phép thử .
Giải pháp. Sự kiện TRONG- chính xác N kiểm tra trước k-lần xuất hiện của sự kiện MỘT là tích của hai biến cố sau:
D-in N bài kiểm tra MỘTđã xảy ra;
C - đầu tiên (n-1) bài kiểm tra MỘTđã xuất hiện (k-1) một lần.
Định lý phép nhân và công thức Bernoulli cho xác suất cần thiết:
Cần lưu ý rằng việc sử dụng luật nhị thức thường đi kèm với những khó khăn trong tính toán. Vì vậy, với giá trị gia tăng N Và tôi nên sử dụng các công thức gần đúng (Poisson, Moivre-Laplace), sẽ được thảo luận trong các phần sau.
1.8. Số lần thành công nhiều khả năng
Cụ thể, phân phối nhị thức (phân phối Bernoulli) cho phép xác định số lần xuất hiện của một sự kiện MỘT rất có thể. Công thức cho số lần thành công rất có thể (sự xuất hiện của một sự kiện) có dạng:
Vì , thì các ranh giới này khác nhau 1. Do đó, là một số nguyên, nó có thể nhận một giá trị khi một số nguyên () , nghĩa là khi (và do đó ) là một số không nguyên hoặc hai giá trị khi một số nguyên.
Ví dụ. Với mục tiêu súng tự động, xác suất bắn trúng mục tiêu di chuyển nhanh là 0,9. Tìm số lần bắn trúng nhiều nhất với 50 lần bắn.
Giải pháp.Đây . Do đó, ta có các bất đẳng thức:
![]()
Kể từ đây, .
Ví dụ. Dữ liệu từ kiểm soát chất lượng dài hạn của các bộ phận tiêu chuẩn được sản xuất cho thấy tỷ lệ loại bỏ trung bình là 7,5%. Xác định số bộ phận hoàn toàn có thể sử dụng được trong một lô gồm 39 bộ phận có khả năng xảy ra cao nhất.
Giải pháp. Biểu thị xác suất sản xuất một bộ phận có thể sử dụng được bằng , chúng ta sẽ có ![]() Và
Và ![]() (nhận được một phần bị lỗi và nhận được một phần có thể sử dụng được là các sự kiện ngược lại). kể từ đây n= 39, thì số mong muốn có thể được tìm thấy từ các bất đẳng thức:
(nhận được một phần bị lỗi và nhận được một phần có thể sử dụng được là các sự kiện ngược lại). kể từ đây n= 39, thì số mong muốn có thể được tìm thấy từ các bất đẳng thức:
Do đó, số lượng bộ phận có thể sửa chữa có thể xảy ra nhất là 36 hoặc 37.
Sự bất bình đẳng về số lần thành công có thể xảy ra nhất cũng cho phép chúng ta giải bài toán nghịch đảo: đối với một giá trị đã cho và một giá trị đã biết r xác định tổng số N tất cả các bài kiểm tra.
Ví dụ. Với số lần bắn bao nhiêu thì số lần trúng nhiều khả năng nhất bằng 16 nếu xác suất trúng một lần là 0,7? T A đến 0,5 thì các công thức này càng chính xác. Đối với các giá trị nhỏ hoặc lớn của xác suất (gần bằng 0 hoặc 1), công thức cho sai số lớn (so với công thức Bernoulli ban đầu). ., chúng tôi tìm thấy, xác suất được suy ra Qua... 45 Chính Mình học thuyết khá phức tạp và chỉ được mô tả chi tiết trong các tài liệu đặc biệt sách giáo khoa Qua công ty...
Sách giáo khoa quản lý Nhà xuất bản St.Petersburg Soyuz
sách giáo khoa... Qua xây dựng bộ máy (hình thức); - Qua bản chất của các đối tượng mô phỏng nội dung). Qua ... xác suất trong mọi trường hợp, sau đó sách giáo khoa Qua lý thuyết xác suất(cũng như cái này chương ... Học thuyết xác suất tình trạng ngẫu nhiên sự kiện, ... tin học. ...
Số thứ tự 2014 Chương trình làm việc trong lớp toán: 5 (trình độ cơ bản)
chương trình làm việcA. G. Toán học. 6 ô sách giáo khoa Qua nội dung Và Qua theo kiểu... chương 6. 4 2 2 - Giới thiệu về xác suất. §53 Chắc chắn, không thể và ngẫu nhiên sự kiện xác suất phản cảm sự kiện. Đáng tin cậy, không thể và ngẫu nhiên sự kiện ...
Dự thảo chương trình giáo dục chính của trường trung học mkou Buturlinovskaya số 1 quận Buturlinovsky, vùng Voronezh giai đoạn 2012-2017
Chương trình giáo dục chính... Ngẫu nhiên sự kiện Và xác suất. Khái niệm của ngẫu nhiên kinh nghiệm và ngẫu nhiên sự kiện. Tính thường xuyên ngẫu nhiên sự kiện. Phương pháp tiếp cận thống kê đối với khái niệm xác suất. xác suấtđối diện sự kiện. Đáng tin cậy và không thể sự kiện. tương đương sự kiện ...
sự kiện ngẫu nhiên -
hai sự kiện không tương thích
lý thuyết xác suất
Đại số các sự kiện ngẫu nhiên, biểu đồ Wienne-Euler.
Tổng các biến cố A và B Một biến cố được gọi là biến cố xảy ra khi A hoặc B hoặc cả hai biến cố xảy ra.
Sản phẩm của A và B gọi là biến cố xảy ra nếu trong nghiệm có cả hai sự kiện.
Biến cố Ā ngược biến cố A là biến cố xảy ra khi biến cố A không xảy ra.
A \ B (thêm A vào B) A xảy ra nhưng B không xảy ra
Định nghĩa cổ điển về xác suất. tổ hợp.
là định nghĩa cổ điển của xác suất.
tôi– tổng số kết quả
N- số kết quả có lợi cho sự xuất hiện của sự kiện A ..
tổ hợp- một nhánh của toán học nghiên cứu sự sắp xếp của các đối tượng theo các quy tắc đặc biệt và đếm số cách sắp xếp như vậy. Tổ hợp phát sinh trong thế kỷ 18. Được coi là một nhánh của lý thuyết tập hợp.
Xây dựng tiên đề của lý thuyết xác suất.
Tiên đề 1."tiên đề không phủ định" P(A)≥0
Tiên đề 2."tiên đề chuẩn hóa" P(Ω)=1
Tiên đề 3."tiên đề cộng tính" Nếu biến cố A và B xung khắc (AB=Ø), thì P(A+B)=P(A)+P(B)
Định lý về xác suất của tổng các biến cố.
Đối với mọi sự kiện P (A + B) \u003d P (A) + P (B) - P (AB) (tài liệu trong bài giảng)
Xác suất có điều kiện. Sự kiện phụ thuộc và độc lập. Các định lý về xác suất sinh ra các biến cố.
P(A|B) – xác suất của sự kiện A, nếu sự kiện B đã xảy ra – xác suất có điều kiện.
Biến cố A được gọi là độc lập, từ biến cố B, nếu xác suất của biến cố A không thay đổi tùy thuộc vào biến cố B có xảy ra hay không.
Định lý nhân xác suất: P(AB) = P(A|B) P(B) = P(B|A) P(A)
Định lý nhân xác suất của các biến cố độc lập: P(AB) = P(A) P(B)
Theo định nghĩa của xác suất có điều kiện,
Công thức xác suất toàn phần.
 Có các biến cố H 1 , H 2 ,…., H n xung khắc với nhau và tạo thành một nhóm hoàn chỉnh. Những sự kiện như vậy được gọi là giả thuyết. Giả sử có biến cố A nào đó. A=AH 1 +AH 2 +…+AH n (các số hạng của tổng này xung khắc từng cặp).
Có các biến cố H 1 , H 2 ,…., H n xung khắc với nhau và tạo thành một nhóm hoàn chỉnh. Những sự kiện như vậy được gọi là giả thuyết. Giả sử có biến cố A nào đó. A=AH 1 +AH 2 +…+AH n (các số hạng của tổng này xung khắc từng cặp).

Công thức Bayes.
 H 1 , H 2 ,…., H n A
H 1 , H 2 ,…., H n A


lược đồ Bernoulli. công thức Bernoulli. Rất có thể số lần thành công.
Giả sử tiến hành một số hữu hạn n phép thử liên tiếp, trong mỗi phép thử có một sự kiện A nào đó có thể xảy ra "thành công" hoặc không "thất bại" và những phép thử này thỏa mãn các điều kiện sau:
· Mỗi bài kiểm tra là ngẫu nhiên liên quan đến sự kiện A.i.e. trước khi kiểm tra, không thể nói liệu A có xuất hiện hay không;
· Các thử nghiệm được thực hiện trong cùng điều kiện theo quan điểm xác suất, nghĩa là xác suất thành công trong mỗi thử nghiệm riêng lẻ là p và không thay đổi từ thử nghiệm này sang thử nghiệm khác;
Các bài kiểm tra là độc lập, tức là kết quả của bất kỳ thử nghiệm nào trong số chúng không ảnh hưởng đến kết quả của các thử nghiệm khác.
Chuỗi các phép thử như vậy được gọi là lược đồ Bernoulli hay lược đồ nhị thức, và bản thân các phép thử đó được gọi là phép thử Bernoulli.
Để tính xác suất P n(k) mà trong một loạt n phép thử Bernoulli có chính xác k thành công, công thức Bernoulli được áp dụng: (k = 0,1,2,…n).
10. Khái niệm về biến ngẫu nhiên. Biến ngẫu nhiên rời rạc, cách thiết lập nó: chuỗi phân phối.
biến ngẫu nhiên một đại lượng được gọi, trong mỗi phép thử (tại mỗi lần quan sát) lấy một trong nhiều giá trị có thể, không biết trước giá trị nào.
rv rời rạc– r.v., tập hợp các giá trị có thể có là hữu hạn hoặc đếm được.
Chuỗi phân phối của r.v.(chuỗi phân phối xác suất). Đồ thị của chuỗi phân phối được cho bởi đa giác phân phối - một đường đứt nét nối các điểm có tọa độ (x i ,p i)
| X | x 1 | x2 | x 3 | … | xk | … |
| P | p1 | p2 | trang 3 | … | pk | … |
Luật phân phối của r.v.: p k =P((X=x k ))
Sự kiện ngẫu nhiên, phân loại của họ. Khái niệm xác suất.
sự kiện ngẫu nhiên - một sự kiện mà, trong các điều kiện của kinh nghiệm, nó có thể xảy ra hoặc không. Hơn nữa, không thể biết trước liệu nó có xảy ra hay không.
hai sự kiện không tương thích nếu sự xuất hiện của một trong số chúng loại trừ sự xuất hiện của cái kia trong cùng một thí nghiệm.
lý thuyết xác suất nghiên cứu các mô hình vốn có trong các hiện tượng ngẫu nhiên hàng loạt. Các khái niệm cơ bản của lý thuyết xác suất đã được trình bày trong thư từ giữa Pascal và Fermat. Những khái niệm này ra đời là kết quả của những nỗ lực mô tả cờ bạc một cách toán học.
Nhu cầu về các phép toán xác suất xuất hiện khi xác suất của một số sự kiện được biết đến và cần tính xác suất của các sự kiện khác có liên quan đến các sự kiện này.
Phép cộng xác suất được sử dụng khi cần tính xác suất của một tổ hợp hoặc một tổng logic của các biến cố ngẫu nhiên.
Tổng số sự kiện MỘT Và b chỉ định MỘT + b hoặc MỘT ∪ b. Tổng của hai biến cố là biến cố xảy ra khi và chỉ khi có ít nhất một biến cố xảy ra. Nó có nghĩa là MỘT + b- một sự kiện xảy ra khi và chỉ khi một sự kiện xảy ra trong quá trình quan sát MỘT hoặc sự kiện b, hoặc đồng thời MỘT Và b.
Nếu các sự kiện MỘT Và b không nhất quán lẫn nhau và xác suất của chúng được đưa ra, thì xác suất mà một trong những sự kiện này sẽ xảy ra do kết quả của một phép thử được tính bằng cách sử dụng phép cộng xác suất.
Định lý cộng xác suất. Xác suất xảy ra một trong hai sự kiện xung khắc lẫn nhau sẽ bằng tổng xác suất của các sự kiện này:
Ví dụ, hai phát súng đã được bắn trong khi đi săn. Sự kiện MỘT– bắn trúng vịt ngay từ phát súng đầu tiên, sự kiện TRONG– đánh từ phát thứ hai, biến cố ( MỘT+ TRONG) - đánh từ phát thứ nhất hoặc thứ hai hoặc từ hai phát. Vì vậy, nếu hai sự kiện MỘT Và TRONG là những sự kiện không tương thích, sau đó MỘT+ TRONG- sự xuất hiện của ít nhất một trong các sự kiện này hoặc hai sự kiện.
ví dụ 1 Một hộp có 30 quả bóng cùng kích thước: 10 quả đỏ, 5 quả xanh và 15 quả trắng. Tính xác suất để lấy được một quả bóng màu (không phải màu trắng) mà không cần nhìn.
Giải pháp. Giả sử rằng sự kiện MỘT– “quả bóng đỏ được lấy”, và sự kiện TRONG- "Quả bóng màu xanh được lấy." Sau đó, sự kiện là "một quả bóng màu (không phải màu trắng) được lấy". Tìm xác suất của biến cố MỘT:
và các sự kiện TRONG:
![]()
Sự kiện MỘT Và TRONG- xung khắc lẫn nhau, vì nếu lấy một bi thì không được lấy các bi khác màu. Do đó, chúng tôi sử dụng phép cộng xác suất:
![]()
Định lý bổ sung xác suất cho một số sự kiện không tương thích. Nếu các sự kiện tạo thành một tập hợp đầy đủ các sự kiện, thì tổng xác suất của chúng bằng 1:
Tổng xác suất của các sự kiện ngược lại cũng bằng 1:
![]()
Các sự kiện đối lập tạo thành một tập hợp đầy đủ các sự kiện và xác suất của một tập hợp đầy đủ các sự kiện là 1.
Xác suất của các sự kiện ngược lại thường được biểu thị bằng các chữ cái nhỏ. P Và q. Đặc biệt,
từ đó các công thức sau đây cho xác suất của các sự kiện ngược lại tuân theo:
ví dụ 2 Mục tiêu trong dấu gạch ngang được chia thành 3 vùng. Xác suất để một xạ thủ nhất định bắn vào mục tiêu ở vùng thứ nhất là 0,15, ở vùng thứ hai - 0,23, ở vùng thứ ba - 0,17. Tìm xác suất để người bắn trúng mục tiêu và xác suất người bắn trượt mục tiêu.
Giải: Tìm xác suất để người bắn trúng mục tiêu:
Tìm xác suất để người bắn trượt mục tiêu:
![]()
Các nhiệm vụ khó hơn mà bạn cần áp dụng cả phép cộng và phép nhân xác suất - trên trang "Các nhiệm vụ khác nhau để cộng và phép nhân xác suất" .
Bổ sung xác suất của các sự kiện chung
Hai biến cố ngẫu nhiên được gọi là đồng quy nếu sự xuất hiện của biến cố này không ngăn cản sự xuất hiện của biến cố thứ hai trong cùng một lần quan sát. Ví dụ, khi ném một con xúc xắc, biến cố MỘTđược coi là sự xuất hiện của số 4, và sự kiện TRONG- bỏ một số chẵn. Vì số 4 là số chẵn nên hai sự kiện tương hợp với nhau. Trong thực tế, có các nhiệm vụ tính toán xác suất xảy ra của một trong các sự kiện chung.
Định lý cộng xác suất cho các sự kiện chung. Xác suất để một trong các sự kiện chung xảy ra bằng tổng xác suất của các sự kiện này, từ đó trừ đi xác suất xảy ra chung của cả hai sự kiện, tức là tích của các xác suất. Công thức cho xác suất của các sự kiện chung như sau:
Bởi vì các sự kiện MỘT Và TRONG tương thích, sự kiện MỘT+ TRONG xảy ra nếu một trong ba sự kiện có thể xảy ra: hoặc AB. Theo định lý cộng các biến cố xung khắc ta tính được như sau:
Sự kiện MỘT xảy ra nếu xảy ra một trong hai sự kiện không tương thích: hoặc AB. Tuy nhiên, xác suất xảy ra một sự kiện từ một số sự kiện không tương thích bằng tổng xác suất của tất cả các sự kiện này:
Tương tự:
Thay biểu thức (6) và (7) vào biểu thức (5), ta thu được công thức xác suất của các biến cố chung:
Khi sử dụng công thức (8), cần lưu ý rằng các sự kiện MỘT Và TRONG có thể:
- Độc lập với nhau;
- Phụ thuộc lẫn nhau.
Công thức xác suất cho các sự kiện độc lập lẫn nhau:
Công thức xác suất cho các sự kiện phụ thuộc lẫn nhau:
Nếu các sự kiện MỘT Và TRONG không nhất quán, thì sự trùng hợp của chúng là một trường hợp không thể và do đó, P(AB) = 0. Công thức xác suất thứ tư cho các sự kiện xung khắc như sau:
ví dụ 3 Trong đua xe ô tô, khi lái xe thứ nhất, xác suất chiến thắng, khi lái xe thứ hai. Tìm thấy:
- xác suất mà cả hai chiếc xe sẽ giành chiến thắng;
- xác suất để có ít nhất một ô tô thắng cuộc;
1) Xác suất xe thứ nhất thắng không phụ thuộc vào kết quả của xe thứ hai nên các biến cố MỘT(xe đầu tiên thắng) và TRONG(chiếc xe thứ hai thắng) - các sự kiện độc lập. Tính xác suất để cả 2 xe đều thắng:
2) Tìm xác suất để một trong hai xe đó thắng:
![]()
Các nhiệm vụ khó hơn mà bạn cần áp dụng cả phép cộng và phép nhân xác suất - trên trang "Các nhiệm vụ khác nhau để cộng và phép nhân xác suất" .
Tự giải bài toán cộng xác suất rồi xem lời giải
Ví dụ 4 Hai đồng xu được tung ra. Sự kiện MỘT- mất huy hiệu trên đồng tiền đầu tiên. Sự kiện b- mất huy hiệu trên đồng xu thứ hai. Tìm xác suất của biến cố C = MỘT + b .
phép nhân xác suất
Phép nhân xác suất được sử dụng khi tính xác suất của một tích logic của các sự kiện.
Trong trường hợp này, các biến cố ngẫu nhiên phải độc lập. Hai biến cố được gọi là độc lập với nhau nếu sự xuất hiện của biến cố này không ảnh hưởng đến xác suất xảy ra biến cố thứ hai.
Định lý nhân xác suất cho các biến cố độc lập. Xác suất xảy ra đồng thời hai biến cố độc lập MỘT Và TRONG bằng tích xác suất của các sự kiện này và được tính theo công thức:
Ví dụ 5Đồng xu được tung ba lần liên tiếp. Tìm xác suất để quốc huy rơi ra cả 3 lần.
Giải pháp. Xác suất để quốc huy rơi vào lần tung đồng xu đầu tiên, lần thứ hai và lần thứ ba. Tìm xác suất để quốc huy rơi ra cả 3 lần:

Tự mình giải các bài toán nhân xác suất rồi xem lời giải
Ví dụ 6 Có một cái hộp với chín quả bóng quần vợt mới. Ba quả bóng được lấy cho trò chơi, sau trò chơi, chúng được đặt trở lại. Khi chọn bóng, họ không phân biệt bóng đã chơi và chưa chơi. Xác suất để sau ba ván không còn bi chưa đánh trong hộp là bao nhiêu?
Ví dụ 7 32 chữ cái trong bảng chữ cái tiếng Nga được viết trên các thẻ bảng chữ cái đã cắt. Năm lá bài được rút ngẫu nhiên, nối tiếp nhau và đặt trên bàn theo thứ tự xuất hiện. Tìm xác suất để các chữ cái sẽ tạo thành từ "kết thúc".
Ví dụ 8 Từ một bộ bài đầy đủ (52 tờ), bốn quân bài được lấy ra cùng một lúc. Tính xác suất để cả 4 quân bài này cùng chất.
Ví dụ 9 Vấn đề tương tự như trong ví dụ 8, nhưng mỗi thẻ được trả lại bộ bài sau khi được rút.
Các nhiệm vụ phức tạp hơn, trong đó bạn cần áp dụng cả phép cộng và phép nhân xác suất, cũng như tính tích của một số sự kiện - trên trang "Các nhiệm vụ khác nhau để cộng và nhân xác suất" .
Xác suất để ít nhất một trong các sự kiện độc lập lẫn nhau sẽ xảy ra có thể được tính bằng cách lấy 1 trừ đi tích xác suất của các sự kiện đối nghịch nhau, nghĩa là theo công thức:
Ví dụ 10 Hàng hóa được vận chuyển bằng ba phương thức vận tải: đường sông, đường sắt và đường bộ. Xác suất hàng hóa được vận chuyển bằng đường sông là 0,82, đường sắt 0,87, đường bộ 0,90. Tìm xác suất để hàng được giao bằng ít nhất một trong ba phương thức vận tải.
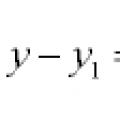 Phương trình đường thẳng và đường cong trong mặt phẳng
Phương trình đường thẳng và đường cong trong mặt phẳng Phương trình thuần nhất tổng quát Phương trình thuần nhất tổng quát cấp 2
Phương trình thuần nhất tổng quát Phương trình thuần nhất tổng quát cấp 2 Nhờ dấu phẩy Do thực tế là trong họ
Nhờ dấu phẩy Do thực tế là trong họ