Bài đạo hàm của hàm mũ số e.” Số e
Đồ thị của hàm số mũ là một đường cong nhẵn không có nếp gấp, tại mỗi điểm mà nó đi qua có thể vẽ được một tiếp tuyến. Thật hợp lý khi giả sử rằng nếu có thể vẽ một tiếp tuyến, thì hàm số sẽ khả vi tại mỗi điểm trong miền xác định của nó.
Hãy hiển thị trên cùng một trục tọa độ một số đồ thị của hàm y \u003d x a, Cho a \u003d 2; một = 2,3; một = 3; một = 3,4.
Tại điểm có tọa độ (0;1). Góc dốc của các tiếp tuyến này sẽ tương ứng là khoảng 35, 40, 48 và 51 độ. Thật hợp lý khi giả sử rằng trong khoảng từ 2 đến 3, có một số mà góc nghiêng của tiếp tuyến sẽ là 45 độ.
Hãy đưa ra công thức chính xác của mệnh đề này: tồn tại một số lớn hơn 2 và nhỏ hơn 3, được ký hiệu bằng chữ e, hàm mũ y = e x tại điểm 0 có đạo hàm bằng 1. Đó là: (e ∆x -1) / ∆x tiến tới 1 còn ∆x tiến tới không.
số đã cho e là số vô tỉ và được viết dưới dạng phân số thập phân vô hạn không tuần hoàn:
e = 2,7182818284…
Vì số e dương và khác 0, nên có một logarit cơ số e. Logarit này được gọi là logarit tự nhiên. Kí hiệu là ln(x) = log e(x).
Đạo hàm của hàm mũ
Định lý: Hàm e x khả vi tại mọi điểm thuộc tập xác định của nó và (e x)’ = e x .
Hàm mũ a x khả vi tại mỗi điểm trong miền xác định của nó, và hơn nữa (a x)’ = (a x)*ln(a).
Hệ quả của định lý này là hàm số mũ liên tục tại mọi điểm trong miền xác định của nó.
Ví dụ: tìm đạo hàm của hàm y = 2 x .
Theo công thức tính đạo hàm của hàm số mũ, ta được:
(2x)' = (2x)*ln(2).
Trả lời: (2x)*ln(2).
Nguyên hàm của hàm số mũ
Đối với hàm mũ a x cho trước trên tập hợp các số thực, nguyên hàm sẽ là hàm (a x)/(ln(a)).
ln(a) là một hằng số nào đó, khi đó (a x / ln(a))’= (1 / ln(a)) * (a x) * ln(a) = a x với mọi x. Ta đã chứng minh định lý này.
Hãy xem xét một ví dụ về việc tìm một hàm số mũ nguyên hàm.
Ví dụ: tìm nguyên hàm của hàm f(x) = 5 x . Hãy sử dụng công thức trên và các quy tắc để tìm các nguyên hàm. Ta được: F(x) = (5 x) / (ln(5)) +C.
Khi rút ra công thức đầu tiên của bảng, chúng ta sẽ tiến hành từ định nghĩa đạo hàm của một hàm tại một điểm. Hãy đi đâu x- bất kỳ số thực nào, nghĩa là, x– bất kỳ số nào từ vùng định nghĩa hàm . Chúng ta hãy viết giới hạn của tỷ lệ gia số của hàm với gia số của đối số tại: ![]()
Cần lưu ý rằng dưới dấu của giới hạn, một biểu thức thu được, không phải là độ không đảm bảo của số 0 chia cho số 0, vì tử số không chứa giá trị vô hạn, mà chính xác bằng không. Nói cách khác, số gia của hàm hằng luôn bằng không.
Như vậy, đạo hàm của một hàm hằngbằng 0 trên toàn miền xác định.
Đạo hàm của một hàm lũy thừa.
Công thức tính đạo hàm của hàm lũy thừa có dạng ![]() , trong đó số mũ P là một số thực bất kỳ.
, trong đó số mũ P là một số thực bất kỳ.
Trước tiên chúng ta hãy chứng minh công thức cho số mũ tự nhiên, nghĩa là cho p = 1, 2, 3, ...
Chúng ta sẽ sử dụng định nghĩa của đạo hàm. Chúng ta hãy viết giới hạn của tỷ số giữa số gia của hàm lũy thừa với số gia của đối số: 
Để đơn giản hóa biểu thức trong tử số, chúng ta chuyển sang công thức nhị thức của Newton: 
Kể từ đây, 
Điều này chứng minh công thức tính đạo hàm của hàm lũy thừa đối với số mũ tự nhiên.
Đạo hàm của hàm mũ.
Ta rút ra được công thức đạo hàm dựa vào định nghĩa:
Đã đến sự không chắc chắn. Để mở rộng nó, chúng tôi giới thiệu một biến mới và cho . Sau đó . Trong lần chuyển đổi cuối cùng, chúng ta đã sử dụng công thức chuyển đổi sang cơ số mới của logarit.
Hãy thực hiện thay thế trong giới hạn ban đầu: 
Nếu chúng ta nhớ lại giới hạn đáng chú ý thứ hai, thì chúng ta sẽ đến công thức tính đạo hàm của hàm mũ: 
Đạo hàm của một hàm logarit.
Hãy để chúng tôi chứng minh công thức tính đạo hàm của hàm logarit cho mọi x từ phạm vi và tất cả các giá trị cơ sở hợp lệ Một logarit. Theo định nghĩa của đạo hàm, ta có: 
Như bạn đã nhận thấy, trong chứng minh, các phép biến đổi được thực hiện bằng cách sử dụng các tính chất của logarit. bình đẳng  là hợp lệ do giới hạn đáng chú ý thứ hai.
là hợp lệ do giới hạn đáng chú ý thứ hai.
Đạo hàm của các hàm lượng giác.
Để rút ra các công thức tính đạo hàm của các hàm lượng giác, chúng ta sẽ phải nhớ lại một số công thức lượng giác, cũng như giới hạn đáng chú ý đầu tiên.
Theo định nghĩa đạo hàm của hàm sin, ta có ![]() .
.
Chúng tôi sử dụng công thức cho sự khác biệt của sin: 
Nó vẫn còn để chuyển sang giới hạn đáng chú ý đầu tiên: 
Vậy đạo hàm của hàm tội x Có cos x.
Công thức của đạo hàm cosin được chứng minh theo cùng một cách. 
Do đó, đạo hàm của hàm cos x Có –sin x.
Việc lập các công thức cho bảng đạo hàm của tiếp tuyến và cotang sẽ được thực hiện bằng cách sử dụng các quy tắc vi phân đã được chứng minh (đạo hàm của một phân số). 
Đạo hàm của hàm hypebol.
Các quy tắc vi phân và công thức tính đạo hàm của hàm mũ từ bảng đạo hàm cho phép chúng ta rút ra các công thức tính đạo hàm của sin, cosin, tiếp tuyến và cotang của hyperbol. 
Đạo hàm của hàm ngược.
Để không có sự nhầm lẫn trong cách trình bày, chúng ta hãy biểu thị đối số của hàm theo đó phân biệt được thực hiện trong chỉ số thấp hơn, nghĩa là nó là đạo hàm của hàm f(x) Qua x.
Bây giờ chúng tôi xây dựng quy tắc tìm đạo hàm của hàm ngược.
Hãy để các chức năng y = f(x) Và x = g(y) nghịch biến nhau, xác định trên các khoảng và tương ứng. Nếu tại một điểm tồn tại một đạo hàm hữu hạn khác 0 của hàm số f(x), thì tại điểm tồn tại đạo hàm hữu hạn của hàm nghịch biến g(y), Và ![]() . Trong một mục khác
. Trong một mục khác ![]() .
.
Quy tắc này có thể được điều chỉnh lại cho bất kỳ x từ khoảng , sau đó chúng tôi nhận được  .
.
Hãy kiểm tra tính hợp lệ của các công thức này.
Hãy tìm hàm ngược của logarit tự nhiên ![]() (Đây y là một chức năng, và x- lý lẽ). Giải phương trình này cho x, chúng tôi nhận được (ở đây x là một chức năng, và y lập luận của cô ấy). Đó là,
(Đây y là một chức năng, và x- lý lẽ). Giải phương trình này cho x, chúng tôi nhận được (ở đây x là một chức năng, và y lập luận của cô ấy). Đó là, ![]() và các hàm nghịch biến lẫn nhau.
và các hàm nghịch biến lẫn nhau.
Từ bảng đạo hàm ta thấy ![]() Và
Và ![]() .
.
Hãy đảm bảo rằng các công thức tìm đạo hàm của hàm ngược đưa chúng ta đến cùng một kết quả: 
Mục tiêu bài học: hình thành một ý tưởng về một số e; Chứng minh tính khả vi của hàm số tại mọi điểm X; xét chứng minh của định lý khả vi của hàm số ; kiểm tra việc hình thành các kỹ năng và khả năng khi giải các ví dụ cho ứng dụng của họ.
Mục tiêu bài học.
Giáo dục: nhắc lại định nghĩa của đạo hàm, quy tắc phân biệt, đạo hàm của các hàm cơ bản, ghi nhớ đồ thị và tính chất của hàm mũ, hình thành khả năng tìm đạo hàm của hàm mũ, kiểm soát kiến thức bằng cách sử dụng nhiệm vụ kiểm tra và Bài kiểm tra.
Phát triển: thúc đẩy sự phát triển của sự chú ý, phát triển tư duy logic, trực giác toán học, khả năng phân tích, áp dụng kiến thức trong các tình huống phi tiêu chuẩn.
Giáo dục: giáo dục văn hóa thông tin, phát triển kỹ năng làm việc theo nhóm và cá nhân.
Phương pháp giảng dạy: lời nói, trực quan, tích cực.
Hình thức bồi dưỡng: tập thể, cá nhân, nhóm.
Thiết bị : sách giáo khoa “Đại số và sự khởi đầu của giải tích” (do Kolmogorov biên tập), tất cả các nhiệm vụ của nhóm B “Phân đoạn khép kín” do A.L. Semenov, I.V. Yashchenko, máy chiếu đa phương tiện.
Các bước làm bài:
- Báo cáo chủ đề, mục tiêu, mục tiêu của bài học (2 phút).
- Chuẩn bị cho việc nghiên cứu tài liệu mới thông qua việc lặp lại nghiên cứu trước đó (15 phút).
- Giới thiệu về tài liệu mới (10 phút)
- Hiểu sơ cấp và củng cố kiến thức mới (15 phút).
- Bài tập về nhà (1 phút).
- Tổng kết (2 phút).
Trong các lớp học
1. Thời điểm tổ chức.
Chủ đề của bài học được thông báo: “Đạo hàm của hàm số mũ. Số e.”, mục tiêu, nhiệm vụ. trượt 1. Bài thuyết trình
2. Hoạt động của kiến thức cơ bản.
Để làm điều này, ở giai đoạn đầu tiên của bài học, chúng tôi sẽ trả lời các câu hỏi và giải quyết các nhiệm vụ để lặp lại. Trang trình bày 2.
Trên bảng đen, hai học sinh làm việc trên thẻ, hoàn thành các nhiệm vụ như B8 SỬ DỤNG.
Nhiệm vụ cho học sinh đầu tiên:
Nhiệm vụ cho học sinh thứ hai:

Các em còn lại hoàn thành bài độc lập theo các phương án:
| lựa chọn 1 | Lựa chọn 2 | ||
| 1. |  |
1. |  |
| 2. |  |
2. |  |
| 3. |  |
3. |  |
| 4. |  |
4. |  |
| 5. |  |
5. |  |
Các cặp trao đổi lời giải và kiểm tra bài làm của nhau, tham khảo đáp án ở slide 3.
Các giải pháp và câu trả lời của học sinh làm việc trên bảng đen được xem xét.
Kiểm tra bài tập số 1904. Chiếu slide 4.
3. Cập nhật chủ đề bài học, tạo tình huống có vấn đề.
Giáo viên yêu cầu đưa ra định nghĩa hàm số mũ và liệt kê các tính chất của hàm số y \u003d 2 x. Đồ thị của các hàm số mũ được hiển thị dưới dạng các đường trơn, có thể vẽ tiếp tuyến tại mỗi điểm. Nhưng sự tồn tại của một hàm số tiếp tuyến với đồ thị tại một điểm có hoành độ x 0 thì tương đương với khả năng khả vi của nó tại x 0.
Đối với đồ thị của hàm y \u003d 2 x và y \u003d 3 x, ta vẽ các tiếp tuyến với chúng tại điểm có hoành độ 0. Góc nghiêng của các tiếp tuyến này với trục hoành xấp xỉ bằng 35 ° và 48 ° , tương ứng. Trang trình bày 5.
Kết luận: nếu cơ số của hàm số mũ MỘT tăng từ 2 lên, chẳng hạn như 10, thì góc giữa tiếp tuyến với đồ thị hàm số tại điểm x=0 và trục x tăng dần từ 35° đến 66,5°. Thật hợp lý khi cho rằng có một lý do MỘT, với góc tương ứng là 45
Người ta chứng minh rằng tồn tại một số lớn hơn 2 và nhỏ hơn 3. Người ta thường ký hiệu nó bằng chữ cái e. Trong toán học, người ta xác định rằng số e- phi lý, tức là là một số thập phân vô hạn không tuần hoàn.
đ = 2,7182818284590…
Lưu ý (không nghiêm trọng lắm). trượt 6.
Ở slide 7 tiếp theo có chân dung của các nhà toán học vĩ đại - John Napier, Leonard Euler và ghi chú ngắn gọn về họ.
- Xem xét các tính chất của hàm y=e x
- Chứng minh Định lý 1. Trang chiếu 8.
- Chứng minh Định lý 2. Trang chiếu 9.
4. Tạm dừng hoặc xả động cho mắt.
(Tư thế bắt đầu - ngồi, mỗi bài tập lặp lại 3-4 lần):
1. Ngả người ra sau, hít sâu rồi rướn người về phía trước, thở ra.
2. Tựa lưng vào ghế, nhắm mắt lại, nhắm chặt mắt không mở mí mắt.
3. Tay dọc theo cơ thể, chuyển động tròn của vai qua lại.
5. Củng cố kiến thức đã học.
5.1 Lời giải bài 538, 540, 544c.
5.2 Ứng dụng kiến thức, kỹ năng và khả năng một cách độc lập. Công tác thẩm tra dưới hình thức trắc nghiệm. Thời gian hoàn thành nhiệm vụ - 5 phút.
Tiêu chí đánh giá:
"5" - 3 điểm
"4" - 2 điểm
“3” - 1 điểm
6. Tổng hợp kết quả, kết quả làm việc trong bài.
- Sự phản xạ.
- chấm điểm.
- Đệ trình các nhiệm vụ thử nghiệm.
7. Bài tập về nhà: tr 41 (1, 2); số 539(a,b,d); 540 (c, d), 544 (a, b).
“Phân khúc khép kín” số 1950, 2142.
Để sử dụng bản xem trước của bản trình bày, hãy tạo tài khoản Google (tài khoản) và đăng nhập: https://accounts.google.com
Chú thích slide:
Đạo hàm của hàm số lũy thừa Số e lớp 11
LẶP LẠI là mẹ của việc học!
Định nghĩa hàm số mũ Hàm số được cho bởi công thức y \u003d a x (trong đó a > 0, a ≠ 1) được gọi là hàm số mũ với cơ số a.
Tính chất của hàm mũ y \u003d a x a > 1 0
Xác định đạo hàm của hàm số tại điểm x 0. là Δ → 0. Đạo hàm của hàm f tại điểm x 0 là số mà quan hệ sai phân có xu hướng là Δx → 0.
Ý nghĩa hình học của đạo hàm x ₀ α A y \u003d f (x) 0 x y k \u003d tg α \u003d f "(x ₀) Hệ số góc của tiếp tuyến với đồ thị hàm số f (x) tại điểm ( x 0; f (x 0) bằng các hàm đạo hàm f "(x ₀). f(x 0)
Trò chơi: "Tìm cặp" (u + v) "cos x e (u v)" n xⁿ ⁻" p (u / v)" - 1 / (sin² x) a (x ⁿ)" - sin x n C "u" v +u v" to (C u)" 1 / (cos ² x) t (sin x)" (u" v - u v") / v² c (cos x)" 0 o (tg x)" u "+v" u (ctg x) "C u" n
Kiểm tra chính mình! (u + v)" u" + v" e (u v)" u" v + u v "đến (u / v)" (u' v –u v") / v² c (x ⁿ)" n x ⁿ ⁻¹ p C" 0 o (Cu)" C u "n (sin x)" Cos x e (cos x)" - sin x n (tg x)" 1 / (cos² x) t (ctg x)" - 1 / (sin² x ) Một
Số mũ là một hàm lũy thừa. Số mũ là một hàm trong đó e là cơ số của logarit tự nhiên.
1 y \u003d e x 45 ° Hàm y \u003d e x được gọi là "số mũ" x ₀ \u003d 0; tg 45° = 1 Tại điểm (0;1) hệ số góc với tiếp tuyến của đồ thị hàm số k = tg 45° = 1 - ý nghĩa hình học của đạo hàm theo số mũ Số mũ y = e x
Định lý 1. Hàm y \u003d e khả vi tại mỗi điểm của miền xác định và (e)" \u003d e x x x Logarit tự nhiên (ln) là logarit cơ số e: ln x \u003d log x e và ( a)" = a ∙ ln a x x Định lý 2 .
Công thức tính đạo hàm của hàm số mũ (e)" = e ; (e)" = k e ; (a)" = a ∙ ln a ; (a)" = k a ∙ ln a . x kx + b x x x kx + b kx + b kx + b F(a x) = + C; F(e x) = e x +C.
"Tập thể dục tạo ra sự tinh thông." Tacitus Publius Cornelius - nhà sử học La Mã cổ đại
Ví dụ: Tìm đạo hàm của các hàm: 1. = 3 e. 2. (e)" = (5x)" e = 5 e. 3. (4)" = 4 ln 4. 4. (2)" = (-7 x) "2 ∙ ln 2 = -7 ∙ 2 ∙ ln 2. 5 x 5 x x (3 e)" 5 x - 7 x x x -7 x -7 x x
Thú vị gần đó
Leonhard Euler 1707 -1783 Nhà khoa học Nga - nhà toán học, vật lý học, thợ cơ khí, nhà thiên văn học... Đưa ra cách gọi tên số e. Chứng minh rằng số e ≈ 2, 718281... là số vô tỉ. John Napier 1550 - 1617 Nhà toán học người Scotland, người phát minh ra logarit. Để vinh danh ông, số e được gọi là "số không ngang hàng".
Sự tăng trưởng và giảm dần của một hàm với tốc độ của một số mũ được gọi là cấp số nhân
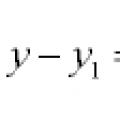 Phương trình đường thẳng và đường cong trong mặt phẳng
Phương trình đường thẳng và đường cong trong mặt phẳng Phương trình thuần nhất tổng quát Phương trình thuần nhất tổng quát cấp 2
Phương trình thuần nhất tổng quát Phương trình thuần nhất tổng quát cấp 2 Nhờ dấu phẩy Do thực tế là trong họ
Nhờ dấu phẩy Do thực tế là trong họ