Y 5x 1 график. Преобразования графиков с модулем

Довольно часто удается выделить важные особенности движения механической системы, не прибегая к интегрированию системы дифференциальных уравнений движения. Это достигается применением общих теорем динамики.

5.1. Основные понятия и определения

Внешние и внутренние силы. Любая сила, действующая на точку механической системы, обязательно является либо активной силой, либо реакцией связи. Всю совокупность сил, действующих на точки системы, можно разделить на два класса иначе: на внешние силы и внутренние силы (индексы е и i - от латинских слов externus - внешний и internus - внутренний). Внешними называются силы, действующие на точки системы со стороны точек и тел, не входящих в состав рассматриваемой системы. Внутренними называются силы взаимодействия между точками и телами рассматриваемой системы.

Это разделение зависит от того, какие материальные точки и тела включены исследователем в рассматриваемую механическую систему. Если расширить состав системы, включив в нее дополнительно точки и тела, то некоторые силы, которые для прежней системы были внешними, для расширенной системы могут стать внутренними.

Свойства внутренних сил. Поскольку эти силы являются силами взаимодействия между частями системы, они входят в полную систему внутренних сил «двойками», организованными в соответствии с аксиомой действия-противодействия. У каждой такой «двойки» сил

главный вектор и главный момент относительно произвольного центра равны нулю. Так как полная система внутренних сил состоит только из «двоек», то

1) главный вектор системы внутренних сил равен нулю,

2) главный момент системы внутренних сил относительно произвольной точки равен нулю.

Массой системы называется арифметическая сумма масс тк всех точек и тел, образующих систему:

Центром масс (центром инерции) механической системы называется геометрическая точка С, радиус-вектор и координаты которой определяются формулами

где - радиусы-векторы и координаты точек, образующих систему.

Для твердого тела, находящегося в однородном поле тяжести, положения центра масс и центра тяжести совпадают, в других случаях это разные геометрические точки.

Вместе с инерциальной системой отсчета часто рассматривают одновременно неинерциальную систему отсчета, движущуюся поступательно. Ее оси координат (оси Кёнига) выбирают так, чтобы начало отсчета С постоянно совпадало с центром масс механической системы. В соответствии с определением центр масс неподвижен в осях Кёнига и находится в начале координат.

Моментом инерции системы относительно оси называется скалярная величина равная сумме произведений масс тк всех точек системы на квадраты их расстояний до оси:

Если механической системой является твердое тело, для нахождения 12 можно воспользоваться формулой

где - плотность, объем, занимаемый телом.

Лекция 3. Общие теоремы динамики

Динамика системы материальных точек является важным разделом теоретической механики. Здесь в основном рассматриваются задачи о движении механических систем (систем материальных точек) с конечным числом степеней свободы – максимальным числом независимых параметров, определяющих положение системы. Главная задача динамики системы – изучение законов движения твердого тела и механических систем.

Наиболее простой подход к исследованию движения системы, состоящий из N материальных точек, сводиться к рассмотрению движений каждой отдельной точки системы. При этом должны быть определены все силы, действующие на каждую точку системы, в том числе и силы взаимодействия между точками.

Определяя ускорения каждой точки в соответствии со вторым законом Ньютона (1.2), получим для каждой точки три скалярных дифференциальных закона движения второго порядка, т.е. 3 N дифференциальных закона движения для всей системы.

Для нахождения уравнений движения механической системы по заданным силам и начальным условиям для каждой точки системы, полученные дифференциальные законы нужно проинтегрировать. Эта задача трудна даже в случае двух материальных точек, которые движутся только под действием сил взаимодействия по закону всемирного притяжения (задача о двух телах), и исключительно трудна в случае трех взаимодействующих точек (задача о трех телах).

Поэтому необходимо отыскать такие методы решения задач, которые бы приводили к решаемым уравнениям и давали представление о движении механической системы. Общие теоремы динамики, являясь следствием дифференциальных законов движения, позволяют избежать сложности, возникающие при интегрировании и получать необходимые результаты.

3. 1. Общие замечания

Точки механической системы будем нумеровать индексами i , j , k и т.д., которые пробегают все значения 1, 2, 3… N , где N – число точек системы. Физические величины, относящиеся к k -й точке, обозначаются таким же индексом, что и точка. Например, выражают соответственно радиус-вектор и скорость k -й точки.

На каждую из точек системы действуют силы двоякого происхождения: во-первых, силы, источники которых лежат вне системы, называемые внешними силами и обозначаемые ; во-вторых, силы со стороны других точек данной системы, называемые внутренними силами и обозначаемые . Внутренние силы удовлетворяют третьему закону Ньютона. Рассмотрим простейшие свойства внутренних сил, действующих на всю механическую систему в любом ее состоянии.

Первое свойство. Геометрическая сумма всех внутренних сил системы (главный вектор внутренних сил) равна нулю .

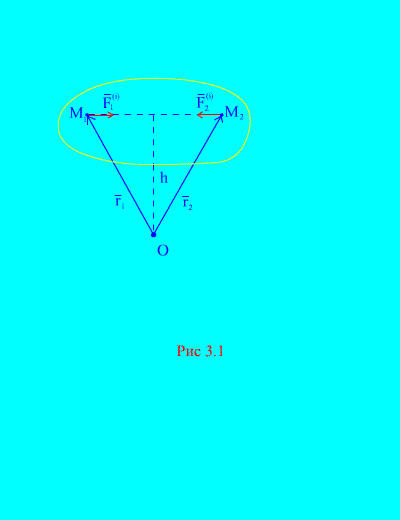
Действительно, если рассмотреть какие-либо две произвольные точки системы, например и (рис. 3.1) , то для них , т.к. силы действия и противодействия всегда равны по модулю, действуют вдоль одной линии действия в противоположном направлении, которое соединяет взаимодействующие точки. Главный вектор внутренних сил состоит из пар сил взаимодействующих точек, следовательно

(3.1)

Второе свойство. Геометрическая сумма моментов всех внутренних сил относительно произвольной точки пространства равна нулю .

Рассмотрим систему моментов сил и относительно точки О (рис. 3.1) . Из (рис. 3.1) . видно, что

,

т.к. обе силы имеют одинаковые плечи и противоположные направления векторных моментов. Главный момент внутренних сил относительно точки О состоит из векторной суммы таких выражений и равен нулю. Следовательно,

Пусть заданы внешние и внутренние силы, действующие на механическую систему, состоящую из N точек (рис. 3.2) . Если к каждой точке системы приложить равнодействующую внешних сил и равнодействующую всех внутренних сил , то для любой k -й точки системы можно составить дифференциальные уравнения движения. Всего таких уравнений будет N :

а в проекциях на неподвижные оси координат 3 N :

(3.4)

Векторные уравнения (3.3) или эквивалентные им скалярные уравнения (3.4) представляют дифференциальные законы движения материальных точек всей системы. Если все точки движутся параллельно одной плоскости или одной прямой, то число уравнений (3.4) в первом случае будет 2 N , во втором N .

Пример 1. Два груза массой и связаны между собой нерастяжимым тросом, перекинутым через блок (рис. 3.3) . Пренебрегая силами трения, а также массой блока и троса, определить закон движения грузов и натяжения троса.

Решение . Система состоит из двух материальных тел (связанных нерастяжимым тросом), движущихся параллельно одной оси х. Запишем дифференциальные законы движения в проекциях на ось х для каждого тела.

Пусть правый груз опускается с ускорением , тогда левый груз будет подниматься с ускорением . Мысленно освобождаемся от связи (троса) и заменяем ее реакциями и (рис. 3.3) . Считая тела свободными, составим дифференциальные законы движения в проекции на ось х (имеется в виду, что натяжения нити являются внутренними силами, а вес грузов – внешними):

Поскольку и (тела связаны нерастяжимым тросом), получаем

Решая эти уравнения относительно ускорения и натяжения троса Т , получим

.

Отметим, что натяжение троса при не равно силе тяжести соответствующего груза.

3. 2. Теорема о движении центра масс

Известно, что твердое тело и механическая система в плоскости может двигаться достаточно сложно. К первой теореме о движении тела и механической системы можно прийти следующим образом: бросить к.-л. предмет, состоящий из множества скрепленных между собой твердых тел. Ясно, что он полетит по параболе. Это выявилось при изучении движения точки. Однако теперь объект не точка. Он поворачивается, покачивается в процессе полета вокруг некого эффективного центра, который движется по параболе. Первая теорема о движении сложных предметов говорит о том, что некий эффективный центр есть центр масс движущегося предмета. Центр масс не обязательно находится в самом теле, он может лежать и где-то вне его.

Теорема. Центр масс механической системы движется как материальная точка массой равной массе всей системы, к которой приложены все внешние силы, действующие на систему.

Для доказательства теоремы перепишем дифференциальные законы движения (3.3) в следующем виде:

(3.5)

где N – число точек системы.

Сложим почленно уравнения между собой:

(а)

Положение центра масс механической системы относительно выбранной системы координат определяется формулой (2.1): где М – масса системы. Тогда левая часть равенства (а) запишется

Первая сумма, стоящая в правой части равенства (а), равна главному вектору внешних сил, а последняя по свойству внутренних сил равна нулю. Тогда равенство (а), с учетом (б) перепишется

, (3.6)

т.е. произведение массы системы на ускорение центра ее массы равно геометрической сумме всех действующих на систему внешних сил.

Из уравнения (3.6) следует, что внутренние силы непосредственно не влияют на движение центра масс. Однако в ряде случаев являются причиной появления внешних сил, приложенных к системе. Так, внутренние силы, приводящие во вращение ведущие колеса автомобиля, вызывают действие на него внешней силы сцепления, приложенной к ободу колеса.

Пример 2. Механизм, расположенный в вертикальной плоскости, установлен на горизонтальной гладкой плоскости и прикреплен к ней жестко закрепленными с поверхностью брусками К и L (рис. 3.4) .

Диск 1 радиусом R неподвижен. Диск 2 массой m и радиусом r скреплен с кривошипом , длиной R + r в точке С 2 . Кривошип вращается с постоянной

угловой скоростью . В начальный момент кривошип занимал правое горизонтальное положение. Пренебрегая массой кривошипа, определить наибольшее горизонтальное и вертикальное усилия, действующие на бруски, если общая масса станины и колеса 1 равна М. Также рассмотреть поведение механизма при отсутствии брусков.

Решение . Система состоит из двух масс (N =2 ): неподвижного диска 1 со станиной и подвижного диска 2. Направим ось у через центр тяжести неподвижного диска по вертикали вверх, ось х – вдоль горизонтальной плоскости.

Запишем теорему о движении центра масс (3.6) в координатной форме

Внешними силами этой системы являются: вес станины и неподвижного диска – Mg , вес подвижного диска – mg , - суммарная горизонтальная реакция болтов, - нормальная суммарная реакция плоскости. Следовательно,

Тогда законы движения (б) перепишутся

Вычислим координаты центра масс механической системы:

; (г)

как видно из (рис. 3.4) , , , (угол поворота кривошипа ), . Подставляя эти выражения в (г) и вычисляя вторые производные по времени t от , , получим, что

(д)

Подставляя (в) и (д) в (б), находим

Горизонтальное давление, действующее на бруски, имеет наибольшее и наименьшее значения, когда cos = 1 соответственно, т.е

Давление механизма на горизонтальную плоскость имеет наибольшее и наименьшее значения, когда sin соответственно, т.е.

Фактически решена первая задача динамики: по известным уравнениям движения центра масс системы (д) восстанавливаются силы, участвующие в движении.

В условиях отсутствия брусков K и L (рис. 3.4) , механизм может начать подпрыгивать над горизонтальной плоскостью. Это будет иметь место, когда , т.е. когда , отсюда следует, что угловая скорость вращения кривошипа, при которой происходит подпрыгивание механизма, должна удовлетворять равенству

.

3. 3. Закон сохранения движения центра масс

Если главный вектор внешних сил, действующих на систему, равен нулю, т.е. , то из (3.6) следует, что ускорение центра масс равно нулю, следовательно, скорость центра масс является постоянной по модулю и направлению. Если, в частности, в начальный момент центр масс находится в покое, то он покоится в течение всего времени, пока главный вектор внешних сил равен нулю.

Из этой теоремы вытекает несколько следствий.

· Одними внутренними силами нельзя изменить характер движения центра масс системы.

· Если главный вектор внешних сил, действующих на систему, равен нулю, то центр масс находится в покое или движется равномерно и прямолинейно.

· Если проекция главного вектора внешних сил системы на некоторую неподвижную ось равна нулю, то проекция скорости центра масс системы на эту ось не изменяется.

· Пара сил, приложенная к твердому телу, не может изменить движение его центра масс (она может вызвать только вращение тела вокруг центра масс).

Рассмотрим пример, иллюстрирующий закон сохранения движения центра масс.

Пример 3. Два груза массами и соединены нерастяжимой нитью, переброшенной через блок (рис. 3.5) , закрепленный на клине массой М. Клин опирается на гладкую горизонтальную плоскость. В начальный момент система находилась в покое. Найти перемещение клина по плоскости при опускании первого груза на высоту Н. Массой блока и нити пренебречь.

Решение. Внешними силами, действующими на клин вместе с грузами, являются силы тяжести , и Mg , а также нормальная реакция гладкой горизонтальной поверхности N. Следовательно,

Поскольку в начальный момент система находилась в покое, имеем .

Вычислим координату центра масс системы при и в момент t 1 , когда груз весом g опустится на высоту H .

Для момента :

,

где , , х – соответственно координаты центра масс грузов весом g, g и клина весом М g .

Предположим, что клин в момент времени переместится в положительном направлении оси Ox на величину L , если груз весом опустится на высоту Н. Тогда, для момента

т.к. грузы вместе с клином передвинутся на L вправо, a груз переместится на расстояние по клину вверх. Так как , то после вычислений получим

.

3.4. Количество движения системы

3.4.1. Вычисление количества движения системы

Количеством движения материальной точки называется векторная величина, равная произведению массы точки на вектор ее скорости

Единица измерения количества движения -

Количеством движения механической системы называют векторную сумму количества движения отдельных точек системы, т.е.

где N – число точек системы.

Количество движения механической системы можно выразить через массу системы М и скорость центра масс . Действительно,

т.е. количество движения системы равно произведению массы всей системы на скорость ее центра масс. Направление совпадает с направлением (рис. 3.6)

В проекциях на прямоугольные оси имеем

где , , - проекции скорости центра масс системы.

Здесь М – масса механической системы; не меняется при движении системы.

Этими результатами особенно удобно пользоваться при вычислении количеств движения твердых тел.

Из формулы (3.7) видно, что если механическая система движется так, что ее центр масс остается неподвижным, то количество движения системы остается равным нулю.

3.4.2. Элементарный и полный импульс силы

Действие силы на материальную точку в течение времени dt можно охарактеризовать элементарным импульсом . Полный импульс силы за время t , или импульс силы , определяют по формуле

или в проекциях на координаты оси

(3.8а)

Единица импульса силы - .

3.4.3. Теорема об изменении количества движения системы

Пусть к точкам системы приложены внешние и внутренние силы. Тогда для каждой точки системы можно применить дифференциальные законы движения (3.3), имея в виду, что :

.

Суммируя по всем точкам системы, получим

По свойству внутренних сил и по определению имеем

(3.9)

Умножая обе части этого уравнения на dt , получим теорему об изменении количества движения в дифференциальной форме:

, (3.10)

т.е. дифференциал количества движения механической системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на точки механической системы.

Вычисляя интеграл от обеих частей (3.10) по времени от 0 до t , получим теорему в конечной или интегральной форме

(3.11)

В проекциях на координатные оси будем иметь

Изменение количества движения механической системы за время t , равно векторной сумме всех импульсов внешних сил, действующих на точки механической системы за то же время.

Пример 4. Груз массой m спускается вниз по наклонной плоскости из состояния покоя под действием силы F , пропорциональной времени: , где (рис. 3.7) . Какую скорость приобретет тело через t секунд после начала движения, если коэффициент трения скольжения груза о наклонную плоскость равен f .

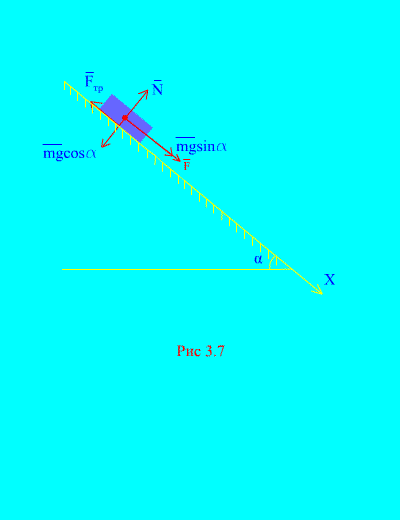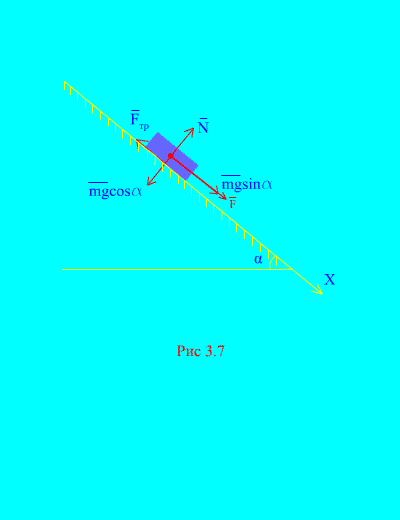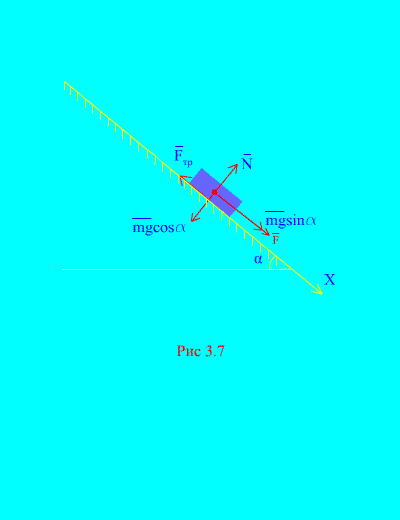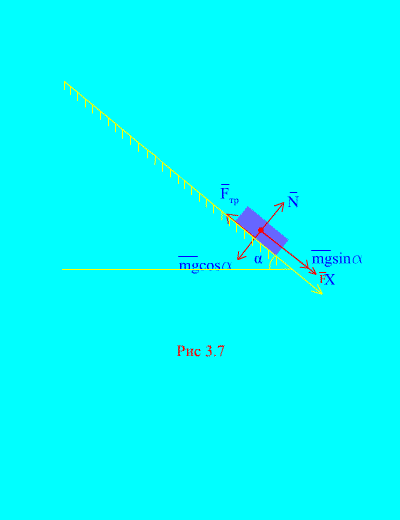
Решение. Изобразим силы, приложенные к грузу: mg – сила тяжести груза, N – нормальная реакция плоскости, - сила трения скольжения груза о плоскость, причем . Направление всех сил изображено на (рис. 3.7) .

Направим ось х вдоль наклонной плоскости вниз. Запишем теорему об изменении количества движения (3.11) в проекции на ось х :

(а)

По условию , т.к. в начальный момент времени груз находился в состоянии покоя. Сумма проекций импульсов всех сил на ось х равна

Следовательно,

,

.

3.4.4. Законы сохранения количества движения

Законы сохранения получаются как частные случаи теоремы об изменении количества движения. Возможны два частных случая.

· Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т.е. , то из теоремы следует (3.9) , что ,

т.е. если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению.

· Если проекция главного вектора внешних сил на какую-либо координатную ось равна нулю, например Ох, т.е. , то проекция количества движения на эту ось величина постоянная .

Рассмотрим пример применения закона сохранения количества движения.

Пример 5. Баллистический маятник представляет собой тело массой , подвешенное на длинной нити (рис. 3.8) .

Пуля массой , движущаяся со скоростью V и попадающая в неподвижное тело, застревает в нем, и тело отклоняется. Какова была скорость пули, если тело поднялось на высоту h ?

Решение. Пусть тело с застрявшей пулей приобрело скорость . Тогда, пользуясь законом сохранения количества движения при взаимодействии двух тел, можно записать .

Скорость можно вычислить, воспользовавшись законом сохранения механической энергии . Тогда . В результате находим

.

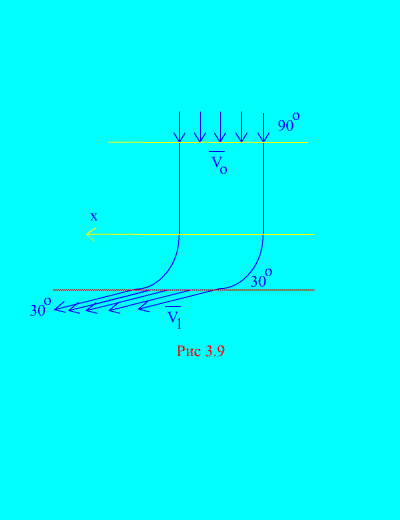
Пример 6 . Вода входит в неподвижный канал (рис. 3.9) переменного сечения со скоростью под углом к горизонту; площадь поперечного сечения канала при входе ; скорость воды у выхода из канала и составляет угол с горизонтом.

Определить горизонтальную составляющую реакции, которую вода оказывает на стенки канала. Плотность воды .

Решение. Будем определять горизонтальную составляющую реакции, оказываемой стенками канала на воду. Эта сила равна по модулю и противоположна по знаку искомой силе. Имеем, согласно (3.11а),

. (а)

Вычисляем массу объема жидкости, поступающей в канал за время t:

Величина rАV 0 называется секундной массой - масса жидкости, протекающей через любое сечение трубы в единицу времени.

Такое же количество воды покидает канал за это же время. Начальная и конечная скорости даны в условии.

Вычислим правую часть равенства (а) которая определяет сумму проекций на горизонтальную ось внешних сил, приложенных к системе (воде). Единственной горизонтальной силой является горизонтальная составляющая равнодействующей реакции стенок R x . Эта сила при установившемся движении воды является постоянной. Поэтому

. (в)

Подставляя (б) и (в) в (а), получаем

3.5. Кинетический момент системы

3.5.1. Главный момент количества движения системы

Пусть - радиус-вектор точки массой системы относительно некоторой точки А, называемой центром (рис. 3.10) .

Моментом количества движения (кинетическим моментом) точки относительно центра А называется вектор , определяемый по формуле

. (3.12)

При этом вектор направлен перпендикулярно плоскости, проходящей через центр А и вектор .

Моментом количества движения (кинетическим моментом) точки относительно оси называется проекция на эту ось момента количества движения точки относительно любого выбранного на данной оси центра.

Главным моментом количества движения (кинетическим моментом) системы относительно центра А называется величина

(3.13)

Главным моментом количества движения (кинетическим моментом) системы относительно оси называется проекция на эту ось главного момента количества движения системы относительно любого выбранного на данной оси центра.

3.5.2. Кинетический момент вращающегося твердого тела относительно оси вращения

Совместим неподвижную точку О тела, лежащую на оси вращения О z , с началом системы координат Оху z , оси которой будут вращаться вместе с телом (рис. 3.11) . Пусть - радиус-вектор точки тела относительно начала координат, его проекции на оси обозначим , , . Проекции вектора угловой скорости тела на те же оси обозначим 0, 0, ().

1. Дробно-линейная функция и ее график

Функция вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, называется дробно-рациональной функцией.

С понятием рациональных чисел вы уже наверняка знакомы. Аналогично рациональные функции – это функции, которые можно представить как частное двух многочленов.

Если дробно-рациональная функция представляет собой частное двух линейных функций – многочленов первой степени, т.е. функцию вида

y = (ax + b) / (cx + d), то ее называют дробно-линейной.

Заметим, что в функции y = (ax + b) / (cx + d), c ≠ 0 (иначе функция становится линейной y = ax/d + b/d) и что a/c ≠ b/d (иначе функция константа). Дробно-линейная функция определена при всех действительных числах, кроме x = -d/c. Графики дробно-линейных функций по форме не отличаются от известного вам графика y = 1/x. Кривая, являющаяся графиком функции y = 1/x, называется гиперболой . При неограниченном увеличении x по абсолютной величине функция y = 1/x неограниченно уменьшается по абсолютной величине и обе ветки графика приближаются к оси абсцисс: правая приближается сверху, а левая – снизу. Прямые, к которым приближаются ветки гиперболы, называются ее асимптотами .

Пример 1.

y = (2x + 1) / (x – 3).

Решение.

Выделим целую часть: (2x + 1) / (x – 3) = 2 + 7/(x – 3).

Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 3 единичных отрезка вправо, растяжением вдоль оси Oy в 7 раз и сдвигом на 2 единичных отрезка вверх.

Любую дробь y = (ax + b) / (cx + d) можно записать аналогичным образом, выделив «целую часть». Следовательно, графики всех дробно-линейных функций есть гиперболы, различным образом сдвинутые вдоль координатных осей и растянутые по оси Oy.

Для построения графика какой-нибудь произвольной дробно-линейной функции совсем не обязательно дробь, задающую эту функцию, преобразовывать. Поскольку мы знаем, что график есть гипербола, будет достаточно найти прямые, к которым приближаются ее ветки – асимптоты гиперболы x = -d/c и y = a/c.

Пример 2.

Найти асимптоты графика функции y = (3x + 5)/(2x + 2).

Решение.

Функция не определена, при x = -1. Значит, прямая x = -1 служит вертикальной асимптотой. Для нахождения горизонтальной асимптоты, выясним, к чему приближаются значения функции y(x), когда аргумент x возрастает по абсолютной величине.

Для этого разделим числитель и знаменатель дроби на x:

y = (3 + 5/x) / (2 + 2/x).

При x → ∞ дробь будет стремиться к 3/2. Значит, горизонтальная асимптота – это прямая y = 3/2.

Пример 3.

Построить график функции y = (2x + 1)/(x + 1).

Решение.

Выделим у дроби «целую часть»:

(2x + 1) / (x + 1) = (2x + 2 – 1) / (x + 1) = 2(x + 1) / (x + 1) – 1/(x + 1) =

2 – 1/(x + 1).

Теперь легко видеть, что график этой функции получается из графика функции y = 1/x следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 2 единичных отрезка вверх по оси Oy.

Область определения D(y) = (-∞; -1)ᴗ(-1; +∞).

Область значений E(y) = (-∞; 2)ᴗ(2; +∞).

Точки пересечения с осями: c Oy: (0; 1); c Ox: (-1/2; 0). Функция возрастает на каждом из промежутков области определения.

Ответ: рисунок 1.

2. Дробно-рациональная функция

Рассмотрим дробно-рациональную функцию вида y = P(x) / Q(x), где P(x) и Q(x) – многочлены, степени выше первой.

Примеры таких рациональных функций:

y = (x 3 – 5x + 6) / (x 7 – 6) или y = (x – 2) 2 (x + 1) / (x 2 + 3).

Если функция y = P(x) / Q(x) представляет собой частное двух многочленов степени выше первой, то ее график будет, как правило, сложнее, и построить его точно, со всеми деталями бывает иногда трудно. Однако, часто достаточно применить приемы, аналогичные тем, с которыми мы уже познакомились выше.

Пусть дробь – правильная (n < m). Известно, что любую несократимую рациональную дробь можно представить, и притом единственным образом, в виде суммы конечного числа элементарных дробей, вид которых определяется разложением знаменателя дроби Q(x) в произведение действительных сомножителей:

P(x)/Q(x) = A 1 /(x – K 1) m1 + A 2 /(x – K 1) m1-1 + … + A m1 /(x – K 1) + …+

L 1 /(x – K s) ms + L 2 /(x – K s) ms-1 + … + L ms /(x – K s) + …+

+ (B 1 x + C 1) / (x 2 +p 1 x + q 1) m1 + … + (B m1 x + C m1) / (x 2 +p 1 x + q 1) + …+

+ (M 1 x + N 1) / (x 2 +p t x + q t) m1 + … + (M m1 x + N m1) / (x 2 +p t x + q t).

Очевидно, что график дробно-рациональной функции можно получить как сумму графиков элементарных дробей.

Построение графиков дробно-рациональных функций

Рассмотрим несколько способов построения графиков дробно-рациональной функции.

Пример 4.

Построить график функции y = 1/x 2 .

Решение.

Используем график функции y = x 2 для построения графика y = 1/x 2 и воспользуемся приемом «деления» графиков.

Область определения D(y) = (-∞; 0)ᴗ(0; +∞).

Область значений E(y) = (0; +∞).

Точек пересечения с осями нет. Функция четная. Возрастает при все х из интервала (-∞; 0), убывает при x от 0 до +∞.

Ответ: рисунок 2.

Пример 5.

Построить график функции y = (x 2 – 4x + 3) / (9 – 3x).

Решение.

Область определения D(y) = (-∞; 3)ᴗ(3; +∞).

y = (x 2 – 4x + 3) / (9 – 3x) = (x – 3)(x – 1) / (-3(x – 3)) = -(x – 1)/3 = -x/3 + 1/3.

Здесь мы использовали прием разложения на множители, сокращения и приведения к линейной функции.

Ответ: рисунок 3.

Пример 6.

Построить график функции y = (x 2 – 1)/(x 2 + 1).

Решение.

Область определения D(y) = R. Так как функция четная, то график симметричен относительно оси ординат. Прежде чем строить график, опять преобразуем выражение, выделив целую часть:

y = (x 2 – 1)/(x 2 + 1) = 1 – 2/(x 2 + 1).

Заметим, что выделение целой части в формуле дробно-рациональной функции является одним из основных при построении графиков.

Если x → ±∞, то y → 1, т.е. прямая y = 1 является горизонтальной асимптотой.

Ответ: рисунок 4.

Пример 7.

Рассмотрим функцию y = x/(x 2 + 1) и попробуем точно найти наибольшее ее значение, т.е. самую высокую точку правой половины графика. Чтобы точно построить этот график, сегодняшних знаний недостаточно. Очевидно, что наша кривая не может «подняться» очень высоко, т.к. знаменатель довольно быстро начинает «обгонять» числитель. Посмотрим, может ли значение функции равняться 1. Для этого нужно решить уравнение x 2 + 1 = x, x 2 – x + 1 = 0. Это уравнение не имеет действительных корней. Значит, наше предположение не верно. Чтобы найти самое большое значение функции, надо узнать, при каком самом большом А уравнение А = x/(x 2 + 1) будет иметь решение. Заменим исходное уравнение квадратным: Аx 2 – x + А = 0. Это уравнение имеет решение, когда 1 – 4А 2 ≥ 0. Отсюда находим наибольшее значение А = 1/2.

Ответ: рисунок 5, max y(x) = ½.

Остались вопросы? Не знаете, как строить графики функций?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2 , изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3) .

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4) .

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7) .

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8) .

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11) .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.