Уравнение на права, минаваща през 2. Уравнение на права - видове уравнение на права: минаващо през точка, общо, канонично, параметрично и др.
Определение.В декартовата правоъгълна координатна система вектор с компоненти (A, B) е перпендикулярен на правата линия, дадена от уравнението Ax + By + C = 0.
Пример. Намерете уравнението на правата, минаваща през точката A(1, 2), перпендикулярна на вектора (3, -1).
Решение. При A = 3 и B = -1, нека съставим уравнението на правата: 3x – y + C = 0. За да намерим коефициента C, заместваме координатите на дадената точка A в получения израз.Получаваме: 3 – 2 + C = 0, следователно C = -1. Общо: необходимото уравнение: 3x – y – 1 = 0.
Уравнение на права, минаваща през две точки
Нека две точки M 1 (x 1, y 1, z 1) и M 2 (x 2, y 2, z 2) са дадени в пространството, тогава уравнението на правата, минаваща през тези точки, е:

Ако някой от знаменателите е равен на нула, съответният числител трябва да е равен на 0. На равнината уравнението на правата, написана по-горе, е опростено:

ако x 1 ≠ x 2 и x = x 1, ако x 1 = x 2.
Дробта = k се нарича наклонправ.
Пример. Намерете уравнението на правата, минаваща през точки A(1, 2) и B(3, 4).
Решение.Прилагайки формулата, написана по-горе, получаваме:

Уравнение на права от точка и наклон
Ако общото уравнение на правата Ax + By + C = 0 се редуцира до формата:

и посочете  , тогава полученото уравнение се нарича уравнение на права линия с наклонк.
, тогава полученото уравнение се нарича уравнение на права линия с наклонк.
Уравнение на права от точка и насочващ вектор
По аналогия с точката, разглеждаща уравнението на права линия през нормален вектор, можете да въведете дефиницията на права линия през точка и насочващия вектор на правата линия.
Определение.Всеки ненулев вектор (α 1, α 2), компонентите на който отговарят на условието A α 1 + B α 2 = 0, се нарича насочващ вектор на правата.
Ax + Wu + C = 0.
Пример. Намерете уравнението на права линия с насочващ вектор (1, -1) и минаваща през точката A(1, 2).
Решение.Ще търсим уравнението на желаната линия във формата: Ax + By + C = 0. В съответствие с дефиницията коефициентите трябва да отговарят на условията:
1 * A + (-1) * B = 0, т.е. А = Б.
Тогава уравнението на правата има формата: Ax + Ay + C = 0, или x + y + C / A = 0. за x = 1, y = 2 получаваме C/ A = -3, т.е. необходимо уравнение:
Уравнение на права в отсечки
Ако в общото уравнение на правата Ах + Ву + С = 0 С≠0, тогава, разделяйки на –С, получаваме:  или
или

Геометричният смисъл на коефициентите е, че коефициентът А е координатата на пресечната точка на правата с оста Ox, и b – координатата на пресечната точка на правата с оста Oy.
Пример.Дадено е общото уравнение на правата x – y + 1 = 0. Намерете уравнението на тази права в отсечки.
C = 1, , a = -1, b = 1.
Нормално уравнение на права
Ако двете страни на уравнението Ax + By + C = 0 се разделят на числото  което се нарича нормализиращ фактор, тогава получаваме
което се нарича нормализиращ фактор, тогава получаваме
xcosφ + ysinφ - p = 0 –
нормално уравнение на права. Знакът ± на нормализиращия фактор трябва да бъде избран така, че μ * C< 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Пример. Дадено е общото уравнение на правата 12x – 5y – 65 = 0. Необходимо е да се напишат различни видове уравнения за тази права.
уравнение на тази линия в сегменти: 
уравнение на тази права с наклон: (разделете на 5)

нормално уравнение на линия:
 ; cos φ = 12/13; sin φ= -5/13; p = 5.
; cos φ = 12/13; sin φ= -5/13; p = 5.
C Трябва да се отбележи, че не всяка линия може да бъде представена чрез уравнение в сегменти, например линии, успоредни на оси или минаващи през началото.
Пример. Правата линия отрязва равни положителни отсечки по координатните оси. Напишете уравнение на права линия, ако площта на триъгълника, образуван от тези сегменти, е 8 cm 2.
Решение.Уравнението на правата има вида: , ab /2 = 8; а = 4; -4. a = -4 не е подходящ според условията на проблема. Общо: или x + y – 4 = 0.
Пример. Напишете уравнение за права линия, минаваща през точка A(-2, -3) и началото.
Решение.
Уравнението на правата линия е:  , където x 1 = y 1 = 0; х 2 = -2; y 2 = -3.
, където x 1 = y 1 = 0; х 2 = -2; y 2 = -3.
Нека да разгледаме как да създадем уравнение за права, минаваща през две точки, използвайки примери.
Пример 1.
Напишете уравнение за права линия, минаваща през точки A(-3; 9) и B(2;-1).
Метод 1 - създайте уравнение на права линия с ъглов коефициент.
Уравнението на права линия с ъглов коефициент има формата . Замествайки координатите на точките A и B в уравнението на правата (x= -3 и y=9 - в първия случай, x=2 и y= -1 - във втория), получаваме система от уравнения от които намираме стойностите на k и b:
Събирайки 1-во и 2-ро уравнения член по член, получаваме: -10=5k, откъдето k= -2. Замествайки k= -2 във второто уравнение, намираме b: -1=2·(-2)+b, b=3.
Така y= -2x+3 е търсеното уравнение.
Метод 2 - нека създадем общо уравнение на права линия.
Общото уравнение на права има формата . Замествайки координатите на точки A и B в уравнението, получаваме системата:
Тъй като броят на неизвестните е по-голям от броя на уравненията, системата не е разрешима. Но всички променливи могат да бъдат изразени чрез една. Например чрез b.
Чрез умножаване на първото уравнение на системата по -1 и добавяне на член по член с второто:
получаваме: 5a-10b=0. Следователно a=2b.
Нека заместим получения израз във второто уравнение: 2·2b -b+c=0; 3b+c=0; c= -3b.
Заместете a=2b, c= -3b в уравнението ax+by+c=0:
2bx+по-3b=0. Остава да разделим двете страни на b:
Общото уравнение на права линия може лесно да се сведе до уравнението на права линия с ъглов коефициент:
Метод 3 - създайте уравнение на права линия, минаваща през 2 точки.
Уравнението на права, минаваща през две точки е:
![]()
Нека заместим координатите на точки A(-3; 9) и B(2;-1) в това уравнение
(т.е. x 1 = -3, y 1 =9, x 2 =2, y 2 = -1):
![]()
и опростете:
откъдето 2x+y-3=0.
В училищните курсове най-често се използва уравнението на права линия с ъглов коефициент. Но най-лесният начин е да изведем и използваме формулата за уравнението на права, минаваща през две точки.
Коментирайте.
Ако при заместване на координатите на дадени точки, един от знаменателите на уравнението
![]()
се оказва равно на нула, то търсеното уравнение се получава чрез приравняване на съответния числител на нула.
Пример 2.
Напишете уравнение за права линия, минаваща през две точки C(5; -2) и D(7;-2).
Заместваме координатите на точки C и D в уравнението на права линия, минаваща през 2 точки.
Тази статия е част от темата уравнение на права в равнина. Тук ще го разгледаме от всички страни: ще започнем с доказателството на теоремата, която определя формата на общото уравнение на права, след това ще разгледаме непълно общо уравнение на права, ще дадем примери за непълни уравнения на линия с графични илюстрации и в заключение ще се спрем на прехода от общо уравнение на линия към други видове уравнения на тази линия и ще дадем подробни решения на типични задачи за съставяне на общото уравнение на права линия.
Навигация в страницата.
Общо уравнение на права линия - основна информация.
Нека анализираме този алгоритъм при решаване на пример.
Пример.
Напишете параметрични уравнения на права, която е дадена от общото уравнение на права ![]() .
.
Решение.
Първо, намаляваме първоначалното общо уравнение на правата до каноничното уравнение на правата:
Сега приемаме лявата и дясната страна на полученото уравнение за равни на параметъра. Ние имаме 
Отговор:

От общо уравнение на права линия е възможно да се получи уравнение на права линия с ъглов коефициент само когато . Какво трябва да направите, за да направите прехода? Първо, от лявата страна на общото уравнение на права линия, оставете само члена, останалите членове трябва да бъдат преместени в дясната страна с противоположния знак: ![]() . Второ, разделете двете страни на полученото равенство на числото B, което е различно от нула,
. Второ, разделете двете страни на полученото равенство на числото B, което е различно от нула, ![]() . Това е всичко.
. Това е всичко.
Пример.
Права линия в правоъгълна координатна система Oxy се дава от общото уравнение на права линия. Вземете уравнението на тази права с наклона.
Решение.
Да извършим необходимите действия: .
Отговор:
Когато една права е дадена от пълното общо уравнение на правата, лесно е да се получи уравнението на правата в сегменти от формата. За да направим това, прехвърляме числото C в дясната страна на равенството с противоположен знак, разделяме двете страни на полученото равенство на –C и накрая прехвърляме коефициентите за променливите x и y към знаменателите: 
Разгледайте уравнението на права линия, минаваща през точка и нормален вектор. Нека в координатната система са дадени точка и ненулев вектор (фиг. 1).
Определение
Както виждаме, има една права линия, която минава през точката, перпендикулярна на посоката на вектора (в този случай се нарича нормален векторнаправо).

Ориз. 1
Нека докажем, че линейното уравнение
това е уравнение на права, тоест координатите на всяка точка от правата отговарят на уравнение (1), но координатите на точка, която не лежи върху, не отговарят на уравнение (1).
За да докажем това, нека отбележим, че скаларното произведение на вектори и = в координатна форма съвпада с лявата страна на уравнение (1).
След това използваме очевидното свойство на линията: векторите и са перпендикулярни тогава и само ако точката лежи на . И при условие, че и двата вектора са перпендикулярни, тяхното скаларно произведение (2) се превръща в за всички точки, които лежат върху и само за тях. Това означава, че (1) е уравнението на правата линия.
Определение
Уравнение (1) се нарича уравнение на правата, която минава през дадена точкас нормален вектор = .
Нека трансформираме уравнение (1)
Означавайки = , получаваме
По този начин линейно уравнение под формата (3) съответства на права линия. Напротив, като се използва дадено уравнение под формата (3), където поне един от коефициентите не е равен на нула, може да се построи права линия.
Наистина, нека чифт числа удовлетворяват уравнение (3), т.е
Изваждайки последното от (3), получаваме връзката, която определя правата зад вектора и точката.
Изследване на общото уравнение на линия
Полезно е да знаете особеностите на поставяне на линия в определени случаи, когато едно или две от числата са равни на нула.
1. Общото уравнение изглежда така: . Точката го удовлетворява, което означава, че правата минава през началото. Може да се запише: = – x (виж фиг. 2).

Ориз. 2
Ние вярваме, че:
Ако поставим , тогава , получаваме още една точка (виж фиг. 2).
2. , тогава уравнението изглежда така, където = –. Нормалният вектор лежи върху оста, права линия. Така правата линия е перпендикулярна в точка , или успоредна на оста (виж Фиг. 3). По-специално, ако и , тогава и уравнението е уравнението на ординатната ос.

Ориз. 3
3. По същия начин, когато уравнението е написано, където . Векторът принадлежи на оста. Права линия в точка (фиг. 4).

Ако, тогава уравнението на оста е .
Изследването може да се формулира в следната форма: правата линия е успоредна на координатната ос, промяната на която отсъства в общото уравнение на правата линия.
Например:
Нека построим права линия, използвайки общото уравнение, при условие че - не са равни на нула. За да направите това, достатъчно е да намерите две точки, които лежат на тази линия. Понякога е по-удобно да се намерят такива точки на координатни оси.
Нека тогава = –.
Когато , тогава = –.
Нека означим – = , – = . Точки и бяха намерени. Нека начертаем и начертаем права линия върху осите и през тях (виж фиг. 5).

Ориз. 5
От общото можете да преминете към уравнение, което ще включва числата и:
И тогава се оказва:
Или, според нотацията, получаваме уравнението
Което се нарича уравнение на права линия в сегменти. Числата и с точност до знака са равни на сегментите, които са отрязани от права линия на координатните оси.
Уравнение на права линия с наклон
За да разберете какво е уравнението на права линия с наклон, разгледайте уравнение (1):
Означавайки – = , получаваме
уравнение на права, която минава през точка в дадена посока. Геометричното съдържание на коефициента е ясно от фиг. 6.
B = = , където е най-малкият ъгъл, с който положителната посока на оста трябва да се завърти около общата точка, докато се изравни с правата линия. Очевидно, ако ъгълът е остър, тогава title="Rendered by QuickLaTeX.com" height="17" width="97" style="vertical-align: -4px;">; если же – тупой угол, тогда .!}
Нека отворим скобите в (5) и го опростим:
Където . Връзка (6) – уравнение права линия с наклон. Когато , е сегмент, който пресича права линия на оста (виж Фиг. 6).
Забележка!
За да преминете от общо уравнение на права линия към уравнение с коефициент на наклон, първо трябва да решите за .

Ориз. 6
= – x + – =
където е означено = –, = –. Ако, тогава от изследването на общото уравнение вече е известно, че такава права линия е перпендикулярна на оста.
Нека да разгледаме каноничното уравнение на права линия, използвайки пример.
Нека в координатната система са зададени точка и ненулев вектор (фиг. 7).

Ориз. 7
Необходимо е да се създаде уравнение за права линия, която минава през точка, успоредна на вектора, която се нарича вектор на посоката. Произволна точка принадлежи на тази линия, ако и само ако . Тъй като векторът е даден, а векторът е , тогава, съгласно условието за паралелност, координатите на тези вектори са пропорционални, т.е.
Определение
Връзката (7) се нарича уравнение на права, която минава през дадена точка в дадена посока или канонично уравнение на права.
Нека отбележим, че можем да преминем към уравнение под формата (7), например от уравнението на молив от линии (4)
или от уравнението на права линия през точка и нормален вектор (1):
По-горе беше прието, че векторът на посоката е различен от нула, но може да се случи една от неговите координати, например . Тогава изразът (7) ще бъде формално записан:
което изобщо няма смисъл. Ние обаче приемаме и получаваме уравнението на правата, перпендикулярна на оста. Наистина, от уравнението става ясно, че правата линия се определя от точка и насочващ вектор, перпендикулярен на оста. Ако премахнем знаменателя от това уравнение, тогава получаваме:
Или - уравнението на права линия, перпендикулярна на оста. Подобен резултат би се получил за вектора .
Параметрично уравнение на права
За да разберете какво е параметрично уравнение на линия, трябва да се върнете към уравнение (7) и да приравните всяка дроб (7) към параметър. Тъй като поне един от знаменателите в (7) не е равен на нула и съответният числител може да придобие произволни стойности, тогава областта на промяна на параметъра е цялата цифрова ос.
Определение
Уравнение (8) се нарича параметрично уравнение на права линия.
Примери за задачи с права линия
Разбира се, трудно е да решите нещо само въз основа на дефиниции, защото трябва да решите сами поне няколко примера или задачи, които ще ви помогнат да консолидирате материала, който сте покрили. Затова нека анализираме основните задачи в права линия, тъй като подобни проблеми често се срещат на изпити и тестове.
Канонично и параметрично уравнение
Пример 1
На права линия, дадена от уравнението, намерете точка, която се намира на разстояние 10 единици от точката на тази права линия.
Решение:
Позволявам търсенточка на права линия, то за разстоянието пишем . Като се има предвид, че. Тъй като точката принадлежи на права, която има нормален вектор, тогава уравнението на правата може да бъде написано: = = и тогава се оказва:
След това разстоянието. Предмет на , или . От параметричното уравнение:
Пример 2
Задача
Точката се движи равномерно със скорост по посока на вектора от началната точка. Намерете координатите на точката през от началото на движението.
Решение
Първо трябва да намерите единичния вектор. Неговите координати са насочващи косинуси:
Тогава векторът на скоростта:
X = x = .
Каноничното уравнение на линията сега ще бъде написано:
= = , = – параметрично уравнение. След това трябва да използвате параметричното уравнение на правата линия при .
Решение:
Уравнението на права, която минава през точка, се намира с помощта на формулата за молив от линии, където наклонза права линия и = за права линия.
Имайки предвид фигурата, където можете да видите, че между прави линии и - има два ъгъла: единият е остър, а вторият е тъп. Според формула (9), това е ъгълът между правите линии и с който трябва да завъртите правата линия обратно на часовниковата стрелка спрямо тяхната пресечна точка, докато се изравни с правата линия.

И така, запомнихме формулата, разбрахме ъглите и сега можем да се върнем към нашия пример. Това означава, че като вземем предвид формула (9), първо намираме уравненията на крака.

Тъй като завъртането на правата линия под ъгъл обратно на часовниковата стрелка спрямо точката води до подравняване с правата линия, тогава във формула (9) , a . От уравнението:
Използвайки формулата на лъча, уравнението на права линия ще бъде написано:
По същия начин намираме и
Уравнение на линията:
Уравнение на права – видове уравнение на права: минаващо през точка, общо, канонично, параметрично и др.актуализиран: 22 ноември 2019 г. от: Научни статии.Ru
Свойства на права линия в евклидовата геометрия.
Безкрайно много прави линии могат да бъдат начертани през всяка точка.
През всеки две несъвпадащи точки може да се прекара една права линия.
Две различни прави в една равнина се пресичат в една точка или се пресичат
паралелен (следва от предишния).
В триизмерното пространство има три варианта за взаимното разположение на две линии:
- линиите се пресичат;
- линиите са успоредни;
- пресичат се прави линии.
Направо линия— алгебрична крива от първи ред: права линия в декартовата координатна система
се дава на равнината чрез уравнение от първа степен (линейно уравнение).
Общо уравнение на права линия.
Определение. Всяка права линия в равнината може да бъде определена чрез уравнение от първи ред
Ax + Wu + C = 0,
и постоянна А, Бне са равни на нула едновременно. Това уравнение от първи ред се нарича общ
уравнение на права линия.В зависимост от стойностите на константите А, БИ СЪСВъзможни са следните специални случаи:
. C = 0, A ≠ 0, B ≠ 0- права линия минава през началото
. A = 0, B ≠0, C ≠0 (By + C = 0)- права линия, успоредна на оста о
. B = 0, A ≠0, C ≠ 0 (Ax + C = 0)- права линия, успоредна на оста OU
. B = C = 0, A ≠0- правата линия съвпада с оста OU
. A = C = 0, B ≠0- правата линия съвпада с оста о
Уравнението на права линия може да бъде представено в различни форми в зависимост от всяка даденост
начални условия.
Уравнение на права от точка и нормален вектор.
Определение. В декартова правоъгълна координатна система вектор с компоненти (A, B)
перпендикулярна на правата, дадена от уравнението
Ax + Wu + C = 0.
Пример. Намерете уравнението на права, минаваща през точка A(1, 2)перпендикулярен на вектора (3, -1).
Решение. При A = 3 и B = -1, нека съставим уравнението на правата линия: 3x - y + C = 0. За да намерим коефициента C
Нека заместим в получения израз координатите на дадената точка A. Получаваме: 3 - 2 + C = 0, следователно
C = -1. Общо: необходимото уравнение: 3x - y - 1 = 0.
Уравнение на права, минаваща през две точки.
Нека в пространството са дадени две точки M 1 (x 1, y 1, z 1)И M2 (x 2, y 2, z 2),Тогава уравнение на права,
преминавайки през тези точки:
Ако някой от знаменателите е нула, съответният числител трябва да бъде равен на нула. На
равнина, уравнението на правата линия, написано по-горе, е опростено:

Ако x 1 ≠ x 2И x = x 1, Ако x 1 = x 2 .
Фракция = kНаречен наклон прав.
Пример. Намерете уравнението на правата, минаваща през точки A(1, 2) и B(3, 4).
Решение. Прилагайки формулата, написана по-горе, получаваме:

Уравнение на права линия с помощта на точка и наклон.
Ако общото уравнение на правата Ax + Wu + C = 0води до:

и посочете  , тогава полученото уравнение се нарича
, тогава полученото уравнение се нарича
уравнение на права линия с наклон k.
Уравнение на права от точка и насочващ вектор.
По аналогия с точката, разглеждаща уравнението на права линия през нормалния вектор, можете да въведете задачата
права линия през точка и насочващ вектор на права линия.
Определение. Всеки ненулев вектор (α 1, α 2), чиито компоненти отговарят на условието
Aα 1 + Bα 2 = 0Наречен насочващ вектор на права линия.
Ax + Wu + C = 0.
Пример. Намерете уравнението на права линия с насочващ вектор (1, -1) и минаваща през точката A(1, 2).
Решение. Ще търсим уравнението на желаната права във формата: Ax + By + C = 0.Според определението,
коефициентите трябва да отговарят на следните условия:
1 * A + (-1) * B = 0, т.е. А = Б.
Тогава уравнението на правата има формата: Ax + Ay + C = 0,или x + y + C / A = 0.
при x = 1, y = 2получаваме C/A = -3, т.е. необходимо уравнение:
x + y - 3 = 0
Уравнение на права линия в отсечки.
Ако в общото уравнение на правата Ах + Ву + С = 0 С≠0, тогава, разделяйки на -С, получаваме:
 или къде
или къде

Геометричният смисъл на коефициентите е, че коефициентът a е координатата на пресечната точка
права с ос оА b- координата на пресечната точка на правата с оста OU.
Пример. Дадено е общото уравнение на права линия x - y + 1 = 0.Намерете уравнението на тази права в сегменти.
C = 1, , a = -1, b = 1.
Нормално уравнение на права.
Ако и двете страни на уравнението Ax + Wu + C = 0разделяне на число  което се нарича
което се нарича
нормализиращ фактор, тогава получаваме
xcosφ + ysinφ - p = 0 -нормално уравнение на права.
Знакът ± на нормализиращия фактор трябва да бъде избран така, че μ*C< 0.
Р- дължината на перпендикуляра, пуснат от началото до правата линия,
А φ - ъгълът, образуван от този перпендикуляр с положителната посока на оста о
Пример. Дадено е общото уравнение на правата 12x - 5y - 65 = 0. Изисква се за писане на различни видове уравнения
тази права линия.
Уравнението на тази права в сегменти:

Уравнението на тази права с наклона: (раздели на 5)

Уравнение на права:

cos φ = 12/13; sin φ= -5/13; p = 5.
Трябва да се отбележи, че не всяка права линия може да бъде представена чрез уравнение в сегменти, например прави линии,
успоредни на осите или минаващи през началото.
Ъгълът между прави в равнина.
Определение. Ако са дадени два реда y = k 1 x + b 1, y = k 2 x + b 2, тогава острия ъгъл между тези прави
ще се определи като

Две прави са успоредни, ако k 1 = k 2. Две линии са перпендикулярни
Ако k 1 = -1/ k 2 .
Теорема.
Директен Ax + Wu + C = 0И A 1 x + B 1 y + C 1 = 0паралелно, когато коефициентите са пропорционални
A 1 = λA, B 1 = λB. Ако също С 1 = λС, тогава линиите съвпадат. Координати на пресечната точка на две прави
се намират като решение на системата от уравнения на тези прави.
Уравнението на права, минаваща през дадена точка, перпендикулярна на дадена права.
Определение. Права, минаваща през точка M 1 (x 1, y 1)и перпендикулярна на правата y = kx + b
представено от уравнението:

Разстояние от точка до права.
Теорема. Ако се даде точка M(x 0, y 0),след това разстоянието до правата линия Ax + Wu + C = 0дефиниран като:

Доказателство. Нека точката M 1 (x 1, y 1)- основата на перпендикуляр, пуснат от точка Мза даденост
директен. След това разстоянието между точките МИ М 1:
![]() (1)
(1)
Координати х 1И на 1може да се намери като решение на системата от уравнения:

Второто уравнение на системата е уравнението на права линия, минаваща през дадена точка M 0 перпендикулярно
дадена права линия. Ако трансформираме първото уравнение на системата във вида:
A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,
тогава, решавайки, получаваме:

Замествайки тези изрази в уравнение (1), намираме:

Теоремата е доказана.
 Николай Мартинов, убил в дуел М
Николай Мартинов, убил в дуел М Проекции на вектора на преместване Модул на преместване на тялото във времето
Проекции на вектора на преместване Модул на преместване на тялото във времето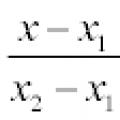 Уравнение на права - видове уравнение на права: минаващо през точка, общо, канонично, параметрично и др.
Уравнение на права - видове уравнение на права: минаващо през точка, общо, канонично, параметрично и др.