Kakvi su termini. Smanjenje sličnih pojmova (Wolfson G.I.)
Višekratnik je broj koji je djeljiv sa dati broj bez traga. Najmanji zajednički višekratnik (LCM) grupe brojeva je najmanji broj koji je jednako djeljiv sa svakim brojem u grupi. Da biste pronašli najmanji zajednički umnožak, morate pronaći proste faktore datih brojeva. Također, LCM se može izračunati korištenjem niza drugih metoda koje su primjenjive na grupe od dva ili više brojeva.
Koraci
Serija višestrukih
- Na primjer, pronađite najmanji zajednički umnožak brojeva 5 i 8. To su mali brojevi, pa se ova metoda može koristiti.
-
Višekratnik broja je broj koji je djeljiv datim brojem bez ostatka. Više brojeva se može naći u tablici množenja.
- Na primjer, brojevi koji su višestruki od 5 su: 5, 10, 15, 20, 25, 30, 35, 40.
-
Zapišite niz brojeva koji su višekratnici prvog broja. Uradite to pod višekratnicima prvog broja da biste uporedili dva reda brojeva.
- Na primjer, brojevi koji su višekratnici broja 8 su: 8, 16, 24, 32, 40, 48, 56 i 64.
-
Pronađite najmanji broj koji se pojavljuje u oba niza višekratnika. Možda ćete morati napisati duge nizove višestrukih brojeva da biste ih pronašli ukupan broj. Najmanji broj koji se pojavljuje u oba niza višekratnika je najmanji zajednički višekratnik.
- Na primjer, najmanji broj, koji se pojavljuje u nizu višekratnika 5 i 8, je broj 40. Dakle, 40 je najmanji zajednički višekratnik brojeva 5 i 8.
Prime faktorizacija
-
Pogledaj ove brojke. Ovdje opisani metod najbolje je koristiti kada su data dva broja, svaki veći od 10. Ako je dat manji brojevi, koristite drugu metodu.
- Na primjer, pronađite najmanji zajednički višekratnik brojeva 20 i 84. Svaki od brojeva je veći od 10, tako da se ovaj metod može koristiti.
-
Faktorizirajte prvi broj. Odnosno, trebate pronaći takve proste brojeve, kada se pomnožite, dobijete dati broj. Nakon što ste pronašli proste faktore, zapišite ih kao jednakost.
- Na primjer, 2 × 10 = 20 (\displaystyle (\mathbf (2) )\puta 10=20) I 2 × 5 = 10 (\displaystyle (\mathbf (2) )\puta (\mathbf (5) )=10). Dakle, prosti činioci broja 20 su brojevi 2, 2 i 5. Zapišite ih kao izraz: .
-
Faktori drugi broj u proste faktore. Uradite to na isti način kao što ste rastavili na faktore prvi broj, odnosno pronađite takve proste brojeve koji će, kada se pomnože, dobiti ovaj broj.
- Na primjer, 2 × 42 = 84 (\displaystyle (\mathbf (2) )\puta 42=84), 7 × 6 = 42 (\displaystyle (\mathbf (7) )\puta 6=42) I 3 × 2 = 6 (\displaystyle (\mathbf (3) )\puta (\mathbf (2) )=6). Dakle, prosti činioci broja 84 su brojevi 2, 7, 3 i 2. Zapišite ih kao izraz: .
-
Zapišite faktore zajedničke za oba broja. Napišite takve faktore kao operaciju množenja. Dok zapisujete svaki faktor, precrtajte ga u oba izraza (izrazi koji opisuju dekompoziciju brojeva na proste faktore).
- Na primjer, zajednički faktor za oba broja je 2, pa napišite 2 × (\displaystyle 2\puta) i precrtaj 2 u oba izraza.
- Zajednički faktor za oba broja je još jedan faktor 2, pa napišite 2 × 2 (\displaystyle 2\puta 2) i precrtajte drugo 2 u oba izraza.
-
Dodajte preostale faktore operaciji množenja. To su faktori koji nisu precrtani u oba izraza, odnosno faktori koji nisu zajednički za oba broja.
- Na primjer, u izrazu 20 = 2 × 2 × 5 (\displaystyle 20=2\puta 2\puta 5) obje dvije (2) su precrtane jer su zajednički faktori. Faktor 5 nije precrtan, pa zapišite operaciju množenja na sljedeći način: 2 × 2 × 5 (\displaystyle 2\puta 2\puta 5)
- U izrazu 84 = 2 × 7 × 3 × 2 (\displaystyle 84=2\puta 7\puta 3\puta 2) obje dvojke (2) su također precrtane. Faktori 7 i 3 nisu precrtani, pa zapišite operaciju množenja na sljedeći način: 2 × 2 × 5 × 7 × 3 (\displaystyle 2\puta 2\puta 5\puta 7\puta 3).
-
Izračunajte najmanji zajednički višekratnik. Da biste to učinili, pomnožite brojeve u pismenoj operaciji množenja.
- Na primjer, 2 × 2 × 5 × 7 × 3 = 420 (\displaystyle 2\puta 2\puta 5\puta 7\puta 3=420). Dakle, najmanji zajednički višekratnik 20 i 84 je 420.
Pronalaženje zajedničkih djelitelja
-
Nacrtajte mrežu kao što biste to učinili za igru tic-tac-toe. Takva mreža se sastoji od dvije paralelne linije koje se sijeku (pod pravim uglom) s dvije druge paralelne prave. Ovo će rezultirati tri reda i tri kolone (rešetka liči na znak #). Upišite prvi broj u prvi red i drugu kolonu. Upišite drugi broj u prvi red i treću kolonu.
- Na primjer, pronađite najmanji zajednički višekratnik 18 i 30. U prvi red i drugu kolonu upišite 18, a u prvi red i treću kolonu upišite 30.
-
Pronađite djelitelj zajednički za oba broja. Zapišite to u prvi red i prvu kolonu. Bolje je tražiti proste djelitelje, ali to nije preduvjet.
- Na primjer, 18 i 30 su parni brojevi, dakle oni zajednički djeliteljće biti broj 2. Dakle, napišite 2 u prvom redu i prvoj koloni.
-
Podijelite svaki broj sa prvim djeliteljem. Upišite svaki količnik ispod odgovarajućeg broja. Kvocijent je rezultat dijeljenja dva broja.
- Na primjer, 18 ÷ 2 = 9 (\displaystyle 18\div 2=9), pa napiši 9 ispod 18.
- 30 ÷ 2 = 15 (\displaystyle 30\div 2=15), pa napiši 15 ispod 30.
-
Pronađite djelitelj zajednički za oba količnika. Ako ne postoji takav djelitelj, preskočite sljedeća dva koraka. U suprotnom, zapišite djelitelj u drugom redu i prvoj koloni.
- Na primjer, 9 i 15 su djeljivi sa 3, pa upišite 3 u drugi red i prvi stupac.
-
Podijelite svaki količnik sa drugim djeliteljem. Zapišite svaki rezultat dijeljenja pod odgovarajućim količnikom.
- Na primjer, 9 ÷ 3 = 3 (\displaystyle 9\div 3=3), pa upiši 3 ispod 9.
- 15 ÷ 3 = 5 (\displaystyle 15\div 3=5), pa napiši 5 ispod 15.
-
Ako je potrebno, dopunite mrežu dodatnim ćelijama. Ponavljajte gornje korake dok količniki ne budu imali zajednički djelitelj.
-
Zaokružite brojeve u prvom stupcu i posljednjem redu mreže. Zatim napišite označene brojeve kao operaciju množenja.
- Na primjer, brojevi 2 i 3 su u prvom stupcu, a brojevi 3 i 5 su u posljednjem redu, pa napišite operaciju množenja ovako: 2 × 3 × 3 × 5 (\displaystyle 2\puta 3\puta 3\puta 5).
-
Pronađite rezultat množenja brojeva. Ovo će izračunati najmanji zajednički višekratnik od dva data broja.
- Na primjer, 2 × 3 × 3 × 5 = 90 (\displaystyle 2\puta 3\puta 3\puts 5=90). Dakle, najmanji zajednički višekratnik 18 i 30 je 90.
Euklidov algoritam
-
Zapamtite terminologiju povezanu s operacijom podjele. Dividenda je broj koji se dijeli. Delitelj je broj kojim se dijeli. Kvocijent je rezultat dijeljenja dva broja. Ostatak je broj koji ostaje kada se podijele dva broja.
- Na primjer, u izrazu 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) odmor. 3:
15 je djeljivo
6 je djelitelj
2 je privatno
3 je ostatak.
- Na primjer, u izrazu 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) odmor. 3:
Pogledaj ove brojke. Ovdje opisani metod najbolje je koristiti kada su data dva broja, svaki manji od 10. Ako je dat veliki brojevi, koristite drugu metodu.
Nastavimo raspravu o najmanjem zajedničkom višekratniku koju smo započeli u LCM-u - Najmanji zajednički višekratnik, definicija, primjeri. U ovoj temi ćemo pogledati načine kako pronaći LCM za tri ili više broja, analizirat ćemo pitanje kako pronaći LCM negativnog broja.
Yandex.RTB R-A-339285-1
Izračunavanje najmanjeg zajedničkog višekratnika (LCM) kroz gcd
Već smo uspostavili odnos između najmanjeg zajedničkog višekratnika i najvećeg zajedničkog djelitelja. Sada ćemo naučiti kako definirati LCM kroz GCD. Prvo, hajde da shvatimo kako to učiniti za pozitivni brojevi.
Definicija 1
Najmanji zajednički višekratnik možete pronaći kroz najveći zajednički djelitelj koristeći formulu LCM (a, b) \u003d a b: GCD (a, b) .
Primjer 1
Potrebno je pronaći LCM brojeva 126 i 70.
Rješenje
Uzmimo a = 126 , b = 70 . Zamijenite vrijednosti u formuli za izračunavanje najmanjeg zajedničkog višekratnika kroz najveći zajednički djelitelj LCM (a, b) = a · b: GCD (a, b) .
Pronalazi GCD brojeva 70 i 126. Za ovo nam je potreban Euklid algoritam: 126 = 70 1 + 56 , 70 = 56 1 + 14 , 56 = 14 4 , dakle gcd (126 , 70) = 14 .
Izračunajmo LCM: LCM (126, 70) = 126 70: GCD (126, 70) = 126 70: 14 = 630.
odgovor: LCM (126, 70) = 630.
Primjer 2
Pronađite nok brojeva 68 i 34.
Rješenje
GCD in ovaj slučaj Pronaći ga je lako, jer je 68 deljivo sa 34. Izračunajte najmanji zajednički višekratnik koristeći formulu: LCM (68, 34) = 68 34: GCD (68, 34) = 68 34: 34 = 68.
odgovor: LCM(68, 34) = 68.
U ovom primjeru koristili smo pravilo za pronalaženje najmanjeg zajedničkog višekratnika pozitivnih cijelih brojeva a i b: ako je prvi broj djeljiv drugim, tada će LCM ovih brojeva biti jednak prvom broju.
Pronalaženje LCM-a razlaganjem brojeva u proste faktore
Pogledajmo sada način da pronađemo LCM, koji se zasniva na dekompoziciji brojeva na proste faktore.
Definicija 2
Da bismo pronašli najmanji zajednički višekratnik, moramo izvršiti nekoliko jednostavnih koraka:
- sastaviti proizvod svih primarni faktori brojevi za koje trebamo pronaći LCM;
- iz njihovih dobijenih proizvoda isključujemo sve primarne faktore;
- proizvod koji se dobije nakon eliminacije zajedničkih prostih faktora biće jednak LCM datih brojeva.
Ovaj način pronalaženja najmanjeg zajedničkog višekratnika zasniva se na jednakosti LCM (a, b) = a b: GCD (a, b) . Ako pogledate formulu, bit će vam jasno: proizvod brojeva a i b jednak je proizvodu svih faktora koji su uključeni u proširenje ova dva broja. U ovom slučaju, GCD dva broja jednak je proizvodu svi prosti faktori koji su istovremeno prisutni u faktorizaciji data dva broja.
Primjer 3
Imamo dva broja 75 i 210. Možemo ih izdvojiti ovako: 75 = 3 5 5 I 210 = 2 3 5 7. Ako napravite proizvod svih faktora dva originalna broja, dobijete: 2 3 3 5 5 5 7.
Ako izuzmemo faktore 3 i 5 zajedničke za oba broja, dobićemo proizvod sledeće vrste: 2 3 5 5 7 = 1050. Ovaj proizvod će biti naš LCM za brojeve 75 i 210.
Primjer 4
Pronađite LCM brojeva 441 I 700 , razlažući oba broja u proste faktore.
Rješenje
Nađimo sve proste faktore brojeva datih u uslovu:
441 147 49 7 1 3 3 7 7
700 350 175 35 7 1 2 2 5 5 7
Dobijamo dva lanca brojeva: 441 = 3 3 7 7 i 700 = 2 2 5 5 7 .
Proizvod svih faktora koji su učestvovali u ekspanziji ovih brojeva će izgledati ovako: 2 2 3 3 5 5 7 7 7. Hajde da pronađemo zajedničke faktore. Ovaj broj je 7. Isključimo to iz zajednički proizvod: 2 2 3 3 5 5 7 7. Ispostavilo se da je NOC (441 , 700) = 2 2 3 3 5 5 7 7 = 44 100.
odgovor: LCM (441 , 700) = 44 100 .
Hajde da damo još jednu formulaciju metode za pronalaženje LCM dekomponovanjem brojeva na proste faktore.
Definicija 3
Prethodno smo isključili iz ukupnog broja faktora koji su zajednički za oba broja. Sada ćemo to učiniti drugačije:
- Razložimo oba broja na proste faktore:
- dodaj proizvodu prostih faktora prvog broja faktore koji nedostaju drugog broja;
- dobijamo proizvod, koji će biti željeni LCM od dva broja.
Primjer 5
Vratimo se na brojeve 75 i 210 , za koje smo već tražili LCM u jednom od prethodnih primjera. Podijelimo ih na jednostavne faktore: 75 = 3 5 5 I 210 = 2 3 5 7. Na proizvod faktora 3, 5 i 5 broj 75 dodaj faktore koji nedostaju 2 I 7 brojevi 210 . Dobijamo: 2 3 5 5 7 . Ovo je LCM brojeva 75 i 210.
Primjer 6
Potrebno je izračunati LCM brojeva 84 i 648.
Rješenje
Hajde da dekomponujemo brojeve iz uslova na proste faktore: 84 = 2 2 3 7 I 648 = 2 2 2 3 3 3 3. Dodajte proizvodu faktora 2 , 2 , 3 i 7
brojevi 84 nedostajući faktori 2 , 3 , 3 i
3
brojevi 648 . Dobijamo proizvod 2 2 2 3 3 3 3 7 = 4536 . Ovo je najmanji zajednički višekratnik 84 i 648.
odgovor: LCM (84, 648) = 4536.
Pronalaženje LCM od tri ili više brojeva
Bez obzira s kojim brojevima imamo posla, algoritam naših akcija će uvijek biti isti: stalno ćemo pronaći LCM dva broja. Za ovaj slučaj postoji teorema.
Teorema 1
Pretpostavimo da imamo cijele brojeve a 1 , a 2 , … , a k. NOC m k ovih brojeva nalazi se u sekvencijalnom proračunu m 2 = LCM (a 1 , a 2) , m 3 = LCM (m 2 , a 3) , … , m k = LCM (m k − 1 , a k) .
Pogledajmo sada kako se teorema može primijeniti na specifične probleme.
Primjer 7
Morate izračunati najmanji zajednički višekratnik od četiri broja 140 , 9 , 54 i 250 .
Rješenje
Hajde da uvedemo notaciju: a 1 = 140, a 2 = 9, a 3 = 54, a 4 = 250.
Počnimo s izračunavanjem m 2 = LCM (a 1 , a 2) = LCM (140 , 9) . Koristimo Euklidov algoritam da izračunamo GCD brojeva 140 i 9: 140 = 9 15 + 5 , 9 = 5 1 + 4 , 5 = 4 1 + 1 , 4 = 1 4 . Dobijamo: GCD (140, 9) = 1, LCM (140, 9) = 140 9: GCD (140, 9) = 140 9: 1 = 1260. Dakle, m 2 = 1 260 .
Sada izračunajmo prema istom algoritmu m 3 = LCM (m 2 , a 3) = LCM (1 260 , 54) . U toku proračuna dobijamo m 3 = 3 780.
Ostaje nam da izračunamo m 4 = LCM (m 3, a 4) = LCM (3 780, 250) . Postupamo po istom algoritmu. Dobijamo m 4 \u003d 94 500.
LCM od četiri broja iz primjera uvjeta je 94500.
odgovor: LCM (140, 9, 54, 250) = 94.500.
Kao što vidite, proračuni su jednostavni, ali prilično naporni. Da uštedite vrijeme, možete ići drugim putem.
Definicija 4
Nudimo vam sljedeći algoritam akcija:
- rastaviti sve brojeve na proste faktore;
- proizvodu faktora prvog broja dodajte faktore koji nedostaju iz proizvoda drugog broja;
- dodati faktore trećeg broja koji nedostaju proizvodu dobijenom u prethodnoj fazi, itd.;
- rezultirajući proizvod će biti najmanji zajednički višekratnik svih brojeva iz uvjeta.
Primjer 8
Potrebno je pronaći LCM od pet brojeva 84 , 6 , 48 , 7 , 143 .
Rješenje
Razložimo svih pet brojeva na proste faktore: 84 = 2 2 3 7 , 6 = 2 3 , 48 = 2 2 2 2 3 , 7 , 143 = 11 13 . Prosti brojevi, a to je broj 7, ne mogu se rastaviti u proste faktore. Takvi brojevi se poklapaju sa njihovom dekompozicijom na proste faktore.
Sada uzmimo proizvod prostih faktora 2, 2, 3 i 7 broja 84 i dodajmo im faktore koji nedostaju drugog broja. Rasporedili smo broj 6 na 2 i 3. Ovi faktori su već u proizvodu prvog broja. Stoga ih izostavljamo.
Nastavljamo sa sabiranjem množitelja koji nedostaju. Okrećemo se broju 48, od proizvoda prostih faktora od kojih uzimamo 2 i 2. Zatim dodajemo jednostavan faktor 7 od četvrtog broja i faktore 11 i 13 od petog. Dobijamo: 2 2 2 2 3 7 11 13 = 48,048. Ovo je najmanji zajednički višekratnik od pet originalnih brojeva.
odgovor: LCM (84, 6, 48, 7, 143) = 48.048.
Pronalaženje najmanjeg zajedničkog višestrukog negativnih brojeva
Da pronađemo najmanji zajednički višekratnik negativni brojevi, ovi brojevi se prvo moraju zamijeniti brojevima sa suprotan znak, a zatim izvršite proračune prema gore navedenim algoritmima.
Primjer 9
LCM(54, −34) = LCM(54, 34) i LCM(−622,−46, −54,−888) = LCM(622, 46, 54, 888) .
Takve radnje su dozvoljene zbog činjenice da ako se to prihvati a I − a- suprotni brojevi
zatim skup višekratnika a poklapa se sa skupom višekratnika broja − a.
Primjer 10
Potrebno je izračunati LCM negativnih brojeva − 145 I − 45 .
Rješenje
Hajde da promenimo brojeve − 145 I − 45 na njihove suprotne brojeve 145 I 45 . Sada, koristeći algoritam, izračunavamo LCM (145 , 45) = 145 45: GCD (145 , 45) = 145 45: 5 = 1 305 , nakon što smo prethodno odredili GCD koristeći Euklid algoritam.
Dobijamo da je LCM brojeva − 145 i − 45 jednaki 1 305 .
odgovor: LCM (− 145 , − 45) = 1 305 .
Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter
Definicija. Naziva se najveći prirodni broj kojim su brojevi a i b djeljivi bez ostatka najveći zajednički djelitelj (gcd) ovi brojevi.
Nađimo najveći zajednički djelitelj brojeva 24 i 35.
Delitelji 24 će biti brojevi 1, 2, 3, 4, 6, 8, 12, 24, a djelitelji 35 će biti brojevi 1, 5, 7, 35.
Vidimo da brojevi 24 i 35 imaju samo jedan zajednički djelitelj - broj 1. Takvi brojevi se nazivaju coprime.
Definicija. Prirodni brojevi se nazivaju coprime ako je njihov najveći zajednički djelitelj (gcd) 1.
Najveći zajednički djelitelj (GCD) može se naći bez ispisivanja svih djelitelja datih brojeva.
Rastavljajući na faktore brojeve 48 i 36, dobijamo:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Iz faktora uključenih u proširenje prvog od ovih brojeva brišemo one koji nisu uključeni u proširenje drugog broja (tj. dvije dvojke).
Ostaju faktori 2 * 2 * 3. Njihov proizvod je 12. Ovaj broj je najveći zajednički djelitelj brojeva 48 i 36. Pronađen je i najveći zajednički djelitelj tri ili više brojeva.
Naći najveći zajednički djelitelj
2) iz faktora uključenih u proširenje jednog od ovih brojeva precrtati one koji nisu uključeni u proširenje drugih brojeva;
3) naći proizvod preostalih faktora.
Ako su svi dati brojevi djeljivi sa jednim od njih, onda je i ovaj broj najveći zajednički djelitelj date brojeve.
Na primjer, najveći zajednički djelitelj 15, 45, 75 i 180 je 15, jer dijeli sve ostale brojeve: 45, 75 i 180.
Najmanji zajednički višekratnik (LCM)
Definicija. Najmanji zajednički višekratnik (LCM) prirodni brojevi a i b su najmanji prirodni broj koji je višekratnik i a i b. Najmanji zajednički višekratnik (LCM) brojeva 75 i 60 može se pronaći bez pisanja višekratnika ovih brojeva u nizu. Da bismo to učinili, razlažemo 75 i 60 na jednostavne faktore: 75 = 3 * 5 * 5 i 60 = 2 * 2 * 3 * 5.
Zapisujemo faktore uključene u proširenje prvog od ovih brojeva i dodajemo im faktore koji nedostaju 2 i 2 iz proširenja drugog broja (tj. kombinujemo faktore).
Dobijamo pet faktora 2 * 2 * 3 * 5 * 5, čiji je proizvod 300. Ovaj broj je najmanji zajednički višekratnik brojeva 75 i 60.
Također pronađite najmanji zajednički višekratnik tri ili više brojeva.
To pronađite najmanji zajednički višekratnik nekoliko prirodnih brojeva, potrebno je:
1) razložiti ih na proste faktore;
2) ispisati faktore uključene u proširenje jednog od brojeva;
3) dodati im faktore koji nedostaju iz proširenja preostalih brojeva;
4) naći proizvod rezultujućih faktora.
Imajte na umu da ako je jedan od ovih brojeva djeljiv sa svim ostalim brojevima, onda je ovaj broj najmanji zajednički višekratnik ovih brojeva.
Na primjer, najmanji zajednički višekratnik od 12, 15, 20 i 60 bi bio 60, jer je djeljiv sa svim datim brojevima.
Pitagora (VI vek pne) i njegovi učenici proučavali su pitanje deljivosti brojeva. Broj, jednak zbiru sve njegove djelitelje (bez samog broja), nazivali su savršenim brojem. Na primjer, brojevi 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) su savršeni. Sljedeći savršeni brojevi su 496, 8128, 33 550 336. Pitagorejci su poznavali samo prva tri savršena broja. Četvrti - 8128 - postao je poznat u 1. vijeku. n. e. Peti - 33 550 336 - pronađen je u 15. vijeku. Do 1983. već je bilo poznato 27 savršenih brojeva. Ali do sada naučnici ne znaju da li postoje neparni savršeni brojevi, da li postoji najveći savršeni broj.
Interes starih matematičara za proste brojeve je zbog činjenice da je bilo koji broj ili prost ili se može predstaviti kao proizvod primarni brojevi, tj. prosti brojevi su, takoreći, cigle od kojih se grade ostali prirodni brojevi.
Vjerovatno ste primijetili da se prosti brojevi u nizu prirodnih brojeva javljaju neravnomjerno - u nekim dijelovima niza ih ima više, u drugim - manje. Ali što dalje idemo dalje numeričke serije, rjeđi prosti brojevi su. Postavlja se pitanje: postoji li posljednji (najveći) prost broj? Drevni grčki matematičar Euklid (3. vek pre nove ere), u svojoj knjizi „Počeci“, koja je dve hiljade godina bila glavni udžbenik matematike, dokazao je da postoji beskonačno mnogo prostih brojeva, odnosno da iza svakog prostog broja postoji paran broj. veći prost broj.
Za pronalaženje prostih brojeva, drugi grčki matematičar iz istog vremena, Eratosten, smislio je takvu metodu. Zapisao je sve brojeve od 1 do nekog broja, a zatim precrtao jedinicu, koja nije ni prost ni složeni broj, zatim kroz jedan precrtao sve brojeve nakon 2 (brojeve koji su višestruki od 2, tj. 4, 6, 8, itd.). Prvi preostali broj nakon 2 bio je 3. Zatim, nakon dva, svi brojevi iza 3 su precrtani (brojevi koji su višestruki od 3, tj. 6, 9, 12, itd.). na kraju su ostali neprecrtani samo prosti brojevi.
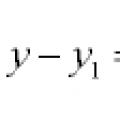 Jednačine linija i krivulja u ravni
Jednačine linija i krivulja u ravni Uopštene homogene jednačine Generalizovane homogene jednačine drugog reda
Uopštene homogene jednačine Generalizovane homogene jednačine drugog reda Hvala zarezu Zbog činjenice da je u njihovoj
Hvala zarezu Zbog činjenice da je u njihovoj