Apstraktne logaritamske nejednakosti. Rješavanje logaritamskih jednadžbi i nejednačina
MBOU srednja škola br. 1 Novobelokatay selo
Radna tema:
"Moja najbolja lekcija"
nastavnik matematike:
Mukhametova Fauzia Karamatovna
Predmet predavao matematiku
2014
Tema lekcije:
"Nestandardni način rješavanja logaritamskih nejednakosti"
razred 11( nivo profila)
Obrazac za lekciju kombinovano
Ciljevi lekcije:
Ovladavanje novim načinom rješavanja logaritamskih nejednačina, te sposobnošću primjene ovu metodu pri rješavanju zadataka C3 (17) USE 2015 iz matematike.
Ciljevi lekcije:
- edukativni:sistematizuju, generalizuju, proširuju vještine i znanja u vezi sa upotrebom metoda za rješavanje logaritamskih nejednačina; Sposobnost primjene znanja u rješavanju USE 2015 zadataka iz matematike.
Obrazovni : formirati vještine samoobrazovanja, samoorganiziranja, sposobnosti analiziranja, poređenja, generalizacije, zaključivanja; Razvoj logičko razmišljanje, pažnja, pamćenje, izgled.
edukativni: odgojiti samostalnost, sposobnost slušanja drugih, sposobnost komuniciranja u grupi. Povećanje interesa za rješavanje problema, formiranje samokontrole i aktivacije mentalna aktivnost tokom izvršavanja zadataka.
Metodološka osnova:
Zdravstveno-štedna tehnologija po sistemu V.F. Bazarny;
Tehnologija višestepenog obrazovanja;
Tehnologija grupnog učenja;
Informaciona tehnologija (pratiti lekciju prezentacijom),
Oblici organizacije aktivnosti učenja : frontalni, grupni, individualni, samostalni.
Oprema: učenika na radnom mestu evaluacijski listovi, kartice sa samostalan rad, prezentacija lekcije, kompjuter, multimedijalni projektor.
Koraci lekcije:
Učiteljica Zdravo momci!
Drago mi je da vas sve vidim na lekciji i nadam se plodnom zajedničkom radu.
2. Motivacioni trenutak: napisano u prezentaciji IKT tehnologija
Neka epigraf naše lekcije budu riječi:
"Učenje može biti samo zabavno...
Da bi se svarilo znanje, potrebno ga je apsorbovati s apetitom. Anatole Franz.
Zato budimo aktivni i pažljivi, jer će nam znanje biti od koristi prilikom polaganja ispita.
3. Faza postavljanja i ciljevi časa:
Danas ćemo u lekciji proučavati rješenje logaritamskih nejednačina nestandardna metoda. S obzirom da je za rješavanje cijele varijante potrebno 235 minuta, za zadatak C3 je potrebno oko 30 minuta, tako da je potrebno pronaći takvo rješenje kako biste potrošili manje vremena. Zadaci preuzeti iz Naknade za korištenje 2015. iz matematike.
4. Faza ažuriranja znanja.
Tehnologija vrednovanja obrazovnog uspjeha.
Na klupama imate evaluacione listove koje učenici popunjavaju tokom časa, a na kraju ih predaju nastavniku. Nastavnik objašnjava kako popuniti list za ocjenjivanje.
Uspjeh zadatka je označen simbolom:
"!" - govorim slobodno
"+" - Mogu odlučiti, ponekad grešim
"-"- još treba raditi
Definicija logaritamskih nejednakosti | Sposobnost rješavanja jednostavnih logaritamskih nejednačina | Sposobnost korištenja svojstava logaritama | Sposobnost korištenja metode dekompozicije | Raditi u parovima | Mogu i sama | ukupno |
4. Prednji rad
Ponavlja se definicija logaritamskih nejednakosti. Poznate metode rješenja i njihov algoritam na konkretnim primjerima.
Učitelju.
Ljudi, pogledajmo u ekran, usmeno odlučimo.
1) Riješite jednačinu
2) Izračunajte
a B C)
Upišite odgovarajući broj u tabelu datu u odgovoru ispod svakog slova.
odgovor:
Faza 5 Učenje novog materijala
Tehnologija učenja problema
Učitelju
Pogledajmo slajd. Moramo riješiti ovu nejednakost. Kako se ova nejednakost može riješiti? Teorija za nastavnika:
Metoda razlaganja
Metoda razlaganja je zamjena složen izraz F(x) na jednostavniji izraz G(x) za koji je nejednakost G(x)^0 ekvivalentna nejednakosti F(x)^0 u domeni F(x).
Postoji nekoliko F izraza i odgovarajuća dekompozicija Gs, gdje su k, g, h, p, q izrazi sa promjenljivom X (h>0; h≠1; f>0, k>0), a je fiksni broj (a>0, a≠1).
Izraz F | G izraz |
|
(a-1)(f-k) (a-1)(f-a) (a-1)(f-1) |
||
(h-1)(f-k) (h-1)(f-h) (h-1)(f-1) |
||
(k≠1, f≠1) | (f-1)(k-1)(h-1)(k-f) |
|
(h-1)(f-k) (h-1)f |
||
(f>0; k>0) | (f-k)h |
|
|f| - |k| | (f-k)(f+k) |
Iz ovih izraza mogu se zaključiti neke posljedice (uzimajući u obzir domen definicije):
0 ⬄ 0
U naznačenim ekvivalentnim prijelazima, simbol ^ zamjenjuje jedan od znakova nejednakosti: >,
Na slajdu je zadatak koji nastavnik razumije.
Razmotrimo primjer rješavanja logaritamske nejednakosti pomoću dvije metode
1. Metoda intervala
O.D.Z.
a) b)
Odgovor: (;
Učitelju
Ova nejednakost se može riješiti na drugi način.
2. Metoda razlaganja
Odgovori
Na primjeru rješavanja ove nejednakosti vidjeli smo da je svrsishodnije koristiti metodu dekompozicije.
Razmotrimo primjenu ove metode na nekoliko nejednakosti
Vježba 1
Odgovor: (-1,5; -1) U (-1; 0) U (0; 3)
Zadatak2
Sažetak lekcije "Rješenje logaritamskih nejednačina." 11. razred
Razvio i vodi učiteljica prve kategorije Shaydulina G.S.
Naš moto je: “Put će savladati onaj ko hoda, a matematiku mislilac.”
Mnogi fizičari se šale da je "Matematika, kraljica nauka, ali sluga fizike!" Isto mogu i hemičari, astronomi, pa čak i muzičari. Zaista, matematika je osnova većine nauka i riječi engleskog filozofa Rogera Bacona iz 16. stoljeća: „Onaj ko ne zna matematiku ne može znati nijednu drugu nauku, pa čak ni otkriti sopstvenog neznanja." trenutno relevantno
Tema naše lekcije je "Logaritmske nejednakosti".
Svrha lekcije:
1) generalizovati znanje o temi
"Logaritamske nejednakosti"
2) razmotriti tipične poteškoće sa kojima se susreću pri rešavanju logaritamskih nejednačina;
3) ojačati praktičnu orijentaciju ove teme za kvalitetnu pripremu za ispit.
Zadaci:
Tutorijali:ponavljanje, generalizacija i sistematizacija gradiva teme, kontrola usvajanja znanja i vještina.
u razvoju:razvoj matematičkog i opšteg pogleda, mišljenja, govora, pažnje i pamćenja.
edukativni:razvijanje interesa za matematiku, aktivnost, komunikacijske vještine, opću kulturu.
Oprema: kompjuter, multimedijalni projektor, platno, kartice sa zadacima, sa logaritamskim formulama.
Struktura lekcije:
Organiziranje vremena.
Ponavljanje gradiva. usmeni rad.
Istorijska referenca.
Radite na materijalu.
Zadaća.
Sažetak lekcije.
logaritamske nejednakosti V KORISTI opcije posvećena matematici zadatak C3 . Svaki učenik treba da nauči rješavanje zadataka C3 sa Jedinstvenog državnog ispita iz matematike ako želi na predstojećem ispitu položiti kao „dobar“ ili „odličan“.
Istorijska referenca.
John Napier posjeduje termin "logaritam", koji je preveo kao "vještački broj". John Napier je Škot. Sa 16 godina odlazi na kontinent, gdje pet godina studira matematiku i druge nauke na raznim univerzitetima u Evropi. Zatim je ozbiljno studirao astronomiju i matematiku. na ideju logaritamski proračuni Napier se vratio 80-ih godine XVI vijeka, ali je svoje tabele objavio tek 1614. godine, nakon 25 godina proračuna. Izašli su pod naslovom "Opis divnih logaritamskih tablica".
Započnimo čas oralnim zagrijavanjem. Spreman?
Rad na tabli.
Tokom usmeni rad sa razredom, dva učenika rješavaju primjere na karticama na tabli.
1. Riješite nejednačinu
2. Riješite nejednačinu
(Učenici koji su završili zadatke na tabli komentarišu svoje odluke, pozivajući se na odgovarajuće teorijski materijal i izvršite prilagođavanja po potrebi.)
1) Navedite pogrešnu jednakost. Koje pravilo treba koristiti za ovo?
a) log 3 27 = 3
b) log 2 0,125 = - 3
a) log 0,5 0,5 = 1
a) log 10000 = 5.
2) Uporedite vrednosti logaritma sa nulom.Koje pravilo treba koristiti za ovo?
A)lg 7
b)log 0,4 3
V)log 6 0,2
e)log ⅓ 0,6
3) Želim teponuditi da igramo morsku bitku. Ja imenujem slovo reda i broj kolone, a vi imenujete odgovor i tražite odgovarajuće slovo u tabeli.
4) Koje od navedenih logaritamskih funkcija rastu, a koje opadaju. Od čega zavisi?
5) Koja je domena logaritamske funkcije? Pronađite opseg funkcije:
Razgovarajte o rješenju na tabli.
Kako se rješavaju logaritamske nejednakosti?
Šta je osnova za rješavanje logaritamskih nejednačina?
Na kakve nejednakosti to izgleda?
(Rješenje logaritamskih nejednačina zasniva se na monotonosti logaritamske funkcije, uzimajući u obzir domen logaritamske funkcije i zajednička svojstva nejednakosti.)
Algoritam za rješavanje logaritamskih nejednačina:
A) Pronađite oblast definicije nejednakosti (podblogaritamski izraz Iznad nule).
B) Predstavite (ako je moguće) lijevi i desni dio nejednačine kao logaritme u istoj osnovi.
B) Odredite da li se vrijednost povećava ili smanjuje. logaritamska funkcija: ako je t>1, onda raste; ako je 01, onda se smanjuje.
D) Idi na više jednostavna nejednakost(sublogaritamski izrazi), s obzirom na to da će predznak nejednakosti biti sačuvan ako se funkcija povećava, a promijenit će se ako se smanjuje.
Provjera d.z.
1. log 8 (5x-10)< log 8 (14.).
2. log 3 (x+2) +log 3 x =< 1.
3. log 0,5 (3x+1)< log 0,5 (2-x)
Učenje na tuđim greškama!!!
Ko će prvi pronaći grešku.
1.Nađi grešku u rješavanju nejednakosti:
A)log 8 (5x-10)< log 8 (14-e),
5 x-10 < 14- x,
6 x < 24,
x < 4.
Odgovor: x € (-∞; 4).
Greška: obim nejednakosti nije uzet u obzir.
Komentirajte odluku
log 8 (5x-10)< log 8 (14's)
![]()
2<
x <4.
2<
x <4.
Odgovor: x € (2; 4).
2.Nađi grešku u rješavanju nejednakosti:
![]()
![]()
![]()
Greška: domen definicije izvorne nejednakosti nije uzet u obzir.Prava odluka
![]()
![]()
Odgovor: x .
3.Nađi grešku u rješavanju nejednakosti:
log 0,5
(3x+1)<
log 0,5
(2-x)

Odgovor: x €
Greška: osnova logaritma nije uzeta u obzir.
Prava odluka:
log 0,5
(3x+1)<
log 0,5
(2-x)

Odgovor: x €
Analizirajući opcije prijemnih ispita iz matematike, možete vidjeti da se iz teorije logaritama na ispitima često javljaju logaritamske nejednakosti koje sadrže varijablu ispod logaritma i u osnovi logaritma.
Pronađite grešku u rješavanju nejednakosti:
4
.


Kako drugačije možete riješiti nejednakost #4?
Ko je riješio na drugačiji način?
Dakle, ljudi, postoji mnogo zamki pri rješavanju logaritamskih nejednačina.
Na šta treba obratiti posebnu pažnju pri rješavanju logaritamskih nejednačina? Kako misliš?
Dakle, šta treba da odlučitelogaritamske jednačine i nejednačine?
prvo,pažnju. Nemojte praviti greške u svojim konverzijama. Pazite da svaka vaša radnja ne širi ili sužava područje dozvoljene vrijednosti nejednakost, odnosno nije dovela ni do gubitka ni do sticanja stranih rješenja.
drugo,sposobnost logičkog razmišljanja. Sastavljači USE iz matematike sa zadacima C3 testiraju sposobnost učenika da operišu konceptima kao što su sistem nejednačina (presek skupova), skup nejednačina (agregacija skupova), da biraju rešenja za nejednakost, vodeći se njegov raspon prihvatljivih vrijednosti.
Treće, jasnoznanjesvojstva svih elementarnih funkcija (potencijalnih, racionalnih, eksponencijalnih, logaritamskih, trigonometrijskih) izučavanih u školskom predmetu matematike irazumijevanjenjihovo značenje.
PAŽNJA!
1. ODZ izvorne nejednakosti.
2. Osnova logaritma.
Riješite jednačinu:
Rješenje. Raspon dozvoljenih vrijednosti jednadžbe određen je sistemom nejednačina:

Razmotrimo graf logaritamske funkcije i graf direktne proporcionalnosti
Imajte na umu da funkcija raste preko domene.Bez grafa, ovo se može odrediti iz baze logaritma. Jer gdje je x>0, ako je baza logaritma veća od nule, ali manja od jedan, tada je funkcija opadajuća, ako je baza logaritma veća od jedan, tada se funkcija povećava.
Važno je napomenuti da logaritamska funkcija uzima pozitivne vrijednosti na skupu brojeva većih od jedan, pišemo ovu izjavu koristeći simbole f(x)atx
Direktna proporcionalnost y=x u ovom slučaju, na intervalu od jedan do plus beskonačnost, također uzima pozitivne vrijednosti veće od jedan. Je li ovo slučajnost ili obrazac? O svemu po redu.
Nejednakosti oblika nazivaju se logaritamske, gdje je a pozitivan broj različit od 1 i >0,)>0
Pretvorimo nejednakost u oblik. Kada se članovi prenesu iz jednog dijela nejednakosti u drugi, predznak člana se mijenja u suprotan. Po svojstvu logaritma, razlika logaritama sa istu bazu možemo zamijeniti logaritam količnika, tako da naša nejednakost ima oblik.
Označite izraz t, Onda nejednakost će poprimiti oblik.
Razmotrimo ovu nejednakost u odnosu na bazu A, veći od jedan, a u odnosu na bazu a, veći od nule i manji od jedan.
Ako je osnova logaritma A, veći od jedan, tada funkcija raste u domeni definicije i uzima pozitivne vrijednosti za t veće od jedan. Vratimo se zamjeni. Dakle, razlomak mora biti veći od jedan. To znači da je f(x)>g(x).
Ako je osnova logaritma veća od nule i manja od jedan, tada funkcija opada u domenu definicije i poprima pozitivne vrijednosti kada je t veće od nule i manje od jedan. Pod obrnutom zamjenom, nejednakost je ekvivalentna nejednakosti i vrijedi za f(x) da zaključimo: Ako)>0 i za a>1 logaritamska nejednakost je ekvivalentna nejednakosti istog značenja)>), i u 0 Ekvivalentno nejednakosti suprotnog značenja)<) Razmotrimo primjere rješavanja logaritamskih nejednačina. Riješite nejednačinu: Nejednakosti >0 i raspon važećih vrijednosti varijable za datu logaritamsku nejednakost. Osnova logaritma je pet i veća je od jedan, pa je originalna nejednakost ekvivalentna nejednakosti. Rezultirajući sistem nejednačina rješavamo odvajanjem varijable za ovo. U prvoj nejednakosti pomičemo četiri na desnu stranu nejednakosti mijenjajući znak minus u plus. Primit ćemo. U drugoj nejednačini jedinicu pomjerimo na desnu stranu i zapišemo je kao minus jedan. Dobijamo nejednakost U trećoj nejednakosti pomjerimo minus četiri na desnu stranu, zapišemo to kao plus četiri i X pomaknite se na lijevu stranu i upišite kao minus x. Dobijamo nejednakost. U njemu možete donijeti slične članove na lijevoj i desnoj strani nejednakosti. Dobijamo nejednakost. U prvoj nejednakosti dijelimo lijevi i desni dio nejednakosti sa 2. Dobijamo nejednakost. Sistem dobijen tokom rešavanja ima predznak jednog smera, u takvim slučajevima je očigledno da skup brojeva veći od pet zadovoljava ovaj sistem. Lako je vidjeti da pet također zadovoljava sistem nejednakosti. U suprotnom, možete izgraditi geometrijski model ovog sistema i vidjeti rješenje. Zabilježite na koordinatnoj liniji brojeve minus jedan, dva i pet. Štoviše, brojevi -1 i 2 odgovarat će svijetloj tački, a broj pet - tamnoj tački. Primijenimo "šrafiranje" desno od 2 za prvu nejednakost, desno od 1 za drugu nejednakost i desno od pet za treću nejednakost. Presjek šrafura označava skup brojeva većih i jednakih pet. Odgovor zapisujemo kao izraz Primjer 2. Riješite nejednačinu Hajde da napravimo sistem nejednakosti. Nejednakosti >0 i >0 definiraju raspon prihvatljivih vrijednosti nejednakosti. Osnova logaritma je 0,3, veća je od nule, ali manja od jedan, što znači da je logaritamska nejednakost ekvivalentna nejednakosti suprotnog predznaka: Rezultirajući sistem je teško paralelno rješavati nejednakosti. Riješit ćemo svaki od njih posebno i razmotriti opće rješenje na geometrijskom modelu. Nejednakost je kvadratna i rješava se svojstvima kvadratne funkcije čiji je graf parabola s granama prema gore. Pronalazimo nule ove funkcije, za to izjednačavamo njenu desnu stranu sa nulom i rezultujuću jednačinu rješavamo faktorizacijom. Da bismo to učinili, izvlačimo zajednički faktor x iz zagrada, u zagradama ostaje od prvog člana - šest, od drugog člana - minus x. Proizvod je jednak nuli kada je jedan od faktora jednak nuli, dok drugi ne gubi smisao. Dakle, prvi faktor x je nula, ili drugi faktor šest minus x je nula. Tada su korijeni jednadžbe nula i šest. Označavamo ih na koordinatnoj liniji u obliku svjetlosnih tačaka, pošto je kvadratna nejednakost koju treba riješiti stroga i crtamo parabolu sa granama nadole, prolazeći kroz te tačke. Kvadratna funkcija uzima pozitivne vrijednosti u intervalu od nule do šest, što znači da je rješenje nejednakosti skup brojeva x Nejednakost je linearna. Sadrži negativne članove, zbog pogodnosti množimo oba dijela nejednakosti sa minus jedan. U ovom slučaju, znak nejednakosti će biti obrnut. Dobijamo nejednakost. Pomjerimo osam na desnu stranu nejednačine i zapišemo je kao minus osam. Dakle, rješenje nejednakosti je skup brojeva od minus beskonačno do minus osam. Rješenje nejednačine zapisujemo u obliku izraza x.
Nejednakost se svodi na kvadratnu nejednakost, za to prenosimo minus osam i minus x na lijevu stranu nejednakosti. Dobijamo nejednakost i donosimo slične 6x i x, Dobijamo 7x, jednačina poprima oblik. Rješava se svojstvima kvadratne funkcije čiji je graf parabola s granama nadolje. Pronađite nule funkcije.0 na =0 i rezultujuću kvadratnu jednačinu riješite kroz diskriminantnu formulu Pošto je koeficijent b jednako minus sedam, koeficijent A jednako minus jedan, i With je 8, tada je diskriminanta jednadžbe 81. Prvi korijen nalazimo po formuli, to je -1, drugi korijen je 8. Dobivene vrijednosti označavamo na koordinatnoj liniji tamnim tačkama, pa se razmatrana kvadratna nejednakost odnosi na nestroge nejednakosti. Nacrtajte parabolu sa granama nadole na koordinatnoj liniji. Kvadratna funkcija uzima vrijednosti manje i jednake nuli na skupu brojeva od minus beskonačno do uključujući i od 8 do plus beskonačno uključujući 8. Rješenje ove nejednakosti zapisujemo kao izraz ] Dakle, sve tri nejednačine su riješene, njihova rješenja bilježimo na jednoj koordinatnoj liniji. Ne postoji vrijednost varijable koja istovremeno zadovoljava sve tri nejednakosti, što znači da izvorna logaritamska nejednakost nema rješenja. Odgovor: Ne postoje rješenja. Ova činjenica se mogla uočiti nakon rješavanja linearne nejednačine, budući da su rješenja prve kvadratne nejednakosti pozitivni brojevi od jedan do šest, a rješenja druge nejednačine negativni brojevi, onda za ove dvije nejednakosti ne postoje opšta rješenja i originalna logaritamska nejednakost nema rješenja. Logaritmi imaju zanimljiva svojstva koja pojednostavljuju proračune i izraze, prisjetimo se nekih od njih Primjer 3. Riješite nejednačinu: Nejednakost treba pretvoriti u oblik. Da bismo to učinili, jedinicu zapisujemo kao logaritam od 2 prema bazi dva. A na lijevoj strani nejednakosti zamjenjujemo zbir logaritama svojstvom izrazom koji mu je identično jednak - logaritmom proizvoda. Dobijamo nejednakost oblika Hajde da napravimo sistem nejednakosti. Nejednakosti koje definiraju raspon prihvatljivih vrijednosti nejednakosti određene su izvornom nejednakošću, pa će >0 i >0 biti prve dvije nejednakosti sistema. Pošto logaritam ima bazu 2, veći je od jedan, onda je nejednakost U prvoj nejednakosti minus tri prenosimo na desnu stranu, dobijamo nejednačinu x> 3, u drugoj - minus dva prenosimo na desnu stranu, dobijamo nejednačinu x > 2. U trećem, širimo zagrade na lijevoj strani nejednakosti množenjem svakog člana prvog polinoma sa svakim članom drugog polinoma. Dobijamo nejednakost. Treću nejednačinu rješavamo posebno: dvije prenesemo na lijevu stranu nejednačine i zapišemo je sa minusom. Pojednostavimo rezultirajući moral na formu. Zbir koeficijenata ove jednadžbe jednak je nuli, tada je, prema svojstvu koeficijenata, prvi korijen jednak jedan, a drugi je jednak količniku od c na A i jednaka je u ovom slučaju 4. Ove jednačine se također mogu riješiti pomoću diskriminantne formule, korijeni ne zavise od metode rješenja. Ove korijene označavamo na koordinatnoj liniji u obliku tamnih tačaka, kroz njih crtamo parabolu s granama prema gore. Nejednakost radi na skupu brojeva od 1 do 4 uključujući 1 i 4. Rješenje prve i druge nejednačine označavamo na jednoj koordinatnoj liniji, za to pravimo šrafiranje desno od tri za prvu nejednačinu i desno od dva za drugu nejednačinu i šrafiranje od 1 do 4 za drugu nejednakost. Tri nejednakosti vrijede istovremeno samo na skupu brojeva od 3 do 4, uključujući i 4. To znači da će to biti rješenje izvorne logaritamske nejednakosti. Zaključak: Prilikom rješavanja logaritamskih nejednačina Ako je a>1, onda se ide na rješenje sistema nejednačina koje određuju raspon dozvoljenih vrijednosti nejednakosti, i nejednakosti podlogaritamskih izraza istog znaka. Ako je 0 slajd 1) Svrha lekcije: Struktura lekcije: 1. Organizacija početka časa. TOKOM NASTAVE 1. Organizacioni momenat 2. Provjera domaćeg zadatka(Aplikacija
, slajd 2) 3. Ponavljanje(Aplikacija
, slajd 4) 4. Ažuriranje vodećih znanja i metoda djelovanja – U jednoj od prethodnih lekcija imali smo situaciju u kojoj nismo mogli riješiti eksponencijalnu jednačinu, što je dovelo do uvođenja novog matematičkog koncepta. Uveli smo definiciju logaritma, proučavali svojstva i razmatrali graf logaritamske funkcije. U prethodnim lekcijama smo rješavali logaritamske jednadžbe koristeći teoremu i svojstva logaritama. Primjenom svojstava logaritamske funkcije uspjeli smo riješiti najjednostavnije nejednačine. Ali opis svojstava svijeta oko nas nije ograničen na najjednostavnije nejednakosti. Šta učiniti u slučaju kada dobijemo nejednakosti koje se ne mogu nositi sa raspoloživom količinom znanja? Odgovor na ovo pitanje dobićemo u ovoj i narednim lekcijama. 5. Organizacija usvajanja novih znanja i metoda djelovanja (Aplikacija
, slajdovi 5-12). 1) Tema, svrha lekcije. 2) (Aplikacija
, slajd 5) Definicija logaritamske nejednakosti: logaritamske nejednakosti su nejednakosti oblika i nejednakosti koje se svode na ovaj oblik. 3) (Aplikacija
, slajd 6) Da bismo riješili nejednakost, provodimo sljedeće rezonovanje: Dobijamo 2 slučaja: a> 1 i 0<a < 1. (Aplikacija
, slajd 7) Dobijamo teoremu: ako f(x) > 0 i g(x)
> 0),
zatim log logaritamske nejednakosti a f(x) > log a g(x) je ekvivalentna nejednakosti istog značenja f(x)
> g(x) at a > 1 4) U praksi, prilikom rješavanja nejednačina, one prelaze na ekvivalentan sistem nejednačina ( Aplikacija
, slajd 8): 5) Primjer 1 ( Aplikacija
, slajd 9) Iz treće nejednakosti proizlazi da je prva nejednakost suvišna. Iz treće nejednakosti proizlazi da je druga nejednakost suvišna. Primjer 2 ( Aplikacija
, slajd 10) Ako vrijedi druga nejednakost, vrijedi i prva (ako je A >
16, onda sve više A > 0). Dakle 16 + 4 x – x 2 >
16, x 2 – 4 <
0, x(x –
4) <
0, 

Ekvivalentno nejednakosti (x-3)(x-2)2.
2. Provjera domaćeg zadatka.
3. Ponavljanje.
4. Aktuelizacija vodećih znanja i metoda djelovanja.
5. Organizacija usvajanja novih znanja i metoda djelovanja.
6. Primarni test razumijevanja, razumijevanja i konsolidacije.
7. Domaći.
8. Refleksija. Sažetak lekcije.

Ako a>1, zatim log nejednakosti a t> 0 se odvija ako i samo ako je t > 1, dakle , tj. f(x)
> g(x)
(imajte na umu da g(x)
> 0).
Ako je 0<a < 1, то неравенство loga t> 0, odvija se ako i samo ako je 0<t < 1, значит ,
т.е. f(x) < g(x) (uzmite to u obzir g(x) > 0 i f(x) > 0).
log logaritamske nejednakosti a f(x) > log a g(x) je ekvivalentna suprotnoj nejednakosti f(x)
< g(x),
ako je 0<a < 1.


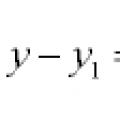 Jednačine linija i krivulja u ravni
Jednačine linija i krivulja u ravni Uopštene homogene jednačine Generalizovane homogene jednačine drugog reda
Uopštene homogene jednačine Generalizovane homogene jednačine drugog reda Hvala zarezu Zbog činjenice da je u njihovoj
Hvala zarezu Zbog činjenice da je u njihovoj