Λειτουργεί με λύσεις μονάδων. Μετασχηματισμοί γραφημάτων με ενότητα
Αντίγραφο
1 Περιφερειακό επιστημονικό και πρακτικό συνέδριο εκπαιδευτικών και ερευνητικών εργασιών μαθητών στις τάξεις 6-11 «Εφαρμοσμένα και θεμελιώδη ζητήματα των μαθηματικών» Μεθοδολογικές πτυχές της μελέτης των μαθηματικών Κατασκευή γραφημάτων συναρτήσεων που περιέχουν την ενότητα Gabova Angela Yuryevna, 10η τάξη, MOBU «Γυμνάσιο 3 ” Kudymkar, Pikuleva Nadezhda Ivanovna, καθηγήτρια μαθηματικών του δημοτικού εκπαιδευτικού ιδρύματος “Gymnasium 3”, Kudymkar Perm, 2016
2 Περιεχόμενα: Εισαγωγή...3 σελίδες I. Κύριο μέρος...6 σελίδες 1.1Ιστορικό υπόβαθρο..6 σελίδες 2.Βασικοί ορισμοί και ιδιότητες συναρτήσεων σελίδα 2.1 Τετραγωνική συνάρτηση..7 σελίδες 2.2 Γραμμική συνάρτηση.. .8 σελ. 2.3 Κλασματική-ορθολογική συνάρτηση 8 σελ. 3. Αλγόριθμοι κατασκευής γραφημάτων με συνάρτηση 9 σελ. 3.2 Προσδιορισμός γραφημάτων που περιέχει στον τύπο «φωλιασμένες ενότητες».10 σελ. 3.4 Αλγόριθμος κατασκευής γραφημάτων της μορφής y = a 1 x x 1 + a 2 x a n x x n + ax + b... 3.5 Αλγόριθμος κατασκευής γραφικών παραστάσεων συνάρτηση με συντελεστή.14 σελ. 3.6 Αλγόριθμος σχεδίασης κλασματικής ορθολογικής συνάρτησης με συντελεστή. 15 σελ. 4. Μεταβολές στη γραφική παράσταση μιας τετραγωνικής συνάρτησης ανάλογα με τη θέση του πρόσημου της απόλυτης τιμής..17π. II. Συμπέρασμα...26 σελ. III. Κατάλογος αναφορών και πηγών...27 σελ. IV. Παράρτημα....28σελ. 2
3 Εισαγωγή Η κατασκευή γραφημάτων συναρτήσεων είναι ένα από τα πιο ενδιαφέροντα θέματα στα σχολικά μαθηματικά. Ο μεγαλύτερος μαθηματικός της εποχής μας, ο Israel Moiseevich Gelfand, έγραψε: «Η διαδικασία κατασκευής γραφημάτων είναι ένας τρόπος μετατροπής τύπων και περιγραφών σε γεωμετρικές εικόνες. Αυτή η γραφική παράσταση είναι ένα μέσο για να δείτε τύπους και συναρτήσεις και να δείτε πώς αλλάζουν αυτές οι συναρτήσεις. Για παράδειγμα, αν γράφεται y =x 2, τότε βλέπετε αμέσως μια παραβολή. Αν y = x 2-4, βλέπετε μια παραβολή χαμηλωμένη κατά τέσσερις μονάδες. αν y = -(x 2 4), τότε βλέπετε την προηγούμενη παραβολή γυρισμένη προς τα κάτω. Αυτή η ικανότητα να βλέπουμε αμέσως έναν τύπο και τη γεωμετρική του ερμηνεία είναι σημαντική όχι μόνο για τη μελέτη των μαθηματικών, αλλά και για άλλα μαθήματα. Είναι μια δεξιότητα που σας μένει για μια ζωή, όπως το ποδήλατο, η πληκτρολόγηση ή η οδήγηση αυτοκινήτου». Τα βασικά για την επίλυση εξισώσεων με ενότητες αποκτήθηκαν στις τάξεις 6ης-7ης τάξης. Επέλεξα το συγκεκριμένο θέμα γιατί πιστεύω ότι απαιτεί βαθύτερη και πιο ενδελεχή έρευνα. Θέλω να αποκτήσω περισσότερες γνώσεις για το μέτρο των αριθμών, διαφορετικούς τρόπους κατασκευής γραφημάτων που περιέχουν το πρόσημο της απόλυτης τιμής. Όταν το πρόσημο του συντελεστή περιλαμβάνεται σε «τυποποιημένες» εξισώσεις γραμμών, παραβολών και υπερβολών, τα γραφήματα τους γίνονται ασυνήθιστα και ακόμη και όμορφα. Για να μάθετε πώς να δημιουργείτε τέτοια γραφήματα, πρέπει να μάθετε τις τεχνικές κατασκευής βασικών σχημάτων, καθώς και να γνωρίζετε και να κατανοείτε σταθερά τον ορισμό του συντελεστή μέτρησης ενός αριθμού. Στο μάθημα των σχολικών μαθηματικών, τα γραφήματα με την ενότητα δεν συζητούνται αρκετά σε βάθος, γι' αυτό ήθελα να επεκτείνω τις γνώσεις μου σε αυτό το θέμα και να πραγματοποιήσω τη δική μου έρευνα. Χωρίς να γνωρίζουμε τον ορισμό του συντελεστή, είναι αδύνατο να κατασκευάσουμε ακόμη και το απλούστερο γράφημα που περιέχει μια απόλυτη τιμή. Ένα χαρακτηριστικό γνώρισμα των γραφημάτων συναρτήσεων που περιέχουν εκφράσεις με πρόσημο συντελεστή είναι το 3
4 είναι η παρουσία συστροφών σε εκείνα τα σημεία στα οποία η έκφραση κάτω από το πρόσημο του συντελεστή αλλάζει πρόσημο. Σκοπός της εργασίας: να εξετάσει την κατασκευή μιας γραφικής παράστασης γραμμικών, τετραγωνικών και κλασματικά ορθολογικών συναρτήσεων που περιέχει μια μεταβλητή κάτω από το πρόσημο του συντελεστή. Στόχοι: 1) Μελετήστε τη βιβλιογραφία για τις ιδιότητες της απόλυτης τιμής γραμμικών, τετραγωνικών και κλασματικών ορθολογικών συναρτήσεων. 2) Διερευνήστε τις αλλαγές στα γραφήματα συναρτήσεων ανάλογα με τη θέση του πρόσημου της απόλυτης τιμής. 3) Μάθετε να γράφετε εξισώσεις. Αντικείμενο μελέτης: γραφικές παραστάσεις γραμμικών, τετραγωνικών και κλασματικά ορθολογικών συναρτήσεων. Αντικείμενο έρευνας: αλλαγές στη γραφική παράσταση γραμμικών, τετραγωνικών και κλασματικά ορθολογικών συναρτήσεων ανάλογα με τη θέση του πρόσημου της απόλυτης τιμής. Η πρακτική σημασία της δουλειάς μου έγκειται στη: 1) χρήση της αποκτηθείσας γνώσης σχετικά με αυτό το θέμα, καθώς και στην εμβάθυνσή της και στην εφαρμογή της σε άλλες συναρτήσεις και εξισώσεις. 2) στη χρήση ερευνητικών δεξιοτήτων σε περαιτέρω εκπαιδευτικές δραστηριότητες. Συνάφεια: Οι εργασίες γραφικής παράστασης είναι παραδοσιακά ένα από τα πιο δύσκολα θέματα στα μαθηματικά. Εμείς οι απόφοιτοι βρισκόμαστε αντιμέτωποι με το πρόβλημα της επιτυχούς επιτυχίας στις Κρατικές και στην Ενιαία Κρατική. Ερευνητικό πρόβλημα: κατασκευή γραφημάτων συναρτήσεων που περιέχουν το πρόσημο συντελεστή από το δεύτερο μέρος του GIA. Ερευνητική υπόθεση: η χρήση μιας μεθοδολογίας για την επίλυση εργασιών στο δεύτερο μέρος του GIA, που αναπτύχθηκε με βάση γενικές μεθόδους για την κατασκευή γραφημάτων συναρτήσεων που περιέχουν ένα σύμβολο συντελεστή, θα επιτρέψει στους μαθητές να λύσουν αυτές τις εργασίες 4
5 σε συνειδητή βάση, επιλέξτε την πιο ορθολογική μέθοδο λύσης, εφαρμόστε διαφορετικές μεθόδους λύσης και περάστε τις Κρατικές Εξετάσεις με μεγαλύτερη επιτυχία. Μέθοδοι έρευνας που χρησιμοποιήθηκαν στην εργασία: 1.Ανάλυση μαθηματικής βιβλιογραφίας και πόρων του Διαδικτύου για αυτό το θέμα. 2. Αναπαραγωγική αναπαραγωγή του μελετημένου υλικού. 3. Γνωστική και ερευνητική δραστηριότητα. 4.Ανάλυση και σύγκριση δεδομένων για αναζήτηση λύσεων σε προβλήματα. 5. Δήλωση υποθέσεων και επαλήθευση τους. 6. Σύγκριση και γενίκευση μαθηματικών γεγονότων. 7. Ανάλυση των αποτελεσμάτων που προέκυψαν. Κατά τη συγγραφή αυτής της εργασίας χρησιμοποιήθηκαν οι ακόλουθες πηγές: Διαδικτυακοί πόροι, τεστ OGE, μαθηματική βιβλιογραφία. 5
6 I. Κύριο μέρος 1.1 Ιστορική αναδρομή. Στο πρώτο μισό του 17ου αιώνα άρχισε να εμφανίζεται η ιδέα της συνάρτησης ως εξάρτησης μιας μεταβλητής από μια άλλη. Έτσι, οι Γάλλοι μαθηματικοί Pierre Fermat () και Rene Descartes () φαντάστηκαν μια συνάρτηση ως την εξάρτηση της τεταγμένης ενός σημείου από μια καμπύλη από την τετμημένη του. Και ο Άγγλος επιστήμονας Isaac Newton () κατάλαβε μια συνάρτηση ως τη συντεταγμένη ενός κινούμενου σημείου που αλλάζει ανάλογα με το χρόνο. Ο όρος «συνάρτηση» (από τη λατινική συνάρτηση execution, accomplishment) εισήχθη για πρώτη φορά από τον Γερμανό μαθηματικό Gottfried Leibniz(). Συνέδεσε μια συνάρτηση με μια γεωμετρική εικόνα (το γράφημα μιας συνάρτησης). Στη συνέχεια, ο Ελβετός μαθηματικός Johann Bernoulli() και μέλος της Ακαδημίας Επιστημών της Αγίας Πετρούπολης, ο διάσημος μαθηματικός του 18ου αιώνα Leonard Euler(), θεώρησαν τη συνάρτηση ως αναλυτική έκφραση. Ο Euler έχει επίσης μια γενική κατανόηση της συνάρτησης ως την εξάρτηση μιας μεταβλητής από μια άλλη. Η λέξη «module» προέρχεται από τη λατινική λέξη «modulus», που σημαίνει «μέτρο». Πρόκειται για μια πολυσηματική λέξη (ομώνυμο), που έχει πολλές σημασίες και χρησιμοποιείται όχι μόνο στα μαθηματικά, αλλά και στην αρχιτεκτονική, τη φυσική, την τεχνολογία, τον προγραμματισμό και άλλες ακριβείς επιστήμες. Στην αρχιτεκτονική, αυτή είναι η αρχική μονάδα μέτρησης που καθιερώθηκε για μια δεδομένη αρχιτεκτονική δομή και χρησιμοποιείται για να εκφράσει πολλαπλές αναλογίες των συστατικών της στοιχείων. Στην τεχνολογία, αυτός είναι ένας όρος που χρησιμοποιείται σε διάφορους τομείς της τεχνολογίας, ο οποίος δεν έχει καθολική σημασία και χρησιμεύει για να προσδιορίσει διάφορους συντελεστές και ποσότητες, για παράδειγμα, συντελεστή εμπλοκής, συντελεστή ελαστικότητας κ.λπ. 6
7 Ο συντελεστής όγκου (στη φυσική) είναι ο λόγος της κανονικής τάσης σε ένα υλικό προς τη σχετική επιμήκυνση. 2. Βασικοί ορισμοί και ιδιότητες των συναρτήσεων Η συνάρτηση είναι μια από τις πιο σημαντικές μαθηματικές έννοιες. Μια συνάρτηση είναι μια εξάρτηση της μεταβλητής y από τη μεταβλητή x έτσι ώστε κάθε τιμή της μεταβλητής x αντιστοιχεί σε μια μεμονωμένη τιμή της μεταβλητής y. Μέθοδοι για τον καθορισμό μιας συνάρτησης: 1) αναλυτική μέθοδος (η συνάρτηση καθορίζεται με χρήση μαθηματικού τύπου). 2) μέθοδος πίνακα (η συνάρτηση καθορίζεται χρησιμοποιώντας έναν πίνακα). 3) περιγραφική μέθοδος (η λειτουργία καθορίζεται με λεκτική περιγραφή). 4) γραφική μέθοδος (η συνάρτηση καθορίζεται χρησιμοποιώντας ένα γράφημα). Η γραφική παράσταση μιας συνάρτησης είναι το σύνολο όλων των σημείων του επιπέδου συντεταγμένων, των οποίων οι τετμημένες είναι ίσες με την τιμή του ορίσματος και οι τεταγμένες ίσες με τις αντίστοιχες τιμές της συνάρτησης. 2.1 Τετραγωνική συνάρτηση Μια συνάρτηση που ορίζεται από τον τύπο y = ax 2 + σε + c, όπου x και y είναι μεταβλητές και οι παράμετροι a, b και c είναι οποιοιδήποτε πραγματικοί αριθμοί, και a = 0, ονομάζεται τετραγωνική. Η γραφική παράσταση της συνάρτησης y=ax 2 +in+c είναι παραβολή. ο άξονας συμμετρίας της παραβολής y=ax 2 +in+c είναι ευθεία γραμμή, για a>0 τα «κλαδιά» της παραβολής κατευθύνονται προς τα πάνω, για ένα<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7
8 (για συναρτήσεις μιας μεταβλητής). Η κύρια ιδιότητα των γραμμικών συναρτήσεων: η αύξηση της συνάρτησης είναι ανάλογη με την αύξηση του ορίσματος. Δηλαδή, η συνάρτηση είναι γενίκευση της ευθείας αναλογικότητας. Το γράφημα μιας γραμμικής συνάρτησης είναι μια ευθεία γραμμή, από όπου προέρχεται και το όνομά της. Αυτό αφορά μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής. 1) Όταν, η ευθεία σχηματίζει οξεία γωνία με τη θετική φορά του άξονα της τετμημένης. 2) Όταν, η ευθεία σχηματίζει αμβλεία γωνία με τη θετική φορά του άξονα x. 3) είναι ο δείκτης τεταγμένων του σημείου τομής της ευθείας με τον άξονα τεταγμένων. 4) Όταν, η ευθεία διέρχεται από την αρχή. , 2.3 Κλασματική-ορθολογική συνάρτηση είναι ένα κλάσμα του οποίου ο αριθμητής και ο παρονομαστής είναι πολυώνυμα. Έχει τη μορφή όπου, πολυώνυμα σε οποιοδήποτε αριθμό μεταβλητών. Μια ειδική περίπτωση είναι οι ορθολογικές συναρτήσεις μιας μεταβλητής:, όπου και είναι πολυώνυμα. 1) Οποιαδήποτε έκφραση μπορεί να ληφθεί από μεταβλητές χρησιμοποιώντας τέσσερις αριθμητικές πράξεις είναι μια ορθολογική συνάρτηση. 8
9 2) Το σύνολο των ορθολογικών συναρτήσεων είναι κλειστό κάτω από τις αριθμητικές πράξεις και την πράξη σύνθεσης. 3) Οποιαδήποτε ορθολογική συνάρτηση μπορεί να αναπαρασταθεί ως άθροισμα απλών κλασμάτων - αυτό χρησιμοποιείται στην αναλυτική ολοκλήρωση.. , 3. Αλγόριθμοι για την κατασκευή γραφημάτων με μέτρο 3.1 Ορισμός συντελεστή Ο συντελεστής ενός πραγματικού αριθμού a είναι ο ίδιος ο αριθμός a, εάν είναι μη αρνητικός και ο αριθμός απέναντι από το a, αν το a είναι αρνητικός. a = 3.2 Αλγόριθμος για την κατασκευή γραφήματος γραμμικής συνάρτησης με συντελεστή Για να κατασκευάσετε γραφήματα συναρτήσεων y = x πρέπει να γνωρίζετε ότι για θετικό x έχουμε x = x. Αυτό σημαίνει ότι για θετικές τιμές του ορίσματος, το γράφημα y= x συμπίπτει με το γράφημα y=x, δηλαδή, αυτό το τμήμα του γραφήματος είναι μια ακτίνα που αναδύεται από την αρχή υπό γωνία 45 μοιρών ως προς τον άξονα της τετμημένης . Στο x< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9
10 Για να κατασκευάσουμε, παίρνουμε πόντους (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2). Τώρα ας φτιάξουμε ένα γράφημα y= x-1 Αν το A είναι ένα σημείο στο γράφημα y= x με συντεταγμένες (a; a), τότε το σημείο στο γράφημα y= x-1 με την ίδια τιμή της τεταγμένης Y θα. να είναι το σημείο A1(a+1; a). Αυτό το σημείο του δεύτερου γραφήματος μπορεί να ληφθεί από το σημείο A(a; a) του πρώτου γραφήματος μετατοπίζοντας παράλληλα προς τον άξονα Ox προς τα δεξιά. Αυτό σημαίνει ότι ολόκληρη η γραφική παράσταση της συνάρτησης y= x-1 προκύπτει από τη γραφική παράσταση της συνάρτησης y= x μετατοπίζοντας παράλληλα προς τον άξονα Ox προς τα δεξιά κατά 1. Ας κατασκευάσουμε τα γραφήματα: y= x-1 Για να κατασκευάσουμε , πάρτε τους βαθμούς (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1). 3.3 Κατασκευή γραφημάτων συναρτήσεων που περιέχουν «ένθετες ενότητες» στον τύπο Ας εξετάσουμε τον αλγόριθμο κατασκευής χρησιμοποιώντας ένα συγκεκριμένο παράδειγμα Κατασκευάστε ένα γράφημα μιας συνάρτησης: 10
11 y=i-2-ix+5ii 1. Να φτιάξετε μια γραφική παράσταση της συνάρτησης. 2. Εμφανίζουμε τη γραφική παράσταση του κάτω ημιεπιπέδου προς τα πάνω συμμετρικά σε σχέση με τον άξονα OX και παίρνουμε τη γραφική παράσταση της συνάρτησης. έντεκα
12 3. Εμφανίζουμε τη γραφική παράσταση της συνάρτησης προς τα κάτω συμμετρικά σε σχέση με τον άξονα OX και παίρνουμε τη γραφική παράσταση της συνάρτησης. 4. Εμφανίζουμε τη γραφική παράσταση της συνάρτησης προς τα κάτω συμμετρικά σε σχέση με τον άξονα OX και παίρνουμε μια γραφική παράσταση της συνάρτησης 5. Εμφανίζουμε τη γραφική παράσταση της συνάρτησης σε σχέση με τον άξονα OX και παίρνουμε ένα γράφημα. 12
13 6. Ως αποτέλεσμα, το γράφημα της συνάρτησης μοιάζει με αυτό 3.4. Αλγόριθμος κατασκευής γραφημάτων συναρτήσεων της μορφής y = a 1 x x 1 + a 2 x x a n x x n + ax + b. Στο προηγούμενο παράδειγμα, ήταν αρκετά εύκολο να αποκαλυφθούν τα σημάδια του συντελεστή. Εάν υπάρχουν περισσότερα αθροίσματα μονάδων, τότε είναι προβληματικό να εξεταστούν όλοι οι πιθανοί συνδυασμοί σημείων υπομονάδων παραστάσεων. Πώς, σε αυτή την περίπτωση, να κατασκευάσετε ένα γράφημα της συνάρτησης; Σημειώστε ότι η γραφική παράσταση είναι μια διακεκομμένη γραμμή, με κορυφές σε σημεία με τετμημένες -1 και 2. Στα x = -1 και x = 2, οι υπο-αρθρωτές εκφράσεις είναι ίσες με μηδέν. Στην πράξη, έχουμε πλησιάσει τον κανόνα για την κατασκευή τέτοιων γραφημάτων: Η γραφική παράσταση μιας συνάρτησης της μορφής y = a 1 x x 1 + a 2 x x a n x x n + ax + b είναι μια διακεκομμένη γραμμή με άπειρους ακραίους συνδέσμους. Για να κατασκευάσουμε μια τέτοια διακεκομμένη γραμμή, αρκεί να γνωρίζουμε όλες τις κορυφές της (τα τετμημένα των κορυφών είναι τα μηδενικά των υπομονάδων παραστάσεων) και ένα σημείο ελέγχου στον αριστερό και τον δεξιό άπειρο σύνδεσμο. 13
14 Πρόβλημα. Να σχηματίσετε γραφικά τη συνάρτηση y = x + x 1 + x + 1 και να βρείτε τη μικρότερη τιμή της. Λύση: 1. Μηδενικά υπομονάδων παραστάσεων: 0; -1; Κορυφές της πολυγραμμής (0; 2); (-13); (1; 3) (αντικαθιστούμε τα μηδενικά των υπομονάδων παραστάσεων στην εξίσωση) 3 Σημείο ελέγχου στα δεξιά (2; 6), στα αριστερά (-2; 6). Κατασκευάζουμε ένα γράφημα (Εικ. 7), η μικρότερη τιμή της συνάρτησης είναι Αλγόριθμος για την κατασκευή γραφήματος τετραγωνικής συνάρτησης με την ενότητα Σχεδίαση αλγορίθμων για τη μετατροπή γραφημάτων συναρτήσεων. 1. Σχεδίαση γραφικής παράστασης της συνάρτησης y= f(x). Εξ ορισμού μιας ενότητας, αυτή η συνάρτηση χωρίζεται σε ένα σύνολο δύο λειτουργιών. Συνεπώς, η γραφική παράσταση της συνάρτησης y= f(x) αποτελείται από δύο γραφήματα: y= f(x) στο δεξί ημιεπίπεδο, y= f(-x) στο αριστερό ημιεπίπεδο. Με βάση αυτό, μπορεί να διαμορφωθεί ένας κανόνας (αλγόριθμος). Η γραφική παράσταση της συνάρτησης y= f(x) προκύπτει από τη γραφική παράσταση της συνάρτησης y= f(x) ως εξής: στο x 0 διατηρείται η γραφική παράσταση και στο x< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14
15 3. Για να δημιουργήσετε μια γραφική παράσταση της συνάρτησης y= f(x), πρέπει πρώτα να δημιουργήσετε μια γραφική παράσταση της συνάρτησης y= f(x) για x> 0 και μετά για x< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15
16 Για να λάβετε αυτό το γράφημα, πρέπει απλώς να μετατοπίσετε το γράφημα που λάβατε προηγουμένως τρεις μονάδες προς τα δεξιά. Σημειώστε ότι αν ο παρονομαστής του κλάσματος περιείχε την παράσταση x + 3, τότε θα μετατοπίζαμε τη γραφική παράσταση προς τα αριστερά: Τώρα πρέπει να πολλαπλασιάσουμε όλες τις τεταγμένες επί δύο για να πάρουμε τη γραφική παράσταση της συνάρτησης δύο μονάδες: Το τελευταίο πράγμα που πρέπει να κάνουμε είναι , αυτό είναι να σχεδιάσουμε ένα γράφημα μιας δεδομένης συνάρτησης εάν περικλείεται κάτω από το σύμβολο του συντελεστή. Για να γίνει αυτό, αντικατοπτρίζουμε συμμετρικά προς τα πάνω ολόκληρο το τμήμα του γραφήματος του οποίου οι τεταγμένες είναι αρνητικές (εκείνο το τμήμα που βρίσκεται κάτω από τον άξονα x): Εικ. 4 16
17 4.Μεταβολές στη γραφική παράσταση μιας τετραγωνικής συνάρτησης ανάλογα με τη θέση του πρόσημου της απόλυτης τιμής. Κατασκευάστε μια γραφική παράσταση της συνάρτησης y = x 2 - x -3 1) Επειδή x = x στο x 0, η απαιτούμενη γραφική παράσταση συμπίπτει με την παραβολή y = 0,25 x 2 - x - 3. Αν x<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. β) Επομένως, ολοκληρώνω την κατασκευή για το x<0 часть графика, симметричную построенной относительно оси ОУ. 17
18 Εικ. 4 Η γραφική παράσταση της συνάρτησης y = f (x) συμπίπτει με τη γραφική παράσταση της συνάρτησης y = f (x) στο σύνολο των μη αρνητικών τιμών του ορίσματος και είναι συμμετρική με αυτήν ως προς τον άξονα του OU στο σύνολο των αρνητικών τιμών του επιχειρήματος. Απόδειξη: Αν x 0, τότε f (x) = f (x), δηλ. στο σύνολο των μη αρνητικών τιμών του ορίσματος, οι γραφικές παραστάσεις των συναρτήσεων y = f (x) και y = f (x) συμπίπτουν. Εφόσον η y = f (x) είναι άρτια συνάρτηση, η γραφική παράσταση της είναι συμμετρική ως προς τον op-amp. Έτσι, η γραφική παράσταση της συνάρτησης y = f (x) μπορεί να ληφθεί από τη γραφική παράσταση της συνάρτησης y = f (x) ως εξής: 1. Κατασκευάστε μια γραφική παράσταση της συνάρτησης y = f (x) για x>0; 2. Για x<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. Για x<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х
19 Αν x 2 - x -6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 και συμμετρικά ανακλώμενο μέρος y = f(x) στο y<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, μετά f (x) = f (x), που σημαίνει ότι σε αυτό το μέρος η γραφική παράσταση της συνάρτησης y = f (x) συμπίπτει με τη γραφική παράσταση της ίδιας της συνάρτησης y = f (x). Αν f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19
20 Εικ.5 Συμπέρασμα: Για να φτιάξετε μια γραφική παράσταση της συνάρτησης y= f(x) 1. Κατασκευάστε μια γραφική παράσταση της συνάρτησης y=f(x) ; 2. Σε περιοχές όπου η γραφική παράσταση βρίσκεται στο κάτω μισό επίπεδο, δηλ. όπου f(x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20
21 Ερευνητική εργασία για την κατασκευή γραφημάτων της συνάρτησης y = f (x) Χρησιμοποιώντας τον ορισμό της απόλυτης τιμής και παραδείγματα που συζητήθηκαν προηγουμένως, θα κατασκευάσουμε γραφήματα της συνάρτησης: y = 2 x - 3 y = x 2-5 x y = x 2 -2 και βγάλτε συμπεράσματα. Για να φτιάξετε μια γραφική παράσταση της συνάρτησης y = f (x) πρέπει: 1. Να φτιάξετε μια γραφική παράσταση της συνάρτησης y = f (x) για x>0. 2. Κατασκευάστε το δεύτερο μέρος του γραφήματος, δηλαδή αντικατοπτρίστε το κατασκευασμένο γράφημα συμμετρικά σε σχέση με τον op-amp, επειδή Αυτή η λειτουργία είναι ομοιόμορφη. 3. Μετατρέψτε τα τμήματα του γραφήματος που προκύπτει που βρίσκονται στο κάτω ημιεπίπεδο στο άνω μισό επίπεδο συμμετρικά στον άξονα OX. Κατασκευάστε μια γραφική παράσταση της συνάρτησης y = 2 x - 3 (1η μέθοδος για τον προσδιορισμό του συντελεστή) 1. Κατασκευάστε y = 2 x - 3, για 2 x - 3 > 0, x >1,5 δηλ. Χ< -1,5 и х>1,5 α) y = 2x - 3, για x>0 β) για x<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 β) για το x<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) Κατασκευάζουμε μια ευθεία γραμμή, συμμετρική με αυτήν που κατασκευάστηκε σε σχέση με τον άξονα του op-amp. 3) Εμφανίζω τμήματα του γραφήματος που βρίσκονται στο κάτω ημιεπίπεδο συμμετρικά σε σχέση με τον άξονα OX. Συγκρίνοντας και τα δύο γραφήματα, βλέπουμε ότι είναι τα ίδια. 21
22 Παραδείγματα προβλημάτων Παράδειγμα 1. Θεωρήστε τη γραφική παράσταση της συνάρτησης y = x 2 6x +5. Εφόσον το x είναι τετράγωνο, ανεξάρτητα από το πρόσημο του αριθμού x, μετά τον τετραγωνισμό θα είναι θετικό. Από αυτό προκύπτει ότι η γραφική παράσταση της συνάρτησης y = x 2-6x +5 θα είναι πανομοιότυπη με τη γραφική παράσταση της συνάρτησης y = x 2-6x +5, δηλ. γράφημα μιας συνάρτησης που δεν περιέχει σύμβολο απόλυτης τιμής (Εικ. 2). Εικ.2 Παράδειγμα 2. Θεωρούμε τη γραφική παράσταση της συνάρτησης y = x 2 6 x +5. Χρησιμοποιώντας τον ορισμό του συντελεστή ενός αριθμού, αντικαθιστούμε τον τύπο y = x 2 6 x +5 Τώρα έχουμε να κάνουμε με την τμηματική ανάθεση εξάρτησης που μας είναι γνωστή. Θα φτιάξουμε ένα γράφημα ως εξής: 1) να φτιάξουμε μια παραβολή y = x 2-6x +5 και να κυκλώσουμε το μέρος που είναι 22
Το 23 αντιστοιχεί σε μη αρνητικές τιμές του x, δηλ. το τμήμα που βρίσκεται στα δεξιά του άξονα Oy. 2) στο ίδιο επίπεδο συντεταγμένων, κατασκευάστε μια παραβολή y = x 2 +6x +5 και κυκλώστε το τμήμα που αντιστοιχεί σε αρνητικές τιμές του x, δηλ. το τμήμα που βρίσκεται στα αριστερά του άξονα Oy. Τα κυκλωμένα μέρη των παραβολών μαζί σχηματίζουν μια γραφική παράσταση της συνάρτησης y = x 2-6 x +5 (Εικ. 3). Εικ.3 Παράδειγμα 3. Θεωρούμε τη γραφική παράσταση της συνάρτησης y = x 2-6 x +5. Επειδή η γραφική παράσταση της εξίσωσης y = x 2 6x +5 είναι η ίδια με τη γραφική παράσταση της συνάρτησης χωρίς το σύμβολο του συντελεστή (που συζητείται στο παράδειγμα 2), προκύπτει ότι η γραφική παράσταση της συνάρτησης y = x 2 6 x +5 είναι πανομοιότυπη στη γραφική παράσταση της συνάρτησης y = x 2 6 x +5 , που εξετάζεται στο παράδειγμα 2 (Εικ. 3). Παράδειγμα 4. Ας φτιάξουμε μια γραφική παράσταση της συνάρτησης y = x 2 6x +5. Για να γίνει αυτό, ας φτιάξουμε ένα γράφημα της συνάρτησης y = x 2-6x. Για να λάβετε μια γραφική παράσταση της συνάρτησης y = x 2-6x από αυτήν, πρέπει να αντικαταστήσετε κάθε σημείο της παραβολής με μια αρνητική τεταγμένη με ένα σημείο με την ίδια τεταγμένη, αλλά με την αντίθετη (θετική) τεταγμένη. Με άλλα λόγια, το τμήμα της παραβολής που βρίσκεται κάτω από τον άξονα x πρέπει να αντικατασταθεί με μια γραμμή συμμετρική προς αυτήν σε σχέση με τον άξονα x. Επειδή πρέπει να δημιουργήσουμε μια γραφική παράσταση της συνάρτησης y = x 2-6x +5, τότε η γραφική παράσταση της συνάρτησης που θεωρήσαμε y = x 2-6x πρέπει απλώς να ανυψωθεί κατά μήκος του άξονα y κατά 5 μονάδες προς τα πάνω (Εικ. 4 ). 23
24 Εικ.4 Παράδειγμα 5. Ας σχεδιάσουμε τη συνάρτηση y = x 2-6x+5. Για να το κάνουμε αυτό, θα χρησιμοποιήσουμε τη γνωστή συνάρτηση piecewise. Ας βρούμε τα μηδενικά της συνάρτησης y = 6x +5 6x + 5 = 0 στο. Ας εξετάσουμε δύο περιπτώσεις: 1) Αν, τότε η εξίσωση θα πάρει τη μορφή y = x 2 6x -5. Ας κατασκευάσουμε αυτήν την παραβολή και ας κυκλώσουμε το μέρος όπου. 2) Αν, τότε η εξίσωση παίρνει τη μορφή y = x 2 + 6x +5. Ας σταθούμε σε αυτή την παραβολή και ας κυκλώσουμε με συντεταγμένες εκείνο το τμήμα της που βρίσκεται στα αριστερά του σημείου (Εικ. 5). 24
25 Εικ.5 Παράδειγμα6. Ας φτιάξουμε μια γραφική παράσταση της συνάρτησης y = x 2 6 x +5. Για να γίνει αυτό, θα φτιάξουμε ένα γράφημα της συνάρτησης y = x 2-6 x +5. Κατασκευάσαμε αυτό το γράφημα στο Παράδειγμα 3. Εφόσον η συνάρτησή μας είναι εντελώς κάτω από το πρόσημο του συντελεστή, για να φτιάξουμε ένα γράφημα της συνάρτησης y = x 2 6 x +5, χρειαζόμαστε κάθε σημείο της γραφικής παράστασης της συνάρτησης y = x 2 6 x + 5 με αρνητική τεταγμένη θα πρέπει να αντικατασταθεί από ένα σημείο με την ίδια τετμημένη, αλλά με την αντίθετη (θετική) τεταγμένη, δηλ. το τμήμα της παραβολής που βρίσκεται κάτω από τον άξονα Ox πρέπει να αντικατασταθεί με μια γραμμή συμμετρική προς αυτόν σε σχέση με τον άξονα Ox (Εικ. 6). Εικ.6 25
26 II Συμπέρασμα «Οι μαθηματικές πληροφορίες μπορούν να χρησιμοποιηθούν επιδέξια και χρήσιμα μόνο εάν τις κατακτήσουν δημιουργικά, ώστε ο μαθητής να δει μόνος του πώς θα μπορούσε να τις καταφέρει μόνος του». ΕΝΑ. Κολμογκόροφ. Τα προβλήματα αυτά παρουσιάζουν μεγάλο ενδιαφέρον για τους μαθητές της ένατης τάξης, καθώς είναι πολύ συνηθισμένα στα τεστ OGE. Η δυνατότητα κατασκευής γραφημάτων δεδομένων συναρτήσεων θα σας επιτρέψει να περάσετε την εξέταση με μεγαλύτερη επιτυχία. Οι Γάλλοι μαθηματικοί Pierre Fermat () και Rene Descartes () φαντάστηκαν μια συνάρτηση ως την εξάρτηση της τεταγμένης ενός σημείου από μια καμπύλη στην τετμημένη του. Και ο Άγγλος επιστήμονας Isaac Newton () κατάλαβε μια συνάρτηση ως τη συντεταγμένη ενός κινούμενου σημείου που αλλάζει ανάλογα με το χρόνο. 26
27 III Κατάλογος αναφορών και πηγών 1. Galitsky M. L., Goldman A. M., Zvavich L. I. Συλλογή προβλημάτων στην άλγεβρα για τις τάξεις 8-9: Σχολικό βιβλίο. εγχειρίδιο για μαθητές σχολείων. και προχωρημένων τάξεων μελετημένος Μαθηματικά 2η έκδ. M.: Διαφωτισμός, Dorofeev G.V. Αλγεβρα. Λειτουργίες. Ανάλυση δεδομένων. 9η τάξη: m34 Εκπαιδευτικά. για σπουδές γενικής παιδείας. ίδρυση 2η έκδ., στερεότυπο. M.: Bustard, Solomonik V.S Συλλογή ερωτήσεων και προβλημάτων στα μαθηματικά M.: «Γυμνάσιο», Yashchenko I.V. GIA. Μαθηματικά: τυπικές επιλογές εξετάσεων: Σχετικά με τις επιλογές.μ.: «Εθνική Παιδεία», σελ. 5. Yashchenko I.V. OGE. Μαθηματικά: τυπικές επιλογές εξετάσεων: Σχετικά με τις επιλογές.μ.: «Εθνική Παιδεία», σελ. 6. Yashchenko I.V. OGE. Μαθηματικά: τυπικές επιλογές εξετάσεων: Σχετικά με τις επιλογές.μ.: «Εθνική Παιδεία», με
28 Παράρτημα 28
29 Παράδειγμα 1. Να σχηματίσετε γραφική παράσταση τη συνάρτηση y = x 2 8 x Λύση. Ας προσδιορίσουμε την ισοτιμία της συνάρτησης. Η τιμή για το y(-x) είναι ίδια με την τιμή για το y(x), επομένως αυτή η συνάρτηση είναι άρτια. Τότε η γραφική παράσταση του είναι συμμετρική ως προς τον άξονα Oy. Σχεδιάζουμε τη συνάρτηση y = x 2 8x + 12 για x 0 και εμφανίζουμε συμμετρικά το γράφημα ως προς το Oy για αρνητικό x (Εικ. 1). Παράδειγμα 2. Η ακόλουθη γραφική παράσταση της μορφής y = x 2 8x Αυτό σημαίνει ότι η γραφική παράσταση της συνάρτησης προκύπτει ως εξής: δημιουργήστε μια γραφική παράσταση της συνάρτησης y = x 2 8x + 12, αφήστε το τμήμα της γραφικής παράστασης που βρίσκεται παραπάνω ο άξονας Ox αμετάβλητος και το τμήμα του γραφήματος που βρίσκεται κάτω από τον άξονα της τετμημένης και εμφανίζεται συμμετρικά σε σχέση με τον άξονα Ox (Εικ. 2). Παράδειγμα 3. Για να σχεδιάσουμε μια γραφική παράσταση της συνάρτησης y = x 2 8 x + 12, πραγματοποιείται συνδυασμός μετασχηματισμών: y = x 2 8x + 12 y = x 2 8 x + 12 y = x 2 8 x Απάντηση: Εικόνα 3. Παράδειγμα 4 Έκφραση κάτω από το πρόσημο συντελεστή, αλλάζει πρόσημο στο σημείο x=2/3. Στο x<2/3 функция запишется так: 29
30 Για x>2/3 η συνάρτηση θα γραφτεί ως εξής: Δηλαδή, το σημείο x=2/3 χωρίζει το επίπεδο των συντεταγμένων μας σε δύο περιοχές, στη μία από τις οποίες (δεξιά) χτίζουμε μια συνάρτηση και στην άλλη (στα αριστερά) χτίζουμε μια γραφική παράσταση της συνάρτησης: Παράδειγμα 5 Επόμενο Το γράφημα είναι επίσης σπασμένο, αλλά έχει δύο σημεία διακοπής, αφού περιέχει δύο εκφράσεις κάτω από τα σημάδια του συντελεστή: Ας δούμε σε ποια σημεία αλλάζουν πρόσημο οι υποαρθρικές εκφράσεις: Ας τακτοποιήστε τα σημάδια για τις υπομονάδες παραστάσεις στη γραμμή συντεταγμένων: 30
31 Επεκτείνουμε τις ενότητες στο πρώτο διάστημα: Στο δεύτερο διάστημα: Στο τρίτο διάστημα: Έτσι, στο διάστημα (- ; 1.5] έχουμε ένα γράφημα γραμμένο από την πρώτη εξίσωση, στο διάστημα ένα γράφημα γραμμένο από τη δεύτερη εξίσωση , και στο μεσοδιάστημα)
 Βούληση: λειτουργίες, έννοια, κύρια χαρακτηριστικά
Βούληση: λειτουργίες, έννοια, κύρια χαρακτηριστικά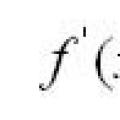 Γεωμετρική και μηχανική σημασία της παραγώγου
Γεωμετρική και μηχανική σημασία της παραγώγου Ιδιότητες εξουσιών επιπλέον
Ιδιότητες εξουσιών επιπλέον