Grondbeginselen van de waarschijnlijkheidstheorie en wiskundige statistiek. Basisconcepten van waarschijnlijkheidstheorie en wiskundige statistiek
Waarschijnlijkheidstheorie en wiskundige statistiek
- Agekyan TA Grondbeginselen van de foutentheorie voor astronomen en natuurkundigen (2e ed.). M.: Nauka, 1972 (djvu, 2,44 M)
- Agekyan TA Waarschijnlijkheidstheorie voor astronomen en natuurkundigen. M.: Nauka, 1974 (djvu, 2,59 M)
- Anderson T. Statistische analyse van tijdreeksen. M.: Mir, 1976 (djvu, 14 M)
- Bakelman I.Ya. Werner AL Kantor BE Inleiding tot differentiële meetkunde "in het algemeen". M.: Nauka, 1973 (djvu, 5,71 M)
- Bernstein S.N. Waarschijnlijkheids theorie. M.-L.: GI, 1927 (djvu, 4,51 M)
- Billingsley P. Convergentie van waarschijnlijkheidsmetingen. M.: Nauka, 1977 (djvu, 3,96 M)
- Box J. Jenkins G. Tijdreeksanalyse: voorspelling en beheer. Uitgave 1. M.: Mir, 1974 (djvu, 3,38 M)
- Box J. Jenkins G. Tijdreeksanalyse: voorspelling en beheer. Nummer 2. M.: Mir, 1974 (djvu, 1,72 M)
- Borel E. Waarschijnlijkheid en betrouwbaarheid. M.: Nauka, 1969 (djvu, 1,19 M)
- Van der Waerden B.L. Wiskundige statistieken. M.: IL, 1960 (djvu, 6,90 M)
- Vapnik V.N. Afhankelijkheden herstellen op basis van empirische gegevens. M.: Nauka, 1979 (djvu, 6,18M)
- Ventzel E.S. Inleiding tot operationeel onderzoek. M.: Sovjetradio, 1964 (djvu, 8,43 M)
- Ventzel E.S. Elementen van de speltheorie (2e ed.). Serie: Populaire lezingen over wiskunde. Uitgave 32. M.: Nauka, 1961 (djvu, 648 K)
- Ventstel E.S. Waarschijnlijkheidstheorie (4e ed.). M.: Nauka, 1969 (djvu, 8,05 M)
- Ventstel E.S., Ovcharov L.A. Waarschijnlijkheids theorie. Taken en oefeningen. M.: Nauka, 1969 (djvu, 7,71 M)
- Vilenkin N.Ya., Potapov V.G. Een praktisch werkboek over kansrekening met elementen uit de combinatoriek en wiskundige statistiek. M.: Onderwijs, 1979 (djvu, 1,12M)
- Gmurman V.E. Een gids voor het oplossen van problemen in de waarschijnlijkheidstheorie en wiskundige statistiek (3e ed.). M.: Hoger. school, 1979 (djvu, 4,24 M)
- Gmurman V.E. Waarschijnlijkheidstheorie en wiskundige statistiek (4e ed.). M.: Hogere school, 1972 (djvu, 3,75 M)
- Gnedenko B.V., Kolmogorov A.N. Beperk distributies voor sommen van onafhankelijke willekeurige variabelen. M.-L.: GITTL, 1949 (djvu, 6,26 M)
- Gnedenko B.V., Khinchin A.Ya. Een elementaire inleiding tot de waarschijnlijkheidstheorie (7e ed.). M.: Nauka, 1970 (djvu, 2,48 M)
- Eiken J.L. Probabilistische processen. M.: IL, 1956 (djvu, 8,48 M)
- David G. Ordinale statistieken. M.: Nauka, 1979 (djvu, 2,87M)
- Ibragimov IA, Linnik Yu.V. Onafhankelijke en stationair gerelateerde hoeveelheden. M.: Nauka, 1965 (djvu, 6,05M)
- Idier V., Dryard D., James F., Rus M., Sadoulet B. Statistische methoden in de experimentele natuurkunde. M.: Atomizdat, 1976 (djvu, 5,95M)
- Kamalov M.K. Verdeling van kwadratische vormen in steekproeven uit een normale populatie. Tasjkent: Academie van Wetenschappen van de UzSSR, 1958 (djvu, 6,29M)
- Cassandra ON, Lebedev V.V. Verwerking van observatieresultaten. M.: Nauka, 1970 (djvu, 867 K)
- Katz M. Waarschijnlijkheid en aanverwante kwesties in de natuurkunde. M.: Mir, 1965 (djvu, 3,67 M)
- Katz M. Verschillende probabilistische problemen van de natuurkunde en wiskunde. M.: Nauka, 1967 (djvu, 1,50 M)
- Katz M. Statistische onafhankelijkheid in waarschijnlijkheidstheorie, analyse en getaltheorie. M.: IL, 1963 (djvu, 964 K)
- Kendall M., Moran P. Geometrische waarschijnlijkheden. M.: Nauka, 1972 (djvu, 1,40 M)
- Kendall M., Stewart A. Deel 2. Statistische gevolgtrekking en verbindingen. M.: Nauka, 1973 (djvu, 10 M)
- Kendall M., Stewart A. Deel 3. Multivariate statistische analyse en tijdreeksen. M.: Nauka, 1976 (djvu, 7,96 M)
- Kendall M., Stewart A. Vol. 1. Theorie van distributies. M.: Nauka, 1965 (djvu, 6,02 M)
- Kolmogorov A.N. Basisconcepten van de waarschijnlijkheidstheorie (2e ed.) M.: Nauka, 1974 (djvu, 2,14M)
- Kolchin VF, Sevastyanov BA, Chistyakov V.P. Willekeurige plaatsingen. M.: Nauka, 1976 (djvu, 2,96 M)
- Kramer G. Wiskundige statistische methoden (2e ed.). M.: Mir, 1976 (djvu, 9,63 M)
- Leman E. Statistische hypothesen testen. M.: Wetenschap. 1979 (djvu, 5,18 M)
- Linnik Yu.V., Ostrovski I.V. Ontledingen van willekeurige variabelen en vectoren. M.: Nauka, 1972 (djvu, 4,86 M)
- Licholetov II, Matskevitsj I.P. Een gids voor het oplossen van problemen in de hogere wiskunde, kansrekening en wiskundige statistiek (2e ed.). Mn.: Vysh. school, 1969 (djvu, 4,99 M)
- Loev M. Waarschijnlijkheidstheorie. M.: IL, 1962 (djvu, 7,38 M)
- Malakhov A.N. Cumulante analyse van willekeurige niet-Gaussiaanse processen en hun transformaties. M.: Sov. radio, 1978 (djvu, 6,72 M)
- Meshalkin L.D. Verzameling van problemen op het gebied van de waarschijnlijkheidstheorie. M.: MSU, 1963 (djvu, 1 004 K)
- Mitropolsky A.K. Theorie van momenten. M.-L.: GIKSL, 1933 (djvu, 4,49 M)
- Mitropolsky A.K. Technieken van statistisch computergebruik (2e ed.). M.: Nauka, 1971 (djvu, 8,35 M)
- Mosteller F., Rurke R., Thomas J. Waarschijnlijkheid. M.: Mir, 1969 (djvu, 4,82 M)
- Nalimov V.V. Toepassing van wiskundige statistiek bij de analyse van materie. M.: GIFML, 1960 (djvu, 4,11 miljoen)
- Neveu J. Wiskundige grondslagen van de waarschijnlijkheidstheorie. M.: Mir, 1969 (djvu, 3,62 M)
- Preston K. Wiskunde. Nieuw in buitenlandse wetenschap nr.7. Gibbs zegt over telbare sets. M.: Mir, 1977 (djvu, 2,15 M)
- Savelyev L.Ya. Elementaire waarschijnlijkheidstheorie. Deel 1. Novosibirsk: NSU, 2005 (
Velen worden bang als ze geconfronteerd worden met het concept van de ‘waarschijnlijkheidstheorie’, omdat ze denken dat het iets overweldigends en heel complex is. Maar eigenlijk is alles niet zo tragisch. Vandaag zullen we kijken naar het basisconcept van de waarschijnlijkheidstheorie en leren hoe we problemen kunnen oplossen met behulp van specifieke voorbeelden.
De wetenschap
Wat bestudeert een tak van de wiskunde als de ‘waarschijnlijkheidstheorie’? Ze noteert patronen en hoeveelheden. Wetenschappers raakten voor het eerst geïnteresseerd in dit onderwerp in de achttiende eeuw, toen ze gokken bestudeerden. Het basisconcept van de waarschijnlijkheidstheorie is een gebeurtenis. Het is elk feit dat door ervaring of observatie wordt vastgesteld. Maar wat is ervaring? Een ander basisconcept van de waarschijnlijkheidstheorie. Het betekent dat deze omstandigheden niet door toeval zijn ontstaan, maar voor een specifiek doel. Wat de observatie betreft, hier neemt de onderzoeker zelf niet deel aan het experiment, maar is hij eenvoudigweg getuige van deze gebeurtenissen; hij heeft op geen enkele manier invloed op wat er gebeurt.
Evenementen
We hebben geleerd dat het basisconcept van de waarschijnlijkheidstheorie een gebeurtenis is, maar we hebben de classificatie niet overwogen. Ze zijn allemaal onderverdeeld in de volgende categorieën:
- Betrouwbaar.
- Onmogelijk.
- Willekeurig.
Ongeacht wat voor soort gebeurtenissen het zijn, waargenomen of gecreëerd tijdens de ervaring, ze vallen allemaal onder deze classificatie. Wij nodigen u uit om elk type afzonderlijk te leren kennen.
Betrouwbaar evenement

Dit is een omstandigheid waarvoor het noodzakelijke pakket aan maatregelen is genomen. Om de essentie beter te begrijpen, is het beter om een paar voorbeelden te geven. Natuurkunde, scheikunde, economie en hogere wiskunde zijn onderworpen aan deze wet. De waarschijnlijkheidstheorie omvat zo'n belangrijk concept als een betrouwbare gebeurtenis. Hier zijn enkele voorbeelden:
- Wij werken en ontvangen een vergoeding in de vorm van loon.
- We zijn goed geslaagd voor de examens, zijn geslaagd voor de competitie en hiervoor ontvangen we een beloning in de vorm van toelating tot een onderwijsinstelling.
- We hebben geld op de bank belegd en als het nodig is, krijgen we het terug.
Dergelijke gebeurtenissen zijn betrouwbaar. Als we aan alle noodzakelijke voorwaarden hebben voldaan, zullen we zeker het verwachte resultaat behalen.
Onmogelijke gebeurtenissen
Nu beschouwen we elementen van de waarschijnlijkheidstheorie. Wij stellen voor om verder te gaan met een verklaring van het volgende type gebeurtenis, namelijk het onmogelijke. Laten we eerst de belangrijkste regel vaststellen: de waarschijnlijkheid van een onmogelijke gebeurtenis is nul.
Bij het oplossen van problemen kan van deze formulering niet worden afgeweken. Ter verduidelijking volgen hier voorbeelden van dergelijke evenementen:
- Het water bevroor bij een temperatuur van plus tien (dit is onmogelijk).
- Het gebrek aan elektriciteit heeft geen enkele invloed op de productie (net zo onmogelijk als in het vorige voorbeeld).
Het is niet de moeite waard om nog meer voorbeelden te geven, omdat de hierboven beschreven voorbeelden heel duidelijk de essentie van deze categorie weerspiegelen. Tijdens een experiment zal onder geen enkele omstandigheid een onmogelijke gebeurtenis plaatsvinden.
Willekeurige gebeurtenissen

Bij het bestuderen van de elementen moet speciale aandacht worden besteed aan dit specifieke type evenement. Dit is wat de wetenschap bestudeert. Als gevolg van de ervaring kan er wel of niet iets gebeuren. Bovendien kan de test een onbeperkt aantal keren worden uitgevoerd. Levendige voorbeelden zijn onder meer:
- Het opgooien van een munt is een ervaring of test, het landen van de kop is een gebeurtenis.
- Blindelings een bal uit een zak trekken is een test; een rode bal krijgen is een gebeurtenis, enzovoort.
Er kunnen een onbeperkt aantal van dergelijke voorbeelden zijn, maar over het algemeen moet de essentie duidelijk zijn. Om de kennis die is opgedaan over de gebeurtenissen samen te vatten en te systematiseren, wordt een tabel verstrekt. De waarschijnlijkheidstheorie bestudeert alleen het laatste type van alle gepresenteerde typen.
Naam | definitie | |
Betrouwbaar | Gebeurtenissen die plaatsvinden met 100% garantie als aan bepaalde voorwaarden wordt voldaan. | Toelating tot een onderwijsinstelling na goed slagen voor het toelatingsexamen. |
Onmogelijk | Gebeurtenissen die onder geen enkele omstandigheid zullen plaatsvinden. | Het sneeuwt bij een luchttemperatuur van plus dertig graden Celsius. |
Willekeurig | Een gebeurtenis die wel of niet kan plaatsvinden tijdens een experiment/test. | Een schot in de roos als je een basketbal in een hoepel gooit. |
Wetten
Waarschijnlijkheidstheorie is een wetenschap die de mogelijkheid bestudeert dat een gebeurtenis plaatsvindt. Net als de anderen heeft het enkele regels. De volgende wetten van de waarschijnlijkheidstheorie bestaan:
- Convergentie van reeksen willekeurige variabelen.
- Wet van de grote getallen.
Wanneer u de mogelijkheid van iets complexs berekent, kunt u een reeks eenvoudige gebeurtenissen gebruiken om op een eenvoudiger en snellere manier een resultaat te bereiken. Merk op dat de wetten van de waarschijnlijkheidstheorie gemakkelijk kunnen worden bewezen met behulp van bepaalde stellingen. Wij raden u aan eerst kennis te maken met de eerste wet.
Convergentie van reeksen willekeurige variabelen

Merk op dat er verschillende soorten convergentie zijn:
- De reeks willekeurige variabelen convergeert in waarschijnlijkheid.
- Bijna onmogelijk.
- Beteken vierkante convergentie.
- Convergentie van de distributie.
Het is dus heel moeilijk om de essentie meteen te begrijpen. Hier volgen definities die u zullen helpen dit onderwerp te begrijpen. Laten we beginnen met de eerste weergave. De reeks wordt genoemd convergent in waarschijnlijkheid Als aan de volgende voorwaarde is voldaan: n neigt naar oneindig, is het getal waarnaar de reeks neigt groter dan nul en dichtbij één.
Laten we verder gaan naar de volgende weergave, bijna zeker. Er wordt gezegd dat de reeks convergeert bijna zeker naar een willekeurige variabele waarbij n naar oneindig neigt en P naar een waarde dicht bij de eenheid neigt.
Het volgende type is gemiddelde kwadratische convergentie. Bij gebruik van SC-convergentie wordt de studie van willekeurige vectorprocessen beperkt tot de studie van hun gecoördineerde willekeurige processen.
Het laatste type blijft bestaan, laten we er kort naar kijken, zodat we direct verder kunnen gaan met het oplossen van problemen. Convergentie in distributie heeft een andere naam: 'zwak', en we zullen later uitleggen waarom. Zwakke convergentie is de convergentie van distributiefuncties op alle punten van continuïteit van de beperkende distributiefunctie.
We zullen onze belofte zeker nakomen: zwakke convergentie verschilt van al het bovenstaande doordat de willekeurige variabele niet is gedefinieerd in de waarschijnlijkheidsruimte. Dit is mogelijk omdat de voorwaarde uitsluitend wordt gevormd met behulp van distributiefuncties.
Wet van grote aantallen
Stellingen van de waarschijnlijkheidstheorie, zoals:
- De ongelijkheid van Tsjebysjev.
- De stelling van Chebyshev.
- Gegeneraliseerde stelling van Chebyshev.
- Markovs stelling.
Als we al deze stellingen in overweging nemen, kan deze vraag enkele tientallen vellen aanslepen. Onze hoofdtaak is het toepassen van de waarschijnlijkheidstheorie in de praktijk. Wij raden u aan dit nu meteen te doen. Maar laten we eerst eens kijken naar de axioma's van de waarschijnlijkheidstheorie; zij zullen de belangrijkste assistenten zijn bij het oplossen van problemen.
Axioma's

De eerste ontmoetten we al toen we spraken over een onmogelijke gebeurtenis. Laten we niet vergeten: de waarschijnlijkheid van een onmogelijke gebeurtenis is nul. We gaven een heel levendig en gedenkwaardig voorbeeld: er viel sneeuw bij een luchttemperatuur van dertig graden Celsius.
De tweede is als volgt: er vindt een betrouwbare gebeurtenis plaats met een waarschijnlijkheid gelijk aan één. Nu zullen we laten zien hoe we dit in wiskundige taal kunnen schrijven: P(B)=1.
Ten derde: een willekeurige gebeurtenis kan wel of niet plaatsvinden, maar de mogelijkheid varieert altijd van nul tot één. Hoe dichter de waarde bij één ligt, hoe groter de kansen; als de waarde nul nadert, is de waarschijnlijkheid zeer laag. Laten we dit in wiskundige taal schrijven: 0<Р(С)<1.
Laten we eens kijken naar het laatste, vierde axioma, dat als volgt klinkt: de waarschijnlijkheid van de som van twee gebeurtenissen is gelijk aan de som van hun kansen. We schrijven het in wiskundige taal: P(A+B)=P(A)+P(B).
De axioma's van de waarschijnlijkheidstheorie zijn de eenvoudigste regels die niet moeilijk te onthouden zijn. Laten we proberen enkele problemen op te lossen op basis van de kennis die we al hebben verworven.
Loterij ticket

Laten we eerst eens kijken naar het eenvoudigste voorbeeld: een loterij. Stel je voor dat je één lot voor geluk hebt gekocht. Wat is de kans dat u minstens twintig roebel wint? In totaal nemen duizend kaartjes deel aan de oplage, waarvan er één een prijs van vijfhonderd roebel heeft, tien daarvan hebben elk honderd roebel, vijftig hebben een prijs van twintig roebel en honderd hebben een prijs van vijf. Waarschijnlijkheidsproblemen zijn gebaseerd op het vinden van de mogelijkheid van geluk. Nu zullen we samen de oplossing voor de bovenstaande taak analyseren.
Als we de letter A gebruiken om een winst van vijfhonderd roebel aan te duiden, dan is de kans om A te krijgen gelijk aan 0,001. Hoe hebben we dit gekregen? U hoeft alleen maar het aantal “gelukstickets” te delen door hun totale aantal (in dit geval: 1/1000).
B is een overwinning van honderd roebel, de kans is 0,01. Nu handelden we volgens hetzelfde principe als bij de vorige actie (10/1000)
C - de winst is twintig roebel. We vinden de waarschijnlijkheid, deze is gelijk aan 0,05.
We zijn niet geïnteresseerd in de resterende tickets, omdat hun prijzengeld lager is dan aangegeven in de voorwaarde. Laten we het vierde axioma toepassen: de kans om minstens twintig roebel te winnen is P(A)+P(B)+P(C). De letter P geeft de waarschijnlijkheid aan van het optreden van een bepaalde gebeurtenis; we hebben ze al in eerdere acties gevonden. Het enige dat overblijft is het optellen van de benodigde gegevens, en het antwoord dat we krijgen is 0,061. Dit nummer is het antwoord op de taakvraag.
Spel kaarten
Problemen in de kansrekening kunnen complexer zijn; laten we bijvoorbeeld de volgende taak nemen. Voor je ligt een kaartspel met zesendertig kaarten. Jouw taak is om twee kaarten op rij te trekken zonder de stapel te schudden, de eerste en tweede kaart moeten azen zijn, de reeks doet er niet toe.
Laten we eerst de waarschijnlijkheid vinden dat de eerste kaart een aas zal zijn, hiervoor delen we vier door zesendertig. Ze hebben het terzijde gelegd. We halen de tweede kaart eruit, het wordt een aas met een waarschijnlijkheid van drie vijfendertigsten. De waarschijnlijkheid van de tweede gebeurtenis hangt af van welke kaart we als eerste hebben getrokken, we vragen ons af of het een aas was of niet. Hieruit volgt dat gebeurtenis B afhankelijk is van gebeurtenis A.
De volgende stap is het vinden van de waarschijnlijkheid van gelijktijdig optreden, dat wil zeggen, we vermenigvuldigen A en B. Hun product wordt als volgt gevonden: we vermenigvuldigen de waarschijnlijkheid van de ene gebeurtenis met de voorwaardelijke waarschijnlijkheid van een andere, die we berekenen, ervan uitgaande dat de eerste gebeurtenis heeft plaatsgevonden, dat wil zeggen dat we een aas hebben getrokken met de eerste kaart.
Om alles duidelijk te maken, laten we een aanduiding geven aan een dergelijk element als gebeurtenissen. Het wordt berekend in de veronderstelling dat gebeurtenis A heeft plaatsgevonden. Het wordt als volgt berekend: P(B/A).
Laten we doorgaan met het oplossen van ons probleem: P(A * B) = P(A) * P(B/A) of P(A * B) = P(B) * P(A/B). De waarschijnlijkheid is gelijk aan (4/36) * ((3/35)/(4/36). We berekenen door af te ronden op het dichtstbijzijnde honderdste. We hebben: 0,11 * (0,09/0,11) = 0,11 * 0, 82 = 0,09. De kans dat we twee azen op rij trekken is negenhonderdste. De waarde is erg klein, hieruit volgt dat de kans dat de gebeurtenis plaatsvindt extreem klein is.
Vergeten nummer
We stellen voor om nog een aantal varianten van taken te analyseren die door de waarschijnlijkheidstheorie worden bestudeerd. Je hebt in dit artikel al voorbeelden gezien van het oplossen van een aantal ervan. Laten we proberen het volgende probleem op te lossen: de jongen vergat het laatste cijfer van het telefoonnummer van zijn vriend, maar omdat de oproep erg belangrijk was, begon hij alles één voor één te bellen . We moeten de kans berekenen dat hij niet vaker dan drie keer zal bellen. De oplossing voor het probleem is het eenvoudigst als de regels, wetten en axioma's van de waarschijnlijkheidstheorie bekend zijn.
Probeer het eerst zelf op te lossen voordat u naar de oplossing kijkt. We weten dat het laatste cijfer van nul tot negen kan zijn, dat wil zeggen tien waarden in totaal. De kans dat je de juiste krijgt is 1/10.
Vervolgens moeten we de opties voor de oorsprong van de gebeurtenis overwegen, stel dat de jongen het goed heeft geraden en onmiddellijk de juiste heeft getypt, de kans op een dergelijke gebeurtenis is 1/10. Tweede optie: de eerste oproep mist en de tweede ligt op schema. Laten we de waarschijnlijkheid van een dergelijke gebeurtenis berekenen: vermenigvuldig 9/10 met 1/9, en als resultaat krijgen we ook 1/10. De derde optie: de eerste en tweede oproep bleken op het verkeerde adres te zijn, pas bij de derde kwam de jongen waar hij wilde. We berekenen de waarschijnlijkheid van een dergelijke gebeurtenis: 9/10 vermenigvuldigd met 8/9 en 1/8, wat resulteert in 1/10. We zijn niet geïnteresseerd in andere opties afhankelijk van de omstandigheden van het probleem, dus we hoeven alleen maar de verkregen resultaten bij elkaar op te tellen, uiteindelijk hebben we 3/10. Antwoord: de kans dat de jongen maximaal drie keer belt is 0,3.
Kaarten met cijfers

Er liggen negen kaarten voor je, waarop op elk een getal van één tot en met negen staat geschreven, de getallen worden niet herhaald. Ze werden in een doos gedaan en grondig gemengd. Je moet de kans hierop berekenen
- er verschijnt een even getal;
- twee cijfers.
Voordat we verder gaan met de oplossing, stellen we vast dat m het aantal succesvolle gevallen is, en n het totale aantal opties. Laten we de waarschijnlijkheid berekenen dat het getal even is. Het zal niet moeilijk zijn om te berekenen dat er vier even getallen zijn, dit zal onze m zijn, er zijn in totaal negen mogelijke opties, dat wil zeggen m=9. Dan is de kans 0,44 of 4/9.
Laten we het tweede geval eens bekijken: het aantal opties is negen, en er kunnen helemaal geen succesvolle resultaten zijn, dat wil zeggen dat m gelijk is aan nul. De kans dat de getrokken kaart een getal van twee cijfers bevat, is eveneens nul.
INVOERING
Veel dingen zijn voor ons onbegrijpelijk, niet omdat onze concepten zwak zijn;
maar omdat deze zaken niet binnen het bereik van onze concepten vallen.
Kozma Prutkov
Het belangrijkste doel van het studeren van wiskunde in secundaire gespecialiseerde onderwijsinstellingen is om studenten een reeks wiskundige kennis en vaardigheden te geven die nodig zijn voor het bestuderen van andere programmadisciplines die wiskunde in een of andere mate gebruiken, voor het vermogen om praktische berekeningen uit te voeren, voor de vorming en ontwikkeling van logisch denken.
In dit werk zijn alle basisconcepten van het deel van de wiskunde "Fundamentals of Probability Theory and Mathematical Statistics", voorzien door het programma en de State Educational Standards of Secondary Vocational Education (Ministerie van Onderwijs van de Russische Federatie. M., 2002) ), consequent worden geïntroduceerd, worden de belangrijkste stellingen geformuleerd, waarvan de meeste niet bewezen zijn. Er wordt aandacht besteed aan de belangrijkste problemen en methoden om deze op te lossen, en aan technologieën om deze methoden toe te passen bij het oplossen van praktische problemen. De presentatie gaat vergezeld van gedetailleerd commentaar en talrijke voorbeelden.
Methodologische instructies kunnen worden gebruikt voor de eerste kennismaking met de bestudeerde stof, bij het maken van aantekeningen bij hoorcolleges, ter voorbereiding op praktische lessen, om verworven kennis, vaardigheden en capaciteiten te consolideren. Bovendien zal de handleiding ook nuttig zijn voor studenten als naslagwerk, waardoor ze zich snel kunnen herinneren wat eerder is bestudeerd.
Aan het einde van het werk staan voorbeelden en taken die leerlingen in zelfcontrolemodus kunnen uitvoeren.
De richtlijnen zijn bedoeld voor deeltijd- en voltijdstudenten.
BASISCONCEPTEN
De waarschijnlijkheidstheorie bestudeert de objectieve patronen van massale willekeurige gebeurtenissen. Het is de theoretische basis voor wiskundige statistiek, die zich bezighoudt met de ontwikkeling van methoden voor het verzamelen, beschrijven en verwerken van observatieresultaten. Door observaties (testen, experimenten), d.w.z. ervaring in de brede zin van het woord, kennis van de verschijnselen van de echte wereld ontstaat.
Bij onze praktische activiteiten komen we vaak verschijnselen tegen waarvan de uitkomst niet kan worden voorspeld en waarvan de uitkomst afhangt van het toeval.
Een willekeurig fenomeen kan worden gekarakteriseerd door de verhouding tussen het aantal keren dat het voorkomt en het aantal pogingen, waarbij het in elk ervan, onder dezelfde omstandigheden van alle pogingen, wel of niet zou kunnen voorkomen.
Waarschijnlijkheidstheorie is een tak van de wiskunde waarin willekeurige verschijnselen (gebeurtenissen) worden bestudeerd en patronen worden geïdentificeerd wanneer ze zich massaal herhalen.
Wiskundige statistiek is een tak van de wiskunde die zich bezighoudt met de studie van methoden voor het verzamelen, systematiseren, verwerken en gebruiken van statistische gegevens om wetenschappelijk onderbouwde conclusies te verkrijgen en beslissingen te nemen.
In dit geval worden statistische gegevens opgevat als een reeks getallen die de kwantitatieve kenmerken vertegenwoordigen van de kenmerken van de onderzochte objecten die ons interesseren. Statistische gegevens worden verkregen als resultaat van speciaal ontworpen experimenten en observaties.
Statistische gegevens zijn in wezen afhankelijk van veel willekeurige factoren. Daarom is wiskundige statistiek nauw verwant aan de waarschijnlijkheidstheorie, die de theoretische basis ervan vormt.
I. WAARSCHIJNLIJKHEID. Stellingen van optelling en vermenigvuldiging van waarschijnlijkheden
1.1. Basisconcepten van combinatoriek
In de tak van de wiskunde, die combinatoriek wordt genoemd, worden enkele problemen opgelost die verband houden met het overwegen van verzamelingen en de samenstelling van verschillende combinaties van elementen van deze verzamelingen. Als we bijvoorbeeld 10 verschillende getallen 0, 1, 2, 3,: , 9 nemen en daar combinaties van maken, krijgen we verschillende getallen, bijvoorbeeld 143, 431, 5671, 1207, 43, enz.
We zien dat sommige van deze combinaties alleen verschillen in de volgorde van de cijfers (bijvoorbeeld 143 en 431), andere - in de cijfers die erin zijn opgenomen (bijvoorbeeld 5671 en 1207), en andere verschillen ook in het aantal cijfers (bijvoorbeeld 143 en 43).
De resulterende combinaties voldoen dus aan verschillende voorwaarden.
Afhankelijk van de compositieregels kunnen drie soorten combinaties worden onderscheiden: permutaties, plaatsingen, combinaties.
Laten we eerst kennis maken met het concept faculteit.
Het product van alle natuurlijke getallen van 1 tot en met n wordt genoemd n-factorieel en schrijf.
Bereken: a) ; B) ; V).
Oplossing. A) .
b) Sinds ![]() , dan kunnen we het tussen haakjes zetten
, dan kunnen we het tussen haakjes zetten
Dan krijgen wij
V) ![]() .
.
Herschikkingen.
Een combinatie van n elementen die alleen van elkaar verschillen in de volgorde van de elementen wordt een permutatie genoemd.
Permutaties worden aangegeven met het symbool Pn , waarbij n het aantal elementen is dat in elke permutatie is opgenomen. ( R- eerste letter van een Frans woord permutatie- herschikking).
Het aantal permutaties kan worden berekend met behulp van de formule
of gebruik faculteit:
Laten we dat onthouden 0!=1 en 1!=1.
Voorbeeld 2. Op hoeveel manieren kunnen zes verschillende boeken op één plank worden gerangschikt?
Oplossing. Het vereiste aantal manieren is gelijk aan het aantal permutaties van 6 elementen, d.w.z.
Plaatsingen.
Berichten van M elementen erin N in elk worden dergelijke verbindingen genoemd die van elkaar verschillen, hetzij door de elementen zelf (minstens één), hetzij door de volgorde van hun rangschikking.
Plaatsingen worden aangegeven door het symbool, waar M- het aantal van alle beschikbare elementen, N- het aantal elementen in elke combinatie. ( A- eerste letter van een Frans woord regeling, wat ‘plaatsing, orde brengen’ betekent).
Tegelijkertijd wordt aangenomen dat nm.
Met behulp van de formule kan het aantal plaatsingen worden berekend
![]() ,
,
die. aantal van alle mogelijke plaatsingen vanaf M elementen door N gelijk is aan het product N opeenvolgende gehele getallen, waarvan de grootste is M.
Laten we deze formule in faculteitsvorm schrijven:
Voorbeeld 3. Hoeveel opties voor het uitdelen van drie vouchers aan sanatoria met verschillende profielen kunnen voor vijf aanvragers worden samengesteld?
Oplossing. Het vereiste aantal opties is gelijk aan het aantal plaatsingen van 5 elementen van 3 elementen, d.w.z.
![]() .
.
Combinaties.
Combinaties zijn alle mogelijke combinaties van M elementen door N, die op ten minste één element van elkaar verschillen (hier M En N- natuurlijke getallen, en n m).
Aantal combinaties van M elementen door N worden aangegeven met ( MET-de eerste letter van een Frans woord combinatie- combinatie).
Over het algemeen is het aantal M elementen door N gelijk aan het aantal plaatsingen van M elementen door N, gedeeld door het aantal permutaties van N elementen:
Met behulp van factoriële formules voor het aantal plaatsingen en permutaties verkrijgen we:
![]()
Voorbeeld 4. In een team van 25 mensen moet je er vier inzetten om in een bepaald gebied te werken. Op hoeveel manieren kan dit gedaan worden?
Oplossing. Omdat de volgorde van de vier gekozen mensen er niet toe doet, zijn er manieren om dit te doen.
We vinden met behulp van de eerste formule
![]() .
.
Bovendien worden bij het oplossen van problemen de volgende formules gebruikt, die de basiseigenschappen van combinaties weergeven:
(ze gaan per definitie uit van en);
![]() .
.
1.2. Combinatorische problemen oplossen
Taak 1. Er worden 16 vakken bestudeerd aan de faculteit. Voor maandag moet je 3 vakken in je agenda zetten. Op hoeveel manieren kan dit gedaan worden?
Oplossing. Er zijn net zoveel manieren om drie van de zestien items te plannen als u de plaatsing van zestien items per drie kunt regelen.
Taak 2. Van de 15 objecten moet je 10 objecten selecteren. Op hoeveel manieren kan dit gedaan worden?

Taak 3. Vier teams namen deel aan de competitie. Hoeveel opties zijn er mogelijk om de zetels onderling te verdelen?
![]() .
.
Probleem 4. Op hoeveel manieren kan een patrouille van drie soldaten en één officier worden gevormd als er 80 soldaten en drie officieren zijn?
Oplossing. Je kunt een soldaat op patrouille kiezen
manieren, en officieren op manieren. Omdat elke officier met elk team soldaten kan meegaan, zijn er maar een beperkt aantal manieren.
Taak 5. Vind , als bekend is dat .
Sinds , krijgen we
![]() ,
,
![]() ,
,
![]()
Per definitie van een combinatie volgt dat , . Dat. .
1.3. Het concept van een willekeurige gebeurtenis. Soorten evenementen. Waarschijnlijkheid van de gebeurtenis
Elke actie, fenomeen, observatie met verschillende uitkomsten, gerealiseerd onder een gegeven reeks omstandigheden, zal worden genoemd test.
Het resultaat van deze actie of observatie wordt genoemd evenement .
Als een gebeurtenis onder bepaalde omstandigheden wel of niet kan plaatsvinden, wordt deze gebeurtenis genoemd willekeurig . Wanneer het zeker is dat een gebeurtenis zal plaatsvinden, wordt deze opgeroepen betrouwbaar , en in het geval dat het duidelijk niet kan gebeuren, - onmogelijk.
De evenementen worden genoemd onverenigbaar , als er maar één ervan elke keer kan verschijnen.
De evenementen worden genoemd gewricht indien, onder gegeven omstandigheden, het optreden van een van deze gebeurtenissen het optreden van een ander tijdens dezelfde test niet uitsluit.
De evenementen worden genoemd tegenovergestelde , als deze, als enige uitkomsten, onder de testomstandigheden onverenigbaar zijn.
Gebeurtenissen worden meestal aangegeven met hoofdletters van het Latijnse alfabet: EEN, B, C, D, : .
Een compleet systeem van gebeurtenissen A 1 , A 2 , A 3 , : , An is een reeks incompatibele gebeurtenissen, waarvan het optreden van ten minste één verplicht is tijdens een bepaalde test.
Als een compleet systeem uit twee incompatibele gebeurtenissen bestaat, worden dergelijke gebeurtenissen tegengesteld genoemd en aangeduid met A en .
Voorbeeld. De doos bevat 30 genummerde ballen. Bepaal welke van de volgende gebeurtenissen onmogelijk, betrouwbaar of tegenstrijdig zijn:
pakte een genummerde bal (A);
kreeg een bal met een even getal (IN);
kreeg een bal met een oneven nummer (MET);
kreeg een bal zonder nummer (D).
Wie van hen vormt een complete groep?
Oplossing . A- betrouwbaar evenement; D- onmogelijke gebeurtenis;
In en MET- tegengestelde gebeurtenissen.
De volledige groep evenementen bestaat uit A En D, V En MET.
De waarschijnlijkheid van een gebeurtenis wordt beschouwd als een maatstaf voor de objectieve mogelijkheid dat een willekeurige gebeurtenis plaatsvindt.
1.4. Klassieke definitie van waarschijnlijkheid
Een getal dat de mate van de objectieve mogelijkheid van een gebeurtenis uitdrukt, wordt genoemd waarschijnlijkheid deze gebeurtenis en wordt aangegeven door het symbool R(A).
Definitie. Waarschijnlijkheid van de gebeurtenis A is de verhouding van het aantal uitkomsten m dat het optreden van een bepaalde gebeurtenis bevordert A, naar het nummer N alle uitkomsten (inconsistent, alleen mogelijk en even mogelijk), d.w.z. .
Om de waarschijnlijkheid van een gebeurtenis te bepalen, is het daarom noodzakelijk, nadat we verschillende uitkomsten van de test hebben overwogen, alle mogelijke inconsistente uitkomsten te berekenen. N, kies het aantal uitkomsten m waarin we geïnteresseerd zijn en bereken de verhouding M Naar N.
Uit deze definitie volgen de volgende eigenschappen:
De waarschijnlijkheid van elke test is een niet-negatief getal dat niet groter is dan één.
Het aantal m van de vereiste gebeurtenissen ligt inderdaad binnen . Beide delen verdelen in N, we krijgen
2. De waarschijnlijkheid van een betrouwbare gebeurtenis is gelijk aan één, omdat .
3. De waarschijnlijkheid van een onmogelijke gebeurtenis is nul, aangezien .
Probleem 1. In een loterij van 1000 loten zijn er 200 winnende loten. Er wordt willekeurig één kaartje uitgenomen. Wat is de kans dat dit ticket een winnaar is?
Oplossing. Het totale aantal verschillende uitkomsten is N=1000. Het aantal uitkomsten dat gunstig is voor het winnen is m=200. Volgens de formule krijgen we
![]() .
.
Probleem 2. In een batch van 18 onderdelen zijn er 4 defecte. Er worden willekeurig 5 delen geselecteerd. Bereken de kans dat twee van deze vijf onderdelen defect zijn.
Oplossing. Aantal van alle even mogelijke onafhankelijke uitkomsten N gelijk aan het aantal combinaties van 18 bij 5, d.w.z.
Laten we het getal m tellen dat de voorkeur geeft aan gebeurtenis A. Onder de vijf willekeurig genomen onderdelen moeten er drie goede en twee defecte zijn. Het aantal manieren om twee defecte onderdelen te selecteren uit 4 bestaande defecte onderdelen is gelijk aan het aantal combinaties van 4 bij 2:
Het aantal manieren om drie kwaliteitsonderdelen te selecteren uit 14 beschikbare kwaliteitsonderdelen is gelijk aan
![]() .
.
Elke groep goede onderdelen kan worden gecombineerd met elke groep defecte onderdelen, dus het totale aantal combinaties M bedraagt
De vereiste waarschijnlijkheid van gebeurtenis A is gelijk aan de verhouding van het aantal uitkomsten m gunstig voor deze gebeurtenis en het aantal n van alle even mogelijke onafhankelijke uitkomsten:
![]() .
.
De som van een eindig aantal gebeurtenissen is een gebeurtenis die bestaat uit het optreden van ten minste één ervan.
De som van twee gebeurtenissen wordt aangegeven met het symbool A+B en de som N gebeurtenissen met het symbool A 1 +A 2 + : +A n.
Waarschijnlijkheidsadditiestelling.
De waarschijnlijkheid van de som van twee onverenigbare gebeurtenissen is gelijk aan de som van de waarschijnlijkheden van deze gebeurtenissen.
Gevolg 1. Als de gebeurtenis A 1, A 2, :,A n een compleet systeem vormen, dan is de som van de kansen op deze gebeurtenissen gelijk aan één.
Gevolg 2. De som van de kansen op tegengestelde gebeurtenissen en is gelijk aan één.
![]() .
.
Probleem 1. Er zijn 100 loten. Het is bekend dat 5 kaartjes elk 20.000 roebel winnen, 10 kaartjes 15.000 roebel winnen, 15 kaartjes 10.000 roebel winnen, 25 kaartjes 2.000 roebel winnen. en voor de rest niets. Bereken de kans dat het gekochte ticket een winst van minimaal 10.000 roebel zal opleveren.
Oplossing. Laat A, B en C evenementen zijn die erin bestaan dat het gekochte ticket een winst ontvangt van respectievelijk 20.000, 15.000 en 10.000 roebel. aangezien de gebeurtenissen A, B en C dus onverenigbaar zijn
Taak 2. De correspondentieafdeling van een technische school ontvangt tests in wiskunde van steden A, B En MET. Waarschijnlijkheid van het ontvangen van een test van de stad A gelijk aan 0,6, vanuit de stad IN- 0,1. Bereken de kans dat de volgende test uit de stad komt MET.
Moeder heeft het frame gewassen
Aan het einde van de lange zomervakantie is het tijd om langzaam terug te keren naar de hogere wiskunde en plechtig het lege Verdov-bestand te openen om een nieuwe sectie te maken - . Ik geef toe dat de eerste regels niet eenvoudig zijn, maar de eerste stap is de helft, dus ik raad iedereen aan het inleidende artikel zorgvuldig te bestuderen, waarna het beheersen van het onderwerp twee keer gemakkelijker zal zijn! Ik overdrijf helemaal niet. …Aan de vooravond van de volgende 1 september herinner ik me het eerste leerjaar en de primer…. Letters vormen lettergrepen, lettergrepen vormen woorden, woorden vormen korte zinnen - mama waste het frame. Het beheersen van turver- en wiskundige statistieken is net zo eenvoudig als leren lezen! Hiervoor moet u echter de belangrijkste termen, concepten en aanduidingen kennen, evenals enkele specifieke regels, die het onderwerp van deze les vormen.
Maar accepteer eerst mijn felicitaties voor het begin (voortzetting, voltooiing, markeer wat van toepassing is) van het schooljaar en accepteer het geschenk. Het beste cadeau is een boek, en voor zelfstandig werk raad ik de volgende literatuur aan:
1) Gmurman V.E. Waarschijnlijkheidstheorie en wiskundige statistiek
Een legendarisch leerboek dat meer dan tien herdrukken heeft gehad. Het onderscheidt zich door zijn begrijpelijkheid en uiterst eenvoudige presentatie van de stof, en de eerste hoofdstukken zijn, denk ik, al volledig toegankelijk voor studenten in de groepen 6-7.
2) Gmurman V.E. Gids voor het oplossen van problemen in de waarschijnlijkheidstheorie en wiskundige statistiek
Een oplossingenboek van dezelfde Vladimir Efimovich met gedetailleerde voorbeelden en problemen.
NODIG download beide boeken van internet of ontvang de papieren originelen! De versie uit de jaren 60 en 70 zal ook werken, wat nog beter is voor dummies. Hoewel de uitdrukking "waarschijnlijkheidstheorie voor dummies" nogal belachelijk klinkt, omdat bijna alles beperkt is tot elementaire rekenkundige bewerkingen. Ze slaan echter op sommige plaatsen over derivaten En integralen, maar dit is alleen op plaatsen.
Ik zal proberen dezelfde helderheid van presentatie te bereiken, maar ik moet waarschuwen dat mijn cursus daarop gericht is probleemoplossing en theoretische berekeningen worden tot een minimum beperkt. Dus als je een gedetailleerde theorie nodig hebt, bewijzen van stellingen (stellingen-stellingen!), raadpleeg dan het leerboek. Nou ja, wie wil problemen leren oplossen in waarschijnlijkheidstheorie en wiskundige statistiek in de kortst mogelijke tijd, Volg mij!
Dat is genoeg om te beginnen =)
Terwijl u de artikelen leest, is het raadzaam om (althans kort) kennis te maken met aanvullende taken van de beschouwde typen. Op de pagina Kant-en-klare oplossingen voor hogere wiskunde De bijbehorende pdf's met voorbeelden van oplossingen worden geplaatst. Er zal ook aanzienlijke hulp worden verleend IDZ 18.1 Rjaboesjko(eenvoudiger) en loste IDZ op volgens de collectie van Chudesenko(moeilijker).
1) Hoeveelheid twee gebeurtenissen en de gebeurtenis wordt genoemd, namelijk dat deze zal plaatsvinden of evenement of evenement of beide gebeurtenissen tegelijkertijd. In het geval dat evenementen onverenigbaar, de laatste optie verdwijnt, dat wil zeggen dat deze kan voorkomen of evenement of evenement .
De regel geldt ook voor een groter aantal termen, bijvoorbeeld de gebeurtenis ![]() is wat er zal gebeuren minstens een uit evenementen
is wat er zal gebeuren minstens een uit evenementen ![]() , A als gebeurtenissen onverenigbaar zijn – dan één ding en maar één ding evenement vanaf dit bedrag: of evenement , of evenement , of evenement , of evenement , of evenement .
, A als gebeurtenissen onverenigbaar zijn – dan één ding en maar één ding evenement vanaf dit bedrag: of evenement , of evenement , of evenement , of evenement , of evenement .
Er zijn genoeg voorbeelden:
Gebeurtenissen (bij het gooien van een dobbelsteen verschijnen geen 5 punten) zijn wat er zal verschijnen of 1, of 2, of 3, of 4, of 6 punten.
Gebeurtenis (zal dalen niet meer twee punten) is dat er 1 verschijnt of 2punten.
Evenement ![]() (er zal een even aantal punten zijn) is wat verschijnt of 2 of 4 of 6 punten.
(er zal een even aantal punten zijn) is wat verschijnt of 2 of 4 of 6 punten.
De gebeurtenis is dat er een rode kaart (hart) uit de stapel wordt getrokken of tamboerijn), en de gebeurtenis ![]() – dat de “foto” wordt geëxtraheerd (jack of dame of koning of ace).
– dat de “foto” wordt geëxtraheerd (jack of dame of koning of ace).
Iets interessanter is het geval bij gezamenlijke evenementen:
Het evenement is dat er een club uit het kaartspel wordt getrokken of zeven of zeven clubs Volgens de hierboven gegeven definitie, tenminste iets- of welke club dan ook, of welke zeven dan ook, of hun "kruispunt" - zeven van clubs. Het is eenvoudig te berekenen dat deze gebeurtenis overeenkomt met 12 elementaire uitkomsten (9 clubkaarten + 3 resterende zevens).
De afspraak is dat het morgen om 12.00 uur zal zijn TEN MINSTE EEN van de optelbare gezamenlijke evenementen, namelijk:
– of er is alleen maar regen / alleen onweer / alleen zon;
– of er zullen slechts enkele gebeurtenissen plaatsvinden (regen + onweer / regen + zon / onweer + zon);
– of alle drie de gebeurtenissen verschijnen tegelijkertijd.
Dat wil zeggen dat de gebeurtenis zeven mogelijke uitkomsten omvat.
De tweede pijler van de algebra van gebeurtenissen:
2) Het werk twee gebeurtenissen en noem een gebeurtenis die bestaat uit het gezamenlijk optreden van deze gebeurtenissen, met andere woorden, vermenigvuldiging betekent dat er onder bepaalde omstandigheden En evenement , En evenement . Een soortgelijke uitspraak geldt voor een groter aantal gebeurtenissen; een werk impliceert bijvoorbeeld dat het onder bepaalde omstandigheden zal gebeuren En evenement , En evenement , En evenement , …, En evenement .
Overweeg een test waarbij twee munten worden opgeworpen en de volgende evenementen:
– er verschijnt kop op de eerste munt;
– de eerste munt levert kop op;
– er verschijnt kop op de 2e munt;
– de 2e munt levert kop op.
Dan:
En op de 2e) verschijnen er koppen;
– de gebeurtenis is dat op beide munten (op de 1e En op de 2e) zullen het koppen zijn;
– de gebeurtenis is dat de eerste munt kop oplevert En de 2e munt is staarten;
– de gebeurtenis is dat de eerste munt kop oplevert En op de 2e munt staat een adelaar.
Het is gemakkelijk om die gebeurtenissen te zien onverenigbaar (omdat het bijvoorbeeld niet 2 kop en 2 munt tegelijk kan zijn) en vorm volledige groep (sindsdien in aanmerking genomen Alle mogelijke uitkomsten van het opgooien van twee munten). Laten we deze gebeurtenissen samenvatten: . Hoe moet dit bericht worden geïnterpreteerd? Heel eenvoudig: vermenigvuldiging betekent een logische verbinding EN, en toevoeging – OF. Het bedrag is dus gemakkelijk af te lezen in begrijpelijke menselijke taal: “Er zullen twee hoofden verschijnen of twee hoofden of de eerste munt zal kop opleveren En op de 2e staarten of de eerste munt zal kop opleveren En op de 2e munt staat een adelaar"
Dit was een voorbeeld toen in één proef Er zijn meerdere voorwerpen bij betrokken, in dit geval twee munten. Een ander veel voorkomend schema bij praktische problemen is opnieuw testen , wanneer bijvoorbeeld dezelfde dobbelsteen drie keer achter elkaar wordt gegooid. Beschouw ter demonstratie de volgende gebeurtenissen:
– bij de 1e worp krijg je 4 punten;
– bij de 2e worp krijg je 5 punten;
– bij de 3e worp krijg je 6 punten.
Dan het evenement ![]() is dat je bij de eerste worp 4 punten krijgt En bij de 2e worp krijg je 5 punten En bij de 3e worp krijg je 6 punten. Het is duidelijk dat er in het geval van een kubus aanzienlijk meer combinaties (uitkomsten) zullen zijn dan wanneer we een munt zouden opgooien.
is dat je bij de eerste worp 4 punten krijgt En bij de 2e worp krijg je 5 punten En bij de 3e worp krijg je 6 punten. Het is duidelijk dat er in het geval van een kubus aanzienlijk meer combinaties (uitkomsten) zullen zijn dan wanneer we een munt zouden opgooien.
...Ik begrijp dat de geanalyseerde voorbeelden misschien niet erg interessant zijn, maar dit zijn zaken die je vaak tegenkomt bij problemen en waar je niet aan kunt ontsnappen. Naast een munt wachten een kubus en een pak kaarten op je, urnen met veelkleurige ballen, verschillende anonieme mensen die op een doelwit schieten, en een onvermoeibare werker die voortdurend wat details uitwerkt =)
Waarschijnlijkheid van de gebeurtenis
Waarschijnlijkheid van de gebeurtenis is het centrale concept van de waarschijnlijkheidstheorie. ...Een moordend logisch iets, maar we moesten ergens beginnen =) Er zijn verschillende benaderingen voor de definitie ervan:
;
Geometrische definitie van waarschijnlijkheid
;
Statistische definitie van waarschijnlijkheid
.
In dit artikel zal ik me concentreren op de klassieke definitie van waarschijnlijkheid, die het meest wordt gebruikt in onderwijstaken.
Benamingen. De waarschijnlijkheid van een bepaalde gebeurtenis wordt aangegeven met een Latijnse hoofdletter, en de gebeurtenis zelf wordt tussen haakjes gezet en fungeert als een soort argument. Bijvoorbeeld:
Ook wordt de kleine letter veel gebruikt om waarschijnlijkheid aan te duiden. In het bijzonder kunt u de omslachtige aanduidingen van gebeurtenissen en hun waarschijnlijkheden achterwege laten ![]() ten gunste van de volgende stijl::
ten gunste van de volgende stijl::
– de kans dat een toss kop oplevert;
– de kans dat een dobbelsteenworp 5 punten oplevert;
– de kans dat een kaart van de klaverenkleur uit de stapel wordt getrokken.
Deze optie is populair bij het oplossen van praktische problemen, omdat u hiermee de opname van de oplossing aanzienlijk kunt verminderen. Net als in het eerste geval is het handig om hier “pratende” subscripts/superscripts te gebruiken.
Iedereen heeft de cijfers die ik zojuist hierboven heb opgeschreven al lang geraden, en nu zullen we ontdekken hoe ze zijn uitgekomen:
Klassieke definitie van waarschijnlijkheid:
De waarschijnlijkheid dat een gebeurtenis zich voordoet in een bepaalde test wordt de ratio genoemd, waarbij:
– totaal aantal van allemaal evengoed mogelijk, elementair uitkomsten van deze test, welke vorm volledige groep evenementen;
- hoeveelheid elementair uitkomsten, gunstig evenement.
Bij het opgooien van een munt kunnen er kop of munt uitvallen - deze gebeurtenissen vormen zich volledige groep, dus het totale aantal uitkomsten; tegelijkertijd, elk van hen elementair En evengoed mogelijk. De gebeurtenis wordt begunstigd door de uitkomst (koppen). Volgens de klassieke definitie van waarschijnlijkheid: ![]() .
.
Op dezelfde manier kunnen, als gevolg van het gooien van een dobbelsteen, elementaire, even mogelijke uitkomsten verschijnen, waardoor een complete groep wordt gevormd, en de gebeurtenis wordt begunstigd door een enkele uitkomst (een vijf gooien). Daarom: ![]() DIT IS NIET AANVAARD (hoewel het niet verboden is om percentages in je hoofd te schatten).
DIT IS NIET AANVAARD (hoewel het niet verboden is om percentages in je hoofd te schatten).
Het is gebruikelijk om fracties van een eenheid te gebruiken, en uiteraard kan de waarschijnlijkheid variëren binnen . Bovendien, als , dan is er sprake van een gebeurtenis onmogelijk, Als - betrouwbaar, en als , dan hebben we het over willekeurig evenement.
! Als u tijdens het oplossen van een probleem een andere waarschijnlijkheidswaarde krijgt, zoek dan naar de fout!
In de klassieke benadering van het bepalen van de waarschijnlijkheid worden extreme waarden (nul en één) verkregen door precies dezelfde redenering. Laat willekeurig 1 bal trekken uit een bepaalde urn met daarin 10 rode ballen. Denk eens aan de volgende gebeurtenissen:
in een enkele proef zal een gebeurtenis met een lage kans niet optreden.
Dit is de reden waarom u de jackpot in de loterij niet wint als de waarschijnlijkheid van deze gebeurtenis bijvoorbeeld 0,00000001 is. Ja, ja, jij bent het – met het enige ticket in een bepaalde oplage. Een groter aantal kaartjes en een groter aantal trekkingen zullen je echter niet veel helpen. ...Als ik anderen hierover vertel, hoor ik vrijwel altijd als reactie: “maar iemand wint.” Oké, laten we dan het volgende experiment doen: koop vandaag of morgen een lot voor een willekeurige loterij (wacht niet langer!). En als je wint... nou ja, tenminste meer dan 10 kilo, meld je dan aan - ik zal uitleggen waarom dit gebeurde. Voor een percentage natuurlijk =) =)
Maar er is geen reden om verdrietig te zijn, want er is een tegengesteld principe: als de waarschijnlijkheid van een bepaalde gebeurtenis heel dicht bij één ligt, dan zal dat in één enkele proef ook zo zijn. bijna zeker zal gebeuren. Daarom is het niet nodig om bang te zijn voordat je met een parachute springt, integendeel: glimlach! Er moeten immers volkomen ondenkbare en fantastische omstandigheden ontstaan voordat beide parachutes falen.
Hoewel dit allemaal lyriek is, kan het eerste principe, afhankelijk van de inhoud van de gebeurtenis, vrolijk blijken te zijn, en het tweede – droevig; of zelfs beide zijn parallel.
Misschien is dat genoeg voor nu, in de klas Klassieke waarschijnlijkheidsproblemen we halen het maximale uit de formule. In het laatste deel van dit artikel zullen we één belangrijke stelling beschouwen:
De som van de kansen op gebeurtenissen die een complete groep vormen, is gelijk aan één. Grof gezegd: als gebeurtenissen een complete groep vormen, zal er met 100% waarschijnlijkheid één van deze gebeurtenissen plaatsvinden. In het eenvoudigste geval wordt een complete groep gevormd door tegengestelde gebeurtenissen, bijvoorbeeld:
– als gevolg van het opgooien van munten verschijnen er koppen;
– het resultaat van een toss is kop.
Volgens de stelling: ![]()
Het is absoluut duidelijk dat deze gebeurtenissen evengoed mogelijk zijn en dat hun kansen hetzelfde zijn ![]() .
.
Vanwege de gelijkheid van kansen worden vaak even mogelijke gebeurtenissen genoemd even waarschijnlijk . En hier is een tongbreker om de mate van dronkenschap te bepalen =)
Voorbeeld met een kubus: gebeurtenissen zijn dus tegengesteld ![]() .
.
De stelling in kwestie is handig omdat je hiermee snel de waarschijnlijkheid van de tegenovergestelde gebeurtenis kunt vinden. Dus als de kans bekend is dat er een vijf wordt gegooid, is het eenvoudig om de kans te berekenen dat deze niet wordt gegooid:
![]()
Dit is veel eenvoudiger dan het optellen van de waarschijnlijkheden van vijf elementaire uitkomsten. Voor elementaire uitkomsten geldt deze stelling overigens ook:
. Als dit bijvoorbeeld de kans is dat de schutter het doel zal raken, dan is dit ook de kans dat hij zal missen.
! In de waarschijnlijkheidstheorie is het onwenselijk om letters voor andere doeleinden te gebruiken.
Ter ere van de Kennisdag geef ik geen huiswerk op =), maar het is wel heel belangrijk dat je de volgende vragen kunt beantwoorden:
– Welke soorten evenementen bestaan er?
– Wat is kans en gelijke mogelijkheid van een gebeurtenis?
– Hoe begrijp je de termen compatibiliteit/incompatibiliteit van evenementen?
– Wat is een complete groep gebeurtenissen, tegengestelde gebeurtenissen?
– Wat betekent optellen en vermenigvuldigen van gebeurtenissen?
– Wat is de essentie van de klassieke definitie van waarschijnlijkheid?
– Waarom is de stelling voor het optellen van de waarschijnlijkheden van gebeurtenissen die een complete groep vormen nuttig?
Nee, je hoeft niets te proppen, dit zijn slechts de basisprincipes van de waarschijnlijkheidstheorie - een soort primer die snel in je hoofd past. En om dit zo snel mogelijk te laten gebeuren, stel ik voor dat u vertrouwd raakt met de lessen
Waarschijnlijkheidstheorie en wiskundige statistiek
1. THEORETISCH DEEL
1 Convergentie van reeksen willekeurige variabelen en kansverdelingen
In de waarschijnlijkheidstheorie heeft men te maken met verschillende soorten convergentie van willekeurige variabelen. Laten we de volgende hoofdtypen van convergentie bekijken: door waarschijnlijkheid, met waarschijnlijkheid één, door middel van orde p, door verdeling.
Laten,... willekeurige variabelen zijn die zijn gedefinieerd op een bepaalde waarschijnlijkheidsruimte (, Ф, P).
Definitie 1. Van een reeks willekeurige variabelen, ... wordt gezegd dat ze in waarschijnlijkheid convergeren naar een willekeurige variabele (notatie:), als er een > 0 is
Definitie 2. Er wordt gezegd dat een reeks willekeurige variabelen, ... met waarschijnlijkheid één (vrijwel zeker, bijna overal) convergeert naar een willekeurige variabele als
die. als de reeks uitkomsten waarvoor () niet convergeert naar () een waarschijnlijkheid van nul heeft.
Dit type convergentie wordt als volgt aangegeven: , of, of.
Definitie 3. Een reeks willekeurige variabelen ... wordt gemiddeld-convergent van orde p, 0 genoemd< p < , если
Definitie 4. Van een reeks willekeurige variabelen... wordt gezegd dat deze in de distributie convergeert naar een willekeurige variabele (notatie :) als er een begrensde continue functie is
Convergentie in de verdeling van willekeurige variabelen wordt alleen gedefinieerd in termen van de convergentie van hun distributiefuncties. Daarom is het zinvol om over dit soort convergentie te praten, zelfs als willekeurige variabelen in verschillende waarschijnlijkheidsruimten zijn gespecificeerd.
Stelling 1.
a) Voor (P-a.s.) is het noodzakelijk en voldoende dat voor elke > 0
) De reeks () is fundamenteel met waarschijnlijkheid één als en slechts als voor elke > 0.
Bewijs.
a) Zij A = (: |- | ), A = A. Dan
Daarom is bewering a) het resultaat van de volgende reeks implicaties:
P(: )= 0 P() = 0 = 0 P(A) = 0, m 1 P(A) = 0, > 0 P() 0, n 0, > 0 P( ) 0,
n 0, > 0.) Laten we = (: ), = aanduiden. Dan is (: (()) niet fundamenteel ) = en op dezelfde manier als in a) wordt aangetoond dat (: (()) niet fundamenteel is ) = 0 P( ) 0, n.
De stelling is bewezen
Stelling 2. (Cauchy-criterium voor vrijwel zekere convergentie)
Om ervoor te zorgen dat een reeks willekeurige variabelen () convergeert met waarschijnlijkheid één (naar een willekeurige variabele), is het noodzakelijk en voldoende dat deze fundamenteel is met waarschijnlijkheid één.
Bewijs.
Als, dan +
waaruit volgt de noodzaak van de voorwaarden van de stelling.
Laat nu de reeks () fundamenteel zijn met waarschijnlijkheid één. Laten we L = (: (()) niet fundamenteel) aanduiden. Dan is de nummerreeks () voor iedereen van fundamenteel belang en bestaat er, volgens het Cauchy-criterium voor nummerreeksen, (). Laten we
Deze gedefinieerde functie is een willekeurige variabele en.
De stelling is bewezen.
2 Werkwijze karakteristieke functies
De methode van karakteristieke functies is een van de belangrijkste instrumenten van het analytische apparaat van de waarschijnlijkheidstheorie. Naast willekeurige variabelen (waarbij reële waarden worden aangenomen), vereist de theorie van karakteristieke functies het gebruik van willekeurige variabelen met complexe waarden.
Veel van de definities en eigenschappen met betrekking tot willekeurige variabelen kunnen gemakkelijk worden overgedragen naar het complexe geval. Dus de wiskundige verwachting M ?willekeurige variabele met complexe waarde ?=?+?? wordt als zeker beschouwd als de wiskundige verwachtingen M zijn bepaald ?hen ?. In dit geval nemen we per definitie aan dat M ?= M ? + ?M ?. Uit de definitie van onafhankelijkheid van willekeurige elementen volgt dat complex gewaardeerde grootheden ?1 =?1+??1 , ?2=?2+??2zijn onafhankelijk als en slechts als paren willekeurige variabelen onafhankelijk zijn ( ?1 , ?1) En ( ?2 , ?2), of, wat hetzelfde is, onafhankelijk ?-algebra F ?1, ?1 en F ?2, ?2.
Samen met de ruimte L 2echte willekeurige variabelen met een eindig tweede moment, kunnen we de Hilbertruimte van willekeurige variabelen met complexe waarden introduceren ?=?+?? met M | ?|2?|2= ?2+?2, en het scalaire product ( ?1 , ?2)=M ?1?2¯ , Waar ?2¯ - complexe geconjugeerde willekeurige variabele.
Bij algebraïsche bewerkingen worden vectoren Rn behandeld als algebraïsche kolommen,
Als rijvectoren is a* - (a1,a2,…,an). Als Rn, dan zal hun scalaire product (a,b) worden opgevat als een hoeveelheid. Het is duidelijk dat
Als aRn en R=||rij|| is dan een matrix van orde nхn
Definitie 1. Stel F = F(x1,...,xn) - n-dimensionale verdelingsfunctie in (, ()). De karakteristieke functie ervan wordt de functie genoemd
Definitie 2 . Als? = (?1,…,?n) is een willekeurige vector gedefinieerd op een waarschijnlijkheidsruimte met waarden in, dan wordt de karakteristieke functie ervan de functie genoemd
waar is F? = F?(х1,….,хn) - vectorverdelingsfunctie?=(?1,…, ?n).
Als de verdelingsfunctie F(x) dichtheid f = f(x) heeft, dan
In dit geval is de karakteristieke functie niets anders dan de Fourier-transformatie van de functie f(x).
Uit (3) volgt dat de karakteristieke functie ??(t) van een willekeurige vector ook kan worden gedefinieerd door de gelijkheid
Basiseigenschappen van karakteristieke functies (in het geval van n=1).
Laten zijn? = ?(?) - willekeurige variabele, F? =F? (x) is de verdelingsfunctie en de karakteristieke functie.
Opgemerkt moet worden dat als, dan.
Inderdaad,
waarbij we gebruik maakten van het feit dat de wiskundige verwachting van het product van onafhankelijke (begrensde) willekeurige variabelen gelijk is aan het product van hun wiskundige verwachtingen.
Eigenschap (6) is van cruciaal belang bij het bewijzen van limietstellingen voor sommen van onafhankelijke willekeurige variabelen met behulp van de methode van karakteristieke functies. In dit opzicht wordt de distributiefunctie op een veel complexere manier uitgedrukt via de distributiefuncties van individuele termen, namelijk waarbij het *-teken een convolutie van de distributies betekent.
Elke verdelingsfunctie kan worden geassocieerd met een willekeurige variabele die deze functie als verdelingsfunctie heeft. Daarom kunnen we ons bij het presenteren van de eigenschappen van karakteristieke functies beperken tot het beschouwen van de karakteristieke functies van willekeurige variabelen.
Stelling 1. Laten zijn? - een willekeurige variabele met verdelingsfunctie F=F(x) en - zijn karakteristieke functie.
De volgende eigenschappen vinden plaats:
) is uniform continu in;
) is een functie met reële waarde als en slechts als de verdeling van F symmetrisch is
)als voor sommige n? 1, dan zijn er voor iedereen derivaten en
)Als het bestaat en eindig is, dan
) Laat voor alle n ? 1 en
dan voor alle |t| De volgende stelling laat zien dat de karakteristieke functie op unieke wijze de verdelingsfunctie bepaalt. Stelling 2 (uniciteit). Laat F en G twee verdelingsfuncties zijn met dezelfde karakteristieke functie, dat wil zeggen voor iedereen De stelling zegt dat de verdelingsfunctie F = F(x) op unieke wijze kan worden hersteld vanuit zijn karakteristieke functie. De volgende stelling geeft een expliciete weergave van de functie F in termen van. Stelling 3 (generalisatieformule). Laat F = F(x) de verdelingsfunctie zijn en de karakteristieke functie ervan. a) Voor twee willekeurige punten a, b (a< b), где функция F = F(х) непрерывна, ) Als dan de verdelingsfunctie F(x) dichtheid f(x) heeft, Stelling 4. Om ervoor te zorgen dat de componenten van een willekeurige vector onafhankelijk zijn, is het noodzakelijk en voldoende dat zijn karakteristieke functie het product is van de karakteristieke functies van de componenten: Stelling van Bochner-Khinchin .
Laat het een continue functie zijn. Om karakteristiek te zijn, is het noodzakelijk en voldoende dat het niet-negatief definitief is, dat wil zeggen voor elke reële t1, ..., tn en alle complexe getallen Stelling 5. Laat de karakteristieke functie van een willekeurige variabele zijn. a) Als voor sommigen de willekeurige variabele een rooster met een stap is ) Als er voor twee verschillende punten een irrationeel getal is, is het dan een willekeurige variabele? is gedegenereerd: waarbij a een constante is. c) Zo ja, is het dan een willekeurige variabele? ontaarden. 1.3 Centrale limietstelling voor onafhankelijke, identiek verdeelde willekeurige variabelen Laat () een reeks onafhankelijke, identiek verdeelde willekeurige variabelen zijn. Verwachting M= a, variantie D= , S = , en Ф(х) is de verdelingsfunctie van de normale wet met parameters (0,1). Laten we nog een reeks willekeurige variabelen introduceren Stelling. Als 0<<, то при n P(< x) Ф(х) равномерно относительно х (). In dit geval wordt de reeks () asymptotisch normaal genoemd. Uit het feit dat M = 1 en uit de continuïteitsstellingen volgt dat er, naast de zwakke convergentie, FM f() Mf() voor elke continu begrensde f, er ook convergentie Mf() Mf() is voor elke continue f , zodat |f(x)|< c(1+|x|) при каком-нибудь. Bewijs. Uniforme convergentie is hier een gevolg van zwakke convergentie en continuïteit van Ф(x). Verder kunnen we, zonder verlies van algemeenheid, aannemen dat a = 0, omdat we anders de reeks () zouden kunnen beschouwen, en de reeks () niet zou veranderen. Om de vereiste convergentie te bewijzen is het daarom voldoende om aan te tonen dat (t) e wanneer a = 0. Dat hebben we gedaan (t) = , waarbij =(t). Omdat M bestaat, bestaat de ontbinding en is deze geldig Daarom is voor n De stelling is bewezen. 1.4 De belangrijkste taken van wiskundige statistiek, hun korte beschrijving Het vaststellen van patronen die massale willekeurige verschijnselen beheersen, is gebaseerd op de studie van statistische gegevens - de resultaten van observaties. De eerste taak van wiskundige statistiek is het aangeven van manieren om statistische informatie te verzamelen en te groeperen. De tweede taak van wiskundige statistiek is het ontwikkelen van methoden voor het analyseren van statistische gegevens, afhankelijk van de doelstellingen van het onderzoek. Bij het oplossen van elk probleem van de wiskundige statistiek zijn er twee informatiebronnen. De eerste en meest definitieve (expliciete) is het resultaat van waarnemingen (experiment) in de vorm van een steekproef uit een algemene populatie van een scalaire of vectorwillekeurige variabele. In dit geval kan de steekproefomvang n worden vastgesteld, of deze kan tijdens het experiment toenemen (dat wil zeggen dat er zogenaamde sequentiële statistische analyseprocedures kunnen worden gebruikt). De tweede bron is alle a priori informatie over de eigenschappen van belang van het object dat wordt bestudeerd, die tot op heden is verzameld. Formeel wordt de hoeveelheid a priori-informatie weerspiegeld in het initiële statistische model dat wordt gekozen bij het oplossen van het probleem. Het is echter niet nodig om te praten over een geschatte bepaling in de gebruikelijke zin van de waarschijnlijkheid van een gebeurtenis op basis van de resultaten van experimenten. Met het bij benadering vaststellen van welke grootheid dan ook wordt doorgaans bedoeld dat het mogelijk is foutgrenzen aan te geven waarbinnen geen fout zal optreden. De frequentie van de gebeurtenis is willekeurig voor een willekeurig aantal experimenten vanwege de willekeur van de resultaten van individuele experimenten. Vanwege de willekeur van de resultaten van individuele experimenten kan de frequentie aanzienlijk afwijken van de waarschijnlijkheid van de gebeurtenis. Door de onbekende waarschijnlijkheid van een gebeurtenis te definiëren als de frequentie van deze gebeurtenis over een groot aantal experimenten, kunnen we daarom de grenzen van de fout niet aangeven en garanderen dat de fout deze grenzen niet zal overschrijden. Daarom praten we in de wiskundige statistiek meestal niet over geschatte waarden van onbekende grootheden, maar over hun geschikte waarden, schattingen. Het probleem van het schatten van onbekende parameters doet zich voor in gevallen waarin de populatieverdelingsfunctie tot op een bepaalde parameter bekend is. In dit geval is het noodzakelijk een statistiek te vinden waarvan de steekproefwaarde voor de beschouwde implementatie xn van een willekeurige steekproef zou kunnen worden beschouwd als een geschatte waarde van de parameter. Een statistiek waarvan de steekproefwaarde voor elke realisatie xn wordt genomen als een geschatte waarde van een onbekende parameter, wordt een puntschatting of eenvoudigweg een schatting genoemd, en is de waarde van de puntschatting. Een puntschatting moet aan zeer specifieke eisen voldoen, wil de steekproefwaarde ervan overeenkomen met de werkelijke waarde van de parameter. Een andere benadering om het beschouwde probleem op te lossen is ook mogelijk: vind dergelijke statistieken en, met waarschijnlijkheid? de volgende ongelijkheid geldt: In dit geval spreken we over intervalschatting voor. Interval wordt het betrouwbaarheidsinterval voor genoemd met de betrouwbaarheidscoëfficiënt?. Nadat een of ander statistisch kenmerk is beoordeeld op basis van de resultaten van experimenten, rijst de vraag: hoe consistent is de veronderstelling (hypothese) dat het onbekende kenmerk precies de waarde heeft die werd verkregen als resultaat van de evaluatie ervan met de experimentele gegevens? Dit is hoe de tweede belangrijke klasse van problemen in de wiskundige statistiek ontstaat: problemen bij het testen van hypothesen. In zekere zin is het probleem van het testen van een statistische hypothese het omgekeerde van het probleem van het schatten van parameters. Bij het schatten van een parameter weten we niets over de werkelijke waarde ervan. Bij het testen van een statistische hypothese wordt om de een of andere reden aangenomen dat de waarde ervan bekend is en het is noodzakelijk om deze veronderstelling te verifiëren op basis van de resultaten van het experiment. Bij veel problemen van de wiskundige statistiek wordt rekening gehouden met reeksen willekeurige variabelen, die op de een of andere manier naar een bepaalde grens (willekeurige variabele of constante) convergeren. De belangrijkste taken van de wiskundige statistiek zijn dus de ontwikkeling van methoden voor het vinden van schattingen en het bestuderen van de nauwkeurigheid van hun benadering van de beoordeelde kenmerken, en de ontwikkeling van methoden voor het testen van hypothesen. 5 Testen van statistische hypothesen: basisconcepten De taak van het ontwikkelen van rationele methoden voor het testen van statistische hypothesen is een van de hoofdtaken van de wiskundige statistiek. Een statistische hypothese (of eenvoudigweg een hypothese) is elke uitspraak over het type of de eigenschappen van de verdeling van willekeurige variabelen die in een experiment worden waargenomen. Stel dat er een steekproef is die een realisatie is van een willekeurige steekproef uit een algemene populatie, waarvan de distributiedichtheid afhangt van een onbekende parameter. Statistische hypothesen over de onbekende werkelijke waarde van een parameter worden parametrische hypothesen genoemd. Bovendien, als het een scalair is, hebben we het over hypothesen met één parameter, en als het een vector is, dan hebben we het over hypothesen met meerdere parameters. Een statistische hypothese wordt eenvoudig genoemd als deze de vorm heeft waar is een gespecificeerde parameterwaarde. Een statistische hypothese wordt complex genoemd als deze de vorm heeft waar is een reeks parameterwaarden die uit meer dan één element bestaan. In het geval van het testen van twee eenvoudige statistische hypothesen van het formulier waar twee gegeven (verschillende) waarden van de parameter zijn, wordt de eerste hypothese gewoonlijk de hoofdhypothese genoemd, en de tweede de alternatieve of concurrerende hypothese. Het criterium, of statistisch criterium, voor het testen van hypothesen is de regel waarmee, op basis van steekproefgegevens, een beslissing wordt genomen over de geldigheid van de eerste of de tweede hypothese. Het criterium wordt gespecificeerd met behulp van een kritische set, die een subset is van de steekproefruimte van een willekeurige steekproef. De beslissing wordt als volgt genomen: ) als de steekproef tot de kritische set behoort, verwerp dan de hoofdhypothese en accepteer de alternatieve hypothese; ) als de steekproef niet tot de kritische set behoort (dat wil zeggen, hij behoort tot het complement van de set tot de steekproefruimte), dan wordt de alternatieve hypothese verworpen en wordt de hoofdhypothese geaccepteerd. Bij gebruik van een criterium zijn de volgende soorten fouten mogelijk: 1) accepteer een hypothese als deze waar is - een fout van de eerste soort; )Het accepteren van een hypothese terwijl deze waar is, is een type II-fout. De kansen op het begaan van fouten van het eerste en tweede type worden aangegeven met: waar is de waarschijnlijkheid van een gebeurtenis, op voorwaarde dat de hypothese waar is. De aangegeven kansen worden berekend met behulp van de verdelingsdichtheidsfunctie van een willekeurige steekproef: De kans op het begaan van een type I-fout wordt ook wel het criterium significantieniveau genoemd. De waarde die gelijk is aan de waarschijnlijkheid dat de hoofdhypothese wordt verworpen als deze waar is, wordt de kracht van de test genoemd. 1.6 Onafhankelijkheidscriterium Er is een steekproef ((XY), ..., (XY)) uit een tweedimensionale verdeling L met een onbekende verdelingsfunctie waarvoor het nodig is om de hypothese H: te testen: waar zijn enkele eendimensionale verdelingsfuncties. Op basis van de methodologie kan een eenvoudige goodness-of-fit-test voor hypothese H worden geconstrueerd. Deze techniek wordt gebruikt voor discrete modellen met een eindig aantal uitkomsten, dus we zijn het erover eens dat de willekeurige variabele een eindig aantal s van sommige waarden aanneemt, die we met letters zullen aanduiden, en de tweede component - k-waarden. Als het oorspronkelijke model een andere structuur heeft, worden de mogelijke waarden van willekeurige variabelen voorlopig afzonderlijk gegroepeerd in de eerste en tweede component. In dit geval wordt de set verdeeld in s-intervallen, de waarde in k-intervallen en de waarde zelf in N=sk-rechthoeken. Laten we aangeven met het aantal waarnemingen van het paar (het aantal monsterelementen dat bij de rechthoek hoort, als de gegevens gegroepeerd zijn), zodat. Het is handig om de waarnemingsresultaten te rangschikken in de vorm van een kruistabel met twee tekens (tabel 1.1). In toepassingen worden met dit meestal twee criteria bedoeld waarmee observatieresultaten worden geclassificeerd. Stel P, i=1,…,s, j=1,…,k. Dan betekent de onafhankelijkheidshypothese dat er s+k-constanten zijn zodanig dat en, d.w.z. Tabel 1.1 Som . . .. . .. . . . . .. . .. . . . . . . . . . . . . . .Som . . .N Hypothese H komt dus neer op de stelling dat frequenties (hun aantal is N = sk) worden verdeeld volgens een polynomiale wet waarbij de kansen op uitkomsten de gespecificeerde specifieke structuur hebben (de vector van de kansen op uitkomsten p wordt bepaald door de waarden r = s + k-2 van onbekende parameters. Om deze hypothese te testen, zullen we schattingen van de maximale waarschijnlijkheid vinden voor de onbekende parameters die het beschouwde schema bepalen. Als de nulhypothese waar is, heeft de waarschijnlijkheidsfunctie de vorm L(p)= waarbij de vermenigvuldiger c niet afhankelijk is van de onbekende parameters. Vanaf hier verkrijgen we, met behulp van de Lagrange-methode van onbepaalde vermenigvuldigers, dat de vereiste schattingen de vorm hebben Daarom statistieken L() op, aangezien het aantal vrijheidsgraden in de limietverdeling gelijk is aan N-1-r=sk-1-(s+k-2)=(s-1)(k-1). Voor een voldoende grote n kan dus de volgende hypothesetestregel worden gebruikt: hypothese H wordt verworpen als en slechts als de statistische waarde van t, berekend op basis van de feitelijke gegevens, voldoet aan de ongelijkheid. Dit criterium heeft een asymptotisch (op) gegeven significantieniveau en wordt het onafhankelijkheidscriterium genoemd. 2. PRAKTIJK DEEL 1 Oplossingen voor problemen met soorten convergentie 1. Bewijs dat convergentie vrijwel zeker convergentie in waarschijnlijkheid impliceert. Geef een testvoorbeeld om aan te tonen dat het omgekeerde niet waar is. Oplossing. Laat een reeks willekeurige variabelen vrijwel zeker convergeren naar een willekeurige variabele x. Dus, voor iemand? > 0 Sindsdien en uit de convergentie van xn naar x volgt vrijwel zeker dat xn qua waarschijnlijkheid naar x convergeert, aangezien in dit geval Maar de tegenovergestelde bewering is niet waar. Laten we een reeks onafhankelijke willekeurige variabelen zijn met dezelfde verdelingsfunctie F(x), gelijk aan nul bij x? 0 en gelijk voor x > 0. Beschouw de reeks Deze reeks convergeert naar nul in waarschijnlijkheid, aangezien neigt naar nul voor elke vaste? En. Convergentie naar nul zal echter vrijwel zeker niet plaatsvinden. Echt neigt naar eenheid, dat wil zeggen, met waarschijnlijkheid 1 voor any en n zullen er realisaties in de reeks zijn die groter zijn dan ?. Merk op dat in de aanwezigheid van enkele aanvullende voorwaarden die aan de grootheden xn worden opgelegd, convergentie in waarschijnlijkheid vrijwel zeker convergentie impliceert. Laat xn een monotone reeks zijn. Bewijs dat in dit geval de convergentie van xn naar x in waarschijnlijkheid de convergentie van xn naar x met waarschijnlijkheid 1 met zich meebrengt. Oplossing. Laat xn dus een monotoon afnemende rij zijn. Om onze redenering te vereenvoudigen, nemen we aan dat x º 0, xn ³ 0 voor alle n. Laat xn in waarschijnlijkheid convergeren naar x, maar convergentie vindt vrijwel zeker niet plaats. Bestaat het dan? > 0, zodat voor alle n Maar wat er is gezegd betekent ook dat voor alle n wat in tegenspraak is met de convergentie van xn naar x in waarschijnlijkheid. Dus voor een monotone reeks convergeert xn, die in waarschijnlijkheid naar x convergeert, ook met waarschijnlijkheid 1 (vrijwel zeker). Laat de reeks xn in waarschijnlijkheid convergeren naar x. Bewijs dat het uit deze reeks mogelijk is een reeks te isoleren die convergeert naar x met een waarschijnlijkheid van 1. Oplossing. Laat een reeks positieve getallen zijn, en laat en zijn positieve getallen zodat de reeks. Laten we een reeks indices n1 construeren Dan de serie Aangezien de reeks convergeert, geldt dat dan voor iedereen? > 0, de rest van de reeks neigt naar nul. Maar dan neigt het naar nul en Bewijs dat convergentie in het gemiddelde van elke positieve orde convergentie in waarschijnlijkheid impliceert. Geef een voorbeeld waaruit blijkt dat het omgekeerde niet waar is. Oplossing. Laat de reeks xn convergeren naar een gemiddelde waarde x van de orde p > 0, dat wil zeggen Laten we de algemene Chebyshev-ongelijkheid gebruiken: voor willekeurig? > 0 en p > 0 Door te regisseren en daar rekening mee te houden, verkrijgen we dat dat wil zeggen, xn convergeert naar x in waarschijnlijkheid. Convergentie in waarschijnlijkheid brengt echter geen convergentie in het gemiddelde van de orde p > 0 met zich mee. Dit wordt geïllustreerd door het volgende voorbeeld. Beschouw de waarschijnlijkheidsruimte áW, F, Rñ, waarbij F = B de Borel s-algebra is en R de Lebesgue-maat. Laten we een reeks willekeurige variabelen als volgt definiëren: De reeks xn convergeert in waarschijnlijkheid naar 0, aangezien maar voor elke p > 0 dat wil zeggen dat het gemiddeld niet zal convergeren. Laten we, wat voor alle n . Bewijs dat in dit geval xn convergeert naar x in het gemiddelde kwadraat. Oplossing. Let daar op... Laten we een schatting maken. Laten we een willekeurige variabele bekijken. Laten zijn? - een willekeurig positief getal. Toen om en om. Als, dan en. Vandaar, . En omdat? willekeurig klein en dan in het gemiddelde vierkant. Bewijs dat als xn in waarschijnlijkheid naar x convergeert, er sprake is van zwakke convergentie. Geef een testvoorbeeld om aan te tonen dat het omgekeerde niet waar is. Oplossing. Laten we bewijzen dat als dan op elk punt x, dat een punt van continuïteit is (dit is een noodzakelijke en voldoende voorwaarde voor zwakke convergentie), de verdelingsfunctie is van de waarde xn, en - de waarde van x. Laat x een continuïteitspunt zijn van de functie F. Als, dan is minstens één van de ongelijkheden of waar. Dan Hetzelfde geldt voor ten minste één van de ongelijkheden of en Zo ja, dan voor zo klein als gewenst? > 0 er bestaat N zodat voor alle n > N Aan de andere kant, als x een punt van continuïteit is, is het dan mogelijk om zoiets als dit te vinden? > 0, wat voor willekeurig klein is Dus, zo klein als je wilt? en er bestaat N zodanig dat voor n >N of, wat is hetzelfde, Dit betekent dat convergentie plaatsvindt op alle punten van continuïteit. Bijgevolg volgt een zwakke convergentie uit de convergentie in waarschijnlijkheid. De omgekeerde verklaring gaat in het algemeen niet op. Om dit te verifiëren, nemen we een reeks willekeurige variabelen die niet gelijk zijn aan constanten met waarschijnlijkheid 1 en dezelfde verdelingsfunctie F(x) hebben. We nemen aan dat voor alle n de hoeveelheden onafhankelijk zijn. Het is duidelijk dat er sprake is van zwakke convergentie, aangezien alle leden van de reeks dezelfde verdelingsfunctie hebben. Overwegen: |Uit de onafhankelijkheid en identieke waardenverdeling volgt dat Laten we kiezen uit alle verdelingsfuncties van niet-gedegenereerde willekeurige variabelen zoals F(x) die niet nul zullen zijn voor alle voldoende kleine ?. Dan neigt het niet naar nul met een onbeperkte groei van n en zal er geen convergentie in waarschijnlijkheid plaatsvinden. 7. Er is sprake van een zwakke convergentie, waarbij er met waarschijnlijkheid 1 een constante is. Bewijs dat in dit geval het zal convergeren naar waarschijnlijkheid. Oplossing. Laat waarschijnlijkheid 1 gelijk zijn aan a. Zwakke convergentie betekent dan convergentie voor iedereen. Sindsdien, dan om en om. Dat wil zeggen, op en op. Volgt dat voor iemand? > 0 waarschijnlijkheid neiging tot nul. Het betekent dat neigt naar nul bij, dat wil zeggen convergeert naar in waarschijnlijkheid. 2.2 Problemen oplossen op de CV-centrale De waarde van de gammafunctie Г(x) bij x= wordt berekend met de Monte Carlo-methode. Laten we het minimaal benodigde aantal tests vinden, zodat we met een waarschijnlijkheid van 0,95 kunnen verwachten dat de relatieve fout van de berekeningen minder dan één procent zal zijn. Tot op zekere hoogte hebben we dat Het is bekend dat Nadat we een verandering in (1) hebben aangebracht, komen we tot de integraal over een eindig interval: Bij ons dus Zoals u kunt zien, kan het worden weergegeven in de vorm waarin en gelijkmatig wordt verdeeld. Laat statistische tests uitvoeren. Dan is de statistische analogie de hoeveelheid waarbij, onafhankelijke willekeurige variabelen zijn met een uniforme verdeling. Waarin Uit de CLT volgt dat deze asymptotisch normaal is met de parameters. Dit betekent dat het minimumaantal tests dat met waarschijnlijkheid de relatieve fout van de berekening garandeert, niet meer dan gelijk is. We beschouwen een reeks van 2000 onafhankelijke, identiek verdeelde willekeurige variabelen met een wiskundige verwachting van 4 en een variantie van 1,8. Het rekenkundig gemiddelde van deze grootheden is een willekeurige variabele. Bepaal de waarschijnlijkheid dat de willekeurige variabele een waarde zal aannemen in het interval (3,94; 4,12). Laat …,… een reeks onafhankelijke willekeurige variabelen zijn met dezelfde verdeling met M=a=4 en D==1,8. Dan is de CLT van toepassing op de reeks (). Willekeurige waarde Waarschijnlijkheid dat het een waarde zal aannemen in het interval (): Voor n=2000 krijgen we 3,94 en 4,12 3 Hypotheses testen met behulp van het onafhankelijkheidscriterium Als resultaat van het onderzoek werd vastgesteld dat 782 vaders met lichtogige ogen ook zonen met lichtogige ogen hebben, en 89 vaders met lichtogige zonen. 50 vaders met donkere ogen hebben ook zonen met donkere ogen, en 79 vaders met donkere ogen hebben zonen met lichte ogen. Is er een verband tussen de oogkleur van vaders en de oogkleur van hun zonen? Stel dat het betrouwbaarheidsniveau 0,99 is. Tabel 2.1 KinderenVadersSomLichtogigDonkerogigLichtogig78279861Donkerogig8950139Som8711291000 H: Er is geen verband tussen de oogkleur van kinderen en vaders. H: Er is een verband tussen de oogkleur van kinderen en vaders. s=k=2 =90,6052 met 1 vrijheidsgraad De berekeningen zijn gemaakt in Mathematica 6. Aangezien > , moet hypothese H, over het ontbreken van een relatie tussen de oogkleur van vaders en kinderen, op significantieniveau, worden verworpen en moet de alternatieve hypothese H worden aanvaard. Er wordt gesteld dat het effect van het medicijn afhangt van de wijze van toepassing. Controleer deze verklaring met behulp van de gegevens in de tabel. 2.2 Stel dat het betrouwbaarheidsniveau 0,95 is. Tabel 2.2 Resultaat Toepassingswijze ABC Ongunstig 111716 Gunstig 202319 Oplossing. Om dit probleem op te lossen, zullen we een kruistabel met twee kenmerken gebruiken. Tabel 2.3 Resultaat Toepassingswijze Hoeveelheid ABC Ongunstig 11171644 Gunstig 20231962 Hoeveelheid 314035106 H: het effect van medicijnen is niet afhankelijk van de wijze van toediening H: het effect van medicijnen hangt af van de wijze van aanbrengen Statistieken worden berekend met behulp van de volgende formule s=2, k=3, =0,734626 met 2 vrijheidsgraden. Berekeningen gemaakt in Mathematica 6 Uit de verdelingstabellen vinden we dat. Omdat de< , то гипотезу H, про отсутствия зависимости действия лекарств от способа применения, при уровне значимости, следует принять. Conclusie Dit artikel presenteert theoretische berekeningen uit de sectie "Onafhankelijkheidscriterium", evenals "Grensstellingen van de waarschijnlijkheidstheorie", de cursus "Kansrekening en wiskundige statistiek". Tijdens de werkzaamheden werd het onafhankelijkheidscriterium in de praktijk getoetst; Ook werd voor bepaalde reeksen onafhankelijke willekeurige variabelen gecontroleerd of aan de centrale limietstelling werd voldaan. Dit werk heeft mij geholpen mijn kennis van deze delen van de waarschijnlijkheidstheorie te verbeteren, met literaire bronnen te werken en de techniek van het controleren van het criterium van onafhankelijkheid goed onder de knie te krijgen. probabilistische statistische hypothesestelling Lijst met koppelingen 1. Verzameling van problemen uit de kansrekening met oplossingen. Uch. toelage / red. V.V. Semenets. - Charkov: KhTURE, 2000. - 320 p. Gikhman II, Skorokhod AV, Yadrenko MI Waarschijnlijkheidstheorie en wiskundige statistiek. - K.: Vishchaschool, 1979. - 408 p. Ivchenko GI, Medvedev Yu.I., Wiskundige statistiek: leerboek. tegemoetkoming voor hogescholen. - M.: Hoger. school, 1984. - 248 blz., . Wiskundige statistiek: leerboek. voor universiteiten / V.B. Goryainov, I.V. Pavlov, G.M. Tsvetkova en anderen; Ed. V.S. Zarubina, AP Krischenko. - M.: Uitgeverij van MSTU im. N.E. Bauman, 2001. - 424 p. Hulp nodig bij het bestuderen van een onderwerp?
Onze specialisten adviseren of geven bijles over onderwerpen die u interesseren. Bijles
Dien uw aanvraag in door het onderwerp nu aan te geven om meer te weten te komen over de mogelijkheid om een consultatie te verkrijgen.
 Verzameling Russische freaks en bodymodifiers
Verzameling Russische freaks en bodymodifiers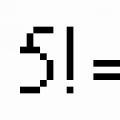 Waarschijnlijkheidstheorie en wiskundige statistiek
Waarschijnlijkheidstheorie en wiskundige statistiek Basisconcepten van waarschijnlijkheidstheorie en wiskundige statistiek
Basisconcepten van waarschijnlijkheidstheorie en wiskundige statistiek