Eksempel

Del et segment i to

Biseksjonsproblem. Bruk et kompass og linjal for å dele dette segmentet AB i to like deler. En av løsningene er vist i figuren:

• Ved hjelp av et kompass tegner vi sirkler med sentre ved punkter EN Og B radius AB.
• Finne skjæringspunkter P Og Q to konstruerte sirkler (buer).
• Bruk en linjal til å tegne et segment eller en linje som går gjennom punktene P Og Q.
• Finne ønsket midtpunkt av segmentet AB- skjæringspunkt AB Og PQ.

Formell definisjon

I konstruksjonsproblemer vurderes settet med alle punkter i flyet, settet med alle rette linjer i planet og settet med alle sirkler i flyet, hvor følgende operasjoner er tillatt:

1. Velg et punkt fra settet med alle punkter:
   1. vilkårlig poeng
   2. vilkårlig punkt på en gitt linje
   3. vilkårlig punkt på en gitt sirkel
   4. skjæringspunktet mellom to gitte linjer
   5. skjæringspunkt/tangens for en gitt linje og en gitt sirkel
   6. skjæringspunkter/tangens av to gitte sirkler
2. "Ved bruk av herskere» velg en linje fra settet med alle linjer:
   1. vilkårlig rett linje
   2. en vilkårlig rett linje som går gjennom et gitt punkt
   3. en rett linje som går gjennom to gitte punkter
3. "Ved bruk av kompass» velg en krets fra settet med alle kretser:
   1. vilkårlig sirkel
   2. en vilkårlig sirkel med et senter i et gitt punkt
   3. en vilkårlig sirkel med en radius lik avstanden mellom to gitte punkter
   4. en sirkel med sentrum i et gitt punkt og med en radius lik avstanden mellom to gitte punkter

I betingelsene for problemet er et visst sett med punkter spesifisert. Det er nødvendig, ved å bruke et begrenset antall operasjoner blant de tillatte operasjonene som er oppført ovenfor, for å konstruere et annet sett med punkter som er i et gitt forhold til det opprinnelige settet.

Løsningen på konstruksjonsproblemet inneholder tre vesentlige deler:

1. Beskrivelse av metoden for å konstruere et gitt sett.
2. Bevis på at settet konstruert på den beskrevne måten faktisk står i et gitt forhold til det originale settet. Vanligvis utføres beviset for konstruksjonen som et vanlig bevis for teoremet, basert på aksiomer og andre påviste teoremer.
3. Analyse av den beskrevne konstruksjonsmetoden for dens anvendelighet til forskjellige versjoner av startforholdene, samt for det unike eller ikke-unike av løsningen oppnådd ved den beskrevne metoden.

kjente problemer

• Apollonius' problem med å konstruere en sirkel som tangerer tre gitte sirkler. Hvis ingen av de gitte sirklene ligger inne i den andre, har dette problemet 8 vesentlig forskjellige løsninger.
• Brahmaguptas problem med å konstruere en innskrevet firkant ved å bruke de fire sidene.

Konstruksjon av regulære polygoner

Gamle geometre visste hvordan de skulle konstruere riktig n-gons for , , og .

Mulige og umulige konstruksjoner

Alle konstruksjoner er ikke annet enn løsninger på en eller annen ligning, og koeffisientene til denne ligningen er relatert til lengdene til gitte segmenter. Derfor er det praktisk å snakke om å konstruere et tall - en grafisk løsning på en ligning av en bestemt type. Innenfor rammen av kravene ovenfor er følgende konstruksjoner mulig:

• Konstruksjon av løsninger til lineære ligninger.
• Konstruere løsninger på andregradsligninger.

Det er med andre ord bare mulig å konstruere tall som er lik aritmetiske uttrykk ved å bruke kvadratroten av de opprinnelige tallene (lengder på segmenter). For eksempel,

Variasjoner og generaliseringer

• Konstruksjoner med ett kompass. I følge Mohr-Mascheroni-teoremet kan du ved hjelp av ett kompass konstruere hvilken som helst figur som kan konstrueres med et kompass og en linjal. I dette tilfellet anses en rett linje som konstruert hvis to punkter er spesifisert på den.
• Konstruksjoner med én linjal. Det er lett å se at ved hjelp av en linjal kan kun prosjektive-invariante konstruksjoner utføres. Spesielt er det umulig å dele et segment i to like deler, eller finne midten av en tegnet sirkel. Men hvis det er en forhåndstegnet sirkel på planet med et markert senter, ved hjelp av en linjal, kan du utføre de samme konstruksjonene som med kompass og en linjal (Poncelet-Steiner teorem ( Engelsk)), 1833. Hvis det er to hakk på en linjal, så tilsvarer konstruksjoner som bruker den konstruksjoner som bruker kompass og en linjal (Napoleon tok et viktig skritt for å bevise dette).
• Konstruksjoner som bruker verktøy med begrenset kapasitet. I problemer av denne typen anses verktøy (i motsetning til den klassiske formuleringen av problemet) som ikke ideelle, men begrensede: en rett linje gjennom to punkter kan tegnes ved hjelp av en linjal bare hvis avstanden mellom disse punktene ikke overstiger en viss verdi; radiusen til sirkler tegnet med et kompass kan begrenses ovenfra, under eller både over og under.
• Konstruksjoner med flat origami. se Hujit-reglene

se også

• Dynamiske geometriprogrammer lar deg utføre konstruksjoner ved hjelp av et kompass og linjal på en datamaskin.

Notater

Litteratur

• A. Adler Teori om geometriske konstruksjoner / Oversettelse fra tysk av G. M. Fikhtengolts. - Tredje utgave. - L.: Uchpedgiz, 1940. - 232 s.
• I. I. Alexandrov Samling av geometriske konstruksjonsproblemer. - Attende utgave. - M.: Uchpedgiz, 1950. - 176 s.
• B. I. Argunov, M. B. Balk. - Andre utgave. - M.: Uchpedgiz, 1957. - 268 s.
• A. M. Voronets Geometrien til kompasset. - M.-L.: ONTI, 1934. - 40 s. - (Populært bibliotek om matematikk under generell redaksjon av L. A. Lyusternik).
• V. A. Geiler Uløselige konstruksjonsproblemer // kjølevæske. - 1999. - Nr. 12. - S. 115-118.
• V. A. Kirichenko Konstruksjoner med kompass og linjal og Galois teori // Sommerskole "Moderne matematikk". - Dubna, 2005.
• Yu. I. Manin Bok IV. Geometri // Encyclopedia of elementary mathematics. - M.: Fizmatgiz, 1963. - 568 s.
• Y. Petersen Metoder og teorier for å løse geometriske konstruksjonsproblemer. - M.: Trykkeri av E. Lissner og Y. Roman, 1892. - 114 s.
• V. V. Prasolov Tre klassiske konstruksjonsproblemer. Doble en terning, tredelt en vinkel, kvadratisk en sirkel. - M.: Nauka, 1992. - 80 s. - (Populære forelesninger om matematikk).
• J. Steiner Geometriske konstruksjoner utført ved hjelp av en rett linje og en fast sirkel. - M.: Uchpedgiz, 1939. - 80 s.
• Valgfritt kurs i matematikk. 7-9 / Komp. I. L. Nikolskaya. - M.: Education, 1991. - S. 80. - 383 s. - ISBN 5-09-001287-3

Wikimedia Foundation. 2010.

Se hva "Konstruksjon med kompass og linjal" er i andre ordbøker:

Linjaler - få en fungerende kupong for rabatt på AllInstruments hos Akademika eller kjøp linjaler med fortjeneste med gratis levering på salg hos AllInstruments

En gren av euklidisk geometri, kjent siden antikken. I konstruksjonsoppgaver er følgende operasjoner mulig: Marker et vilkårlig punkt på planet, et punkt på en av de konstruerte linjene, eller skjæringspunktet mellom to konstruerte linjer. Med hjelp av... ... Wikipedia

Konstruksjoner som bruker kompass og linjaler er en gren av euklidisk geometri kjent siden antikken. I byggeoppgaver er følgende operasjoner mulig: Merk et vilkårlig punkt på planet, et punkt på en av de konstruerte linjene, eller et punkt... ... Wikipedia

Substantiv, s., brukt. sammenligne ofte Morfologi: (nei) hva? konstruksjon, hva? konstruksjon, (jeg ser) hva? konstruksjon, hva? konstruksjon, om hva? om konstruksjon; pl. Hva? konstruksjon, (nei) hva? konstruksjoner, hva? konstruksjoner, (jeg ser) hva? konstruksjon, med hva?... ... Dmitrievs forklarende ordbok

LITEN VITENSKAPSAKADEMY FOR SKOLEBARN PÅ KRIM

"SØKER"

Seksjon "Matematikk"

GEOMETRISKE KONSTRUKSJONER MED EN DOBBELSIDIG LINAL

Jeg har gjort jobben EN

_____________

Klasseelev

Vitenskapelig leder

INNLEDNING………………………………………………………………………………………………..…..3

I. GEOMETRISKE KONSTRUKSJONER PÅ FLYET………………...4

I.1. Generelle aksiomer for konstruktiv geometri. Aksiomer for matematiske instrumenter………………………………………………………………………………………………..4

I.2. ……………………….....5

I.3. Geometriske konstruksjoner med én linjal…………………………………..7

Jeg.4. Grunnleggende oppgaver for å bygge med tosidig linjal………………..8

I.5. Løse ulike konstruksjonsproblemer …………………………………………12

I.6. Konstruksjoner med ensidig linjal…………………………………………………20

I.7. Utskiftbarhet av en tosidig linjal med et kompass og en linjal....21

KONKLUSJON……………………………………………………………………….24

Liste over referanser…………………………………..………….25

Introduksjon

Problemer som involverer konstruksjon med begrensede midler inkluderer problemer som involverer konstruksjon med kun kompass og linjal, som vurderes i skolens læreplan. Er det mulig å løse konstruksjonsproblemer med bare en linjal? Ofte har du ikke et kompass for hånden, men du kan alltid finne en linjal.

Problemer med konstruksjoner i geometri er et fascinerende avsnitt. Interessen for det skyldes skjønnheten og enkelheten i dets geometriske innhold. Relevansen av å vurdere disse problemene øker på grunn av at de brukes i praksis. Evnen til å bruke en linjal for å løse problemene som vurderes i dette arbeidet er av stor betydning i praktiske aktiviteter, fordi Vi står stadig overfor problemer med å dele et segment i to, doble et gitt segment osv.

Denne artikkelen undersøker de viktigste konstruksjonsproblemene som tjener som grunnlag for å løse mer komplekse problemer.

Som erfaringen viser, vekker byggeoppgaver interesse og bidrar til aktivisering av mental aktivitet. Når du løser dem, brukes kunnskap om egenskapene til figurer aktivt, evnen til å resonnere utvikles og ferdighetene til geometriske konstruksjoner forbedres. Som et resultat utvikles konstruktive evner, som er et av målene med å studere geometri.

Hypotese: alle konstruksjonsproblemer som kan løses ved hjelp av kompass og linjal kan bare løses ved hjelp av en tosidig linjal.

Studieobjekt: byggeoppgaver og tosidig linjal.

Forskningsmål: å bevise at alle konstruksjonsproblemer bare kan løses ved hjelp av en tosidig linjal.

Forskningsmål: å studere det teoretiske grunnlaget for å løse konstruksjonsproblemer; løse grunnleggende konstruksjonsproblemer ved å bruke en tosidig linjal; gi eksempler på mer komplekse konstruksjonsproblemer; systematisere teoretisk og praktisk materiale.

I. GEOMETRISKE KONSTRUKSJONER PÅ FLYET

I.1. Generelle aksiomer for konstruktiv geometri. Aksiomer for matematiske verktøy

For konstruktiv geometri er det nødvendig å ha en nøyaktig og, for matematiske formål, fullstendig beskrivelse av et bestemt verktøy. Denne beskrivelsen er gitt i form av aksiomer. Disse aksiomene i abstrakt matematisk form uttrykker egenskapene til ekte tegneinstrumenter som brukes til geometriske konstruksjoner.

De mest brukte geometriske konstruksjonsverktøyene er:linjal (ensidig) , kompass, tosidig linjal (med parallelle kanter) og noen andre.

A. Herskeraksiom.

Linjalen lar deg utføre følgende geometriske konstruksjoner:
a) konstruer et segment som forbinder to konstruerte punkter;

b) konstruer en rett linje som går gjennom to konstruerte punkter;

c) konstruer en stråle som kommer fra et konstruert punkt og går gjennom et annet konstruert punkt.

B. Kompassaksiomet.

Kompasset lar deg utføre følgende geometriske konstruksjoner:
a) konstruer en sirkel hvis sentrum av sirkelen og et segment som er lik radiusen til sirkelen (eller dens ender) er konstruert;

B. Aksiom for en tosidig linjal.

Den dobbeltsidige linjalen lar deg:

a) utføre noen av konstruksjonene oppført i aksiom A;

b) i hvert av halvplanene definert av den konstruerte linjen, konstruer en linje parallelt med denne linjen og som går fra den i en avstandEN, Hvor EN - et segment fast for en gitt linjal (bredden på linjalen);

c) hvis to punkter A og B er konstruert, avgjør om AB vil være større enn et bestemt fast segmentEN (linjalbredde), og hvis AB >EN , konstruer deretter to par parallelle linjer som går gjennom punktene A og B henholdsvis og med avstand fra hverandreEN .

I tillegg til de oppførte verktøyene kan du bruke andre verktøy for geometriske konstruksjoner: en vilkårlig vinkel, en firkant, en linjal med merker, et par rette vinkler, forskjellige enheter for å tegne spesielle kurver, etc.

I.2. Generelle prinsipper for løsning av konstruksjonsproblemer

Byggeoppgave består i det faktum at det er nødvendig å konstruere en viss figur med de spesifiserte verktøyene hvis en annen figur er gitt og visse forhold mellom elementene i den ønskede figuren og elementene i denne figuren er indikert.

Hver figur som tilfredsstiller betingelsene for problemet kallesbeslutning denne oppgaven.

Finn en løsning konstruksjonsoppgave betyr å redusere den til et begrenset antall grunnleggende konstruksjoner, det vil si å indikere en begrenset sekvens av grunnleggende konstruksjoner, hvoretter den ønskede figuren allerede vil bli ansett som konstruert i kraft av de aksepterte aksiomer for konstruktiv geometri. Listen over akseptable grunnleggende konstruksjoner, og følgelig fremdriften med å løse problemet, avhenger betydelig av hvilke spesifikke verktøy som brukes til konstruksjoner.

Løs konstruksjonsproblemet - Midler, finne alle sine løsninger .

Den siste definisjonen krever en viss avklaring. Figurer som tilfredsstiller betingelsene for problemet kan variere både i form eller størrelse, og plassering på planet. Forskjeller i posisjon på planet tas i betraktning eller ikke tatt i betraktning avhengig av utformingen av selve konstruksjonsproblemet, om tilstanden til problemet gir eller ikke sørger for en bestemt plassering av ønsket figur i forhold til noen gitte figurer .

Hvis en løsning på et problem blir funnet, er det i fremtiden tillatt å bruke denne løsningen "som helhet", det vil si uten å dele den inn i hovedkonstruksjoner.

Det finnes en rekke enkle geometriske konstruksjonsproblemer, som spesielt ofte inngår som komponenter i løsning av mer komplekse problemer. Vi vil kalle dem elementære geometriske konstruksjonsproblemer. Listen over elementære oppgaver er selvfølgelig betinget. Grunnleggende oppgaver inkluderer vanligvis følgende:

Del dette segmentet i to.

Del en gitt vinkel i to.

Å konstruere på en gitt linje et segment som er lik den gitte.

Konstruere en vinkel lik en gitt.

Konstruere en linje som går gjennom et gitt punkt parallelt med en gitt linje.

Konstruere en linje som går gjennom et gitt punkt og vinkelrett på en gitt linje.

Inndeling av et segment i denne forbindelse.

Konstruere en trekant med tre gitte sider.

Konstruere en trekant ved hjelp av en side og to tilstøtende vinkler.

Konstruere en trekant med to sider og vinkelen mellom dem.

Når man skal løse et hvilket som helst noe komplekst konstruksjonsproblem, oppstår spørsmålet om hvordan man skal resonnere for å finne en måte å løse problemet på, for å få alle løsninger på problemet, for å finne ut betingelsene for muligheten for å løse problemet osv. Derfor , når de løser konstruktive problemer, bruker de et løsningsskjema , som består av følgende fire stadier:

1) analyse;
2) konstruksjon;
3) bevis;
4) forskning.

I.3. Geometriske konstruksjoner med én linjal

Vi vil vurdere linjalen fra to synsvinkler: som en linjal og som en tosidig linjal.

1. Tosidig linjal bredde EN vi vil kalle en linjal med parallelle kanter plassert på avstand EN fra hverandre, noe som gjør det mulig å bygge direkte:

a) en vilkårlig rett linje;

b) en rett linje som går gjennom to punkter gitt eller oppnådd i prosessen med å løse problemet;

c) parallelle linjer, som hver går gjennom ett av punktene, hvor avstandene mellom disse er størreEN (i denne konstruksjonen er linjalen i en slik posisjon at på hver av de to parallelle kantene er det ett av de to gitte punktene; i dette tilfellet vil vi snakke om direkte konstruksjon).

Bredden på linjalen i denne konstruksjonen anses som konstant, og derfor, hvis det i ferd med å løse et spesifikt problem blir det nødvendig å utføre en direkte konstruksjon i forhold til noen oppnådde punkterEN Og I , så må vi bevise at lengdenAB lengre EN .

Vi vil vurdere et punkt som skal konstrueres hvis det er en av dataene eller er skjæringspunktet mellom to konstruerte linjer; på sin side vil vi vurdere en rett linje som skal konstrueres hvis den går gjennom de konstruerte eller gitte punktene.

Ved å bruke en tosidig linjal kan du konstruere følgende.

a) Gjennom to punkter kan du tegne en rett linje, og bare ett.

b) Uansett den rette linjen, er det nøyaktig to rette linjer i planet, parallelle med det og atskilt fra det med en avstanden .

c) Gjennom to punkter A og B ved AB EN det er mulig å trekke to par parallelle rett; med AB = EN du kan tegne et par parallelle linjer, avstanden mellom dem er likEN .

Hvis ett, to, tre poeng gis, kan ingen nye poeng konstrueres

(Figur 1);

hvis fire punkter er gitt, hvorav noen tre (eller alle fire) ligger på samme linje, kan ingen andre punkter konstrueres (fig. 2);

Hvis du får fire punkter som ligger ved toppunktene til et parallellogram, kan du konstruere bare ett punkt - dets sentrum. (Fig.3).

Etter å ha akseptert det ovennevnte, la oss se separat på problemene som er løst av en tosidig linjal.

Jeg.4. Grunnleggende oppgaver for å bygge med tosidig linjal

1
. Konstruer halveringslinjen til vinkel ABC.

Løsning: (Fig. 4)

EN  (I C) Og b  (Et band  b = D .

Vi får B D– halveringslinje  ABC.

Faktisk oppnådd av

å konstruere et parallellogram er

rombe, siden dens høyder er like. ID –

diagonalen til en rombe er en halveringslinje ABC. Fig.4

2
. Doble den gitte vinkelen ABC

Løsning : (fig. 5) a) EN  (AB),

EN  (I C)= D , gjennom punkt B og D

b direkte;

b) gjennom punktene B ogD m  b

direkte,b Ç a = F .

Vi får Ð AB F = 2 Ð ABC .

Fig.5

3 . Til en gitt rett linje M N i dette

tegne en vinkelrett på punkt A

Løsning : (Fig.6)

1) (AA 1) || (BB 1) || (SS 1) –

direkte (B (M N),

MED Î (M N)); 2) til A og B

m || n - direkte,

m Ç (SS 1) = D .

Vi får (A D )  (M N ).

Fig.6.

4
. Gjennom et gitt punkt ikke ligge på

gitt linje, tegne en vinkelrett

Til denne linjen.

Løsning: Gjennom dette punktet O tegner vi

to linjer som skjærer en gitt

rett linje AB, og doble vinklene til den resulterende

trekanter ved siden av denne

rett.  OA N = 2  OAV og

OB N = 2  OVA (fig. 7).

Fig.7

5. Konstruer et punkt symmetrisk til en gitt linje i forhold til en gitt linje.

Løsning: se oppgave 4. (punkt O er symmetrisk til punktN. Fig. 7)

6. Utfør en rett linje parallelt med denne

P
rett M N , gjennom punkt A, ikke

som tilhører linjen M N .

Løsning 1: (Fig. 8)

1)(AA 1) || (BB 1) || (SS 1) || (DD 1 ) || (КК 1) -

– direkte, (SA)Ç (BB1) = C2;

2) (Med 2 K) Ç (DD 1 ) = F .

(EN F ) er den ønskede rette linjen.

Fig 8

Løsning 2 . På fig. 8 er 1 nummerert

rekkefølge av rette linjer,

hvorav 1, 2 og 3 er parallelle i

direkte konstruksjon;

(EN F) || (M N).

Fig.8 1

7
. Del dette segmentet AB i to.

Løsning 1. (Fig. 9) (bare for tilfellet når bredden på linjalen er mindre enn lengden på dette segmentet). Tegn to par parallelle linjer direkte gjennom

endene av dette segmentet, og deretter diagonalen

den resulterende romben. O – midt AB.

Ris. 9.

Løsning 2. (Fig. 9, a)

1) a || (Et band b || (AB) – direkte;

2) (AR), (AR)Ç a = C, (AP) Ç b = D ;

3) (D I) Ç a = M, (SV) Ç b = N ;

4) (M N ) Ç (AB) = K;

5) (D TIL) Ç (EN N ) = F ;

6) (B F ) Ç b = D 1, (B F ) Ç a = C1;

7) (D I ) Ç (EN D 1 ) = X,

(AC 1) Ç (SV) = Z.

8) (X Z) Ç (AB) =O. Vi får AO = OB.

Fig. 9, a

Løsning 3 .( Ris. 9,b)

Som kjent , i midten trapes

baser, skjæringspunkt

diagonaler og skjæringspunkt

forlengelser av sidene

ligge på samme rette linje.

1) m || (AB) – direkte;

2) C Î m , D Î m , (SOM) Ç (I D ) = TIL; Fig. 9, b

3) (NE) Ç (EN D ) = F ; 4) (K F ) Ç (AB) =O. Vi får AO = OB.

I.5. Løse ulike konstruksjonsproblemer

For å løse de følgende konstruksjonsproblemene med kun en tosidig linjal, brukes den direkte konstruksjonen av parallelle linjer og de syv hovedoppgavene gitt ovenfor.

1. Tegn to innbyrdes vinkelrette linjer gjennom dette punktet.

R løsning: la oss gå gjennom dette punktet

to vilkårlige linjer,

og deretter - halveringslinjer

tilstøtende hjørner. (fig.10)

Fig.10

2. Gitt et segment A D gitt lengde a.

Konstruer et segment hvis lengde er lik .

R
beslutning : La oss gjennomføre m  EN Og h || m gjennom

punkt A. f || (EN D ) , k || (AD) direkte.

La oss tegne AB og AC, hvor B =f  m ,

a C = m  k . På kjent måte

del AB og AC i to og

la oss tegne medianene til trekanten

ABC. Etter eiendommen til medianer

trekant, O D = - ettertraktet

segment (fig. 11)

Ris. elleve

3. Konstruer et segment hvis lengde er

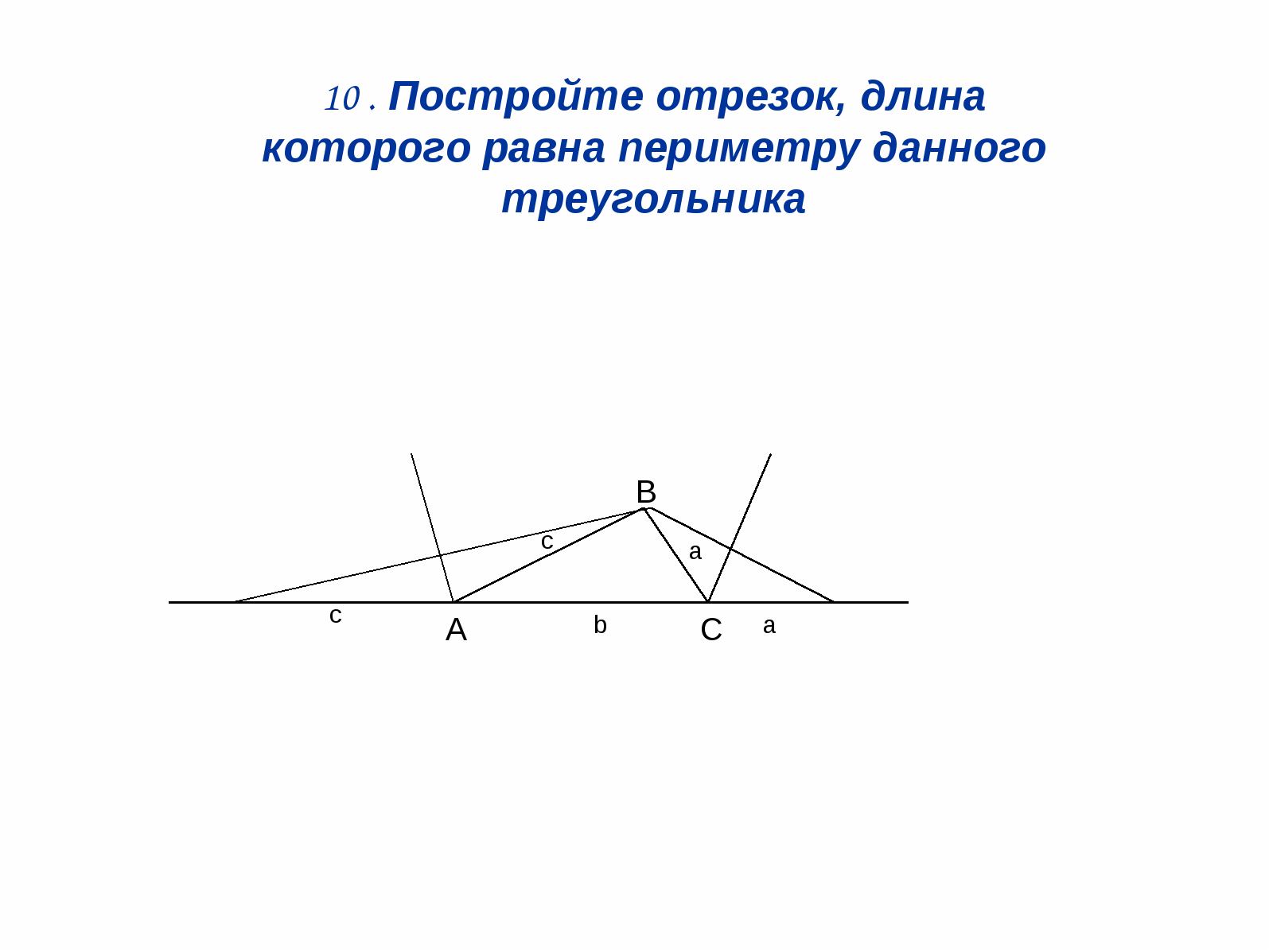lik omkretsen til den gitte trekanten.

Løsning: (Fig. 12). La oss konstruere halveringslinjer

to ytre hjørner av trekanten, og deretter

3 topper I la oss tegne perpendikulære

til disse halveringslinjene.

DE = et + b + s

Fig.12

4. Gitt et segment med lengde a. Konstruer lengdesegmenter 2a, 3a.

R løsning: (Fig. 13)

1M N) || (AB) og (M 1 N 1 ) || (M N) || (M 2 N 2 ) –

Direkte;

2) (CA) og (CB) til A og B.

Segmentene A 1 B 1 og A 2 B 2 er påkrevd.

En annen løsning på dette problemet kan være

hentet fra løsningen på oppgave 7.

Ris. 1. 3

5. To segmenter er gitt på en rett linje, hvor lengdene er a og b . Konstruer segmenter hvis lengder er lik en + b , b -A, ( en + b )/2 og ( b - en )/2 .

Løsning: og for en + b(Fig. 14, a)

Fig. 14, a

b) for ( en + b)/2 (fig. 14, b)

1) (A 1 B 1) || (A 2 B 2) || (AB) – direkte;

2) M Î (A 2 B 2), (MX) Ç (A 1 B 1 ) = N, (M H) Ç (A 1 B 1 ) = P;

3) (PY) Ç (A 2 B 2) = L, (LZ ) Ç (A 1 B 1 ) = Å,

Vi får: N O = NP + P.O. =
.

Ris. 14, f

c) for b - A(Fig. 14, c)

Ris. 14,v

c) for ( b - en )/2 (Fig. 14,d)

Ris. 14,g

6
. Konstruer midten av denne sirkelen.

Løsning : (Fig. 15) La oss tegne en rett linje AB,

krysser sirkelen ved punktene A og B;

Sol  AB, hvor C er skjæringspunktet

med en sirkel.

Gjennom punkt C trekker vi parallelt med AB

rett C D; MEDDskjærer en sirkel

på punktetD.

Ved å koble tilDmed B og A med C, får vi

det ønskede punktet er sentrum av sirkelen. Ris. 15

Løsning 2: (Fig. 16) Konstruer to parallelle akkorder med en tosidig linjalAD OgB.C. . Vi får en likebenet trapesABCD. LaK OgP - skjæringspunkter for linjerA.C. OgBD , AB OgDC . Så rettP K går gjennom midtpunktene til basene til trapesen vinkelrett på dem, noe som betyr at den går gjennom midten av den gitte sirkelen. Ved på samme måte å konstruere en annen slik rett linje, finner vi sentrum av sirkelen.

Ris. 16

7. En sirkelbue er gitt. Konstruer midten av sirkelen

Løsning . (Fig. 17) Marker tre punkter A, B og C på denne buen. Bruk en linjal på endene av segmentet AB og skriv av kantene. Vi får to parallelle linjer. Ved å endre posisjonen til linjalen tegner vi ytterligere to parallelle linjer. Vi får en rombe (et parallellogram med like høyder). En av diagonalene til en rombe er den vinkelrette halveringslinjen til segmentetAB , siden diagonalen til en rombe ligger på den vinkelrette halveringslinjen til den andre diagonalen. På samme måte konstruerer vi den vinkelrette halveringslinjen til segmentetA.C. . Skjæringspunktet til de konstruerte halveringslinjene er sentrum av den ønskede sirkelen.

Ris. 17

8. Gitt et segment AB, en ikke-parallell linje l og et punkt M på den. Konstruer skjæringspunktene til rett linje l med en sirkel med radius AB med sentrum M med en tosidig linjal.

Løsning: (fig.18)

La oss fullføre trekantenA.B.M. til parallellogramABNM . La oss konstruere halveringslinjene MT ogMSvinkler mellomMNog rettl . La oss trekke gjennom poengetN linjer parallelle med disse halveringslinjene:NQ || MS, NR || M.T.. MT│ MSsom halveringslinjer for tilstøtende vinkler. Midler,NQ │ MT, det vil si i en trekantNMQhalveringslinjen er høyden, derfor er trekanten likebenet:MQ = MN. Like måte,MR. = MN. PoengQOgRettertraktet.

Ris. 18

9. Gitt en linje l og et segment OA parallelt med l. Konstruer skjæringspunktene til rett linje l med en sirkel med radius OA med sentrum O ved hjelp av en tosidig linjal.

Løsning: (Fig. 19, a)

La oss lage en direktel 1 , parallelt med linjenO.A. og fjernt fra det på avstanden . La oss ta det på en rett linjel vilkårlig poengB . LaB 1 - skjæringspunkt for linjerO.B. Ogl 1 . La oss trekke gjennom poengetB 1 rett, parallellAB ; denne linjen skjærer linjenO.A. på punktetEN 1 . La oss nå trekke gjennom punkteneO OgEN 1 et par parallelle linjer, avstanden mellom dem eren (det kan være to slike par med linjer); laX OgX 1 - skjæringspunkter for en linje som går gjennom et punktO , med rette linjerl Ogl 1 . FordiO.A. 1 = OKSE 1 og ∆O.A. 1 X 1 ∆ OAX , så OA = OX, punktX ettertraktet.

På samme måte konstruerer vi det andre skjæringspunktet mellom sirkelen og linjen - punktetY(Fig. 18, b).

Ris. 18,a

Ris. 18, f

I.6.Konstruksjoner med ensidig linjal

Z
Her tar vi for oss et spesielt tilfelle: la poeng P gis,Q, R 1 OgQ 1 . og de ligger på toppene av trapesen.

1. Del segmentet P Q i halvparten

Løsning vist i figur 19

Gitt poeng P,Q, R 1 OgQ 1 og parallelle linjer

RQ, R 1 Q 1 . La oss utføre RQ 1  QR 1 = B , RR 1  QQ 1 = A

La oss koble sammen punktene A og B. AB RQ = F- midten

segment PQ.

Ris. 19

2. Doble segmentet R 1 Q 1.

R
beslutning vist i figur 20. La oss bygge

punktF– midten av segmentet PQog koble den til

MedQ 1. R 1 Q FQ 1 = M. La oss gjennomføre RM. RM R 1 Q 1 = R

likestillingRQog P 1 Q 1 følger av likheten

trekanter RMFOg RMQ 1 ,

FMQOg R 1 MQ 1 , og likheter PFOgFQ.

Ris. 20

3
. Konstruer et lengdesegment n  R 1 Q 1 .

m – 1 like segmenter PQ 2 , Q 2 Q 3, … Q m -1 Q m

Så bygger vi (RR 1 ) OgQ m Q 1 og koble til

deres skjæringspunkt A med punkter

Q 2 , Q 3, … Q m Mottattm -1 direkte

dele oppR 1 Q 1 påm lik deler.

Tilm = 4 løsningen er vist i figur 22

Fig.22

I.7. Utskiftbarhet av tosidig linjal med kompass og linjal

La oss bevise at en tosidig linjal kan byttes ut med et kompass og en linjal. For å gjøre dette beviser vi følgende utsagn:

Påstand 1: alle konstruksjoner som kan gjøres med kompass og linjal kan gjøres med tosidig linjal.

Siden når man konstruerer med et kompass og en linjal, trekker linjalen en linje gjennom to punkter, og kompasset konstruerer en sirkel (finner et sett med punkter like langt fra en gitt), så reduseres alle konstruksjoner med et kompass og en linjal til konstruere skjæringspunktet mellom to rette linjer, to sirkler og en sirkel med en rett linje.

Skjæringspunktet mellom to rette linjer kan konstrueres ved hjelp av en linjal.

Skjæringspunktet mellom en sirkel og en rett linje (fig. 23):

Konstruksjon:La segmentet AB gis - radiusen til sirkelen, en rett linjel , sentrum av sirkel O, deretter:

1) Vi utfører OS ||l , OS = AB.

2) Vi utfører OS ||kog fjernkontroll til en.

3) Vi gjennomførerO.D., O.D. l = D; O.D. k) Som følge av Thales’ teorem

4) I henhold til loven om transitivitet av likheter

5) VurderOMQE. OMQEer et parallellogram, siden OM ||EQog OE ||M.C.(sidene av linjalen er parallelle). La oss bevise at dette er en rombe.

5.1) OppførselQZ O.C.OgQG PÅ, DeretterQG = QZ = en.

5.2)  OMQ =  RQM(ligger på tvers);  OS =PÅ, som var det som måtte bevises.

Skjæringspunktet mellom to sirkler: lignende.

Utsagn 2: alle konstruksjoner som kan gjøres med tosidig linjal kan gjøres med kompass og rette.

For å gjøre dette vil vi utføre konstruksjonsstandarden for en tosidig linjal ved hjelp av et kompass og en linjal.

1) En rett linje med to punkter konstrueres enkelt ved hjelp av en linjal.

2) Konstruksjon av en rett linje parallelt med en gitt og fjernet fra den i en gitt avstand:

2.1) La det gis en rett linjekog lengdesegmenten.

2.2) Konstruer en vilkårlig rett linjeb k, lak b= B.

2.3) Påbpå begge sider av punktetBpå en rett linjebsett til side et stykke lengdeen, la poengeneCOgD.

2.4) Gjennom et punktCbygge en rett linjec k.

2.5) Gjennom et punktDbygge en rett linjed k.

2.6) DirektecOgd-påkrevd, fordiB.C.OgBDlikenved konstruksjon og er lik avstanden mellom den rette linjenkog rett

3) Konstruksjon av rette linjer parallelle med hverandre og som går gjennom to gitte punkter, og avstanden mellom dem er lik det gitte segmentet:

3.1) La poeng gisENOgBog lengdesegmenten.

3.2) Konstruere en sirkel med et senter i et punktENog radiusen.

3.3) Konstruer en tangent til en gitt sirkel gjennom et punktB; det er to slike tangenter ifBligger utenfor sirkelen (hvisAB> en), en hvisBligger på sirkelen (hvisAB= en), ingen hvisBligger inne i sirkelen (AB< en). Denne tangenten er en av linjene vi ser etter; det gjenstår å passere gjennom punktetENrett linje parallelt med den.

3.4) Siden en av linjene er vinkelrett på radiusen til sirkelen som en tangent, er den andre også vinkelrett på den (siden de er parallelle), derfor er avstanden mellom dem lik radiusen, som ved konstruksjon er liken, som er det som kreves for å få tak i.

Dermed har vi bevist utskiftbarheten av en tosidig linjal og et kompass og linjal.

Konklusjon: En tosidig linjal kan byttes ut med et kompass og en linjal.

Konklusjon

Så spørsmålet om muligheten for å bruke en linjal til å løse klassiske konstruksjonsproblemer ved å bruke et kompass og en linjal har blitt vurdert og løst. Det viser seg at konstruksjonsproblemer kan løses med kun en linjal med parallelle kanter. Ved løsning av mer komplekse problemer bør man videre stole på de såkalte grunnkonstruksjonene som er omtalt i dette arbeidet.

Det presenterte materialet kan brukes direkte ikke bare i matematikktimer, i matematikksirkelklasser, men også i praktiske aktiviteter.

Liste over brukt litteratur

Aliev A.V. Geometriske konstruksjoner. Matematikk på skolen. 1978 nr. 3

Glazer G.I. Matematikkens historie på skolen. M., Opplysning. 1981.

Depman I.Ya. Bak sidene i en lærebok i matematikk. M.. Opplysning. 1989.

Elensky Shch. I fotsporene til Pythagoras. M., Detgiz. 1961.

Encyklopedisk ordbok for en ung matematiker. M., Pedagogikk. 1985

I konstruksjonsoppgaver vil vi vurdere konstruksjonen av en geometrisk figur, som kan gjøres ved hjelp av linjal og kompass.

Ved å bruke en linjal kan du:

vilkårlig rett linje;

en vilkårlig rett linje som går gjennom et gitt punkt;

en rett linje som går gjennom to gitte punkter.

Ved hjelp av et kompass kan du beskrive en sirkel med en gitt radius fra et gitt senter.

Ved å bruke et kompass kan du plotte et segment på en gitt linje fra et gitt punkt.

La oss vurdere de viktigste byggeoppgavene.

Oppgave 1. Konstruer en trekant med gitte sider a, b, c (fig. 1).

Løsning. Bruk en linjal, tegn en vilkårlig rett linje og ta på den et vilkårlig punkt B. Ved hjelp av en kompassåpning lik a beskriver vi en sirkel med sentrum B og radius a. La C være skjæringspunktet med linjen. Med en kompassåpning lik c beskriver vi en sirkel fra sentrum B, og med en kompassåpning lik b beskriver vi en sirkel fra sentrum C. La A være skjæringspunktet for disse sirklene. Trekant ABC har sider lik a, b, c.

Kommentar. For at tre rette segmenter skal tjene som sider i en trekant, er det nødvendig at den største av dem er mindre enn summen av de to andre (og< b + с).

Oppgave 2.

Løsning. Denne vinkelen med toppunkt A og strålen OM er vist i figur 2.

La oss tegne en vilkårlig sirkel med sentrum i toppunktet A av den gitte vinkelen. La B og C være skjæringspunktene for sirkelen med sidene av vinkelen (fig. 3, a). Med radius AB tegner vi en sirkel med sentrum i punktet O - startpunktet til denne strålen (fig. 3, b). La oss betegne skjæringspunktet for denne sirkelen med denne strålen som C 1 . La oss beskrive en sirkel med sentrum C 1 og radius BC. Punkt B 1 i skjæringspunktet mellom to sirkler ligger på siden av ønsket vinkel. Dette følger av likheten Δ ABC = Δ OB 1 C 1 (det tredje tegnet på likhet i trekanter).

Oppgave 3. Konstruer halveringslinjen til denne vinkelen (fig. 4).

Løsning. Fra toppunktet A i en gitt vinkel, som fra sentrum, tegner vi en sirkel med vilkårlig radius. La B og C være punktene for skjæringspunktet med sidene av vinkelen. Fra punktene B og C beskriver vi sirkler med samme radius. La D være deres skjæringspunkt, forskjellig fra A. Stråle AD halverer vinkel A. Dette følger av likheten Δ ABD = Δ ACD (det tredje kriteriet for trekanters likhet).

Oppgave 4. Tegn en vinkelrett halveringslinje til dette segmentet (fig. 5).

Løsning. Ved hjelp av en vilkårlig, men identisk kompassåpning (større enn 1/2 AB), beskriver vi to buer med senter i punktene A og B, som vil skjære hverandre i noen punkter C og D. Den rette linjen CD vil være den ønskede perpendikulæren. Faktisk, som det kan sees fra konstruksjonen, er hvert av punktene C og D like langt fra A og B; derfor må disse punktene ligge på den vinkelrette halveringslinjen til segment AB.

Oppgave 5. Del dette segmentet i to. Det løses på samme måte som oppgave 4 (se fig. 5).

Oppgave 6. Gjennom et gitt punkt tegne en linje vinkelrett på den gitte linjen.

Løsning. Det er to mulige tilfeller:

1) et gitt punkt O ligger på en gitt rett linje a (fig. 6).

Fra punkt O tegner vi en sirkel med en vilkårlig radius som skjærer linje a i punktene A og B. Fra punktene A og B tegner vi sirkler med samme radius. La O 1 være skjæringspunktet deres, forskjellig fra O. Vi får OO 1 ⊥ AB. Faktisk er punktene O og O 1 like langt fra endene av segmentet AB og ligger derfor på den vinkelrette halveringslinjen til dette segmentet.

Kommunal budsjettutdanningsinstitusjon

ungdomsskole nr. 34 med fordypning i enkeltfag

MAN, fysikk og matematikk seksjon

"Geometriske konstruksjoner med kompass og linjal"

Fullført av: elev av klasse 7 "A"

Batishcheva Victoria

Leder: Koltovskaya V.V.

Voronezh, 2013

3. Konstruere en vinkel lik den gitte.

P La oss tegne en vilkårlig sirkel med et senter i toppunktet A i en gitt vinkel (fig. 3). La B og C være skjæringspunktene for sirkelen med sidene av vinkelen. Med radius AB tegner vi en sirkel med sentrum i punktet O, startpunktet for denne halvlinjen. La oss betegne skjæringspunktet for denne sirkelen med denne halvlinjen som C 1 . La oss beskrive en sirkel med sentrum C 1 og fig. 3

radius til flyet. Punkt B 1 skjæringspunktet mellom de konstruerte sirklene i det angitte halvplanet ligger på siden av ønsket vinkel.

6. Konstruksjon av vinkelrette linjer.

Vi tegner en sirkel med en vilkårlig radius r med et senter i punktet O i fig. 6. Sirkelen skjærer linjen i punktene A og B.Fra punktene A og B tegner vi sirkler med radius AB. La melankoli C være skjæringspunktet mellom disse sirklene. Vi oppnådde punktene A og B i det første trinnet, når vi konstruerte en sirkel med en vilkårlig radius.

Den ønskede rette linjen går gjennom punktene C og O.

Fig.6

kjente problemer

1.Brahmaguptas problem

Konstruer en innskrevet firkant ved å bruke de fire sidene. En løsning bruker Apollonius-sirkelen.La oss løse Apollonius' problem ved å bruke analogien mellom en trisirkel og en trekant. Hvordan finner vi en sirkel innskrevet i en trekant: vi konstruerer skjæringspunktet til halveringslinjen, slipper perpendikulære fra den til sidene av trekanten, basene til perpendikulærene (skjæringspunktene til perpendikulæren med siden den på er droppet) og gi oss tre poeng som ligger på ønsket sirkel. Tegn en sirkel gjennom disse tre punktene - løsningen er klar. Vi vil gjøre det samme med Apollonius' problem.

2. Apollonius' problem

Bruk et kompass og linjal, konstruer en sirkel som tangerer de tre gitte sirklene. I følge legenden ble problemet formulert av Apollonius av Perga rundt 220 f.Kr. e. i boken «Touch», som gikk tapt, men ble restaurert i 1600 av François Viète, den «galliske Apollonius», som hans samtidige kalte ham.

Hvis ingen av de gitte sirklene ligger inne i den andre, har dette problemet 8 vesentlig forskjellige løsninger.

Konstruksjon av regulære polygoner.

P

riktig (eller likesidet ) triangel - Dette vanlig polygonmed tre sider, den første av de regulære polygonene. Alle sidene av en vanlig trekant er like hverandre, og alle vinklene er 60°. For å konstruere en likesidet trekant, må du dele sirkelen i 3 like deler. For å gjøre dette er det nødvendig å tegne en bue med radius R av denne sirkelen fra bare den ene enden av diameteren, vi får den første og andre divisjonen. Den tredje divisjonen er i motsatt ende av diameteren. Ved å koble sammen disse punktene får vi en likesidet trekant.

Vanlig sekskant Kankonstruere ved hjelp av kompass og linjal. Underbyggemetoden er gittgjennom å dele sirkelen i 6 deler. Vi bruker likheten mellom sidene av en regulær sekskant til radiusen til den omskrevne sirkelen. Fra de motsatte ender av en av diameteren til sirkelen beskriver vi buer med radius R. Skjæringspunktene til disse buene med en gitt sirkel vil dele den i 6 like deler. Ved å sekvensielt koble de funnet punktene, oppnås en vanlig sekskant.

Bygging av en vanlig femkant.

P
en vanlig femkant kan værekonstruert ved hjelp av et kompass og linjal, eller ved å passe det inn i en gittsirkel, eller konstruksjon basert på en gitt side. Denne prosessen er beskrevet av Euclidi hans Elementer omkring 300 f.Kr. e.

Her er en metode for å konstruere en vanlig femkant i en gitt sirkel:

Konstruer en sirkel som femkanten skal skrives inn i, og merk sentrum somO . (Dette er den grønne sirkelen i diagrammet til høyre).

Velg et punkt på sirkelenEN , som vil være en av toppunktene i femkanten. Konstruer en rett linje gjennomO OgEN .

Konstruer en linje vinkelrett på linjenO.A. , passerer gjennom punktetO . Angi et av skjæringspunktene med sirkelen som et punktB .

Tegn et poengC midt mellomO OgB .

C gjennom punktetEN . Marker skjæringspunktet med linjenO.B. (inne i den opprinnelige sirkelen) som et punktD .

Tegn en sirkel med sentrum klEN gjennom punkt D, marker skjæringspunktet mellom denne sirkelen med originalen (grønn sirkel) som punkterE OgF .

Tegn en sirkel med sentrum klE gjennom punktetEN G .

Tegn en sirkel med sentrum klF gjennom punktetEN . Merk det andre skjæringspunktet med den opprinnelige sirkelen som et punktH .

Konstruer en vanlig femkantAEGHF .

Uløselige problemer

Følgende tre byggeoppgaver ble satt i antikken:

Tredeling av en vinkel - dele en vilkårlig vinkel i tre like deler.

Med andre ord er det nødvendig å konstruere vinkeltrisektorer - stråler som deler vinkelen i tre like deler. P. L. Wanzel beviste i 1837 at problemet kun kan løses når for eksempel tredeling er mulig for vinkler α = 360°/n, forutsatt at hele tallet n ikke er delelig med 3. Men i pressen fra tid til annen (feilaktig ) metoder for tredeling av en vinkel med kompass og linjal er publisert.

Dobling av kuben - klassisk gammelt problem med å konstruere kanten av en terning med kompass og linjal, hvis volumet er dobbelt så stort som volumet til en gitt terning.

I moderne notasjon er problemet redusert til å løse ligningen. Det hele kommer ned til problemet med å konstruere et lengdesegment. P. Wantzel beviste i 1837 at dette problemet ikke kunne løses ved hjelp av kompass og rett kant.

Kvadrate en sirkel - en oppgave som består i å finne en konstruksjon ved hjelp av et kompass og en linjal av en firkant som i areal er lik den gitte sirkelen.

Som du vet kan du ved hjelp av et kompass og en linjal utføre alle de 4 regneoperasjonene og trekke ut kvadratroten; det følger at det er mulig å kvadrere sirkelen hvis og bare hvis det ved hjelp av et begrenset antall slike handlinger er mulig å konstruere et segment med lengden π. Dermed følger uløseligheten av dette problemet fra den ikke-algebraiske naturen (transcendens) til tallet π, som ble bevist i 1882 av Lindemann.

Et annet velkjent problem som ikke kan løses med kompass og linjal erkonstruere en trekant ved å bruke tre gitte halveringslengder .

Dessuten forblir dette problemet uløselig selv i nærvær av en trisektor.

Det var først på 1800-tallet at det ble bevist at alle tre problemene var uløselige kun ved bruk av kompass og rette. Spørsmålet om muligheten for konstruksjon er fullstendig løst ved algebraiske metoder basert på Galois teori.

VISSTE DU AT...

(fra historien til geometriske konstruksjoner)

En gang i tiden ble det investert en mystisk betydning i konstruksjonen av vanlige polygoner.

Således pytagoreerne, tilhengere av den religiøse og filosofiske læren grunnlagt av Pythagoras, og som levde i antikkens Hellas (V Jeg-jeg Vårhundrer f.Kr BC), adopterte som et tegn på deres forening en stjerneformet polygon dannet av diagonalene til en vanlig femkant.

Reglene for den strenge geometriske konstruksjonen av noen vanlige polygoner er fastsatt i boken "Elementer" av den gamle greske matematikeren Euclid, som bodde iIIIV. f.Kr. For å utføre disse konstruksjonene foreslo Euclid å bruke bare en linjal og et kompass, som på den tiden ikke hadde en hengslet enhet for å koble bena (en slik begrensning i instrumenter var et uforanderlig krav i gammel matematikk).

Vanlige polygoner ble mye brukt i gammel astronomi. Hvis Euclid var interessert i konstruksjonen av disse figurene fra et matematisk synspunkt, viste det seg for den gamle greske astronomen Claudius Ptolemaios (ca. 90 - 160 e.Kr.) å være nødvendig som et hjelpeverktøy for å løse astronomiske problemer. Så, i den første boken til Almagests, er hele det tiende kapittelet viet til konstruksjonen av vanlige femkanter og dekagoner.

Men i tillegg til rent vitenskapelige arbeider var konstruksjonen av vanlige polygoner en integrert del av bøker for byggere, håndverkere og kunstnere. Evnen til å skildre disse figurene har lenge vært nødvendig innen arkitektur, smykker og kunst.

De "ti bøker om arkitektur" til den romerske arkitekten Vitruvius (som levde ca. 63-14 f.Kr.) sier at bymurene skulle ha form av en vanlig polygon i plan, og tårnene på festningen "bør gjøres runde eller polygonale , for en firkant som er ganske ødelagt av beleiringsvåpen.»

Utformingen av byer var av stor interesse for Vitruvius, som mente at det var nødvendig å planlegge gatene slik at hovedvindene ikke blåste langs dem. Det ble antatt at det var åtte slike vinder og at de blåste i visse retninger.

Under renessansen var konstruksjonen av regulære polygoner, og spesielt femkanten, ikke et enkelt matematisk spill, men var en nødvendig forutsetning for bygging av festninger.

Den vanlige sekskanten var gjenstand for en spesiell studie av den store tyske astronomen og matematikeren Johannes Kepler (1571-1630), som han snakker om i sin bok «Nyttårsgave, eller sekskantede snøfnugg». Når han diskuterer årsakene til at snøflak har en sekskantet form, bemerker han spesielt følgende: "... et fly kan dekkes uten hull bare med følgende figurer: likesidede trekanter, firkanter og vanlige sekskanter. Blant disse figurene dekker den vanlige sekskanten det største området."

En av de mest kjente forskerne involvert i geometriske konstruksjoner var den store tyske kunstneren og matematikeren Albrecht Durer (1471 -1528), som dedikerte en betydelig del av sin bok "Manualer..." til dem. Han foreslo regler for å konstruere vanlige polygoner med 3, 4, 5 ... 16 sider. Metodene for å dele en sirkel foreslått av Dürer er ikke universelle; en individuell teknikk brukes i hvert enkelt tilfelle.

Dürer brukte metoder for å konstruere vanlige polygoner i kunstnerisk praksis, for eksempel ved å lage ulike typer ornamenter og mønstre for parkett. Han tegnet slike mønstre under en reise til Nederland, hvor det ble funnet parkettgulv i mange hus.

Dürer komponerte ornamenter fra vanlige polygoner, som er forbundet til ringer (ringer med seks likesidede trekanter, fire firkanter, tre eller seks sekskanter, fjorten sjukanter, fire åttekanter).

Konklusjon

Så,geometriske konstruksjoner er en metode for å løse et problem der svaret er innhentet grafisk. Konstruksjoner utføres ved hjelp av tegneverktøy med maksimal presisjon og nøyaktighet av arbeidet, siden riktigheten av løsningen avhenger av dette.

Takket være dette arbeidet ble jeg kjent med historien om kompassets opprinnelse, ble mer kjent med reglene for utførelse av geometriske konstruksjoner, fikk ny kunnskap og brukte den i praksis.
Å løse problemer som involverer konstruksjon med kompass og linjal er et nyttig tidsfordriv som lar deg ta en ny titt på de kjente egenskapene til geometriske figurer og deres elementer.Denne artikkelen diskuterer de mest presserende problemene knyttet til geometriske konstruksjoner ved bruk av kompass og linjaler. Hovedproblemene vurderes og deres løsninger er gitt. De oppgitte problemstillingene er av vesentlig praktisk interesse, befester tilegnet kunnskap i geometri og kan brukes til praktisk arbeid.
Dermed er målet med arbeidet nådd, de tildelte oppgavene er utført.

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt=">Konstruksjon med linjal og kompassgeometri">!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="> Konstruer et segment lik det gitte Ú Oppgave A B"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="> Konstruere en vinkel lik en gitt en Tenk på trekanter"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="> Konstruere halveringslinjen til en vinkel Oppgave Ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="> Konstruksjon av vinkelrette linjer Ú Problem gitt en linje"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="> Konstruere midtpunktet til et segment Oppgave Ú a Konstruere midtpunktet gitt"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}