Heve en sum av tall til en potens. Formler for krefter og røtter
Hvis du fortsetter samtalen om kraften til et tall, er det logisk å finne ut hvordan du finner verdien av potensen. Denne prosessen kalles eksponentiering. I denne artikkelen skal vi studere hvordan eksponentiering utføres, mens vi skal berøre alle mulige eksponenter – naturlig, heltall, rasjonell og irrasjonell. Og ifølge tradisjonen skal vi vurdere i detalj løsninger på eksempler på å heve tall til ulike makter.
Sidenavigering.
Hva betyr "eksponentiering"?
La oss starte med å forklare hva som kalles eksponentiering. Her er den relevante definisjonen.
Definisjon.
Eksponentiering- dette er å finne verdien av potensen til et tall.
Dermed er det samme å finne verdien av potensen til et tall a med eksponent r og heve tallet a til potensen r. For eksempel, hvis oppgaven er "beregn verdien av potensen (0,5) 5", kan den omformuleres som følger: "Høy tallet 0,5 til potensen 5."
Nå kan du gå direkte til reglene som eksponentieringen utføres etter.
Heve et tall til en naturlig kraft
I praksis brukes likestilling basert på vanligvis i skjemaet . Det vil si at når man hever et tall a til en brøkpotens m/n, tas først den n-te roten av tallet a, hvoretter det resulterende resultatet heves til en heltallspott m.
La oss se på løsninger på eksempler på å heve til en brøkstyrke.
Eksempel.
Regn ut verdien av graden.
Løsning.
Vi viser to løsninger.
Første vei. Per definisjon av en grad med en brøkeksponent. Vi beregner verdien av graden under rottegnet, og trekker deretter ut kuberoten:  .
.
Andre vei. Ved definisjonen av en grad med en brøkeksponent og basert på egenskapene til røttene, er følgende likheter sanne:  . Nå trekker vi ut roten
. Nå trekker vi ut roten ![]() , til slutt hever vi den til en heltalls potens
, til slutt hever vi den til en heltalls potens ![]() .
.
Det er klart at de oppnådde resultatene av å heve til en brøkkraft sammenfaller.
Svar:
Legg merke til at en brøkeksponent kan skrives som en desimalbrøk eller et blandet tall, i disse tilfellene bør den erstattes med den tilsvarende ordinære brøken, og deretter heves til en potens.
Eksempel.
Regn ut (44,89) 2,5.
Løsning.
La oss skrive eksponenten i form av en vanlig brøk (om nødvendig, se artikkelen):  . Nå utfører vi hevingen til en brøkstyrke:
. Nå utfører vi hevingen til en brøkstyrke: 
Svar:
(44,89) 2,5 =13 501,25107 .
Det skal også sies at det å heve tall til rasjonelle potenser er en ganske arbeidskrevende prosess (spesielt når telleren og nevneren til brøkeksponenten inneholder tilstrekkelig store tall), som vanligvis utføres ved hjelp av datateknologi.
For å konkludere med dette punktet, la oss dvele ved å heve tallet null til en brøkpotens. Vi ga følgende betydning til brøkkraften til null i formen: når vi har  , og ved null til m/n-effekten er ikke definert. Så null til en brøkdel positiv potens er null, for eksempel,
, og ved null til m/n-effekten er ikke definert. Så null til en brøkdel positiv potens er null, for eksempel,  . Og null i en negativ brøkpotens gir ikke mening, for eksempel gir ikke uttrykkene 0 -4,3 mening.
. Og null i en negativ brøkpotens gir ikke mening, for eksempel gir ikke uttrykkene 0 -4,3 mening.
Heve til en irrasjonell makt
Noen ganger blir det nødvendig å finne ut verdien av potensen til et tall med en irrasjonell eksponent. I dette tilfellet er det for praktiske formål vanligvis tilstrekkelig å oppnå verdien av graden nøyaktig til et bestemt tegn. La oss umiddelbart merke seg at i praksis beregnes denne verdien ved hjelp av elektroniske datamaskiner, siden å heve den til en irrasjonell kraft manuelt krever et stort antall tungvinte beregninger. Men vi vil likevel beskrive essensen av handlingene i generelle termer.
For å få en tilnærmet verdi av potensen til et tall a med en irrasjonell eksponent, tas en desimal tilnærming av eksponenten og verdien av potensen beregnes. Denne verdien er en omtrentlig verdi av potensen til tallet a med en irrasjonell eksponent. Jo mer nøyaktig desimaltilnærmingen til et tall tas i utgangspunktet, desto mer nøyaktig vil verdien av graden oppnås til slutt.
Som et eksempel, la oss beregne den omtrentlige verdien av potensen 2 1,174367... . La oss ta følgende desimaltilnærming av den irrasjonelle eksponenten: . Nå hever vi 2 til den rasjonelle kraften 1.17 (vi beskrev essensen av denne prosessen i forrige avsnitt), vi får 2 1.17 ≈2.250116. Dermed, 2 1,174367... ≈2 1,17 ≈2,250116 . Hvis vi tar en mer nøyaktig desimal tilnærming av den irrasjonelle eksponenten, for eksempel, får vi en mer nøyaktig verdi av den opprinnelige eksponenten: 2 1,174367... ≈2 1,1743 ≈2,256833 .
Bibliografi.
- Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S., Shvartsburd S.I. Matematikk lærebok for 5. klasse. utdanningsinstitusjoner.
- Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: lærebok for 7. klasse. utdanningsinstitusjoner.
- Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: lærebok for 8. klasse. utdanningsinstitusjoner.
- Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: lærebok for 9. klasse. utdanningsinstitusjoner.
- Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. Algebra og begynnelsen av analyse: Lærebok for 10. - 11. klassetrinn ved allmennutdanningsinstitusjoner.
- Gusev V.A., Mordkovich A.G. Matematikk (en manual for de som går inn på tekniske skoler).
Kalkulatoren hjelper deg raskt å heve et tall til en potens på nettet. Grunnlaget for graden kan være et hvilket som helst tall (både heltall og reelle tall). Eksponenten kan også være et heltall eller reell, og kan også være positiv eller negativ. Husk at for negative tall er det udefinert å heve til en ikke-heltalls potens, så kalkulatoren vil rapportere en feil hvis du prøver det.
Gradskalkulator
Hev til makten
Eksponentiseringer: 94722
Hva er en naturlig kraft til et tall?
Tallet p kalles den n-te potensen av et tall hvis p er lik tallet a multiplisert med seg selv n ganger: p = a n = a·...·a
n - kalt eksponent, og tallet a er gradsgrunnlag.
Hvordan heve et tall til en naturlig kraft?
For å forstå hvordan du øker forskjellige tall til naturlige krefter, kan du vurdere noen eksempler:
Eksempel 1. Hev tallet tre til fjerde potens. Det vil si at det er nødvendig å beregne 3 4
Løsning: som nevnt ovenfor, 3 4 = 3·3·3·3 = 81.
Svar: 3 4 = 81 .
Eksempel 2. Hev tallet fem til femte potens. Det vil si at det er nødvendig å beregne 5 5
Løsning: tilsvarende, 55 = 5·5·5·5·5 = 3125.
Svar: 5 5 = 3125 .
For å heve et tall til en naturlig potens, trenger du bare å multiplisere det med seg selv n ganger.
Hva er en negativ potens av et tall?
Den negative potensen -n av a er en dividert med a til potensen av n: a -n = .I dette tilfellet eksisterer en negativ potens bare for tall som ikke er null, siden deling med null ellers ville forekomme.
Hvordan heve et tall til en negativ heltallspotens?
For å heve et tall som ikke er null til en negativ potens, må du beregne verdien av dette tallet til samme positive potens og dele en på resultatet.
Eksempel 1. Hev tallet to til den negative fjerde potensen. Det vil si at du må beregne 2 -4
Løsning: som angitt ovenfor, 2 -4 = = = 0,0625.Svar: 2 -4 = 0.0625 .
Vi fant ut hva en potens av et tall faktisk er. Nå må vi forstå hvordan vi beregner det riktig, dvs. heve tall til makter. I dette materialet vil vi analysere de grunnleggende reglene for beregning av grader i tilfelle av heltalls-, naturlige, brøk-, rasjonelle og irrasjonelle eksponenter. Alle definisjoner vil bli illustrert med eksempler.
Konseptet med eksponentiering
La oss starte med å formulere grunnleggende definisjoner.
Definisjon 1
Eksponentiering- dette er beregningen av verdien av kraften til et visst tall.
Det vil si at ordene "beregne verdien av en makt" og "å heve til en makt" betyr det samme. Så hvis problemet sier "Høy tallet 0, 5 til femte potens", bør dette forstås som "beregn verdien av potensen (0, 5) 5.
Nå presenterer vi de grunnleggende reglene som må følges når du gjør slike beregninger.
La oss huske hva potensen til et tall med en naturlig eksponent er. For en potens med grunntall a og eksponent n vil dette være produktet av det n-te antall faktorer, som hver er lik a. Dette kan skrives slik:
For å beregne verdien av en grad, må du utføre en multiplikasjonshandling, det vil si multiplisere basene til graden det angitte antallet ganger. Selve konseptet med en grad med en naturlig eksponent er basert på evnen til raskt å multiplisere. La oss gi eksempler.
Eksempel 1
Tilstand: heve - 2 til styrke 4.
Løsning
Ved å bruke definisjonen ovenfor skriver vi: (− 2) 4 = (− 2) · (− 2) · (− 2) · (− 2) . Deretter trenger vi bare å følge disse trinnene og få 16.
La oss ta et mer komplisert eksempel.
Eksempel 2
Regn ut verdien 3 2 7 2
Løsning
Denne oppføringen kan skrives om til 3 2 7 · 3 2 7 . Tidligere har vi sett på hvordan man korrekt multipliserer de blandede tallene nevnt i betingelsen.
La oss utføre disse trinnene og få svaret: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Hvis problemet indikerer behovet for å heve irrasjonelle tall til en naturlig potens, må vi først runde av basene deres til sifferet som vil tillate oss å få et svar med den nødvendige nøyaktigheten. La oss se på et eksempel.
Eksempel 3
Utfør kvadratet av π.
Løsning
Først, la oss runde det av til hundredeler. Så π 2 ≈ (3, 14) 2 = 9, 8596. Hvis π ≈ 3. 14159, da får vi et mer nøyaktig resultat: π 2 ≈ (3, 14159) 2 = 9, 8695877281.
Merk at behovet for å beregne potenser av irrasjonelle tall oppstår relativt sjelden i praksis. Vi kan da skrive svaret som potensen (ln 6) 3 selv, eller omregne om mulig: 5 7 = 125 5 .
Separat skal det angis hva den første potensen av et tall er. Her kan du ganske enkelt huske at ethvert tall hevet til første potens forblir seg selv:
Dette fremgår tydelig av opptaket  .
.
Det avhenger ikke av graden.
Eksempel 4
Så, (− 9) 1 = − 9, og 7 3 hevet til første potens vil forbli lik 7 3.
For enkelhets skyld vil vi undersøke tre tilfeller separat: hvis eksponenten er et positivt heltall, om det er null og om det er et negativt heltall.
I det første tilfellet er dette det samme som å heve til en naturlig potens: tross alt tilhører positive heltall settet med naturlige tall. Vi har allerede snakket ovenfor om hvordan man jobber med slike grader.
La oss nå se hvordan du kan heve til nullstyrken. For et annet grunnlag enn null gir denne beregningen alltid 1. Vi har tidligere forklart at 0. potens av a kan defineres for ethvert reelt tall som ikke er lik 0, og a 0 = 1.
Eksempel 5
5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1
0 0 - ikke definert.
Vi sitter igjen med bare tilfellet av en grad med en heltalls negativ eksponent. Vi har allerede diskutert at slike grader kan skrives som en brøk 1 a z, der a er et hvilket som helst tall, og z er et negativt heltall. Vi ser at nevneren til denne brøken ikke er noe mer enn en vanlig potens med en positiv heltallseksponent, og vi har allerede lært hvordan vi beregner den. La oss gi eksempler på oppgaver.
Eksempel 6
Hev 2 til makten - 3.
Løsning
Ved å bruke definisjonen ovenfor skriver vi: 2 - 3 = 1 2 3
La oss regne ut nevneren til denne brøken og få 8: 2 3 = 2 · 2 · 2 = 8.
Da er svaret: 2 - 3 = 1 2 3 = 1 8
Eksempel 7
Øk 1,43 til -2-styrken.
Løsning
La oss omformulere: 1, 43 - 2 = 1 (1, 43) 2
Vi regner ut kvadratet i nevneren: 1,43·1,43. Desimaler kan multipliseres på denne måten: 
Som et resultat fikk vi (1, 43) - 2 = 1 (1, 43) 2 = 1 2, 0449. Alt vi trenger å gjøre er å skrive dette resultatet i form av en vanlig brøk, som vi må gange det med 10 tusen (se materialet om å konvertere brøker).
Svar: (1, 43) - 2 = 10000 20449
Et spesielt tilfelle er å heve et tall til minus første potens. Verdien av denne graden er lik den gjensidige av den opprinnelige verdien av basen: a - 1 = 1 a 1 = 1 a.
Eksempel 8
Eksempel: 3 − 1 = 1 / 3
9 13 - 1 = 13 9 6 4 - 1 = 1 6 4 .
Hvordan heve et tall til en brøkpotens
For å utføre en slik operasjon, må vi huske den grunnleggende definisjonen av en grad med en brøkeksponent: a m n = a m n for enhver positiv a, heltall m og naturlig n.
Definisjon 2
Dermed må beregningen av en brøkpotens utføres i to trinn: heve til en heltallspotens og finne roten til n-te potens.
Vi har likheten a m n = a m n , som, tatt i betraktning røttenes egenskaper, vanligvis brukes til å løse problemer i formen a m n = a n m . Dette betyr at hvis vi hever et tall a til en brøkpotens m / n, så tar vi først den n-te roten av a, så hever vi resultatet til en potens med en heltallseksponent m.
La oss illustrere med et eksempel.
Eksempel 9
Regn ut 8-2 3.
Løsning
Metode 1: I følge grunndefinisjonen kan vi representere dette som: 8 - 2 3 = 8 - 2 3
La oss nå beregne graden under roten og trekke ut den tredje roten fra resultatet: 8 - 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Metode 2. Transformer den grunnleggende likheten: 8 - 2 3 = 8 - 2 3 = 8 3 - 2
Etter dette trekker vi ut roten 8 3 - 2 = 2 3 3 - 2 = 2 - 2 og kvadrerer resultatet: 2 - 2 = 1 2 2 = 1 4
Vi ser at løsningene er identiske. Du kan bruke den som du vil.
Det er tilfeller der graden har en indikator uttrykt som et blandet tall eller en desimalbrøk. For å forenkle beregningene er det bedre å erstatte den med en vanlig brøk og beregne som angitt ovenfor.
Eksempel 10
Hev 44, 89 til styrken 2, 5.
Løsning
La oss konvertere verdien av indikatoren til en vanlig brøk: 44, 89 2, 5 = 44, 89 5 2.
Nå utfører vi i rekkefølge alle handlingene som er angitt ovenfor: 44, 89 5 2 = 44, 89 5 = 44, 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = 01001 = 01007 1 = 01 501, 25107
Svar: 13 501, 25107.
Hvis telleren og nevneren til en brøkeksponent inneholder store tall, er det en ganske vanskelig jobb å beregne slike eksponenter med rasjonelle eksponenter. Det krever vanligvis datateknologi.
La oss dvele separat ved potenser med nullbase og brøkeksponent. Et uttrykk på formen 0 m n kan gis følgende betydning: hvis m n > 0, så 0 m n = 0 m n = 0; hvis m n< 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную - значения не имеет: 0 - 4 3 .
Hvordan heve et tall til en irrasjonell makt
Behovet for å beregne verdien av en potens hvis eksponent er et irrasjonelt tall oppstår ikke så ofte. I praksis er oppgaven vanligvis begrenset til å beregne en omtrentlig verdi (opptil et visst antall desimaler). Dette beregnes vanligvis på en datamaskin på grunn av kompleksiteten til slike beregninger, så vi vil ikke dvele på dette i detalj, vi vil bare indikere hovedbestemmelsene.
Hvis vi trenger å beregne verdien av en potens a med en irrasjonell eksponent a, tar vi desimaltilnærmingen til eksponenten og teller fra den. Resultatet vil være et omtrentlig svar. Jo mer nøyaktig desimaltilnærmingen er, jo mer nøyaktig er svaret. La oss vise med et eksempel:
Eksempel 11
Regn ut tilnærmingen til 2 i potensen 1,174367....
Løsning
La oss begrense oss til desimaltilnærmingen a n = 1, 17. La oss utføre beregninger ved å bruke dette tallet: 2 1, 17 ≈ 2, 250116. Hvis vi for eksempel tar tilnærmingen a n = 1, 1743, vil svaret være litt mer nøyaktig: 2 1, 174367. . . ≈ 2 1, 1743 ≈ 2, 256833.
Hvis du oppdager en feil i teksten, merk den og trykk Ctrl+Enter
Gradsformler brukes i prosessen med å redusere og forenkle komplekse uttrykk, i å løse likninger og ulikheter.
Antall c er n-te potens av et tall en Når:
Operasjoner med grader.
1. Ved å multiplisere grader med samme base, legges indikatorene deres til:
en m·a n = a m + n .
2. Når du deler grader med samme grunntall, trekkes eksponentene deres fra:

3. Graden av produktet av 2 eller flere faktorer er lik produktet av gradene av disse faktorene:
(abc...) n = a n · b n · c n …
4. Graden av en brøk er lik forholdet mellom gradene av utbytte og divisor:
(a/b) n = a n /b n .
5. Ved å heve en potens til en potens multipliseres eksponentene:
(a m) n = a m n .
Hver formel ovenfor er sann i retningene fra venstre til høyre og omvendt.
For eksempel. (2 3 5/15)² = 2² 3² 5²/15² = 900/225 = 4.
Operasjoner med røtter.
1. Roten til produktet av flere faktorer er lik produktet av røttene til disse faktorene:
2. Roten av et forholdstall er lik forholdet mellom utbyttet og divisoren til røttene:
![]()
3. Når du hever en rot til en makt, er det nok å heve det radikale tallet til denne makten:

4. Hvis du øker graden av roten inn n en gang og samtidig bygge inn n potensen er et radikalt tall, så endres ikke verdien av roten:
![]()
5. Hvis du reduserer graden av roten i n trekke ut roten samtidig n-te potens av et radikalt tall, vil verdien av roten ikke endres:

En grad med negativ eksponent. Potensen til et visst tall med en ikke-positiv (heltalls) eksponent er definert som en dividert med potensen til samme tall med en eksponent lik den absolutte verdien av den ikke-positive eksponenten:

Formel en m:a n =a m - n kan brukes ikke bare til m> n, men også med m< n.
For eksempel. en4:a 7 = a 4 - 7 = a -3.
Til formel en m:a n =a m - n ble rettferdig når m=n, tilstedeværelsen av null grader er nødvendig.
En grad med nullindeks. Potensen til et tall som ikke er lik null med en nulleksponent er lik en.
For eksempel. 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Grad med en brøkeksponent. For å heve et reelt tall EN til den grad m/n, må du trekke ut roten n grad av m-te potens av dette tallet EN.
Eksponentiering er en operasjon som er nært knyttet til multiplikasjon; denne operasjonen er resultatet av gjentatte ganger multiplisere et tall med seg selv. La oss representere det med formelen: a1 * a2 * … * an = an.
For eksempel, a=2, n=3: 2 * 2 * 2=2^3 = 8 .
Generelt brukes eksponentiering ofte i ulike formler innen matematikk og fysikk. Denne funksjonen har et mer vitenskapelig formål enn de fire viktigste: Addisjon, Subtraksjon, Multiplikasjon, Divisjon.
Å heve et tall til en makt
Å heve et tall til en potens er ikke en komplisert operasjon. Det er relatert til multiplikasjon på en lignende måte som forholdet mellom multiplikasjon og addisjon. Notasjonen an er en kort notasjon av det n-te antallet tall "a" multiplisert med hverandre.
Vurder eksponentiering ved å bruke de enkleste eksemplene, gå videre til komplekse.
For eksempel, 42. 42 = 4 * 4 = 16. Fire kvadrater (til andre potens) er lik seksten. Hvis du ikke forstår multiplikasjon 4 * 4, så les vår artikkel om multiplikasjon.
La oss se på et annet eksempel: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125 . Fem terninger (til tredje potens) er lik hundre og tjuefem.
Et annet eksempel: 9^3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729 . Ni terninger tilsvarer syv hundre og tjueni.
Eksponentieringsformler
For å heve til en potens på riktig måte, må du huske og kjenne formlene gitt nedenfor. Det er ikke noe ekstra naturlig i dette, det viktigste er å forstå essensen og da vil de ikke bare bli husket, men vil også virke enkle.

Å heve en monomial til en makt
Hva er et monomial? Dette er et produkt av tall og variabler i en hvilken som helst mengde. For eksempel er to en monomial. Og denne artikkelen handler nettopp om å heve slike monomialer til makter.
Ved å bruke formlene for eksponentiering vil det ikke være vanskelig å beregne eksponentieringen til en monomial.
For eksempel, (3x^2y^3)^2= 3^2 * x^2 * 2 * y^(3 * 2) = 9x^4y^6; Hvis du hever en monomial til en potens, så heves hver komponent av monomial til en potens.
Ved å heve en variabel som allerede har en potens til en potens, multipliseres potensene. For eksempel, (x^2)^3 = x^(2 * 3) = x^6 ;
Heve til en negativ makt
En negativ potens er den gjensidige av et tall. Hva er det gjensidige tallet? Den gjensidige av ethvert tall X er 1/X. Det vil si X-1=1/X. Dette er essensen av den negative graden.
Tenk på eksemplet (3Y)^-3:
(3Y)^-3 = 1/(27Y^3).
Hvorfor det? Siden det er minus i graden, overfører vi ganske enkelt dette uttrykket til nevneren, og hever det så til tredje potens. Enkelt er det ikke?
Heve til en brøkdel
La oss starte med å se på problemet med et spesifikt eksempel. 43/2. Hva betyr grad 3/2? 3 – teller, betyr å heve et tall (i dette tilfellet 4) til en kube. Tallet 2 er nevneren; det er ekstraksjonen av den andre roten av et tall (i dette tilfellet 4).
Da får vi kvadratroten av 43 = 2^3 = 8. Svar: 8.
Så, nevneren til en brøkpotens kan være enten 3 eller 4 eller opp til uendelig et hvilket som helst tall, og dette tallet bestemmer graden av kvadratroten tatt fra et gitt tall. Selvsagt kan ikke nevneren være null.
Å heve en rot til en makt
Hvis roten heves til en grad lik graden av selve roten, så vil svaret være et radikalt uttrykk. For eksempel, (√x)2 = x. Og så i alle fall er graden av roten og graden av heving av roten like.
Hvis (√x)^4. Deretter (√x)^4=x^2. For å sjekke løsningen konverterer vi uttrykket til et uttrykk med brøkpotens. Siden roten er kvadratisk, er nevneren 2. Og hvis roten heves til fjerde potens, så er telleren 4. Vi får 4/2=2. Svar: x = 2.
I alle fall er det beste alternativet å konvertere uttrykket til et uttrykk med brøkstyrke. Hvis brøken ikke kansellerer, så er dette svaret, forutsatt at roten til det gitte tallet ikke er isolert.
Heve et komplekst tall til makten
Hva er et komplekst tall? Et komplekst tall er et uttrykk som har formelen a + b * i; a, b er reelle tall. i er et tall som gir tallet -1 når det er kvadratisk.
La oss se på et eksempel. (2 + 3i)^2.
(2 + 3i)^2 = 22 +2 * 2 * 3i +(3i)^2 = 4+12i^-9=-5+12i.
Meld deg på kurset "Fremskynde hoderegning, IKKE hoderegning" for å lære hvordan du raskt og riktig kan addere, subtrahere, multiplisere, dividere, kvadrattall og til og med trekke ut røtter. På 30 dager lærer du hvordan du bruker enkle triks for å forenkle aritmetiske operasjoner. Hver leksjon inneholder nye teknikker, klare eksempler og nyttige oppgaver.
Eksponentiering på nett
Ved å bruke kalkulatoren vår kan du beregne økningen av et tall til en potens:
Eksponentiering 7. klasse
Skoleelever begynner å øke til en makt først i syvende klasse.
Eksponentiering er en operasjon som er nært knyttet til multiplikasjon; denne operasjonen er resultatet av gjentatte ganger multiplisere et tall med seg selv. La oss representere det med formelen: a1 * a2 * … * an=an.
For eksempel, a=2, n=3: 2 * 2 * 2 = 2^3 = 8.
Eksempler på løsning:

Eksponentieringspresentasjon
Presentasjon om maktheving, designet for sjuendeklassinger. Presentasjonen kan oppklare noen uklare punkter, men disse punktene vil trolig ikke bli oppklart takket være vår artikkel.
Bunnlinjen
Vi har kun sett på toppen av isfjellet, for å forstå matematikk bedre – meld deg på kurset vårt: Akselererende hoderegning – IKKE hoderegning.
Fra kurset vil du ikke bare lære dusinvis av teknikker for forenklet og rask multiplikasjon, addisjon, multiplikasjon, divisjon og beregning av prosenter, men du vil også øve på dem i spesielle oppgaver og pedagogiske spill! Mentalregning krever også mye oppmerksomhet og konsentrasjon, som trenes aktivt når man løser interessante problemer.
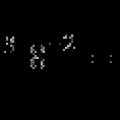 Formler for krefter og røtter
Formler for krefter og røtter Endelte setninger (8. klasse) Russisk språk alternativ 2 Gamle russiske arkitekter
Endelte setninger (8. klasse) Russisk språk alternativ 2 Gamle russiske arkitekter Når brukes komma?
Når brukes komma?