Як виник принцип найменшої дії. Принцип найменшої дії

Коли я вперше дізнався про цей принцип, у мене виникло відчуття якоїсь містики. Таке враження, що природа таємниче перебирає всі можливі шляхи руху системи і вибирає з них найкращий.

Сьогодні я хочу трохи розповісти про один із найчудовіших фізичних принципів – принцип найменшої дії.

Передісторія

З часів Галілея було відомо, що тіла, на які не діють жодні сили, рухаються прямими лініями, тобто найкоротшим шляхом. По прямих лініях поширюються і світлові промені.

При відображенні світло також рухається таким чином, щоб дістатися з однієї точки до іншої найкоротшим шляхом. На картинці найкоротшим буде зелений шлях, при якому кут падіння дорівнює куту відображення. Будь-який інший шлях, наприклад, червоний, виявиться довшим.

Це нескладно довести, просто відбивши шляхи променів на протилежний бік від дзеркала. На зображенні вони показані пунктиром.

Видно, що зелений шлях ACB перетворюється на пряму ACB'. А червоний шлях перетворюється на зламану лінію ADB', яка, звичайно, довша за зелену.

У 1662 році П'єр Ферма припустив, що швидкість світла в щільній речовині, наприклад, у склі, менша, ніж у повітрі. До цього загальноприйнятою була версія Декарта, згідно з якою швидкість світла в речовині повинна бути більшою, ніж у повітрі, щоб виходив правильний закон заломлення. Для Ферма припущення, що світло може рухатися в більш щільному середовищі швидше, ніж у розрідженому здавалося протиприродним. Тому він припустив, що все точно навпаки і довів дивовижну річ – при такому припущенні світло заломлюється так, щоб досягти місця призначення за мінімальний час.

На малюнку знову зеленим кольором показаний шлях, яким насправді рухається світловий промінь. Шлях, позначений червоним кольором, є найкоротшим, але не найшвидшим, тому що світові доводиться більший шлях проходити у склі, а в ньому його швидкість менша. Найшвидшим є реальний шлях проходження світлового променя.

Всі ці факти наводили на думку, що природа діє якимось раціональним чином, світло і тіла рухаються найбільш оптимально, витрачаючи якнайменше зусиль. Але що це за зусилля і як їх порахувати залишалося загадкою.

У 1744 році Мопертюї вводить поняття «дії» і формулює принцип, згідно з яким справжня траєкторія частки відрізняється від будь-якої іншої тим, що дія для неї є мінімальною. Однак сам Мопертюї, так і не зміг дати чіткого визначення чому ця дія. Суворе математичне формулювання принципу найменшої дії було розроблено вже іншими математиками – Ейлером, Лагранжем, і остаточно було дано Вільямом Гамільтоном:

Математичною мовою принцип найменшої дії формулюється досить коротко, проте не для всіх читачів може бути зрозумілий зміст позначень, що використовуються. Я хочу спробувати пояснити цей принцип більш наочно та простими словами.

Вільне тіло

Отже, уявіть, що ви сидите в машині в точці і в момент часу вам дане просте завдання: на момент часу вам потрібно доїхати на машині до точки.

Паливо для машини дорого коштує і, звичайно, вам хочеться витратити його якнайменше. Машина у вас зроблена за новітніми супер-технологіями і може розганятися або гальмувати як завгодно швидко. Проте, влаштована вона так, що чим швидше вона їде, то більше споживає палива. Причому споживання палива пропорційне квадрату швидкості. Якщо ви їдете вдвічі швидше, то за той самий проміжок часу споживаєте вчетверо більше палива. Крім швидкості, на споживання палива, звичайно, впливає і маса автомобіля. Чим важчий наш автомобіль, тим більше палива він споживає. У нашого автомобіля споживання палива в кожний момент часу рівне, тобто. точно точно кінетичної енергії автомобіля.

То як же треба їхати, щоб дістатися пункту до точно призначеного часу і витратити палива якнайменше? Зрозуміло, що їхати треба прямою. При збільшенні відстані палива, що проїжджається, витратиться точно не менше. А далі можна вибрати різні тактики. Наприклад, можна швидко приїхати в пункт заздалегідь і просто посидіти, почекати, коли настане час. Швидкість їзди, а значить і споживання палива в кожний момент часу, при цьому вийде великий, але й час їзди скоротиться. Можливо, загальна витрата палива при цьому буде не така вже й велика. Або можна їхати рівномірно, з однією і тією ж швидкістю, такою, щоб, не поспішаючи, точно приїхати в момент часу. Або частину шляху проїхати швидко, а частина повільніша. Як краще їхати?

Виявляється, що найоптимальніший, найекономніший спосіб їзди - це їхати з постійною швидкістю, такою, щоб опинитися в пункті в точно призначений час. При будь-якому іншому варіанті палива витрачається більше. Можете самі перевірити на кількох прикладах. Причина полягає в тому, що споживання палива зростає пропорційно квадрату швидкості. Тому зі збільшенням швидкості споживання палива зростає швидше, ніж скорочується час їзди, і загальна витрата палива також зростає.

Отже, ми з'ясували, що якщо автомобіль у кожний момент часу споживає паливо пропорційно своєї кінетичної енергії, то найекономніший спосіб дістатися з точки в крапку до точно призначеного часу - це їхати рівномірно і прямолінійно, точно так, як рухається тіло без діючих на нього сил. Будь-який інший спосіб руху призведе до більшої загальної витрати палива.

У полі тяжкості

Тепер давайте трохи вдосконалимо наш автомобіль. Давайте приробимо до нього реактивні двигуни, щоб він міг вільно літати у будь-якому напрямку. Загалом конструкція залишилася тією ж, тому витрата палива знову залишилася суворо пропорційною кінетичній енергії автомобіля. Якщо тепер дано завдання вилетіти з точки в момент часу і прилетіти в точку до моменту часу, то найбільш економічний спосіб, як і раніше, буде летіти рівномірно і прямолінійно, щоб опинитися в точці в точно призначений час. Це знову відповідає вільному руху тіла у тривимірному просторі.

Проте в останню модель автомобіля встановили незвичайний апарат. Цей апарат може виробляти паливо практично з нічого. Але конструкція така, що чим вище знаходиться автомобіль, тим більше палива кожен момент часу виробляє апарат. Вироблення палива прямо пропорційне висоті, на якій в даний момент знаходиться автомобіль. Також, чим важчий автомобіль, тим потужніший апарат на ньому встановлений і тим більше палива він виробляє, і вироблення прямо пропорційне масі автомобіля. Апарат вийшов таким, що виробництво палива точно дорівнює (де – прискорення вільного падіння), тобто. потенційної енергії автомобіля.

Споживання палива в кожен момент часу виходить рівним кінетичній енергії мінус потенційної енергії автомобіля (мінус потенційної енергії, тому що встановлений апарат виробляє паливо, а не витрачає). Тепер наше завдання найекономнішого руху автомобіля між пунктами і стає складнішим. Прямолінійний рівномірний рух виявляється в даному випадку не найефективнішим. Виявляється, оптимальніше - трохи набрати висоти, якийсь час там затриматися, виробивши більше палива, а потім уже спуститися в крапку. При правильній траєкторії польоту загальне вироблення палива за рахунок набору висоти перекриє додаткові витрати палива на збільшення довжини шляху та збільшення швидкості. Якщо акуратно порахувати, то найекономнішим способом для автомобіля летітиме по параболі, точно за такою траєкторією і з точно такою швидкістю, з якою летів би камінь у полі тяжіння Землі.

Тут варто роз'яснити. Звичайно, можна з точки кинути камінь багатьма різними способами так, щоб він потрапив у крапку. Але кидати його потрібно так, щоб він, вилетівши з точки в момент часу, потрапив у крапку точно в момент часу. Саме цей рух буде найекономнішим для нашого автомобіля.

Функція Лагранжа та принцип найменшої дії

Тепер ми можемо перенести цю аналогію реальні фізичні тіла. Аналог інтенсивності споживання палива для тіл називають функцією Лагранжа або Лагранжіаном (на честь Лагранжа) та позначають буквою . Лагранжіан показує, наскільки багато «палива» споживає тіло в даний момент часу. Для тіла, що рухається в потенційному полі, Лагранжіан дорівнює його кінетичній енергії мінус потенційної енергії.

Аналог загальної кількості витраченого палива весь час руху, тобто. значення Лагранжіана, накопичене весь час руху, називається «дією».

Принцип найменшої дії полягає в тому, що тіло рухається таким чином, щоб дія (яка залежить від траєкторії руху) була мінімальною. У цьому не слід забувати, що задані початкове і кінцеве умови, тобто. де тіло знаходиться в момент часу та в момент часу.

При цьому тіло не обов'язково має рухатись у однорідному полі тяжіння, яке ми розглядали для нашого автомобіля. Можна розглядати зовсім інші ситуації. Тіло може коливатися на гумці, гойдатися на маятнику чи літати навколо Сонця, у всіх випадках воно рухається те щоб мінімізувати «загальний витрата палива» тобто. дія.

Якщо система складається з кількох тіл, то Лагранжіан такої системи дорівнюватиме сумарній кінетичній енергії всіх тіл мінус сумарної потенційної енергії всіх тіл. І знову всі тіла будуть узгоджено рухатися так, щоб дія всієї системи при такому русі була мінімальною.

Не все так просто

Насправді я трохи обдурив, сказавши, що тіла завжди рухаються так, щоб мінімізувати дію. Хоча в дуже багатьох випадках це справді так, можна вигадати ситуації, в яких дія явно не мінімальна.

Наприклад, візьмемо кульку і помістимо її в порожній простір. На деякому віддаленні від нього поставимо пружну стінку. Припустимо, ми хочемо, щоб через деякий час кулька опинилася в тому самому місці. За таких заданих умов кулька може рухатися двома різними способами. По-перше, може просто залишатися дома. По-друге, можна його штовхнути у напрямку до стіни. Кулька долетить до стінки, відскочить від неї і повернеться назад. Зрозуміло, що можна штовхнути його з такою швидкістю, щоб він повернувся у потрібний час.

Обидва варіанти руху кульки можливі, але дія у другому випадку вийде більше, тому що весь цей час кулька рухатиметься з ненульовою кінетичною енергією.

Як же врятувати принцип найменшої дії, щоб він був справедливим і в таких ситуаціях? Про це ми поговоримо у .

Ми коротко розглянули один із найчудовіших фізичних принципів - принцип найменшої дії, і зупинилися на прикладі, який, здавалося б, йому суперечить. У цій статті ми розберемося з цим принципом трохи докладніше і подивимося, що відбувається у цьому прикладі.

На цей раз нам знадобиться трохи більше математики. Однак основну частину статті я знову намагатимуся викласти на елементарному рівні. Трохи суворіші та складніші моменти я виділятиму кольором, їх можна пропустити без шкоди для основного розуміння статті.

Граничні умови

Почнемо ми з найпростішого об'єкта – кулі, що вільно рухається в просторі, на яку не діють жодні сили. Така куля, як відомо, рухається рівномірно та прямолінійно. Для простоти, припустимо, що він рухається вздовж осі:

Щоб точно описати його рух, зазвичай задаються початкові умови. Наприклад, задається, що в початковий момент часу куля знаходилася в точці з координатою і мала швидкість . Задавши початкові умови у такому вигляді, ми однозначно визначаємо подальший рух кулі - він буде рухатися з постійною швидкістю, і його становище в момент часу дорівнюватиме початковому положенню плюс швидкість, помножена на час: . Такий спосіб завдання початкових умов дуже природний та інтуїтивно звичний. Ми задали всю необхідну інформацію про рух кулі в початковий момент часу і далі її рух визначається законами Ньютона.

Однак це не єдиний спосіб завдання руху кулі. Інший альтернативний спосіб - це задати положення кулі в два різні моменти часу і . Тобто. поставити, що:

1) в момент часу куля знаходилася в точці (з координатою);
2) в момент часу куля знаходилася в точці (з координатою).

Вираз «знаходився в точці» не означає, що куля спочивала в точці . У момент часу він міг пролітати через крапку. Мається на увазі, що його становище в момент часу збігалося з точкою . Те саме стосується і точки.

Ці дві умови також однозначно визначають рух кулі. Його рух легко вирахувати. Щоб задовольнити обох умов, швидкість кулі, очевидно, повинна бути . Положення кулі в момент часу знову дорівнює початковому положенню плюс швидкість, помножена на минулий час:

Зауважте, що в умовах завдання нам не потрібно було задавати початкову швидкість. Вона однозначно визначилася з умов 1) та 2).

Завдання умов другим способом виглядає незвично. Можливо, незрозуміло навіщо взагалі може знадобитися задавати їх у такому вигляді. Однак, у принципі найменшої дії використовуються саме умови у вигляді 1) та 2), а не у вигляді завдання початкового стану та початкової швидкості.

Траєкторія з найменшою дією

Тепер трохи відвернемося від реального вільного руху кулі та розглянемо наступне суто математичне завдання. Припустимо, у нас є куля, яку ми можемо вручну переміщати будь-яким способом. При цьому нам потрібно виконати умови 1) та 2). Тобто. в проміжок часу між і ми повинні перемістити його з точки в крапку. Це можна зробити абсолютно різними способами. Кожен такий спосіб ми будемо називати траєкторією руху кулі і він може бути описаний функцією положення кулі від часу. Відкладемо кілька таких траєкторій на графіку залежності положення кульки від часу:

Наприклад, ми можемо переміщати кульку з тією самою швидкістю, що дорівнює (зелена траєкторія). Або ми можемо половину часу тримати його в точці, а потім з подвійною швидкістю перемістити в крапку (синя траєкторія). Можна спершу рухати його в протилежний відбік, а потім уже перемістити в (коричнева траєкторія). Можна рухати його взад і вперед (червона траєкторія). Загалом, можна пересувати його як завгодно, аби дотримувалися умови 1) та 2).

Для кожної такої траєкторії ми можемо порівняти число. У прикладі, тобто. без будь-яких сил, що діють на кулю, це число дорівнює загальної накопиченої кінетичної енергії за весь час його руху в проміжок часу між і називається дією.

У разі слово «накопичена» кінетична енергія не дуже точно передає сенс. Реально кінетична енергія ніде не накопичується, накопичення використовується лише обчислення дії для траєкторії. У математиці для такого накопичення є дуже хороше поняття – інтеграл:

Дія зазвичай позначається буквою. Символ означає кінетичну енергію. Цей інтеграл означає, що дія дорівнює накопиченої кінетичної енергії кулі за проміжок часу від .

Як приклад, давайте візьмемо кулю масою 1 кг., задамо якісь граничні умови і обчислимо дію для двох різних траєкторій. Нехай точка знаходиться на відстані 1 метр від точки , а час від часу на 1 секунду. Тобто. ми повинні перемістити кулю, яка в початковий момент часу була в точці за одну секунду на відстань 1 м. вздовж осі .

У першому прикладі (зелена траєкторія) ми переміщали кулю поступово, тобто. з однаковою швидкістю, яка, очевидно, повинна дорівнювати: м/с. Кінетична енергія кулі в кожний момент часу дорівнює: = 1/2 Дж. За одну секунду накопичиться 1/2 Дж з кінетичної енергії. Тобто. дійство для такої траєкторії одно: Дж с.

Тепер давайте кулю будемо не відразу переносити з точки в точку, а півсекунди притримаємо її в точці, а потім, за час, що залишився, рівномірно перенесемо його в точку. У перші півсекунди куля спочиває і її кінетична енергія дорівнює нулю. Тому внесок у дію цієї частини траєкторії також дорівнює нулю. Другі півсекунди ми переносимо кулю з подвійною швидкістю: м/с. Кінетична енергія при цьому дорівнюватиме = 2 Дж. Вклад цього проміжку часу в дію дорівнюватиме 2 Дж помножити на півсекунди, тобто. 1 Дж с. Тому загальна дія для такої траєкторії виходить одно Дж с.

Аналогічно, будь-який інший траєкторії із заданими нами крайовими умовами 1) і 2) відповідає деяке число, що дорівнює дії для даної траєкторії. Серед усіх таких траєкторій є траєкторія, у якої найменша дія. Можна довести, що траєкторією є зелена траєкторія, тобто. рівномірний рух кулі. Для будь-якої іншої траєкторії, якою б хитрою вона не була, дія буде більшою за 1/2.

У математиці таке зіставлення кожної функції певного числа називається функціоналом. Досить часто у фізиці та математиці виникають завдання подібні до нашої, тобто. на відшукання такої функції, на яку значення певного функціонала мінімально. Наприклад, одне із завдань, що мали велике історичне значення для розвитку математики – це завдання про бахістохрон. Тобто. знаходження такої кривої, по якій кулька скочується найшвидше. Знову, кожну криву можна уявити функцією h(x), і кожної функції зіставити число, у разі час скочування кульки. Знову завдання зводиться до знаходження такої функції, котрій значення функціонала мінімально. Область математики, яка займається такими завданнями, називається варіаційним обчисленням.

Принцип найменшої дії

У розібраних вище прикладах ми з'явилися дві спеціальні траєкторії, отримані двома різними способами.

Перша траєкторія отримана із законів фізики і відповідає реальній траєкторії вільної кулі, на яку не діють жодні сили і для якої задані граничні умови у вигляді 1) та 2).

Друга траєкторія отримана з математичної задачі знаходження траєкторії із заданими граничними умовами 1) та 2), для якої дія мінімальна.

Принцип найменшої дії стверджує, що ці дві траєкторії мають співпадати. Іншими словами, якщо відомо, що кулька рухалася так, що виконувались граничні умови 1) і 2), то вона обов'язково рухалася по траєкторії, для якої дія мінімальна порівняно з будь-якою іншою траєкторією з тими самими граничними умовами.

Можна було б вважати це простим збігом. Чи мало завдань, у яких з'являються рівномірні траєкторії та прямі лінії. Проте принцип найменшої дії виявляється дуже загальним принципом, справедливим та інших ситуаціях, наприклад, для руху кулі в рівномірному полі тяжкості. Для цього тільки потрібно замінити кінетичну енергію на різницю кінетичної та потенційної енергії. Цю різницю називають Лагранжіаном або функцією Лагранжа і дія тепер стає рівною загальному накопиченому Лагранжіану. Фактично, функція Лагранжа містить усю необхідну інформацію про динамічні властивості системи.

Якщо ми запустимо кулю в рівномірному полі тяжкості таким чином, щоб вона пролетіла крапку в момент часу і прилетіла в точку в момент часу, то вона, згідно із законами Ньютона, полетить параболою. Саме ця парабола збігатиметься з траєкторій, для якої дія буде мінімальною.

Таким чином, для тіла, що рухається в потенційному полі, наприклад, гравітаційному полі Землі, функція Лагранжа дорівнює: . Кінетична енергія залежить від швидкості тіла, а потенційна - з його становища, тобто. координат. В аналітичній механіці всю сукупність координат, що визначають положення системи, зазвичай позначають однією літерою. Для кулі, що вільно рухається в полі тяжкості, означає координати , і .

Для позначення швидкості зміни будь-якої величини у фізиці дуже часто просто ставлять крапку над цією величиною. Наприклад, означає швидкість зміни координати , або, іншими словами, швидкість тіла в напрямку . Використовуючи ці угоди, швидкість нашої кулі в аналітичній механіці позначається як . Тобто. означає компоненти швидкості.

Оскільки функція Лагранжа залежить швидкості та координат, а також може явно залежати від часу (явно залежить від часу означає, що значення в різні моменти часу різне, при однакових швидкостях та положеннях кулі) то дія у загальному вигляді записується як

Не завжди мінімальне

Однак наприкінці попередньої частини ми розглянули приклад, коли принцип найменшої дії явно не працює. Для цього ми знову взяли вільну кульку, на яку не діють жодні сили і помістили поряд з нею пружну стінку.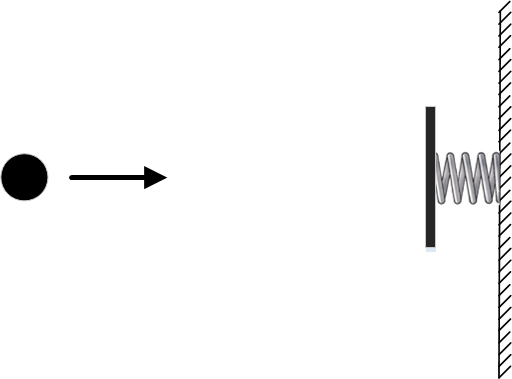

Граничні умови ми поставили такими, що крапки і збігаються. Тобто. і в момент часу і в момент часу куля повинна опинитися в одній точці . Однією з можливих траєкторій буде стояння кулі на місці. Тобто. весь проміжок часу між і він простоїть у точці. Кінетична і потенційна енергія в цьому випадку дорівнюватимуть нулю, тому дія для такої траєкторії також дорівнюватиме нулю.

Строго кажучи, потенційну енергію можна взяти рівною не нулю, а будь-якому числу, оскільки важлива різниця потенційної енергії у різних точках простору. Однак зміна значення потенційної енергії не впливає на пошук траєкторії з мінімальною дією. Просто для всіх траєкторій значення дії зміниться на те саме число, і траєкторія з мінімальною дією так і залишиться траєкторією з мінімальною дією. Для зручності, для нашої кулі ми виберемо потенційну енергію, що дорівнює нулю.

Іншою можливою фізичною траєкторією з тими ж граничними умовами буде траєкторія, при якій кулька спочатку летить вправо, пролітаючи крапку в момент часу. Потім він стикається з пружиною, стискає її, пружина, розпрямляючись, відштовхує кульку назад, і він знову пролітає повз крапку. Можна підібрати швидкість руху кулі такою, щоб вона, відскочивши від стінки, пролетіла крапку точно в момент . Дія при такій траєкторії буде в основному рівною накопиченої кінетичної енергії під час польоту між точкою і стінкою і назад. Буде якийсь проміжок часу, коли кулька стисне пружину і її потенційна енергія збільшиться, і в цей проміжок часу потенційна енергія зробить негативний внесок у дію. Але такий проміжок часу буде не дуже великим і сильно не зменшить дію.

На малюнку намальовані обидві фізично можливі траєкторії руху кулі. Зелена траєкторія відповідає кулі, що покоїться, у той час як синя відповідає кулі, що відскочила від пружинної стінки.

Однак мінімальну дію має тільки одна з них, а саме перша! У другій траєкторії дія більша. Виходить, що в цьому завданні є дві фізично можливі траєкторії і всього одна з мінімальною дією. Тобто. у разі принцип найменшого дії не працює.

Стаціонарні точки

Щоб зрозуміти в чому тут справа, давайте відвернемося поки що від принципу найменшої дії і займемося звичайними функціями. Давайте візьмемо якусь функцію та намалюємо її графік:

На графіку я відзначив зеленим кольором чотири особливі точки. Що загальне для цих точок? Уявимо, що графік функції – це реальна гірка, якою може котитися кулька. Чотири позначені точки особливі тим, що якщо встановити кульку точно в дану точку, то вона нікуди не покотиться. В інших точках, наприклад, точці E він не зможе встояти на місці і почне скочуватися вниз. Такі точки називають стаціонарними. Знаходження таких точок є корисним завданням, оскільки будь-який максимум або мінімум функції, якщо вона не має різких зламів, обов'язково має бути стаціонарною точкою.

Якщо точніше класифікувати ці точки, то точка A є абсолютним мінімумом функції, тобто. її значення менше, ніж будь-яке інше значення функції. Точка B - не є ні максимумом, ні мінімумом і називається сідловою точкою. Точка З називається локальним максимумом, тобто. значення у ній більше, ніж у сусідніх точках функції. А точка D – локальним мінімумом, тобто. значення у ній менше, ніж у сусідніх точках функції.

Пошуком таких точок займається розділ математики, який називається математичним аналізом. Інакше його іноді називають аналізом нескінченно малих, оскільки він вміє працювати з нескінченно малими величинами. З точки зору математичного аналізу стаціонарні точки мають одну особливу властивість, завдяки якій їх і знаходять. Щоб зрозуміти, що це за властивість, нам потрібно зрозуміти, як виглядає функція дуже малих відстанях від цих точок. Для цього ми візьмемо мікроскоп і подивимося на наші точки. На малюнку показано як виглядає функція навколо різних точок при різному збільшенні.

Видно, що при дуже великому збільшенні (тобто при дуже малих відхиленнях x) стаціонарні точки виглядають абсолютно однаково та сильно відрізняються від нестаціонарної точки. Легко зрозуміти у чому полягає ця відмінність – графік функції у стаціонарній точці зі збільшенням стає строго горизонтальної лінією, а нестаціонарної – похилої. Саме тому кулька, встановлена ​​в стаціонарній точці, не скочуватиметься.

Горизонтальність функції в стаціонарній точці можна виразити інакше: функція в стаціонарній точці практично не змінюється при дуже малій зміні свого аргументу, навіть у порівнянні із зміною аргументу. Функція ж у нестаціонарній точці при малій зміні змінюється пропорційно до зміни. І що більше кут нахилу функції, то сильніше змінюється функція за зміни . Насправді, функція зі збільшенням стає дедалі більше схожа дотичну до графіку в точці.

Суворою математичною мовою вираз «функція практично не змінюється в точці при дуже малій зміні» означає, що відношення зміни функції та зміни її аргументу прагне до 0 при прагненні до 0:

$$display$$\lim_(∆x \to 0) \frac (∆y(x_0))(∆x) = \lim_(x \to 0) \frac (y(x_0+∆x)-y(x_0) )(∆x) = 0$$display$$

Для нестаціонарної точки це ставлення прагне ненульовому числу, яке дорівнює тангенсу кута нахилу функції у цій точці. Це число називають похідної функції у цій точці. Похідна функції показує, наскільки швидко змінюється функція біля цієї точки при невеликій зміні її аргументу. Отже, стаціонарні точки – це точки, у яких похідна функції дорівнює 0.

Стаціонарні траєкторії

За аналогією зі стаціонарними точками можна запровадити поняття стаціонарних траєкторій. Згадаймо, що з кожної траєкторії відповідає певне значення дії, тобто. якесь число. Тоді може бути така траєкторія, що з близьких до неї траєкторій із тими самими граничними умовами, відповідні їм значення дії мало відрізнятимуться від дії для самої стаціонарної траєкторії. Така траєкторія називається стаціонарною. Іншими словами, будь-яка траєкторія близька до стаціонарної мати значення дії, дуже мало відрізняється від дії для цієї стаціонарної траєкторії.

Знову, математичною мовою «мало відрізняється» має наступний точний зміст. Припустимо, що ми заданий функціонал для функцій з необхідними граничними умовами 1) і 2), тобто. та . Припустимо, що траєкторія – стаціонарна.

Ми можемо взяти будь-яку іншу функцію , таку, що у кінцях вона приймає нульові значення, тобто. = = 0. Також візьмемо змінну , яку ми робитимемо дедалі менше. З цих двох функцій та змінної ми можемо скласти третю функцію, яка також задовольнятиме граничним умовам та. При зменшенні траєкторія, відповідна функції , все сильніше наближатися до траєкторії .

При цьому для стаціонарних траєкторій при малих значення функціоналу у траєкторій буде відрізнятися дуже мало від значення функціоналу навіть для порівняння з . Тобто.

$$display$$\lim_(ε\to 0) \frac (S(x"(t))-S(x(t)))ε=\lim_(ε\to 0) \frac (S(x( t)+εg(t))-S(x(t)))ε = 0$$display$$

Причому це має бути справедливо для будь-якої траєкторії, що задовольняє граничні умови = = 0.

Зміна функціоналу при малій зміні функції (точніше, лінійна частина зміни функціоналу, пропорційна до зміни функції) називається варіацією функціоналу і позначається . Від терміна «варіація» і походить назва «варіаційне обчислення».

Для стаціонарних траєкторій варіація функціоналу.

Метод знаходження стаціонарних функцій (як для принципу найменшого дії, а й багатьох інших завдань) знайшли два математика - Ейлер і Лагранж. Виявляється, що стаціонарна функція, чий функціонал виражається інтегралом, подібним до інтегралу дії, повинна задовольняти певному рівнянню, яке тепер називається рівнянням Ейлера-Лагранжа.

Принцип стаціонарної дії

Ситуація з мінімумом дії для траєкторій аналогічна ситуації з мінімумом функцій. Щоб траєкторія мала найменшою дією, вона повинна бути стаціонарною траєкторією. Проте чи всі стаціонарні траєкторії – це траєкторії з мінімальною дією. Наприклад, стаціонарна траєкторія може мати мінімальну дію локально. Тобто. у неї дія буде меншою, ніж у будь-якої іншої сусідньої траєкторії. Однак десь далеко можуть бути інші траєкторії, для яких дія буде ще меншою.

Виявляється, реальні тіла можуть рухатися не обов'язково траєкторіями з найменшою дією. Вони можуть рухатися ширшим набором спеціальних траєкторій, а саме - стаціонарним траєкторіям. Тобто. реальна траєкторія тіла завжди буде стаціонарною. Тому принцип найменшого впливу правильніше назвати принципом стаціонарного впливу. Однак за традицією, що склалася, його часто називають принципом найменшої дії, маючи на увазі за цим не тільки мінімальність, а й стаціонарність траєкторій.

Тепер ми можемо записати принцип стаціонарного впливу математичною мовою, як його зазвичай записують у підручниках: .

Тут – це узагальнені координати, тобто. набір змінних, що однозначно задають положення системи.
- Швидкості зміни узагальнених координат.
- функція Лагранжа, яка залежить від узагальнених координат, їх швидкостей та, можливо, часу.
- Дія, яка залежить від конкретної траєкторії руху системи (тобто від).

Реальні траєкторії системи стаціонарні, тобто. для них варіація дії.

Якщо повернутись наприклад з кулею і пружною стінкою, то пояснення цієї ситуації тепер стає дуже простим. За заданих граничних умов, що куля повинна і під час і під час опинитися в точці існують дві стаціонарні траєкторії. І за будь-якою з цих траєкторій може реально рухатися куля. Щоб явно вибрати одну з траєкторій, на рух кулі можна накласти додаткову умову. Наприклад, сказати, що куля має відскочити від стінки. Тоді траєкторія визначиться однозначно.

З принципу найменшої (точніше стаціонарної) дії випливають деякі чудові наслідки, про які ми поговоримо в наступній частині.

Йому підкоряються, у зв'язку з чим цей принцип одна із ключових положень сучасної фізики. Одержувані з його допомогою рівняння руху мають назву рівнянь Ейлера-Лагранжа.

Перше формулювання принципу дав П. Мопертюї (P. Maupertuis) у році, відразу ж вказавши на його універсальну природу, вважаючи його придатним до оптики та механіки. З цього принципу він вивів закони відображення та заломлення світла.

Історія

Мопертюї прийшов до цього принципу з відчуття, що досконалість Всесвіту потребує певної економії в природі та суперечить будь-яким марним витратам енергії. Природний рух має бути таким, щоб зробити певну величину мінімальною. Треба було тільки знайти цю величину, що він і продовжував робити. Вона була добутком тривалості (час) руху в межах системи на подвоєну величину, яку ми тепер називаємо кінетичною енергією системи.

Ейлер (в «Reflexions sur quelques loix générales de la nature», 1748) приймає принцип найменшої кількості дії, називаючи дію "зусиллям". Його вираз у статиці відповідає тому, що ми тепер назвали б потенційною енергією, так що його затвердження найменшої дії у статиці еквівалентне умові мінімуму потенційної енергії для конфігурації рівноваги.

У класичній механіці

Принцип найменшої дії служить фундаментальною та стандартною основою лагранжевої та гамільтонової формулювань механіки.

Спочатку розглянемо побудову таким чином лагранжової механіки. На прикладі фізичної системи з одним ступенем свободи, нагадаємо, що дія - це функціонал щодо (узагальнених) координат (у разі одного ступеня свободи - однієї координати), тобто виражається через так, що кожному мислимому варіанту функції зіставляється деяка кількість - дія (у цьому сенсі можна сказати, що дія як функціонал є правило, що дозволяє для будь-якої заданої функції обчислити цілком певну кількість - також називається дією). Дія має вигляд:

де є лагранжіан системи, що залежить від узагальненої координати, її першої похідної за часом, а також, можливо, і явно від часу. Якщо система має більшу кількість ступенів свободи, то лагранжіан залежить від більшої кількості узагальнених координат та їх перших похідних за часом. Таким чином, дія є скалярним функціоналом, що залежить від траєкторії тіла.

Те, що дія є скаляром, дозволяє легко записати його в будь-яких узагальнених координатах, головне тільки, щоб положення (конфігурація) системи однозначно ними характеризувалося (наприклад, замість декартових це можуть бути полярні координати, відстані між точками системи, кути або їх функції тощо) д.).

Дію можна обчислити для абсолютно довільної траєкторії, якою б «дикою» та «неприродною» вона не була б. Однак у класичній механіці серед усього набору можливих траєкторій існує одна-єдина, якою тіло дійсно піде. Принцип стаціонарності дії якраз і дає відповідь на питання, як дійсно рухатиметься тіло:

Це означає, що якщо заданий лагранжіан системи, то ми за допомогою варіаційного обчислення можемо встановити, як саме рухатиметься тіло, спочатку отримавши рівняння руху – рівняння Ейлера – Лагранжа, а потім вирішивши їх. Це дозволяє не тільки серйозно узагальнити формулювання механіки, але й вибирати найбільш зручні координати для кожної певної задачі, не обмежуючись декартовими, що може бути дуже корисно для отримання найпростіших рівнянь, що легко вирішуються.

де – функція Гамільтона даної системи; - (узагальнені) координати, - пов'язані ним (узагальнені) імпульси, що характеризують разом у кожний момент часу динамічний стан системи і, будучи кожним функцією часу, характеризуючи, в такий спосіб, еволюцію (рух) системи. У цьому випадку для отримання рівнянь руху системи у формі канонічних рівнянь Гамільтона треба проваріювати записану так дію незалежно по всіх і .

Слід зазначити, що з умов завдання принципово можна знайти закон руху, це автоматично неозначає, що можна побудувати функціонал, що набуває стаціонарного значення при істинному русі. Прикладом може служити спільний рух електричних зарядів і монополій - магнітних зарядів - в електромагнітному полі. Їхні рівняння руху неможливо вивести з принципу стаціонарності дії. Аналогічно деякі гамільтонові системи мають рівняння руху, які не виводяться з цього принципу.

Приклади

Тривіальні приклади допомагають оцінювати використання принципу дії через рівняння Ейлера-Лагранжа. Вільна частка (маса mта швидкість v) в Евклідовому просторі переміщається прямою лінією. Використовуючи рівняння Ейлера Лагранжа, це можна показати в полярних координатах наступним чином. За відсутності потенціалу функція Лагранжа просто дорівнює кінетичній енергії

в ортогональній системі координат.

У полярних координатах кінетична енергія, отже, функція Лагранжа стає

Радіальна та кутова компонента рівнянь стають, відповідно:

Розв'язання цих двох рівнянь

Тут - це умовний запис нескінченно функціонального інтегрування по всіх траєкторіях x(t), а - постійна Планка. Підкреслимо, що в принципі дія в експоненті з'являється (або може з'являтися) сама, при вивченні оператора еволюції в квантовій механіці, проте для систем, що мають точний класичний (неквантовий) аналог, воно точно дорівнює звичайному класичному дії.

Математичний аналіз цього висловлювання у класичному межі - за досить великих , тобто за дуже швидких осциляціях уявної експоненти - показує, що переважна більшість усіляких траєкторій у тому інтегралі взаємозменшуються у своїй межі (формально при ). Для майже будь-якого шляху знайдеться такий шлях, на якому набіг фази буде протилежним, і вони в сумі дадуть нульовий внесок. Не скорочуються ті траєкторії, котрим дія близька до екстремального значення (для більшості систем - мінімуму). Це - суто математичний факт з теорії функцій комплексного змінного; на ньому, наприклад, заснований метод стаціонарної фази.

В результаті частка в повній згоді з законами квантової механіки рухається одночасно по всіх траєкторіях, але в звичайних умовах в значення, що спостерігаються, дають вклад тільки траєкторії, близькі до стаціонарних (тобто класичних). Оскільки квантова механіка перетворюється на класичну межі великих енергій, можна вважати, що це - квантовомеханічне виведення класичного принципу стаціонарності дії.

У квантовій теорії поля

У квантовій теорії поля принцип стаціонарності дії також успішно застосовується. У лагранжеву густину тут входять оператори відповідних квантових полів. Хоча правильніше тут по суті (за винятком класичної межі і частково квазікласики) говорити не про принцип стаціонарності дії, а про фейнманівське інтегрування по траєкторіях у конфігураційному або фазовому просторі цих полів - з використанням згаданої щойно лагранжової щільності.

Подальші узагальнення

Найбільш широко, під впливом розуміють функціонал, що задає відображення з конфігураційного простору на безліч речових чисел і, загалом, він не повинен бути інтегралом, тому що нелокальні події в принципі можливі, принаймні, теоретично. Понад те, конфігураційний простір необов'язково є функціональним простором, оскільки може мати некомутативну геометрію.

Принцип найменшої дії, вперше точно сформульований Якобі, аналогічний принципу Гамільтона, але менш загальний і важчий для доказу. Цей принцип застосовується тільки до того випадку, коли зв'язки та силова функція не залежать від часу і, отже, існує інтеграл живої сили.

Цей інтеграл має вигляд:

Принцип Гамільтона, викладений вище, стверджує, що варіація інтеграла

дорівнює нулю при переході дійсного руху до будь-якого іншого нескінченно близького руху, який переводить систему з того самого початкового положення в той же кінцевий стан за той самий проміжок часу.

Принцип Якобі, навпаки, виражає властивість, рухи, що не залежить від часу. Якобі розглядає інтеграл

визначальний дію. Встановлений ним принцип стверджує, що варіація цього інтеграла дорівнює нулю, коли ми порівнюємо дійсний рух системи з будь-яким іншим нескінченно близьким рухом, що переводить систему з того самого початкового положення в той же кінцевий стан. При цьому ми не звертаємо уваги на проміжок часу, що витрачається, але дотримуємось рівняння (1), тобто рівняння живої сили з тим же значенням постійної h, що і в дійсному русі.

Ця необхідна умова екстремуму приводить, взагалі кажучи, до мінімуму інтеграла (2), звідки і походить назва принцип найменшої дії. Умова мінімуму є найбільш природною, оскільки величина Т істотно позитивна, і тому інтеграл (2) необхідно мати мінімум. Існування мінімуму може бути суворо доведено, якщо проміжок часу - досить малий. Доказ цього можна знайти у відомому курсі Дарбу з теорії поверхонь. Ми, однак, не наводитимемо його тут і обмежимося виведенням умови

432. Доказ принципу найменшої дії.

При дійсному обчисленні ми зустрічаємося з одним складним трудом, якого немає в доказі теореми Гамільтона. Змінна t не залишається більш незалежною від варіацій; тому варіації q i та q. пов'язані з варіацією t складним співвідношенням, яке випливає з рівняння (1). Найпростіший спосіб обійти це утруднення полягає в тому, щоб змінити незалежну змінну, вибравши таку, значення якої розташовувалися б між постійними межами, що не залежать від часу. Нехай є нова незалежна змінна, межі якої і передбачаються не залежать від t. При переміщенні системи параметри та t будуть функціями від цієї змінної

Нехай літери зі штрихами q позначатимуть похідні від параметрів q за часом.

Оскільки зв'язку, за припущенням, не залежить від часу, то декартові координати х, у, z є функціями від q, які містять час. Тому їх похідні будуть однорідними лінійними функціями від q і 7 буде однорідною квадратичною формою від q, коефіцієнти якої суть функції від q. Маємо

Щоб відрізняти похідні q за часом, позначимо за допомогою дужок, (q), похідні від q, взяті за і покладемо відповідно до цього

тоді матимемо

і інтеграл (2), виражений через нову незалежну змінну А, набуде вигляду;

Похідну можна виключити з допомогою теореми живої сили. Справді, інтеграл живої сили буде

Підставивши цей вираз у формулу для наведемо інтеграл (2) до виду

Інтеграл, що визначає дію, набув, таким чином, остаточного вигляду (3). Підінтегральна функція є квадратний корінь із квадратичної форми від величин

Покажемо, що диференціальні рівняння екстремалей інтеграла (3) є точності рівняння Лагранжа. Рівняння екстремалей на підставі загальних формул варіаційного обчислення будуть:

Помножимо рівняння на 2 і виконаємо приватні диференціювання, зважаючи на те, що не містить тоді отримаємо, якщо не писати індексу ,

Це рівняння екстремалей, виражені через незалежну змінну. Завдання полягає тепер у тому, щоб повернутися до незалежної змінної.

Оскільки Г є однорідна функція другого ступеня від - однорідна функція першого ступеня, то маємо

З іншого боку, до множників при похідних у рівняннях екстремалей можна застосувати теорему живої сили, яка призводить, як ми бачили вище, до підстановки

В результаті всіх підстановок рівняння екстремалей наводяться до вигляду

Таким чином, ми прийшли до рівнянь Лагранжа.

433. Випадок, коли немає рушійних сил.

У випадку, коли рушійних сил немає, рівняння живої сили є і ми маємо

Умова, що інтеграл є мінімум, полягає в даному випадку в тому, що відповідне значення -10 має бути найменшим. Таким чином, коли рушійних сил немає, то серед усіх рухів, при яких жива сила зберігає одне й те саме дане значення, дійсний рух є те, що переводить систему з її початкового положення в кінцеве положення в найкоротший час.

Якщо система зводиться до однієї точки, що рухається нерухомою поверхнею, то дійсний рух, серед усіх рухів по поверхні, що відбуваються з тією ж швидкістю, є такий рух, при якому точка переходить зі свого початкового положення в кінцеве положення в найкоротший

проміжок часу. Інакше висловлюючись, точка описує лежить на поверхні найкоротшу лінію між двома її положеннями, т. е. геодезичну лінію.

434. Зауваження.

Принцип найменшої дії передбачає, що система має кілька ступенів свободи, оскільки якби була лише одна ступінь свободи, то одного рівняння було б достатньо для визначення руху. Так як рух може бути в даному випадку цілком визначено рівнянням живої сили, то дійсний рух буде єдиним, що задовольняє цього рівняння, і тому не може бути порівнюваним з іншим рухом.

P. Maupertuis) в 1744-году, відразу ж вказавши на його універсальну природу і вважаючи його придатним до оптики та механіки. З цього принципу він вивів закони відображення та заломлення світла.

Енциклопедичний YouTube

• 1 / 5

  Математичне дослідження та розвиток принципу Ферма провів Християн Гюйгенс, після чого тему активно обговорювали найбільші вчені XVII століття. Лейбніц в 1669 році ввів у фізику фундаментальне поняття дії: «Формальні дії руху пропорційні добутку кількості матерії, відстаней, на які вони пересуваються, і швидкості».

  Паралельно з аналізом основ механіки розвивалися методи розв'язання варіаційних завдань. Ісаак Ньютон у своїх «Математичних початку натуральної філософії » (1687 рік) поставив і вирішив перше варіаційне завдання: знайти таку форму тіла обертання, що рухається в опірному середовищі вздовж своєї осі, для якої випробовуваний опір було б наи. Майже одночасно з'явилися й інші варіаційні проблеми: задача про брахістохрон (1696), форма ланцюгової лінії та ін.

  Вирішальні події сталися 1744 року. Леонард Ейлер опублікував першу загальну роботу з варіаційного обчислення («Метод знаходження кривих, що володіють властивостями максимуму або мінімуму»), а П'єр Луї де Мопертюі в трактаті «Узгодження різних законів природи, які до цього здавалися на перший погляд. «шлях, якого дотримується світло, є шляхом, для якого кількість дії буде найменшою». Він продемонстрував виконання цього закону як для відображення, так і для заломлення світла. У відповідь на статтю Мопертюї Ейлер опублікував (у тому ж 1744) роботу «Про визначення руху кинутих тіл у неопірному середовищі методом максимумів і мінімумів», і в цій праці він надав принципу Мопертюї загальномеханічний характер: «Оскільки всі явища природи слідують якому- ні закону максимуму чи мінімуму, немає жодного сумніву, що й кривих ліній, які описують кинуті тіла, коли ними діють якісь сили, має місце якась властивість максимуму чи мінімуму. Далі Ейлер сформулював цей закон: траєкторія тіла здійснює мінімум ∫ m v d s (\displaystyle \int mv\ ds). Потім він застосував його, вивівши закони руху в однорідному полі тяжкості та в кількох інших випадках.

  У 1746 році Мопертюї в новій роботі погодився з думкою Ейлера і проголосив найзагальнішу версію свого принципу: «Коли в природі відбувається деяка зміна, кількість дії, яка потрібна для цієї зміни, є найменшою можливою. Кількість дії є добуток маси тіл на їхню швидкість і на відстань, яку вони пробігають». У широкої дискусії, що розгорнулася, Ейлер підтримав пріоритет Мопертюї і аргументував загальний характер нового закону: «вся динаміка і гідродинаміка можуть бути з дивовижною легкістю розкриті за допомогою одного тільки методу максимумів і мінімумів».

  Новий етап почався в 1760-1761 роках, коли Жозеф, Луї, Лагранж ввів суворе поняття варіації функції, надав варіаційному обчисленню сучасний вигляд і поширив принцип найменшого впливу на довільну механічну систему (тобто не тільки на вільні матеріальні точки). Тим самим було започатковано аналітичну механіку. Подальше узагальнення принципу здійснив Карл, Густав, Якоб, Які в 1837 році - він розглянув проблему геометрично, як знаходження екстремалей варіаційного завдання в конфігураційному просторі з неевклідовою метрикою. Зокрема, Якобі зазначив, що за відсутності зовнішніх сил траєкторія системи є геодезичною лінією в конфігураційному просторі.

  Підхід Гамільтона виявився універсальним і високоефективним у математичних моделях фізики, особливо для квантової механіки. Його евристична сила була підтверджена при створенні Загальної теорії відносності, коли Давид Гільберт застосував гамільтонів принцип для виведення остаточних рівнянь гравітаційного поля (1915 рік).

  У класичній механіці

  Принцип найменшої дії служить фундаментальною та стандартною основою лагранжевої та гамільтонової формулювань механіки.

  Спочатку розглянемо побудову таким чином лагранжової механіки. На прикладі фізичної системи з одним ступенем свободи, нагадаємо, що дія - це функціонал щодо (узагальнених) координат (у разі одного ступеня свободи - однієї координати), тобто воно виражається через q(t) (\displaystyle q(t))так, що кожному можливим варіантом функції q(t) (\displaystyle q(t))зіставляється деяке число - дію (у цьому сенсі можна сказати, що дія як функціонал є правило, що дозволяє для будь-якої заданої функції q(t) (\displaystyle q(t))обчислити цілком певну кількість - також називається дією). Дія має вигляд:

  S [q] = ∫ L (q (t), q ˙ (t), t) d t, (\displaystyle S [q] = int (\mathcal (L)) (q(t),(\dot ( q)) (t), t) dt,)

  де L (q (t) , q ˙ (t) , t) (\displaystyle (\mathcal (L))є лагранжіан системи, який залежить від узагальненої координати q (\displaystyle q), її першою похідною за часом q ˙ (\displaystyle (\dot (q))), а також, можливо, і явно від часу t (\displaystyle t). Якщо система має більшу кількість ступенів свободи n (\displaystyle n), то лагранжіан залежить від більшої кількості узагальнених координат q i (t) , i = 1 , 2 , … , n (\displaystyle q_(i)(t),\ i=1,2,\dots ,n)та їх перших похідних за часом. Таким чином, дія є скалярним функціоналом, що залежить від траєкторії тіла.

  Те, що дія є скаляром, дозволяє легко записати його в будь-яких узагальнених координатах, головне тільки щоб положення (конфігурація) системи однозначно ними характеризувалося (наприклад, замість декартових це можуть бути полярні координати, відстані між точками системи, кути або їх функції і т.п. д.).

  Дія можна обчислити для довільної траєкторії q(t) (\displaystyle q(t))Якою б «дикою» та «неприродною» вона б не була. Однак у класичній механіці серед всього набору можливих траєкторій існує одна-єдина, по якій тіло дійсно піде. Принцип стаціонарності дії якраз і дає відповідь на питання, як дійсно рухатиметься тіло:

  Це означає, що якщо заданий лагранжіан системи, то ми за допомогою варіаційного обчислення можемо встановити, як саме рухатиметься тіло, спочатку отримавши рівняння руху - рівняння Ейлера - Лагранжа, а потім вирішивши їх. Це дозволяє не тільки серйозно узагальнити формулювання механіки, але й вибирати найбільш зручні координати для кожного певного завдання, не обмежуючись декартовими, що може бути дуже корисно для отримання найпростіших рівнянь, що легко вирішуються.

  S [ p , q ] = ∫ (∑ i p i d q i − H (q , p , t) d t) = ∫ (∑ i p i q ˙ i − H (q , p , t)) d t , (\displaystyle S=\int (\ big()\sum _(i)p_(i)dq_(i)-(\mathcal(H))(q,p,t)dt(\big))=\int (\big()\sum _( i)p_(i)(\dot(q))_(i)-(\mathcal(H))(q,p,t)(\big))dt,)

  де H (q , p , t) ≡ H (q 1 , q 2 , … , q N , p 1 , p 2 , … , p N , t) (\displaystyle (\mathcal (H))(q,p, t)\equiv (\mathcal (H))(q_(1),q_(2),\dots ,q_(N),p_(1),p_(2),\dots ,p_(N),t) )- функція Гамільтона цієї системи; q ≡ q 1 , q 2 , … , q N (\displaystyle q\equiv q_(1),q_(2),\dots ,q_(N))- (Узагальнені) координати, p ≡ p 1 , p 2 , … , p N (\displaystyle p\equiv p_(1),p_(2),\dots ,p_(N))- сполучені ним (узагальнені) імпульси, що характеризують разом у кожний момент часу динамічний стан системи і, будучи кожною функцією часу, характеризуючи, таким чином, еволюцію (рух) системи. У цьому випадку для отримання рівнянь руху системи у формі канонічних рівнянь Гамільтона треба проваріювати записану так дію незалежно по всіх q i (\displaystyle q_(i))і p i (\displaystyle p_(i)).

  Слід зазначити, що з умов завдання принципово можна знайти закон руху, це автоматично неозначає, що можна побудувати функціонал, що набуває стаціонарного значення при істинному русі. Прикладом може служити спільний рух електричних зарядів і монополій - магнітних зарядів - в електромагнітному полі. Їхні рівняння руху неможливо вивести з принципу стаціонарності дії. Аналогічно деякі гамільтонові системи мають рівняння руху, не виведені з цього принципу.

  Приклади

  Тривіальні приклади допомагають оцінювати використання принципу дії через рівняння Ейлера-Лагранжа. Вільна частка (маса mта швидкість v) в евклідовому просторі переміщається по прямій лінії. Використовуючи рівняння Ейлера-Лагранжа, це можна показати в полярних координатах наступним чином. За відсутності потенціалу функція Лагранжа просто дорівнює кінетичній енергії

  1 2 m v 2 = 1 2 m (x 2 + y 2) (\displaystyle (\frac(1)(2))mv^(2)=(\frac(1)(2))m\left( (\dot (x))^(2)+(\dot (y))^(2)\right)) ψ = ∫ [D x ] e (i S [ x ] / ℏ) . (\displaystyle \psi =\int e^(((iS[x])/(\hbar )))\,.)

  Тут ∫ [D x ] (\displaystyle \int )- це умовний запис нескінченно функціонального інтегрування по всіх траєкторіях x(t), а ℏ (\displaystyle \hbar )- Постійна Планка. Підкреслимо, що в принципі дія в експоненті з'являється (або може з'являтися) сама, при вивченні оператора еволюції в квантовій механіці, проте для систем, що мають точний класичний (неквантовий) аналог, воно точно дорівнює звичайному класичному дії.

  Математичний аналіз цього виразу в класичній межі - за досить великих S / ℏ (\displaystyle S/\hbar ), тобто при дуже швидких осциляціях уявної експоненти - показує, що переважна більшість усіляких траєкторій у цьому інтегралі взаємозменшуються при цьому у межі (формально при S / ℏ → ∞ (\displaystyle S/\hbar \rightarrow \infty )). Для майже будь-якого шляху знайдеться такий шлях, на якому набіг фази буде протилежним, і вони в сумі дадуть нульовий внесок. Не скорочуються ті траєкторії, котрим дія близька до екстремального значення (для більшості систем - мінімуму). Це - суто математичний факт з