Chuỗi phân phối của c rời rạc trong x. Ví dụ giải bài toán về chủ đề “Biến ngẫu nhiên”
Chương 1. Biến ngẫu nhiên rời rạc
§ 1. Khái niệm về biến ngẫu nhiên.
Luật phân phối của một biến ngẫu nhiên rời rạc.
Sự định nghĩa : Ngẫu nhiên là đại lượng, do kết quả thử nghiệm, chỉ lấy một giá trị trong tập hợp các giá trị có thể có của nó, không xác định trước và tùy thuộc vào lý do ngẫu nhiên.
Có hai loại biến ngẫu nhiên: rời rạc và liên tục.
Sự định nghĩa : Biến ngẫu nhiên X được gọi là rời rạc (không liên tục) nếu tập các giá trị của nó là hữu hạn hoặc vô hạn nhưng đếm được.
Nói cách khác, các giá trị có thể có của một biến ngẫu nhiên rời rạc có thể được đánh số lại.
Một biến ngẫu nhiên có thể được mô tả bằng luật phân phối của nó.
Sự định nghĩa : Luật phân phối của một biến ngẫu nhiên rời rạc gọi sự tương ứng giữa các giá trị có thể có của một biến ngẫu nhiên và xác suất của chúng.
Luật phân phối của biến ngẫu nhiên rời rạc X có thể được chỉ định dưới dạng bảng, ở hàng đầu tiên trong đó tất cả các giá trị có thể có của biến ngẫu nhiên được biểu thị theo thứ tự tăng dần và ở hàng thứ hai xác suất tương ứng của các giá trị này các giá trị, tức là
trong đó р1+ р2+…+ рn=1
Bảng như vậy được gọi là chuỗi phân phối của một biến ngẫu nhiên rời rạc.
Nếu tập hợp các giá trị có thể có của một biến ngẫu nhiên là vô hạn thì chuỗi p1+ p2+…+ pn+… hội tụ và tổng của nó bằng 1.
Quy luật phân phối của biến ngẫu nhiên rời rạc X có thể được mô tả bằng đồ họa, trong đó một đường đứt nét được xây dựng theo hệ tọa độ hình chữ nhật, nối các điểm tuần tự với tọa độ (xi; pi), i=1,2,…n. Dòng kết quả được gọi là đa giác phân phối (Hình 1).
Hóa hữu cơ" href="/text/category/organicheskaya_hiimya/" rel="bookmark">Hóa hữu cơ lần lượt là 0,7 và 0,8. Hãy vẽ luật phân phối cho biến ngẫu nhiên X - số bài kiểm tra mà học sinh sẽ vượt qua.
Giải pháp. Biến ngẫu nhiên X được coi là kết quả của bài kiểm tra có thể nhận một trong các giá trị sau: x1=0, x2=1, x3=2.
Hãy tìm xác suất của các giá trị này và ký hiệu các sự kiện:
https://pandia.ru/text/78/455/images/image004_81.jpg" width="259" Height="66 src=">
 |
Vì vậy, luật phân phối của biến ngẫu nhiên X được cho bởi bảng:
Kiểm soát: 0,6+0,38+0,56=1.
§ 2. Chức năng phân phối
Một mô tả đầy đủ về một biến ngẫu nhiên cũng được đưa ra bởi hàm phân phối.
Sự định nghĩa: Hàm phân phối của biến ngẫu nhiên rời rạc X được gọi là hàm F(x), xác định với mỗi giá trị x xác suất mà biến ngẫu nhiên X sẽ nhận giá trị nhỏ hơn x:
F(x)=P(X<х)
Về mặt hình học, hàm phân phối được hiểu là xác suất để biến ngẫu nhiên X sẽ lấy giá trị được biểu thị trên trục số bởi một điểm nằm bên trái điểm x.
1)0 2) F(x) là hàm không giảm trên (-∞;+∞); 3) F(x) - liên tục bên trái tại các điểm x= xi (i=1,2,...n) và liên tục tại tất cả các điểm còn lại; 4) F(-∞)=P (X<-∞)=0 как вероятность невозможного события Х<-∞, F(+∞)=P(X<+∞)=1 как вероятность достоверного события Х<-∞. Nếu luật phân phối của biến ngẫu nhiên rời rạc X được cho dưới dạng bảng: thì hàm phân phối F(x) được xác định theo công thức: https://pandia.ru/text/78/455/images/image007_76.gif" Height="110"> 0 với x< x1, р1 tại x1< х≤ x2, F(x)= р1 + р2 tại x2< х≤ х3 1 cho x>xn. Đồ thị của nó được hiển thị trong Hình 2: §
3. Đặc tính số của biến ngẫu nhiên rời rạc. Một trong những đặc tính số quan trọng là kỳ vọng toán học. Sự định nghĩa: Kỳ vọng toán học M(X)
Biến ngẫu nhiên rời rạc X là tổng các tích của tất cả các giá trị của nó và xác suất tương ứng của chúng: M(X) =
∑ xiрi= x1р1 + x2р2+…+ xnрn Kỳ vọng toán học đóng vai trò là đặc tính của giá trị trung bình của một biến ngẫu nhiên. Tính chất của kỳ vọng toán học:
1)M(C)=C, trong đó C là giá trị không đổi; 2)M(C X)=C M(X), 3)M(X±Y)=M(X) ±M(Y); 4)M(X Y)=M(X) M(Y), trong đó X, Y là các biến ngẫu nhiên độc lập; 5)M(X±C)=M(X)±C, trong đó C là giá trị không đổi; Để mô tả mức độ phân tán của các giá trị có thể có của một biến ngẫu nhiên rời rạc xung quanh giá trị trung bình của nó, người ta sử dụng độ phân tán. Sự định nghĩa:
Phương sai
D
(
X
)
biến ngẫu nhiên X là kỳ vọng toán học của độ lệch bình phương của biến ngẫu nhiên so với kỳ vọng toán học của nó:
Đặc tính phân tán:
1)D(C)=0, trong đó C là giá trị không đổi; 2)D(X)>0, trong đó X là biến ngẫu nhiên; 3)D(C X)=C2 D(X), trong đó C là giá trị không đổi; 4)D(X+Y)=D(X)+D(Y), trong đó X, Y là các biến ngẫu nhiên độc lập; Để tính phương sai, thường thuận tiện khi sử dụng công thức: D(X)=M(X2)-(M(X))2, trong đó M(X)=∑ xi2рi= x12р1 + x22р2+…+ xn2рn Phương sai D(X) có thứ nguyên của một biến ngẫu nhiên bình phương, điều này không phải lúc nào cũng thuận tiện. Do đó, giá trị √D(X) cũng được sử dụng làm chỉ báo về độ phân tán của các giá trị có thể có của một biến ngẫu nhiên. Sự định nghĩa: Độ lệch chuẩn σ(X)
Biến ngẫu nhiên X được gọi là căn bậc hai của phương sai: Nhiệm vụ số 2. Biến ngẫu nhiên rời rạc X được xác định theo luật phân phối: Tìm P2, hàm phân phối F(x) và vẽ đồ thị của nó, cũng như M(X), D(X), σ(X). Giải pháp:
Vì tổng xác suất của các giá trị có thể có của biến ngẫu nhiên X bằng 1 nên Р2=1- (0,1+0,3+0,2+0,3)=0,1 Hãy tìm hàm phân phối F(x)=P(X Về mặt hình học, đẳng thức này có thể được hiểu như sau: F(x) là xác suất để biến ngẫu nhiên lấy giá trị được biểu thị trên trục số bởi điểm nằm bên trái điểm x. Nếu x≤-1 thì F(x)=0, vì không có một giá trị nào của biến ngẫu nhiên này trên (-∞;x); Nếu -1<х≤0, то F(х)=Р(Х=-1)=0,1, т. к. в промежуток (-∞;х) попадает только одно значение x1=-1; Nếu 0<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т. к. в промежуток (-∞;x) có hai giá trị x1=-1 và x2=0; Nếu 1<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т. к. в промежуток (-∞;х) попадают три значения x1=-1, x2=0 и x3=1; Nếu 2<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т. к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1 и х4=2; Nếu x>3 thì F(x)=P(X=-1) + P(X=0)+ P(X=1)+ P(X=2)+P(X=3)= 0,1 +0,1 +0,3+0,2+0,3=1, vì bốn giá trị x1=-1, x2=0, x3=1, x4=2 rơi vào khoảng (-∞;x) và x5=3. https://pandia.ru/text/78/455/images/image006_89.gif" width="14 chiều cao=2" chiều cao="2"> 0 tại x≤-1, 0,1 tại -1<х≤0, 0,2 tại 0<х≤1, F(x)= 0,5 tại 1<х≤2, 0,7 lúc 2<х≤3, 1 tại x>3 Hãy biểu thị hàm F(x) bằng đồ họa (Hình 3): https://pandia.ru/text/78/455/images/image014_24.jpg" width="158 chiều cao=29" chiều cao="29">≈1.2845. §
4. Luật phân phối nhị thức biến ngẫu nhiên rời rạc, định luật Poisson. Sự định nghĩa: nhị thức
được gọi là quy luật phân phối của biến ngẫu nhiên rời rạc X - số lần xuất hiện của sự kiện A trong n phép thử lặp lại độc lập, trong đó mỗi sự kiện A có thể xảy ra với xác suất p hoặc không xảy ra với xác suất q = 1-p. Khi đó P(X=m) - xác suất xảy ra sự kiện A đúng m lần trong n phép thử được tính bằng công thức Bernoulli: Р(Х=m)=Сmnpmqn-m Kỳ vọng, độ phân tán và độ lệch chuẩn toán học của biến ngẫu nhiên X được phân phối theo luật nhị phân tương ứng được tìm thấy bằng cách sử dụng các công thức: https://pandia.ru/text/78/455/images/image016_31.gif" width="26"> Xác suất của sự kiện A - “ra năm” trong mỗi lần thử là như nhau và bằng 1/6 , tức là . P(A)=p=1/6, khi đó P(A)=1-p=q=5/6, trong đó - “không đạt được điểm A.” Biến ngẫu nhiên X có thể nhận các giá trị sau: 0;1;2;3. Chúng tôi tìm xác suất của từng giá trị có thể có của X bằng công thức Bernoulli: Р(Х=0)=Р3(0)=С03р0q3=1 (1/6)0 (5/6)3=125/216; Р(Х=1)=Р3(1)=С13р1q2=3 (1/6)1 (5/6)2=75/216; Р(Х=2)=Р3(2)=С23р2q =3 (1/6)2 (5/6)1=15/216; Р(Х=3)=Р3(3)=С33р3q0=1 (1/6)3 (5/6)0=1/216. Cái đó. luật phân phối của biến ngẫu nhiên X có dạng: Điều khiển: 125/216+75/216+15/216+1/216=1. Hãy tìm các đặc tính số của biến ngẫu nhiên X: M(X)=np=3 (1/6)=1/2, D(X)=npq=3 (1/6) (5/6)=5/12, Nhiệm vụ số 4. Máy tự động dán tem các bộ phận. Xác suất để một bộ phận được sản xuất bị lỗi là 0,002. Tìm xác suất để trong số 1000 phần được chọn sẽ có: a) 5 chiếc có khuyết tật; b) ít nhất một chiếc bị lỗi. Giải pháp:
Số n=1000 lớn, xác suất tạo ra một bộ phận bị lỗi p=0,002 là nhỏ và các sự kiện đang được xem xét (bộ phận đó hóa ra là bị lỗi) là độc lập, do đó công thức Poisson đúng: Рn(m)= e-
λ
λm Hãy tìm λ=np=1000 0,002=2. a) Tìm xác suất để có 5 bộ phận bị lỗi (m=5): Р1000(5)= e-2
25
= 32 0,13534
= 0,0361 b) Tìm xác suất để có ít nhất một bộ phận bị lỗi. Sự kiện A - “ít nhất một trong các bộ phận được chọn bị lỗi” ngược lại với sự kiện – “tất cả các bộ phận được chọn đều không bị lỗi”. Do đó, P(A) = 1-P(). Do đó xác suất mong muốn bằng: P(A)=1-P1000(0)=1- e-2
20
= 1- e-2=1-0,13534≈0,865. Nhiệm vụ cho công việc độc lập.
1.1
1.2.
Biến ngẫu nhiên phân tán X được xác định bởi luật phân phối: Tìm p4, hàm phân phối F(X) và vẽ đồ thị của nó, cũng như M(X), D(X), σ(X). 1.3.
Trong hộp có 9 cái bút đánh dấu, trong đó có 2 cái không còn viết nữa. Lấy ngẫu nhiên 3 điểm đánh dấu. Biến ngẫu nhiên X là số lượng bút viết trong số những bút được lấy. Xây dựng quy luật phân phối của một biến ngẫu nhiên. 1.4.
Có 6 cuốn sách giáo khoa được sắp xếp ngẫu nhiên trên kệ thư viện, trong đó có 4 cuốn được đóng bìa. Thủ thư lấy ngẫu nhiên 4 cuốn sách. Biến ngẫu nhiên X là số lượng sách giáo khoa đóng trong số sách được lấy. Xây dựng quy luật phân phối của một biến ngẫu nhiên. 1.5.
Có hai nhiệm vụ trên vé. Xác suất giải đúng bài toán thứ nhất là 0,9, câu thứ hai là 0,7. Biến ngẫu nhiên X là số bài toán được giải đúng trong phiếu. Hãy vẽ luật phân phối, tính kỳ vọng và phương sai toán học của biến ngẫu nhiên này, đồng thời tìm hàm phân phối F(x) và xây dựng đồ thị của nó. 1.6.
Ba xạ thủ đang bắn vào một mục tiêu. Xác suất bắn trúng mục tiêu bằng một phát bắn là 0,5 đối với người bắn đầu tiên, 0,8 đối với người bắn thứ hai và 0,7 đối với người bắn thứ ba. Biến ngẫu nhiên X là số lần bắn trúng mục tiêu nếu người bắn bắn từng phát một. Tìm luật phân phối, M(X),D(X). 1.7.
Một cầu thủ bóng rổ ném bóng vào rổ với xác suất mỗi cú ném trúng là 0,8. Với mỗi lần đánh, anh ta nhận được 10 điểm, và nếu trượt, anh ta sẽ không được thưởng điểm. Hãy vẽ luật phân phối cho biến ngẫu nhiên X - số điểm mà một cầu thủ bóng rổ nhận được sau 3 lượt đánh. Tìm M(X),D(X), cũng như xác suất để người đó được nhiều hơn 10 điểm. 1.8.
Các chữ cái được viết trên thẻ, có tổng cộng 5 nguyên âm và 3 phụ âm. 3 lá bài được chọn ngẫu nhiên và mỗi lần lấy lá bài sẽ được trả lại. Biến ngẫu nhiên X là số nguyên âm trong số những nguyên âm được lấy. Hãy vẽ luật phân phối và tìm M(X),D(X),σ(X). 1.9.
Trung bình, dưới 60% hợp đồng, công ty bảo hiểm trả số tiền bảo hiểm liên quan đến việc xảy ra sự kiện được bảo hiểm. Hãy vẽ luật phân phối cho biến ngẫu nhiên X - số lượng hợp đồng được trả số tiền bảo hiểm trong số bốn hợp đồng được chọn ngẫu nhiên. Tìm các đặc tính số của đại lượng này. 1.10.
Đài phát thanh sẽ gửi các dấu hiệu cuộc gọi (không quá bốn) theo những khoảng thời gian nhất định cho đến khi thiết lập được liên lạc hai chiều. Xác suất nhận được phản hồi đối với dấu hiệu cuộc gọi là 0,3. Biến ngẫu nhiên X là số lượng tín hiệu cuộc gọi được gửi đi. Hãy vẽ luật phân phối và tìm F(x). 1.11.
Có 3 chìa khóa, trong đó chỉ có một chìa khóa được. Hãy lập luật phân phối biến ngẫu nhiên X-số lần thử mở ổ khóa, nếu chìa khóa đã thử không tham gia vào các lần thử tiếp theo. Tìm M(X),D(X). 1.12.
Các thử nghiệm độc lập liên tiếp của ba thiết bị được thực hiện để đảm bảo độ tin cậy. Mỗi thiết bị tiếp theo chỉ được kiểm tra nếu thiết bị trước đó đáng tin cậy. Xác suất vượt qua bài kiểm tra cho mỗi thiết bị là 0,9. Vẽ luật phân phối cho biến ngẫu nhiên X-số lượng thiết bị được thử nghiệm. 1.13
.Biến ngẫu nhiên rời rạc X có ba giá trị có thể có: x1=1, x2, x3 và x1<х2<х3. Вероятность того, что Х примет значения х1 и х2, соответственно равны 0,3 и 0,2. Известно, что М(Х)=2,2, D(X)=0,76. Составить закон распределения случайной величины. 1.14.
Khối thiết bị điện tử chứa 100 phần tử giống hệt nhau. Xác suất hư hỏng của mỗi phần tử trong thời gian T là 0,002. Các phần tử hoạt động độc lập. Tìm xác suất để có không quá hai phần tử bị hỏng trong thời gian T. 1.15.
Sách giáo khoa đã được xuất bản với số lượng phát hành 50.000 bản. Xác suất để cuốn sách được đóng bìa không đúng cách là 0,0002. Tìm xác suất để vòng tuần hoàn chứa: a) bốn cuốn sách bị lỗi, b) ít hơn hai cuốn sách bị lỗi. 1
.16.
Số cuộc gọi đến PBX mỗi phút được phân bổ theo định luật Poisson với tham số λ=1,5. Tìm xác suất để trong một phút sẽ có những thứ sau: a) hai cuộc gọi; b) ít nhất một cuộc gọi. 1.17.
Tìm M(Z),D(Z) nếu Z=3X+Y. 1.18.
Định luật phân phối của hai biến ngẫu nhiên độc lập được đưa ra: Tìm M(Z),D(Z) nếu Z=X+2Y. Câu trả lời:
https://pandia.ru/text/78/455/images/image007_76.gif" Height="110"> 1.1.
p3=0,4; 0 tại x<-2, 0,3 tại -2<х≤0, F(x)= 0,5 tại 0<х≤2, 0,9 lúc 2<х≤5, 1 tại x>5 0,3 tại -1<х≤0, 0,4 lúc 0<х≤1, F(x)= 0,6 tại 1<х≤2, 0,7 lúc 2<х≤3, 1 tại x>3 M(X)=1; D(X)=2,6; σ(X) ≈1.612. https://pandia.ru/text/78/455/images/image025_24.gif" width="2 chiều cao=98" chiều cao="98"> 0 tại x≤0, 0,03 tại 0<х≤1, F(x)= 0,37 tại 1<х≤2, 1 cho x>2 M(X)=2; D(X)=0,62 M(X)=2,4; D(X)=0,48, P(X>10)=0,896 1.
8
.
M(X)=15/8; D(X)=45/64; σ(X) ≈ M(X)=2,4; D(X)=0,96 https://pandia.ru/text/78/455/images/image008_71.gif" width="14"> 1.11.
M(X)=2; D(X)=2/3 1.14.
1,22 e-0,2≈0,999 1.15.
a)0,0189; b) 0,00049 1.16.
a) 0,0702; b)0,77687 1.17.
3,8; 14,2 1.18.
11,2; 4. Chương 2. Biến ngẫu nhiên liên tục
Sự định nghĩa: Tiếp diễn
Họ gọi một đại lượng là tất cả các giá trị có thể có của nó lấp đầy một khoảng hữu hạn hoặc vô hạn của trục số. Rõ ràng, số lượng giá trị có thể có của một biến ngẫu nhiên liên tục là vô hạn. Một biến ngẫu nhiên liên tục có thể được xác định bằng hàm phân phối. Sự định nghĩa: F Chức năng phân phối
biến ngẫu nhiên liên tục X được gọi là hàm F(x), hàm này xác định cho từng giá trị xhttps://pandia.ru/text/78/455/images/image028_11.jpg" width="14" Height="13"> R Hàm phân phối đôi khi được gọi là hàm phân phối tích lũy. Tính chất của hàm phân phối:
1)1< F(x) <1 2) Đối với một biến ngẫu nhiên liên tục, hàm phân phối liên tục tại bất kỳ điểm nào và khả vi ở mọi nơi, ngoại trừ, có lẽ, tại các điểm riêng lẻ. 3) Xác suất để biến ngẫu nhiên X rơi vào một trong các khoảng (a;b), [a;b], [a;b] bằng hiệu giữa các giá trị của hàm F(x) tại các điểm a và b, tức là R(a)<Х 4) Xác suất để biến ngẫu nhiên liên tục X lấy một giá trị riêng biệt là 0. 5) F(-∞)=0, F(+∞)=1 Việc chỉ định một biến ngẫu nhiên liên tục bằng hàm phân phối không phải là cách duy nhất. Hãy để chúng tôi giới thiệu khái niệm về mật độ phân bố xác suất (mật độ phân phối). Sự định nghĩa
:
Mật độ phân bố xác suất
f
(
x
)
của biến ngẫu nhiên liên tục X là đạo hàm của hàm phân phối của nó, tức là: Hàm mật độ xác suất đôi khi được gọi là hàm phân phối vi phân hoặc luật phân phối vi phân. Đồ thị của phân bố mật độ xác suất f(x) được gọi là đường cong phân bố xác suất
.
Tính chất của phân bố mật độ xác suất:
1) f(x) ≥0, tại xhttps://pandia.ru/text/78/455/images/image029_10.jpg" width="285" Height="141">DIV_ADBLOCK13"> https://pandia.ru/text/78/455/images/image032_23.gif" Height="38 src="> +∞ 2 6 +∞ 6 6 ∫ f(x)dx=∫ 0dx+ ∫ c(x-2)dx +∫ 0dx= c∫ (x-2)dx=c(x2/2-2x) =c(36/2-12-(4/ 2-4))=8 giây; b) Biết rằng F(x)= ∫ f(x)dx Vì vậy, x nếu x 2 thì F(x)= ∫ 0dx=0; https://pandia.ru/text/78/455/images/image032_23.gif" Height="38 src="> 2 6 x 6 6 nếu x>6, thì F(x)= ∫ 0dx+∫ 1/8(x-2)dx+∫ 0dx=1/8∫(x-2)dx=1/8(x2/2-2x) = 1/8(36/2-12-(4/2+4))=1/8 8=1. Như vậy, 0 tại x 2, F(x)= (x-2)2/16 tại 2<х≤6, 1 cho x>6. Đồ thị của hàm F(x) được thể hiện trên Hình 3 https://pandia.ru/text/78/455/images/image034_23.gif" width="14" Height="62 src="> 0 tại x<0, F(x)= (3 arctan x)/π tại 0<х≤√3, 1 cho x>√3. Tìm hàm phân phối vi phân f(x) Giải pháp:
Vì f(x)=F’(x), nên DIV_ADBLOCK14"> · Kỳ vọng toán học M (X)
biến ngẫu nhiên liên tục X được xác định bởi đẳng thức: M(X)= ∫ x f(x)dx, với điều kiện tích phân này hội tụ tuyệt đối. · phân tán
D
(
X
)
biến ngẫu nhiên liên tục X được xác định bởi đẳng thức: D(X)= ∫ (x-M(x)2) f(x)dx, hoặc D(X)= ∫ x2 f(x)dx - (M(x))2 · Độ lệch chuẩn σ(X)
biến ngẫu nhiên liên tục được xác định bởi đẳng thức: Tất cả các tính chất của kỳ vọng và phân tán toán học, đã thảo luận trước đó đối với các biến ngẫu nhiên phân tán, cũng có giá trị đối với các biến ngẫu nhiên phân tán. Nhiệm vụ số 3. Biến ngẫu nhiên X được xác định bởi hàm vi phân f(x): https://pandia.ru/text/78/455/images/image036_19.gif" Height="38"> -∞ 2 X3/9 + x2/6 = 8/9-0+9/6-4/6=31/18, https://pandia.ru/text/78/455/images/image032_23.gif" Height="38"> +∞ D(X)= ∫ x2 f(x)dx-(M(x))2=∫ x2 x/3 dx+∫1/3x2 dx=(31/18)2=x4/12 + x3/9 - - (31/18)2=16/12-0+27/9-8/9-(31/18)2=31/9- (31/18)2==31/9(1-31/36)=155/324, https://pandia.ru/text/78/455/images/image032_23.gif" Height="38"> P(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х2/6 +1/3х = 4/6-1/6+1-2/3=5/6. Vấn đề cho giải pháp độc lập.
2.1.
Biến ngẫu nhiên liên tục X được xác định bởi hàm phân phối: 0 tại x 0, F(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" Height="86"> 0 cho x π/6, F(x)= - cos 3x tại π/6<х≤ π/3, 1 cho x> π/3. Tìm hàm phân phối vi phân f(x), và cũng Р(2π /9<Х< π /2). 2.3.
0 tại x 2, f(x)= c x tại 2<х≤4, 0 cho x>4. 2.4.
Biến ngẫu nhiên liên tục X được xác định bởi mật độ phân bố: 0 tại x 0, f(x)= c √x tại 0<х≤1, 0 cho x>1. Tìm: a) số c; b) M(X), D(X). 2.5.
https://pandia.ru/text/78/455/images/image041_3.jpg" width="36" Height="39"> tại x, 0 tại x. Tìm: a) F(x) và xây dựng đồ thị của nó; b) M(X),D(X), σ(X); c) xác suất để trong bốn phép thử độc lập giá trị của X sẽ bằng đúng 2 lần giá trị thuộc khoảng (1;4). 2.6.
Mật độ phân bố xác suất của biến ngẫu nhiên liên tục X được cho: f(x)= 2(x-2) tại x, 0 tại x. Tìm: a) F(x) và xây dựng đồ thị của nó; b) M(X),D(X), σ (X); c) xác suất để trong ba phép thử độc lập giá trị của X sẽ bằng đúng 2 lần giá trị thuộc đoạn . 2.7.
Hàm f(x) được cho là: https://pandia.ru/text/78/455/images/image045_4.jpg" width="43" Height="38 src=">.jpg" width="16" Height="15">[-√ 3/2; √3/2]. 2.8.
Hàm f(x) được cho là: https://pandia.ru/text/78/455/images/image046_5.jpg" width="45" Height="36 src="> .jpg" width="16" Height="15">[- π /4 ; π /4]. Tìm: a) giá trị của hằng số c mà tại đó hàm số sẽ là mật độ xác suất của một biến ngẫu nhiên X nào đó; b) hàm phân phối F(x). 2.9.
Biến ngẫu nhiên X, tập trung vào khoảng (3;7), được xác định bởi hàm phân phối F(x)= . Tìm xác suất để Biến ngẫu nhiên X sẽ lấy giá trị: a) nhỏ hơn 5, b) không nhỏ hơn 7. 2.10.
Biến ngẫu nhiên X, tập trung vào khoảng (-1;4), được cho bởi hàm phân phối F(x)= . Tìm xác suất để Biến ngẫu nhiên X sẽ lấy giá trị: a) nhỏ hơn 2, b) không nhỏ hơn 4. 2.11.
https://pandia.ru/text/78/455/images/image049_6.jpg" width="43" Height="44 src="> .jpg" width="16" Height="15">. Tìm: a) số c; b) M(X); c) xác suất P(X> M(X)). 2.12.
Biến ngẫu nhiên được xác định bởi hàm phân phối vi phân: https://pandia.ru/text/78/455/images/image050_3.jpg" width="60" Height="38 src=">.jpg" width="16 Height=15" Height="15"> . Tìm: a) M(X); b) xác suất P(X 2.13.
Phân phối Rem được tính bằng mật độ xác suất: https://pandia.ru/text/78/455/images/image052_5.jpg" width="46" Height="37"> cho x ≥0. Chứng minh rằng f(x) thực sự là một hàm mật độ xác suất. 2.14.
Mật độ phân bố xác suất của biến ngẫu nhiên liên tục X được cho: DIV_ADBLOCK17"> https://pandia.ru/text/78/455/images/image055_3.jpg" width="187 chiều cao=136" chiều cao="136">(Hình 5) 2.16.
Biến ngẫu nhiên X được phân phối theo định luật “tam giác vuông” trong khoảng (0;4) (Hình 5). Tìm biểu thức giải tích cho mật độ xác suất f(x) trên toàn bộ trục số. câu trả lời
0 tại x 0, f(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" Height="86"> 0 cho x π/6, F(x)= 3sin 3x tại π/6<х≤ π/3,
Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т. е. 0 cho x f(x)= cho một<х 0 cho x ≥b. Đồ thị của hàm f(x) được biểu diễn trên Hình 2. 1 F(x)= https://pandia.ru/text/78/455/images/image077_3.jpg" width="30" Height="37">, D(X)=, σ(X)=. Nhiệm vụ số 1. Biến ngẫu nhiên X được phân bố đều trên đoạn. Tìm thấy: a) mật độ phân bố xác suất f(x) và vẽ đồ thị đó; b) hàm phân phối F(x) và vẽ đồ thị đó; c) M(X),D(X), σ(X). Giải pháp:
Sử dụng các công thức đã thảo luận ở trên, với a=3, b=7, chúng ta tìm thấy: https://pandia.ru/text/78/455/images/image081_2.jpg" width="22" Height="39"> tại 3 х 7, 0 cho x>7 Hãy xây dựng biểu đồ của nó (Hình 3): https://pandia.ru/text/78/455/images/image038_17.gif" width="14" Height="86 src="> 0 tại x<3, F(x)= https://pandia.ru/text/78/455/images/image084_3.jpg" width="203" Height="119 src=">Hình 4 D(X) = ==https://pandia.ru/text/78/455/images/image089_1.jpg" width="37" Height="43">==https://pandia.ru/text/ 78/455/images/image092_10.gif" width="14" Height="49 src="> 0 tại x<0, f(x)= λе-λх với x ≥0. Hàm phân phối của biến ngẫu nhiên X phân bố theo định luật hàm mũ được cho bởi công thức: DIV_ADBLOCK19"> https://pandia.ru/text/78/455/images/image095_4.jpg" width="161" Height="119 src="> Hình 6 Kỳ vọng toán học, phương sai và độ lệch chuẩn của phân bố mũ lần lượt bằng: M(X)= , D(X)=, σ (Х)= Do đó, kỳ vọng toán học và độ lệch chuẩn của phân bố mũ bằng nhau. Xác suất để X rơi vào khoảng (a;b) được tính theo công thức: P(a<Х Nhiệm vụ số 2. Thời gian hoạt động không xảy ra lỗi trung bình của thiết bị là 100 giờ. Giả sử thời gian hoạt động không xảy ra lỗi của thiết bị có luật phân phối mũ, hãy tìm: a) mật độ phân bố xác suất; b) hàm phân phối; c) xác suất thời gian hoạt động không hỏng hóc của thiết bị sẽ vượt quá 120 giờ. Giải pháp:
Theo điều kiện, phân phối toán học M(X)=https://pandia.ru/text/78/455/images/image098_10.gif" Height="43 src="> 0 tại x<0, a) f(x)= 0,01e -0,01x đối với x ≥0. b) F(x)= 0 tại x<0, 1-e -0,01x tại x ≥0. c) Chúng ta tìm xác suất mong muốn bằng hàm phân phối: P(X>120)=1-F(120)=1-(1- e -1.2)= e -1.2≈0.3. §
3. Luật phân phối chuẩn Sự định nghĩa:
Một biến ngẫu nhiên liên tục X có luật phân phối chuẩn (định luật Gauss),
nếu mật độ phân bố của nó có dạng: trong đó m=M(X), σ2=D(X), σ>0. Đường cong phân phối chuẩn được gọi là đường cong bình thường hoặc Gaussian
(Hình 7) Hàm phân phối của biến ngẫu nhiên X phân phối theo định luật chuẩn tắc được biểu diễn thông qua hàm Laplace Ф(x) theo công thức: hàm Laplace ở đâu Bình luận:
Hàm Ф(x) là số lẻ (Ф(-х)=-Ф(х)), ngoài ra, với x>5 chúng ta có thể giả sử Ф(х) ≈1/2. Đồ thị của hàm phân phối F(x) được biểu diễn trên Hình 2. số 8 https://pandia.ru/text/78/455/images/image106_4.jpg" width="218" Height="33"> Xác suất để giá trị tuyệt đối của độ lệch nhỏ hơn số dương δ được tính theo công thức: Cụ thể, với m=0 đẳng thức sau đây đúng: "Quy tắc ba Sigma"
Nếu một biến ngẫu nhiên X có luật phân phối chuẩn với các tham số m và σ thì gần như chắc chắn rằng giá trị của nó nằm trong khoảng (a-3σ; a+3σ), bởi vì https://pandia.ru/text/78/455/images/image110_2.jpg" width="157" Height="57 src=">a) b) Sử dụng công thức: https://pandia.ru/text/78/455/images/image112_2.jpg" width="369" Height="38 src="> Từ bảng giá trị hàm Ф(х) ta tìm được Ф(1.5)=0,4332, Ф(1)=0,3413. Vì vậy, xác suất mong muốn: P(28 Nhiệm vụ cho công việc độc lập
3.1.
Biến ngẫu nhiên X được phân bố đều trong khoảng (-3;5). Tìm thấy: b) hàm phân bố F(x); c) đặc tính số; d) xác suất P(4<х<6). 3.2.
Biến ngẫu nhiên X được phân bố đều trên đoạn. Tìm thấy: a) mật độ phân bố f(x); b) hàm phân bố F(x); c) đặc tính số; d) xác suất P(3<х<6). 3.3.
Trên đường cao tốc có đèn giao thông tự động, đèn xanh sáng trong 2 phút, đèn vàng trong 3 giây, đèn đỏ trong 30 giây, v.v. Một ô tô chạy dọc đường cao tốc vào một thời điểm ngẫu nhiên. Tìm xác suất để một ô tô vượt đèn giao thông mà không dừng lại. 3.4.
Tàu điện ngầm chạy thường xuyên với khoảng thời gian 2 phút. Một hành khách bước vào sân ga vào một thời điểm ngẫu nhiên. Xác suất để một hành khách phải chờ tàu hơn 50 giây là bao nhiêu? Tìm kỳ vọng toán học của biến ngẫu nhiên X - thời gian chờ tàu. 3.5.
Tìm phương sai và độ lệch chuẩn của phân bố mũ do hàm phân phối cho trước: F(x)= 0 tại x<0, 1-8x cho x ≥0. 3.6.
Biến ngẫu nhiên liên tục X được xác định bởi mật độ phân bố xác suất: f(x)= 0 tại x<0, 0,7 e-0,7x tại x ≥0. a) Nêu quy luật phân phối của biến ngẫu nhiên đang xét. b) Tìm hàm phân phối F(X) và các đặc tính số của biến ngẫu nhiên X. 3.7.
Biến ngẫu nhiên X được phân bố theo quy luật hàm mũ được xác định bởi mật độ phân bố xác suất: f(x)= 0 tại x<0, 0,4 e-0,4 x tại x ≥0. Tìm xác suất mà kết quả của phép thử X sẽ lấy giá trị từ khoảng (2,5;5). 3.8.
Biến ngẫu nhiên liên tục X được phân phối theo quy luật hàm mũ được xác định bởi hàm phân phối: F(x)= 0 tại x<0, Thứ 1-0,6x tại x ≥0 Tìm xác suất mà theo kết quả kiểm tra, X sẽ lấy một giá trị từ phân khúc. 3.9.
Giá trị kỳ vọng và độ lệch chuẩn của một biến ngẫu nhiên có phân phối chuẩn lần lượt là 8 và 2. Tìm: a) mật độ phân bố f(x); b) xác suất mà kết quả của phép thử X sẽ lấy giá trị từ khoảng (10;14). 3.10.
Biến ngẫu nhiên X thường được phân phối với kỳ vọng toán học là 3,5 và phương sai là 0,04. Tìm thấy: a) mật độ phân bố f(x); b) xác suất mà kết quả của phép thử X sẽ lấy một giá trị từ đoạn . 3.11.
Biến ngẫu nhiên X có phân phối chuẩn với M(X)=0 và D(X)=1. Sự kiện nào: |X|<0,6 hoặc |X|>0,6 có nhiều khả năng xảy ra hơn? 3.12.
Biến ngẫu nhiên X được phân phối chuẩn với M(X)=0 và D(X)=1. Từ khoảng nào (-0,5;-0,1) hoặc (1;2) thì có nhiều khả năng nhận được một giá trị trong một lần kiểm tra? 3.13.
Giá hiện tại trên mỗi cổ phiếu có thể được mô hình hóa bằng luật phân phối chuẩn với M(X)=10 den. các đơn vị và σ(X)=0,3 den. các đơn vị Tìm thấy: a) xác suất giá cổ phiếu hiện tại sẽ từ 9,8 den. các đơn vị lên tới 10,4 ngày các đơn vị; b) sử dụng “quy tắc ba sigma”, tìm ranh giới mà giá cổ phiếu hiện tại sẽ nằm trong đó. 3.14.
Chất được cân mà không có lỗi hệ thống. Các lỗi cân ngẫu nhiên tuân theo quy luật thông thường với tỷ lệ bình phương trung bình σ=5g. Tìm xác suất để trong bốn thí nghiệm độc lập không xảy ra sai số trong ba lần cân ở giá trị tuyệt đối 3r. 3.15.
Biến ngẫu nhiên X có phân phối chuẩn với M(X)=12,6. Xác suất để một biến ngẫu nhiên rơi vào khoảng (11,4;13,8) là 0,6826. Tìm độ lệch chuẩn σ. 3.16.
Biến ngẫu nhiên X được phân phối chuẩn với M(X)=12 và D(X)=36. Tìm khoảng mà biến ngẫu nhiên X sẽ rơi vào đó do kết quả của phép thử với xác suất là 0,9973. 3.17.
Một bộ phận được sản xuất bằng máy tự động được coi là bị lỗi nếu độ lệch X của tham số được điều khiển của nó so với giá trị danh nghĩa vượt quá modulo 2 đơn vị đo. Giả sử biến ngẫu nhiên X có phân phối chuẩn với M(X)=0 và σ(X)=0,7. Máy tạo ra bao nhiêu phần trăm bộ phận bị lỗi? 3.18.
Tham số X của bộ phận được phân phối bình thường với kỳ vọng toán học là 2 bằng giá trị danh nghĩa và độ lệch chuẩn là 0,014. Tìm xác suất để độ lệch của X so với giá trị danh nghĩa sẽ không vượt quá 1% giá trị danh nghĩa. câu trả lời
https://pandia.ru/text/78/455/images/image116_9.gif" width="14" Height="110 src="> b) 0 với x<-3, F(x)= trái"> 3.10.
a)f(x)= , b) Р(3,1<Х<3,7) ≈0,8185. 3.11.
|x| ≥0,6. 3.12.
(-0,5;-0,1). 3.13.
a) P(9,8<Х<10,4) ≈0,6562. 3.14.
0,111. 3.15.
σ=1,2. 3.16.
(-6;30). 3.17.
0,4%. Ví dụ giải bài toán về chủ đề “Biến ngẫu nhiên”.
Nhiệm vụ 1
. Có 100 vé được phát hành để xổ số. Một chiến thắng trị giá 50 USD đã được rút ra. và mười chiến thắng trị giá 10 USD mỗi chiến thắng. Tìm quy luật phân phối của giá trị X - chi phí của số tiền thắng có thể có. Giải pháp. Các giá trị có thể có của X: x 1
= 0; x 2
= 10 và x 3
= 50. Vì có 89 vé “rỗng” nên p 1
= 0,89, xác suất trúng 10$. (10 vé) – p 2
= 0,10 và giành được 50 USD -P 3
= 0,01. Như vậy: 0,89
0,10
0,01
Dễ dàng điều khiển: . Nhiệm vụ 2.
Xác suất người mua đã đọc trước quảng cáo sản phẩm là 0,6 (p = 0,6). Việc kiểm soát có chọn lọc chất lượng quảng cáo được thực hiện bằng cách khảo sát người mua trước người đầu tiên đã nghiên cứu trước về quảng cáo. Vẽ một chuỗi phân phối cho số lượng người mua được khảo sát. Giải pháp. Theo điều kiện của bài toán thì p = 0,6. Từ: q=1 -p = 0,4. Thay thế các giá trị này, chúng tôi nhận được: và xây dựng một chuỗi phân phối: số Pi 0,24
Nhiệm vụ 3.
Một máy tính bao gồm ba thành phần hoạt động độc lập: bộ phận hệ thống, màn hình và bàn phím. Với một lần tăng mạnh điện áp, xác suất hỏng hóc của từng phần tử là 0,1. Dựa trên phân bố Bernoulli, hãy vẽ luật phân bố cho số phần tử bị lỗi khi có sự đột biến điện năng trong mạng. Giải pháp. Hãy xem xét Phân phối Bernoulli(hoặc nhị thức): xác suất để N kiểm tra, sự kiện A sẽ xuất hiện chính xác k một lần: q N P N TRONG Hãy quay trở lại nhiệm vụ. Các giá trị có thể có cho X (số lần thất bại): x 0 =0 – không có phần tử nào bị lỗi; x 1 =1 – hỏng một phần tử; x 2 =2 – hỏng hai phần tử; x 3 =3 – hỏng toàn bộ phần tử. Vì, theo điều kiện, p = 0,1 thì q = 1 – p = 0,9. Sử dụng công thức Bernoulli, chúng ta có được , ,
, .
Điều khiển: . Do đó, luật phân phối cần thiết: 0,729
0,243
0,027
0,001
Vấn đề 4. 5000 viên đạn được sản xuất. Xác suất một hộp mực bị lỗi Giải pháp. Áp dụng Phân bố Poisson: Phân phối này được sử dụng để xác định xác suất rằng, đối với rất lớn số lần thử nghiệm (thử nghiệm hàng loạt), trong đó xác suất xảy ra sự kiện A rất nhỏ thì sự kiện A sẽ xảy ra k lần: Ở đây n = 5000, p = 0,0002, k = 3. Khi đó ta tìm được xác suất mong muốn: Vấn đề 5. Khi bắn cho đến phát đầu tiên với xác suất trúng p
= 0,6 khi bắn, bạn cần tìm xác suất để lần bắn thứ 3 sẽ trúng đích. Giải pháp. Chúng ta hãy áp dụng phân bố hình học: tiến hành các thử nghiệm độc lập, trong mỗi biến cố A có xác suất xảy ra p (và không xảy ra q = 1 – p). Thử nghiệm kết thúc ngay khi sự kiện A xảy ra. Trong điều kiện như vậy, xác suất để sự kiện A xảy ra ở lần thử thứ k được xác định theo công thức: . Ở đây p = 0,6; q = 1 – 0,6 = 0,4;k = 3. Do đó, . Vấn đề 6. Cho định luật phân phối của biến ngẫu nhiên X: Tìm kỳ vọng toán học. Giải pháp. . Lưu ý rằng ý nghĩa xác suất của kỳ vọng toán học là giá trị trung bình của một biến ngẫu nhiên. Vấn đề 7. Tìm phương sai của biến ngẫu nhiên X tuân theo luật phân phối sau: Giải pháp. Đây
.
Luật phân phối cho giá trị bình phương của X 2
:
X 2
Phương sai yêu cầu: . Độ phân tán đặc trưng cho thước đo độ lệch (độ phân tán) của một biến ngẫu nhiên so với kỳ vọng toán học của nó. Vấn đề 8. Cho một biến ngẫu nhiên theo phân phối: 10m Tìm các đặc tính số của nó. Giải: m, m 2
,
M 2
, m. Về biến ngẫu nhiên X chúng ta có thể nói: kỳ vọng toán học của nó là 6,4 m với phương sai là 13,04 m 2
, hoặc – kỳ vọng toán học của nó là 6,4 m với độ lệch là m. Công thức thứ hai rõ ràng hơn. Nhiệm vụ 9.
Giá trị ngẫu nhiên X được cho bởi hàm phân phối: Tìm xác suất mà kết quả của phép thử là giá trị X sẽ lấy giá trị chứa trong khoảng Giải pháp. Xác suất X sẽ lấy một giá trị từ một khoảng nhất định bằng với mức tăng của hàm tích phân trong khoảng này, tức là. . Trong trường hợp của chúng tôi và do đó Nhiệm vụ 10.
Biến ngẫu nhiên rời rạc X được cho bởi luật phân phối: Tìm hàm phân phối F(x ) và vẽ đồ thị đó. Giải pháp. Vì hàm phân phối Tại ; Tại ; Tại ; Tại ; Biểu đồ liên quan: Vấn đề 11. Biến ngẫu nhiên liên tục X được đưa ra bởi hàm phân phối vi phân: Tìm xác suất trúng X mỗi khoảng Giải pháp. Lưu ý rằng đây là trường hợp đặc biệt của luật phân phối mũ. Hãy sử dụng công thức: Nhiệm vụ 12.
Tìm các đặc tính số của biến ngẫu nhiên rời rạc X theo quy luật phân phối: –5
X2: X 2 .
,
Ở đâu Các giá trị của hàm này được tìm thấy bằng bảng. Trong trường hợp của chúng ta: . Từ bảng chúng tôi tìm thấy: , do đó: Định nghĩa 1 Một biến ngẫu nhiên $X$ được gọi là rời rạc (không liên tục) nếu tập hợp các giá trị của nó là vô hạn hoặc hữu hạn nhưng có thể đếm được. Nói cách khác, một đại lượng được gọi là rời rạc nếu các giá trị của nó có thể đánh số được. Một biến ngẫu nhiên có thể được mô tả bằng luật phân phối. Luật phân phối của biến ngẫu nhiên rời rạc $X$ có thể được chỉ định dưới dạng bảng, dòng đầu tiên cho biết tất cả các giá trị có thể có của biến ngẫu nhiên theo thứ tự tăng dần và dòng thứ hai chứa xác suất tương ứng của các giá trị này giá trị: Bức tranh 1. trong đó $р1+ р2+ ... + рn = 1$. Bảng này là gần phân phối của một biến ngẫu nhiên rời rạc. Nếu tập hợp các giá trị có thể có của một biến ngẫu nhiên là vô hạn thì chuỗi $р1+ р2+ ... + рn+ ...$ hội tụ và tổng của nó sẽ bằng $1$. Luật phân phối của một biến ngẫu nhiên rời rạc $X$ có thể được biểu diễn bằng đồ họa, trong đó một đường gãy được xây dựng trong hệ tọa độ (hình chữ nhật), nối các điểm một cách tuần tự với tọa độ $(xi;pi), i=1,2, ... n$. Dòng chúng tôi nhận được được gọi là đa giác phân phối. Hình 2. Luật phân phối của biến ngẫu nhiên rời rạc $X$ cũng có thể được biểu diễn bằng phương pháp giải tích (sử dụng công thức): $P(X=xi)= \varphi (xi),i =1,2,3 ... n$. Khi giải nhiều bài toán lý thuyết xác suất, cần thực hiện các phép tính nhân một biến ngẫu nhiên rời rạc với một hằng số, cộng hai biến ngẫu nhiên, nhân chúng, thay lũy thừa. Trong những trường hợp này, cần tuân thủ các quy tắc sau đối với số lượng rời rạc ngẫu nhiên: Định nghĩa 3 Phép nhân của một biến ngẫu nhiên rời rạc $X$ theo một hằng số $K$ là một biến ngẫu nhiên rời rạc $Y=KX,$ được xác định bởi các đẳng thức: $y_i=Kx_i,\ \ p\left(y_i\right)=p\ left(x_i\right)= p_i,\ \ i=\overline(1,\ n).$ Định nghĩa 4 Hai biến ngẫu nhiên $x$ và $y$ được gọi độc lập, nếu luật phân phối của một trong số chúng không phụ thuộc vào giá trị có thể có của đại lượng thứ hai. Định nghĩa 5 Số lượng hai biến ngẫu nhiên rời rạc độc lập $X$ và $Y$ được gọi là biến ngẫu nhiên $Z=X+Y,$ được xác định bởi các đẳng thức: $z_(ij)=x_i+y_j$, $P\left(z_(ij )\right)= P\left(x_i\right)P\left(y_j\right)=p_ip"_j$, $i=\overline(1,n)$, $j=\overline(1,m)$ , $P\left (x_i\right)=p_i$, $P\left(y_j\right)=p"_j$. Định nghĩa 6 Phép nhân hai biến ngẫu nhiên rời rạc độc lập $X$ và $Y$ được gọi là biến ngẫu nhiên $Z=XY,$ được xác định bởi các đẳng thức: $z_(ij)=x_iy_j$, $P\left(z_(ij)\right) =P\left( x_i\right)P\left(y_j\right)=p_ip"_j$, $i=\overline(1,n)$, $j=\overline(1,m)$, $P\ left(x_i\right )=p_i$, $P\left(y_j\right)=p"_j$. Chúng ta hãy tính đến việc một số sản phẩm $x_(i\ \ \ \ )y_j$ có thể bằng nhau. Trong trường hợp này, xác suất thêm sản phẩm bằng tổng các xác suất tương ứng. Ví dụ: nếu $x_2\ \ y_3=x_5\ \ y_7,\ $thì xác suất của $x_2y_3$ (hoặc $x_5y_7$ tương tự) sẽ bằng $p_2\cdot p"_3+p_5\cdot p"_7 .$ Những điều trên cũng áp dụng cho số tiền. Nếu $x_1+\ y_2=x_4+\ \ y_6,$ thì xác suất của $x_1+\ y_2$ (hoặc $x_4+\ y_6$ tương tự) sẽ bằng $p_1\cdot p"_2+p_4\cdot p"_6. $ Các biến ngẫu nhiên $X$ và $Y$ được quy định bởi luật phân phối: Hình 3. Trong đó $p_1+p_2+p_3=1,\ \ \ p"_1+p"_2=1.$ Khi đó luật phân phối của tổng $X+Y$ sẽ có dạng Hinh 4. Và quy luật phân phối của sản phẩm $XY$ sẽ có dạng Hình 5. Một mô tả đầy đủ về một biến ngẫu nhiên cũng được đưa ra bởi hàm phân phối. Về mặt hình học, hàm phân phối được giải thích là xác suất để biến ngẫu nhiên $X$ nhận giá trị được biểu thị trên trục số bởi điểm nằm bên trái điểm $x$. Chúng ta có thể nêu bật các quy luật phân phối phổ biến nhất của các biến ngẫu nhiên rời rạc: Đối với các phân bố nhất định của các biến ngẫu nhiên rời rạc, việc tính xác suất giá trị của chúng, cũng như các đặc tính số (kỳ vọng toán học, phương sai, v.v.) được thực hiện bằng cách sử dụng một số "công thức" nhất định. Vì vậy, điều rất quan trọng là phải biết các loại phân phối này và các tính chất cơ bản của chúng. Biến ngẫu nhiên rời rạc $X$ tuân theo luật phân phối xác suất nhị thức nếu nó nhận các giá trị $0,\ 1,\ 2,\ \dots ,\ n$ với xác suất $P\left(X=k\right)= C^k_n\cdot p^k\cdot (\left(1-p\right))^(n-k)$. Trong thực tế, biến ngẫu nhiên $X$ là số lần xuất hiện của sự kiện $A$ trong $n$ phép thử độc lập. Định luật phân bố xác suất của biến ngẫu nhiên $X$: $\begin(array)(|c|c|) Đối với một biến ngẫu nhiên như vậy, kỳ vọng toán học là $M\left(X\right)=np$, phương sai là $D\left(X\right)=np\left(1-p\right)$. Ví dụ
. Gia đình có hai người con. Giả sử xác suất sinh con trai và con gái bằng $0,5$, hãy tìm quy luật phân phối của biến ngẫu nhiên $\xi$ - số con trai trong gia đình. Gọi biến ngẫu nhiên $\xi $ là số con trai trong gia đình. Các giá trị mà $\xi có thể nhận:\ 0,\ 1,\ 2$. Xác suất của các giá trị này có thể được tìm thấy bằng công thức $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot (\left(1-p\right))^(n-k )$, trong đó $n =2$ là số lần thử độc lập, $p=0,5$ là xác suất của một sự kiện xảy ra trong một chuỗi $n$ thử nghiệm. Chúng tôi nhận được: $P\left(\xi =0\right)=C^0_2\cdot (0,5)^0\cdot (\left(1-0,5\right))^(2-0)=(0, 5)^2=0,25;$ $P\left(\xi =1\right)=C^1_2\cdot 0.5\cdot (\left(1-0.5\right))^(2-1)=2\cdot 0.5\ cdot 0.5=0.5;$ $P\left(\xi =2\right)=C^2_2\cdot (0.5)^2\cdot (\left(1-0.5\right))^(2-2)=(0, 5)^2 =0,25.$ Khi đó luật phân phối của biến ngẫu nhiên $\xi $ là sự tương ứng giữa các giá trị $0,\ 1,\ 2$ và xác suất của chúng, đó là: $\begin(array)(|c|c|) Tổng các xác suất trong luật phân phối phải bằng $1$, nghĩa là $\sum _(i=1)^(n)P(\xi _((\rm i)))=0,25+0,5+ 0, 25=$1. Kỳ vọng $M\left(\xi \right)=np=2\cdot 0.5=1$, phương sai $D\left(\xi \right)=np\left(1-p\right)=2\ cdot 0.5\ cdot 0,5=0,5$, độ lệch chuẩn $\sigma \left(\xi \right)=\sqrt(D\left(\xi \right))=\sqrt(0.5 )\khoảng $0,707. Nếu một biến ngẫu nhiên rời rạc $X$ chỉ có thể nhận các giá trị nguyên không âm $0,\ 1,\ 2,\ \dots ,\ n$ với xác suất $P\left(X=k\right)=((( \lambda )^k )\over (k}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.!} Bình luận. Điểm đặc biệt của phân phối này là, dựa trên dữ liệu thử nghiệm, chúng ta tìm thấy các ước tính $M\left(X\right),\ D\left(X\right)$, nếu các ước tính thu được gần nhau thì chúng ta có lý do để khẳng định rằng biến ngẫu nhiên tuân theo quy luật phân phối Poisson. Ví dụ
. Ví dụ về các biến ngẫu nhiên tuân theo luật phân phối Poisson có thể là: số lượng ô tô sẽ được trạm xăng phục vụ vào ngày mai; số sản phẩm bị lỗi trong sản phẩm sản xuất. Ví dụ
. Nhà máy đã gửi $500$ sản phẩm đến cơ sở. Xác suất hư hỏng sản phẩm trong quá trình vận chuyển là $0,002$. Tìm quy luật phân phối của biến ngẫu nhiên $X$ bằng số sản phẩm bị hư hỏng; $M\left(X\right),\ D\left(X\right)$ là gì. Gọi biến ngẫu nhiên rời rạc $X$ là số lượng sản phẩm bị hư hỏng. Một biến ngẫu nhiên như vậy tuân theo luật phân phối Poisson với tham số $\lambda =np=500\cdot 0,002=1$. Xác suất của các giá trị bằng $P\left(X=k\right)=(((\lambda )^k)\over (k}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.!} $P\left(X=0\right)=((1^0)\over (0}\cdot e^{-1}=0,368;$!} $P\left(X=1\right)=((1^1)\over (1}\cdot e^{-1}=0,368;$!} $P\left(X=2\right)=((1^2)\over (2}\cdot e^{-1}=0,184;$!} $P\left(X=3\right)=((1^3)\over (3}\cdot e^{-1}=0,061;$!} $P\left(X=4\right)=((1^4)\over (4}\cdot e^{-1}=0,015;$!} $P\left(X=5\right)=((1^5)\over (5}\cdot e^{-1}=0,003;$!} $P\left(X=6\right)=((1^6)\over (6}\cdot e^{-1}=0,001;$!} $P\left(X=k\right)=(((\lambda )^k)\over (k}\cdot e^{-\lambda }$!} Luật phân phối biến ngẫu nhiên $X$: $\begin(array)(|c|c|) Đối với một biến ngẫu nhiên như vậy, kỳ vọng toán học và phương sai bằng nhau và bằng tham số $\lambda $, nghĩa là $M\left(X\right)=D\left(X\right)=\lambda =1$. Nếu một biến ngẫu nhiên rời rạc $X$ chỉ có thể lấy các giá trị tự nhiên $1,\ 2,\ \dots ,\ n$ với xác suất $P\left(X=k\right)=p(\left(1-p\ right)) ^(k-1),\ k=1,\ 2,\ 3,\ \dots $, thì người ta nói rằng một biến ngẫu nhiên $X$ như vậy tuân theo định luật phân bố xác suất hình học. Trên thực tế, phân bố hình học là phép thử Bernoulli cho đến lần thành công đầu tiên. Ví dụ
. Ví dụ về các biến ngẫu nhiên có phân bố hình học có thể là: số lần bắn trước khi phát bắn trúng mục tiêu đầu tiên; số lần kiểm tra thiết bị cho đến lần thất bại đầu tiên; số lần tung đồng xu cho đến khi mặt ngửa đầu tiên xuất hiện, v.v. Kỳ vọng toán học và phương sai của một biến ngẫu nhiên tuân theo phân bố hình học lần lượt bằng $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right )/p^ $2. Ví dụ
. Trên đường di chuyển của cá đến nơi sinh sản có một ổ khóa $4$. Xác suất để cá lọt qua mỗi ổ khóa là $p=3/5$. Xây dựng một chuỗi phân phối của biến ngẫu nhiên $X$ - số lượng ổ khóa mà con cá đã đi qua trước khi bị mắc kẹt lần đầu tiên tại ổ khóa. Tìm $M\left(X\right),\ D\left(X\right),\ \sigma \left(X\right)$. Gọi biến ngẫu nhiên $X$ là số ổ khóa mà con cá đã vượt qua trước lần bắt đầu tiên ở ổ khóa. Một biến ngẫu nhiên như vậy tuân theo quy luật phân bố xác suất hình học. Các giá trị mà biến ngẫu nhiên $X có thể nhận:$ 1, 2, 3, 4. Xác suất của các giá trị này được tính bằng công thức: $P\left(X=k\right)=pq^(k -1)$, trong đó: $ p=2/5$ - xác suất cá bị giữ qua ổ khóa, $q=1-p=3/5$ - xác suất cá đi qua ổ khóa, $k=1,\ 2,\ 3,\ 4$. $P\left(X=1\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^0=((2)\ trên (5))=0,4;$ $P\left(X=2\right)=((2)\over (5))\cdot ((3)\over (5))=((6)\over (25))=0,24; $ $P\left(X=3\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^2=((2)\ trên (5))\cdot ((9)\trên (25))=((18)\trên (125))=0.144;$ $P\left(X=4\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^3+(\left(( (3)\over (5))\right))^4=((27)\over (125))=0.216.$ $\begin(array)(|c|c|) Gia trị được ki vọng: $M\left(X\right)=\sum^n_(i=1)(x_ip_i)=1\cdot 0.4+2\cdot 0.24+3\cdot 0.144+4\cdot 0.216=2.176.$ Phân tán: $D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2=)0.4\cdot (\ left( 1-2,176\right))^2+0,24\cdot (\left(2-2,176\right))^2+0,144\cdot (\left(3-2,176\right))^2+$ $+\0,216\cdot (\left(4-2,176\right))^2\khoảng 1,377.$ Độ lệch chuẩn: $\sigma \left(X\right)=\sqrt(D\left(X\right))=\sqrt(1.377)\khoảng 1.173.$ Nếu các đối tượng $N$, trong đó các đối tượng $m$ có một thuộc tính nhất định. Các đối tượng $n$ được truy xuất ngẫu nhiên mà không quay trở lại, trong đó có các đối tượng $k$ có thuộc tính nhất định. Phân bố siêu hình học giúp ước tính xác suất để các đối tượng $k$ chính xác trong mẫu có một thuộc tính nhất định. Đặt biến ngẫu nhiên $X$ là số đối tượng trong mẫu có thuộc tính nhất định. Khi đó xác suất của các giá trị của biến ngẫu nhiên $X$: $P\left(X=k\right)=((C^k_mC^(n-k)_(N-m))\over (C^n_N))$ Bình luận. Hàm thống kê HYPERGEOMET của trình hướng dẫn hàm $f_x$ trong Excel cho phép bạn xác định xác suất thành công của một số lần kiểm tra nhất định. $f_x\to$ thống kê$\đến$ siêu hình học$\đến$ ĐƯỢC RỒI. Một hộp thoại sẽ xuất hiện mà bạn cần điền vào. Trong cột Số_số_thành_công_trong_mẫu chỉ ra giá trị $k$. cỡ mẫu bằng $n$. Trong cột Số_số_thành công_cùng nhau chỉ ra giá trị $m$. quy mô dân số bằng $N$. Kỳ vọng toán học và phương sai của một biến ngẫu nhiên rời rạc $X$, tuân theo định luật phân phối hình học, tương ứng bằng $M\left(X\right)=nm/N$, $D\left(X\right)= ((nm\left(1 -((m)\over (N))\right)\left(1-((n)\over (N))\right))\over (N-1))$. Ví dụ
. Bộ phận tín dụng của ngân hàng tuyển dụng 5 chuyên gia có trình độ học vấn cao hơn về tài chính và 3 chuyên gia có trình độ cao hơn về pháp luật. Ban lãnh đạo ngân hàng quyết định cử 3 chuyên gia đi nâng cao trình độ, lựa chọn theo thứ tự ngẫu nhiên. a) Thực hiện phân bổ số lượng chuyên gia có trình độ học vấn cao hơn về tài chính có thể được cử đi nâng cao tay nghề; b) Tìm các đặc tính số của phân bố này. Gọi biến ngẫu nhiên $X$ là số chuyên gia có trình độ học vấn tài chính cao hơn trong số ba chuyên gia được chọn. Các giá trị mà $X có thể nhận: 0,\ 1,\ 2,\ 3$. Biến ngẫu nhiên $X$ này được phân phối theo phân phối siêu hình học với các tham số sau: $N=8$ - quy mô dân số, $m=5$ - số lần thành công trong dân số, $n=3$ - cỡ mẫu, $ k=0,\ 1, \2,\3$ - số lần thành công trong mẫu. Khi đó, xác suất $P\left(X=k\right)$ có thể được tính bằng công thức: $P(X=k)=(C_(m)^(k) \cdot C_(N-m)^(n-k) \ trên C_(N)^(n) ) $. Chúng ta có: $P\left(X=0\right)=((C^0_5\cdot C^3_3)\over (C^3_8))=((1)\over (56))\khoảng 0,018;$ $P\left(X=1\right)=((C^1_5\cdot C^2_3)\over (C^3_8))=((15)\over (56))\khoảng 0,268;$ $P\left(X=2\right)=((C^2_5\cdot C^1_3)\over (C^3_8))=((15)\over (28))\khoảng 0,536;$ $P\left(X=3\right)=((C^3_5\cdot C^0_3)\over (C^3_8))=((5)\over (28))\khoảng 0,179.$ Khi đó chuỗi phân phối của biến ngẫu nhiên $X$: $\begin(array)(|c|c|) Chúng ta hãy tính các đặc tính số của biến ngẫu nhiên $X$ bằng cách sử dụng các công thức chung của phân bố siêu hình học. $M\left(X\right)=((nm)\over (N))=((3\cdot 5)\over (8))=((15)\over (8))=1,875.$ $D\left(X\right)=((nm\left(1-((m)\over (N))\right)\left(1-((n)\over (N))\right)) \over (N-1))=((3\cdot 5\cdot \left(1-((5)\over (8))\right)\cdot \left(1-((3)\over (8 ))\right))\over (8-1))=((225)\over (448))\khoảng 0,502.$ $\sigma \left(X\right)=\sqrt(D\left(X\right))=\sqrt(0,502)\khoảng 0,7085.$ X; nghĩa F(5); xác suất mà biến ngẫu nhiên X sẽ lấy các giá trị từ phân khúc. Xây dựng một đa giác phân phối. Đặt luật phân phối của một biến ngẫu nhiên X dưới dạng một cái bàn. Tìm hàm phân phối của một biến ngẫu nhiên X. Xây dựng đồ thị hàm số và . Tính toán kỳ vọng, phương sai, mode và trung vị của một biến ngẫu nhiên X. Mẫu A: 6 9 7 6 4 4 Mẫu B: 55 72 54 53 64 53 59 48 42 46 50 63 71 56 54 59 54 44 50 43 51 52 60 43 50 70 68 59 53 58 62 49 59 51 52 47 57 71 60 46 55 58 72 47 60 65 63 63 58 56 55 51 64 54 54 63 56 44 73 41 68 54 48 52 52 50 55 49 71 67 58 46 50 51 72 63 64 48 47 55 Phương án 17. Tính toán kỳ vọng và phương sai toán học của nó. Tìm hàm phân phối của một biến ngẫu nhiên X. Xây dựng đồ thị hàm số và . Tính kỳ vọng toán học, phương sai, mode và trung vị của biến ngẫu nhiên X. · mẫu trung bình; · phương sai mẫu; Chế độ và trung vị; Mẫu A: 0 0 2 2 1 4 · mẫu trung bình; · phương sai mẫu; độ lệch mẫu chuẩn; · Chế độ và trung vị; Mẫu B: 166 154 168 169 178 182 169 159 161 150 149 173 173 156 164 169 157 148 169 149 157 171 154 152 164 157 177 155 167 169 175 166 167 150 156 162 170 167 161 158 168 164 170 172 173 157 157 162 156 150 154 163 143 170 170 168 151 174 155 163 166 173 162 182 166 163 170 173 159 149 172 176 Phương án 18. Tính toán kỳ vọng và phương sai toán học của nó. Tìm hàm phân phối của biến ngẫu nhiên X. Vẽ đồ thị của hàm số và . Tính toán kỳ vọng, phương sai, mode và trung vị của một biến ngẫu nhiên X. · mẫu trung bình; · phương sai mẫu; độ lệch mẫu chuẩn; · Chế độ và trung vị; Mẫu A: 4 7 6 3 3 4 · mẫu trung bình; · phương sai mẫu; độ lệch mẫu chuẩn; · Chế độ và trung vị; Mẫu B: 152 161 141 155 171 160 150 157 154 164 138 172 155 152 177 160 168 157 115 128 154 149 150 141 172 154 144 177 151 128 150 147 143 164 156 145 156 170 171 142 148 153 152 170 142 153 162 128 150 146 155 154 163 142 171 138 128 158 140 160 144 150 162 151 163 157 177 127 141 160 160 142 159 147 142 122 155 144 170 177 Phương án 19. 1. Có 16 phụ nữ và 5 nam giới làm việc tại công trường. 3 người được chọn ngẫu nhiên dựa trên số lượng nhân sự của họ. Tìm xác suất để tất cả những người được chọn đều là nam giới. 2. Tung bốn đồng xu. Tìm xác suất để chỉ có hai đồng xu có “huy hiệu”. 3. Từ “TÂM LÝ” được tạo thành từ các tấm thẻ, mỗi tấm thẻ có một chữ cái viết trên đó. Các lá bài được xáo trộn và lấy ra lần lượt mà không cần quay lại. Tìm xác suất để các chữ cái được lấy ra tạo thành một từ: a) TÂM LÝ; b) NHÂN VIÊN. 4. Chiếc bình chứa 6 quả bóng đen và 7 quả bóng trắng. 5 quả bóng được rút ngẫu nhiên. Tìm xác suất để trong số đó có: Một. 3 quả bóng trắng; b. ít hơn 3 quả bóng màu trắng; c. ít nhất một quả bóng màu trắng. 5. Xác suất xảy ra sự kiện MỘT trong một lần thử là bằng 0,5. Tìm xác suất của các biến cố sau: Một. sự kiện MỘT xuất hiện 3 lần trong chuỗi 5 thử nghiệm độc lập; b. sự kiện MỘT sẽ xuất hiện ít nhất 30 và không quá 40 lần trong chuỗi 50 lần thử. 6. Có 100 máy có cùng công suất, hoạt động độc lập với nhau trong cùng một chế độ, trong đó bộ dẫn động của chúng được bật trong 0,8 giờ làm việc. Xác suất để tại một thời điểm bất kỳ có từ 70 đến 86 máy được bật là bao nhiêu? 7. Chiếc bình thứ nhất chứa 4 quả bóng trắng và 7 quả bóng đen, chiếc bình thứ hai chứa 8 quả bóng trắng và 3 quả bóng đen. Lấy ngẫu nhiên 4 quả bóng từ thùng thứ nhất và 1 quả bóng từ thùng thứ hai. Tìm xác suất để trong số bi rút ra chỉ có 4 bi đen. 8. Showroom bán xe hàng ngày tiếp nhận xe của 3 hãng với số lượng: “Moskvich” – 40%; "Được" - 20%; "Volga" - 40% tổng số ô tô nhập khẩu. Trong số xe Moskvich, 0,5% có thiết bị chống trộm, Oka – 0,01%, Volga – 0,1%. Tìm xác suất để chiếc xe được đem đi kiểm tra có thiết bị chống trộm. 9. Các số và được chọn ngẫu nhiên trên đoạn đó. Tìm xác suất để những số này thỏa mãn các bất đẳng thức. 10. Đưa ra định luật phân phối biến ngẫu nhiên X: Tìm hàm phân phối của một biến ngẫu nhiên X; nghĩa F(2); xác suất mà biến ngẫu nhiên X sẽ lấy các giá trị từ khoảng . Xây dựng một đa giác phân phối.
1.2.
p4=0,1; 0 tại x<-1,
https://pandia.ru/text/78/455/images/image038_17.gif" width="14" Height="86"> 0 cho x
,
Đường cong pháp tuyến đối xứng với đường thẳng x=m, có cực đại tại x=a, bằng .
,
, hoặc:
. Xác suất để có đúng 3 hộp mực bị lỗi trong cả lô là bao nhiêu?
, Ở đâu .
.
.
.
.
Vì 
, Cái đó
.
.
– Hàm Laplace.
Các phép toán trên xác suất rời rạc
Chức năng phân phối
1. Luật phân phối nhị thức.
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end(mảng)$
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi) & 0,25 & 0,5 & 0,25 \\
\hline
\end(mảng)$2. Định luật phân bố Poisson.
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & ... & k \\
\hline
P_i & 0,368; & 0,368 & 0,184 & 0,061 & 0,015 & 0,003 & 0,001 & ... & (((\lambda )^k)\over (k}\cdot e^{-\lambda } \\!}
\hline
\end(mảng)$3. Định luật phân bố hình học.
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end(mảng)$4. Định luật phân bố siêu hình học.
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end(mảng)$ X
–28
–20
–12
–4
P
0,22
0,44
0,17
0,1
0,07
X
P
0,1
0,2
0,3
0,4
Xem “Quân đoàn (số)” là gì trong các từ điển khác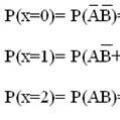
Ví dụ giải bài toán về chủ đề “Biến ngẫu nhiên”
Tôi đang đọc bài thơ “Sương giá, mũi đỏ” của Nekrasov