Kako se vektori sabiraju i oduzimaju. Svojstva množenja vektora brojem

Za ispravan prikaz zakona prirode u fizici, potrebni su odgovarajući matematički alati.

U geometriji i fizici postoje veličine koje se karakterišu i numerička vrijednost, i smjer.

Preporučljivo ih je predstaviti kao usmjerene segmente ili vektori.

Takve vrijednosti imaju početak (predstavljen tačkom) i kraj, označen strelicom. Dužina segmenta se naziva (dužina).

brzina;
ubrzanje;
puls;
snaga;
momenat;
snaga;
kretanje;
jačina polja itd.

Koordinate ravnine

Definirajmo segment na ravni usmjerenoj od tačke A (x1, y1) do tačke B (x2, y2). Njegove koordinate a (a1, a2) su brojevi a1=x2-x1, a2=y2-y1.

Modul se izračunava pomoću Pitagorine teoreme:

Nulti vektor ima početak i kraj. Koordinate i dužina su 0.

Zbir vektora

Postoji nekoliko pravila za izračunavanje iznosa

pravilo trougla;
pravilo poligona;
pravilo paralelograma.

Pravilo sabiranja vektora može se objasniti korištenjem zadataka iz dinamike i mehanike. Razmotrimo sabiranje vektora prema pravilu trokuta na primjeru sila koje djeluju na tačkasto tijelo i uzastopnih pomjeranja tijela u prostoru.

Pretpostavimo da se tijelo prvo kretalo od tačke A do tačke B, a zatim od tačke B do tačke C. Konačni pomak je segment usmjeren od početne tačke A do krajnje tačke C.

Rezultat dva pomaka ili njihov zbir s = s1+ s2. Takav metod se zove pravilo trougla.

Strelice se redaju u lancu jedna za drugom, ako je potrebno, vršeći paralelni prijenos. Ukupan segment zatvara niz. Njegov početak poklapa se s početkom prvog, kraj - s krajem posljednjeg. U stranim udžbenicima ovu metodu pozvao "rep uz glavu".

Koordinate rezultata c = a + b jednake su zbiru odgovarajućih koordinata članova c (a1+ b1, a2+ b2).

Zbir paralelnih (kolinearnih) vektora je također određen pravilom trougla.

Ako su dva početna segmenta okomita jedan na drugi, onda je rezultat njihovog zbrajanja hipotenuza od pravougaonog trougla. Dužina sume se izračunava pomoću Pitagorine teoreme.

Primjeri:

Brzina tijela bačenog vodoravno okomito ubrzanje slobodan pad.
Sa uniformom rotaciono kretanje linijska brzina tijelo je okomito na centripetalno ubrzanje.

Dodavanje tri ili više vektora proizvoditi prema pravilo poligona, "rep uz glavu"

Pretpostavimo da su sile F1 i F2 primijenjene na tijelo tačke.

Iskustvo dokazuje da je kombinovani učinak ovih sila ekvivalentan djelovanju jedne sile usmjerene dijagonalno duž paralelograma izgrađenog na njima. Ova rezultujuća sila jednaka je njihovom zbroju F = F1 + F 2. Gornja metoda sabiranja naziva se pravilo paralelograma.

Dužina se u ovom slučaju izračunava po formuli

Gdje je θ ugao između stranica.

Pravila trougla i paralelograma su zamjenjiva. U fizici se češće koristi pravilo paralelograma, jer se usmjerene količine sila, brzina i ubrzanja obično primjenjuju na tijelo u jednoj tački. U 3D koordinatnom sistemu primjenjuje se pravilo kutije.

Algebarski elementi

Zbrajanje je binarna operacija: možete dodati samo par po jedan.
komutativnost: zbir iz permutacije članova ne mijenja a + b = b + a. Ovo je jasno iz pravila paralelograma: dijagonala je uvijek ista.
Asocijativnost: zbir proizvoljnog broja vektora ne zavisi od redosleda njihovog sabiranja (a + b) + c = a + (b + c).
Zbrajanje sa nultim vektorom ne mijenja smjer ili dužinu: a +0= a .
Za svaki vektor postoji suprotno. Njihov zbir je jednak nuli a +(-a)=0, a dužine su iste.

Oduzimanje usmjerenog segmenta je ekvivalentno dodavanju suprotnog. Koordinate su jednake razlici odgovarajućih koordinata. dužina je:

Za oduzimanje možete koristiti modificirano pravilo trokuta.

Množenje skalarom

Rezultat množenja skalarom je vektor.

Koordinate proizvoda se dobijaju množenjem skalarom odgovarajućih koordinata izvora.

skalar - numerička vrijednost sa znakom plus ili minus, veći ili manji od jedan.

Primjeri skalarima u fizici:

težina;
vrijeme;
punjenje;
dužina;
kvadrat;
volumen;
gustina;
temperatura;
energije.

Primjeri:

Pomak jednoliko pokretnog tijela jednak je proizvodu vremena i brzine s = vt.
Moć kretanja tijela je masa pomnožena sa brzinom p = mv.
Njutnov drugi zakon. Proizvod tjelesne mase i ubrzanja je u prilogu rezultantna sila ma=F.
Sila koja djeluje na nabijenu česticu u električnom polju proporcionalna je naboju F = qE.

Skalarni proizvod usmjerenih segmenata a i b jednak je proizvodu modula i kosinusa ugla između njih. Skalarni proizvod međusobno okomitih segmenata jednak je nuli.

Primjer:

Posao jeste skalarni proizvod sile i pomaci A = Fs .

X i y zove vektor z takav da z+y=x.

Opcija 1. Početne tačke svih vektora poklapaju se sa ishodištem.

Konstruirajmo razliku vektora i .

Zacrtati razliku vektora z=x-y, morate dodati vektor x sa suprotnim od y vektor y". Opposite Vector y" izgrađen je jednostavno:

Vector y" je suprotan vektoru y, jer y+y"= 0, gdje je 0 nulti vektor odgovarajuće veličine. Zatim se vrši sabiranje vektora x i y":

Iz izraza (1) se može vidjeti da je za konstruiranje razlike vektora dovoljno izračunati razlike odgovarajućih koordinata vektora x i y.

Rice. jedan

Na sl. 1 u dvodimenzionalnom prostoru predstavlja razliku vektora x=(10,3) i y=(2,4).

Compute z=x-y=(10-3,3-4)=(7,-1). Uporedimo dobijeni rezultat sa geometrijskom interpretacijom. Zaista, nakon konstruisanja vektora y" i paralelno kretanje početne tačke vektora y" do krajnje tačke vektora x, dobijamo vektor y"", i nakon dodavanja vektora x i y"", dobijamo vektor z.

Opcija 2. Početne tačke vektora su proizvoljne.

Rice. 2

Na sl. 2 u dvodimenzionalnom prostoru je razlika vektora x=AB i y=CD, gdje A(1,0), B(11,3), C(1,2), D(3.6). Za izračunavanje vektora z=x-y, konstruisan suprotno od vektora y vektor y":

Zatim morate dodati vektore x i y". Vector y" kreće se paralelno tako da tačka C" poklopio sa tačkom B. Da biste to učinili, izračunavaju se razlike u koordinatama tačaka B i OD.

ov, prvo morate razumjeti takav koncept kao što je odlaganje vektora iz date tačke.

Definicija 1

Ako je tačka $A$ početak nekog vektora $\overrightarrow(a)$, tada se kaže da je vektor $\overrightarrow(a)$ odvojen od tačke $A$ (slika 1).

Slika 1. $\overrightarrow(a)$ iscrtana iz tačke $A$

Uvodimo sljedeću teoremu:

Teorema 1

Iz bilo koje tačke $K$ može se nacrtati vektor $\overrightarrow(a)$ i to samo jedan.

Dokaz.

postojanje: Ovdje treba razmotriti dva slučaja:

Vektor $\overrightarrow(a)$ je nula.

U ovom slučaju, očigledno je da je željeni vektor vektor $\overrightarrow(KK)$.

Vektor $\overrightarrow(a)$ je različit od nule.

Neka tačka $A$ označava početak vektora $\overrightarrow(a)$, a tačka $B$ kraj vektora $\overrightarrow(a)$. Povučemo pravu $b$ kroz tačku $K$ paralelno sa vektorom$\overrightarrow(a)$. Nacrtajmo segmente $\left|KL\right|=|AB|$ i $\left|KM\right|=|AB|$ na ovoj pravoj liniji. Razmotrimo vektore $\overrightarrow(KL)$ i $\overrightarrow(KM)$. Od ova dva vektora, željeni će biti onaj koji će biti ko-usmjeren sa $\overrightarrow(a)$ vektorom (slika 2)

Slika 2. Ilustracija teoreme 1

Jedinstvenost: jedinstvenost odmah proizilazi iz konstrukcije izvedene u pododjeljku "postojanje".

Teorema je dokazana.

Oduzimanje vektora. Pravilo jedno

Neka nam budu dati vektori $\overrightarrow(a)$ i $\overrightarrow(b)$.

Definicija 2

Razlika dva vektora $\overrightarrow(a)$ i $\overrightarrow(b)$ je vektor $\overrightarrow(c)$ koji, kada se doda vektoru $\overrightarrow(b)$, daje vektor $\ overrightarrow(a)$ , tj

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

Oznaka:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

Razmotrićemo konstrukciju razlike dva vektora koristeći problem.

Primjer 1

Neka su dati vektori $\overrightarrow(a)$ i $\overrightarrow(b)$. Konstruirajte vektor $\overrightarrow(a)-\overrightarrow(b)$.

Rješenje.

Konstruirajmo proizvoljnu tačku $O$ i iz nje nacrtajmo vektore $\overrightarrow(OA)=\overrightarrow(a)$ i $\overrightarrow(OB)=\overrightarrow(b)$. Povezujući tačku $B$ sa tačkom $A$, dobijamo vektor $\overrightarrow(BA)$ (slika 3).

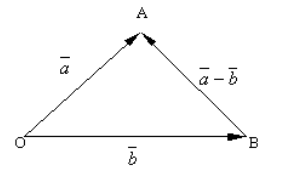
Slika 3. Razlika dva vektora

Prema pravilu trougla za konstruisanje zbira dva vektora, vidimo da

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

Iz definicije 2 dobijamo to

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

odgovor:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

Iz ovog problema dobijamo sledeće pravilo za pronalaženje razlike dva vektora. Da biste pronašli razliku $\overrightarrow(a)-\overrightarrow(b)$ koja vam je potrebna proizvoljna tačka$O$ ostavi po strani vektore $\overrightarrow(OA)=\overrightarrow(a)$ i $\overrightarrow(OB)=\overrightarrow(b)$ i spoji kraj drugog vektora sa krajem prvog vektora.

Oduzimanje vektora. Pravilo dva

Prisjetimo se sljedećeg pojma koji nam je potreban.

Definicija 3

Vektor $\overrightarrow(a_1)$ naziva se proizvoljnim za vektor $\overrightarrow(a)$ ako su ovi vektori suprotno usmjereni i imaju istu dužinu.

Oznaka: Vektor $(-\overrightarrow(a))$ je suprotan vektoru $\overrightarrow(a)$.

Da bismo uveli drugo pravilo za razliku dva vektora, prvo moramo uvesti i dokazati sljedeću teoremu.

Teorema 2

Za bilo koja dva vektora $\overrightarrow(a)$ i $\overrightarrow(b)$ vrijedi sljedeća jednakost:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

Dokaz.

Prema definiciji 2, imamo

Dodajte na oba dijela vektor $\left(-\overrightarrow(b)\right)$, dobijamo

Pošto su vektori $\overrightarrow(b)$ i $\left(-\overrightarrow(b)\right)$ suprotni, onda je $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\ strelica preko desno (0)$. Imamo

Teorema je dokazana.

Iz ove teoreme dobijamo sljedeće pravilo za razliku dva vektora: Da bismo pronašli razliku $\overrightarrow(a)-\overrightarrow(b)$, moramo odgoditi vektor $\overrightarrow(OA)=\overrightarrow( a)$ iz proizvoljne tačke $O$, zatim, iz dobijene tačke $A$, odgoditi vektor $\overrightarrow(AB)=-\overrightarrow(b)$ i povezati početak prvog vektora sa krajem drugi vektor.

Primjer problema o konceptu razlike vektora

Primjer 2

Neka je $ADCD$ paralelogram čije se dijagonale sijeku u $O$. $\overrightarrow(AB)=\overrightarrow(a)$, $\overrightarrow(AD)=\overrightarrow(b)$ (slika 4). Izrazite sljedeće vektore u terminima $\overrightarrow(a)$ i $\overrightarrow(b)$:

a) $\overrightarrow(DC)+\overrightarrow(CB)$

b) $\overrightarrow(BO)-\overrightarrow(OC)$

Slika 4. Paralelogram

Rješenje.

a) Sabiramo prema pravilu trougla, dobijamo

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

Iz prvog pravila za razliku dva vektora dobijamo

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

b) Pošto je $\overrightarrow(OC)=\overrightarrow(AO)$, dobijamo

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

Prema teoremi 2, imamo

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

Koristeći pravilo trougla, konačno imamo

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

ov, prvo morate razumjeti takav koncept kao što je odlaganje vektora iz date tačke.

Definicija 1

Ako je tačka $A$ početak nekog vektora $\overrightarrow(a)$, tada se kaže da je vektor $\overrightarrow(a)$ odvojen od tačke $A$ (slika 1).

Slika 1. $\overrightarrow(a)$ iscrtana iz tačke $A$

Uvodimo sljedeću teoremu:

Teorema 1

Iz bilo koje tačke $K$ može se nacrtati vektor $\overrightarrow(a)$ i to samo jedan.

Dokaz.

postojanje: Ovdje treba razmotriti dva slučaja:

Vektor $\overrightarrow(a)$ je nula.

U ovom slučaju, očigledno je da je željeni vektor vektor $\overrightarrow(KK)$.

Vektor $\overrightarrow(a)$ je različit od nule.

Neka tačka $A$ označava početak vektora $\overrightarrow(a)$, a tačka $B$ kraj vektora $\overrightarrow(a)$. Nacrtajmo pravu $b$ paralelnu vektoru $\overrightarrow(a)$ kroz tačku $K$. Nacrtajmo segmente $\left|KL\right|=|AB|$ i $\left|KM\right|=|AB|$ na ovoj pravoj liniji. Razmotrimo vektore $\overrightarrow(KL)$ i $\overrightarrow(KM)$. Od ova dva vektora, željeni će biti onaj koji će biti ko-usmjeren sa $\overrightarrow(a)$ vektorom (slika 2)

Slika 2. Ilustracija teoreme 1

Jedinstvenost: jedinstvenost odmah proizilazi iz konstrukcije izvedene u pododjeljku "postojanje".

Teorema je dokazana.

Oduzimanje vektora. Pravilo jedno

Neka nam budu dati vektori $\overrightarrow(a)$ i $\overrightarrow(b)$.

Definicija 2

Razlika dva vektora $\overrightarrow(a)$ i $\overrightarrow(b)$ je vektor $\overrightarrow(c)$ koji, kada se doda vektoru $\overrightarrow(b)$, daje vektor $\ overrightarrow(a)$ , tj

\[\overrightarrow(b)+\overrightarrow(c)=\overrightarrow(a)\]

Oznaka:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(c)$.

Razmotrićemo konstrukciju razlike dva vektora koristeći problem.

Primjer 1

Neka su dati vektori $\overrightarrow(a)$ i $\overrightarrow(b)$. Konstruirajte vektor $\overrightarrow(a)-\overrightarrow(b)$.

Rješenje.

Slika 3. Razlika dva vektora

Prema pravilu trougla za konstruisanje zbira dva vektora, vidimo da

\[\overrightarrow(OB)+\overrightarrow(BA)=\overrightarrow(OA)\]

\[\overrightarrow(b)+\overrightarrow(BA)=\overrightarrow(a)\]

Iz definicije 2 dobijamo to

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)\]

odgovor:$\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(BA)$.

Iz ovog problema dobijamo sledeće pravilo za pronalaženje razlike dva vektora. Da bismo pronašli razliku $\overrightarrow(a)-\overrightarrow(b)$, iz proizvoljne tačke $O$ moramo odvojiti vektore $\overrightarrow(OA)=\overrightarrow(a)$ i $\overrightarrow( OB)=\overrightarrow(b)$ i povežite kraj drugog vektora sa krajem prvog vektora.

Oduzimanje vektora. Pravilo dva

Prisjetimo se sljedećeg pojma koji nam je potreban.

Definicija 3

Vektor $\overrightarrow(a_1)$ naziva se proizvoljnim za vektor $\overrightarrow(a)$ ako su ovi vektori suprotno usmjereni i imaju istu dužinu.

Oznaka: Vektor $(-\overrightarrow(a))$ je suprotan vektoru $\overrightarrow(a)$.

Da bismo uveli drugo pravilo za razliku dva vektora, prvo moramo uvesti i dokazati sljedeću teoremu.

Teorema 2

Za bilo koja dva vektora $\overrightarrow(a)$ i $\overrightarrow(b)$ vrijedi sljedeća jednakost:

\[\overrightarrow(a)-\overrightarrow(b)=\overrightarrow(a)+(-\overrightarrow(b))\]

Dokaz.

Prema definiciji 2, imamo

Dodajte na oba dijela vektor $\left(-\overrightarrow(b)\right)$, dobijamo

Pošto su vektori $\overrightarrow(b)$ i $\left(-\overrightarrow(b)\right)$ suprotni, onda je $\overrightarrow(b)+\left(-\overrightarrow(b)\right)=\ strelica preko desno (0)$. Imamo

Teorema je dokazana.

Primjer problema o konceptu razlike vektora

Primjer 2

a) $\overrightarrow(DC)+\overrightarrow(CB)$

b) $\overrightarrow(BO)-\overrightarrow(OC)$

Slika 4. Paralelogram

Rješenje.

a) Sabiramo prema pravilu trougla, dobijamo

\[\overrightarrow(DC)+\overrightarrow(CB)=\overrightarrow(DB)\]

Iz prvog pravila za razliku dva vektora dobijamo

\[\overrightarrow(DB)=\overrightarrow(a)-\overrightarrow(b)\]

b) Pošto je $\overrightarrow(OC)=\overrightarrow(AO)$, dobijamo

\[\overrightarrow(BO)-\overrightarrow(OC)=\overrightarrow(BO)-\overrightarrow(AO)\]

Prema teoremi 2, imamo

\[\overrightarrow(BO)-\overrightarrow(AO)=\overrightarrow(BO)+\left(-\overrightarrow(AO)\right)=\overrightarrow(BO)+\overrightarrow(OA)\]

Koristeći pravilo trougla, konačno imamo

\[\overrightarrow(BO)+\overrightarrow(OA)=\overrightarrow(BA)=-\overrightarrow(AB)=-\overrightarrow(a)\]

Kako se vektori dodaju nije uvijek jasno učenicima. Djeca nemaju pojma šta je iza njih. Samo morate zapamtiti pravila, a ne razmišljati o suštini. Dakle, upravo o principima sabiranja i oduzimanja vektorskih veličina potrebno je dosta znanja.

Dodavanje dva ili više vektora uvijek rezultira još jednim. Štoviše, uvijek će biti isti, bez obzira na prijem na njegovoj lokaciji.

Najčešće u školski kurs geometrija razmatra dodavanje dva vektora. Može se izvesti prema pravilu trougla ili paralelograma. Ovi crteži izgledaju drugačije, ali rezultat akcije je isti.

Kako se vrši sabiranje prema pravilu trougla?

Koristi se kada vektori nisu kolinearni. To jest, ne leže na istoj liniji ili paraleli.

U ovom slučaju, prvi vektor mora biti odgođen iz neke proizvoljne tačke. Od njegovog kraja potrebno je povući paralelu i jednaku drugom. Rezultat će biti vektor koji počinje od početka prvog i završava se na kraju drugog. Crtež izgleda kao trokut. Otuda i naziv pravila.

Ako su vektori kolinearni, onda se ovo pravilo također može primijeniti. Samo će se crtež nalaziti duž jedne linije.

Kako se izvodi sabiranje paralelograma?

Još jednom? odnosi se samo na kolinearni vektori. Izgradnja se izvodi po drugačijem principu. Iako je početak isti. Moramo odgoditi prvi vektor. I od svog početka - drugi. Na osnovu njih dovršite paralelogram i nacrtajte dijagonalu od početka oba vektora. Ona će biti rezultat. Ovako se vektori sabiraju prema pravilu paralelograma.

Do sada su bila dva. Ali šta ako ih ima 3 ili 10? Koristite sljedeći trik.

Kako i kada se primjenjuje pravilo poligona?

Ako trebate izvršiti sabiranje vektora, čiji je broj veći od dva, ne treba se bojati. Dovoljno je da ih sve redom odložite i povežete početak lanca s njegovim krajem. Ovaj vektor će biti željeni zbir.

Koja svojstva vrijede za operacije na vektorima?

O nultom vektoru. Koja tvrdi da kada se tome doda, dobije se original.

O suprotnom vektoru. Odnosno, o onom koji ima suprotan smjer i jednaku vrijednost u apsolutnoj vrijednosti. Njihov zbir će biti nula.

O komutativnosti sabiranja.Šta se od tada zna osnovna škola. Promjena mjesta pojmova ne mijenja rezultat. Drugim riječima, nije važno koji vektor prvi odložiti. Odgovor će i dalje biti tačan i jedinstven.

O asocijativnosti sabiranja. Ovaj zakon vam omogućava da u parovima dodate sve vektore iz trojke i dodate im treći. Ako ovo zapišemo pomoću simbola, dobićemo sljedeće:

prvi + (drugi + treći) = drugi + (prvi + treći) = treći + (prvi + drugi).

Šta se zna o razlici vektora?

Ne postoji posebna operacija oduzimanja. To je zbog činjenice da je to, u stvari, dodatak. Samo drugom od njih dat je suprotan smjer. I onda se sve radi kao da se razmatra dodavanje vektora. Stoga praktično ne govore o svojoj različitosti.

Da bi se pojednostavio rad sa njihovim oduzimanjem, modifikovano je pravilo trougla. Sada (pri oduzimanju) drugi vektor mora biti odložen od početka prvog. Odgovor će biti onaj koji povezuje krajnju tačku minuenda sa njom. Iako je moguće odgoditi kako je ranije opisano, jednostavno promjenom smjera sekunde.

Kako pronaći zbir i razliku vektora u koordinatama?

U zadatku su date koordinate vektora i potrebno je saznati njihove vrijednosti za konačni. U tom slučaju konstrukcije nije potrebno izvoditi. To jest, možete koristiti jednostavne formule koje opisuju pravilo za dodavanje vektora. izgledaju ovako:

a(x, y, z) + b(k, l, m) = c(x+k, y+l, z+m);

a (x, y, z) -in (k, l, m) \u003d c (x-k, y-l, z-m).

Lako je vidjeti da koordinate samo treba dodati ili oduzeti, ovisno o konkretnom zadatku.

Prvi primjer sa rješenjem

Stanje. Dat je pravougaonik ABCD. Njegove stranice su 6 i 8 cm.Tačka presjeka dijagonala označena je slovom O. Potrebno je izračunati razliku između vektora AO i VO.

Rješenje. Prvo morate nacrtati ove vektore. Oni su usmjereni od vrhova pravokutnika do točke presjeka dijagonala.

Ako pažljivo pogledate crtež, možete vidjeti da su vektori već poravnati tako da je drugi od njih u kontaktu s krajem prvog. Samo je njegov pravac pogrešan. Mora početi od ove tačke. Ovo je ako se vektori saberu, au zadatku - oduzmu. Stani. Ova akcija znači da morate dodati suprotni vektor. Dakle, VO mora biti zamijenjen OB. I ispostavilo se da su dva vektora već formirala par stranica iz pravila trougla. Dakle, rezultat njihovog sabiranja, odnosno željene razlike je vektor AB.

I poklapa se sa stranom pravougaonika. Da biste snimili brojčani odgovor, trebat će vam sljedeće. Nacrtajte pravougaonik po dužini tako da najduža strana bude vodoravna. Numeracija vrhova počinje od donjeg lijevog i ide u smjeru suprotnom od kazaljke na satu. Tada će dužina vektora AB biti jednaka 8 cm.

Odgovori. Razlika između AO i VO je 8 cm.

Drugi primjer i njegovo detaljno rješenje

Stanje. Romb ABCD ima dijagonale 12 i 16 cm. Tačka njihovog preseka je označena slovom O. Izračunajte dužinu vektora formiranog razlikom vektora AO i BO.

Rješenje. Neka je oznaka vrhova romba ista kao u prethodnom zadatku. Slično rješenju prvog primjera, ispada da je željena razlika jednaka vektoru AB. A njegova dužina je nepoznata. Rješenje zadatka svelo se na izračunavanje jedne od stranica romba.

U tu svrhu morate uzeti u obzir trokut ABO. Pravougaona je jer se dijagonale romba seku pod uglom od 90 stepeni. A njegove noge su jednake polovini dijagonala. To jest, 6 i 8 cm.Tražena stranica u zadatku poklapa se sa hipotenuzom u ovom trouglu.

Da biste ga pronašli, potrebna vam je Pitagorina teorema. Kvadrat hipotenuze će biti jednak je zbiru brojevi 6 2 i 8 2 . Nakon kvadriranja dobivaju se vrijednosti: 36 i 64. Njihov zbir je 100. Iz toga slijedi da je hipotenuza 10 cm.

Odgovori. Razlika između vektora AO i VO je 10 cm.

Treći primjer sa detaljnim rješenjem

Stanje. Izračunajte razliku i zbir dva vektora. Njihove koordinate su poznate: prva ima 1 i 2, druga ima 4 i 8.

Rješenje. Da biste pronašli zbroj, trebate zbrojiti prvu i drugu koordinate u parovima. Rezultat će biti brojevi 5 i 10. Odgovor će biti vektor sa koordinatama (5; 10).

Za razliku, trebate oduzeti koordinate. Nakon izvođenja ove radnje dobiće se brojevi -3 i -6. Oni će biti koordinate željenog vektora.

Odgovori. Zbir vektora je (5; 10), njihova razlika je (-3; -6).

Četvrti primjer

Stanje. Dužina vektora AB je 6 cm, BC - 8 cm.Drugi se odvaja od kraja prvog pod uglom od 90 stepeni. Izračunajte: a) razliku između modula vektora BA i BC i modula razlike između BA i BC; b) zbir istih modula i modul zbira.

Rješenje: a) Dužine vektora su već date u zadatku. Stoga nije teško izračunati njihovu razliku. 6 - 8 = -2. Situacija s modulom razlike je nešto složenija. Prvo morate saznati koji će vektor biti rezultat oduzimanja. U tu svrhu treba izdvojiti vektor BA na koji se usmjerava Suprotna strana AB. Zatim nacrtajte vektor BC sa njegovog kraja, usmjeravajući ga u smjeru suprotnom od prvobitnog. Rezultat oduzimanja je CA vektor. Njegov modul se može izračunati pomoću Pitagorine teoreme. Jednostavni proračuni dovode do vrijednosti od 10 cm.

b) Zbir modula vektora je 14 cm.Da bismo pronašli drugi odgovor, potrebna je neka transformacija. Vektor BA je suprotan od datog - AB. Oba vektora su usmjerena iz iste tačke. U ovoj situaciji možete koristiti pravilo paralelograma. Rezultat sabiranja bit će dijagonala, i to ne samo paralelogram, već pravougaonik. Njegove dijagonale su jednake, što znači da je modul sume isti kao u prethodnom pasusu.

Odgovor: a) -2 i 10 cm; b) 14 i 10 cm.