Συνημίτονο της γωνίας μεταξύ δύο επιπέδων. Εύρεση της γωνίας μεταξύ των επιπέδων (διεδρική γωνία)

Στόχοι:

να αναπτύξουν την ικανότητα να εξετάζουν διαφορετικές προσεγγίσεις για την επίλυση προβλημάτων και να αναλύουν την «επίδραση» της χρήσης αυτών των μεθόδων επίλυσης·
να αναπτύξει την ικανότητα του μαθητή να επιλέγει μια μέθοδο για την επίλυση ενός προβλήματος σύμφωνα με τις μαθηματικές του προτιμήσεις, με βάση πιο στέρεες γνώσεις και αυτοπεποίθηση δεξιοτήτων·
να αναπτύξουν την ικανότητα να καταρτίζουν ένα σχέδιο διαδοχικών σταδίων για την επίτευξη αποτελεσμάτων.
να αναπτύξουν την ικανότητα να αιτιολογούν όλα τα βήματα και τους υπολογισμούς που έγιναν·
επανάληψη και ενίσχυση διάφορα θέματακαι ζητήματα στερεομετρίας και επιπεδομετρίας, τυπικές στερεομετρικές δομές που σχετίζονται με την επίλυση τρεχόντων προβλημάτων.
αναπτύξουν χωρική σκέψη.

ανάλυση διάφορες μεθόδουςεπίλυση προβλημάτων: μέθοδος διανύσματος συντεταγμένων, εφαρμογή του θεωρήματος συνημιτόνου, εφαρμογή του θεωρήματος των τριών καθέτων.
σύγκριση των πλεονεκτημάτων και των μειονεκτημάτων κάθε μεθόδου·
επανάληψη των ιδιοτήτων ενός κύβου, τριγωνικό πρίσμα, κανονικό εξάγωνο.
προετοιμασία για την επιτυχία της Ενιαίας Κρατικής Εξέτασης ·
ανάπτυξη ανεξαρτησίας στη λήψη αποφάσεων.

Περίγραμμα μαθήματος

Κόκκος αρωματικός ABCDA 1 B 1 C 1 D 1με άκρη 1 σημείο O – κέντρο προσώπου Α Β Γ Δ.

α) η γωνία μεταξύ των ευθειών Α 1 ΔΚαι Β.Ο.;

β) απόσταση από το σημείο σιστη μέση του τμήματος Α 1 Δ.

Λύση στο σημείο α).

Ας τοποθετήσουμε τον κύβο μας ορθογώνιο σύστημασυντεταγμένες όπως φαίνεται στο σχήμα, κορυφές Α1 (1; 0; 1), D (1; 1; 0), Β1 (0; 0; 1), Ο (½; ½; 0).

Διανύσματα κατεύθυνσης ευθειών Α 1 ΔΚαι B 1 O:

(0; 1; -1) και (½; ½; -1);

βρίσκουμε την επιθυμητή γωνία φ μεταξύ τους χρησιμοποιώντας τον τύπο:

cos∠φ = ,
από όπου ∠φ = 30°.

Μέθοδος 2. Χρησιμοποιούμε το θεώρημα συνημιτόνου.

1) Ας τραβήξουμε μια ευθεία γραμμή Β 1 Γπαράλληλα με τη γραμμή Α 1 Δ. Γωνία CB 1 Oθα είναι αυτό που ψάχνετε.

2) Από ορθογώνιο τρίγωνο BB 1 Oσύμφωνα με το Πυθαγόρειο θεώρημα:

3) Με το θεώρημα των συνημιτόνων από ένα τρίγωνο CB 1 Oυπολογίστε τη γωνία CB 1 O:

cos CB 1 O = , η απαιτούμενη γωνία είναι 30°.

Σχόλιο. Όταν λύνετε το πρόβλημα με τον 2ο τρόπο, μπορείτε να παρατηρήσετε ότι σύμφωνα με το θεώρημα των τριών καθέτων COB 1 = 90°, επομένως από ορθογώνιο Δ CB 1 OΕίναι επίσης εύκολο να υπολογιστεί το συνημίτονο της επιθυμητής γωνίας.

Λύση στο σημείο β).

1 τρόπος. Ας χρησιμοποιήσουμε τον τύπο για την απόσταση μεταξύ δύο σημείων

Αφήστε το θέμα μι- Μέσης Α 1 Δ, μετά τις συντεταγμένες Ε (1; 1/2; ½), Β (0; 0; 0).

BE = .

Μέθοδος 2. Σύμφωνα με το Πυθαγόρειο θεώρημα

Από ορθογώνιο Δ Η Β.Α.Ε.με απευθείας Η Β.Α.Ε.βρίσκουμε ΕΙΝΑΙ = .

Στα δεξιά τριγωνικό πρίσμα ABCA 1 B 1 C 1όλες οι άκρες είναι ίσες ένα. Βρείτε τη γωνία μεταξύ των γραμμών ΑΒΚαι Α 1 C.

1 τρόπος. Μέθοδος διανύσματος συντεταγμένων

Συντεταγμένες των κορυφών του πρίσματος σε ένα ορθογώνιο σύστημα όταν το πρίσμα είναι τοποθετημένο όπως στο σχήμα: Α (0; 0; 0), Β (α; 0), Α1 (0; 0; α), C (0; α; 0).

Διανύσματα κατεύθυνσης ευθειών Α 1 CΚαι ΑΒ:

(0; α; -α)Και (ένα; ; 0} ;

cos φ = ;

Μέθοδος 2. Χρησιμοποιούμε το θεώρημα συνημιτόνου

Θεωρούμε το Δ Α 1 Β 1 Γ, στο οποίο Α 1 Β 1 || ΑΒ. Εχουμε

cos φ = .

(Από τη συλλογή Ενιαίων Κρατικών Εξετάσεων-2012. Μαθηματικά: τυπικά επιλογές εξετάσεωνεπεξεργάστηκε από A.L. Semenova, I.V. Yashchenko)

Σε κανονικό εξαγωνικό πρίσμα ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, του οποίου όλες οι ακμές είναι ίσες με 1, βρείτε την απόσταση από το σημείο μισε ευθεία γραμμή Β 1 Γ 1.

1 τρόπος. Μέθοδος διανύσματος συντεταγμένων

1) Τοποθετήστε το πρίσμα σε ένα ορθογώνιο σύστημα συντεταγμένων, τοποθετώντας τους άξονες συντεταγμένων όπως φαίνεται στο σχήμα. SS 1, ΒΑΚαι SEείναι κάθετοι σε ζεύγη, ώστε να μπορείτε να κατευθύνετε τους άξονες συντεταγμένων κατά μήκος τους. Παίρνουμε τις συντεταγμένες:

C 1 (0; 0; 1), E (; 0; 0), B 1 (0;1;1).

2) Να βρείτε τις συντεταγμένες των διανυσμάτων κατεύθυνσης για τις ευθείες Από 1 έως 1Και Γ 1 Ε:

(0;1;0), (;0;-1).

3) Να βρείτε το συνημίτονο της μεταξύ τους γωνίας Από 1 έως 1Και Γ 1 Εχρησιμοποιώντας κλιμακωτό προϊόνφορείς και:

cos β = = 0 => β = 90° => C 1 E – η απαιτούμενη απόσταση.

4)C 1 E = = 2.

Συμπέρασμα: γνώση διαφορετικές προσεγγίσειςη επίλυση στερεομετρικών προβλημάτων σας επιτρέπει να επιλέξετε την προτιμώμενη μέθοδο για κάθε μαθητή, π.χ. Αυτό που ο μαθητής κατακτά με σιγουριά, βοηθά στην αποφυγή λαθών, οδηγεί στην επιτυχή επίλυση του προβλήματος και στη λήψη καλής βαθμολογίας στις εξετάσεις. Μέθοδος συντεταγμένωνέχει ένα πλεονέκτημα έναντι άλλων μεθόδων στο ότι απαιτεί λιγότερες στερεομετρικές σκέψεις και όραμα και βασίζεται στη χρήση τύπων που έχουν πολλές επιπεδομετρικές και αλγεβρικές αναλογίες που είναι πιο γνωστές στους μαθητές.

Η μορφή του μαθήματος είναι ένας συνδυασμός της εξήγησης του δασκάλου με τη μετωπική συλλογική εργασία των μαθητών.

Τα εν λόγω πολύεδρα εμφανίζονται στην οθόνη χρησιμοποιώντας βιντεοπροβολέα, ο οποίος επιτρέπει τη σύγκριση διάφορους τρόπουςλύσεις.

Εργασία για το σπίτι: λύστε το πρόβλημα 3 με άλλο τρόπο, για παράδειγμα χρησιμοποιώντας το θεώρημα των τριών κάθετων .

Βιβλιογραφία

1. Ershova A.P., Goloborodko V.V. Ανεξάρτητη και δοκιμαστικά χαρτιάστη γεωμετρία για την τάξη 11. – Μ.: ΗΛΕΚΣΑ, – 2010. – 208 σελ.

2. Γεωμετρία, 10-11: σχολικό βιβλίο για Εκπαιδευτικά ιδρύματα: βασικά επίπεδα και προφίλ / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev et al. - M.: Education, 2007. - 256 p.

3. Ενιαία Κρατική Εξέταση-2012. Μαθηματικά: τυπικές επιλογές εξετάσεων: 10 επιλογές / εκδ. A.L. Semenova, I.V. Yashchenko. - Μ.: Εθνική παιδεία, 2011. – 112 σελ. – (ΧΡΗΣΗ-2012. FIPI - σχολείο).

Το άρθρο μιλά για την εύρεση της γωνίας μεταξύ των επιπέδων. Αφού δώσουμε τον ορισμό, ας δώσουμε μια γραφική απεικόνιση και ας εξετάσουμε λεπτομερής μέθοδοςεύρεση με τη μέθοδο συντεταγμένων. Λαμβάνουμε έναν τύπο για τεμνόμενα επίπεδα, ο οποίος περιλαμβάνει τις συντεταγμένες κανονικά διανύσματα.

Yandex.RTB R-A-339285-1

Το υλικό θα χρησιμοποιήσει δεδομένα και έννοιες που είχαν μελετηθεί προηγουμένως σε άρθρα σχετικά με το επίπεδο και τη γραμμή στο διάστημα. Πρώτον, είναι απαραίτητο να προχωρήσουμε στη συλλογιστική που μας επιτρέπει να έχουμε μια συγκεκριμένη προσέγγιση για τον προσδιορισμό της γωνίας μεταξύ δύο τεμνόμενων επιπέδων.

Δίνονται δύο τεμνόμενα επίπεδα γ 1 και γ 2. Η διασταύρωσή τους θα πάρει τον χαρακτηρισμό γ. Η κατασκευή του επιπέδου χ σχετίζεται με την τομή αυτών των επιπέδων. Το επίπεδο χ διέρχεται από το σημείο Μ ως ευθεία c. Η τομή των επιπέδων γ 1 και γ 2 θα γίνει χρησιμοποιώντας το επίπεδο χ. Παίρνουμε τον προσδιορισμό της ευθείας που τέμνει γ 1 και χ ως ευθεία a, και την ευθεία που τέμνει το γ 2 και χ ως ευθεία b. Διαπιστώνουμε ότι η τομή των ευθειών a και b δίνει το σημείο M.

Η θέση του σημείου Μ δεν επηρεάζει τη γωνία μεταξύ των τεμνόμενων ευθειών a και b και το σημείο Μ βρίσκεται στην ευθεία c, από την οποία διέρχεται το επίπεδο χ.

Είναι απαραίτητο να κατασκευαστεί ένα επίπεδο χ 1 κάθετο στην ευθεία c και διαφορετικό από το επίπεδο χ. Η τομή των επιπέδων γ 1 και γ 2 με τη βοήθεια του χ 1 θα πάρει τον προσδιορισμό των ευθειών a 1 και b 1.

Μπορεί να φανεί ότι κατά την κατασκευή των χ και χ 1, οι ευθείες a και b είναι κάθετες στην ευθεία c, τότε οι a 1, b 1 βρίσκονται κάθετες στην ευθεία c. Βρίσκοντας ευθείες a και a 1 στο επίπεδο γ 1 με κάθετο στην ευθεία c, τότε μπορούν να θεωρηθούν παράλληλες. Με τον ίδιο τρόπο, η θέση των b και b 1 στο επίπεδο γ 2 με κάθετο στην ευθεία c δηλώνει τον παραλληλισμό τους. Αυτό σημαίνει ότι είναι απαραίτητο να γίνει παράλληλη μεταφορά του επιπέδου χ 1 στο χ, όπου παίρνουμε δύο ευθείες που συμπίπτουν a και a 1, b και b 1. Διαπιστώνουμε ότι η γωνία μεταξύ των τεμνόμενων ευθειών a και b είναι 1 ίσο με γωνίατεμνόμενες ευθείες α και β.

Ας δούμε το παρακάτω σχήμα.

Η πρόταση αυτή αποδεικνύεται από το γεγονός ότι μεταξύ των τεμνόμενων ευθειών a και b υπάρχει γωνία που δεν εξαρτάται από τη θέση του σημείου Μ, δηλαδή από το σημείο τομής. Αυτές οι γραμμές βρίσκονται στα επίπεδα γ 1 και γ 2. Στην πραγματικότητα, η γωνία που προκύπτει μπορεί να θεωρηθεί η γωνία μεταξύ δύο τεμνόμενων επιπέδων.

Ας προχωρήσουμε στον προσδιορισμό της γωνίας μεταξύ των υφιστάμενων τεμνόμενων επιπέδων γ 1 και γ 2.

Ορισμός 1

Η γωνία μεταξύ δύο τεμνόμενων επιπέδων γ 1 και γ 2ονομάζεται η γωνία που σχηματίζεται από την τομή των ευθειών a και b, όπου τα επίπεδα γ 1 και γ 2 τέμνονται με το επίπεδο χ που είναι κάθετο στην ευθεία c.

Σκεφτείτε το παρακάτω σχήμα.

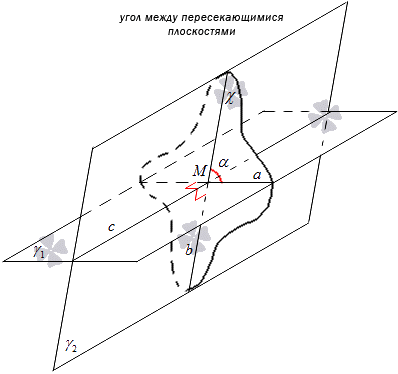
Η απόφαση μπορεί να υποβληθεί με άλλη μορφή. Όταν τα επίπεδα γ 1 και γ 2 τέμνονται, όπου c είναι η ευθεία πάνω στην οποία τέμνονται, σημειώστε ένα σημείο M μέσα από το οποίο σχεδιάστε ευθείες a και b κάθετες στην ευθεία c και βρίσκονται στα επίπεδα γ 1 και γ 2, τότε η γωνία μεταξύ Οι ευθείες α και β θα είναι η γωνία μεταξύ των επιπέδων. Στην πράξη, αυτό ισχύει για την κατασκευή της γωνίας μεταξύ των επιπέδων.

Κατά τη διασταύρωση σχηματίζεται γωνία μικρότερη από 90 μοίρες, δηλαδή μέτρο βαθμούΗ γωνία ισχύει σε ένα διάστημα αυτού του τύπου (0, 90]. Ταυτόχρονα, αυτά τα επίπεδα ονομάζονται κάθετα εάν σχηματίζεται ορθή γωνία στην τομή. Η γωνία μεταξύ των παράλληλων επιπέδων θεωρείται ίση με μηδέν.

Ο συνήθης τρόπος εύρεσης της γωνίας μεταξύ των τεμνόμενων επιπέδων είναι η εκτέλεση πρόσθετων κατασκευών. Αυτό βοηθά στον προσδιορισμό του με ακρίβεια και αυτό μπορεί να γίνει χρησιμοποιώντας σημάδια ισότητας ή ομοιότητας τριγώνου, ημιτόνων και συνημιτόνων μιας γωνίας.

Ας εξετάσουμε την επίλυση προβλημάτων χρησιμοποιώντας ένα παράδειγμα από Προβλήματα Ενιαίας Κρατικής Εξέτασηςμπλοκ C 2.

Παράδειγμα 1

Σειρά κυβοειδές A B C D A 1 B 1 C 1 D 1, όπου η πλευρά A B = 2, A D = 3, A A 1 = 7, το σημείο E διαιρεί την πλευρά A A 1 σε αναλογία 4: 3. Να βρείτε τη γωνία μεταξύ των επιπέδων A B C και B E D 1.

Λύση

Για λόγους σαφήνειας, είναι απαραίτητο να κάνετε ένα σχέδιο. Το καταλαβαίνουμε

Μια οπτική αναπαράσταση είναι απαραίτητη για να καταστεί πιο βολική η εργασία με τη γωνία μεταξύ των επιπέδων.

Καθορίζουμε την ευθεία κατά μήκος της οποίας συμβαίνει η τομή των επιπέδων A B C και B E D 1. Το σημείο Β είναι κοινό σημείο. Πρέπει να βρεθεί άλλος κοινό σημέιοδιασταυρώσεις. Ας εξετάσουμε τις ευθείες D A και D 1 E, οι οποίες βρίσκονται στο ίδιο επίπεδο A D D 1. Η θέση τους δεν υποδηλώνει παραλληλισμό, σημαίνει ότι έχουν κοινό σημείο τομής.

Ωστόσο, η ευθεία D A βρίσκεται στο επίπεδο A B C και η D 1 E στο B E D 1. Από αυτό παίρνουμε ότι οι ευθείες γραμμές Δ ΑΚαι Δ 1 Εέχουν ένα κοινό σημείο τομής, το οποίο είναι κοινό για τα επίπεδα A B C και B E D 1. Υποδεικνύει το σημείο τομής των γραμμών Δ Ακαι Δ 1 Ε γράμμα ΣΤ. Από αυτό προκύπτει ότι η B F είναι η ευθεία κατά μήκος της οποίας τέμνονται τα επίπεδα A B C και B E D 1.

Ας δούμε το παρακάτω σχήμα.

Για να λάβουμε την απάντηση, είναι απαραίτητο να κατασκευάσουμε ευθείες ευθείες που βρίσκονται στα επίπεδα A B C και B E D 1 που διέρχονται από ένα σημείο που βρίσκεται στην ευθεία B F και είναι κάθετες σε αυτό. Τότε η γωνία που προκύπτει μεταξύ αυτών των ευθειών θεωρείται η επιθυμητή γωνία μεταξύ των επιπέδων A B C και B E D 1.

Από αυτό μπορούμε να δούμε ότι το σημείο Α είναι η προβολή του σημείου Ε στο επίπεδο A B C. Είναι απαραίτητο να σχεδιάσουμε μια ευθεία γραμμή που τέμνει τη γραμμή B F σε ορθή γωνία στο σημείο M. Μπορεί να φανεί ότι η ευθεία γραμμή A M είναι η προβολή της ευθείας E M στο επίπεδο A B C, με βάση το θεώρημα για αυτές τις καθέτους A M ⊥ B F . Σκεφτείτε την παρακάτω εικόνα.

∠ A M E είναι η επιθυμητή γωνία που σχηματίζεται από τα επίπεδα A B C και B E D 1. Από το προκύπτον τρίγωνο A E M μπορούμε να βρούμε το ημίτονο, το συνημίτονο ή την εφαπτομένη της γωνίας και στη συνέχεια την ίδια τη γωνία, μόνο εάν είναι γνωστές οι δύο πλευρές της. Υπό τον όρο, έχουμε ότι το μήκος A E βρίσκεται με αυτόν τον τρόπο: η ευθεία A A 1 διαιρείται με το σημείο E σε αναλογία 4: 3, που σημαίνει ότι το συνολικό μήκος της ευθείας είναι 7 μέρη, τότε A E = 4 μέρη. Βρίσκουμε το Α Μ.

Πρέπει να εξεταστεί ορθογώνιο τρίγωνο A B F . Έχουμε ορθή γωνία Α με ύψος Α Μ. Από τη συνθήκη A B = 2, τότε μπορούμε να βρούμε το μήκος A F με την ομοιότητα των τριγώνων D D 1 F και A E F. Παίρνουμε ότι A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Είναι απαραίτητο να βρούμε το μήκος της πλευράς B F του τριγώνου A B F χρησιμοποιώντας το Πυθαγόρειο θεώρημα. Παίρνουμε ότι B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Το μήκος της πλευράς A M βρίσκεται μέσα από το εμβαδόν του τριγώνου A B F. Έχουμε ότι το εμβαδόν μπορεί να είναι ίσο και με το S A B C = 1 2 · A B · A F και το S A B C = 1 2 · B F · A M .

Παίρνουμε ότι A M = A B A F B F = 2 4 2 5 = 4 5 5

Τότε μπορούμε να βρούμε την τιμή της εφαπτομένης της γωνίας του τριγώνου A E M. Παίρνουμε:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Η επιθυμητή γωνία που προκύπτει από την τομή των επιπέδων A B C και B E D 1 είναι ίση με a r c t g 5, κατόπιν με απλοποίηση λαμβάνουμε r c t g 5 = a r c sin 30 6 = a r c cos 6 6.

Απάντηση: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Ορισμένες περιπτώσεις εύρεσης της γωνίας μεταξύ τεμνόμενων γραμμών καθορίζονται χρησιμοποιώντας επίπεδο συντεταγμένων O x y z και η μέθοδος συντεταγμένων. Ας ρίξουμε μια πιο προσεκτική ματιά.

Εάν δίνεται πρόβλημα όπου είναι απαραίτητο να βρεθεί η γωνία μεταξύ των τεμνόμενων επιπέδων γ 1 και γ 2, συμβολίζουμε την επιθυμητή γωνία ως α.

Επειτα δεδομένο σύστημαοι συντεταγμένες δείχνει ότι έχουμε τις συντεταγμένες των κανονικών διανυσμάτων των τεμνόμενων επιπέδων γ 1 και γ 2. Τότε συμβολίζουμε ότι n 1 → = n 1 x, n 1 y, n 1 z είναι το κανονικό διάνυσμα του επιπέδου γ 1, και n 2 → = (n 2 x, n 2 y, n 2 z) - για το επίπεδο γ 2. Ας εξετάσουμε τον λεπτομερή προσδιορισμό της γωνίας που βρίσκεται μεταξύ αυτών των επιπέδων σύμφωνα με τις συντεταγμένες των διανυσμάτων.

Είναι απαραίτητο να ορίσουμε την ευθεία κατά την οποία τα επίπεδα γ 1 και γ 2 τέμνονται με το γράμμα c. Στην ευθεία c έχουμε ένα σημείο Μ μέσα από το οποίο σχεδιάζουμε ένα επίπεδο χ κάθετο στη c. Το επίπεδο χ κατά μήκος των ευθειών a και b τέμνει τα επίπεδα γ 1 και γ 2 στο σημείο M. από τον ορισμό προκύπτει ότι η γωνία μεταξύ των τεμνόμενων επιπέδων γ 1 και γ 2 είναι ίση με τη γωνία των τεμνόμενων ευθειών a και b που ανήκουν σε αυτά τα επίπεδα, αντίστοιχα.

Στο χ επίπεδο σχεδιάζουμε κανονικά διανύσματα από το σημείο Μ και τα συμβολίζουμε n 1 → και n 2 → . Το διάνυσμα n 1 → βρίσκεται σε μια ευθεία κάθετη στην ευθεία a, και το διάνυσμα n 2 → βρίσκεται σε μια ευθεία κάθετη στην ευθεία b. Από εδώ το καταλαβαίνουμε δεδομένο αεροπλάνοΤο χ έχει κανονικό διάνυσμα ευθείας a ίσο με n 1 → και για ευθεία b ίσο με n 2 →. Σκεφτείτε το παρακάτω σχήμα.

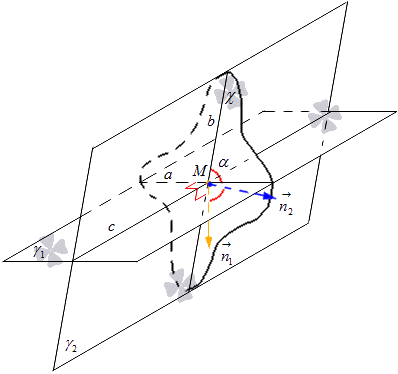
Από εδώ λαμβάνουμε έναν τύπο με τον οποίο μπορούμε να υπολογίσουμε το ημίτονο της γωνίας των τεμνόμενων γραμμών χρησιμοποιώντας τις συντεταγμένες των διανυσμάτων. Βρήκαμε ότι το συνημίτονο της γωνίας μεταξύ των ευθειών a και b είναι το ίδιο με το συνημίτονο μεταξύ των τεμνόμενων επιπέδων γ 1 και γ 2, το οποίο προέρχεται από τύπους cosα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, όπου έχουμε ότι n 1 → = (n 1 x, n 1 y, n 1 z) και n 2 → = (n 2 x, n 2 y, n 2 z) είναι οι συντεταγμένες του τα διανύσματα των αναπαρασταθέντων επιπέδων.

Η γωνία μεταξύ τεμνόμενων γραμμών υπολογίζεται χρησιμοποιώντας τον τύπο

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

Παράδειγμα 2

Σύμφωνα με την συνθήκη δίνεται το παραλληλεπίπεδο A B C D A 1 B 1 C 1 D 1 , όπου A B = 2, A D = 3, A A 1 = 7, και το σημείο E διαιρεί την πλευρά A A 1 4: 3. Να βρείτε τη γωνία μεταξύ των επιπέδων A B C και B E D 1.

Λύση

Από τη συνθήκη είναι ξεκάθαρο ότι οι πλευρές του είναι κατά ζεύγη κάθετες. Αυτό σημαίνει ότι είναι απαραίτητο να εισαχθεί ένα σύστημα συντεταγμένων O x y z με την κορυφή στο σημείο C και τους άξονες συντεταγμένων O x, O y, O z. Είναι απαραίτητο να ρυθμίσετε την κατεύθυνση στις κατάλληλες πλευρές. Σκεφτείτε το παρακάτω σχήμα.

Τέμνοντα επίπεδα Α Β ΓΚαι Β Ε Δ 1σχηματίστε μια γωνία που μπορεί να βρεθεί χρησιμοποιώντας τον τύπο α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, όπου n 1 → = (n 1 x, n 1 y, n 1 z) και n 2 → = (n 2 x, n 2 y, n 2 z ) είναι κανονικά διανύσματα του αυτά τα αεροπλάνα. Είναι απαραίτητο να καθοριστούν οι συντεταγμένες. Από το σχήμα βλέπουμε ότι άξονα συντεταγμένωνΤο O x y συμπίπτει με το επίπεδο A B C, που σημαίνει ότι οι συντεταγμένες του κανονικού διανύσματος k → είναι ίσες με την τιμή n 1 → = k → = (0, 0, 1).

Το κανονικό διάνυσμα του επιπέδου B E D 1 λαμβάνεται ως το διανυσματικό γινόμενο B E → και B D 1 →, όπου οι συντεταγμένες τους βρίσκονται με συντεταγμένες ακραία σημείαΒ, Ε, Δ 1, τα οποία καθορίζονται με βάση τις συνθήκες του προβλήματος.

Παίρνουμε ότι B (0, 3, 0), D 1 (2, 0, 7). Επειδή A E E A 1 = 4 3, από τις συντεταγμένες των σημείων A 2, 3, 0, A 1 2, 3, 7 βρίσκουμε E 2, 3, 4. Βρίσκουμε ότι B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 · i → - 6 j → - 6 k → ⇔ n 2 → = (12 , - 6 , - 6)

Είναι απαραίτητο να αντικατασταθούν οι ευρεθείσες συντεταγμένες στον τύπο για τον υπολογισμό της γωνίας μέσω του συνημιτόνου τόξου. Παίρνουμε

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

Η μέθοδος συντεταγμένων δίνει ένα παρόμοιο αποτέλεσμα.

Απάντηση: a r c cos 6 6 .

Το τελικό πρόβλημα εξετάζεται με στόχο την εύρεση της γωνίας μεταξύ των τεμνόμενων επιπέδων με τις υπάρχουσες γνωστές εξισώσεις των επιπέδων.

Παράδειγμα 3

Υπολογίστε το ημίτονο, συνημίτονο της γωνίας και την τιμή της γωνίας που σχηματίζεται από δύο τεμνόμενες ευθείες, οι οποίες ορίζονται στο σύστημα συντεταγμένων O x y z και δίνονται από τις εξισώσεις 2 x - 4 y + z + 1 = 0 και 3 y - z - 1 = 0.

Λύση

Όταν μελετάτε ένα θέμα γενική εξίσωσηευθεία της μορφής A x + B y + C z + D = 0 αποκάλυψε ότι τα A, B, C είναι συντελεστές ίσοι με τις συντεταγμένες του κανονικού διανύσματος. Αυτό σημαίνει ότι n 1 → = 2, - 4, 1 και n 2 → = 0, 3, - 1 είναι κανονικά διανύσματα των δεδομένων γραμμών.

Είναι απαραίτητο να αντικατασταθούν οι συντεταγμένες των κανονικών διανυσμάτων των επιπέδων στον τύπο για τον υπολογισμό της επιθυμητής γωνίας των τεμνόμενων επιπέδων. Τότε το καταλαβαίνουμε

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Από εδώ έχουμε ότι το συνημίτονο της γωνίας παίρνει τη μορφή cos α = 13 210. Τότε η γωνία των τεμνόμενων γραμμών δεν είναι αμβλεία. Αντικατάσταση σε τριγωνομετρική ταυτότητα, βρίσκουμε ότι η τιμή του ημιτόνου της γωνίας είναι ίση με την έκφραση. Ας το υπολογίσουμε και ας το βρούμε

sin α = 1 - cos 2 α = 1 - 13.210 = 41.210

Απάντηση: sin α = 41,210, cos α = 13,210, α = a r c cos 13,210 = a r c sin 41,210.

Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter

Στην εργασία C2 στα μαθηματικά, τις περισσότερες φορές χρειάζεται να λύσετε ένα πρόβλημα στο οποίο πρέπει να προσδιορίσετε:

Απόσταση μεταξύ δύο σημείων
Απόσταση από σημείο σε γραμμή
Απόσταση από σημείο σε αεροπλάνο
Απόσταση μεταξύ των γραμμών διέλευσης
Γωνία μεταξύ δύο ευθειών
Γωνία μεταξύ ευθείας γραμμής και επιπέδου
Γωνία μεταξύ των επιπέδων

Οι εργασίες είναι στοιχειώδεις αν ακολουθήσετε τον αλγόριθμο λύσης C2 και θυμηθείτε τα βασικά τριγωνομετρικές ιδιότητες, όπως οι ιδιότητες των διαγωνίων ή η επιφάνεια ενός πολυεδρικού. Οι βασικές εργασίες θα σας βοηθήσουν να θυμάστε αυτές τις βασικές ιδιότητες.

Τώρα ας περάσουμε απευθείας στους αλγόριθμους.

1. Για να προσδιορίσουμε την απόσταση μεταξύ δύο σημείων Α και Β, χρησιμοποιούμε μία από τις δύο μεθόδους:

Περιλαμβάνουμε το ΑΒ σε κάποιο τρίγωνο και βρίσκουμε το μήκος του ως πλευρά του τριγώνου
Σύμφωνα με τον τύπο

Επιπλέον, η μέθοδος συντεταγμένων, κατά τη γνώμη μου, είναι η απλούστερη· απλά πρέπει να προσδιορίσετε προσεκτικά τις συντεταγμένες κάθε σημείου.

2. Για να προσδιορίσετε την απόσταση από ένα σημείο σε μια ευθεία, υπολογίστε

ως το μήκος ενός κάθετου τμήματος, εάν είναι δυνατόν να συμπεριληφθεί αυτό το τμήμα σε κάποιο τρίγωνο ως ένα από τα ύψη

χρησιμοποιώντας τη μέθοδο συντεταγμένων χρησιμοποιώντας τύπους για τον υπολογισμό του εμβαδού, στους οποίους η απαιτούμενη απόσταση θα είναι το ύψος και

3. Η απόσταση από ένα σημείο σε ένα επίπεδο είναι

το μήκος της καθέτου που έπεσε από αυτό το σημείο στο επίπεδο. Για να γίνει αυτό, κατασκευάζουμε προσεκτικά ένα τμήμα που είναι κάθετο στο επίπεδο και διέρχεται από αυτό δεδομένο σημείο. Η απαιτούμενη απόσταση θα είναι ίση με το ύψος του προκύπτοντος νέου πολυέδρου.
Χρησιμοποιώντας τη μέθοδο συντεταγμένων

Η εξίσωση βρίσκεται αντικαθιστώντας τις συντεταγμένες τριών σημείων που ανήκουν σε αυτό το επίπεδο

Χρησιμοποιώντας τη μέθοδο του διανύσματος

Για να το κάνετε αυτό, πρέπει να θυμάστε τους κανόνες για την πρόσθεση και την αφαίρεση διανυσμάτων, ότι το γινόμενο κάθετα διανύσματαισούται με μηδέν.

Χρησιμοποιώντας τη μέθοδο όγκου, εάν υπάρχει μια πυραμίδα ABCM, τότε η απόσταση από το σημείο M έως το επίπεδο που περιέχει το τρίγωνο ABC υπολογίζεται με τον τύπο

Χρησιμοποιώντας τη μέθοδο των προβλημάτων αναφοράς, τα οποία μπορούν να προβληθούν

4. Η απόσταση μεταξύ των γραμμών διέλευσης μπορεί να λυθεί χρησιμοποιώντας

4.1. Βήμα προς βήμα υπολογιστική μέθοδος:

Κατασκευάστε μια κοινή κάθετο δύο τεμνόμενων ευθειών και βρείτε το μήκος της.
κατασκευάστε ένα επίπεδο που περιέχει μια από τις ευθείες και παράλληλη με τη δεύτερη. Τότε η απαιτούμενη απόσταση θα είναι ίση με την απόσταση από το σημείο μέχρι την ευθεία που κατασκευάζεται στο επίπεδο.
περικλείω δεδομένες γραμμές σε παράλληλα επίπεδα που διέρχονται από δεδομένες τεμνόμενες ευθείες, βρείτε την απόσταση μεταξύ αυτών των επιπέδων
κατασκευάστε ένα επίπεδο κάθετο σε μία από αυτές τις ευθείες και κατασκευάστε μια ορθογώνια προβολή της δεύτερης γραμμής

4.2. Μέθοδος διανυσματικών συντεταγμένων

Να βρείτε τις συντεταγμένες των άκρων ενός τμήματος που είναι κοινή κάθετη σε δύο τεμνόμενες ευθείες
Εύρεση της απόστασης μεταξύ δύο σημείων

4.3. Διανυσματική μέθοδος
Μειώνουμε το πρόβλημα στον προσδιορισμό του μήκους ενός διανύσματος που ανήκει σε μια κάθετο που είναι η κοινή κάθετο δύο λοξών γραμμών

6. Γωνία μεταξύ ευθείας γραμμής και επιπέδουπροσδιορίζεται συμπεριλαμβάνοντάς το σε ένα ορθογώνιο τρίγωνο ως μία από τις οξείες γωνίες ή με τη μέθοδο διανύσματος-συντονιστή

Θα δούμε πώς καθορίζεται η γωνία μεταξύ των επιπέδων στο επόμενο μάθημα. Αυτοί οι αλγόριθμοι για την επίλυση του C2 συμβάλλουν στην ολοκληρωμένη κατανόηση της μεθόδου επίλυσης του προβλήματος. «Ένα περιοδικό για τους μαθητές και τους γονείς τους για να βοηθήσουν τους μαθητές». Διαβάστε περισσότερα: http://education-club.ru/#ixzz2IXf5GOJU

7. Γωνία μεταξύ των επιπέδων(γεωμετρική μέθοδος)

1. Βρείτε την ευθεία κατά την οποία τέμνονται τα επίπεδα.
2. Επιλέξτε ένα σημείο σε αυτή την ευθεία και σχεδιάστε δύο κάθετες σε αυτό, που βρίσκονται σε αυτά τα επίπεδα. Ή σχεδιάστε ένα επίπεδο κάθετο στη γραμμή τομής των επιπέδων.
3. Να βρείτε την τριγωνομετρική συνάρτηση της γωνίας που σχηματίζουν οι κάθετοι στην ευθεία τομής των επιπέδων. Κατά κανόνα, το κάνουμε αυτό μέσω ενός τριγώνου που περιλαμβάνει την επιθυμητή γωνία.
4. Γράψτε την τιμή της γωνίας στην απάντησή σας, ή τριγωνομετρική συνάρτησηγωνία.

Γωνία μεταξύ των επιπέδων. Μέθοδος συντεταγμένων. Εργασία Γ2

Δύο τεμνόμενα επίπεδα σχηματίζουν δύο ζεύγη ίσων διεδρικών γωνιών:

Το μέγεθος της διεδρικής γωνίας μετριέται με το μέγεθος της αντίστοιχης γραμμικής γωνίας.

Για να κατασκευάσετε μια γραμμική γωνία μιας διεδρικής γωνίας, πρέπει να πάρετε τη γραμμή τομής των επιπέδων αυθαίρετο σημείο, και σε κάθε επίπεδο σχεδιάστε μια ακτίνα σε αυτό το σημείο κάθετη στη γραμμή τομής των επιπέδων. Η γωνία που σχηματίζεται από αυτές τις ακτίνες είναι η γραμμική γωνία της διεδρικής γωνίας:

Το μέγεθος της γωνίας μεταξύ των επιπέδων είναι το μέγεθος της μικρότερης από τη διεδρική γωνία.

Ας οριστούν τα επίπεδά μας από τις εξισώσεις:

Το συνημίτονο της γωνίας μεταξύ των επιπέδων βρίσκεται με τον ακόλουθο τύπο:

Στην απάντηση γράφουμε , αφού η τιμή της γωνίας μεταξύ των επιπέδων είναι η τιμή της μικρότερης διεδρικής γωνίας.

Σε κανονικό τετράγωνο πρίσμα με πλευρά βάσης 12 και ύψος 21, λαμβάνεται ένα σημείο Μ στην άκρη έτσι ώστε . Το σημείο Κ λαμβάνεται στην άκρη έτσι ώστε . Βρείτε τη γωνία μεταξύ του επιπέδου και του επιπέδου.

Ας κάνουμε ένα σχέδιο. Εφόσον θα χρησιμοποιήσουμε τη μέθοδο συντεταγμένων, θα εισαγάγουμε αμέσως ένα σύστημα συντεταγμένων: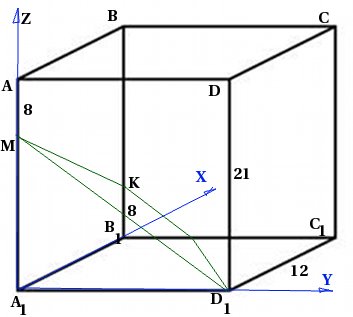

Τώρα βρισκόμαστε αντιμέτωποι με το καθήκον να γράψουμε τις εξισώσεις επιπέδου και επιπέδου.

Περιέγραψα έναν λεπτομερή αλγόριθμο για την εύρεση της εξίσωσης ενός επιπέδου χρησιμοποιώντας τρία σημεία.

Αφού βρούμε τους συντελεστές στις εξισώσεις επιπέδου και επιπέδου, τους αντικαθιστούμε στον τύπο για να βρούμε το συνημίτονο της γωνίας μεταξύ των επιπέδων και να βρούμε τη γωνία.

Σας προτείνω να παρακολουθήσετε μια λεπτομερή λύση βίντεο για αυτό το πρόβλημα:

Μια άλλη εργασία από την Inna Vladimirovna Feldman

Μαθήματα βίντεο "Μέθοδος συντονισμού για την επίλυση προβλημάτων s-2"

Μάθημα 2 http://youtu.be/dKQWG8OZRGo
Μάθημα 3 http://youtu.be/ddgr0PnbFno
Μάθημα 4 http://youtu.be/n6yx2pQC0Lo
Μάθημα 5 http://youtu.be/JkWbxAw1YLI
Μάθημα 6 http://youtu.be/gybIqCMKBiI
μάθημα 7 http://youtu.be/_LpARpYxp5g
μάθημα 8 http://youtu.be/XJhyZQoofD8

Η γωνία μεταξύ δύο διαφορετικών επιπέδων μπορεί να προσδιοριστεί για οποιοδήποτε σχετική θέσηαεροπλάνα.

Μια ασήμαντη περίπτωση αν τα επίπεδα είναι παράλληλα. Τότε η γωνία μεταξύ τους θεωρείται ίση με μηδέν.

Μια μη τετριμμένη περίπτωση αν τέμνονται τα επίπεδα. Η υπόθεση αυτή αποτελεί αντικείμενο περαιτέρω συζήτησης. Πρώτα χρειαζόμαστε την έννοια της διεδρικής γωνίας.

9.1 Διεδρική γωνία

Διεδρική γωνία είναι δύο ημιεπίπεδα με κοινή ευθεία γραμμή (η οποία ονομάζεται ακμή της διεδρικής γωνίας). Στο Σχ. 50 δείχνει μια δίεδρη γωνία που σχηματίζεται από ημιεπίπεδα και. το άκρο αυτής της διεδρικής γωνίας είναι η ευθεία γραμμή a, κοινή σε αυτά τα ημιεπίπεδα.

Ρύζι. 50. Διεδρική γωνία

Η διεδρική γωνία μπορεί να μετρηθεί σε μοίρες ή ακτίνια με μια λέξη, εισαγάγετε τη γωνιακή τιμή της διεδρικής γωνίας. Αυτό γίνεται ως εξής.

Στην άκρη της δίεδρης γωνίας που σχηματίζουν τα ημιεπίπεδα και, παίρνουμε ένα αυθαίρετο σημείο Μ. Ας σχεδιάσουμε τις ακτίνες ΜΑ και ΜΒ, αντίστοιχα που βρίσκονται σε αυτά τα ημιεπίπεδα και κάθετα στην άκρη (Εικ. 51).

Ρύζι. 51. Γραμμική διεδρική γωνία

Η προκύπτουσα γωνία AMB είναι η γραμμική γωνία της διεδρικής γωνίας. Η γωνία " = \AMB είναι ακριβώς η γωνιακή τιμή της διεδρικής μας γωνίας.

Ορισμός. Το γωνιακό μέγεθος μιας διεδρικής γωνίας είναι το μέγεθος της γραμμικής γωνίας μιας δεδομένης διεδρικής γωνίας.

Όλες οι γραμμικές γωνίες μιας διεδρικής γωνίας είναι ίσες μεταξύ τους (εξάλλου, λαμβάνονται μεταξύ τους με παράλληλη μετατόπιση). Να γιατί αυτόν τον ορισμόσωστή: η τιμή "δεν εξαρτάται από συγκεκριμένη επιλογήσημεία Μ στην άκρη μιας διεδρικής γωνίας.

9.2 Προσδιορισμός της γωνίας μεταξύ των επιπέδων

Όταν τέμνονται δύο επίπεδα, λαμβάνονται τέσσερις διεδρικές γωνίες. Αν έχουν όλοι το ίδιο μέγεθος(κατά 90), τότε τα επίπεδα ονομάζονται κάθετα. Η γωνία μεταξύ των επιπέδων είναι τότε 90.

Εάν δεν είναι όλες οι διεδρικές γωνίες ίδιες (δηλαδή υπάρχουν δύο οξείες και δύο αμβλείες), τότε η γωνία μεταξύ των επιπέδων είναι η τιμή της οξείας διεδρικής γωνίας (Εικ. 52).

Ρύζι. 52. Γωνία μεταξύ επιπέδων

9.3 Παραδείγματα επίλυσης προβλημάτων

Ας δούμε τρία προβλήματα. Το πρώτο είναι απλό, το δεύτερο και το τρίτο είναι περίπου στο επίπεδο Γ2 στην Ενιαία Κρατική Εξέταση στα μαθηματικά.

Πρόβλημα 1. Βρείτε τη γωνία μεταξύ δύο όψεων ενός κανονικού τετραέδρου.

Λύση. Έστω το ABCD ένα κανονικό τετράεδρο. Ας σχεδιάσουμε τις διάμεσες AM και DM των αντίστοιχων όψεων, καθώς και το ύψος του τετραέδρου DH (Εικ. 53).

Ρύζι. 53. Στην εργασία 1

Όντας διάμεσοι, το AM και το DM είναι επίσης ύψη ισόπλευρων τρίγωνα ABCκαι DBC. Επομένως, η γωνία " = \AMD είναι η γραμμική γωνία της διεδρικής γωνίας που σχηματίζεται από τις όψεις ABC και DBC. Την βρίσκουμε από το τρίγωνο DHM:

			1 ΜΜ

Απάντηση: arccos 1 3 .

Πρόβλημα 2. Σε μια κανονική τετραγωνική πυραμίδα SABCD (με κορυφή S), η πλευρική ακμή είναι ίση με την πλευρά της βάσης. Το σημείο Κ είναι το μέσο της ακμής SA. Βρείτε τη γωνία μεταξύ των επιπέδων

Λύση. Η ευθεία BC είναι παράλληλη με το AD και επομένως παράλληλη στο επίπεδο ADS. Επομένως, το επίπεδο KBC τέμνει το επίπεδο ADS κατά μήκος της ευθείας KL παράλληλης προς το BC (Εικ. 54).

Ρύζι. 54. Στην εργασία 2

Σε αυτήν την περίπτωση, το KL θα είναι επίσης παράλληλο στη γραμμή AD. επομένως KL ΜΕΣΑΙΑ ΣΕΙΡΑτρίγωνο ADS, και το σημείο L είναι το μέσο του DS.

Ας βρούμε το ύψος της πυραμίδας SO. Έστω N το μέσο του DO. Τότε το LN είναι η μεσαία γραμμή του τριγώνου DOS, και επομένως LN k SO. Αυτό σημαίνει ότι το LN είναι κάθετο στο επίπεδο ABC.

Από το σημείο N κατεβάζουμε την κάθετη NM στην ευθεία BC. Η ευθεία γραμμή NM θα είναι η προβολή του κεκλιμένου LM στο επίπεδο ABC. Από το θεώρημα των τριών κάθετων προκύπτει ότι το LM είναι επίσης κάθετο στο BC.

Έτσι, η γωνία " = \LMN είναι η γραμμική γωνία της διεδρικής γωνίας που σχηματίζεται από τα ημιεπίπεδα KBC και ABC. Θα αναζητήσουμε αυτή τη γωνία από το ορθογώνιο τρίγωνο LMN.

Έστω η άκρη της πυραμίδας ίση με α. Πρώτα βρίσκουμε το ύψος της πυραμίδας:

SO=σελ

Λύση. Έστω L το σημείο τομής των ευθειών A1 K και AB. Στη συνέχεια, το επίπεδο A1 KC τέμνει το επίπεδο ABC κατά μήκος της ευθείας CL (Εικ.55).

ΕΝΑ ντο

Ρύζι. 55. Στο πρόβλημα 3

Τα τρίγωνα A1 B1 K και KBL είναι ίσα σε σκέλος και οξεία γωνία. Επομένως, τα άλλα σκέλη είναι ίσα: A1 B1 = BL.

Εξετάστε το τρίγωνο ACL. Σε αυτό BA = BC = BL. Η γωνία CBL είναι 120. επομένως, \BCL = 30 . Επίσης, \BCA = 60 . Επομένως \ACL = \BCA + \BCL = 90 .

Λοιπόν, LC; ΜΕΤΑ ΧΡΙΣΤΟΝ. Αλλά η γραμμή AC χρησιμεύει ως προβολή της γραμμής A1 C στο επίπεδο ABC. Με το θεώρημα των τριών καθέτων συμπεραίνουμε ότι το LC ? Α1 Γ.

Έτσι, η γωνία A1 CA είναι η γραμμική γωνία της διεδρικής γωνίας που σχηματίζεται από τα ημιεπίπεδα A1 KC και ABC. Αυτή είναι η επιθυμητή γωνία. Από το ισοσκελές ορθογώνιο τρίγωνο A1 AC βλέπουμε ότι είναι ίσο με 45.

\(\μαύρο τρίγωνο\) Διεδρική γωνία είναι μια γωνία που σχηματίζεται από δύο ημιεπίπεδα και μια ευθεία γραμμή \(a\), που είναι το κοινό τους όριο.

\(\blacktriangleright\) Για να βρείτε τη γωνία μεταξύ των επιπέδων \(\xi\) και \(\pi\) , πρέπει να βρείτε τη γραμμική γωνία (και αρωματώδηςή ευθεία) διεδρική γωνία που σχηματίζεται από τα επίπεδα \(\xi\) και \(\pi\) :

Βήμα 1: έστω \(\xi\cap\pi=a\) (η γραμμή τομής των επιπέδων). Στο επίπεδο \(\xi\) σημειώνουμε ένα αυθαίρετο σημείο \(F\) και σχεδιάζουμε \(FA\perp a\) ;

Βήμα 2: πραγματοποιήστε \(FG\perp \pi\) ;

Βήμα 3: σύμφωνα με το TTP (\(FG\) – κάθετο, \(FA\) – λοξό, \(AG\) – προβολή) έχουμε: \(AG\perp a\) ;

Βήμα 4: Η γωνία \(\γωνία FAG\) ονομάζεται γραμμική γωνία της διεδρικής γωνίας που σχηματίζεται από τα επίπεδα \(\xi\) και \(\pi\) .

Σημειώστε ότι το τρίγωνο \(AG\) είναι ορθογώνιο.
Σημειώστε επίσης ότι το επίπεδο \(AFG\) που κατασκευάστηκε με αυτόν τον τρόπο είναι κάθετο και στα δύο επίπεδα \(\xi\) και \(\pi\) . Επομένως, μπορούμε να το πούμε διαφορετικά: γωνία μεταξύ των επιπέδωνΤα \(\xi\) και \(\pi\) είναι η γωνία μεταξύ δύο τεμνόμενων γραμμών \(c\in \xi\) και \(b\in\pi\) που σχηματίζουν ένα επίπεδο κάθετο στο και \(\xi\ ) και \(\pi\) .

Εργασία 1 #2875

Επίπεδο εργασίας: Πιο δύσκολο από το Unified State Exam

Ντάνα τετράγωνη πυραμίδα, του οποίου όλες οι άκρες είναι ίσες και η βάση είναι τετράγωνο. Βρείτε το \(6\cos \alpha\) , όπου \(\alpha\) είναι η γωνία μεταξύ των παρακείμενων πλευρικών του όψεων.

Έστω \(SABCD\) μια δεδομένη πυραμίδα (\(S\) είναι μια κορυφή) της οποίας οι ακμές είναι ίσες με \(a\) . Επομένως, τα πάντα πλαϊνά πρόσωπαείναι ίσα ισόπλευρα τρίγωνα. Ας βρούμε τη γωνία μεταξύ των όψεων \(SAD\) και \(SCD\) .

Ας κάνουμε \(CH\perp SD\) . Επειδή \(\τρίγωνο SAD=\τρίγωνο SCD\), τότε το \(AH\) θα είναι επίσης το ύψος του \(\τριγώνου SAD\) . Επομένως, εξ ορισμού, \(\γωνία AHC=\alpha\) είναι η γραμμική γωνία της διεδρικής γωνίας μεταξύ των επιφανειών \(SAD\) και \(SCD\) .
Εφόσον η βάση είναι τετράγωνο, τότε \(AC=a\sqrt2\) . Σημειώστε επίσης ότι \(CH=AH\) είναι το ύψος ισόπλευρο τρίγωνομε την πλευρά \(a\) , επομένως, \(CH=AH=\frac(\sqrt3)2a\) .
Στη συνέχεια, με το θεώρημα συνημιτόνου από \(\τρίγωνο AHC\) : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Απάντηση: -2

Εργασία 2 #2876

Επίπεδο εργασίας: Πιο δύσκολο από το Unified State Exam

Τα επίπεδα \(\pi_1\) και \(\pi_2\) τέμνονται υπό γωνία της οποίας το συνημίτονο είναι ίσο με \(0,2\). Τα επίπεδα \(\pi_2\) και \(\pi_3\) τέμνονται κάθετα και η γραμμή τομής των επιπέδων \(\pi_1\) και \(\pi_2\) είναι παράλληλη προς τη γραμμή τομής του επίπεδα \(\pi_2\) και \(\ pi_3\) . Βρείτε το ημίτονο της γωνίας μεταξύ των επιπέδων \(\pi_1\) και \(\pi_3\) .

Έστω η γραμμή τομής των \(\pi_1\) και \(\pi_2\) είναι ευθεία γραμμή \(a\), η γραμμή τομής των \(\pi_2\) και \(\pi_3\) είναι ευθεία γραμμή \(b\), και η γραμμή τομής \(\pi_3\) και \(\pi_1\) – ευθεία γραμμή \(c\) . Αφού \(a\παράλληλο b\) , τότε \(c\παράλληλο a\παράλληλο b\) (σύμφωνα με το θεώρημα από το τμήμα της θεωρητικής αναφοράς "Γεωμετρία στο διάστημα" \(\δεξιό βέλος\) "Εισαγωγή στη στερεομετρία, παραλληλισμός").

Ας σημειώσουμε τα σημεία \(A\in a, B\in b\) έτσι ώστε \(AB\perp a, AB\perp b\) (αυτό είναι δυνατό αφού \(a\παράλληλο b\) ). Ας σημειώσουμε \(C\in c\) έτσι ώστε \(BC\perp c\) , επομένως, \(BC\perp b\) . Στη συνέχεια, \(AC\perp c\) και \(AC\perp a\) .
Πράγματι, εφόσον \(AB\perp b, BC\perp b\) , τότε το \(b\) είναι κάθετο στο επίπεδο \(ABC\) . Εφόσον \(c\παράλληλο a\παράλληλο b\), τότε οι ευθείες \(a\) και \(c\) είναι επίσης κάθετες στο επίπεδο \(ABC\), και επομένως σε οποιαδήποτε ευθεία από αυτό το επίπεδο, ειδικότερα , η γραμμή \ (AC\) .

Από αυτό προκύπτει ότι \(\γωνία BAC=\γωνία (\pi_1, \pi_2)\), \(\γωνία ABC=\γωνία (\pi_2, \pi_3)=90^\circ\), \(\γωνία BCA=\γωνία (\pi_3, \pi_1)\). Αποδεικνύεται ότι το \(\τρίγωνο ABC\) είναι ορθογώνιο, που σημαίνει \[\sin \angle BCA=\cos \angle BAC=0.2.\]

Απάντηση: 0,2

Εργασία 3 #2877

Επίπεδο εργασίας: Πιο δύσκολο από το Unified State Exam

Δίνονται ευθείες γραμμές \(a, b, c\) που τέμνονται σε ένα σημείο και η γωνία μεταξύ οποιωνδήποτε δύο από αυτές είναι ίση με \(60^\circ\) . Βρείτε το \(\cos^(-1)\alpha\) , όπου \(\alpha\) είναι η γωνία μεταξύ του επιπέδου που σχηματίζεται από τις ευθείες \(a\) και \(c\) και του επιπέδου που σχηματίζεται από τις γραμμές \( b\ ) και \(c\) . Δώστε την απάντησή σας σε μοίρες.

Αφήστε τις ευθείες να τέμνονται στο σημείο \(O\) . Εφόσον η γωνία μεταξύ οποιωνδήποτε δύο από αυτές είναι ίση με \(60^\circ\), τότε και οι τρεις ευθείες δεν μπορούν να βρίσκονται στο ίδιο επίπεδο. Ας σημειώσουμε το σημείο \(A\) στη γραμμή \(a\) και ας σχεδιάσουμε \(AB\perp b\) και \(AC\perp c\) . Επειτα \(\τρίγωνο AOB=\τρίγωνο AOC\)ως ορθογώνιο κατά μήκος της υποτείνουσας και οξεία γωνία. Επομένως, \(OB=OC\) και \(AB=AC\) .
Ας κάνουμε \(AH\perp (BOC)\) . Στη συνέχεια, από το θεώρημα περίπου τρεις κάθετες \(HC\perp c\) , \(HB\perp b\) . Αφού \(AB=AC\) , λοιπόν \(\τρίγωνο AHB=\τρίγωνο AHC\)ως ορθογώνιο κατά μήκος της υποτείνουσας και του ποδιού. Επομένως, \(HB=HC\) . Αυτό σημαίνει ότι το \(OH\) είναι η διχοτόμος της γωνίας \(BOC\) (καθώς το σημείο \(H\) απέχει από τις πλευρές της γωνίας).

Σημειώστε ότι με αυτόν τον τρόπο κατασκευάσαμε επίσης τη γραμμική γωνία της διεδρικής γωνίας που σχηματίζεται από το επίπεδο που σχηματίζεται από τις ευθείες \(a\) και \(c\) και το επίπεδο που σχηματίζεται από τις γραμμές \(b\) και \(c \) . Αυτή είναι η γωνία \(ACH\) .

Ας βρούμε αυτή τη γωνία. Επειδή επιλέξαμε το σημείο \(A\) αυθαίρετα, ας το επιλέξουμε έτσι ώστε \(OA=2\) . Στη συνέχεια σε ορθογώνιο \(\τρίγωνο AOC\) : \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ]Εφόσον το \(OH\) είναι διχοτόμος, τότε \(\γωνία HOC=30^\circ\) , επομένως, σε ένα ορθογώνιο \(\τρίγωνο HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\]Στη συνέχεια από το ορθογώνιο \(\τρίγωνο ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Απάντηση: 3

Εργασία 4 #2910

Επίπεδο εργασίας: Πιο δύσκολο από το Unified State Exam

Τα επίπεδα \(\pi_1\) και \(\pi_2\) τέμνονται κατά μήκος της ευθείας \(l\) στην οποία βρίσκονται τα σημεία \(M\) και \(N\). Τα τμήματα \(MA\) και \(MB\) είναι κάθετα στην ευθεία \(l\) και βρίσκονται στα επίπεδα \(\pi_1\) και \(\pi_2\) αντίστοιχα, και \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Βρείτε το \(3\cos\alpha\) , όπου \(\alpha\) είναι η γωνία μεταξύ των επιπέδων \(\pi_1\) και \(\pi_2\) .

Το τρίγωνο \(AMN\) είναι ορθογώνιο, \(AN^2 = AM^2 + MN^2\), από όπου \ Το τρίγωνο \(BMN\) είναι ορθογώνιο, \(BN^2 = BM^2 + MN^2\), από το οποίο \Γράφουμε το θεώρημα συνημιτόνου για το τρίγωνο \(AMB\): \ Επειτα \ Αφού η γωνία \(\άλφα\) μεταξύ των επιπέδων είναι αιχμηρή γωνία, και η \(\γωνία AMB\) αποδείχθηκε αμβλεία, και μετά \(\cos\alpha=\dfrac5(12)\) . Επειτα \

Απάντηση: 1,25

Εργασία 5 #2911

Επίπεδο εργασίας: Πιο δύσκολο από το Unified State Exam

Το \(ABCDA_1B_1C_1D_1\) είναι ένα παραλληλεπίπεδο, το \(ABCD\) είναι ένα τετράγωνο με πλευρά \(a\), το σημείο \(M\) είναι η βάση της κάθετης που έπεσε από το σημείο \(A_1\) στο επίπεδο \ ((ABCD)\) , επιπλέον, \(M\) είναι το σημείο τομής των διαγωνίων του τετραγώνου \(ABCD\) . Είναι γνωστό ότι \(A_1M = \dfrac(\sqrt(3))(2)a\). Βρείτε τη γωνία μεταξύ των επιπέδων \((ABCD)\) και \((AA_1B_1B)\) . Δώστε την απάντησή σας σε μοίρες.

Ας κατασκευάσουμε το \(MN\) κάθετο στο \(AB\) όπως φαίνεται στο σχήμα.

Εφόσον το \(ABCD\) είναι ένα τετράγωνο με πλευρά \(a\) και \(MN\perp AB\) και \(BC\perp AB\) , τότε \(MN\παράλληλη BC\) . Εφόσον \(M\) είναι το σημείο τομής των διαγωνίων του τετραγώνου, τότε το \(M\) είναι το μέσο του \(AC\), επομένως, \(MN\) είναι η μεσαία γραμμή και \(MN =\frac12BC= \frac(1)(2)a\).
Το \(MN\) είναι η προβολή του \(A_1N\) στο επίπεδο \((ABCD)\), και το \(MN\) είναι κάθετο στο \(AB\), στη συνέχεια, με το θεώρημα τριών καθέτων, \ Το (A_1N\) είναι κάθετο στο \(AB \) και η γωνία μεταξύ των επιπέδων \((ABCD)\) και \(AA_1B_1B)\) είναι \(\γωνία A_1NM\) .
\[\mathrm(tg)\, \γωνία A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

Απάντηση: 60

Εργασία 6 #1854

Επίπεδο εργασίας: Πιο δύσκολο από το Unified State Exam

Σε τετράγωνο \(ABCD\) : \(O\) – το σημείο τομής των διαγωνίων. \(S\) – δεν βρίσκεται στο επίπεδο του τετραγώνου, \(SO \perp ABC\) . Βρείτε τη γωνία μεταξύ των επιπέδων \(ASD\) και \(ABC\) εάν \(SO = 5\) και \(AB = 10\) .

Τα ορθογώνια τρίγωνα \(\τρίγωνο SAO\) και \(\τρίγωνο SDO\) είναι ίσα σε δύο πλευρές και η γωνία μεταξύ τους (\(SO \perp ABC\) \(\Δεξιοβέλος\) \(\γωνία SOA = \γωνία SOD = 90^\circ\); \(AO = DO\) , επειδή \(O\) – σημείο τομής των διαγωνίων του τετραγώνου, \(SO\) – κοινή πλευρά) \(\Δεξί βέλος\) \(AS = SD\) \(\Δεξί βέλος\) \(\τρίγωνο ASD\) – ισοσκελές. Το σημείο \(K\) είναι το μέσο του \(AD\), τότε \(SK\) είναι το ύψος στο τρίγωνο \(\triangle ASD\) και \(OK\) είναι το ύψος στο τρίγωνο \( AOD\) \(\ Rightarrow\) επίπεδο \(SOK\) είναι κάθετο στα επίπεδα \(ASD\) και \(ABC\) \(\Rightarrow\) \(\γωνία SKO\) – γραμμική γωνία ίση με την επιθυμητή δίεδρος γωνία.

Στο \(\τρίγωνο SKO\) : \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) – ισοσκελές ορθογώνιο τρίγωνο \(\Rightarrow\) \(\angle SKO = 45^\circ\) .

Απάντηση: 45

Εργασία 7 #1855

Επίπεδο εργασίας: Πιο δύσκολο από το Unified State Exam

Τα ορθογώνια τρίγωνα \(\τρίγωνο SAO\) , \(\τρίγωνο SDO\) , \(\τρίγωνο SOB\) και \(\τρίγωνο SOC\) είναι ίσα σε δύο πλευρές και η μεταξύ τους γωνία (\(SO \perp ABC \) \(\Δεξί βέλος\) \(\γωνία SOA = \γωνία SOD = \γωνία SOB = \γωνία SOC = 90^\circ\); \(AO = OD = OB = OC\), επειδή \(O\) – σημείο τομής των διαγωνίων του τετραγώνου, \(SO\) – κοινή πλευρά) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \( Το \triangle ASD\) και \(\triangle BSC\) είναι ισοσκελές. Το σημείο \(K\) είναι το μέσο του \(AD\), τότε \(SK\) είναι το ύψος στο τρίγωνο \(\triangle ASD\) και \(OK\) είναι το ύψος στο τρίγωνο \( AOD\) \(\ Δεξιό βέλος\) Το επίπεδο \(SOK\) είναι κάθετο στο επίπεδο \(ASD\) . Το σημείο \(L\) είναι το μέσο του \(BC\), τότε \(SL\) είναι το ύψος στο τρίγωνο \(\τρίγωνο BSC\), και \(OL\) είναι το ύψος στο τρίγωνο \( BOC\) \(\ Δεξιό βέλος\) το επίπεδο \(SOL\) (γνωστό και ως επίπεδο \(SOK\)) είναι κάθετο στο επίπεδο \(BSC\) . Έτσι, λαμβάνουμε ότι η \(\γωνία KSL\) είναι μια γραμμική γωνία ίση με την επιθυμητή διεδρική γωνία.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Δεξί βέλος\) \(OL = 5\) ; \(SK = SL\) – ίσα ύψη ισοσκελές τρίγωνα, το οποίο μπορεί να βρεθεί χρησιμοποιώντας το Πυθαγόρειο θεώρημα: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Μπορεί να παρατηρηθεί ότι \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)Το \(\Δεξί βέλος\) για ένα τρίγωνο \(\triangle KSL\) ικανοποιείται θεώρημα αντίστροφης Pythagoras \(\Rightarrow\) \(\triangle KSL\) – ορθογώνιο τρίγωνο \(\Rightarrow\) \(\angle KSL = 90^\circ\) .

Απάντηση: 90

Η προετοιμασία των μαθητών για να λάβουν τις εξετάσεις του Unified State στα μαθηματικά, κατά κανόνα, ξεκινά με την επανάληψη βασικών τύπων, συμπεριλαμβανομένων εκείνων που σας επιτρέπουν να προσδιορίσετε τη γωνία μεταξύ των επιπέδων. Παρά το γεγονός ότι αυτό το τμήμα της γεωμετρίας καλύπτεται με επαρκείς λεπτομέρειες εντός σχολικό πρόγραμμα σπουδών, πολλοί απόφοιτοι χρειάζεται να επαναλάβουν τη βασική ύλη. Κατανοώντας πώς να βρουν τη γωνία μεταξύ των επιπέδων, οι μαθητές γυμνασίου θα μπορούν να υπολογίσουν γρήγορα τη σωστή απάντηση κατά την επίλυση ενός προβλήματος και να υπολογίζουν στη λήψη αξιοπρεπών βαθμολογιών στα αποτελέσματα της επιτυχίας της ενιαίας κρατικής εξέτασης.

Βασικές αποχρώσεις

Για να διασφαλίσετε ότι το ζήτημα του τρόπου εύρεσης μιας διεδρικής γωνίας δεν προκαλεί δυσκολίες, συνιστούμε να ακολουθήσετε έναν αλγόριθμο λύσης που θα σας βοηθήσει να ανταπεξέλθετε στις εργασίες της Ενιαίας Πολιτικής Εξέτασης.

Πρώτα πρέπει να προσδιορίσετε την ευθεία κατά μήκος της οποίας τέμνονται τα επίπεδα.

Στη συνέχεια, πρέπει να επιλέξετε ένα σημείο σε αυτή τη γραμμή και να σχεδιάσετε δύο κάθετες σε αυτό.

Το επόμενο βήμα είναι να βρεθεί η τριγωνομετρική συνάρτηση της διεδρικής γωνίας που σχηματίζεται από τις κάθετες. Ο πιο βολικός τρόπος για να γίνει αυτό είναι με τη βοήθεια του τριγώνου που προκύπτει, μέρος του οποίου είναι η γωνία.

Η απάντηση θα είναι η τιμή της γωνίας ή η τριγωνομετρική της συνάρτηση.

Η προετοιμασία για το τεστ εξετάσεων με το Shkolkovo είναι το κλειδί της επιτυχίας σας

Κατά τη διάρκεια των μαθημάτων την προηγούμενη μέρα περνώντας από την Ενιαία Κρατική ΕξέτασηΠολλοί μαθητές αντιμετωπίζουν το πρόβλημα της εύρεσης ορισμών και τύπων που τους επιτρέπουν να υπολογίζουν τη γωνία μεταξύ 2 επιπέδων. Ένα σχολικό εγχειρίδιο δεν είναι πάντα διαθέσιμο ακριβώς όταν χρειάζεται. Και να βρεις απαραίτητες φόρμουλεςκαι παραδείγματα σωστής χρήσης τους, συμπεριλαμβανομένης της εύρεσης της γωνίας μεταξύ των αεροπλάνων στο Διαδίκτυο, κάτι που μερικές φορές απαιτεί πολύ χρόνο.

Η μαθηματική πύλη "Shkolkovo" προσφέρει νέα προσέγγισηγια προετοιμασία για τις κρατικές εξετάσεις. Τα μαθήματα στον ιστότοπό μας θα βοηθήσουν τους μαθητές να εντοπίσουν τις πιο δύσκολες ενότητες για τον εαυτό τους και να καλύψουν τα κενά στη γνώση.

Ετοιμάσαμε και παρουσιάσαμε με σαφήνεια όλο το απαραίτητο υλικό. Βασικοί ορισμοίκαι οι τύποι παρουσιάζονται στην ενότητα «Θεωρητικές πληροφορίες».

Για την καλύτερη κατανόηση της ύλης προτείνουμε και την εξάσκηση των κατάλληλων ασκήσεων. Μεγάλη επιλογή εργασιών ποικίλους βαθμούςΗ πολυπλοκότητα, για παράδειγμα, παρουσιάζεται στην ενότητα "Κατάλογος". Όλες οι εργασίες περιέχουν έναν λεπτομερή αλγόριθμο για την εύρεση της σωστής απάντησης. Ο κατάλογος των ασκήσεων στον ιστότοπο συμπληρώνεται και ενημερώνεται συνεχώς.

Ενώ εξασκούνται στην επίλυση προβλημάτων που απαιτούν την εύρεση της γωνίας μεταξύ δύο επιπέδων, οι μαθητές έχουν την ευκαιρία να αποθηκεύσουν οποιαδήποτε εργασία στο διαδίκτυο ως "Αγαπημένα". Χάρη σε αυτό θα μπορέσουν να επιστρέψουν σε αυτόν απαιτούμενο ποσόχρόνο και να συζητήσει την πρόοδο της απόφασής του με δασκάλα σχολείουή δάσκαλος.