Εξίσωση ευθείας που διέρχεται από 2. Εξίσωση ευθείας - είδη εξίσωσης ευθείας: διέλευση από σημείο, γενική, κανονική, παραμετρική κ.λπ.
Ορισμός.Στο καρτεσιανό ορθογώνιο σύστημα συντεταγμένων, ένα διάνυσμα με συνιστώσες (Α, Β) είναι κάθετο στην ευθεία που δίνεται από την εξίσωση Ax + By + C = 0.
Παράδειγμα. Να βρείτε την εξίσωση της ευθείας που διέρχεται από το σημείο Α(1, 2) κάθετο στο διάνυσμα (3, -1).
Λύση. Με A = 3 και B = -1, ας συνθέσουμε την εξίσωση της ευθείας: 3x – y + C = 0. Για να βρούμε τον συντελεστή C, αντικαθιστούμε τις συντεταγμένες του δεδομένου σημείου Α στην παράσταση που προκύπτει. 3 – 2 + C = 0, επομένως C = -1. Σύνολο: η απαιτούμενη εξίσωση: 3x – y – 1 = 0.
Εξίσωση ευθείας που διέρχεται από δύο σημεία
Έστω δύο σημεία M 1 (x 1, y 1, z 1) και M 2 (x 2, y 2, z 2) στο διάστημα, τότε η εξίσωση της ευθείας που διέρχεται από αυτά τα σημεία είναι:

Εάν κάποιος από τους παρονομαστές είναι ίσος με μηδέν, ο αντίστοιχος αριθμητής πρέπει να είναι ίσος με μηδέν. Στο επίπεδο, η εξίσωση της ευθείας που γράφτηκε παραπάνω απλοποιείται:

αν x 1 ≠ x 2 και x = x 1, εάν x 1 = x 2.
Λέγεται το κλάσμα = k κλίσηευθεία.
Παράδειγμα. Να βρείτε την εξίσωση της ευθείας που διέρχεται από τα σημεία A(1, 2) και B(3, 4).
Λύση.Εφαρμόζοντας τον τύπο που γράφτηκε παραπάνω, παίρνουμε:

Εξίσωση ευθείας από σημείο και κλίση
Αν η γενική εξίσωση της ευθείας Ax + By + C = 0 μειωθεί στη μορφή:

και ορίζουν  , τότε καλείται η εξίσωση που προκύπτει εξίσωση ευθείας με κλίσηκ.
, τότε καλείται η εξίσωση που προκύπτει εξίσωση ευθείας με κλίσηκ.
Εξίσωση ευθείας από σημείο και διάνυσμα κατεύθυνσης
Κατ' αναλογία με το σημείο που εξετάζει την εξίσωση μιας ευθείας γραμμής μέσω ενός κανονικού διανύσματος, μπορείτε να εισαγάγετε τον ορισμό μιας ευθείας γραμμής μέσω ενός σημείου και το κατευθυντικό διάνυσμα της ευθείας γραμμής.
Ορισμός.Κάθε μη μηδενικό διάνυσμα (α 1, α 2), τα συστατικά του οποίου ικανοποιούν τη συνθήκη A α 1 + B α 2 = 0 ονομάζεται κατευθυντικό διάνυσμα της ευθείας
Ax + Wu + C = 0.
Παράδειγμα. Να βρείτε την εξίσωση μιας ευθείας με διάνυσμα κατεύθυνσης (1, -1) και που διέρχεται από το σημείο Α(1, 2).
Λύση.Θα αναζητήσουμε την εξίσωση της επιθυμητής γραμμής με τη μορφή: Ax + By + C = 0. Σύμφωνα με τον ορισμό, οι συντελεστές πρέπει να πληρούν τις προϋποθέσεις:
1 * A + (-1) * B = 0, δηλ. Α = Β.
Τότε η εξίσωση της ευθείας έχει τη μορφή: Ax + Ay + C = 0, ή x + y + C / A = 0. για x = 1, y = 2 παίρνουμε C/ A = -3, δηλ. απαιτούμενη εξίσωση:
Εξίσωση ευθείας σε τμήματα
Αν στη γενική εξίσωση της ευθείας Ах + Ву + С = 0 С≠0, τότε, διαιρώντας με –С, παίρνουμε:  ή
ή

Η γεωμετρική σημασία των συντελεστών είναι ότι ο συντελεστής ΕΝΑ είναι η συντεταγμένη του σημείου τομής της ευθείας με τον άξονα Ox, και σι – η συντεταγμένη του σημείου τομής της ευθείας με τον άξονα Oy.
Παράδειγμα.Δίνεται η γενική εξίσωση της ευθείας x – y + 1 = 0. Να βρείτε την εξίσωση αυτής της ευθείας σε τμήματα.
C = 1, , a = -1, b = 1.
Κανονική εξίσωση μιας γραμμής
Αν και οι δύο πλευρές της εξίσωσης Ax + By + C = 0 διαιρεθούν με τον αριθμό  η οποία ονομάζεται κανονικοποιητικό παράγοντα, τότε παίρνουμε
η οποία ονομάζεται κανονικοποιητικό παράγοντα, τότε παίρνουμε
xcosφ + ysinφ - p = 0 –
κανονική εξίσωση μιας γραμμής. Το πρόσημο ± του κανονικοποιητικού παράγοντα πρέπει να επιλέγεται έτσι ώστε μ * C< 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Παράδειγμα. Δίνεται η γενική εξίσωση της ευθείας 12x – 5y – 65 = 0. Απαιτείται να γραφούν διάφοροι τύποι εξισώσεων για αυτή τη γραμμή.
εξίσωση αυτής της γραμμής σε τμήματα: 
εξίσωση αυτής της γραμμής με κλίση: (διαιρέστε με 5)

κανονική εξίσωση ευθείας:
 ; cos φ = 12/13; αμαρτία φ= -5/13; p = 5.
; cos φ = 12/13; αμαρτία φ= -5/13; p = 5.
C Πρέπει να σημειωθεί ότι δεν μπορεί να αναπαρασταθεί κάθε γραμμή με εξίσωση σε τμήματα, για παράδειγμα, γραμμές παράλληλες προς άξονες ή που διέρχονται από την αρχή.
Παράδειγμα. Η ευθεία γραμμή κόβει ίσα θετικά τμήματα στους άξονες συντεταγμένων. Γράψτε μια εξίσωση ευθείας γραμμής εάν το εμβαδόν του τριγώνου που σχηματίζεται από αυτά τα τμήματα είναι 8 cm 2.
Λύση.Η εξίσωση της ευθείας έχει τη μορφή: , ab /2 = 8; a = 4; -4. Το a = -4 δεν είναι κατάλληλο σύμφωνα με τις συνθήκες του προβλήματος. Σύνολο: ή x + y – 4 = 0.
Παράδειγμα. Να γράψετε μια εξίσωση για μια ευθεία που διέρχεται από το σημείο Α(-2, -3) και την αρχή.
Λύση.
Η εξίσωση της ευθείας είναι:  , όπου x 1 = y 1 = 0; x 2 = -2; y 2 = -3.
, όπου x 1 = y 1 = 0; x 2 = -2; y 2 = -3.
Ας δούμε πώς να δημιουργήσουμε μια εξίσωση για μια ευθεία που διέρχεται από δύο σημεία χρησιμοποιώντας παραδείγματα.
Παράδειγμα 1.
Γράψτε μια εξίσωση για μια ευθεία που διέρχεται από τα σημεία A(-3; 9) και B(2;-1).
Μέθοδος 1 - δημιουργήστε μια εξίσωση ευθείας γραμμής με συντελεστή γωνίας.
Η εξίσωση ευθείας με γωνιακό συντελεστή έχει τη μορφή . Αντικαθιστώντας τις συντεταγμένες των σημείων Α και Β στην εξίσωση της ευθείας (x= -3 και y=9 - στην πρώτη περίπτωση, x=2 και y= -1 - στη δεύτερη), παίρνουμε ένα σύστημα εξισώσεων από το οποίο βρίσκουμε τις τιμές των k και b:
Προσθέτοντας την 1η και τη 2η εξίσωση όρο προς όρο, παίρνουμε: -10=5k, από όπου k= -2. Αντικαθιστώντας k= -2 στη δεύτερη εξίσωση, βρίσκουμε το b: -1=2·(-2)+b, b=3.
Έτσι, y= -2x+3 είναι η απαιτούμενη εξίσωση.
Μέθοδος 2 - ας δημιουργήσουμε μια γενική εξίσωση μιας ευθείας γραμμής.
Η γενική εξίσωση μιας ευθείας έχει τη μορφή . Αντικαθιστώντας τις συντεταγμένες των σημείων Α και Β στην εξίσωση, παίρνουμε το σύστημα:
Δεδομένου ότι ο αριθμός των αγνώστων είναι μεγαλύτερος από τον αριθμό των εξισώσεων, το σύστημα δεν είναι επιλύσιμο. Αλλά όλες οι μεταβλητές μπορούν να εκφραστούν μέσω μιας. Για παράδειγμα, μέσω του β.
Πολλαπλασιάζοντας την πρώτη εξίσωση του συστήματος με -1 και προσθέτοντας όρο προς όρο με τη δεύτερη:
παίρνουμε: 5a-10b=0. Άρα a=2b.
Ας αντικαταστήσουμε την έκφραση που προκύπτει στη δεύτερη εξίσωση: 2·2b -b+c=0; 3b+c=0; c= -3b.
Αντικαταστήστε τα a=2b, c= -3b στην εξίσωση ax+by+c=0:
2bx+by-3b=0. Απομένει να διαιρεθούν και οι δύο πλευρές με το b:
Η γενική εξίσωση μιας ευθείας γραμμής μπορεί εύκολα να μειωθεί στην εξίσωση μιας ευθείας με γωνιακό συντελεστή:
Μέθοδος 3 - δημιουργήστε μια εξίσωση μιας ευθείας γραμμής που διέρχεται από 2 σημεία.
Η εξίσωση μιας ευθείας που διέρχεται από δύο σημεία είναι:
![]()
Ας αντικαταστήσουμε τις συντεταγμένες των σημείων A(-3; 9) και B(2;-1) σε αυτήν την εξίσωση
(δηλαδή, x 1 = -3, y 1 =9, x 2 =2, y 2 = -1):
![]()
και απλοποιήστε:
από όπου 2x+y-3=0.
Στα σχολικά μαθήματα χρησιμοποιείται συχνότερα η εξίσωση ευθείας με συντελεστή γωνίας. Αλλά ο ευκολότερος τρόπος είναι να εξαγάγετε και να χρησιμοποιήσετε τον τύπο για την εξίσωση μιας ευθείας που διέρχεται από δύο σημεία.
Σχόλιο.
Αν, κατά την αντικατάσταση των συντεταγμένων των δεδομένων σημείων, ένας από τους παρονομαστές της εξίσωσης
![]()
αποδεικνύεται ίση με μηδέν, τότε η απαιτούμενη εξίσωση προκύπτει εξισώνοντας τον αντίστοιχο αριθμητή με μηδέν.
Παράδειγμα 2.
Γράψτε μια εξίσωση για μια ευθεία που διέρχεται από δύο σημεία C(5; -2) και D(7;-2).
Αντικαθιστούμε τις συντεταγμένες των σημείων Γ και Δ στην εξίσωση μιας ευθείας που διέρχεται από 2 σημεία.
Αυτό το άρθρο είναι μέρος της εξίσωσης θέματος μιας γραμμής σε ένα επίπεδο. Εδώ θα το δούμε από όλες τις πλευρές: θα ξεκινήσουμε με την απόδειξη του θεωρήματος που καθορίζει τη μορφή της γενικής εξίσωσης μιας ευθείας, στη συνέχεια θα εξετάσουμε μια ημιτελή γενική εξίσωση μιας γραμμής, θα δώσουμε παραδείγματα ημιτελών εξισώσεων μιας γραμμής με γραφικές απεικονίσεις, και εν κατακλείδι θα σταθούμε στη μετάβαση από μια γενική εξίσωση μιας γραμμής σε άλλους τύπους εξισώσεων αυτής της γραμμής και θα δώσουμε λεπτομερείς λύσεις σε τυπικά προβλήματα για τη σύνθεση της γενικής εξίσωσης μιας ευθείας γραμμής.
Πλοήγηση στη σελίδα.
Γενική εξίσωση ευθείας - βασικές πληροφορίες.
Ας αναλύσουμε αυτόν τον αλγόριθμο όταν λύνουμε ένα παράδειγμα.
Παράδειγμα.
Να γράψετε παραμετρικές εξισώσεις μιας ευθείας που δίνεται από τη γενική εξίσωση μιας ευθείας ![]() .
.
Λύση.
Αρχικά, μειώνουμε την αρχική γενική εξίσωση της γραμμής στην κανονική εξίσωση της γραμμής:
Τώρα παίρνουμε την αριστερή και τη δεξιά πλευρά της εξίσωσης που προκύπτει να είναι ίση με την παράμετρο. Εχουμε 
Απάντηση:

Από μια γενική εξίσωση μιας ευθείας γραμμής, είναι δυνατό να ληφθεί μια εξίσωση ευθείας γραμμής με συντελεστή γωνίας μόνο όταν . Τι πρέπει να κάνετε για να κάνετε τη μετάβαση; Αρχικά, στην αριστερή πλευρά της γενικής εξίσωσης ευθείας γραμμής, αφήστε μόνο τον όρο , οι υπόλοιποι όροι πρέπει να μετακινηθούν στη δεξιά πλευρά με το αντίθετο πρόσημο: ![]() . Δεύτερον, διαιρέστε και τις δύο πλευρές της ισότητας που προκύπτει με τον αριθμό Β, ο οποίος είναι μη μηδενικός,
. Δεύτερον, διαιρέστε και τις δύο πλευρές της ισότητας που προκύπτει με τον αριθμό Β, ο οποίος είναι μη μηδενικός, ![]() . Αυτό είναι όλο.
. Αυτό είναι όλο.
Παράδειγμα.
Μια ευθεία γραμμή σε ένα ορθογώνιο σύστημα συντεταγμένων Oxy δίνεται από τη γενική εξίσωση μιας ευθείας γραμμής. Πάρτε την εξίσωση αυτής της ευθείας με την κλίση.
Λύση.
Ας κάνουμε τις απαραίτητες ενέργειες: .
Απάντηση:
Όταν μια γραμμή δίνεται από την πλήρη γενική εξίσωση της γραμμής, είναι εύκολο να ληφθεί η εξίσωση της γραμμής σε τμήματα της φόρμας. Για να γίνει αυτό, μεταφέρουμε τον αριθμό C στη δεξιά πλευρά της ισότητας με το αντίθετο πρόσημο, διαιρούμε και τις δύο πλευρές της ισότητας που προκύπτει με –C και τέλος μεταφέρουμε τους συντελεστές για τις μεταβλητές x και y στους παρονομαστές: 
Θεωρήστε την εξίσωση μιας ευθείας που διέρχεται από ένα σημείο και ένα κανονικό διάνυσμα. Έστω ένα σημείο και ένα μη μηδενικό διάνυσμα στο σύστημα συντεταγμένων (Εικ. 1).
Ορισμός
Όπως μπορούμε να δούμε, υπάρχει μια ενιαία ευθεία γραμμή που διέρχεται από το σημείο που είναι κάθετο προς την κατεύθυνση του διανύσματος (στην περίπτωση αυτή ονομάζεται κανονικό διάνυσμαευθεία ).

Ρύζι. 1
Ας αποδείξουμε ότι η γραμμική εξίσωση
αυτή είναι μια εξίσωση μιας ευθείας, δηλαδή, οι συντεταγμένες κάθε σημείου της ευθείας ικανοποιούν την εξίσωση (1), αλλά οι συντεταγμένες ενός σημείου που δεν βρίσκεται πάνω δεν ικανοποιούν την εξίσωση (1).
Για να το αποδείξουμε αυτό, ας σημειώσουμε ότι το βαθμωτό γινόμενο των διανυσμάτων και = σε μορφή συντεταγμένων συμπίπτει με την αριστερή πλευρά της εξίσωσης (1).
Στη συνέχεια χρησιμοποιούμε την προφανή ιδιότητα της ευθείας: τα διανύσματα και είναι κάθετα αν και μόνο αν το σημείο βρίσκεται στο . Και με την προϋπόθεση ότι και τα δύο διανύσματα είναι κάθετα, το βαθμωτό γινόμενο τους (2) μετατρέπεται σε για όλα τα σημεία που βρίσκονται και μόνο για αυτά. Αυτό το μέσο (1) είναι η εξίσωση της ευθείας γραμμής.
Ορισμός
Καλείται η εξίσωση (1). εξίσωση της ευθείας που διέρχεται από ένα δεδομένο σημείομε κανονικό διάνυσμα = .
Ας μετατρέψουμε την εξίσωση (1)
Δηλώνοντας = , παίρνουμε
Έτσι, μια γραμμική εξίσωση της μορφής (3) αντιστοιχεί σε μια ευθεία γραμμή. Αντίθετα, χρησιμοποιώντας μια δεδομένη εξίσωση της μορφής (3), όπου τουλάχιστον ένας από τους συντελεστές δεν είναι ίσος με μηδέν, μπορεί να κατασκευαστεί μια ευθεία γραμμή.
Πράγματι, έστω ένα ζεύγος αριθμών ικανοποιεί την εξίσωση (3), δηλαδή
Αφαιρώντας το τελευταίο από το (3), παίρνουμε τη σχέση που καθορίζει την ευθεία πίσω από το διάνυσμα και το σημείο.
Μελέτη της γενικής εξίσωσης μιας ευθείας
Είναι χρήσιμο να γνωρίζετε τα χαρακτηριστικά της τοποθέτησης μιας γραμμής σε ορισμένες περιπτώσεις όταν ένας ή δύο από τους αριθμούς είναι ίσοι με μηδέν.
1. Η γενική εξίσωση μοιάζει με αυτό: . Το σημείο το ικανοποιεί, που σημαίνει ότι η γραμμή διέρχεται από την αρχή. Μπορεί να γραφεί: = – x (βλ. Εικ. 2).

Ρύζι. 2
Πιστεύουμε ότι:
Αν βάλουμε , τότε , παίρνουμε ένα άλλο σημείο (βλ. Εικ. 2).
2. , τότε η εξίσωση μοιάζει με αυτό, όπου = –. Το κανονικό διάνυσμα βρίσκεται στον άξονα, μια ευθεία γραμμή. Έτσι, η ευθεία είναι κάθετη στο σημείο , ή παράλληλη προς τον άξονα (βλ. Εικ. 3). Συγκεκριμένα, αν και , τότε και η εξίσωση είναι η εξίσωση του άξονα τεταγμένων.

Ρύζι. 3
3. Ομοίως, όταν γράφεται η εξίσωση, όπου . Το διάνυσμα ανήκει στον άξονα. Ευθεία γραμμή σε σημείο (Εικ. 4).

Αν, τότε η εξίσωση του άξονα είναι .
Η μελέτη μπορεί να διατυπωθεί με αυτή τη μορφή: η ευθεία είναι παράλληλη προς τον άξονα συντεταγμένων, η αλλαγή του οποίου απουσιάζει στη γενική εξίσωση της ευθείας.
Για παράδειγμα:
Ας κατασκευάσουμε μια ευθεία γραμμή χρησιμοποιώντας τη γενική εξίσωση, με την προϋπόθεση ότι - δεν είναι ίσα με το μηδέν. Για να γίνει αυτό, αρκεί να βρείτε δύο σημεία που βρίσκονται σε αυτή τη γραμμή. Μερικές φορές είναι πιο βολικό να βρίσκουμε τέτοια σημεία σε άξονες συντεταγμένων.
Ας μας λοιπόν = –.
Όταν , τότε = –.
Ας συμβολίσουμε – = , – = . Πόντοι και βρέθηκαν. Ας σχεδιάσουμε και σχεδιάσουμε μια ευθεία γραμμή στους άξονες και μέσα από αυτούς (βλ. Εικ. 5).

Ρύζι. 5
Από το γενικό, μπορείτε να προχωρήσετε σε μια εξίσωση που θα περιλαμβάνει τους αριθμούς και:
Και μετά αποδεικνύεται:
Ή, σύμφωνα με τη σημείωση, λαμβάνουμε την εξίσωση
Η οποία ονομάζεται εξίσωση ευθείας σε τμήματα. Οι αριθμοί και, με ακρίβεια στο πρόσημο, είναι ίσοι με τα τμήματα που κόβονται με ευθεία γραμμή στους άξονες συντεταγμένων.
Εξίσωση ευθείας με κλίση
Για να μάθετε ποια είναι η εξίσωση μιας ευθείας με μια κλίση, εξετάστε την εξίσωση (1):
Δηλώνοντας – = , παίρνουμε
εξίσωση μιας ευθείας που διέρχεται από ένα σημείο σε μια δεδομένη κατεύθυνση. Το γεωμετρικό περιεχόμενο του συντελεστή είναι σαφές από το Σχ. 6.
B = = , όπου είναι η μικρότερη γωνία κατά την οποία η θετική κατεύθυνση του άξονα πρέπει να περιστραφεί γύρω από το κοινό σημείο μέχρι να ευθυγραμμιστεί με την ευθεία. Προφανώς, εάν η γωνία είναι οξεία, τότε title="Rendered by QuickLaTeX.com" height="17" width="97" style="vertical-align: -4px;">; если же – тупой угол, тогда .!}
Ας ανοίξουμε τις αγκύλες στο (5) και ας το απλοποιήσουμε:
Οπου . Σχέση (6) – εξίσωση ευθεία με κλίση. Όταν , είναι ένα τμήμα που κόβει μια ευθεία γραμμή στον άξονα (βλ. Εικ. 6).
Σημείωση!
Για να μετακινηθείτε από μια γενική εξίσωση ευθείας γραμμής σε μια εξίσωση με συντελεστή κλίσης, πρέπει πρώτα να λύσετε για .

Ρύζι. 6
= – x + – =
όπου συμβολίζεται = –, = –. Αν, τότε από τη μελέτη της γενικής εξίσωσης είναι ήδη γνωστό ότι μια τέτοια ευθεία είναι κάθετη στον άξονα.
Ας δούμε την κανονική εξίσωση μιας ευθείας χρησιμοποιώντας ένα παράδειγμα.
Έστω ένα σημείο και ένα μη μηδενικό διάνυσμα στο σύστημα συντεταγμένων (Εικ. 7).

Ρύζι. 7
Είναι απαραίτητο να δημιουργηθεί μια εξίσωση για μια ευθεία που διέρχεται από ένα σημείο παράλληλο προς το διάνυσμα, το οποίο ονομάζεται διάνυσμα κατεύθυνσης. Ένα αυθαίρετο σημείο ανήκει σε αυτή τη γραμμή εάν και μόνο εάν . Εφόσον το διάνυσμα είναι δεδομένο και το διάνυσμα είναι , τότε, σύμφωνα με τη συνθήκη παραλληλισμού, οι συντεταγμένες αυτών των διανυσμάτων είναι ανάλογες, δηλαδή:
Ορισμός
Σχέση (7) ονομάζεται η εξίσωση μιας ευθείας που διέρχεται από ένα δεδομένο σημείο σε μια δεδομένη κατεύθυνση ή η κανονική εξίσωση μιας ευθείας.
Ας σημειώσουμε ότι μπορούμε να μεταβούμε σε μια εξίσωση της μορφής (7), για παράδειγμα, από την εξίσωση ενός μολυβιού γραμμών (4)
ή από την εξίσωση μιας ευθείας γραμμής μέσω ενός σημείου και ενός κανονικού διανύσματος (1):
Θεωρήθηκε παραπάνω ότι το διάνυσμα κατεύθυνσης είναι μη μηδενικό, αλλά μπορεί να συμβεί μια από τις συντεταγμένες του, για παράδειγμα, . Στη συνέχεια, η έκφραση (7) θα γραφτεί επίσημα:
που δεν βγάζει καθόλου νόημα. Δεχόμαστε όμως και παίρνουμε την εξίσωση της κάθετης στον άξονα ευθείας. Πράγματι, από την εξίσωση είναι σαφές ότι η ευθεία ορίζεται από ένα σημείο και ένα διάνυσμα κατεύθυνσης κάθετα στον άξονα. Εάν αφαιρέσουμε τον παρονομαστή από αυτήν την εξίσωση, τότε παίρνουμε:
Ή - η εξίσωση μιας ευθείας γραμμής κάθετης στον άξονα. Ένα παρόμοιο αποτέλεσμα θα ληφθεί για το διάνυσμα.
Παραμετρική εξίσωση γραμμής
Για να κατανοήσετε τι είναι μια παραμετρική εξίσωση μιας γραμμής, πρέπει να επιστρέψετε στην εξίσωση (7) και να εξισώσετε κάθε κλάσμα (7) με μια παράμετρο. Εφόσον τουλάχιστον ένας από τους παρονομαστές στο (7) δεν είναι ίσος με μηδέν και ο αντίστοιχος αριθμητής μπορεί να αποκτήσει αυθαίρετες τιμές, τότε η περιοχή αλλαγής παραμέτρου είναι ολόκληρος ο αριθμητικός άξονας.
Ορισμός
Η εξίσωση (8) ονομάζεται παραμετρική εξίσωση μιας ευθείας.
Παραδείγματα προβλημάτων ευθείας γραμμής
Φυσικά, είναι δύσκολο να λύσετε οτιδήποτε μόνο με βάση τους ορισμούς, γιατί πρέπει να λύσετε μόνοι σας τουλάχιστον μερικά παραδείγματα ή προβλήματα που θα σας βοηθήσουν να εμπεδώσετε το υλικό που καλύψατε. Επομένως, ας αναλύσουμε τις κύριες εργασίες σε ευθεία γραμμή, καθώς παρόμοια προβλήματα συναντώνται συχνά σε εξετάσεις και τεστ.
Κανονική και παραμετρική εξίσωση
Παράδειγμα 1
Σε μια ευθεία που δίνεται από την εξίσωση, βρείτε ένα σημείο που βρίσκεται σε απόσταση 10 μονάδων από το σημείο αυτής της ευθείας.
Λύση:
Αφήνω περιζήτητοςσημείο μιας ευθείας γραμμής, τότε για την απόσταση γράφουμε . Δεδομένου ότι . Εφόσον το σημείο ανήκει σε μια γραμμή που έχει κανονικό διάνυσμα, τότε η εξίσωση της ευθείας μπορεί να γραφτεί: = = και τότε προκύπτει:
Μετά η απόσταση. Με την επιφύλαξη , ή . Από την παραμετρική εξίσωση:
Παράδειγμα 2
Εργο
Το σημείο κινείται ομοιόμορφα με ταχύτητα προς την κατεύθυνση του διανύσματος από το σημείο εκκίνησης. Βρείτε τις συντεταγμένες του σημείου από την αρχή της κίνησης.
Λύση
Πρώτα πρέπει να βρείτε το μοναδιαίο διάνυσμα. Οι συντεταγμένες του είναι συνημίτονο κατεύθυνσης:
Τότε το διάνυσμα της ταχύτητας:
X = x = .
Η κανονική εξίσωση της γραμμής θα γραφτεί τώρα:
= = , = – παραμετρική εξίσωση. Μετά από αυτό, πρέπει να χρησιμοποιήσετε την παραμετρική εξίσωση της ευθείας στο .
Λύση:
Η εξίσωση μιας ευθείας που διέρχεται από ένα σημείο βρίσκεται χρησιμοποιώντας τον τύπο για ένα μολύβι γραμμών, όπου κλίσηγια ευθεία γραμμή και = για ευθεία γραμμή.
Λαμβάνοντας υπόψη το σχήμα, όπου μπορείτε να δείτε ότι μεταξύ ευθειών και - υπάρχουν δύο γωνίες: η μία είναι οξεία και η δεύτερη είναι αμβλεία. Σύμφωνα με τον τύπο (9), αυτή είναι η γωνία μεταξύ των ευθειών και κατά την οποία πρέπει να περιστρέψετε την ευθεία αριστερόστροφα σε σχέση με το σημείο τομής τους μέχρι να ευθυγραμμιστεί με την ευθεία .

Έτσι, θυμηθήκαμε τον τύπο, καταλάβαμε τις γωνίες και τώρα μπορούμε να επιστρέψουμε στο παράδειγμά μας. Αυτό σημαίνει ότι, λαμβάνοντας υπόψη τον τύπο (9), βρίσκουμε πρώτα τις εξισώσεις του σκέλους.

Εφόσον η περιστροφή της ευθείας κατά γωνία αριστερόστροφα σε σχέση με το σημείο οδηγεί σε ευθυγράμμιση με την ευθεία, τότε στον τύπο (9) , a . Από την εξίσωση:
Χρησιμοποιώντας τον τύπο της δέσμης, θα γραφεί η εξίσωση μιας ευθείας γραμμής:
Ομοίως βρίσκουμε και ,
Εξίσωση γραμμής:
Εξίσωση ευθείας – είδη εξίσωσης ευθείας: διέλευση από σημείο, γενική, κανονική, παραμετρική κ.λπ.ενημερώθηκε: 22 Νοεμβρίου 2019 από: Επιστημονικά άρθρα.Ru
Ιδιότητες ευθείας στην Ευκλείδεια γεωμετρία.
Ένας άπειρος αριθμός ευθειών μπορεί να σχεδιαστεί σε οποιοδήποτε σημείο.
Μέσω οποιωνδήποτε δύο σημείων που δεν συμπίπτουν μπορεί να σχεδιαστεί μια ευθεία γραμμή.
Δύο αποκλίνουσες ευθείες σε ένα επίπεδο είτε τέμνονται σε ένα μόνο σημείο είτε είναι
παράλληλη (ακολουθεί από την προηγούμενη).
Στον τρισδιάστατο χώρο, υπάρχουν τρεις επιλογές για τη σχετική θέση δύο γραμμών:
- γραμμές τέμνονται?
- οι γραμμές είναι παράλληλες.
- ευθείες γραμμές τέμνονται.
Ευθεία γραμμή— αλγεβρική καμπύλη πρώτης τάξης: ευθεία γραμμή στο καρτεσιανό σύστημα συντεταγμένων
δίνεται στο επίπεδο από εξίσωση πρώτου βαθμού (γραμμική εξίσωση).
Γενική εξίσωση ευθείας γραμμής.
Ορισμός. Οποιαδήποτε ευθεία γραμμή στο επίπεδο μπορεί να προσδιοριστεί με μια εξίσωση πρώτης τάξης
Ax + Wu + C = 0,
και σταθερό Α, Βδεν είναι ίσα με μηδέν ταυτόχρονα. Αυτή η εξίσωση πρώτης τάξης ονομάζεται γενικός
εξίσωση ευθείας γραμμής.Ανάλογα με τις τιμές των σταθερών Α, ΒΚαι ΜΕΕίναι δυνατές οι ακόλουθες ειδικές περιπτώσεις:
. C = 0, A ≠0, B ≠ 0- μια ευθεία διέρχεται από την αρχή
. A = 0, B ≠0, C ≠0 (By + C = 0)- ευθεία παράλληλη προς τον άξονα Ω
. B = 0, A ≠0, C ≠ 0 (Ax + C = 0)- ευθεία παράλληλη προς τον άξονα OU
. B = C = 0, A ≠0- η ευθεία συμπίπτει με τον άξονα OU
. A = C = 0, B ≠0- η ευθεία συμπίπτει με τον άξονα Ω
Η εξίσωση μιας ευθείας γραμμής μπορεί να παρουσιαστεί με διαφορετικές μορφές ανάλογα με κάθε δεδομένο
αρχικές συνθήκες.
Εξίσωση ευθείας από σημείο και κανονικό διάνυσμα.
Ορισμός. Σε ένα καρτεσιανό ορθογώνιο σύστημα συντεταγμένων, ένα διάνυσμα με συνιστώσες (Α, Β)
κάθετη στην ευθεία που δίνεται από την εξίσωση
Ax + Wu + C = 0.
Παράδειγμα. Να βρείτε την εξίσωση μιας ευθείας που διέρχεται από ένα σημείο A(1, 2)κάθετο στο διάνυσμα (3, -1).
Λύση. Με A = 3 και B = -1, ας συνθέσουμε την εξίσωση της ευθείας: 3x - y + C = 0. Για να βρούμε τον συντελεστή C
Ας αντικαταστήσουμε τις συντεταγμένες του δεδομένου σημείου Α στην παράσταση που προκύπτει. Παίρνουμε: 3 - 2 + C = 0, επομένως
C = -1. Σύνολο: η απαιτούμενη εξίσωση: 3x - y - 1 = 0.
Εξίσωση ευθείας που διέρχεται από δύο σημεία.
Αφήστε δύο σημεία να δίνονται στο διάστημα M 1 (x 1 , y 1 , z 1)Και M2 (x 2, y 2, z 2),Επειτα εξίσωση μιας γραμμής,
περνώντας από αυτά τα σημεία:
Εάν κάποιος από τους παρονομαστές είναι μηδέν, ο αντίστοιχος αριθμητής πρέπει να ισούται με μηδέν. Επί
επίπεδο, η εξίσωση της ευθείας που γράφτηκε παραπάνω απλοποιείται:

Αν x 1 ≠ x 2Και x = x 1, Αν x 1 = x 2 .
Κλάσμα = κπου ονομάζεται κλίση ευθεία.
Παράδειγμα. Να βρείτε την εξίσωση της ευθείας που διέρχεται από τα σημεία A(1, 2) και B(3, 4).
Λύση. Εφαρμόζοντας τον τύπο που γράφτηκε παραπάνω, παίρνουμε:

Εξίσωση ευθείας με χρήση σημείου και κλίσης.
Αν η γενική εξίσωση της ευθείας Ax + Wu + C = 0οδηγεί σε:

και ορίζουν  , τότε καλείται η εξίσωση που προκύπτει
, τότε καλείται η εξίσωση που προκύπτει
εξίσωση ευθείας με κλίση k.
Εξίσωση ευθείας από σημείο και διάνυσμα κατεύθυνσης.
Κατ' αναλογία με το σημείο που εξετάζει την εξίσωση μιας ευθείας γραμμής μέσω του κανονικού διανύσματος, μπορείτε να εισαγάγετε την εργασία
μια ευθεία γραμμή μέσα από ένα σημείο και ένα κατευθυντικό διάνυσμα μιας ευθείας γραμμής.
Ορισμός. Κάθε μη μηδενικό διάνυσμα (α 1 , α 2), τα συστατικά του οποίου ικανοποιούν την προϋπόθεση
Αα 1 + Βα 2 = 0που ονομάζεται κατευθυντικό διάνυσμα μιας ευθείας γραμμής.
Ax + Wu + C = 0.
Παράδειγμα. Να βρείτε την εξίσωση μιας ευθείας με διάνυσμα κατεύθυνσης (1, -1) και που διέρχεται από το σημείο Α(1, 2).
Λύση. Θα αναζητήσουμε την εξίσωση της επιθυμητής γραμμής με τη μορφή: Ax + By + C = 0.Σύμφωνα με τον ορισμό,
Οι συντελεστές πρέπει να πληρούν τις ακόλουθες προϋποθέσεις:
1 * A + (-1) * B = 0, δηλ. Α = Β.
Τότε η εξίσωση της ευθείας έχει τη μορφή: Ax + Ay + C = 0,ή x + y + C / A = 0.
στο x = 1, y = 2παίρνουμε C/A = -3, δηλ. απαιτούμενη εξίσωση:
x + y - 3 = 0
Εξίσωση ευθείας σε τμήματα.
Αν στη γενική εξίσωση της ευθείας Αх + Ву + С = 0 С≠0, τότε, διαιρώντας με -С, παίρνουμε:
 ή πού
ή πού

Η γεωμετρική σημασία των συντελεστών είναι ότι ο συντελεστής a είναι η συντεταγμένη του σημείου τομής
ευθεία με άξονα Ω,ΕΝΑ σι- συντεταγμένη του σημείου τομής της ευθείας με τον άξονα OU.
Παράδειγμα. Δίνεται η γενική εξίσωση μιας ευθείας x - y + 1 = 0.Βρείτε την εξίσωση αυτής της ευθείας σε τμήματα.
C = 1, , a = -1, b = 1.
Κανονική εξίσωση μιας γραμμής.
Αν και οι δύο πλευρές της εξίσωσης Ax + Wu + C = 0διαιρέστε με αριθμό  η οποία ονομάζεται
η οποία ονομάζεται
κανονικοποιητικό παράγοντα, τότε παίρνουμε
xcosφ + ysinφ - p = 0 -κανονική εξίσωση μιας γραμμής.
Το πρόσημο ± του κανονικοποιητικού παράγοντα πρέπει να επιλέγεται έτσι ώστε μ*C< 0.
R- το μήκος της καθέτου που έπεσε από την αρχή στην ευθεία,
ΕΝΑ φ - τη γωνία που σχηματίζει αυτή η κάθετη με τη θετική φορά του άξονα Ω.
Παράδειγμα. Δίνεται η γενική εξίσωση της ευθείας 12x - 5y - 65 = 0. Απαιτείται για τη σύνταξη διαφορετικών τύπων εξισώσεων
αυτή η ευθεία γραμμή.
Η εξίσωση αυτής της ευθείας σε τμήματα:

Η εξίσωση αυτής της ευθείας με την κλίση: (διαιρέστε με 5)

Εξίσωση μιας ευθείας:

cos φ = 12/13; αμαρτία φ= -5/13; p = 5.
Πρέπει να σημειωθεί ότι δεν μπορεί να αναπαρασταθεί κάθε ευθεία με μια εξίσωση σε τμήματα, για παράδειγμα, ευθείες,
παράλληλα με τους άξονες ή περνώντας από την αρχή.
Η γωνία μεταξύ ευθειών σε ένα επίπεδο.
Ορισμός. Αν δίνονται δύο γραμμές y = k 1 x + b 1, y = k 2 x + b 2, τότε η οξεία γωνία μεταξύ αυτών των γραμμών
θα οριστεί ως

Δύο ευθείες είναι παράλληλες αν k 1 = k 2. Δύο ευθείες είναι κάθετες
Αν k 1 = -1 / k 2 .
Θεώρημα.
Απευθείας Ax + Wu + C = 0Και A 1 x + B 1 y + C 1 = 0παράλληλη όταν οι συντελεστές είναι ανάλογοι
A 1 = λA, B 1 = λB. Αν επίσης С 1 = λС, τότε οι γραμμές συμπίπτουν. Συντεταγμένες του σημείου τομής δύο ευθειών
βρίσκονται ως λύση στο σύστημα εξισώσεων αυτών των γραμμών.
Η εξίσωση μιας ευθείας που διέρχεται από ένα δεδομένο σημείο κάθετο σε μια δεδομένη ευθεία.
Ορισμός. Γραμμή που διέρχεται από ένα σημείο M 1 (x 1, y 1)και κάθετα στη γραμμή y = kx + b
παριστάνεται από την εξίσωση:

Απόσταση από ένα σημείο σε μια γραμμή.
Θεώρημα. Αν δοθεί ένας βαθμός M(x 0, y 0),τότε η απόσταση από την ευθεία Ax + Wu + C = 0οριζεται ως:

Απόδειξη. Αφήστε το θέμα M 1 (x 1, y 1)- η βάση μιας κάθετης έπεσε από ένα σημείο Μγια ένα δεδομένο
απευθείας. Στη συνέχεια η απόσταση μεταξύ των σημείων ΜΚαι Μ 1:
![]() (1)
(1)
Συντεταγμένες x 1Και στο 1μπορεί να βρεθεί ως λύση στο σύστημα εξισώσεων:

Η δεύτερη εξίσωση του συστήματος είναι η εξίσωση μιας ευθείας που διέρχεται από ένα δεδομένο σημείο M 0 κάθετα
δεδομένη ευθεία γραμμή. Αν μετατρέψουμε την πρώτη εξίσωση του συστήματος στη μορφή:
A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,
τότε, λύνοντας, παίρνουμε:

Αντικαθιστώντας αυτές τις εκφράσεις στην εξίσωση (1), βρίσκουμε:

Το θεώρημα έχει αποδειχθεί.
 Νικολάι Μαρτίνοφ, ο οποίος σκότωσε τον Μ σε μια μονομαχία
Νικολάι Μαρτίνοφ, ο οποίος σκότωσε τον Μ σε μια μονομαχία Προβολές του διανύσματος μετατόπισης Ενότητα μετατόπισης σώματος σε βάθος χρόνου
Προβολές του διανύσματος μετατόπισης Ενότητα μετατόπισης σώματος σε βάθος χρόνου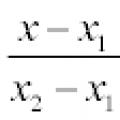 Εξίσωση ευθείας - είδη εξίσωσης ευθείας: διέλευση από σημείο, γενική, κανονική, παραμετρική κ.λπ.
Εξίσωση ευθείας - είδη εξίσωσης ευθείας: διέλευση από σημείο, γενική, κανονική, παραμετρική κ.λπ.