Logaritmid: näited ja lahendused. Logaritm - omadused, valemid, graafik Logaritmide põhiomadused
\(a^(b)=c\) \(\Leftparemnool\) \(\log_(a)(c)=b\)
Selgitame seda lihtsamalt. Näiteks \(\log_(2)(8)\) on võrdne astmega, milleni \(2\) tuleb \(8\) saamiseks tõsta. Sellest on selge, et \(\log_(2)(8)=3\).
|
Näited: |
\(\log_(5)(25)=2\) |
sest \(5^(2)=25\) |
||
|
\(\log_(3)(81)=4\) |
sest \(3^(4)=81\) |
|||
|
\(\log_(2)\)\(\frac(1)(32)\) \(=-5\) |
sest \(2^(-5)=\)\(\frac(1)(32)\) |
Argument ja logaritmi alus
Igal logaritmil on järgmine "anatoomia":
Logaritmi argument kirjutatakse tavaliselt selle tasemel ja alus kirjutatakse logaritmi märgile lähemal asuvas alaindeksis. Ja see sissekanne kõlab järgmiselt: "logaritm kahekümne viiest põhiviieni."
Kuidas arvutada logaritmi?
Logaritmi arvutamiseks peate vastama küsimusele: millisele astmele tuleks argumendi saamiseks baasi tõsta?
Näiteks, arvuta logaritm: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\) sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)
a) Millise astmeni tuleb \(4\) tõsta, et saada \(16\)? Ilmselgelt teine. Sellepärast:
\(\log_(4)(16)=2\)
\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)
c) Millise astmeni tuleb \(\sqrt(5)\) tõsta, et saada \(1\)? Milline jõud teeb ükskõik millisest esikoha? Null, muidugi!
\(\log_(\sqrt(5))(1)=0\)
d) Millise astmeni tuleb \(\sqrt(7)\) suurendada, et saada \(\sqrt(7)\)? Esiteks on suvaline arv esimese astmeni võrdne iseendaga.
\(\log_(\sqrt(7))(\sqrt(7))=1\)
e) Millise astmeni tuleb \(3\) tõsta, et saada \(\sqrt(3)\)? Me teame, et see on murdarvu aste, mis tähendab, et ruutjuur on astme \(\frac(1)(2)\) aste.
\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)
Näide : Arvutage logaritm \(\log_(4\sqrt(2))(8)\)
Lahendus :
|
\(\log_(4\sqrt(2))(8)=x\) |
Peame leidma logaritmi väärtuse, tähistame seda kui x. Nüüd kasutame logaritmi määratlust: |
|
|
\((4\sqrt(2))^(x)=8\) |
Mis ühendab \(4\sqrt(2)\) ja \(8\)? Kaks, sest mõlemat numbrit saab esitada kahega: |
|
|
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\) |
Vasakul kasutame astme omadusi: \(a^(m)\cdot a^(n)=a^(m+n)\) ja \((a^(m))^(n)= a^(m\cdot n)\) |
|
|
\(2^(\frac(5)(2)x)=2^(3)\) |
Alused on võrdsed, liigume edasi näitajate võrdsuse juurde |
|
|
\(\frac(5x)(2)\) \(=3\) |
|
Korrutage võrrandi mõlemad pooled arvuga \(\frac(2)(5)\) |
|
|
Saadud juur on logaritmi väärtus |
Vastus : \(\log_(4\sqrt(2))(8)=1,2\)
Miks leiutati logaritm?
Selle mõistmiseks lahendame võrrandi: \(3^(x)=9\). Võrrandi toimimiseks sobitage lihtsalt \(x\). Muidugi \(x=2\).
Nüüd lahendage võrrand: \(3^(x)=8\). Millega x võrdub? See on asja mõte.
Targemad ütlevad: "X on natuke vähem kui kaks." Kuidas seda numbrit täpselt kirjutada? Sellele küsimusele vastamiseks leiutati logaritm. Tänu temale saab siin vastuse kirjutada kujul \(x=\log_(3)(8)\).
Tahan rõhutada, et \(\log_(3)(8)\), meeldib iga logaritm on vaid arv. Jah, see tundub ebatavaline, kuid on lühike. Sest kui sooviksime seda kirjutada kümnendkohana, näeks see välja järgmine: \(1.892789260714.....\)
Näide : lahendage võrrand \(4^(5x-4)=10\)
Lahendus :
|
\(4^(5x-4)=10\) |
\(4^(5x-4)\) ja \(10\) ei saa tuua samasse baasi. See tähendab, et te ei saa ilma logaritmita hakkama. Kasutame logaritmi definitsiooni: |
|
|
\(\log_(4)(10)=5x-4\) |
Pöörame võrrandi ümber nii, et X on vasakul |
|
|
\(5x-4=\log_(4)(10)\) |
Enne meid. Liigume \(4\) paremale. Ja ärge kartke logaritmi, käsitlege seda kui tavalist arvu. |
|
|
\(5x=\log_(4)(10)+4\) |
Jagage võrrand 5-ga |
|
|
\(x=\)\(\frac(\log_(4)(10)+4)(5)\) |
|
See on meie juur. Jah, see tundub ebatavaline, kuid nad ei vali vastust. |
Vastus : \(\frac(\log_(4)(10)+4)(5)\)
Kümnend- ja naturaallogaritmid
Nagu on öeldud logaritmi definitsioonis, võib selle alus olla mis tahes positiivne arv, välja arvatud üks \((a>0, a\neq1)\). Ja kõigi võimalike aluste hulgas on kaks, mis esinevad nii sageli, et nendega koos olevate logaritmide jaoks leiutati spetsiaalne lühike tähistus:
Naturaalne logaritm: logaritm, mille alus on Euleri arv \(e\) (võrdub ligikaudu \(2,7182818…\)) ja logaritm on kirjutatud kujul \(\ln(a)\).
See on, \(\ln(a)\) on sama mis \(\log_(e)(a)\)
Kümnendlogaritm: Logaritm, mille alus on 10, kirjutatakse \(\lg(a)\).
See on, \(\lg(a)\) on sama mis \(\log_(10)(a)\), kus \(a\) on mingi arv.
Põhiline logaritmiline identiteet
Logaritmidel on palju omadusi. Ühte neist nimetatakse "põhilogaritmiliseks identiteediks" ja see näeb välja järgmine:
| \(a^(\log_(a)(c))=c\) |
See omadus tuleneb otseselt määratlusest. Vaatame täpselt, kuidas see valem tekkis.
Tuletagem meelde logaritmi määratluse lühikest tähistust:
kui \(a^(b)=c\), siis \(\log_(a)(c)=b\)
See tähendab, et \(b\) on sama mis \(\log_(a)(c)\). Siis saame valemis \(a^(b)=c\) kirjutada \(\log_(a)(c)\) asemel \(b\). Selgus \(a^(\log_(a)(c))=c\) - peamine logaritmiline identiteet.
Saate leida muid logaritmide omadusi. Nende abiga saate lihtsustada ja arvutada avaldiste väärtusi logaritmidega, mida on raske otse arvutada.
Näide : leidke avaldise \(36^(\log_(6)(5))\) väärtus
Lahendus :
Vastus : \(25\)
Kuidas kirjutada arv logaritmina?
Nagu eespool mainitud, on iga logaritm vaid arv. Tõsi on ka vastupidi: logaritmina saab kirjutada mis tahes arvu. Näiteks teame, et \(\log_(2)(4)\) on võrdne kahega. Siis saab kahe asemel kirjutada \(\log_(2)(4)\).
Kuid \(\log_(3)(9)\) võrdub ka \(2\), mis tähendab, et saame kirjutada ka \(2=\log_(3)(9)\) . Samamoodi \(\log_(5)(25)\) ja \(\log_(9)(81)\) jne. See tähendab, et selgub
\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)
Seega võime vajaduse korral kirjutada kaks logaritmina suvalise alusega ükskõik kuhu (olgu see siis võrrandisse, avaldisesse või võrratusse) – me kirjutame aluse lihtsalt argumendina ruudus.
Sama on kolmikuga – selle saab kirjutada kui \(\log_(2)(8)\), või \(\log_(3)(27)\) või \(\log_(4)( 64) \)... Siin kirjutame argumendina kuubi aluse:
\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)
Ja neljaga:
\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)
Ja miinus ühega:
\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1) (7)\) \(...\)
Ja ühe kolmandikuga:
\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)
Mis tahes arvu \(a\) saab esitada logaritmina alusega \(b\): \(a=\log_(b)(b^(a))\)
Näide : Leia väljendi tähendus \(\frac(\log_(2)(14))(1+\log_(2)(7))\)
Lahendus :
Vastus : \(1\)
Logaritme, nagu kõiki numbreid, saab igati liita, lahutada ja teisendada. Aga kuna logaritmid pole päris tavalised arvud, siis siin kehtivad reeglid, mida kutsutakse peamised omadused.
Neid reegleid pead kindlasti teadma – ilma nendeta ei saa lahendada ühtegi tõsist logaritmiülesannet. Lisaks on neid väga vähe – ühe päevaga saab kõik selgeks. Nii et alustame.
Logaritmide liitmine ja lahutamine
Vaatleme kahte samade alustega logaritmi: log a x ja logi a y. Seejärel saab neid liita ja lahutada ning:
- logi a x+ palk a y=logi a (x · y);
- logi a x− logi a y=logi a (x : y).
Seega on logaritmide summa võrdne korrutise logaritmiga ja erinevus on võrdne jagatise logaritmiga. Pange tähele: võtmepunkt on siin identsed põhjused. Kui põhjused on erinevad, siis need reeglid ei tööta!
Need valemid aitavad teil arvutada logaritmilise avaldise isegi siis, kui selle üksikuid osi ei arvestata (vt õppetundi "Mis on logaritm"). Vaadake näiteid ja vaadake:
Palk 6 4 + palk 6 9.
Kuna logaritmidel on samad alused, kasutame summa valemit:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Ülesanne. Leidke avaldise väärtus: log 2 48 − log 2 3.
Alused on samad, kasutame erinevuse valemit:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Ülesanne. Leidke avaldise väärtus: log 3 135 − log 3 5.
Jällegi on alused samad, seega on meil:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
Nagu näete, koosnevad algsed avaldised "halbadest" logaritmidest, mida eraldi ei arvutata. Kuid pärast teisendusi saadakse täiesti normaalsed arvud. Paljud testid põhinevad sellel faktil. Jah, ühtsel riigieksamil pakutakse testilaadseid väljendeid täie tõsidusega (mõnikord praktiliselt muudatusteta).
Eksponenti väljavõtmine logaritmist
Teeme nüüd ülesande pisut keerulisemaks. Mis siis, kui logaritmi alus või argument on aste? Seejärel saab selle astme eksponendi logaritmi märgist välja võtta järgmiste reeglite järgi:
On lihtne näha, et viimane reegel järgib kahte esimest. Kuid parem on seda ikkagi meeles pidada - mõnel juhul vähendab see arvutuste mahtu märkimisväärselt.
Muidugi on kõik need reeglid mõistlikud, kui järgitakse logaritmi ODZ-d: a > 0, a ≠ 1, x> 0. Ja veel üks asi: õppige rakendama kõiki valemeid mitte ainult vasakult paremale, vaid ka vastupidi, s.t. Saate sisestada enne logaritmi märki olevad arvud logaritmi endasse. See on see, mida kõige sagedamini nõutakse.
Ülesanne. Leidke avaldise väärtus: log 7 49 6 .
Vabaneme argumendi astmest, kasutades esimest valemit:
log 7 49 6 = 6 log 7 49 = 6 2 = 12
Ülesanne. Leidke väljendi tähendus:
[Pildi pealdis]
Pange tähele, et nimetaja sisaldab logaritmi, mille alus ja argument on täpsed astmed: 16 = 2 4 ; 49 = 7 2. Meil on:
 [Pildi pealdis]
[Pildi pealdis] Ma arvan, et viimane näide nõuab veidi selgitust. Kuhu kadusid logaritmid? Kuni viimase hetkeni töötame ainult nimetajaga. Esitasime seal seisva logaritmi aluse ja argumendi astmetena ning võtsime välja astendajad - saime “kolmekorruselise” murru.
Vaatame nüüd põhifraktsiooni. Lugeja ja nimetaja sisaldavad sama arvu: log 2 7. Kuna log 2 7 ≠ 0, saame murdosa vähendada - 2/4 jääb nimetajasse. Aritmeetika reeglite järgi saab nelja üle kanda lugejasse, mida ka tehti. Tulemuseks oli vastus: 2.
Üleminek uuele vundamendile
Rääkides logaritmide liitmise ja lahutamise reeglitest, rõhutasin konkreetselt, et need töötavad ainult samade alustega. Mis siis, kui põhjused on erinevad? Mis siis, kui need ei ole sama arvu täpsed astmed?
Appi tulevad uuele sihtasutusele ülemineku valemid. Sõnastame need teoreemi kujul:
Olgu antud logaritmi logi a x. Siis suvalise numbri jaoks c selline, et c> 0 ja c≠ 1, võrdsus on tõene:
[Pildi pealdis]
Eelkõige, kui paneme c = x, saame:
[Pildi pealdis]
Teisest valemist järeldub, et logaritmi alust ja argumenti saab vahetada, kuid sel juhul “pööratakse ümber” kogu avaldis, s.t. logaritm ilmub nimetajasse.
Neid valemeid leidub tavalistes arvavaldistes harva. Seda, kui mugavad need on, saab hinnata ainult logaritmiliste võrrandite ja võrratuste lahendamisel.
Siiski on probleeme, mida ei saa üldse lahendada peale uude sihtasutusse kolimise. Vaatame paari neist:
Ülesanne. Leidke avaldise väärtus: log 5 16 log 2 25.
Pange tähele, et mõlema logaritmi argumendid sisaldavad täpseid võimsusi. Võtame välja näitajad: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;
Nüüd pöörame teist logaritmi ümber:
[Pildi pealdis]Kuna tegurite ümberkorraldamisel korrutis ei muutu, korrutasime rahulikult nelja ja kahega ning seejärel tegelesime logaritmidega.
Ülesanne. Leidke avaldise väärtus: log 9 100 lg 3.
Esimese logaritmi alus ja argument on täpsed võimsused. Paneme selle kirja ja vabaneme indikaatoritest:
[Pildi pealdis]Nüüd vabaneme kümnendlogaritmist, liikudes uuele alusele:
[Pildi pealdis]Põhiline logaritmiline identiteet
Sageli on lahendusprotsessis vaja esitada arv logaritmina antud baasile. Sel juhul aitavad meid järgmised valemid:
Esimesel juhul number n muutub argumendis seisva astme näitajaks. Number n võib olla absoluutselt ükskõik, sest see on lihtsalt logaritmi väärtus.
Teine valem on tegelikult parafraseeritud määratlus. Seda nimetataksegi: logaritmiline põhiidentiteet.
Tegelikult, mis saab siis, kui number b tõsta sellise astmeni, et arv b sellele astmele annab numbri a? See on õige: saate sama numbri a. Lugege see lõik uuesti hoolikalt läbi – paljud inimesed jäävad selle peale kinni.
Nagu uude baasi liikumise valemid, on ka põhilogaritmiline identiteet mõnikord ainus võimalik lahendus.
Ülesanne. Leidke väljendi tähendus:
[Pildi pealdis]
Pange tähele, et log 25 64 = log 5 8 - lihtsalt võttis ruudu logaritmi baasist ja argumendist. Võttes arvesse sama baasiga võimsuste korrutamise reegleid, saame:
[Pildi pealdis]Kui keegi veel ei tea, siis see oli päris ühtse riigieksami ülesanne :)
Logaritmiline ühik ja logaritmiline null
Kokkuvõtteks annan kaks identiteeti, mida vaevalt saab omadusteks nimetada – pigem on need logaritmi definitsiooni tagajärjed. Need esinevad pidevalt probleemides ja tekitavad üllataval kombel probleeme isegi "edasijõudnud" õpilastele.
- logi a a= 1 on logaritmiline ühik. Pidage üks kord meeles: logaritm mis tahes baasile a sellest baasist on võrdne ühega.
- logi a 1 = 0 on logaritmiline null. Alus a võib olla ükskõik milline, kuid kui argument sisaldab ühte, on logaritm võrdne nulliga! Sest a 0 = 1 on definitsiooni otsene tagajärg.
See on kõik omadused. Harjutage kindlasti nende rakendamist! Laadige õppetunni alguses petuleht alla, printige see välja ja lahendage probleemid.
Tuleneb selle määratlusest. Ja nii ka arvu logaritm b põhineb A on defineeritud kui astendaja, milleni arv tuleb tõsta a numbri saamiseks b(logaritm eksisteerib ainult positiivsete arvude puhul).
Sellest sõnastusest järeldub, et arvutus x=log a b, on võrdne võrrandi lahendamisega a x =b. Näiteks, log 2 8 = 3 sest 8 = 2 3 . Logaritmi sõnastus võimaldab põhjendada, et kui b=a c, siis arvu logaritm b põhineb a võrdub Koos. Samuti on selge, et logaritmide teema on tihedalt seotud arvu astmete teemaga.
Logaritmidega, nagu kõigi arvudega, saate hakkama liitmise, lahutamise tehted ja muuta igal võimalikul viisil. Kuid kuna logaritmid ei ole täiesti tavalised arvud, kehtivad siin oma erireeglid, mida nimetatakse peamised omadused.
Logaritmide liitmine ja lahutamine.
Võtame kaks samade alustega logaritmi: logi x Ja logi a y. Seejärel on võimalik teha liitmise ja lahutamise toiminguid:
log a x+ log a y= log a (x·y);
log a x - log a y = log a (x:y).
logi a(x 1 . x 2 . x 3 ... x k) = logi x 1 + logi x 2 + logi x 3 + ... + logi a x k.
Alates logaritmi jagatise teoreem Võib saada veel ühe logaritmi omaduse. On üldteada, et logi a 1 = 0, seega
logi a 1 /b=logi a 1 - palk a b= -log a b.
See tähendab, et on olemas võrdsus:
log a 1 / b = - log a b.
Kahe pöördarvu logaritmid samal põhjusel erinevad üksteisest ainult märgi poolest. Niisiis:
Log 3 9= - log 3 1/9 ; log 5 1 / 125 = -log 5 125.
Jätkame logaritmide uurimist. Selles artiklis räägime sellest logaritmide arvutamine, seda protsessi nimetatakse logaritm. Kõigepealt mõistame logaritmide arvutamist definitsiooni järgi. Järgmisena vaatame, kuidas leitakse logaritmide väärtused nende omaduste abil. Pärast seda keskendume logaritmide arvutamisele teiste logaritmide algselt määratud väärtuste kaudu. Lõpuks õpime kasutama logaritmitabeleid. Kogu teooria on varustatud näidetega koos üksikasjalike lahendustega.
Leheküljel navigeerimine.
Logaritmide arvutamine definitsiooni järgi
Lihtsamal juhul on võimalik teostada üsna kiiresti ja lihtsalt logaritmi leidmine definitsiooni järgi. Vaatame lähemalt, kuidas see protsess toimub.
Selle olemus on esitada arvu b kujul a c, millest logaritmi definitsiooni järgi on arv c logaritmi väärtus. See tähendab, et definitsiooni järgi vastab logaritmi leidmisele järgmine võrduste ahel: log a b=log a a c =c.
Seega taandub logaritmi arvutamine definitsiooni järgi sellise arvu c leidmisele, et a c = b ja arv c ise on logaritmi soovitud väärtus.
Võttes arvesse eelmistes lõikudes toodud teavet, kui logaritmimärgi all olev arv on antud logaritmi aluse teatud astmega, saate kohe näidata, millega logaritm võrdub - see on võrdne eksponendiga. Näitame näidetele lahendusi.
Näide.
Leidke log 2 2 −3 ja arvutage ka arvu e naturaallogaritm 5,3.
Lahendus.
Logaritmi definitsioon võimaldab kohe öelda, et log 2 2 −3 =−3. Tõepoolest, logaritmi märgi all olev arv võrdub baasiga 2 astmega −3.
Samamoodi leiame teise logaritmi: lne 5.3 =5.3.
Vastus:
log 2 2 −3 = −3 ja lne 5,3 =5,3.
Kui logaritmi märgi all olev arv b pole määratud logaritmi aluse astmena, peate hoolikalt uurima, kas on võimalik arvu b esitus esitada kujul a c . Sageli on see esitus üsna ilmne, eriti kui logaritmimärgi all olev arv on võrdne baasiga astmel 1, 2 või 3, ...
Näide.
Arvutage logaritmid log 5 25 ja .
Lahendus.
On lihtne näha, et 25=5 2, see võimaldab arvutada esimese logaritmi: log 5 25=log 5 5 2 =2.
Liigume edasi teise logaritmi arvutamise juurde. Arvu võib esitada astmena 7:  (vaata vajadusel). Seega
(vaata vajadusel). Seega  .
.
Kirjutame kolmanda logaritmi järgmisel kujul ümber. Nüüd näete seda  , millest järeldame, et
, millest järeldame, et  . Seega logaritmi definitsiooni järgi
. Seega logaritmi definitsiooni järgi  .
.
Lühidalt võiks lahenduse kirjutada järgmiselt: .
Vastus:
log 5 25=2, ![]() Ja
Ja  .
.
Kui logaritmimärgi all on piisavalt suur naturaalarv, ei tee paha seda algteguritesse arvestada. Sageli aitab sellist arvu esitada logaritmi aluse mõne astmena ja seetõttu arvutada see logaritm definitsiooni järgi.
Näide.
Leidke logaritmi väärtus.
Lahendus.
Mõned logaritmide omadused võimaldavad kohe määrata logaritmide väärtuse. Nende omaduste hulka kuuluvad ühe logaritmi omadus ja baasiga võrdse arvu logaritmi omadus: log 1 1=log a a 0 =0 ja log a a=log a a 1 =1. See tähendab, et kui logaritmi märgi all on arv 1 või arv a, mis on võrdne logaritmi alusega, siis nendel juhtudel on logaritmid võrdsed vastavalt 0 ja 1-ga.
Näide.
Millega võrdub logaritm ja log10?
Lahendus.
Kuna , siis logaritmi definitsioonist järeldub ![]() .
.
Teises näites langeb logaritmimärgi all olev arv 10 kokku selle alusega, seega kümnendlogaritm kümnend on võrdne ühega, st lg10=lg10 1 =1.
Vastus:
JA lg10=1 .
Pange tähele, et logaritmide arvutamine definitsiooni järgi (mida arutasime eelmises lõigus) eeldab võrdsuse log a a p =p kasutamist, mis on üks logaritmide omadusi.
Praktikas, kui logaritmi märgi all olev arv ja logaritmi alus on hõlpsasti esitatavad teatud arvu astmena, on väga mugav kasutada valemit  , mis vastab logaritmide ühele omadusele. Vaatame selle valemi kasutamist illustreeriva logaritmi leidmise näidet.
, mis vastab logaritmide ühele omadusele. Vaatame selle valemi kasutamist illustreeriva logaritmi leidmise näidet.
Näide.
Arvutage logaritm.
Lahendus.
Vastus:
![]() .
.
Arvutustes kasutatakse ka ülalmainimata logaritmide omadusi, kuid sellest räägime järgmistes lõikudes.
Logaritmide leidmine teiste teadaolevate logaritmide kaudu
Selle lõigu teave jätkab logaritmide omaduste kasutamise teemat nende arvutamisel. Siin on aga põhiline erinevus selles, et logaritmide omadusi kasutatakse algse logaritmi väljendamiseks teise logaritmi kaudu, mille väärtus on teada. Toome selgituseks näite. Oletame, et teame, et log 2 3≈1.584963, siis leiame näiteks log 2 6, tehes logaritmi atribuute kasutades väikese teisenduse: log 2 6=log 2 (2 3)=log 2 2+log 2 3≈ 1+1,584963=2,584963 .
Ülaltoodud näites piisas, kui kasutasime korrutise logaritmi omadust. Palju sagedamini on aga vaja kasutada laiemat logaritmide omaduste arsenali, et arvutada algne logaritm läbi etteantud.
Näide.
Arvutage logaritm 27-st aluseni 60, kui teate, et log 60 2=a ja log 60 5=b.
Lahendus.
Seega peame leidma logi 60 27 . On lihtne näha, et 27 = 3 3 ja algse logaritmi saab astme logaritmi omaduse tõttu ümber kirjutada kujule 3·log 60 3 .
Nüüd vaatame, kuidas väljendada log 60 3 tuntud logaritmide kaudu. Alusega võrdse arvu logaritmi omadus võimaldab kirjutada võrduslogi 60 60=1. Teisest küljest log 60 60=log60(2 2 3 5)= log 60 2 2 +log 60 3+log 60 5= 2·log 60 2+log 60 3+log 60 5 . Seega 2 log 60 2+log 60 3+log 60 5=1. Seega log 60 3=1–2·log 60 2–log 60 5=1–2·a–b.
Lõpuks arvutame algse logaritmi: log 60 27=3 log 60 3= 3·(1−2·a−b)=3−6·a−3·b.
Vastus:
log 60 27=3·(1–2·a-b)=3–6·a-3·b.
Eraldi tasub mainida valemi tähendust üleminekuks vormi uuele logaritmi alusele  . See võimaldab liikuda mis tahes alusega logaritmidelt kindla baasiga logaritmidele, mille väärtused on teada või neid on võimalik leida. Tavaliselt liiguvad nad algsest logaritmist üleminekuvalemi abil logaritmidesse ühes alustest 2, e või 10, kuna nende aluste jaoks on olemas logaritmitabelid, mis võimaldavad nende väärtusi teatud määral arvutada. täpsust. Järgmises lõigus näitame, kuidas seda tehakse.
. See võimaldab liikuda mis tahes alusega logaritmidelt kindla baasiga logaritmidele, mille väärtused on teada või neid on võimalik leida. Tavaliselt liiguvad nad algsest logaritmist üleminekuvalemi abil logaritmidesse ühes alustest 2, e või 10, kuna nende aluste jaoks on olemas logaritmitabelid, mis võimaldavad nende väärtusi teatud määral arvutada. täpsust. Järgmises lõigus näitame, kuidas seda tehakse.
Logaritmitabelid ja nende kasutamine
Ligikaudseks arvutamiseks võib kasutada logaritmi väärtusi logaritmi tabelid. Kõige sagedamini kasutatav 2 aluse logaritmi tabel, naturaallogaritmi tabel ja kümnendlogaritmi tabel. Kümnendarvusüsteemis töötades on mugav kasutada kümne baasil põhinevat logaritmide tabelit. Tema abiga õpime leidma logaritmide väärtusi.





Esitatud tabel võimaldab leida kümnendkoha täpsusega arvude kümnendlogaritmide väärtused vahemikus 1000 kuni 9999 (kolme kümnendkohaga). Analüüsime logaritmi väärtuse leidmise põhimõtet kümnendlogaritmide tabeli abil konkreetse näite abil - nii on see selgem. Leiame log1.256.
Kümnendlogaritmide tabeli vasakpoolsest veerust leiame arvu 1,256 kaks esimest numbrit, st leiame 1,2 (selguse huvides on see arv sinisega ümbritsetud). Arvu kolmas number 1.256 (number 5) asub topeltreast vasakul esimesel või viimasel real (see number on punasega ümbritsetud). Algarvu 1.256 neljas number (number 6) asub topeltreast paremal esimesel või viimasel real (sellele numbrile on ümbritsetud roheline joon). Nüüd leiame numbrid logaritmitabeli lahtritest märgitud rea ja märgitud veergude ristumiskohalt (need numbrid on esile tõstetud oranžiga). Märgitud arvude summa annab kümnendlogaritmi soovitud väärtuse neljanda kümnendkoha täpsusega, st log1,236≈0,0969+0,0021=0,0990.
Kas ülaltoodud tabeli abil on võimalik leida nende arvude kümnendlogaritmide väärtused, mille pärast koma on rohkem kui kolm kohta, samuti nende arvude kümnendlogaritmide väärtused, mis ületavad vahemikku 1 kuni 9,999? Jah, sa saad. Näitame näitega, kuidas seda tehakse.
Arvutame lg102,76332. Kõigepealt peate üles kirjutama number standardkujul: 102,76332=1,0276332·10 2. Pärast seda tuleks mantiss ümardada kolmanda kümnendkohani 1,0276332 10 2 ≈1,028 10 2, samas kui algne kümnendlogaritm on ligikaudu võrdne saadud arvu logaritmiga, st võtame log102.76332≈lg1.028·10 2. Nüüd rakendame logaritmi omadusi: lg1,028·10 2 = lg1,028+lg10 2 = lg1,028+2. Lõpuks leiame kümnendlogaritmide tabelist logaritmi lg1.028 väärtuse lg1.028≈0.0086+0.0034=0.012. Selle tulemusena näeb kogu logaritmi arvutamise protsess välja järgmine: log102.76332=log1.0276332 10 2 ≈lg1.028 10 2 = log1,028+lg10 2 =log1,028+2≈0,012+2=2,012.
Kokkuvõtteks väärib märkimist, et kümnendlogaritmide tabeli abil saate arvutada mis tahes logaritmi ligikaudse väärtuse. Selleks piisab üleminekuvalemi kasutamisest, et minna kümnendlogaritmidele, leida nende väärtused tabelist ja teha ülejäänud arvutused.
Näiteks arvutame log 2 3 . Vastavalt valemile üleminekuks uuele logaritmi alusele on meil . Kümnendlogaritmide tabelist leiame log3≈0,4771 ja log2≈0,3010. Seega,.
Bibliograafia.
- Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. jt.Algebra ja analüüsi alged: Õpik üldharidusasutuste 10. - 11. klassile.
- Gusev V.A., Mordkovich A.G. Matemaatika (käsiraamat tehnikumidesse astujatele).
Antakse logaritmi põhiomadused, logaritmgraaf, definitsioonipiirkond, väärtuste hulk, põhivalemid, suurenemine ja kahanemine. Vaadeldakse logaritmi tuletise leidmist. Nagu ka integraal, astmeridade laiendamine ja esitamine kompleksarvude abil.
SisuDomeen, väärtuste kogum, kasvav, kahanev
Logaritm on monotoonne funktsioon, seega pole sellel äärmusi. Logaritmi peamised omadused on toodud tabelis.
| Domeen | 0 < x < + ∞ | 0 < x < + ∞ |
| Väärtuste vahemik | - ∞ < y < + ∞ | - ∞ < y < + ∞ |
| Monotoonne | monotoonselt suureneb | monotoonselt väheneb |
| Nullid, y = 0 | x = 1 | x = 1 |
| Lõikepunktid ordinaatteljega, x = 0 | Ei | Ei |
| + ∞ | - ∞ | |
| - ∞ | + ∞ |
Privaatsed väärtused
Nimetatakse logaritm aluse 10ni kümnendlogaritm ja on tähistatud järgmiselt:
Logaritm baasini e helistas naturaallogaritm:
Logaritmide põhivalemid
Pöördfunktsiooni definitsioonist tulenevad logaritmi omadused:
Logaritmide põhiomadus ja selle tagajärjed
Aluse asendamise valem
Logaritm on logaritmi võtmise matemaatiline tehe. Logaritmide võtmisel teisendatakse tegurite korrutised liigeste summadeks.
Potentsiatsioon on logaritmile vastupidine matemaatiline tehe. Potentsieerimise ajal tõstetakse antud alust ekspressiooniastmeni, mille üle potentseerimine sooritatakse. Sel juhul muudetakse terminite summad tegurite korrutisteks.
Logaritmide põhivalemite tõestus
Logaritmidega seotud valemid tulenevad eksponentsiaalfunktsioonide valemitest ja pöördfunktsiooni definitsioonist.
Vaatleme eksponentsiaalfunktsiooni omadust
.
Siis
.
Rakendame eksponentsiaalfunktsiooni omadust
:
.
Tõestame baasi asendamise valemit.
;
.
Eeldades, et c = b, on meil:
Pöördfunktsioon
Logaritmi pöördväärtus baasile a on eksponentsiaalne funktsioon, mille astendaja on a.
Kui siis
Kui siis
Logaritmi tuletis
Mooduli x logaritmi tuletis:
.
N-nda järgu tuletis:
.
Valemite tuletamine >>>
Logaritmi tuletise leidmiseks tuleb see taandada alusele e.
;
.
Integraalne
Logaritmi integraal arvutatakse osade kaupa integreerimisel: .
Niisiis,
Kompleksarve kasutavad avaldised
Mõelge kompleksarvu funktsioonile z:
.
Avaldame kompleksarvu z mooduli kaudu r ja argument φ
:
.
Seejärel, kasutades logaritmi omadusi, saame:
.
Või
Siiski argument φ
ei ole üheselt määratletud. Kui paned
, kus n on täisarv,
siis on see erinevate jaoks sama number n.
Seetõttu ei ole logaritm kui kompleksmuutuja funktsioon ühe väärtusega funktsioon.
Jõuseeria laiendamine
Kui laienemine toimub:
Viited:
I.N. Bronstein, K.A. Semendjajev, matemaatika käsiraamat inseneridele ja üliõpilastele, “Lan”, 2009.
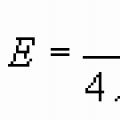 Ostrogradsky-Gaussi teoreem
Ostrogradsky-Gaussi teoreem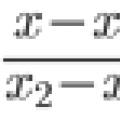 Kuidas õppida lahendama ülesandeid analüütilises geomeetrias?
Kuidas õppida lahendama ülesandeid analüütilises geomeetrias? Sõna merkantiil tähendus Sõna merkantiil tähendus
Sõna merkantiil tähendus Sõna merkantiil tähendus