Kolmnurga kõrguse ja pikkuse võrrand. Kuidas õppida lahendama ülesandeid analüütilises geomeetrias? Kolmnurga tüüpiline ülesanne tasapinnal Kolmnurga mediaanide võrrandid selle tippude koordinaatide põhjal
Mis on funktsioon? See on ühe suuruse sõltuvus teisest. Matemaatilises funktsioonis on enamasti kaks tundmatut: sõltumatu ja sõltuv või vastavalt x ja y.
Mida see tähendab? See tähendab, et x võib omandada absoluutselt mis tahes väärtuse ja y kohandub sellega, muutudes vastavalt funktsiooni koefitsientidele.
On olukordi, kus funktsioonil on mitu muutujat. Sõltuvus on alati 1, kuid seda võib mõjutada mitu tegurit. Sellist funktsiooni ei ole alati võimalik graafikul kuvada. Parimal juhul saate y sõltuvust kahest muutujast graafiliselt kuvada.
Kuidas on kõige lihtsam esitada sõltuvust y(x)?
Jah, väga lihtne. Kujutage ette ärahellitatud last ja rikast, armastavat ema. Nad tulevad koos poodi ja hakkavad kommi kerjama. Kes teab, mitu kommi poiss täna nõuab?
Mitte keegi, aga olenevalt kommide arvust suureneb summa, mille emme kassas maksab. Sel juhul on sõltuvaks muutujaks tšekis olev summa ja sõltumatuks muutujaks maiustuste arv, mida poiss täna soovib.
Väga oluline on mõista, et funktsiooni y üks väärtus vastab alati argumendi x 1 väärtusele. Kuid nagu ruutvõrrandi juurte puhul, võivad need väärtused kokku langeda.
Sirge võrrand
Miks on vaja sirge võrrandit, kui räägime kolmnurga külgede pikkuste võrrandist?
Jah, sest kolmnurga iga külg on segment. Lõik on sirge piiratud osa. See tähendab, et saame määrata sirgjoonte võrrandid. Ja nende ristumispunktides piirake jooni, lõigates sellega sirgjooned ära ja muutes need segmentideks.
Joone võrrand näeb välja selline:
$$y_1=a_1x+b_1$$
$$y_2=a_2x+b_2$$
$$y_3=a_3x+b_3$$
Kolmnurga külgede võrrand
Punktides A(3,7) oleva tippudega kolmnurga külgede pikkuste võrrand tuleb leida; B(5,3); C(12;9)
Kõik koordinaadid on positiivsed, mis tähendab, et kolmnurk asub ühes koordinaatkvadrandis.
Koostame võrrandid kolmnurga iga sirge jaoks ükshaaval.
- Esimene rida on AB. Asendame punktide koordinaadid sirgjoone võrrandis x ja y asemel. Nii saame kahe lineaarvõrrandi süsteemi. Pärast selle lahendamist leiate funktsiooni koefitsientide väärtuse:
A(3,7); B(5,3):
Esimesest võrrandist väljendame b ja asendame selle teisega.
Asendame a väärtuse ja leiame b.
b=7-3a=7-3*(-2)=7+6=13
Koostame sirge võrrandi.
- Loome ülejäänud kaks võrrandit samal viisil.
B(5,3); C(12;9)
9=12a+b=12a+3-5a
$$b=3-5*(6\üle7)=-(9\üle7)$$
$$y=(6\üle7)x-(9\üle7)$$
- A(3,7); C(12;9)
9=12a+b=12a+7-3a=9a+7
$$b=7-(6\over9)=(57\over9)$$
$$y=(2\over9)x+(57\over9)$$
- Kirjutame kolmnurga külgede pikkuste võrrandi:
$$y=(6\üle7)x-(9\üle7)$$
$$y=(2\over9)x+(57\over9)$$
Mida me õppisime?
Õppisime, mis on funktsioon, rääkisime sirge funktsioonist ja õppisime selle tippude koordinaatidest tuletama kolmnurga külgede võrrandeid.
Test teemal
Artikli hinnang
Keskmine hinne: 4.8. Kokku saadud hinnanguid: 45.
Näide. Kolmnurga ABC tipud on antud.Leia: 1) külje AB pikkus; 2) külgede AB ja AC võrrandid ning nende nurkkoefitsiendid; 3) Sisenurk A radiaanides täpsusega 0,01; 4) CD kõrguse ja pikkuse võrrand; 5) ringi võrrand, mille kõrgus CD on läbimõõt; 6) kolmnurka ABC määratlev lineaarvõrratuste süsteem.
Kolmnurga külgede pikkus:
|AB| = 15
|AC| = 11,18
|BC| = 14,14
Kaugus d punktist M: d = 10
Kolmnurga tippude koordinaadid on antud: A(-5,2), B(7,-7), C(5,7).
2) Kolmnurga külgede pikkus
Punktide M 1 (x 1 ; y 1) ja M 2 (x 2 ; y 2) vaheline kaugus d määratakse järgmise valemiga:
8) Sirge võrrand
Punkte A 1 (x 1 ; y 1) ja A 2 (x 2 ; y 2) läbiv sirgjoon on esitatud võrranditega: ![]()
Sirge AB võrrand
![]() või
või
või y = -3 / 4 x -7 / 4 või 4 a + 3x +7 = 0
Sirge AC võrrand
Sirge kanooniline võrrand: ![]() või
või
või y = 1/2 x + 9/2 või 2y -x - 9 = 0
Sirge BC võrrand
Sirge kanooniline võrrand: ![]() või
või
või y = -7x + 42 või y + 7x - 42 = 0
3) Sirgete vaheline nurk
Sirge AB:y võrrand = -3 / 4 x -7 / 4
Sirgevõrrand AC:y = 1/2 x + 9/2
Nurk φ kahe sirge vahel, mis on saadud võrranditega y = k 1 x + b 1 ja y 2 = k 2 x + b 2, arvutatakse järgmise valemiga:
Nende joonte kalded on -3/4 ja 1/2. Kasutame valemit ja võtame selle parempoolse mooduli: 
tg φ = 2
φ = arctan(2) = 63,44 0 või 1,107 rad.
9) Kõrguse võrrand läbi tipu C
Punkti N 0 (x 0 ;y 0) läbival sirgel, mis on risti sirgega Ax + By + C = 0, on suunavektor (A;B) ja seepärast esitatakse seda võrranditega: ![]()
Selle võrrandi võib leida muul viisil. Selleks leiame sirge AB nõlva k 1.
AB võrrand: y = -3 / 4 x -7 / 4, s.o. k 1 = -3/4
Leiame risti nurgateguri k kahe sirge perpendikulaarsuse tingimusest: k 1 *k = -1.
Asendades selle sirge kalde k 1 asemel, saame:
-3/4 k = -1, millest k = 4/3
Kuna risti läbib punkti C(5,7) ja selle k = 4 / 3, siis otsime selle võrrandit kujul: y-y 0 = k(x-x 0).
Asendades x 0 = 5, k = 4/3, y 0 = 7 saame:
y-7 = 4/3 (x-5)
või
y = 4/3 x + 1/3 või 3a -4x - 1 = 0
Leiame sirge AB lõikepunkti:
Meil on kahe võrrandi süsteem:
4a + 3x +7 = 0
3a -4x -1 = 0
Esimesest võrrandist väljendame y ja asendame selle teise võrrandiga.
Saame: x = -1; y=-1
D(-1;-1)
9) Tipust C tõmmatud kolmnurga kõrguse pikkus
Kaugus d punktist M 1 (x 1 ;y 1) sirgjooneni Ax + By + C = 0 on võrdne suuruse absoluutväärtusega: 
Leidke punkti C(5;7) ja sirge AB vaheline kaugus (4y + 3x +7 = 0) 
Kõrguse pikkuse saab arvutada teise valemiga, milleks on punkti C(5;7) ja punkti D(-1;-1) vaheline kaugus.
Kahe punkti vaheline kaugus väljendatakse koordinaatidena järgmise valemiga:
5) ringi võrrand, mille kõrgus CD on läbimõõt;
Raadiusega R ringjoone võrrand, mille keskpunkt on punktis E(a;b), on järgmine:
(x-a) 2 + (y-b) 2 = R 2
Kuna CD on soovitud ringi läbimõõt, on selle keskpunkt E lõigu CD keskpunkt. Kasutades segmendi pooleks jagamise valemeid, saame: ![]()
![]()
Seetõttu E(2;3) ja R = CD / 2 = 5. Valemit kasutades saame soovitud ringi võrrandi: (x-2) 2 + (y-3) 2 = 25 
6) kolmnurka ABC määratlev lineaarvõrratuste süsteem.
Sirge AB võrrand: y = -3 / 4 x -7 / 4
Sirge AC võrrand: y = 1/2 x + 9/2
Sirge BC võrrand: y = -7x + 42
Kuidas õppida lahendama ülesandeid analüütilises geomeetrias?
Tüüpiline probleem kolmnurgaga tasapinnal
See õppetund on loodud ekvaatorile lähenemisest tasapinna geomeetria ja ruumi geomeetria vahel. Hetkel on vaja kogutud info süstematiseerida ja vastata väga olulisele küsimusele: kuidas õppida lahendama ülesandeid analüütilises geomeetrias? Raskus seisneb selles, et geomeetrias on võimalik välja pakkuda lõpmatu arv ülesandeid ning ükski õpik ei sisalda kõiki paljusid ja erinevaid näiteid. Ei ole funktsiooni tuletis viie eristamisreegli, tabeli ja mitme tehnikaga….
Lahendus on olemas! Ma ei hakka valjuhäälselt rääkima sellest, et olen välja töötanud mingi suurejoonelise tehnika, kuid minu arvates on vaadeldavale probleemile tõhus lähenemine, mis võimaldab isegi täielikul mannekeenil saavutada häid ja suurepäraseid tulemusi. Vähemalt geomeetriliste ülesannete lahendamise üldine algoritm võttis minu peas väga selgelt kuju.
MIDA SA PEAD TEADMA JA OSAMA TEHA
geomeetriaülesannete edukaks lahendamiseks?
Sellest pole pääsu – et mitte suvaliselt ninaga nuppe torkida, tuleb omandada analüütilise geomeetria põhitõed. Seega, kui olete just alustanud geomeetria õppimist või selle sootuks unustanud, alustage palun õppetunniga Mannekeenide vektorid. Lisaks vektoritele ja nendega seotud toimingutele peate teadma tasapinna geomeetria põhimõisteid, eriti tasapinna sirge võrrand Ja . Ruumi geomeetria on esitatud artiklites Tasapinnaline võrrand, Ruumi sirge võrrandid, Põhiülesanded sirgel ja tasapinnal ja mõned muud õppetunnid. Kumerad jooned ja teist järku ruumipinnad paistavad mõnevõrra üksteisest eemal ning nendega pole nii palju spetsiifilisi probleeme.
Oletame, et õpilasel on juba algteadmised ja -oskused analüütilise geomeetria lihtsamate ülesannete lahendamisel. Aga see juhtub nii: loed probleemi avaldust ja... tahad kogu asja üldse sulgeda, visata kaugemasse nurka ja unustada, nagu halb unenägu. Pealegi ei sõltu see põhimõtteliselt teie kvalifikatsiooni tasemest, aeg-ajalt puutun ka ise kokku ülesannetega, mille lahendus pole ilmne. Mida sellistel juhtudel teha? Pole vaja karta ülesannet, millest sa aru ei saa!
Esiteks, tuleks paigaldada - Kas see on "tasane" või ruumiline probleem? Näiteks kui tingimus sisaldab vektoreid kahe koordinaadiga, siis loomulikult on see tasapinna geomeetria. Ja kui õpetaja laadis tänulikule kuulajale püramiidi, siis on seal selgelt ruumi geomeetria. Esimese sammu tulemused on juba päris head, sest suutsime ära lõigata tohutu hulga selle ülesande jaoks ebavajalikku infot!
Teiseks. Tingimus puudutab tavaliselt mõnda geomeetrilist kujundit. Tõepoolest, kõndige mööda oma koduülikooli koridore ja näete palju murelikke nägusid.
“Lamedate” ülesannete puhul, rääkimata ilmsetest punktidest ja joontest, on kõige populaarsem kujund kolmnurk. Analüüsime seda väga üksikasjalikult. Edasi tuleb rööpkülik ja palju vähem levinud on ristkülik, ruut, romb, ring ja muud kujundid.
Ruumiülesannetes võivad lennata samad lamedad figuurid + tasapinnad ise ja tavalised rööptahukatega kolmnurksed püramiidid.
Teine küsimus - Kas teate selle kuju kohta kõike? Oletame, et tingimus räägib võrdhaarsest kolmnurgast ja te mäletate väga ähmaselt, milline kolmnurk see on. Avame kooliõpiku ja loeme võrdhaarse kolmnurga kohta. Mis teha... arst ütles romb, see tähendab romb. Analüütiline geomeetria on analüütiline geomeetria, kuid probleemi lahendavad figuuride endi geomeetrilised omadused, meile kooli õppekavast tuntud. Kui te ei tea, mis on kolmnurga nurkade summa, võite pikka aega kannatada.
Kolmandaks. Püüdke ALATI joonist jälgida(mustandil/lõpukoopial/mõtteliselt), isegi kui tingimus seda ei nõua. “Lamedate” probleemide korral käskis Eukleides ise võtta joonlaua ja pliiatsi - ja mitte ainult seisundi mõistmiseks, vaid ka enesekontrolli eesmärgil. Sel juhul on kõige mugavam skaala 1 ühik = 1 cm (2 märkmiku lahtrit). Ärme räägi hoolimatutest õpilastest ja matemaatikutest, kes haudades keerlevad – selliste ülesannete puhul on pea võimatu eksida. Ruumiülesannete jaoks teostame skemaatilise joonise, mis aitab ka seisundit analüüsida.
Joonis või skemaatiline joonis võimaldab sageli kohe näha probleemi lahendamise viisi. Loomulikult peate selleks teadma geomeetria aluseid ja mõistma geomeetriliste kujundite omadusi (vt eelmist lõiku).
Neljandaks. Lahendusalgoritmi väljatöötamine. Paljud geomeetriaülesanded on mitmeastmelised, seega on lahendust ja selle disaini väga mugav punktideks jagada. Sageli tuleb algoritm kohe meelde pärast tingimuse lugemist või joonise lõpetamist. Raskuste korral alustame ülesande KÜSIMUSEGA. Näiteks tingimuse "peate konstrueerima sirge ..." järgi. Siin on kõige loogilisem küsimus: "Millest piisab selle sirgjoone ehitamiseks teadmisest?" Oletame, et "me teame punkti, me peame teadma suunavektorit." Küsime järgmise küsimuse: „Kuidas leida seda suunavektorit? Kuhu?" jne.
Mõnikord on "viga" - probleem ei lahene ja kõik. Peatamise põhjused võivad olla järgmised:
– Tõsine lünk põhiteadmistes. Teisisõnu, sa ei tea ja/või ei näe mõnda väga lihtsat asja.
– Geomeetriliste kujundite omaduste teadmatus.
– Ülesanne oli raske. Jah, see juhtub. Pole mõtet tundide kaupa aurutada ja pisaraid taskurätikusse koguda. Küsige nõu oma õpetajalt, kaasõpilastelt või esitage foorumis küsimus. Veelgi enam, parem on selle avaldus konkreetseks muuta - lahenduse selle osa kohta, millest te aru ei saa. Hüüd vormis "Kuidas probleemi lahendada?" ei näe eriti hea välja... ja eelkõige teie enda maine pärast.
Viies etapp. Otsustame-kontrollime, otsustame-kontrollime, otsustame-kontrollime-anname vastuse. Kasulik on kontrollida ülesande iga punkti kohe pärast selle valmimist. See aitab teil vea kohe tuvastada. Loomulikult ei keela keegi kogu probleemi kiiresti lahendada, kuid on oht, et kirjutatakse kõik uuesti (sageli mitu lehekülge).
Need on ehk kõik peamised kaalutlused, mida tuleks probleemide lahendamisel järgida.
Tunni praktiline osa esitatakse tasapinnalises geomeetrias. Siin on ainult kaks näidet, kuid see ei tundu piisav =)
Vaatame läbi algoritmi lõime, mida ma just oma väikeses teaduslikus töös vaatasin:
Näide 1
Rööpküliku kolm tippu on antud. Leia tipp.
Hakkame mõistma:
Esimene samm: On ilmne, et me räägime "tasasest" probleemist.
Teine samm: Ülesanne käsitleb rööpkülikut. Kas kõik mäletavad seda rööpkülikukuju? Pole vaja naeratada, paljud saavad hariduse 30-40-50 või rohkemgi eluaastat, nii et ka lihtsad faktid võivad mälust kustutada. Rööpküliku definitsiooni leiab tunni näitest nr 3 Vektorite lineaarne (mitte)sõltuvus. Vektorite alused.
Kolmas samm: Teeme joonise, millele märgime kolm teadaolevat tippu. Naljakas on see, et soovitud punkti pole keeruline kohe konstrueerida: 
Selle konstrueerimine on muidugi hea, aga lahendus tuleb sõnastada analüütiliselt.
Neljas samm: Lahendusalgoritmi väljatöötamine. Esimese asjana tuleb meelde, et punkti võib leida sirgete lõikepunktina. Me ei tea nende võrrandeid, seega peame selle probleemiga tegelema:
1) Vastasküljed on paralleelsed. Punktide järgi ![]() Leiame nende külgede suunavektori. See on kõige lihtsam probleem, mida tunnis arutati. Mannekeenide vektorid.
Leiame nende külgede suunavektori. See on kõige lihtsam probleem, mida tunnis arutati. Mannekeenide vektorid.
Märge: õigem on öelda "külge sisaldava sirge võrrand", kuid siin ja edaspidi kasutan lühiduse huvides fraase "külje võrrand", "külje suunavektor" jne.
3) Vastasküljed on paralleelsed. Punkte kasutades leiame nende külgede suunavektori.
4) Koostame punkti ja suunavektori abil sirgjoone võrrandi
Lõigetes 1-2 ja 3-4 lahendasime sama probleemi tegelikult kaks korda, muide, sellest oli juttu õppetunni näites nr 3 Lihtsamad ülesanded sirgjoonega tasapinnal. Sai minna pikemat marsruuti - esmalt leida sirgete võrrandid ja alles siis nendest suunavektorid “välja tõmmata”.
5) Nüüd on sirgete võrrandid teada. Jääb üle vaid vastav lineaarvõrrandisüsteem koostada ja lahendada (vt sama õppetüki näiteid nr 4, 5 Lihtsamad ülesanded sirgjoonega tasapinnal).
Punkt on leitud.
Ülesanne on üsna lihtne ja selle lahendus ilmne, kuid on ka lühem tee!
Teine lahendus:
Rööpküliku diagonaalid poolitatakse nende lõikepunkti järgi. Märkisin punkti ära, aga et joonist mitte segamini ajada, ei joonistanud ma diagonaale ise.
Loome külgmise võrrandi punkt-punkti haaval: 
Kontrollimiseks peaksite mõtteliselt või mustandi põhjal iga punkti koordinaadid saadud võrrandisse asendama. Nüüd leiame kalle. Selleks kirjutame üldvõrrandi ümber kaldekoefitsiendiga võrrandi kujul:
Seega on kalle:
Samamoodi leiame külgede võrrandid. Ma ei näe sama asja kirjeldamisel erilist mõtet, seega annan kohe valmis tulemuse: ![]()
2) Leia külje pikkus. See on klassis käsitletud lihtsaim probleem. Mannekeenide vektorid. Punktide eest ![]() kasutame valemit:
kasutame valemit:
Sama valemi abil on lihtne leida teiste külgede pikkusi. Kontrolli saab tavalise joonlauaga väga kiiresti teha.
Me kasutame valemit  .
.
Leiame vektorid:

Seega:
Muide, teel leidsime külgede pikkused.
Tulemusena:
Tundub, et see on tõsi; veenmiseks võite nurga külge kinnitada kraadiklaasi.
Tähelepanu! Ärge ajage segi kolmnurga nurka sirgjoonte vahelise nurgaga. Kolmnurga nurk võib olla nüri, aga sirgete vaheline nurk mitte (vt artikli viimast lõiku Lihtsamad ülesanded sirgjoonega tasapinnal). Kolmnurga nurga leidmiseks võib aga kasutada ka ülaltoodud õppetunni valemeid, kuid karedus seisneb selles, et need valemid annavad alati teravnurga. Nende abiga lahendasin selle probleemi mustandis ja sain tulemuse. Ja viimasele eksemplarile peaksin veel lisavabandusi kirja panema, et .
4) Kirjutage võrrand sirgele, mis läbib sirgega paralleelset punkti.
Tüüpülesanne, millest on üksikasjalikult juttu tunni näites nr 2 Lihtsamad ülesanded sirgjoonega tasapinnal. Sirge üldvõrrandist ![]() Võtame välja juhtvektori. Koostame punkti ja suunavektori abil sirgjoone võrrandi:
Võtame välja juhtvektori. Koostame punkti ja suunavektori abil sirgjoone võrrandi: 
Kuidas leida kolmnurga kõrgust?
5) Loome kõrguse võrrandi ja leiame selle pikkuse.
Rangetest määratlustest pole pääsu, nii et peate varastama kooliõpikust:
Kolmnurga kõrgus nimetatakse risti, mis on tõmmatud kolmnurga tipust vastaskülge sisaldavale sirgele.
See tähendab, et tipust küljele tõmmatud risti jaoks on vaja luua võrrand. Seda ülesannet käsitletakse õppetunni näidetes nr 6, 7 Lihtsamad ülesanded sirgjoonega tasapinnal. Alates Eq. ![]() eemaldada normaalne vektor. Koostame kõrgusvõrrandi punkti ja suunavektori abil:
eemaldada normaalne vektor. Koostame kõrgusvõrrandi punkti ja suunavektori abil: 

Pange tähele, et me ei tea punkti koordinaate.
Mõnikord leitakse kõrgusvõrrand ristsirgete nurkkoefitsientide suhtest: . Sel juhul siis: . Koostame kõrgusvõrrandi kasutades punkti ja nurgakordajat (vt tunni algust Tasapinna sirgjoone võrrand):
Kõrguse pikkust saab leida kahel viisil.
Seal on ringtee:
a) leid – kõrguse ja külje lõikepunkt;
b) leida kahe teadaoleva punkti abil lõigu pikkus.
Aga klassis Lihtsamad ülesanded sirgjoonega tasapinnal kaaluti mugavat valemit punkti ja sirge kauguse jaoks. Punkt on teada: , sirge võrrand on samuti teada: ![]() , Seega:
, Seega:
6) Arvutage kolmnurga pindala. Ruumis arvutatakse kolmnurga pindala traditsiooniliselt kasutades vektorite vektorkorrutis, kuid siin on meile antud kolmnurk tasapinnal. Kasutame kooli valemit:
– Kolmnurga pindala on võrdne poolega selle aluse ja kõrguse korrutisest.
Sel juhul:
Kuidas leida kolmnurga mediaani?
7) Koostame mediaani võrrandi.
Kolmnurga mediaan nimetatakse lõiguks, mis ühendab kolmnurga tippu vastaskülje keskkohaga.
a) Leia punkt – külje keskkoht. Me kasutame lõigu keskpunkti koordinaatide valemid. Lõigu otste koordinaadid on teada: ![]() , siis keskkoha koordinaadid:
, siis keskkoha koordinaadid: 
Seega: 
Koostame mediaanvõrrandi punktide kaupa ![]() :
:
Võrrandi kontrollimiseks peate sellesse asendama punktide koordinaadid.
8) Leidke kõrguse ja mediaani lõikepunkt. Arvan, et kõik on juba õppinud, kuidas seda iluuisutamise elementi kukkumata sooritada: 

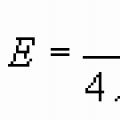 Ostrogradsky-Gaussi teoreem
Ostrogradsky-Gaussi teoreem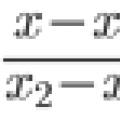 Kuidas õppida lahendama ülesandeid analüütilises geomeetrias?
Kuidas õppida lahendama ülesandeid analüütilises geomeetrias? Sõna merkantiil tähendus Sõna merkantiil tähendus
Sõna merkantiil tähendus Sõna merkantiil tähendus