Vrste vektora. Vektori
Vektor je usmjereni isječak pravca u euklidskom prostoru čiji se jedan kraj (točka A) naziva početkom vektora, a drugi kraj (točka B) krajem vektora (slika 1). Vektori su označeni:

Ako se početak i kraj vektora podudaraju, tada se vektor naziva nulti vektor i naznačen je 0 .
Primjer. Neka početak vektora u dvodimenzionalnom prostoru ima koordinate A(12.6) , a kraj vektora su koordinate B(12.6). Tada je vektor nulti vektor.
Duljina presjeka AB nazvao modul (duljina, pravilo) vektor i označava se sa | a|. Vektor duljine jednake jedan zove se jedinični vektor. Osim modula, vektor karakterizira smjer: vektor ima smjer od A Do B. Vektor se naziva vektor, suprotan vektor.

Dva vektora se nazivaju kolinearni, ako leže na istoj liniji ili na paralelnim pravcima. Na slici Sl. 3 crvena vektora su kolinearna, jer leže na istoj ravnoj liniji, a plavi vektori su kolinearni, jer leže na paralelnim pravcima. Dva kolinearna vektora nazivaju se jednako usmjereni, ako im krajevi leže na istoj strani ravne crte koja povezuje njihove početke. Dva kolinearna vektora nazivaju se suprotno usmjerena, ako im krajevi leže na suprotnim stranama ravne crte koja povezuje njihove početke. Ako dva kolinearna vektora leže na istoj ravnici, nazivaju se identično usmjerenima ako jedna od zraka koju čini jedan vektor u potpunosti sadrži zraku koju čini drugi vektor. U protivnom se kaže da su vektori suprotno usmjereni. Na slici 3 plavi vektori su jednako usmjereni, a crveni vektori suprotno usmjereni.

Dva vektora se nazivaju jednak ako imaju jednake module i iste smjerove. Na slici 2 vektori su jednaki jer njihovi moduli su jednaki i imaju isti smjer.
Vektori se nazivaju komplanarni, ako leže u istoj ravnini ili u paralelnim ravninama.
U n U dimenzionalnom vektorskom prostoru, razmotrite skup svih vektora čija se početna točka podudara s ishodištem koordinata. Tada se vektor može napisati u sljedećem obliku:
| (1) |
Gdje x 1, x 2, ..., x n koordinate krajnje točke vektora x.
Vektor zapisan u obliku (1) nazivamo vektor retka, a vektor zapisan u obliku
| (2) |
nazvao stupac vektor.
Broj n nazvao dimenzija (u redu) vektor. Ako ![]() tada se vektor zove nulti vektor(od početne točke vektora
tada se vektor zove nulti vektor(od početne točke vektora ![]() ). Dva vektora x I g jednaki ako i samo ako su im odgovarajući elementi jednaki.
). Dva vektora x I g jednaki ako i samo ako su im odgovarajući elementi jednaki.
Pri proučavanju raznih grana fizike, mehanike i tehničkih znanosti susreću se veličine koje su u potpunosti određene zadavanjem svojih numeričkih vrijednosti. Takve se količine nazivaju skalar ili, ukratko, skalari.
Skalarne veličine su duljina, površina, volumen, masa, temperatura tijela itd. Osim skalarnih veličina, u raznim zadacima postoje veličine za koje je, osim brojčane vrijednosti, potrebno znati i njihov smjer. Takve se količine nazivaju vektor. Fizikalni primjeri vektorskih veličina mogu biti pomak materijalne točke koja se giba u prostoru, brzina i ubrzanje te točke, kao i sila koja na nju djeluje.
Vektorske veličine su predstavljene pomoću vektora.
Definicija vektora. Vektor je usmjereni segment ravne linije određene duljine.
Vektor karakteriziraju dvije točke. Jedna točka je početna točka vektora, druga točka je krajnja točka vektora. Označimo li početak vektora točkom A , a kraj vektora je točka U , tada se sam vektor označava . Vektor se također može označiti jednim malim latiničnim slovom s crtom iznad njega (na primjer, ).
Grafički, vektor je označen segmentom sa strelicom na kraju.
Početak vektora naziva se njegovu točku primjene. Ako je točka A je početak vektora , tada ćemo reći da je vektor primijenjen u točki A.
Vektor karakteriziraju dvije veličine: duljina i smjer.
Duljina vektora – udaljenost između početne točke A i krajnje točke B. Drugi naziv za duljinu vektora je modul vektora a označen je simbolom . Označava se vektorski modul Vektor , čija je duljina 1 naziva se jedinični vektor. To jest, uvjet za jedinični vektor
Vektor nulte duljine naziva se nulti vektor (označava se s ). Očito je da nulti vektor ima iste početne i krajnje točke. Nulti vektor nema određeni smjer.
Definicija kolinearnih vektora. Vektori koji se nalaze na istoj liniji ili na paralelnim pravcima nazivaju se kolinearima .
Imajte na umu da kolinearni vektori mogu imati različite duljine i različite smjerove.
Određivanje jednakih vektora. Za dva vektora kažemo da su jednaka ako su kolinearni, imaju istu duljinu i isti smjer.
U ovom slučaju pišu:
Komentar. Iz definicije jednakosti vektora proizlazi da se vektor može paralelno prenijeti postavljanjem njegovog ishodišta u bilo koju točku u prostoru (osobito u ravnini).
Svi nulti vektori se smatraju jednakima.
Određivanje suprotnih vektora. Dva vektora se nazivaju suprotnim ako su kolinearni, iste duljine, ali suprotnog smjera.
U ovom slučaju pišu:
Drugim riječima, vektor nasuprot vektoru označava se kao .
Stranica 1 od 2
Pitanje 1.Što je vektor? Kako se označavaju vektori?
Odgovor. Usmjereni segment nazvat ćemo vektor (slika 211). Smjer vektora određuje se označavanjem njegovog početka i kraja. Na crtežu je smjer vektora označen strelicom. Za označavanje vektora koristit ćemo mala latinična slova a, b, c, .... Vektor možete označiti i označavanjem njegovog početka i kraja. U ovom slučaju, početak vektora je postavljen na prvo mjesto. Umjesto riječi "vektor", ponekad se iznad slovne oznake vektora stavlja strelica ili crta. Vektor na slici 211 može se označiti na sljedeći način:
\(\overline(a)\), \(\overdesnastrelica(a)\) ili \(\overline(AB)\), \(\overdesnastrelica(AB)\).
pitanje 2. Koji vektori se nazivaju identično usmjerenim (suprotno usmjerenim)?
Odgovor. Za vektore \(\overline(AB)\) i \(\overline(CD)\) kažemo da su jednako usmjereni ako su polupravci AB i CD jednako usmjereni.
Za vektore \(\overline(AB)\) i \(\overline(CD)\) kažemo da su suprotno usmjereni ako su polupravci AB i CD suprotno usmjereni.
Na slici 212 vektori \(\overline(a)\) i \(\overline(b)\) jednako su usmjereni, a vektori \(\overline(a)\) i \(\overline(c)\ ) su suprotno usmjereni.

pitanje 3. Kolika je apsolutna veličina vektora?
Odgovor. Apsolutna vrijednost (ili modul) vektora je duljina segmenta koji predstavlja vektor. Apsolutna vrijednost vektora \(\overline(a)\) označena je s |\(\overline(a)\)|.
pitanje 4.Što je nulti vektor?
Odgovor. Početak vektora može se podudarati s njegovim krajem. Takav vektor nazvat ćemo nulti vektor. Nulti vektor je označen nulom s crticom (\(\overline(0)\)). Oni ne govore o smjeru nultog vektora. Smatra se da je apsolutna vrijednost nultog vektora jednaka nuli.
pitanje 5. Koji vektori se nazivaju jednakima?
Odgovor. Kaže se da su dva vektora jednaka ako se kombiniraju paralelnom translacijom. To znači da postoji paralelna translacija koja vodi početak i kraj jednog vektora na početak i kraj drugog vektora.
Pitanje 6. Dokažite da jednaki vektori imaju isti smjer i jednaki po apsolutnoj vrijednosti. I obrnuto: jednaki su identično usmjereni vektori koji su jednaki po apsolutnoj vrijednosti.
Odgovor. Tijekom paralelnog prevođenja, vektor zadržava svoj smjer, kao i svoju apsolutnu vrijednost. To znači da jednaki vektori imaju iste smjerove i jednaki su po apsolutnoj vrijednosti.
Neka su \(\overline(AB)\) i \(\overline(CD)\) identično usmjereni vektori, jednaki po apsolutnoj vrijednosti (sl. 213). Paralelna translacija koja pomiče točku C u točku A kombinira polupravac CD s polupravcem AB, budući da imaju isti smjer. A kako su segmenti AB i CD jednaki, tada se točka D poklapa s točkom B, tj. paralelna translacija transformira vektor \(\overline(CD)\) u vektor \(\overline(AB)\). To znači da su vektori \(\overline(AB)\) i \(\overline(CD)\) jednaki, što je i trebalo dokazati.

Pitanje 7. Dokažite da iz bilo koje točke možete nacrtati vektor jednak zadanom vektoru, i to samo jednom.
Odgovor. Neka je CD pravac, a vektor \(\overline(CD)\) dio pravca CD. Neka je AB pravac u koji ide pravac CD tijekom paralelnog prijenosa, \(\overline(AB)\) neka bude vektor u koji vektor \(\overline(CD)\) ide tijekom paralelnog prijenosa, pa stoga vektori \(\ overline(AB)\) i \(\overline(CD)\) su jednaki, a prave AB i CD su paralelne (vidi sliku 213). Kao što znamo, kroz točku koja ne leži na zadanom pravcu, moguće je na ravnini povući najviše jedan pravac paralelan sa zadanim (aksiom paralelnih pravaca). To znači da se kroz točku A može povući jedan pravac paralelan s pravcem CD. Kako je vektor \(\overline(AB)\) dio pravca AB, tada se kroz točku A može povući jedan vektor \(\overline(AB)\), jednak vektoru \(\overline(CD)\ ).
Pitanje 8.Što su vektorske koordinate? Kolika je apsolutna vrijednost vektora s koordinatama a 1, a 2?
Odgovor. Neka vektor \(\overline(a)\) ima početnu točku A 1 (x 1 ; y 1) i krajnju točku A 2 (x 2 ; y 2). Koordinate vektora \(\overline(a)\) bit će brojevi a 1 = x 2 - x 1 , a 2 = y 2 - y 1 . Koordinate vektora ćemo staviti uz slovnu oznaku vektora, u ovom slučaju \(\overline(a)\) (a 1 ; a 2) ili jednostavno \((\overline(a 1 ; a 2 ) )\). Koordinate nulte vektora jednake su nuli.
Iz formule koja izražava udaljenost između dviju točaka preko njihovih koordinata, slijedi da je apsolutna vrijednost vektora s koordinatama a 1 , a 2 jednaka \(\sqrt(a^2 1 + a^2 2 )\).
pitanje 9. Dokažite da jednaki vektori imaju redom jednake koordinate, a da su vektori s redom jednakim koordinatama jednaki.
Odgovor. Neka su A 1 (x 1 ; y 1) i A 2 (x 2 ; y 2) početak i kraj vektora \(\overline(a)\). Budući da je njemu jednak vektor \(\overline(a)\) dobiven iz vektora \(\overline(a)\) paralelnom translacijom, njegov početak i kraj bit će A" 1 (x 1 + c; y 1 + d) odnosno ), A" 2 (x 2 + c; y 2 + d). Ovo pokazuje da oba vektora \(\overline(a)\) i \(\overline(a")\) imaju iste koordinate: x 2 - x 1, y 2 - y 1.
Dokažimo sada obrnutu tvrdnju. Neka su odgovarajuće koordinate vektora \(\overline(A 1 A 2 )\) i \(\overline(A" 1 A" 2 )\) jednake. Dokažimo da su vektori jednaki.
Neka su x" 1 i y" 1 koordinate točke A" 1, a x" 2, y" 2 koordinate točke A" 2. Prema uvjetima teorema, x 2 - x 1 = x" 2 - x" 1, y 2 - y 1 = y" 2 - y" 1. Stoga je x" 2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. Paralelni prijenos zadan formulama
x" = x + x" 1 - x 1, y" = y + y" 1 - y 1,
prenosi točku A 1 u točku A" 1, a točku A 2 u točku A" 2, tj. vektori \(\overline(A 1 A 2 )\) i \(\overline(A" 1 A" 2 )\) su jednaki, što je i trebalo dokazati.
pitanje 10. Definirajte zbroj vektora.
Odgovor. Zbroj vektora \(\overline(a)\) i \(\overline(b)\) s koordinatama a 1 , a 2 i b 1 , b 2 naziva se vektor \(\overline(c)\) s koordinate a 1 + b 1, a 2 + b a 2, tj.
\(\overline(a) (a 1 ; a 2) + \overline(b)(b 1 ; b 2) = \overline(c) (a 1 + b 1 ; a 2 + b 2)\).
 Povijest drevne Kine izvješće, poruka Gdje su živjeli drevni ljudi Kine
Povijest drevne Kine izvješće, poruka Gdje su živjeli drevni ljudi Kine Lekcije iz kemije Obilno ćemo ga namočiti u jod da sve bude sterilno.
Lekcije iz kemije Obilno ćemo ga namočiti u jod da sve bude sterilno.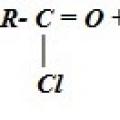 Kemijska svojstva. Priznanica. Dobivanje karboksilnih kiselina Dobivanje karboksilnih kiselina oksidacijom ugljikovodika
Kemijska svojstva. Priznanica. Dobivanje karboksilnih kiselina Dobivanje karboksilnih kiselina oksidacijom ugljikovodika