Y x bereken de periode van de functie. Periodiciteit van functies y = sin x, y = cos x - Kennishypermarkt
Argument x, dan wordt het periodiek genoemd als er een getal T is zodat voor elke x F(x + T) = F(x). Dit getal T wordt de periode van de functie genoemd.
Er kunnen meerdere periodes zijn. De functie F = const neemt bijvoorbeeld dezelfde waarde aan voor elke waarde van het argument, en daarom kan elk getal als de periode ervan worden beschouwd.
Meestal bent u geïnteresseerd in de kleinste periode die niet nul is, van een functie. Kortheidshalve wordt het eenvoudigweg een periode genoemd.
Een klassiek voorbeeld van periodieke functies is trigonometrisch: sinus, cosinus en tangens. Hun periode is hetzelfde en gelijk aan 2π, dat wil zeggen sin(x) = sin(x + 2π) = sin(x + 4π) enzovoort. Trigonometrische functies zijn echter natuurlijk niet de enige periodieke functies.
Voor eenvoudige basisfuncties is berekening de enige manier om te bepalen of ze periodiek of niet-periodiek zijn. Maar voor complexe functies zijn er al verschillende eenvoudige regels.
Als F(x) met periode T is, en er een afgeleide voor gedefinieerd is, dan is deze afgeleide f(x) = F′(x) ook een periodieke functie met periode T. De waarde van de afgeleide op punt x is gelijk aan de raaklijn van de raakhoek van de grafiek van zijn primitieve op dit punt aan de x-as, en aangezien de primitief zich periodiek herhaalt, moet de afgeleide zich ook herhalen. De afgeleide van de functie sin(x) is bijvoorbeeld gelijk aan cos(x), en is periodiek. Als je de afgeleide van cos(x) neemt, krijg je –sin(x). De frequentie blijft ongewijzigd.
Het tegendeel is echter niet altijd waar. De functie f(x) = const is dus periodiek, maar de primitieve functie F(x) = const*x + C niet.
Als F(x) een periodieke functie is met periode T, dan is G(x) = a*F(kx + b), waarbij a, b en k constanten zijn en k niet gelijk is aan nul - ook een periodieke functie , en de periode ervan is T/k. sin(2x) is bijvoorbeeld een periodieke functie en de periode ervan is π. Dit kan visueel als volgt worden weergegeven: door x met een getal te vermenigvuldigen, lijkt het erop dat je de grafiek van de functie precies zo vaak horizontaal comprimeert
Als F1(x) en F2(x) periodieke functies zijn, en hun perioden respectievelijk gelijk zijn aan T1 en T2, dan kan de som van deze functies ook periodiek zijn. De periode ervan zal echter niet een eenvoudige som zijn van de perioden T1 en T2. Als het resultaat van de deling T1/T2 een rationeel getal is, dan is de som van de functies periodiek en is de periode gelijk aan het kleinste gemene veelvoud (LCM) van de perioden T1 en T2. Als de periode van de eerste functie bijvoorbeeld 12 is en de periode van de tweede 15, dan is de periode van hun som gelijk aan LCM (12, 15) = 60.
Dit kan visueel als volgt worden weergegeven: functies hebben verschillende ‘stapbreedtes’, maar als de verhouding tussen hun breedtes rationeel is, zullen ze vroeg of laat (of beter gezegd, juist door de LCM van stappen) weer gelijk worden, en hun som begint een nieuwe periode.
Als de verhouding van perioden echter irrationeel is, zal de totale functie helemaal niet periodiek zijn. Stel bijvoorbeeld dat F1(x) = x mod 2 (de rest als x wordt gedeeld door 2), en F2(x) = sin(x). T1 is hier gelijk aan 2, en T2 is gelijk aan 2π. De verhouding van de perioden is gelijk aan π - een irrationeel getal. Daarom is de functie sin(x) + x mod 2 niet periodiek.
De videoles "Periodiciteit van functies y = sin x, y = cos x" onthult het concept van periodiciteit van een functie, beschouwt een beschrijving van voorbeelden van het oplossen van problemen waarin het concept van periodiciteit van een functie wordt gebruikt. Deze videoles is een visueel hulpmiddel om het onderwerp aan leerlingen uit te leggen. Deze handleiding kan ook een zelfstandig onderdeel van de les worden, waardoor de leraar de vrijheid krijgt om individueel met de leerlingen te werken.
Zichtbaarheid bij het presenteren van dit onderwerp is erg belangrijk. Om het gedrag van een functie weer te geven en in kaart te brengen, moet deze worden gevisualiseerd. Het is niet altijd mogelijk om met schoolbord en krijt constructies zo te maken dat deze voor alle leerlingen begrijpelijk zijn. In de video-tutorial is het mogelijk om tijdens het construeren delen van de tekening met kleur te markeren en transformaties uit te voeren met behulp van animatie. Zo worden de constructies voor de meeste studenten begrijpelijker. Ook dragen de videolesfuncties bij aan een betere memorisatie van de stof.
De demonstratie begint met de introductie van het onderwerp van de les en herinnert de leerlingen aan het materiaal dat ze in eerdere lessen hebben geleerd. In het bijzonder wordt de lijst met eigenschappen samengevat die zijn geïdentificeerd in de functies y = sin x, evenals y = cos x. Onder de eigenschappen van de beschouwde functies worden het definitiedomein, het bereik van waarden, pariteit (vreemdheid) en andere kenmerken opgemerkt: begrensdheid, monotoniciteit, continuïteit, punten van de minste (grootste) waarde. De leerlingen worden geïnformeerd dat in deze les een andere eigenschap van een functie wordt bestudeerd: periodiciteit.
De definitie van een periodieke functie y=f(x), waarbij xϵX, waarin de voorwaarde f(x-Т)= f(x)= f(x+Т) voor sommige Т≠0 wordt gepresenteerd. Anders wordt het getal T de periode van de functie genoemd.
Voor de beschouwde sinus- en cosinusfuncties wordt de vervulling van de voorwaarde gecontroleerd met behulp van reductieformules. Het is duidelijk dat de vorm van de identiteit sin(x-2π)=sinx=sin(x+2π) overeenkomt met de vorm van de uitdrukking die de voorwaarde van periodiciteit van de functie definieert. Dezelfde gelijkheid kan worden opgemerkt voor de cosinus cos (x-2π)= cos x= cos (x+2π). Dit betekent dat deze trigonometrische functies periodiek zijn.
Verder wordt opgemerkt hoe de eigenschap van periodiciteit helpt bij het maken van grafieken van periodieke functies. Er wordt rekening gehouden met de functie y = sin x. Op het scherm wordt een coördinatenvlak geconstrueerd, waarop de abscis van -6π tot 8π wordt gemarkeerd met een stap van π. Een deel van de sinusgrafiek wordt in het vlak uitgezet, weergegeven door één golf op het segment. De figuur laat zien hoe de grafiek van een functie over het gehele definitiedomein wordt gevormd door het geconstrueerde fragment te verschuiven, wat resulteert in een lange sinusoïde.
Een grafiek van de functie y = cos x wordt geconstrueerd met behulp van de eigenschap van zijn periodiciteit. Om dit te doen, wordt in de figuur een coördinatenvlak geconstrueerd, waarop een fragment van de grafiek is afgebeeld. Opgemerkt wordt dat een dergelijk fragment doorgaans wordt geconstrueerd op het segment [-π/2;3π/2]. Net als bij de grafiek van de sinusfunctie, wordt de constructie van de cosinusgrafiek uitgevoerd door het fragment te verschuiven. Als resultaat van de constructie wordt een lange sinusoïde gevormd.
Het grafisch weergeven van een periodieke functie heeft functies die kunnen worden gebruikt. Daarom worden ze in een algemene vorm gegeven. Opgemerkt wordt dat om een grafiek van een dergelijke functie te construeren, eerst een tak van de grafiek wordt geconstrueerd op een bepaald interval met lengte T. Vervolgens is het nodig om de geconstrueerde tak naar rechts en links te verschuiven over T, 2T, 3T, enz. Tegelijkertijd wordt op een ander kenmerk van de periode gewezen: voor elk geheel getal k≠0 is het getal kT ook de periode van de functie. T wordt echter de hoofdperiode genoemd, omdat deze de kleinste van allemaal is. Voor de goniometrische functies sinus en cosinus is de basisperiode 2π. De perioden zijn echter ook 4π, 6π, enz.
Vervolgens wordt voorgesteld om te overwegen de hoofdperiode van de functie y = cos 5x te vinden. De oplossing begint met de aanname dat T de periode van de functie is. Dit betekent dat aan de voorwaarde f(x-T)= f(x)= f(x+T) moet worden voldaan. In deze identiteit is f(x)= cos 5x, en f(x+T)=cos 5(x+T)= cos (5x+5T). In dit geval is cos (5x+5T)= cos 5x, dus 5T=2πn. Nu kun je T=2π/5 vinden. Het probleem is opgelost.
In het tweede probleem moet je de hoofdperiode van de functie y=sin(2x/7) vinden. Er wordt aangenomen dat de hoofdperiode van de T-functie voor een gegeven functie f(x)= sin(2x/7) is, en na een periode f(x+T)=sin(2x/7)(x+T) = zonde(2x/7 +(2/7)T). na reductie krijgen we (2/7)Т=2πn. We moeten echter de hoofdperiode vinden, dus nemen we de kleinste waarde (2/7)T=2π, waaruit we T=7π vinden. Het probleem is opgelost.
Aan het einde van de demonstratie worden de resultaten van de voorbeelden samengevat om een regel te vormen voor het bepalen van de basisperiode van de functie. Opgemerkt wordt dat voor de functies y=sinkx en y=coskx de hoofdperioden 2π/k zijn.

De videoles “Periodiciteit van functies y = sin x, y = cos x” kan gebruikt worden in een traditionele wiskundeles om de effectiviteit van de les te vergroten. Het wordt ook aanbevolen dat dit materiaal wordt gebruikt door een leraar die afstandsonderwijs verzorgt, om de duidelijkheid van de uitleg te vergroten. De video kan worden aanbevolen aan een leerling die het moeilijk heeft om zijn begrip van het onderwerp te verdiepen.
TEKST DECODEREN:
“Periodiciteit van functies y = cos x, y = sin x.”
Om grafieken van de functies y = sin x en y = cos x te construeren, werden de eigenschappen van de functies gebruikt:
1 definitiegebied,
2 waardegebied,
3 even of oneven,
4 eentonigheid,
5 beperking,
6 continuïteit,
7 hoogste en laagste waarde.
Vandaag zullen we een andere eigenschap bestuderen: de periodiciteit van een functie.
DEFINITIE. De functie y = f (x), waarbij x ϵ X (in het Grieks is gelijk aan ef van x, waarbij x tot de verzameling x behoort), wordt periodiek genoemd als er een getal T is dat niet nul is, zodat voor elke x uit voor de verzameling X geldt de dubbele gelijkheid: f (x - T)= f (x) = f (x + T)(eff van x min te is gelijk aan ef van x en gelijk aan ef van x plus te). Het getal T dat aan deze dubbele gelijkheid voldoet, wordt de periode van de functie genoemd

En aangezien sinus en cosinus gedefinieerd zijn op de gehele getallenlijn en voor elke x is voldaan aan de gelijkheden sin(x - 2π)= sin x= sin(x+ 2π) (sinus van x min twee pi is gelijk aan sinus van x en gelijk naar sinus van x plus twee pi ) En
cos (x- 2π)= cos x = cos (x+ 2π) (de cosinus van x min twee pi is gelijk aan de cosinus van x en gelijk aan de cosinus van x plus twee pi), dan zijn sinus en cosinus periodieke functies met een periode van 2π.
Met periodiciteit kunt u snel een grafiek van een functie samenstellen. Om een grafiek van de functie y = sin x te construeren, volstaat het om één golf uit te zetten (meestal op een segment (van nul naar twee pi), en vervolgens het geconstrueerde deel van de grafiek langs de x te verschuiven. -as naar rechts en links met 2π, dan met 4π enzovoort om een sinusgolf te krijgen.
(laat de verschuiving rechts en links zien met 2π, 4π)
Hetzelfde geldt voor de grafiek van de functie
y = cos x, maar we bouwen meestal één golf op het segment [; ] (van min pi gedeeld door twee naar drie pi gedeeld door twee).
Laten we het bovenstaande samenvatten en een conclusie trekken: om een grafiek van een periodieke functie met een periode T te construeren, moet je eerst een tak (of golf, of deel) van de grafiek construeren op een willekeurig interval met lengte T (meestal is dit is een interval met uiteinden op de punten 0 en T of - en (minus te bij twee en te bij twee), en verplaats deze tak vervolgens langs de x(x)-as naar rechts en links over T, 2T, 3T, etc.
Als een functie periodiek is met periode T, dan is voor elk geheel getal k0 (ka niet gelijk aan nul) een getal van de vorm kT (ka te) ook de periode van deze functie. Meestal proberen ze de kleinste positieve periode te isoleren, die de hoofdperiode wordt genoemd.
Als de periode van de functies y = cos x, y = sin x, zou men kunnen nemen - 4π, 4π, - 6π, 6π, enz. (minus vier pi, vier pi, minus zes pi, zes pi, enzovoort) . Maar het getal 2π is de hoofdperiode van beide functies.
Laten we naar voorbeelden kijken.
VOORBEELD 1. Zoek de hoofdperiode van de functie y = cos5x (de y is gelijk aan de cosinus van vijf x).
Oplossing. Laat T de hoofdperiode zijn van de functie y = cos5x. Laten we
f (x) = cos5x, dan f (x + T) = cos5(x + T) = cos (5x + 5T) (eff van x plus te is gelijk aan de cosinus van vijf vermenigvuldigd met de som van x en te is gelijk aan de cosinus van de som van vijf x en vijf te).
cos (5x + 5T) = cos5x. Dus 5T = 2πn (vijf te is gelijk aan twee pi en), maar volgens de voorwaarde moet je de hoofdperiode vinden, wat betekent 5T = 2π. We krijgen T=
(de periode van deze functie is twee pi gedeeld door vijf).
Antwoord: T=.

VOORBEELD 2. Zoek de hoofdperiode van de functie y = sin (de y is gelijk aan de sinus van het quotiënt van twee x bij zeven).
Oplossing. Laat T de hoofdperiode zijn van de functie y = sin. Laten we
f (x) = sin, dan f (x + T) = sin (x + T) = sin (x + T) (ef van x plus te is gelijk aan de sinus van het product van twee zevende en de som van x en te is gelijk aan de sinus van de som van twee septiemen x en twee septiemen te).
Wil het getal T de periode van de functie zijn, dan moet aan de identiteit zijn voldaan
zonde (x + T) = zonde. Dus T= 2πn (twee septiemen te is gelijk aan twee pi en), maar volgens de voorwaarde moet je de hoofdperiode vinden, wat betekent dat T= 2π. We krijgen T=7
(de periode van deze functie is zeven pi).
Antwoord: T=7.
Als we de in de voorbeelden verkregen resultaten samenvatten, kunnen we concluderen: de hoofdperiode van de functies y = sin kx of y = cos kx (y is gelijk aan sinus ka x of y is gelijk aan cosinus ka x) is gelijk aan (twee pi gedeeld door k).
Doel: de kennis van studenten over het onderwerp “Periodiciteit van Functies” samenvatten en systematiseren; vaardigheden ontwikkelen in het toepassen van de eigenschappen van een periodieke functie, het vinden van de kleinste positieve periode van een functie, het construeren van grafieken van periodieke functies; interesse in het studeren van wiskunde bevorderen; cultiveer observatie en nauwkeurigheid.
Uitrusting: computer, multimediaprojector, taakkaarten, dia's, klokken, ornamententafels, elementen van volksambachten
“Wiskunde is wat mensen gebruiken om de natuur en zichzelf te beheersen.”
EEN. Kolmogorov
Tijdens de lessen
I. Organisatorische fase.
Controleren of leerlingen klaar zijn voor de les. Vermeld het onderwerp en de doelstellingen van de les.
II. Huiswerk controleren.
We controleren het huiswerk aan de hand van voorbeelden en bespreken de moeilijkste punten.
III. Generalisatie en systematisering van kennis.
1. Mondeling frontaal werk.
Theorie problemen.
1) Vorm een definitie van de periode van de functie
2) Noem de kleinste positieve periode van de functies y=sin(x), y=cos(x)
3). Wat is de kleinste positieve periode van de functies y=tg(x), y=ctg(x)
4) Bewijs met behulp van een cirkel de juistheid van de relaties:
y=sin(x) = zonde(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+180º)
y=ctg(x) = ctg(x+180º)
tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z

sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z
5) Hoe plot ik een periodieke functie?
Mondelinge oefeningen.
1) Bewijs de volgende relaties
a) zonde(740º) = zonde(20º)
b) cos(54º ) = cos(-1026º)
c) zonde(-1000º) = zonde(80º)
2. Bewijs dat een hoek van 540º één van de perioden is van de functie y= cos(2x)
3. Bewijs dat een hoek van 360º een van de perioden is van de functie y=tg(x)
4. Transformeer deze uitdrukkingen zo dat de daarin opgenomen hoeken in absolute waarde niet groter zijn dan 90°.
a) tg375º
b)ctg530º
c) zonde1268º
d)cos(-7363º)
5. Waar ben je de woorden PERIODE, PERIODICITEIT tegengekomen?
Antwoorden van de leerling: Een periode in de muziek is een structuur waarin een min of meer complete muzikale gedachte wordt gepresenteerd. Een geologische periode maakt deel uit van een tijdperk en is verdeeld in tijdperken met een periode van 35 tot 90 miljoen jaar.
Halfwaardetijd van een radioactieve stof. Periodieke breuk. Periodieken zijn gedrukte publicaties die binnen strikt gedefinieerde deadlines verschijnen. Het periodieke systeem van Mendelejev.
6. De figuren tonen delen van de grafieken van periodieke functies. Bepaal de periode van de functie. Bepaal de periode van de functie.

Antwoord: T=2; T=2; T=4; T=8.
7. Waar in je leven ben je de constructie van herhalende elementen tegengekomen?
Antwoord van de student: Elementen van ornamenten, volkskunst.

IV. Collectieve probleemoplossing.
(Problemen op dia's oplossen.)
Laten we eens kijken naar een van de manieren om een functie op periodiciteit te bestuderen.
Deze methode vermijdt de moeilijkheden die gepaard gaan met het bewijzen dat een bepaalde periode de kleinste is, en elimineert ook de noodzaak om vragen te beantwoorden over rekenkundige bewerkingen op periodieke functies en de periodiciteit van een complexe functie. De redenering is alleen gebaseerd op de definitie van een periodieke functie en op het volgende feit: als T de periode van de functie is, dan is nT(n?0) de periode ervan.
Probleem 1. Vind de kleinste positieve periode van de functie f(x)=1+3(x+q>5)
Oplossing: Neem aan dat de T-periode van deze functie. Dan f(x+T)=f(x) voor alle x € D(f), d.w.z.
1+3(x+T+0,25)=1+3(x+0,25)
(x+T+0,25)=(x+0,25)
Laten we stellen dat x=-0,25 we krijgen
(T)=0 T=n, n € Z
We hebben vastgesteld dat alle perioden van de functie in kwestie (als ze bestaan) tot de gehele getallen behoren. Laten we het kleinste positieve getal uit deze getallen kiezen. Dit is 1. Even kijken of het daadwerkelijk periode 1 wordt.
f(x+1) =3(x+1+0,25)+1
Omdat (T+1)=(T) voor elke T, dan is f(x+1)=3((x+0,25)+1)+1=3(x+0,25)+1=f(x ), d.w.z. 1 – periode f. Omdat 1 het kleinste van alle positieve gehele getallen is, is T=1.
Opgave 2. Laat zien dat de functie f(x)=cos 2 (x) periodiek is en vind de hoofdperiode ervan.

Probleem 3. Zoek de hoofdperiode van de functie
f(x)=sin(1,5x)+5cos(0,75x)
Laten we uitgaan van de T-periode van de functie, dan is voor elke x de relatie geldig
sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)
Als x=0, dan
sin(1,5T)+5cos(0,75T)=sin0+5cos0
sin(1,5T)+5cos(0,75T)=5
Als x=-T, dan
sin0+5cos0=sin(-1,5T)+5cos0,75(-T)
5= – sin(1,5T)+5cos(0,75T)
| sin(1,5T)+5cos(0,75T)=5 – sin(1,5T)+5cos(0,75T)=5 |
Als we dit optellen, krijgen we:
10cos(0,75T)=10
2π n, n € Z
Laten we uit alle ‘verdachte’ getallen voor de periode het kleinste positieve getal kiezen en controleren of het een periode voor f is. Dit nummer
f(x+)=sin(1,5x+4π )+5cos(0,75x+2π )= sin(1,5x)+5cos(0,75x)=f(x)
Dit betekent dat dit de hoofdperiode van de functie f is.
Probleem 4. Laten we controleren of de functie f(x)=sin(x) periodiek is
Laat T de periode van de functie f zijn. Dan voor elke x
zonde|x+Т|=zonde|x|
Als x=0, dan sin|Т|=sin0, sin|Т|=0 Т=π n, n € Z.
Laten we aannemen. Dat voor sommige n het getal π n de periode is
de betreffende functie π n>0. Dan zonde|π n+x|=zonde|x|

Dit impliceert dat n zowel een even als een oneven getal moet zijn, maar dit is onmogelijk. Deze functie is dus niet periodiek.
Taak 5. Controleer of de functie periodiek is
f(x)= 
Laat T dan de periode van f zijn
 , dus sinT=0, Т=π n, n € Z. Laten we aannemen dat voor sommige n het getal π n inderdaad de periode van deze functie is. Dan is het getal 2π n de periode
, dus sinT=0, Т=π n, n € Z. Laten we aannemen dat voor sommige n het getal π n inderdaad de periode van deze functie is. Dan is het getal 2π n de periode

Omdat de tellers gelijk zijn, zijn hun noemers dus ook gelijk

Dit betekent dat de functie f niet periodiek is.
Werk in groepen.
Taken voor groep 1.
Taken voor groep 2.
Controleer of de functie f periodiek is en vind de fundamentele periode ervan (als deze bestaat).
f(x)=cos(2x)+2sin(2x)
Taken voor groep 3.
Aan het einde van hun werk presenteren de groepen hun oplossingen.
VI. De les samenvattend.
Reflectie.
De leraar geeft de leerlingen kaarten met tekeningen en vraagt hen een deel van de eerste tekening in te kleuren, afhankelijk van de mate waarin ze denken de methoden voor het bestuderen van een functie voor periodiciteit onder de knie te hebben, en een deel van de tweede tekening - in overeenstemming met hun bijdrage aan het werk in de les.
VII. Huiswerk
1). Controleer of de functie f periodiek is en vind de fundamentele periode ervan (als deze bestaat)
B). f(x)=x 2 -2x+4
C). f(x)=2tg(3x+5)
2). De functie y=f(x) heeft een periode T=2 en f(x)=x 2 +2x voor x € [-2; 0]. Zoek de waarde van de uitdrukking -2f(-3)-4f(3,5)
Literatuur/
In juli 2020 lanceert NASA een expeditie naar Mars. Het ruimtevaartuig zal Mars een elektronisch medium bezorgen met de namen van alle geregistreerde expeditiedeelnemers.
De inschrijving voor deelnemers is geopend. Koop uw ticket naar Mars via deze link.
Als dit bericht je probleem heeft opgelost of je het gewoon leuk vond, deel dan de link ernaar met je vrienden op sociale netwerken.
Eén van deze codeopties dient u te kopiëren en in de code van uw webpagina te plakken, bij voorkeur tussen tags en of direct na de tag. Volgens de eerste optie laadt MathJax sneller en vertraagt de pagina minder. Maar de tweede optie bewaakt en laadt automatisch de nieuwste versies van MathJax. Als u de eerste code invoert, moet deze periodiek worden bijgewerkt. Als u de tweede code invoegt, worden de pagina's langzamer geladen, maar hoeft u MathJax-updates niet voortdurend in de gaten te houden.
De eenvoudigste manier om MathJax te verbinden is in Blogger of WordPress: voeg in het siteconfiguratiescherm een widget toe die is ontworpen om JavaScript-code van derden in te voegen, kopieer de eerste of tweede versie van de hierboven weergegeven downloadcode erin en plaats de widget dichterbij naar het begin van de sjabloon (dit is overigens helemaal niet nodig, aangezien het MathJax-script asynchroon wordt geladen). Dat is alles. Leer nu de opmaaksyntaxis van MathML, LaTeX en ASCIIMathML, en u bent klaar om wiskundige formules in de webpagina's van uw site in te voegen.
Nog een oudejaarsavond... ijzig weer en sneeuwvlokken op de ruit... Dit alles was voor mij aanleiding om opnieuw te schrijven over... fractals, en wat Wolfram Alpha ervan weet. Er is een interessant artikel over dit onderwerp, dat voorbeelden bevat van tweedimensionale fractale structuren. Hier zullen we kijken naar meer complexe voorbeelden van driedimensionale fractals.
Een fractal kan visueel worden weergegeven (beschreven) als een geometrische figuur of lichaam (wat betekent dat beide een set zijn, in dit geval een set punten), waarvan de details dezelfde vorm hebben als de originele figuur zelf. Dat wil zeggen, dit is een op zichzelf gelijkende structuur, waarbij we de details onderzoeken waarvan we bij vergroting dezelfde vorm zullen zien als zonder vergroting. Terwijl we in het geval van een gewone geometrische figuur (geen fractal) bij vergroting details zullen zien die een eenvoudiger vorm hebben dan de originele figuur zelf. Bij een voldoende hoge vergroting ziet een deel van een ellips er bijvoorbeeld uit als een recht lijnsegment. Dit gebeurt niet bij fractals: bij elke toename ervan zullen we opnieuw dezelfde complexe vorm zien, die bij elke toename steeds opnieuw zal worden herhaald.
Benoit Mandelbrot, de grondlegger van de wetenschap van fractals, schreef in zijn artikel Fractals and Art in the Name of Science: "Fractalen zijn geometrische vormen die net zo complex zijn in hun details als in hun algehele vorm. Dat wil zeggen, als ze deel uitmaken van de fractal zal worden vergroot tot de grootte van het geheel, het zal als een geheel verschijnen, hetzij precies, hetzij misschien met een lichte vervorming."
Trigonometrische functies zijn periodiek, dat wil zeggen dat ze zich na een bepaalde periode herhalen. Als gevolg hiervan is het voldoende om de functie op dit interval te bestuderen en de ontdekte eigenschappen uit te breiden naar alle andere perioden.
Instructies1. Als je een primitieve uitdrukking krijgt waarin er maar één trigonometrische functie is (sin, cos, tg, ctg, sec, cosec), en de hoek binnen de functie met geen enkel getal wordt vermenigvuldigd, en deze zelf niet wordt verhoogd in welke mate dan ook - gebruik de definitie. Voor uitdrukkingen die sin, cos, sec, cosec bevatten, stelt u de periode stoutmoedig in op 2P, en als de vergelijking tg, ctg en dan P bevat. Laten we zeggen dat voor de functie y=2 sinx+5 de periode gelijk zal zijn aan 2P .
2. Als de hoek x onder het teken van een goniometrische functie met een getal wordt vermenigvuldigd, deel dan, om de periode van deze functie te vinden, de typische periode door dit getal. Laten we zeggen dat je een functie y = sin 5x krijgt. De typische periode voor een sinus is 2P; als je deze door 5 deelt, krijg je 2P/5 - dit is de gewenste periode van deze uitdrukking.
3. Om de periode van een goniometrische functie tot een macht te vinden, schat je de pariteit van de macht. Voor een gelijkmatige graad verkort u de typische periode met de helft. Laten we zeggen dat als je de functie y = 3 cos^2x krijgt, de typische periode 2P twee keer afneemt, dus de periode is gelijk aan P. Houd er rekening mee dat de functies tg, ctg periodiek zijn voor P voor elke rang.
4. Als je een vergelijking krijgt die het product of quotiënt van twee goniometrische functies bevat, zoek dan eerst de periode voor ze allemaal afzonderlijk. Zoek hierna het minimumgetal dat het gehele getal van beide perioden zou bevatten. Laten we zeggen dat de functie y=tgx*cos5x is gegeven. Voor de tangens is de periode P, voor cosinus 5x is de periode 2P/5. Het minimale aantal waarin beide periodes kunnen worden ondergebracht is 2P, de gewenste periode is dus 2P.
5. Als je het moeilijk vindt om te doen zoals voorgesteld, of als je twijfelt aan het resultaat, probeer het dan te doen zoals gedefinieerd. Neem T als de periode van de functie; deze is groter dan nul. Vervang de uitdrukking (x + T) in plaats van x in de vergelijking en los de resulterende gelijkheid op alsof T een parameter of een getal is. Als gevolg hiervan ontdekt u de waarde van de trigonometrische functie en kunt u de kleinste periode vinden. Laten we zeggen dat je als resultaat van het reliëf de identiteitszonde (T/2) = 0 krijgt. De minimumwaarde van T waarbij het wordt uitgevoerd is 2P, dit zal het resultaat van de taak zijn.
Een periodieke functie is een functie die zijn waarden herhaalt na een periode die niet nul is. De periode van een functie is een getal dat, wanneer het wordt toegevoegd aan het argument van een functie, de waarde van de functie niet verandert.

Je zal nodig hebben
- Kennis van elementaire wiskunde en basisbeoordeling.
1. Laten we de periode van de functie f(x) aangeven met het getal K. Het is onze taak om deze waarde van K te ontdekken. Stel je hiervoor voor dat de functie f(x), gebruikmakend van de definitie van een periodieke functie, we stellen f(x+K)=f(x) gelijk.
2. We lossen de resulterende vergelijking met betrekking tot de onbekende K op, alsof x een constante is. Afhankelijk van de waarde van K zijn er verschillende opties.
3. Als K>0 – dan is dit de periode van je functie. Als K=0 – dan is de functie f(x) niet periodiek. Als de oplossing van de vergelijking f(x+K)=f(x) dat wel is niet bestaat voor een K die niet gelijk is aan nul, dan wordt zo'n functie aperiodisch genoemd en heeft deze ook geen periode.
Video over het onderwerp
Opmerking!
Alle trigonometrische functies zijn periodiek en alle polynomiale functies met een graad groter dan 2 zijn aperiodisch.
Behulpzaam advies
De periode van een functie bestaande uit 2 periodieke functies is het minst universele veelvoud van de perioden van deze functies.
Trigonometrische vergelijkingen zijn vergelijkingen die trigonometrische functies van een onbekend argument bevatten (bijvoorbeeld: 5sinx-3cosx =7). Om te leren hoe u ze kunt oplossen, moet u enkele manieren kennen om dit te doen.

1. De oplossing van dergelijke vergelijkingen bestaat uit twee fasen: de eerste is het hervormen van de vergelijking om de eenvoudigste vorm te verkrijgen. De eenvoudigste trigonometrische vergelijkingen zijn: Sinx=a; Cosx=a, enz.
2. De tweede is de oplossing van de eenvoudigste verkregen trigonometrische vergelijking. Er zijn basismanieren om dit soort vergelijkingen op te lossen: Algebraïsch oplossen. Deze methode is bekend van school, van een algebracursus. Ook wel de methode van variabele vervanging en substitutie genoemd. Met behulp van reductieformules transformeren we, maken we een vervanging en vinden we vervolgens de wortels.
3. De vergelijking in factoren ontbinden. Eerst verplaatsen we alle termen naar links en ontbinden ze.
4. De vergelijking terugbrengen tot een homogene vergelijking. Vergelijkingen worden homogene vergelijkingen genoemd als alle termen van dezelfde graad zijn en de sinus en cosinus dezelfde hoek hebben. Om het op te lossen, moet je: eerst alle termen van de rechterkant naar de linkerkant overbrengen; plaats alle universele factoren tussen haakjes; factoren en haakjes gelijkstellen aan nul; gelijkgestelde haakjes geven een homogene vergelijking van een lagere graad, die in de hoogste graad moet worden gedeeld door cos (of sin); los de resulterende algebraïsche vergelijking met betrekking tot tan op.
5. De volgende methode is om naar een halve hoek te gaan. Stel, los de vergelijking op: 3 sin x – 5 cos x = 7. Laten we verder gaan met de halve hoek: 6 sin (x / 2) · cos (x / 2) – 5 cos? (x / 2) + 5 zonde ? (x / 2) = 7 zonde? (x / 2) + 7 cos ? (x/ 2) , waarna we alle termen reduceren tot één deel (bij voorkeur de rechterkant) en de vergelijking oplossen.
6. Invoer van hulphoek. Wanneer we de gehele waarde cos(a) of sin(a) vervangen. Het teken “a” is een hulphoek.
7. Methode om een product om te zetten in een som. Hier moet u de juiste formules toepassen. Laten we zeggen gegeven: 2 sin x · sin 3x = cos 4x. Los het op door de linkerkant om te zetten in een som, dat wil zeggen: cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk , x = p/16 + pk/8.
8. De laatste methode wordt multifunctionele substitutie genoemd. We transformeren de uitdrukking en brengen een verandering aan, bijvoorbeeld Cos(x/2)=u, en lossen vervolgens de vergelijking op met de parameter u. Bij aankoop van het totaal rekenen wij de waarde om naar het tegenovergestelde.
Video over het onderwerp
Als we punten op een cirkel beschouwen, dan zijn de punten x, x + 2π, x + 4π, enz. met elkaar samenvallen. Trigonometrische functies op een rechte lijn herhalen dus periodiek hun waarde. Als de periode van een functie bekend is, is het mogelijk om de functie op deze periode te construeren en deze op andere te herhalen.

1. De periode is een getal T zodat f(x) = f(x+T). Om de periode te vinden, lost u de overeenkomstige vergelijking op, waarbij u x en x+T als argument vervangt. In dit geval gebruiken ze de reeds bekende periodes voor functies. Voor de sinus- en cosinusfuncties is de periode 2π, en voor de tangens- en cotangensfuncties is deze π.
2. Laat de functie f(x) = sin^2(10x) gegeven worden. Beschouw de uitdrukking sin^2(10x) = sin^2(10(x+T)). Gebruik de formule om de graad te verminderen: sin^2(x) = (1 – cos 2x)/2. Dan krijg je 1 – cos 20x = 1 – cos 20(x+T) of cos 20x = cos (20x+20T). Wetende dat de periode van de cosinus 2π is, is 20T = 2π. Dit betekent T = π/10. T is de minimaal juiste periode, en de functie wordt herhaald na 2T, en na 3T, en in de andere richting langs de as: -T, -2T, enz.
Behulpzaam advies
Gebruik formules om de graad van een functie te reduceren. Als u de perioden van sommige functies al kent, probeer dan de bestaande functie terug te brengen tot bekende functies.
Het onderzoeken van een functie op gelijkmatigheid en vreemdheid helpt bij het maken van een grafiek van de functie en bij het begrijpen van de aard van zijn gedrag. Voor dit onderzoek moet je deze functie, geschreven voor het argument “x”, vergelijken met het argument “-x”.
1. Schrijf de functie op die je wilt bestuderen in de vorm y=y(x).
2. Vervang het argument van de functie door “-x”. Vervang dit argument door een functionele expressie.
3. Vereenvoudig de uitdrukking.
4. Je hebt dus dezelfde functie geschreven voor de argumenten “x” en “-x”. Kijk eens naar deze twee gegevens. Als y(-x)=y(x), dan is het een even functie. Als y(-x)=-y(x), dan is het een oneven functie. Als het onmogelijk is om Als je over een functie zegt dat y (-x)=y(x) of y(-x)=-y(x), dan is dit volgens de eigenschap van pariteit een functie van universele vorm. Dat wil zeggen: het is noch even, noch oneven.
5. Schrijf je bevindingen op. Nu kunt u ze gebruiken bij het construeren van een grafiek van een functie of bij een toekomstige analytische studie van de eigenschappen van een functie.
6. Het is ook mogelijk om over de evenheid en eigenaardigheid van een functie te praten in het geval dat de grafiek van de functie al gegeven is. Laten we zeggen dat de grafiek het resultaat is van een natuurkundig experiment. Als de grafiek van een functie symmetrisch is rond de ordinaat-as, dan is y(x) een even functie. Als de grafiek van een functie symmetrisch is rond de abscis-as, dan x(y) is een even functie. x(y) is een functie die omgekeerd is aan de functie y(x).Als de grafiek van een functie symmetrisch is rond de oorsprong (0,0), dan is y(x) een oneven functie. De inverse functie x(y) zal ook oneven zijn.
7. Het is belangrijk om te onthouden dat het idee van gelijkheid en eigenaardigheid van een functie een directe verbinding heeft met het domein van de definitie van de functie. Als er bijvoorbeeld geen even of oneven functie bestaat op x=5, dan bestaat deze niet op x=-5, wat niet gezegd kan worden over een functie met een universele vorm. Let bij het vaststellen van even en oneven pariteit op het domein van de functie.
8. Het vinden van een functie voor evenheid en onevenheid correleert met het vinden van een reeks functiewaarden. Om de reeks waarden van een even functie te vinden, volstaat het om naar de helft van de functie te kijken, rechts of links van nul. Als bij x>0 de even functie y(x) waarden van A naar B aanneemt, dan zal deze dezelfde waarden aannemen en bij x0 neemt de oneven functie y(x) het bereik van waarden van A aan naar B, dan bij x sin^2 ? + cos^2 ? = 1. De derde en vierde identiteit worden verkregen door respectievelijk te delen door b^2 en a^2: a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/zonde^ ? of 1 +ctg^2? = 1/sin^2 ?. De vijfde en zesde basisidentiteit worden bewezen door de som van de scherpe hoeken van een rechthoekige driehoek te bepalen, die gelijk is aan 90° of?/2. Moeilijkere trigonometrische identiteiten: formules voor het optellen van argumenten, dubbele en drievoudige hoeken, het verminderen van de graad, het hervormen van de som of producten van functies, evenals formules voor trigonometrische substitutie, namelijk uitdrukkingen van trigonometrische basisfuncties in termen van tan halve hoek: sin ?= (2*tg ?/2)/ (1 + bruin^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg?/2)/(1 – tg^2?/2).
De noodzaak om de minimumwaarde van een wiskundige functie te vinden is van feitelijk belang bij het oplossen van toegepaste problemen, bijvoorbeeld in de economie. Het minimaliseren van verliezen is van groot belang voor bedrijfsactiviteiten.

1. Om de minimumwaarde van de functie te vinden, is het noodzakelijk om te bepalen bij welke waarde van het argument x0 aan de ongelijkheid y(x0) zal worden voldaan? y(x), waar x? x0. Zoals gewoonlijk wordt dit probleem opgelost op een bepaald interval of in elk bereik van waarden van de functie, als er geen is gespecificeerd. Eén aspect van de oplossing is het vinden van vaste punten.
2. Een stationair punt is de waarde van het argument waarbij de afgeleide van de functie nul wordt. Volgens de stelling van Fermat is dit punt stationair als een differentieerbare functie op een bepaald punt een extreme waarde aanneemt (in dit geval een lokaal minimum).
3. Vaak neemt de functie precies op dit punt zijn minimumwaarde aan, maar deze kan niet altijd worden bepaald. Bovendien is het niet altijd mogelijk om met precisie te zeggen waaraan het minimum van de functie gelijk is en of deze een oneindig kleine waarde aanneemt. Vervolgens vinden ze, zoals gewoonlijk, de grens waarheen het neigt als het afneemt.
4. Om de minimumwaarde van een functie te bepalen, is het noodzakelijk om een reeks acties uit te voeren die uit vier fasen bestaan: het vinden van het domein van de definitie van de functie, het verwerven van vaste punten, het beoordelen van de waarden van de functie op deze punten en aan het einde van het interval, het vinden van het minimum.
5. Het blijkt dat een functie y(x) gegeven kan worden op een interval met grenzen op de punten A en B. Zoek het domein van zijn definitie en ontdek of het interval zijn deelverzameling is.
6. Bereken de afgeleide van de functie. Stel de resulterende uitdrukking gelijk aan nul en vind de wortels van de vergelijking. Controleer of deze stationaire punten binnen de opening vallen. Indien dit niet het geval is, wordt er in een later stadium geen rekening mee gehouden.
7. Onderzoek de kloof voor het type grenzen: open, gesloten, samengesteld of onmeetbaar. Dit bepaalt hoe u naar de minimumwaarde zoekt. Laten we zeggen dat het segment [A, B] een gesloten interval is. Sluit ze aan op de functie en bereken de waarden. Doe hetzelfde met een stationair punt. Selecteer het laagste totaal.
8. Met open en onmeetbare intervallen is de situatie iets moeilijker. Hierbij zul je moeten zoeken naar eenzijdige grenzen die niet altijd een eenduidig resultaat opleveren. Stel dat je voor een interval met één gesloten en één doorboorde grens [A, B) een functie zou moeten vinden op x = A en een eenzijdige limiet lim y op x? B-0.

 Kunstmatige zwaartekracht is niet langer sciencefiction
Kunstmatige zwaartekracht is niet langer sciencefiction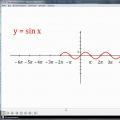 Periodiciteit van functies y = sin x, y = cos x - Kennishypermarkt
Periodiciteit van functies y = sin x, y = cos x - Kennishypermarkt DPR- en LPR-rapporten: krachtige veldslagen bij Gorlovka, beschietingen van Donetsk door artillerie, botsingen langs de hele frontlinie
DPR- en LPR-rapporten: krachtige veldslagen bij Gorlovka, beschietingen van Donetsk door artillerie, botsingen langs de hele frontlinie