Formel for variansen til en tilfeldig variabel. Varians og standardavvik i MS EXCEL

Denne egenskapen alene er imidlertid ikke tilstrekkelig for forskning. tilfeldig variabel. La oss forestille oss to skyttere som skyter mot et mål. Den ene skyter nøyaktig og treffer nær midten, mens den andre... bare har det gøy og sikter ikke engang. Men det som er morsomt er at han gjennomsnitt resultatet blir nøyaktig det samme som det første skytespillet! Denne situasjonen er konvensjonelt illustrert av følgende tilfeldige variabler:

"Snikskyttere" forventet verdi lik imidlertid for " interessant personlighet": – det er også null!

Det er derfor behov for å kvantifisere hvor langt spredt kuler (verdier for tilfeldige variabler) i forhold til midten av målet (matematisk forventning). vel og spredning oversatt fra latin er ingen annen måte enn spredning .

La oss se hvordan denne numeriske egenskapen bestemmes ved å bruke et av eksemplene fra den første delen av leksjonen:

Der fant vi en skuffende matematisk forventning til dette spillet, og nå må vi beregne variansen, som betegnet med gjennom.

La oss finne ut hvor langt gevinstene/tapene er "spredt" i forhold til gjennomsnittsverdien. Det er klart, for dette må vi beregne forskjeller mellom tilfeldige variable verdier og henne matematisk forventning:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Nå ser det ut til at du må oppsummere resultatene, men denne måten er ikke egnet - av den grunn at svingninger til venstre vil oppheve hverandre med svingninger til høyre. Så for eksempel en "amatør" skytespiller (eksempel ovenfor) forskjellene vil være , og når de legges til vil de gi null, så vi vil ikke få noe estimat på spredningen av skytingen hans.

For å omgå dette problemet kan du vurdere moduler forskjeller, men av tekniske årsaker har tilnærmingen slått rot når de kvadres. Det er mer praktisk å formulere løsningen i en tabell:

Og her ber det om å regne vektlagt gjennomsnitt verdien av de kvadrerte avvikene. Hva er det? Det er deres forventet verdi, som er et mål på spredning:

– definisjon avvik. Fra definisjonen er det umiddelbart klart at varians kan ikke være negativ– legg merke til øvelsen!

La oss huske hvordan du finner forventet verdi. Multipliser de kvadrerte forskjellene med de tilsvarende sannsynlighetene (tabellfortsettelse):
– billedlig talt er dette "trekkkraft",
og oppsummer resultatene:

Synes du ikke at i forhold til gevinstene ble resultatet for stort? Det stemmer – vi kvadret det, og for å gå tilbake til dimensjonen av spillet vårt, må vi trekke ut kvadratroten. Denne verdien kalt standardavvik og er betegnet med den greske bokstaven "sigma":

Denne verdien kalles noen ganger standardavvik .

Hva er dens betydning? Hvis vi avviker fra den matematiske forventningen til venstre og høyre med gjennomsnittet standardavvik:

– da vil de mest sannsynlige verdiene til den tilfeldige variabelen være "konsentrert" på dette intervallet. Hva vi faktisk observerer:

Imidlertid har det seg slik at når man analyserer spredning, opererer man nesten alltid med begrepet spredning. La oss finne ut hva det betyr i forhold til spill. Hvis vi når det gjelder piler snakker om "nøyaktigheten" av treff i forhold til midten av målet, så karakteriserer spredning to ting:

For det første er det åpenbart at etter hvert som innsatsene øker, øker også spredningen. Så hvis vi for eksempel øker med 10 ganger, vil den matematiske forventningen øke med 10 ganger, og variansen vil øke med 100 ganger (siden dette er en kvadratisk mengde). Men merk at selve spillereglene ikke har endret seg! Bare prisene har endret seg, grovt sett, før vi satset 10 rubler, nå er det 100.

For det andre, mer interessant poeng er at variansen preger spillestilen. Mentalt fikse spillets innsatser på et visst nivå, og la oss se hva som er hva:

Et spill med lav varians er et forsiktig spill. Spilleren har en tendens til å velge de mest pålitelige ordningene, der han ikke taper/vinner for mye på en gang. For eksempel rød/svart-systemet i rulett (se eksempel 4 i artikkelen Tilfeldige variabler) .

Spill med høy variasjon. Hun blir ofte oppringt dispersive spill. Dette er en eventyrlig eller aggressiv spillestil, der spilleren velger "adrenalin"-opplegg. La oss i det minste huske "Martingale", der beløpene som står på spill er størrelsesordener større enn det "stille" spillet fra forrige punkt.

Situasjonen i poker er veiledende: det er såkalte stramt spillere som har en tendens til å være forsiktige og "shaky" over sine spillemidler (bankroll). Ikke overraskende svinger ikke deres bankroll betydelig (lav varians). Tvert imot, hvis en spiller har høy varians, så er han en aggressor. Han tar ofte risiko, gjør store innsatser og kan enten bryte en enorm bank eller tape i småbiter.

Det samme skjer i Forex, og så videre - det er mange eksempler.

Dessuten spiller det ingen rolle i alle tilfeller om spillet spilles for pennies eller tusenvis av dollar. Hvert nivå har sine lav- og høyspredningsspillere. Vel, som vi husker, er gjennomsnittlig gevinst "ansvarlig" forventet verdi.

Du har sikkert lagt merke til at det å finne varians er en lang og møysommelig prosess. Men matematikk er raus:

Formel for å finne varians

Denne formelen er avledet direkte fra definisjonen av varians, og vi tar den umiddelbart i bruk. Jeg kopierer skiltet med spillet vårt ovenfor:

og den funnet matematiske forventningen.

La oss beregne variansen på den andre måten. La oss først finne den matematiske forventningen - kvadratet til den tilfeldige variabelen. Av fastsettelse av matematisk forventning:

I i dette tilfellet:

Altså, i henhold til formelen:

Som de sier, føl forskjellen. Og i praksis er det selvfølgelig bedre å bruke formelen (med mindre tilstanden krever noe annet).

Vi mestrer teknikken for å løse og designe:

Eksempel 6

Finn dens matematiske forventning, varians og standardavvik.

Denne oppgaven finnes overalt, og går som regel uten meningsfull mening.
Du kan tenke deg flere lyspærer med tall som lyser opp i et galehus med visse sannsynligheter :)

Løsning: Det er praktisk å oppsummere de grunnleggende beregningene i en tabell. Først skriver vi de første dataene i de to øverste linjene. Deretter beregner vi produktene, deretter og til slutt summene i høyre kolonne:

Faktisk er nesten alt klart. Den tredje linjen viser en ferdig matematisk forventning: .

Vi beregner variansen ved å bruke formelen:

Og til slutt, standardavviket:
– Personlig avrunder jeg vanligvis til 2 desimaler.

Alle beregninger kan utføres på en kalkulator, eller enda bedre - i Excel:

Det er vanskelig å gå feil her :)

Svar:

De som ønsker kan forenkle livet sitt enda mer og dra nytte av min kalkulator (demo), som ikke bare løser seg umiddelbart denne oppgaven, men vil også bygge tematisk grafikk (vi kommer dit snart). Programmet kan være last ned fra biblioteket– hvis du har lastet ned minst én undervisningsmateriell, eller få annen vei. Takk for at du støtter prosjektet!

Et par oppgaver for uavhengig avgjørelse:

Eksempel 7

Beregn variansen til den tilfeldige variabelen i forrige eksempel per definisjon.

Og et lignende eksempel:

Eksempel 8

En diskret tilfeldig variabel er spesifisert av dens distribusjonslov:

Ja, tilfeldige variabelverdier kan være ganske store (eksempel fra ekte arbeid) , og her, hvis mulig, bruk Excel. Som forresten i eksempel 7 - det er raskere, mer pålitelig og morsommere.

Løsninger og svar nederst på siden.

På slutten av 2. del av leksjonen skal vi se på en til typisk oppgave, kan man til og med si, en liten rebus:

Eksempel 9

En diskret tilfeldig variabel kan bare ha to verdier: og , og . Sannsynligheten, den matematiske forventningen og variansen er kjent.

Løsning: La oss starte med en ukjent sannsynlighet. Siden en tilfeldig variabel bare kan ta to verdier, er summen av sannsynlighetene for de tilsvarende hendelsene:

og siden da.

Det gjenstår bare å finne..., det er lett å si :) Men jaja, så er det. Per definisjon av matematisk forventning:
– erstatte kjente mengder:

– og ingenting mer kan presses ut av denne ligningen, bortsett fra at du kan skrive den om i vanlig retning:

eller:

OM ytterligere handlinger, jeg tror du kan gjette. La oss komponere og løse systemet:

Desimaler- dette er selvfølgelig en fullstendig skam; multipliser begge ligningene med 10:

og del på 2:

Det er bedre. Fra den første ligningen uttrykker vi:
(dette er den enkleste måten)– bytt inn i den andre ligningen:

Vi bygger kvadrat og gjør forenklinger:

Multipliser med:

Resultatet ble kvadratisk ligning, finner vi det diskriminerende:
- Flott!

og vi får to løsninger:

1) hvis , Det ;

2) hvis , Det.

Betingelsen er oppfylt av det første verdiparet. Med stor sannsynlighet er alt riktig, men la oss likevel skrive ned distribusjonsloven:

og utfør en sjekk, nemlig finn forventningen:

I mange tilfeller blir det nødvendig å introdusere en annen numerisk karakteristikkå måle grad spredning, spredning av verdier, tatt som en tilfeldig variabel ξ , rundt dens matematiske forventning.

Definisjon. Varians av en tilfeldig variabel ξ ringte et nummer.

D ξ= M(ξ-Mξ) 2 . (1)

Med andre ord, spredning er den matematiske forventningen til kvadratavviket til verdiene til en tilfeldig variabel fra gjennomsnittsverdien.

kalt gjennomsnittlig firkant avvik

mengder ξ .

Hvis spredningen preger gjennomsnittlig størrelse kvadratavvik ξ fra Mξ, så kan tallet betraktes som noe gjennomsnittlig karakteristikk selve avviket, mer presist, størrelsen | ξ-Mξ |.

De følgende to egenskapene til spredning følger av definisjon (1).

1. Varians konstant verdi lik null. Dette er ganske i samsvar med den visuelle betydningen av spredning som et "spredningsmål".

Faktisk, hvis

ξ = C, At Mξ = C og det betyr Dξ = M(C-C) 2 = M 0 = 0.

2. Når du multipliserer en tilfeldig variabel ξ på konstant antall C dens varians multipliseres med C 2

D(Cξ) = C 2 Dξ . (3)

Egentlig

D(Cξ) = M(C

= M(C .

3. Følgende formel for å beregne variansen finner sted:

. (4)

Beviset for denne formelen følger av egenskapene til den matematiske forventningen.

Vi har:

4. Hvis verdiene ξ 1 og ξ 2 er uavhengige, så er variansen av summen deres lik summen av deres varians:

Bevis . For å bevise dette bruker vi egenskapene til matematisk forventning. La Mξ 1 = m 1 , Mξ 2 = m 2 da.

Formel (5) er bevist.

Siden variansen til en tilfeldig variabel per definisjon er den matematiske forventningen til verdien ( ξ -m) 2 , hvor m = Mξ, for å beregne variansen kan du bruke formlene som er oppnådd i §7 i kapittel II.

Så hvis ξ det er en DSV med distribusjonslov

x 1	x 2	...
s 1	s 2	...

da vil vi ha:

. (7)

Hvis ξ kontinuerlig tilfeldig variabel med distribusjonstetthet p(x), da får vi:

Dξ= . (8)

Hvis du bruker formel (4) for å beregne variansen, kan du få andre formler, nemlig:

, (9)

hvis verdien ξ diskret, og

Dξ= , (10)

Hvis ξ fordelt med tetthet s(x).

Eksempel 1. La verdien ξ jevnt fordelt på segmentet [ a,b]. Ved å bruke formel (10) får vi:

Det kan vises at variansen til en tilfeldig variabel fordelt etter normalloven med tetthet

p(x)= , (11)

lik σ 2.

Dette tydeliggjør betydningen av parameteren σ inkludert i tetthetsuttrykket (11) for normal lov; σ det er et gjennomsnitt standardavvik verdier ξ.

Eksempel 2. Finn variansen til en tilfeldig variabel ξ , fordelt i henhold til binomialloven.

Løsning . Ved å bruke representasjonen av ξ i skjemaet

ξ = ξ 1 + ξ 2 + ξn(se eksempel 2 §7 kapittel II) og bruke formelen for å legge til varians for uavhengige mengder, vi får

Dξ = Dξ 1 + Dξ 2 +Dξn .

Spredning av noen av mengdene ξi (Jeg= 1,2, n) beregnes direkte:

Dξ i = ​​M(ξ i) 2 - (Mξi) 2 = 0 2 · q+ 1 2 s- s 2 = s(1-s) = pq.

Endelig får vi

Dξ= npq, Hvor q = 1 - s.

For grupperte data gjenværende varians - gjennomsnitt på avvik innen gruppe:

Hvor σ 2 j er intragruppevariansen til den jth gruppen.

For ugrupperte data gjenværende varians– mål for tilnærmingsnøyaktighet, dvs. tilnærming av regresjonslinjen til de opprinnelige dataene:
hvor y(t) er prognosen ved bruk av trendligningen; y t – innledende dynamikkserie; n – antall poeng; p – antall regresjonsligningskoeffisienter (antall forklaringsvariabler).
I dette eksemplet heter det upartisk variansestimator.

Eksempel nr. 1. Fordelingen av arbeidere i tre foretak i en forening i henhold til tariffkategorier er preget av følgende data:

Arbeidstakers tariffkategori	Antall arbeidere ved bedriften
	bedrift 1	bedrift 2	bedrift 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Definere:
1. avvik for hvert foretak (intrakonsernavvik);
2. gjennomsnittet av avvik innen gruppe;
3. spredning mellom grupper;
4. total varians.

Løsning.
Før du begynner å løse problemet, er det nødvendig å finne ut hvilken funksjon som er effektiv og hvilken som er faktoriell. I eksemplet under vurdering er den resulterende attributten "Tariffkategori", og faktorattributten er "Nummer (navn) på foretaket".
Så har vi tre grupper (bedrifter), som det er nødvendig å beregne gruppegjennomsnittet og intragruppeavvikene for:

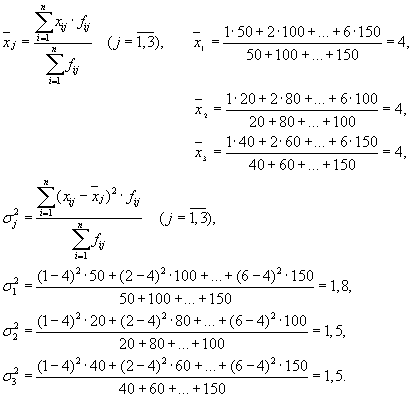
Selskap	Gruppegjennomsnitt,	Avvik innen gruppe,
1	4	1,8

Gjennomsnittet av variasjonene innen gruppe ( gjenværende varians) vil bli beregnet ved hjelp av formelen:

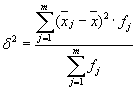
hvor du kan regne ut:
eller:

Deretter:
Den totale variansen vil være lik: s 2 = 1,6 + 0 = 1,6.
Den totale variansen kan også beregnes ved å bruke en av følgende to formler:

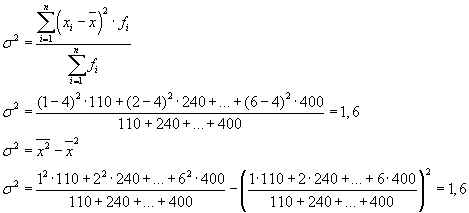
Når man skal løse praktiske problemer, må man ofte forholde seg til en funksjon som kun tar to alternative verdier. I dette tilfellet snakker vi ikke om vekten til en bestemt verdi av en funksjon, men om dens andel i helheten. Hvis andelen populasjonsenheter som har egenskapen som studeres, er angitt med " R", og de som ikke har - gjennom" q", så kan variansen beregnes ved å bruke formelen:
s 2 = p×q

Eksempel nr. 2. Basert på produksjonsdataene til seks arbeidere i et team, bestemme intergruppevariasjonen og evaluer virkningen av arbeidsskiftet på deres arbeidsproduktivitet hvis den totale variansen er 12,2.

Teamarbeider nr.	Arbeiderutgang, stk.
	i første skift	i andre skift
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Løsning. Innledende data

X	f 1	f 2	f 3	f 4	f 5	f 6	Total
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Total	31	33	37	37	40	38

Da har vi 6 grupper som det er nødvendig å beregne gruppemiddel og intragruppevarianser for.
1. Finn gjennomsnittsverdiene for hver gruppe.







2. Finn middelkvadrat for hver gruppe.







La oss oppsummere beregningsresultatene i en tabell:

Gruppenummer	Gruppegjennomsnitt	Avvik innen gruppe
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Avvik innen gruppe karakteriserer endringen (variasjonen) av den studerte (resultative) egenskapen i en gruppe under påvirkning av alle faktorer på den, bortsett fra faktoren som ligger til grunn for grupperingen:
Gjennomsnittet av intragruppeavvikene vil bli beregnet ved å bruke formelen:


4. Intergruppevarians karakteriserer endringen (variasjonen) av den studerte (resultative) karakteristikken under påvirkning av en faktor (faktoriell karakteristikk) som danner grunnlaget for gruppen.
Vi definerer intergruppevarians som:

Hvor


Deretter

Total varians karakteriserer endringen (variasjonen) av den studerte (resultative) karakteristikken under påvirkning av alle faktorer (faktorielle egenskaper) uten unntak. I henhold til betingelsene for problemet er det lik 12,2.
Empirisk korrelasjonsforhold måler hvilken del av den totale variasjonen til den resulterende karakteristikken som er forårsaket av faktoren som studeres. Dette er forholdet mellom faktoravvik og total varians:

Vi definerer den empiriske korrelasjonsrelasjonen:

Forbindelser mellom egenskaper kan være svake og sterke (nære). Kriteriene deres er vurdert på Chaddock-skalaen:
0,1 0,3 0,5 0,7 0,9 I vårt eksempel er forholdet mellom egenskap Y og faktor X svakt
Bestemmelseskoeffisient.

La oss bestemme bestemmelseskoeffisienten:

Dermed skyldes 0,67 % av variasjonen forskjeller mellom egenskaper, og 99,37 % skyldes andre faktorer.
Konklusjon: i dette tilfellet avhenger ikke produksjonen av arbeidere av arbeid på et bestemt skift, dvs. påvirkningen av arbeidsskiftet på deres arbeidsproduktivitet er ikke signifikant og skyldes andre faktorer.

Eksempel nr. 3. Basert på gjennomsnitt lønn og kvadreret avvik fra verdien for to grupper av arbeidere, finn den totale variansen ved å bruke regelen for å legge til avvik:

Løsning:
Gjennomsnitt av avvik innen gruppe

Vi definerer intergruppevarians som:


Den totale variansen vil være: 480 + 13824 = 14304

De viktigste generaliserende indikatorene for variasjon i statistikk er spredninger og standardavvik.

Spredning dette aritmetisk gjennomsnitt kvadrerte avvik for hver karakteristiske verdi fra det totale gjennomsnittet. Variansen kalles vanligvis middelkvadrat av avvik og er betegnet med  2. Avhengig av kildedataene, kan variansen beregnes ved å bruke det enkle eller vektede aritmetiske gjennomsnittet:

 uvektet (enkel) varians;

 variansvektet.

Standardavvik dette er en generaliserende karakteristikk av absolutte størrelser variasjoner tegn i aggregatet. Det uttrykkes i samme måleenheter som attributtet (i meter, tonn, prosent, hektar osv.).

Standardavviket er kvadratroten av variansen og er betegnet med :

 standardavvik uvektet;

 vektet standardavvik.

Standardavviket er et mål på påliteligheten til gjennomsnittet. Jo mindre standardavviket er, jo bedre gjenspeiler det aritmetiske gjennomsnittet hele den representerte populasjonen.

Beregningen av standardavviket innledes med beregningen av variansen.

Prosedyren for å beregne den vektede variansen er som følger:

1) Bestem det vektede aritmetiske gjennomsnittet:

2) beregn avvikene til opsjonene fra gjennomsnittet:

3) kvadrat avviket for hvert alternativ fra gjennomsnittet:

4) multipliser kvadratene av avvik med vekter (frekvenser):

5) oppsummer de resulterende produktene:

6) den resulterende mengden er delt på summen av vektene:

Eksempel 2.1

La oss beregne det vektede aritmetiske gjennomsnittet:

Verdiene av avvik fra gjennomsnittet og deres kvadrater er presentert i tabellen. La oss definere variansen:

Standardavviket vil være lik:

Hvis kildedataene presenteres i form av intervall distribusjonsserie , så må du først bestemme den diskrete verdien av attributtet, og deretter bruke den beskrevne metoden.

Eksempel 2.2

La oss vise variansberegningen for en intervallserie ved å bruke data om fordelingen av sådd areal på en kollektiv gård i henhold til hveteutbytte.

Det aritmetiske gjennomsnittet er:

La oss beregne variansen:

6.3. Beregning av varians ved hjelp av en formel basert på individuelle data

Regneteknikk avvik komplisert, men store verdier alternativer og frekvenser kan være overveldende. Beregninger kan forenkles ved å bruke egenskapene til spredning.

Dispersjonen har følgende egenskaper.

1. Redusering eller økning av vektene (frekvensene) av en varierende karakteristikk med et visst antall ganger endrer ikke spredningen.

2. Reduser eller øk hver verdi av en karakteristikk med samme konstante mengde EN endrer ikke spredningen.

3. Reduser eller øk hver verdi av en karakteristikk med et visst antall ganger k henholdsvis reduserer eller øker variansen i k 2 ganger standardavvik  inn k en gang.

4. Spredningen av en karakteristikk i forhold til en vilkårlig verdi er alltid større enn spredningen i forhold til det aritmetiske gjennomsnittet per kvadrat av differansen mellom gjennomsnittsverdien og vilkårlig verdi:

Hvis EN 0, så kommer vi til følgende likhet:

det vil si at variansen til karakteristikken er lik forskjellen mellom middelkvadraten til de karakteristiske verdiene og kvadratet av gjennomsnittet.

Hver egenskap kan brukes uavhengig eller i kombinasjon med andre ved beregning av varians.

Prosedyren for å beregne varians er enkel:

1) bestemme aritmetisk gjennomsnitt :

2) kvadrat det aritmetiske gjennomsnittet:

3) kvadrat avviket for hver variant av serien:

X Jeg 2 .

4) finn summen av kvadrater av alternativene:

5) del summen av kvadratene til alternativene med antallet, dvs. bestem gjennomsnittlig kvadrat:

6) bestem forskjellen mellom middelkvadraten til karakteristikken og kvadratet av gjennomsnittet:

Eksempel 3.1 Følgende data er tilgjengelig om arbeiderens produktivitet:

La oss gjøre følgende beregninger:

Variansen til en tilfeldig variabel er et mål på spredningen av verdiene til denne variabelen. Lav varians betyr at verdiene er gruppert tett sammen. Stor spredning indikerer sterk spredning av verdier. Konseptet med varians av en tilfeldig variabel brukes i statistikk. For eksempel, hvis du sammenligner variansen til to verdier (som mellom mannlige og kvinnelige pasienter), kan du teste betydningen av en variabel. Dispersjon brukes også ved konstruksjon statistiske modeller, siden lav varians kan være et tegn på at du overpasser verdiene.

Trinn

Beregning av prøvevarians

1. Registrer prøveverdiene. I de fleste tilfeller har statistikere bare tilgang til utvalg av spesifikke populasjoner. For eksempel, som regel analyserer ikke statistikere kostnadene ved å opprettholde totalen av alle biler i Russland - de analyserer tilfeldig utvalg fra flere tusen biler. En slik prøve vil bidra til å bestemme gjennomsnittskostnaden for en bil, men mest sannsynlig vil den resulterende verdien være langt fra den virkelige.

   • La oss for eksempel analysere antall boller solgt på en kafé over 6 dager, tatt i tilfeldig rekkefølge. Prøven har neste visning: 17, 15, 23, 7, 9, 13. Dette er et utvalg, ikke en populasjon, fordi vi ikke har data om solgte boller for hver dag kafeen er åpen.
   • Hvis du får en populasjon i stedet for et utvalg av verdier, fortsett til neste avsnitt.

2. Skriv ned en formel for å beregne prøvevarians. Dispersjon er et mål på spredningen av verdier av en viss mengde. Jo nærmere variansverdien er null, jo nærmere er verdiene gruppert sammen. Når du arbeider med et utvalg av verdier, bruker du følgende formel for å beregne varians:

   • s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))] / (n - 1)
   • s 2 (\displaystyle s^(2))– dette er spredning. Spredning måles i kvadratiske enheter målinger.
   • x i (\displaystyle x_(i))– hver verdi i prøven.
   • x i (\displaystyle x_(i)) du må trekke fra x̅, kvadrere det, og deretter legge til resultatene.
   • x̅ – sample mean (sample mean).
   • n – antall verdier i prøven.

3. Beregn prøvegjennomsnittet. Det er betegnet som x̅. Prøvegjennomsnittet beregnes som et enkelt aritmetisk gjennomsnitt: legg sammen alle verdiene i prøven, og del deretter resultatet på antall verdier i prøven.

   • I vårt eksempel legger du til verdiene i prøven: 15 + 17 + 23 + 7 + 9 + 13 = 84
     Del nå resultatet med antall verdier i prøven (i vårt eksempel er det 6): 84 ÷ 6 = 14.
     Eksempelgjennomsnitt x̅ = 14.
   • Prøvegjennomsnittet er den sentrale verdien som verdiene i utvalget er fordelt rundt. Hvis verdiene i prøveklyngen rundt prøven betyr, er variansen liten; ellers er variansen stor.

4. Trekk prøvegjennomsnittet fra hver verdi i prøven. Beregn nå differansen x i (\displaystyle x_(i))- x̅, hvor x i (\displaystyle x_(i))– hver verdi i prøven. Hvert resultat som oppnås indikerer graden av avvik for en bestemt verdi fra prøvegjennomsnittet, det vil si hvor langt denne verdien er fra prøvegjennomsnittet.

   • I vårt eksempel:
     x 1 (\displaystyle x_(1))- x = 17 - 14 = 3
     x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
     x 3 (\displaystyle x_(3))- x = 23 - 14 = 9
     x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
     x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
     x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
   • Riktigheten av de oppnådde resultatene er lett å kontrollere, siden summen deres skal være lik null. Dette er relatert til bestemmelsen av gjennomsnittsverdien, siden negative verdier(avstander fra gjennomsnittsverdien til mindre verdier) kompenseres fullt ut positive verdier(avstander fra gjennomsnitt til store verdier).

5. Som nevnt ovenfor, summen av forskjellene x i (\displaystyle x_(i))- x̅ må være lik null. Det betyr at gjennomsnittlig varians er alltid lik null, noe som ikke gir noen ide om spredningen av verdier av en viss mengde. For å løse dette problemet, kvadrat hver forskjell x i (\displaystyle x_(i))- x̅. Dette vil resultere i at du bare får positive tall, som når den legges til aldri vil gi 0.

   • I vårt eksempel:
     (x 1 (\displaystyle x_(1))- x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
     (x 2 (\displaystyle (x_(2))- x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
     9 2 = 81
     (-7) 2 = 49
     (-5) 2 = 25
     (-1) 2 = 1
   • Du fant kvadratet av forskjellen - x̅) 2 (\displaystyle ^(2)) for hver verdi i prøven.

6. Regn ut summen av kvadratene av forskjellene. Det vil si, finn den delen av formelen som er skrevet slik: ∑[( x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))]. Her betyr tegnet Σ summen av kvadrerte forskjeller for hver verdi x i (\displaystyle x_(i)) i prøven. Du har allerede funnet de kvadratiske forskjellene (x i (\displaystyle (x_(i))- x̅) 2 (\displaystyle ^(2)) for hver verdi x i (\displaystyle x_(i)) i prøven; nå er det bare å legge til disse rutene.

   • I vårt eksempel: 9 + 1 + 81 + 49 + 25 + 1 = 166 .

7. Del resultatet med n - 1, der n er antall verdier i prøven. For en tid siden, for å beregne prøvevarians, delte statistikere ganske enkelt resultatet på n; i dette tilfellet vil du få gjennomsnittet av den kvadrerte variansen, som er ideell for å beskrive variansen til en gitt prøve. Men husk at enhver prøve er bare en liten del befolkning verdier. Hvis du tar en prøve til og utfører de samme beregningene, får du et annet resultat. Som det viser seg, å dele med n - 1 (ikke bare n) gir mer nøyaktig vurdering populasjonsvarians, som er det du er interessert i. Divisjon med n – 1 er blitt vanlig, så det er inkludert i formelen for beregning av utvalgsvarians.

   • I vårt eksempel inkluderer prøven 6 verdier, det vil si n = 6.
     Prøveavvik = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2

8. Forskjellen mellom varians og standardavvik. Merk at formelen inneholder en eksponent, så spredningen måles i kvadratiske enheter av verdien som analyseres. Noen ganger er en slik størrelse ganske vanskelig å betjene; bruk i slike tilfeller standardavviket, som er lik kvadratrot fra spredning. Det er grunnen til at utvalgsvariansen er betegnet som s 2 (\displaystyle s^(2)), A standardavvik prøver - hvordan s (\displaystyle s).

   • I vårt eksempel er standardavviket til prøven: s = √33,2 = 5,76.

   Beregning av populasjonsvarians

   1. Analyser et sett med verdier. Settet inkluderer alle verdier for kvantumet som vurderes. For eksempel hvis du studerer beboernes alder Leningrad-regionen, så inkluderer befolkningen alderen til alle innbyggere i dette området. Når du arbeider med en populasjon, anbefales det å lage en tabell og legge inn populasjonsverdiene i den. Tenk på følgende eksempel:

      • I et bestemt rom er det 6 akvarier. Hvert akvarium inneholder følgende antall fisk:
        x 1 = 5 (\displaystyle x_(1)=5)
        x 2 = 5 (\displaystyle x_(2)=5)
        x 3 = 8 (\displaystyle x_(3)=8)
        x 4 = 12 (\displaystyle x_(4)=12)
        x 5 = 15 (\displaystyle x_(5)=15)
        x 6 = 18 (\displaystyle x_(6)=18)

   2. Skriv ned en formel for å beregne populasjonsvariansen. Siden populasjonen inkluderer alle verdier av en viss mengde, lar formelen nedenfor deg få den nøyaktige verdien av populasjonsvariasjonen. For å skille populasjonsvarians fra utvalgsvarians (som bare er et estimat), bruker statistikere forskjellige variabler:

      • σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/n
      • σ 2 (\displaystyle ^(2))– befolkningsspredning (leses som "sigma squared"). Dispersjon måles i kvadratiske enheter.
      • x i (\displaystyle x_(i))– hver verdi i sin helhet.
      • Σ – sumtegn. Det vil si fra hver verdi x i (\displaystyle x_(i)) du må trekke fra μ, kvadrere det og legge til resultatene.
      • μ – gjennomsnittlig befolkning.
      • n – antall verdier i befolkningen.

   3. Regn ut gjennomsnittet av befolkningen. Når du arbeider med en populasjon, er gjennomsnittet betegnet som μ (mu). Populasjonsgjennomsnittet beregnes som et enkelt aritmetisk gjennomsnitt: legg sammen alle verdiene i populasjonen, og del deretter resultatet på antall verdier i populasjonen.

      • Husk at gjennomsnitt ikke alltid beregnes som det aritmetiske gjennomsnittet.
      • I vårt eksempel betyr populasjonen: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5

   4. Trekk populasjonsgjennomsnittet fra hver verdi i populasjonen. Jo nærmere forskjellsverdien er null, desto nærmere er den spesifikke verdien populasjonsgjennomsnittet. Finn forskjellen mellom hver verdi i populasjonen og dens gjennomsnitt, og du vil få en første ide om fordelingen av verdier.

      • I vårt eksempel:
        x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
        x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
        x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
        x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
        x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
        x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5

   5. Kvaddra hvert oppnådde resultat. Differanseverdiene vil være både positive og negative; Hvis disse verdiene er plottet på en talllinje, vil de ligge til høyre og venstre for populasjonsgjennomsnittet. Dette er ikke egnet for å beregne varians, siden positiv og negative tall kompensere hverandre. Så kvadrer hver forskjell for å få utelukkende positive tall.

      • I vårt eksempel:
        (x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) for hver populasjonsverdi (fra i = 1 til i = 6):
        (-5,5)2 (\displaystyle ^(2)) = 30,25
        (-5,5)2 (\displaystyle ^(2)), Hvor x n (\displaystyle x_(n)) – siste verdi i den generelle befolkningen.
      • For å beregne gjennomsnittsverdien av de oppnådde resultatene, må du finne summen og dele den på n:(( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2)))/n
      • La oss nå skrive ned forklaringen ovenfor ved å bruke variabler: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n og få en formel for å beregne populasjonsvariansen.