Чому так само і в кубі комплексні числа. Модуль та аргумент комплексного числа
Комплексні числа
Уявні і комплексні числа. Абсциса та ордината
комплексного числа. Сполучені комплексні числа.
Операції із комплексними числами. Геометричне
подання комплексних чисел. Комплексна площина.
Модуль та аргумент комплексного числа. Тригонометрична
Форма комплексного числа. Операції з комплексними
числами у тригонометричній формі. Форма Муавра.
Початкові відомості про уявних і комплексних числах наведено у розділі «Уявні та комплексні числа». Необхідність у цих числах нового типу з'явилася під час вирішення квадратних рівнянь для випадку
D< 0 (здесь D– дискримінант квадратного рівняння). Довгий час ці числа не знаходили фізичного застосування, тому їх і назвали «уявними» числами. Однак зараз вони дуже широко застосовують у різних галузях фізики.та техніки: електротехніці, гідро- та аеродинаміці, теорії пружності та ін.
Комплексні числа записуються у вигляді:a + bi. Тут aі b – дійсні числа , а i – уявна одиниця, т.е. e. i 2 = –1. Число aназивається абсцисою, a b – ординатоюкомплексного числаa + bi.Два комплексні числаa + biі a – bi називаються пов'язанимикомплексними числами.
Основні домовленості:
1. Справжнє число
аможе бути також записано у формікомплексного числа:a + 0 iабо a – 0 i. Наприклад, записи 5 + 0iта 5 – 0 iозначають те саме число 5 .2. Комплексне число 0 + biназивається чисто уявним числом. Записbiозначає те ж саме, що 0 + bi.
3. Два комплексні числаa + bi іc + diвважаються рівними, якщоa = cі b = d. В іншому випадку комплексні числа не рівні.
Додавання. Сумою комплексних чиселa + biі c + diназивається комплексне число (a + c ) + (b + d ) i.Таким чином, при складанні комплексних чисел окремо складаються їх абсциси та ординати.
Це визначення відповідає правилам дій із звичайними багаточленами.
Віднімання. Різницею двох комплексних чиселa + bi(зменшуване) та c + di(віднімається) називається комплексне число (a – c ) + (b – d ) i.
Таким чином, при відніманні двох комплексних чисел окремо віднімаються їх абсциси та ординати.
множення. Добутком комплексних чиселa + biі c + di називається комплексне число:
(ac – bd ) + (ad + bc ) i.Це визначення випливає із двох вимог:
1) числа a + biі c + diповинні перемножуватися, як алгебраїчнідвочлени,
2) число iмає основну властивість:i 2 = – 1.
Примірник. ( a+ bi )(a – bi) = a 2 + b 2 . Отже, твір
двох сполучених комплексних чисел дорівнює дійсному
позитивного числа.
Розподіл. Розділити комплексне числоa + bi (ділене) на іншеc + di(Дільник) - значить знайти третє числоe + f i(чатне), яке будучи помноженим на дільникc + diдає в результаті діленеa + bi.
Якщо дільник не дорівнює нулю, поділ завжди можливий.
П р і м е р. Знайти (8 +i ) : (2 – 3 i) .
Розв'язання. Перепишемо це ставлення у вигляді дробу:
Помноживши її чисельник та знаменник на 2 + 3i
І виконавши всі перетворення, отримаємо:

Геометричне уявлення комплексних чисел. Дійсні числа зображуються точками на числовій прямій:
Тут крапка Aозначає число -3, точкаB- Число 2, і O- Нуль. На відміну від цього, комплексні числа зображуються точками на координатній площині. Виберемо при цьому прямокутні (декартові) координати з однаковими масштабами обох осях. Тоді комплексне числоa + bi буде представлено точкою Р з абсцисою а і ординатою b (Див. рис.). Ця система координат називається комплексною площиною .

Модулем комплексного числа називається довжина вектораOP, що зображує комплексне число на координатній ( комплексної) площині. Модуль комплексного числаa + biпозначається | a + bi| або буквою r
Алгебраїчна форма запису комплексного числа............................................. ................... |
|||
Площина комплексних чисел............................................... .................................................. ... |
|||
Комплексно сполучені числа............................................... .................................................. |
|||
Дії з комплексними числами в формі алгебри........................................... .... |
|||
Додавання комплексних чисел............................................... .................................................. |
|||
Віднімання комплексних чисел............................................... ................................................ |
|||
Множення комплексних чисел............................................... ............................................... |
|||
Розподіл комплексних чисел............................................... .................................................. ... |
|||
Тригонометрична форма запису комплексного числа............................................. .......... |
|||
Дії з комплексними числами в тригонометричній формі. |
|||
Множення комплексних чисел у тригонометричній формі ......................................... |
|||
Розподіл комплексних чисел у тригонометричній формі ............................................ ... |
|||
Зведення комплексного числа в цілий позитивний ступінь .................................. |
|||
Вилучення кореня цілої позитивної міри з комплексного числа..................... |
|||
Зведення комплексного числа в раціональний ступінь............................................ ..... |
|||
Комплексні ряди................................................ .................................................. .................... |
|||
Комплексні числові ряди............................................... .................................................. |
|||
Ступінні ряди в комплексній площині ............................................. ............................ |
|||
Двосторонні статечні ряди в комплексній площині............................................ ... |
|||
Функції комплексного змінного ............................................... ........................................ |
|||
Основні елементарні функції............................................... ......................................... |
|||
Формули Ейлера................................................ .................................................. .................... |
|||
Показова форма подання комплексного числа............................................. . |
|||
Зв'язок між тригонометричними та гіперболічними функціями.......................... |
|||
Логарифмічна функція................................................ .................................................. ... |
|||
Загальна показова та загальна статечна функції ............................................ ............... |
|||
Диференціювання функцій комплексного змінного .............................................. ... |
|||
Умови Коші-Рімана.............................................. .................................................. ............ |
|||
Формули для обчислення похідної .............................................. ................................. |
|||
Властивості операції диференціювання............................................... .............................. |
|||
Властивості дійсної та уявної частин аналітичної функції............................ |
|||
Відновлення функції комплексного змінного за її дійсною чи уявною |
|||
Спосіб №1. За допомогою криволінійного інтеграла.............................................. ....... |
|||
Спосіб №2. Безпосереднє застосування умов Коші-Рімана.......................... |
|||
Спосіб №3. Через похідну шуканої функції.............................................. ......... |
|||
Інтегрування функцій комплексного змінного ................................................. ........... |
|||
Інтегральна формула Коші............................................... .................................................. ... |
|||
Розкладання функцій у ряди Тейлора та Лорана........................................... .......................... |
|||
Нулі і особливі точки функції комплексного змінного ........................................... ..... |
|||
Нулі функції комплексного змінного .............................................. ....................... |
|||
Ізольовані особливі точки функції комплексного змінного ............... |
|||
14.3 Нескінченно віддалена точка як особлива точка функції комплексного змінного
Відрахування................................................. .................................................. ........................................ |
|||
Відрахування в кінцевій точці .............................................. .................................................. ...... |
|||
Відрахування функції у нескінченно віддаленій точці............................................ .................. |
|||
Обчислення інтегралів за допомогою відрахувань............................................. ............................ |
|||
Питання для самоперевірки............................................... .................................................. ....... |
|||
Література................................................. .................................................. ................................. |
|||
Предметний покажчик................................................ .................................................. .............. |
|||
Передмова
Правильно розподілити час і сили при підготовці до теоретичної та практичної частин іспиту або атестації з модуля досить складно, тим більше, що в період сесії часу завжди не вистачає. І, як показує практика, впоратися з цим виходить не у всіх. У результаті на іспиті одні студенти правильно вирішують завдання, але не можуть відповісти на найпростіші теоретичні питання, інші можуть сформулювати теорему, але не можуть її застосувати.
Дані методичні рекомендації для підготовки до іспиту з курсу «Теорія функцій комплексного змінного» (ТФКП) є спробою вирішити цю суперечність та забезпечити одночасне повторення теоретичного та практичного матеріалу курсу. Керуючись принципом «Теорія без практики мертва, практика без теорії сліпа», вони містять як теоретичні положення курсу лише на рівні визначень і формулювань, і приклади, що ілюструють застосування кожного наведеного теоретичного становища, і, полегшують його запам'ятовування і розуміння.
Мета запропонованих методичних рекомендацій – допомогти студенту підготуватися до іспиту на базовому рівні. Іншими словами, складено розширений робочий довідник, що містить основні моменти, що використовуються на заняттях з курсу ТФКП, та необхідні під час виконання домашнього завдання та підготовки до контрольних заходів. Окрім самостійної роботи студентів, справжнє електронне навчальне видання можна використовувати під час проведення занять в інтерактивній формі з використанням електронної дошки або для розміщення у системі дистанційного навчання.
Звертаємо увагу, що справжня праця не замінює собою підручників, ні конспекту лекцій. Для поглибленого вивчення матеріалу рекомендується звертатися до відповідних розділів виданого МГТУ ім. н.е. Баумана базового підручника.
Наприкінці посібника вміщено список рекомендованої літератури та предметний покажчик, до якого входять усі виділені у тексті напівжирним курсивомтерміни. Предметний покажчик складається з гіперпосилань на розділи, у яких ці терміни суворо визначено або описано і де наведено приклади, що ілюструють їх застосування.
Посібник призначений для студентів 2 курсів усіх факультетів МДТУ ім. н.е. Баумана.

1. Алгебраїчна форма запису комплексного числа
Запис виду z = x + iy , де x , y - дійсні числа, i - уявна одиниця (тобто i 2 = − 1)
називають формою алгебри запису комплексного числа z. При цьому x називають дійсною частиною комплексного числа та позначають Re z (x = Re z ), y називають уявною частиною комплексного числа та позначають Im z (y = Im z ).
приклад. У комплексного числа z = 4 − 3i дійсна частина Re z = 4 , а уявна Im z = − 3 .
2. Площина комплексних чисел
У теорії функцій комплексного змінного розглядаютьплощина комплексних чисел, яку позначають або використовують літери, що позначають комплексні числа z , w і т.п.
Горизонтальна вісь комплексної площини називається справжньою віссю, на ній мають дійсні числа z = x + 0 i = x .
Вертикальна вісь комплексної площини називається уявною віссю, на ній розташовують
3. Комплексно сполучені числа
Числа z = x + iy та z = x − iy називають комплексно сполученими. На комплексній площині їм відповідають точки, симетричні щодо дійсної осі.
4. Дії з комплексними числами в алгебраїчній формі
4.1 Додавання комплексних чисел
Сумою двох комплексних чисел |
z 1 = x 1 + iy 1 |
і z 2 = x 2 + iy 2 називається комплексне число |
|||||||||||
z 1 + z 2 |
= (x 1 + iy 1) + (x 2 + iy 2) = (x 1 + x 2) + i (y 1 + y 2). |
операція |
додавання |
||||||||||
комплексних чисел аналогічна операції складання алгебраїчних двочленів. |
|||||||||||||
приклад. Сумою двох комплексних чисел z 1 = 3 + 7i та z 2 |
= −1 +2 i |
буде комплексне число |
|||||||||||
z 1 + z 2 = (3 +7 i) + (-1 +2 i) = (3 -1) + (7 +2) i = 2 +9 i. |
|||||||||||||
Очевидно, |
сумою комплексно |
сполучених |
є |
дійсне |
|||||||||
z + z = (x + iy) + (x - iy) = 2 x = 2 Re z. |
|||||||||||||
4.2 Віднімання комплексних чисел |
|||||||||||||
Різниця двох комплексних чисел z 1 = x 1 + iy 1 |
X 2 +iy 2 |
називається |
комплексне |
||||||||||
число z 1 - z 2 = (x 1 + iy 1) - (x 2 + iy 2) = (x 1 - x 2) + i (y 1 - y 2). |
|||||||||||||
приклад. Різницею двох комплексних чисел |
z 1 = 3 −4 i |
та z 2 |
= −1 +2 i |
буде комплексне |
|||||||||
число z 1 − z 2 = (3 − 4i ) − (− 1+ 2i ) = (3 − (− 1) ) + (− 4 − 2) i = 4 − 6i . |
|||||||||||||
Різниця |
комплексно сполучених |
є |
|||||||||||
z − z = (x + iy) − (x − iy) = 2 iy = 2 i Im z . |
|||||||||||||
4.3 Збільшення комплексних чисел |
|||||||||||||
Добутком двох комплексних чисел |
z 1 = x 1 + iy 1 |
та z 2 = x 2 + iy 2 |
називається комплексне |
||||||||||
z 1z 2 = (x 1 + iy 1 )(x 2 + iy 2 ) = x 1x 2 + iy 1x 2 + iy 2 x 1 + i 2 y 1 y 2 |
= (x 1x 2 − y 1 y 2) + i (y 1x 2 + y 2 x). |
||||||||||||
Таким чином, операція множення комплексних чисел аналогічна до операції множення алгебраїчних двочленів з урахуванням того, що i 2 = − 1.
Комплексні числа - розширення множини дійсних чисел, зазвичай позначається . Будь-яке комплексне число може бути представлене як формальна сума , де і - речові числа, - уявна одиниця.
Запис комплексного числа у вигляді , , називається формою алгебри комплексного числа.
Властивості комплексних чисел. Геометрична інтерпретація комплексного числа.
Дії над комплексними числами, заданими в формі алгебри:
Розглянемо правила, якими проводяться арифметичні дії над комплексними числами.
Якщо дано два комплексні числа α = a + bi і β = c + di, то
α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,
α – β = (a + bi) – (c + di) = (a – c) + (b – d)i . (11)
Це випливає з визначення дій складання та віднімання двох упорядкованих пар дійсних чисел (див. формули (1) та (3)). Ми отримали правила складання та віднімання комплексних чисел: щоб скласти два комплексні числа, треба окремо скласти їх дійсні частини і відповідно уявні частини; щоб від одного комплексного числа відняти інше, необхідно відняти відповідно їх дійсні та уявні частини.
Число – α = – a – bi називають протилежним числу α = a + bi. Сума цих двох чисел дорівнює нулю: - α + α = (- a - bi) + (a + bi) = (-a + a) + (-b + b)i = 0.
Для отримання правила множення комплексних чисел скористаємося формулою (6), тобто тим, що i2 = -1. З огляду на це співвідношення, знаходимо (a + bi) (c + di) = ac + adi + bci + bdi2 = ac + (ad + bc) i – bd, тобто.
(a + bi) (c + di) = (ac - bd) + (ad + bc) i. (12)
Ця формула відповідає формулі (2), якою визначалося множення впорядкованих пар дійсних чисел.
Зазначимо, що сума та добуток двох комплексно сполучених чисел є дійсними числами. Насправді, якщо α = a + bi, = a – bi, то α = (a + bi) = a2 – i2b2 = a2 + b2 , α + = (a + bi) + (a - bi) = ( a + a) + (b - b) i = 2a, тобто.
α + = 2a, α = a2 + b2. (13)
При розподілі двох комплексних чисел в формі алгебри слід очікувати, що приватне виражається також числом того ж виду, тобто α/β = u + vi, де u, v R. Виведемо правило поділу комплексних чисел. Нехай дані числа α = a + bi, β = c + di, причому β ≠ 0, тобто c2 + d2 ≠ 0. Остання нерівність означає, що c і d одночасно в нуль не звертаються (виключається випадок, коли с = 0, d = 0). Застосовуючи формулу (12) та другу з рівностей (13), знаходимо:
Отже, частка двох комплексних чисел визначається формулою:
відповідної формули (4).
За допомогою отриманої формули для числа β = с + di можна знайти зворотне число β-1 = 1/β. Вважаючи у формулі (14) а = 1, b = 0, отримуємо
Ця формула визначає число, обернене даному комплексному числу, відмінному від нуля; це число також є комплексним.
Наприклад: (3+7i) + (4+2i) = 7+9i;
(6 + 5i) - (3 + 8i) = 3 - 3i;
(5 - 4i) (8 - 9i) = 4 - 77i;
Дії над комплексними числами в формі алгебри.

55. Аргумент комплексного числа. Тригонометрична форма запису комплексного числа (висновок).
Арг.ком.числа. – між позитивним напрямком дійсної осі Х вектором, що зображує дане число.
Формула тригон. Числа: ,
ВИЗНАЧЕННЯ
Алгебраїчною формою комплексного числа є запис комплексного числа \(\ z \) у вигляді \(\ z=x+i y \), де \(\ x \) і \(\ y \) - речові числа, \(\ i \ ) - уявна одиниця, що задовольняє співвідношення \(\ i^(2)=-1 \)
Число \(\ x \) називається речовою частиною комплексного числа \(\ z \) і позначається \(\ x=\operatorname(Re) z \)
Число \(\ y \) називається уявною частиною комплексного числа \(\ z \) і позначається \(\ y=\operatorname(Im) z \)
Наприклад:
Комплексне число \(\ z=3-2 i \) та його приєднане число \(\ \overline(z)=3+2 i \)записані в формі алгебри.
Уявна величина (z = 5 i) записується в алгебраїчній формі.
Крім того, залежно від розв'язуваної задачі, ви можете перевести комплексне число в тригонометричну або експоненційну.
Напишіть число \(\ z=\frac(7-i)(4)+13 \) в формі алгебри, знайдіть її дійсну і уявну частини, а також сполучене число.
Застосовуючи термін розподіл фракцій та правило складання дробів, отримаємо:
\(\ z=\frac(7-i)(4)+13=\frac(7)(4)+13-\frac(i)(4)=\frac(59)(4)-\frac( 1) (4) i \)
Тому речова частина комплексного числа \(\ z=\frac(5 g)(4)-\frac(1)(4) i \) є число \(\ x=\operatorname(Re) z=\frac(59) (4) \) , уявна частина - число \(\ y=\operatorname(Im) z=-\frac(1)(4) \)
Сполучене число: \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)
\(\ z=\frac(59)(4)-\frac(1)(4) i \), \(\ \operatorname(Re) z=\frac(59)(4) \), \(\ \operatorname(Im) z=-\frac(1)(4) \), \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)
Дії комплексних чисел в формі алгебри порівняння
Два комплексні числа \(\ z_(1)=x_(1)+i y_(1) \) називаються рівними, якщо \(\ x_(1)=x_(2) \), \(\ y_(1)= y_(2) \) т. e. Їхня дійсна і уявна частини рівні.
Визначити, для яких х і у два комплексних числа \(\ z_(1)=13+y i \) та \(\ z_(2)=x+5 i \) рівні.
За визначенням два комплексні числа рівні, якщо їх дійсна і уявна частини рівні, тобто e. \(\x=13\), \(\y=5\).
додаток
Додавання комплексних чисел \(\ z_(1)=x_(1)+i y_(1) \) виконується шляхом прямого підсумовування речовинної та уявної частин:
\(\ z_(1)+z_(2)=x_(1)+i y_(1)+x_(2)+i y_(2)=\left(x_(1)+x_(2)\right) +i\left(y_(1)+y_(2)\right) \)
Знайти суму комплексних чисел \(\ z_(1)=-7+5 i \), \(\ z_(2)=13-4 i \)
Справжньою частиною комплексного числа \(\ z_(1)=-7+5 i \) є число \(\ x_(1)=\operatorname(Re) z_(1)=-7 \) , уявна частина - число \( \ y_(1)=\mathrm(Im) \), \(\ z_(1)=5 \) . Реальна та уявна частини комплексного числа \(\ z_(2)=13-4 i \) рівні відповідно \(\ x_(2)=\operatorname(Re) z_(2)=13 \) та \(\ y_(2) )=\operatorname(Im) z_(2)=-4 \) .
Отже, сума комплексних чисел:
\(\ z_(1)+z_(2)=\left(x_(1)+x_(2)\right)+i\left(y_(1)+y_(2)\right)=(-7+ 13) + i (5-4) = 6 + i \)
\(\ z_(1)+z_(2)=6+i \)
Докладніше про додавання комплексних чисел в окремій статті: Додавання комплексних чисел.
Віднімання
Віднімання комплексних чисел \(\ z_(1)=x_(1)+i y_(1) \) і \(\ z_(2)=x_(2)+i y_(2) \) виконується шляхом прямого віднімання дійсної і уявної частин:
\(\ z_(1)-z_(2)=x_(1)+i y_(1)-\left(x_(2)+i y_(2)\right)=x_(1)-x_(2) +\left(i y_(1)-i y_(2)\right)=\left(x_(1)-x_(2)\right)+i\left(y_(1)-y_(2)\right ) \)
знайти різницю складних чисел \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \)
Знайдіть дійсну та уявну частини комплексних чисел \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \) :
\(\ x_(1)=\operatorname(Re) z_(1)=17, x_(2)=\operatorname(Re) z_(2)=15 \)
\(\ y_(1)=\operatorname(Im) z_(1)=-35, y_(2)=\operatorname(Im) z_(2)=5 \)
Тому різниця комплексних чисел:
\(\ z_(1)-z_(2)=\left(x_(1)-x_(2)\right)+i\left(y_(1)-y_(2)\right)=(17-15 )+i(-35-5)=2-40 i \)
\(\ z_(1)-z_(2)=2-40 i \) множення
Множення комплексних чисел \(\ z_(1)=x_(1)+i y_(1) \) і \(\ z_(2)=x_(2)+i y_(2) \)виконується шляхом безпосереднього народження чисел в алгебраїчної формі з урахуванням властивості уявної одиниці \(\ i^(2)=-1 \) :
\(\ z_(1) \cdot z_(2)=\left(x_(1)+i y_(1)\right) \cdot\left(x_(2)+i y_(2)\right)=x_ (1) \cdot x_(2)+i^(2) \cdot y_(1) \cdot y_(2)+\left(x_(1) \cdot i y_(2)+x_(2) \cdot i y_(1)\right)= \)
\(\ =\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2) ) \cdot y_(1)\right) \)
Знайти добуток комплексних чисел \(\ z_(1)=1-5 i \)
Комплекс комплексних чисел:
\(\ z_(1) \cdot z_(2)=\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\right)=(1 \cdot 5-(-5) \cdot 2)+i(1 \cdot 2+(-5) \cdot 5 ) = 15-23 i \)
\(\ z_(1) \cdot z_(2)=15-23 i \) поділ
Фактор комплексних чисел \(\ z_(1)=x_(1)+i y_(1) \) і \(\ z_(2)=x_(2)+i y_(2) \) визначається шляхом множення чисельника та знаменника на сполучене число зі знаменником:
\(\ \frac(z_(1))(z_(2))=\frac(x_(1)+i y_(1))(x_(2)+i y_(2))=\frac(\left (x_(1)+i y_(1)\right)\left(x_(2)-i y_(2)\right))(\left(x_(2)+i y_(2)\right)\left (x_(2)-i y_(2)\right))=\frac(x_(1) \cdot x_(2)+y_(1) \cdot y_(2))(x_(2)^(2) +y_(2)^(2))+i \frac(x_(2) \cdot y_(1)-x_(1) \cdot y_(2))(x_(2)^(2)+y_(2) )^(2)) \)
Щоб поділити число 1 на комплексне число \(\z=1+2i).
Оскільки уявна частина дійсного числа 1 дорівнює нулю, фактор дорівнює:
\(\ \frac(1)(1+2 i)=\frac(1 \cdot 1)(1^(2)+2^(2))-i \frac(1 \cdot 2)(1^( 2)+2^(2))=\frac(1)(5)-i \frac(2)(5) \)
\(\ \frac(1)(1+2 i)=\frac(1)(5)-i \frac(2)(5) \)
Нагадаємо необхідні відомості про комплексні числа.
Комплексне число- це вираз виду a + bi, де a, b- дійсні числа, а i- так звана уявна одиниця, символ, квадрат якого дорівнює –1, тобто i 2 = -1. Число aназивається дійсною частиною, а число b - уявною частиноюкомплексного числа z = a + bi. Якщо b= 0, то замість a + 0iпишуть просто a. Видно, що дійсні числа – це окремий випадок комплексних чисел.
Арифметичні дії над комплексними числами самі, як і дійсними: їх можна складати, віднімати, множити і ділити друг на друга. Додавання та віднімання відбуваються за правилом ( a + bi) ± ( c + di) = (a ± c) + (b ± d)i, а множення - за правилом ( a + bi) · ( c + di) = (ac – bd) + (ad + bc)i(тут використовується, що i 2 = -1). Число = a – biназивається комплексно-сполученимдо z = a + bi. Рівність z · = a 2 + b 2 дозволяє зрозуміти, як ділити одне комплексне число на інше (ненульове) комплексне число:
(Наприклад, ![]() .)
.)

У комплексних чисел є зручне та наочне геометричне уявлення: число z = a + biможна зображати вектором з координатами ( a; b) на декартовій площині (або, що майже те саме, точкою - кінцем вектора з цими координатами). При цьому сума двох комплексних чисел зображується як сума відповідних векторів (яку можна знайти за правилом паралелограма). За теоремою Піфагора довжина вектора з координатами ( a; b) дорівнює. Ця величина називається модулемкомплексного числа z = a + biта позначається | z|. Кут, який цей вектор утворює з позитивним напрямом осі абсцис (відрахований проти годинникової стрілки), називається аргументомкомплексного числа zі позначається Arg z. Аргумент визначено не однозначно, а лише з точністю до збільшення величини, кратної 2 π
радіан (або 360 °, якщо рахувати в градусах) - адже ясно, що поворот на такий кут навколо початку координат не змінить вектор. Але якщо вектор довжини rутворює кут φ
з позитивним напрямом осі абсцис, його координати рівні ( r· cos φ
; r· sin φ
). Звідси виходить тригонометрична форма записукомплексного числа: z = |z| · (cos (Arg z) + i sin(Arg z)). Часто буває зручно записувати комплексні числа саме в такій формі, тому що це спрощує викладки. Множення комплексних чисел у тригонометричній формі виглядає дуже просто: z 1 · z 2 = |z 1 | · | z 2 | · (cos (Arg z 1 + Arg z 2) + i sin(Arg z 1 + Arg z 2)) (при множенні двох комплексних чисел їх модулі перемножуються, а аргументи складаються). Звідси випливають формули Муавра: z n = |z|n· (cos ( n· (Arg z)) + i sin( n· (Arg z))). За допомогою цих формул легко навчитися видобувати коріння будь-якого ступеня з комплексних чисел. Корінь n-го ступеня з числа z- це таке комплексне число w, що w n = z. Видно що ![]() , а де kможе приймати будь-яке значення з множини (0, 1, ..., n- 1). Це означає, що завжди є рівно nкоріння n-й ступеня з комплексного числа (на площині вони розташовуються у вершинах правильного n-кутника).
, а де kможе приймати будь-яке значення з множини (0, 1, ..., n- 1). Це означає, що завжди є рівно nкоріння n-й ступеня з комплексного числа (на площині вони розташовуються у вершинах правильного n-кутника).
 Мати дітей Голокосту: Історія Ірини Сендлер
Мати дітей Голокосту: Історія Ірини Сендлер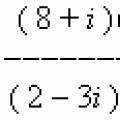 Модуль та аргумент комплексного числа
Модуль та аргумент комплексного числа Як робиться фонетичний аналіз слова: приклад звукового аналізу
Як робиться фонетичний аналіз слова: приклад звукового аналізу