Các tính chất cơ bản của tích phân không xác định. Tính chất đơn giản nhất của tích phân
Trong bài này chúng ta sẽ liệt kê các tính chất chính của tích phân xác định. Hầu hết các tính chất này được chứng minh dựa trên các khái niệm về tích phân xác định Riemann và Darboux.
Việc tính tích phân xác định thường được thực hiện bằng cách sử dụng năm tính chất đầu tiên, vì vậy chúng ta sẽ tham khảo chúng khi cần thiết. Các tính chất còn lại của tích phân xác định chủ yếu được sử dụng để tính các biểu thức khác nhau.
Trước khi tiếp tục tính chất cơ bản của tích phân xác định, chúng ta hãy đồng ý rằng a không vượt quá b.
Đối với hàm y = f(x) được xác định tại x = a, đẳng thức là đúng.
Nghĩa là, giá trị của tích phân xác định có cùng giới hạn tích phân bằng 0. Tính chất này là hệ quả của định nghĩa tích phân Riemann, vì trong trường hợp này, mỗi tổng tích phân cho bất kỳ phân chia nào của khoảng và mọi cách chọn điểm đều bằng 0, do đó, giới hạn của tổng tích phân bằng 0.
Đối với một hàm khả tích trên một khoảng,  .
.
Nói cách khác, khi giới hạn trên và giới hạn dưới của tích phân thay đổi vị trí thì giá trị của tích phân xác định thay đổi theo hướng ngược lại. Tính chất này của tích phân xác định cũng tuân theo khái niệm tích phân Riemann, chỉ việc đánh số phân vùng của đoạn phải bắt đầu từ điểm x = b.
 đối với các hàm tích phân trên một khoảng y = f(x) và y = g(x) .
đối với các hàm tích phân trên một khoảng y = f(x) và y = g(x) .
Bằng chứng.
Hãy viết tổng tích phân của hàm số ![]() đối với một phân vùng nhất định của một phân khúc và một lựa chọn điểm nhất định:
đối với một phân vùng nhất định của một phân khúc và một lựa chọn điểm nhất định: 
trong đó và lần lượt là tổng tích phân của các hàm y = f(x) và y = g(x) đối với một phân vùng đã cho của đoạn đó.
Đi đến giới hạn tại ![]() chúng ta thu được rằng, theo định nghĩa của tích phân Riemann, tương đương với phát biểu về tính chất đang được chứng minh.
chúng ta thu được rằng, theo định nghĩa của tích phân Riemann, tương đương với phát biểu về tính chất đang được chứng minh.
Hệ số không đổi có thể được loại bỏ khỏi dấu của tích phân xác định. Nghĩa là, đối với hàm y = f(x) khả tích trên một khoảng và một số k tùy ý, đẳng thức sau đây đúng:  .
.
Chứng minh tính chất này của tích phân xác định hoàn toàn giống với tính chất trước: 
Cho hàm y = f(x) khả tích trên khoảng X, và ![]() và sau đó
và sau đó  .
.
Thuộc tính này đúng cho cả , và hoặc .
Việc chứng minh có thể được thực hiện dựa trên các tính chất trước đó của tích phân xác định.
Nếu một hàm có thể tích phân trên một khoảng thì nó có thể tích phân trên bất kỳ khoảng bên trong nào.
Bằng chứng dựa trên tính chất của tổng Darboux: nếu các điểm mới được thêm vào phân vùng hiện có của một phân đoạn thì tổng Darboux dưới sẽ không giảm và tổng Darboux trên sẽ không tăng.
Nếu hàm y = f(x) khả tích trên khoảng và với bất kỳ giá trị nào của đối số, thì  .
.
Tính chất này được chứng minh thông qua định nghĩa tích phân Riemann: bất kỳ tổng tích phân nào cho bất kỳ lựa chọn điểm phân chia nào của đoạn thẳng và các điểm tại sẽ không âm (không dương).
Kết quả.
Đối với các hàm y = f(x) và y = g(x) có thể tích phân trên một khoảng, các bất đẳng thức sau đây đúng: 
Tuyên bố này có nghĩa là việc tích hợp các bất đẳng thức là được phép. Ta sẽ sử dụng hệ quả này để chứng minh các tính chất sau.
Cho hàm y = f(x) khả tích trên khoảng , khi đó bất đẳng thức giữ nguyên  .
.
Bằng chứng.
Hiển nhiên là ![]() . Trong tính chất trước, chúng ta đã phát hiện ra rằng bất đẳng thức có thể tích phân từng số hạng, do đó, nó đúng
. Trong tính chất trước, chúng ta đã phát hiện ra rằng bất đẳng thức có thể tích phân từng số hạng, do đó, nó đúng  . Bất đẳng thức kép này có thể được viết là
. Bất đẳng thức kép này có thể được viết là  .
.
Giả sử các hàm y = f(x) và y = g(x) có thể tích phân trên khoảng và với bất kỳ giá trị nào của đối số , thì  , Ở đâu
, Ở đâu ![]() Và
Và ![]() .
.
Việc chứng minh được thực hiện tương tự. Vì m và M là giá trị nhỏ nhất và lớn nhất của hàm y = f(x) trên đoạn , nên ![]() . Nhân bất đẳng thức kép với hàm không âm y = g(x) dẫn chúng ta đến bất đẳng thức kép sau. Tích phân nó vào khoảng , ta đi đến phát biểu được chứng minh.
. Nhân bất đẳng thức kép với hàm không âm y = g(x) dẫn chúng ta đến bất đẳng thức kép sau. Tích phân nó vào khoảng , ta đi đến phát biểu được chứng minh.
Trong phép tính vi phân, bài toán được giải: theo hàm này ƒ(x) tìm đạo hàm của nó(hoặc vi phân). Phép tính tích phân giải bài toán nghịch đảo: tìm hàm F(x), biết đạo hàm F của nó "(x)=ƒ(x) (hoặc vi phân). Hàm tìm F(x) được gọi là nguyên hàm của hàm ƒ(x ).
Hàm F(x) được gọi là phản đạo hàm hàm số ƒ(x) trên khoảng (a; b), nếu với bất kỳ x є (a; b) đẳng thức
F " (x)=ƒ(x) (hoặc dF(x)=ƒ(x)dx).
Ví dụ, nguyên hàm của hàm số y = x 2, x є R, là hàm số, vì
![]()
Rõ ràng, bất kỳ hàm số nào cũng sẽ là nguyên hàm

trong đó C là hằng số, vì
Định lý 29. 1. Nếu hàm F(x) là nguyên hàm của hàm ƒ(x) trên (a;b), thì tập hợp tất cả các nguyên hàm của ƒ(x) được cho bởi công thức F(x)+ C, trong đó C là một hằng số.
▲ Hàm F(x)+C là nguyên hàm của ƒ(x).
Thật vậy, (F(x)+C) " =F " (x)=ƒ(x).
Giả sử Ф(х) là một nguyên hàm khác của hàm ƒ(x), khác với F(x), tức là Ф "(x)=ƒ(х). Khi đó với mọi x є (а; b) ta có
Và điều này có nghĩa (xem Hệ quả 25.1) rằng
trong đó C là một số không đổi. Do đó, Ф(x)=F(x)+С.▼
Tập hợp tất cả các hàm nguyên hàm F(x)+С cho ƒ(x) được gọi là tích phân không xác định của hàm ƒ(x) và được ký hiệu bằng ký hiệu ∫ ƒ(x) dx.
Như vậy, theo định nghĩa 
∫ ƒ(x)dx= F(x)+C.
Ở đây ƒ(x) được gọi là hàm tích phân, ƒ(x)dx — biểu thức tích phân, X - biến tích hợp, ∫ -dấu của tích phân bất định.
Hoạt động tìm tích phân không xác định của một hàm được gọi là tích phân hàm này.
Về mặt hình học, tích phân bất định là một họ các đường cong “song song” y=F(x)+C (mỗi giá trị số của C tương ứng với một đường cong cụ thể của họ) (xem Hình 166). Đồ thị của mỗi nguyên hàm (đường cong) được gọi là đường cong tích phân.
Có phải mọi hàm đều có tích phân không xác định?
Có một định lý phát biểu rằng “mọi hàm số liên tục trên (a;b) đều có nguyên hàm trên khoảng này,” và do đó, là một tích phân không xác định.
Chúng ta hãy lưu ý một số tính chất của tích phân không xác định theo định nghĩa của nó.
1. Vi phân của tích phân không xác định bằng tích phân và đạo hàm của tích phân không xác định bằng tích phân:
d(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) " =ƒ(x).
Thật vậy, d(∫ ƒ(x) dx)=d(F(x)+C)=dF(x)+d(C)=F " (x) dx =ƒ(x) dx
(∫ ƒ (x) dx) " =(F(x)+C)"=F"(x)+0 =ƒ (x).
Nhờ tính chất này, tính đúng đắn của tích phân được kiểm tra bằng vi phân. Ví dụ, sự bình đẳng
∫(3x 2 + 4) dx=х з +4х+С
đúng, vì (x 3 +4x+C)"=3x 2 +4.
2. Tích phân không xác định của vi phân của một hàm số nào đó bằng tổng của hàm số này với một hằng số tùy ý:
∫dF(x)= F(x)+C.
Thật sự,
3. Hệ số hằng số có thể được rút ra khỏi dấu tích phân:
α ≠ 0 là một hằng số.
Thật sự,
(đặt C 1 / a = C.)
4. Tích phân không xác định của tổng đại số của một số hữu hạn các hàm số liên tục bằng tổng đại số của các tích phân của các tổng của các hàm số:
Đặt F"(x)=ƒ(x) và G"(x)=g(x). Sau đó

trong đó C 1 ± C 2 = C.
5. (Tính bất biến của công thức tích phân).
Nếu như ![]() , trong đó u=φ(x) là một hàm tùy ý có đạo hàm liên tục.
, trong đó u=φ(x) là một hàm tùy ý có đạo hàm liên tục.
▲ Cho x là một biến độc lập, ƒ(x) là một hàm liên tục và F(x) là nguyên hàm của nó. Sau đó
![]()
Bây giờ chúng ta đặt u=φ(x), trong đó φ(x) là hàm khả vi liên tục. Xét hàm phức F(u)=F(φ(x)). Do tính bất biến của dạng vi phân bậc nhất của hàm số (xem trang 160), chúng ta có
Từ đây▼
Do đó, công thức tính tích phân không xác định vẫn đúng bất kể biến tích phân là biến độc lập hay bất kỳ hàm nào của nó có đạo hàm liên tục.
Vậy từ công thức ![]() bằng cách thay x bằng u (u=φ(x)) chúng ta nhận được
bằng cách thay x bằng u (u=φ(x)) chúng ta nhận được ![]()
Đặc biệt,

Ví dụ 29.1. Tìm tích phân ![]()
![]()
![]()
trong đó C=C1+C 2 +C 3 +C 4.
Ví dụ 29.2. Tìm nghiệm tích phân:
![]()
![]()
- 29.3. Bảng tích phân bất định cơ bản
Lợi dụng thực tế rằng tích phân là tác động nghịch đảo của vi phân, người ta có thể thu được một bảng tích phân cơ bản bằng cách đảo ngược các công thức tương ứng của phép tính vi phân (bảng vi phân) và sử dụng các tính chất của tích phân không xác định.
Ví dụ, bởi vì
d(sin u)=cos u . bạn
Đạo hàm của một số công thức trong bảng sẽ được đưa ra khi xem xét các phương pháp tích phân cơ bản.
Các tích phân trong bảng dưới đây được gọi là dạng bảng. Họ nên được biết đến bằng trái tim. Trong phép tính tích phân không có quy tắc đơn giản và phổ quát nào để tìm nguyên hàm của các hàm cơ bản, như trong phép tính vi phân. Các phương pháp tìm nguyên hàm (tức là lấy tích phân một hàm số) được rút gọn thành các kỹ thuật biểu thị đưa một tích phân (đã tìm) đã cho vào dạng bảng. Vì vậy, cần phải biết tích phân bảng và nhận biết được chúng.
Lưu ý rằng trong bảng tích phân cơ bản, biến tích phân có thể biểu thị cả biến độc lập và hàm của biến độc lập (theo tính chất bất biến của công thức tích phân).
Tính hợp lệ của các công thức dưới đây có thể được xác minh bằng cách lấy vi phân ở vế phải, nó sẽ bằng tích phân ở vế trái của công thức.
Ví dụ, chúng ta hãy chứng minh tính hợp lệ của công thức 2. Hàm 1/u được xác định và liên tục với tất cả các giá trị của và khác 0.
Nếu u > 0 thì ln|u|=lnu thì ![]() Đó là lý do tại sao
Đó là lý do tại sao
Nếu bạn<0, то ln|u|=ln(-u). Но![]() Có nghĩa
Có nghĩa
Vậy công thức 2 đúng Tương tự, hãy kiểm tra công thức 15:
Bảng tích phân chính


Bạn! Chúng tôi mời bạn thảo luận. Nếu bạn có ý kiến của riêng mình, hãy viết thư cho chúng tôi trong phần bình luận.
Các tính chất này được sử dụng để thực hiện các phép biến đổi của tích phân nhằm giảm nó thành một trong các tích phân cơ bản và tính toán thêm.
1. Đạo hàm của tích phân không xác định bằng tích phân:
2. Vi phân của tích phân không xác định bằng tích phân:
3. Tích phân không xác định của vi phân của một hàm số nào đó bằng tổng của hàm số này với một hằng số tùy ý:
4. Hệ số hằng số có thể được rút ra khỏi dấu tích phân:
Hơn nữa, a ≠ 0
5. Tích phân của tổng (vi phân) bằng tổng (vi phân) của các tích phân:
6. Tài sản là sự kết hợp của tài sản 4 và 5:
Hơn nữa, a ≠ 0 ˄ b ≠ 0
7. Tính chất bất biến của tích phân bất định:
Nếu , thì
8. Tài sản:
Nếu , thì
Trên thực tế, tính chất này là một trường hợp đặc biệt của tích phân sử dụng phương pháp thay đổi biến, sẽ được thảo luận chi tiết hơn trong phần tiếp theo.
Hãy xem một ví dụ:
Đầu tiên chúng ta áp dụng tính chất 5, sau đó là tính chất 4, sau đó sử dụng bảng nguyên hàm và nhận được kết quả.
Thuật toán của máy tính tích phân trực tuyến của chúng tôi hỗ trợ tất cả các thuộc tính được liệt kê ở trên và sẽ dễ dàng tìm ra giải pháp chi tiết cho tích phân của bạn.
Nguyên hàm và tích phân không xác định.
Nguyên hàm của hàm f(x) trên khoảng (a; b) là hàm F(x) sao cho đẳng thức đúng với mọi x từ khoảng đã cho.
Nếu xét đạo hàm của hằng số C bằng 0 thì đẳng thức đúng ![]() . Do đó, hàm f(x) có một tập hợp nguyên hàm F(x)+C, với hằng số C tùy ý, và các nguyên hàm này khác nhau một giá trị hằng số tùy ý.
. Do đó, hàm f(x) có một tập hợp nguyên hàm F(x)+C, với hằng số C tùy ý, và các nguyên hàm này khác nhau một giá trị hằng số tùy ý.
Toàn bộ tập hợp nguyên hàm của hàm f(x) được gọi là tích phân bất định của hàm này và được ký hiệu là ![]() .
.
Biểu thức được gọi là số nguyên và f(x) được gọi là số nguyên. Số nguyên biểu thị vi phân của hàm f(x).
Hoạt động tìm một hàm số chưa biết dựa trên vi phân của nó được gọi là tích phân không xác định, bởi vì kết quả của phép tích phân không phải là một hàm F(x), mà là một tập hợp các nguyên hàm F(x)+C của nó.
Tích phân bảng

Tính chất đơn giản nhất của tích phân
1. Đạo hàm của kết quả tích phân bằng tích phân.
![]()
2. Tích phân không xác định của vi phân của một hàm số bằng tổng của chính hàm đó và một hằng số tùy ý.
3. Hệ số có thể được lấy ra khỏi dấu của tích phân bất định.
![]()
4. Tích phân bất định của tổng/hiệu các hàm số bằng tổng/vi phân của tích phân bất định của các hàm số.
Các đẳng thức trung gian của tính chất thứ nhất và thứ hai của tích phân không xác định được đưa ra để làm rõ.
Để chứng minh tính chất thứ ba và thứ tư, chỉ cần tìm đạo hàm của vế phải của các đẳng thức là đủ:

Các đạo hàm này bằng các tích phân, đây là bằng chứng dựa vào tính chất thứ nhất. Nó cũng được sử dụng trong quá trình chuyển đổi cuối cùng.
Như vậy, bài toán tích phân là nghịch đảo của bài toán vi phân và giữa các bài toán này có mối liên hệ rất chặt chẽ:
thuộc tính đầu tiên cho phép một người kiểm tra tích hợp. Để kiểm tra tính đúng đắn của phép tích phân được thực hiện, việc tính đạo hàm của kết quả thu được là đủ. Nếu hàm thu được do lấy vi phân hóa ra bằng tích phân, điều này có nghĩa là phép tích phân đã được thực hiện chính xác;
Tính chất thứ hai của tích phân không xác định cho phép tìm nguyên hàm của nó từ một vi phân đã biết của một hàm số. Việc tính toán trực tiếp tích phân không xác định dựa trên tính chất này.
1.4.Tính bất biến của các dạng tích phân.
Tích hợp bất biến là một kiểu tích hợp cho các hàm có đối số là các phần tử của một nhóm hoặc các điểm của một không gian đồng nhất (bất kỳ điểm nào trong không gian đó đều có thể được chuyển sang điểm khác bằng một hành động nhất định của nhóm).
hàm f(x) rút gọn thành tính tích phân của dạng vi phân f.w, trong đó
Một công thức rõ ràng cho r(x) được đưa ra dưới đây. Điều kiện thỏa thuận có dạng ![]() .
.
ở đây Tg có nghĩa là toán tử dịch chuyển trên X sử dụng gОG: Tgf(x)=f(g-1x). Cho X=G là một tôpô, một nhóm tự tác động bằng phép dịch trái. Tôi và. tồn tại khi và chỉ khi G compact cục bộ (đặc biệt, trên nhóm vô hạn chiều I.I. không tồn tại). Đối với một tập hợp con của I. và. hàm đặc trưng cA (bằng 1 trên A và 0 bên ngoài A) chỉ định độ đo Xaar bên trái m(A). Thuộc tính xác định của độ đo này là tính bất biến của nó khi dịch chuyển trái: m(g-1A)=m(A) với mọi gОG. Độ đo Haar bên trái của một nhóm được xác định duy nhất với hệ số vô hướng dương. Nếu độ đo Haar m được biết thì I. và. hàm f được cho bởi công thức ![]() . Độ đo Haar bên phải có tính chất tương tự. Có sự đồng cấu liên tục (bản đồ bảo toàn tính chất nhóm) DG của nhóm G vào nhóm (đối với phép nhân) thừa định. những con số mà
. Độ đo Haar bên phải có tính chất tương tự. Có sự đồng cấu liên tục (bản đồ bảo toàn tính chất nhóm) DG của nhóm G vào nhóm (đối với phép nhân) thừa định. những con số mà
trong đó dmr và dmi là số đo Haar bên phải và bên trái. Hàm DG(g) được gọi là mô-đun của nhóm G. Nếu , thì nhóm G được gọi. đơn mô-đun; trong trường hợp này độ đo Haar bên phải và bên trái trùng nhau. Các nhóm nhỏ gọn, nửa đơn và linh năng (đặc biệt là giao hoán) là đơn môđun. Nếu G là nhóm Lie n chiều và q1,...,qn là cơ sở trong không gian dạng 1 bất biến trái trên G thì độ đo Haar trái trên G được cho bởi dạng n. Trong tọa độ địa phương để tính toán
dạng qi, bạn có thể sử dụng bất kỳ cách thực hiện ma trận nào của nhóm G: ma trận dạng 1 g-1dg là bất biến trái và hệ số của nó. là các dạng 1 vô hướng bất biến trái mà từ đó cơ sở bắt buộc được chọn. Ví dụ, nhóm ma trận đầy đủ GL(n, R) là đơn môđun và độ đo Haar trên nó được cho dưới dạng. Cho phép ![]() X=G/H là một không gian đồng nhất trong đó nhóm compact cục bộ G là nhóm biến đổi và nhóm con đóng H là nhóm ổn định của một điểm nhất định. Để một i.i. tồn tại trên X, điều cần và đủ là với mọi hОH đẳng thức DG(h)=DH(h) đúng. Đặc biệt, điều này đúng trong trường hợp H compact hoặc nửa đơn. Lý thuyết hoàn chỉnh về I. và. không tồn tại trên đa tạp vô hạn chiều.
X=G/H là một không gian đồng nhất trong đó nhóm compact cục bộ G là nhóm biến đổi và nhóm con đóng H là nhóm ổn định của một điểm nhất định. Để một i.i. tồn tại trên X, điều cần và đủ là với mọi hОH đẳng thức DG(h)=DH(h) đúng. Đặc biệt, điều này đúng trong trường hợp H compact hoặc nửa đơn. Lý thuyết hoàn chỉnh về I. và. không tồn tại trên đa tạp vô hạn chiều.
Thay thế các biến

Nhiệm vụ chính của phép tính vi phân là tìm đạo hàm f'(x) hoặc vi phân df=f'(x)dx chức năng f(x). Trong phép tính tích phân, bài toán nghịch đảo được giải. Theo chức năng nhất định f(x) bạn cần tìm một hàm như vậy F(x), Cái gì F'(x)=f(x) hoặc dF(x)=F'(x)dx=f(x)dx.
Như vậy, nhiệm vụ chính của phép tính tích phân là sự phục hồi chức năng F(x) bằng đạo hàm (vi phân) đã biết của hàm này. Phép tính tích phân có nhiều ứng dụng trong hình học, cơ học, vật lý và công nghệ. Nó đưa ra một phương pháp chung để tìm diện tích, thể tích, trọng tâm, v.v.
Sự định nghĩa. Chức năngF(x), , được gọi là nguyên hàm của hàm sốf(x) trên tập X nếu nó khả vi với bất kỳ vàF'(x)=f(x) hoặcdF(x)=f(x)dx.
Định lý. Bất kỳ dòng liên tục nào trên khoảng [Một;b] chức năngf(x) có nguyên hàm trên đoạn nàyF(x).
Định lý. Nếu nhưF 1 (x) vàF 2 (x) – hai nguyên hàm khác nhau của cùng một hàm sốf(x) trên tập x thì chúng khác nhau một số hạng không đổi, tức làF 2 (x)=F 1x)+C, trong đó C là hằng số.
- Tích phân không xác định, tính chất của nó.
Sự định nghĩa. Tổng thểF(x)+Từ tất cả các hàm phản đạo hàmf(x) trên tập X được gọi là tích phân không xác định và được ký hiệu:
- (1)Trong công thức (1) f(x)dx gọi điện biểu thức tích phân,f(x) – hàm tích phân, x – biến tích phân, MỘT C – hằng số tích phân.
Chúng ta hãy xem xét các tính chất của tích phân không xác định theo định nghĩa của nó.
1. Đạo hàm của tích phân không xác định bằng tích phân, vi phân của tích phân không xác định bằng tích phân:
Và .2. Tích phân không xác định của vi phân của một hàm nào đó bằng tổng của hàm này và một hằng số tùy ý:
3. Hệ số hằng số a (a≠0) có thể được coi là dấu của tích phân không xác định:
4. Tích phân không xác định của tổng đại số của một số hữu hạn các hàm bằng tổng đại số của các tích phân của các hàm này:
5. Nếu nhưF(x) – nguyên hàm của hàm sốf(x), thì:
6 (bất biến của công thức tích phân). Bất kỳ công thức tích phân nào cũng giữ nguyên dạng của nó nếu biến tích phân được thay thế bằng bất kỳ hàm khả vi nào của biến này:
Ở đâuu là một hàm khả vi.
- Bảng tích phân không xác định.
Hãy cung cấp cho các nguyên tắc cơ bản để tích hợp các hàm.
Hãy cung cấp cho bảng tích phân bất định cơ bản.(Lưu ý rằng ở đây, giống như trong phép tính vi phân, chữ cái bạn có thể được chỉ định là một biến độc lập (bạn=x) và hàm của biến độc lập (bạn=bạn(x)).)
(n≠-1). (a >0, a≠1). (a≠0). (a≠0). (|u| > |a|).(|u|< |a|).
Tích phân 1 – 17 được gọi là dạng bảng.
Một số công thức trên trong bảng tích phân không có công thức tương tự trong bảng đạo hàm, được xác minh bằng cách lấy vi phân vế phải của chúng.
- Thay đổi biến và tích phân từng phần trong tích phân không xác định.
Tích hợp bằng cách thay thế (thay thế biến). Cần phải tính tích phân
, không ở dạng bảng. Bản chất của phương pháp thay thế là trong tích phân biến X thay thế bằng một biến t theo công thức x=φ(t),Ở đâu dx=φ’(t)dt.Định lý. Hãy để chức năngx=φ(t) được xác định và khả vi trên một tập T nhất định và đặt X là tập các giá trị của hàm này mà hàm được xác địnhf(x). Khi đó nếu trên tập X hàmf(
 Hình cầu, quả bóng, đoạn và khu vực
Hình cầu, quả bóng, đoạn và khu vực Chuyên ngành "Điều dưỡng" (bằng cử nhân)
Chuyên ngành "Điều dưỡng" (bằng cử nhân)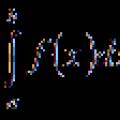 Tính chất đơn giản nhất của tích phân
Tính chất đơn giản nhất của tích phân