رتبة المصفوفة: التعريف ، طرق البحث ، الأمثلة ، الحلول. إيجاد رتبة مصفوفة ما رتبة مصفوفة 1123 5814

وأيضًا ضع في اعتبارك تطبيقًا عمليًا مهمًا للموضوع: دراسة نظام المعادلات الخطية للتوافق.

ما هي رتبة المصفوفة؟

يحتوي النص الفكاهي للمقال على قدر كبير من الحقيقة. عادة ما ترتبط كلمة "رتبة" نفسها بنوع من التسلسل الهرمي ، وغالبًا ما ترتبط بالسلّم الوظيفي. كلما زادت المعرفة والخبرة والقدرات والصلات وما إلى ذلك ، لدى الشخص. - كلما ارتفع مركزه وتنوع الفرص. في مصطلحات الشباب ، يشير الترتيب إلى الدرجة الكلية "المتانة".

ويعيش إخواننا في الرياضيات على نفس المبادئ. دعنا نأخذ في نزهة تعسفية قليلة مصفوفات صفرية:

لنفكر إذا كان في المصفوفة فقط الأصفارإذن ما هي الرتبة التي يمكن أن نتحدث عنها؟ الجميع على دراية بالتعبير غير الرسمي "الصفر الكلي". في مجتمع المصفوفة ، كل شيء هو نفسه تمامًا:

رتبة مصفوفة صفريةأي حجم هو صفر.

ملحوظة : المصفوفة الصفرية يُرمز إليها بالحرف اليوناني "ثيتا"

من أجل فهم رتبة المصفوفة بشكل أفضل ، سأستند فيما يلي إلى المواد الهندسة التحليلية. ضع في اعتبارك الصفر المتجهلفضائنا ثلاثي الأبعاد ، والذي لا يحدد اتجاهًا معينًا وغير مفيد للبناء أساس أفيني. من وجهة نظر جبرية ، تتم كتابة إحداثيات متجه معين مصفوفة"واحد تلو الآخر" ومنطقي (بالمعنى الهندسي المحدد)افترض أن رتبة هذه المصفوفة هي صفر.

الآن دعونا نلقي نظرة على القليل غير صفرية ناقلات العمودو نواقل الصف:

يحتوي كل مثيل على عنصر واحد على الأقل غير فارغ ، وهذا شيء!

رتبة أي متجه غير صفري (متجه العمود) تساوي واحدًا

وبصفة عامة - إذا كان في المصفوفة أحجام عشوائيةيحتوي على عنصر واحد على الأقل غير صفري ، ثم رتبته ليس أقلالوحدات.

متجهات الصفوف والأعمدة الجبرية مجردة إلى حد ما ، لذلك دعنا ننتقل مرة أخرى إلى الارتباط الهندسي. غير صفرية المتجهيحدد اتجاهًا محددًا جيدًا في الفضاء ومناسبًا للبناء أساس، لذلك يُفترض أن تكون رتبة المصفوفة مساوية لواحد.

المرجع النظري : في الجبر الخطي ، المتجه هو عنصر من فضاء متجه (محدد من خلال 8 بديهيات) ، والذي ، على وجه الخصوص ، يمكن أن يكون صفًا (أو عمودًا) مرتبًا من الأرقام الحقيقية مع عمليات الجمع والضرب برقم حقيقي محدد بالنسبة لهم. لمزيد من المعلومات حول النواقل ، راجع المقالة التحولات الخطية.

تعتمد خطيا(معبراً عنها من خلال بعضها البعض). من وجهة نظر هندسية ، يحتوي السطر الثاني على إحداثيات المتجه الخطي التي لم تقدم الأمر في البناء ثلاثي الأبعاد، زائدة عن الحاجة بهذا المعنى. وبالتالي ، فإن رتبة هذه المصفوفة تساوي أيضًا واحدًا.

نعيد كتابة إحداثيات المتجهات في الأعمدة ( انقل المصفوفة):

ما الذي تغير من حيث الرتبة؟ لا شئ. الأعمدة متناسبة ، مما يعني أن المرتبة تساوي واحدًا. بالمناسبة ، لاحظ أن جميع الأسطر الثلاثة متناسبة أيضًا. يمكن التعرف عليها مع الإحداثيات ثلاثةالمتجهات الخطية للمستوى ، منها واحد فقطمفيد لبناء أساس "ثابت". وهذا يتفق تمامًا مع إحساسنا الهندسي بالرتبة.

يتبع بيان مهم من المثال أعلاه:

ترتيب المصفوفة بالصفوف يساوي رتبة المصفوفة بالأعمدة. لقد ذكرت هذا قليلاً بالفعل في الدرس الخاص بالفعالية طرق حساب المحدد.

ملحوظة : التبعية الخطية للصفوف تؤدي إلى تبعية خطية للأعمدة (والعكس صحيح). ولكن من أجل توفير الوقت ، وبدلاً من العادة ، سأتحدث دائمًا عن الاعتماد الخطي للأوتار.

دعونا نواصل تدريب حيواننا الأليف المحبوب. أضف إحداثيات متجه خطي آخر إلى المصفوفة في الصف الثالث :

هل ساعدنا في بناء قاعدة ثلاثية الأبعاد؟ بالطبع لا. تسير المتجهات الثلاثة ذهابًا وإيابًا على نفس المسار ، وتكون رتبة المصفوفة واحدة. يمكنك أن تأخذ العديد من المتجهات الخطية كما تريد ، لنقل 100 ، ضع إحداثياتها في مصفوفة 100 × 3 ، وسيظل ترتيب ناطحة سحاب مثل هذا واحدًا.

دعنا نتعرف على المصفوفة التي صفوفها مستقل خطيا. زوج من النواقل غير الخطية مناسب لبناء أساس ثلاثي الأبعاد. رتبة هذه المصفوفة اثنان.

ما هي رتبة المصفوفة؟ لا يبدو أن الخطوط متناسبة ... لذا ، من الناحية النظرية ، ثلاثة. ومع ذلك ، فإن رتبة هذه المصفوفة تساوي أيضًا اثنين. أضفت أول سطرين وكتبت النتيجة في الأسفل ، أي معبر عنها خطياالخط الثالث من خلال الأولين. هندسيًا ، تتوافق صفوف المصفوفة مع إحداثيات ثلاثة ناقلات متحد المستوى، ومن بين هذا الثلاثي هناك زوج من الرفاق غير المتصلين.

كما ترون الاعتماد الخطيفي المصفوفة المدروسة ليست واضحة ، واليوم سنتعلم فقط كيفية إحضارها "لتنظيف المياه".

أعتقد أن الكثير من الناس يخمنون ما هي رتبة المصفوفة!

النظر في المصفوفة التي صفوفها مستقل خطيا. شكل النواقل أساس أفيني، ورتبة هذه المصفوفة ثلاثة.

كما تعلم ، أي متجه رابع أو خامس أو عاشر للفضاء ثلاثي الأبعاد سيتم التعبير عنه خطيًا من حيث المتجهات الأساسية. لذلك ، إذا تمت إضافة أي عدد من الصفوف إلى المصفوفة ، ثم رتبتها سيظل ثلاثة.

يمكن إجراء تفكير مماثل لمصفوفات ذات أحجام أكبر (بوضوح ، بالفعل بدون معنى هندسي).

تعريف : رتبة المصفوفة هي الحد الأقصى لعدد الصفوف المستقلة خطيًا. أو: رتبة المصفوفة هي الحد الأقصى لعدد الأعمدة المستقلة خطيًا. نعم ، يتطابقون دائمًا.

يتبع دليل عملي مهم مما ورد أعلاه: لا تتجاوز رتبة المصفوفة الحد الأدنى من أبعادها. على سبيل المثال ، في المصفوفة أربعة صفوف وخمسة أعمدة. البعد الأدنى هو أربعة ، وبالتالي ، فإن رتبة هذه المصفوفة لن تتجاوز بالتأكيد 4.

الرموز: في النظرية والتطبيق العالميين ، لا يوجد معيار مقبول بشكل عام لتحديد رتبة المصفوفة ، ويمكن العثور على أكثرها شيوعًا: - كما يقولون ، يكتب رجل إنجليزي شيئًا ، وآخر ألمانيًا. لذلك ، بناءً على الحكاية المعروفة عن الجحيم الأمريكي والروسي ، دعنا نحدد رتبة المصفوفة بكلمة أصلية. فمثلا: . وإذا كانت المصفوفة "بدون اسم" ، والتي يوجد الكثير منها ، فيمكنك ببساطة الكتابة.

كيف تجد رتبة مصفوفة باستخدام القاصرين؟

إذا كان لجدتنا عمود خامس في المصفوفة ، فيجب حساب قاصر آخر من الرتبة الرابعة ("أزرق" ، "توت العليق" + العمود الخامس).

استنتاج: الحد الأقصى لترتيب قاصر غير صفري هو ثلاثة ، لذلك.

ربما لم يستوعب الجميع هذه العبارة تمامًا: الدرجة الرابعة للقاصر تساوي صفرًا ، ولكن بين القاصرين من الدرجة الثالثة كان هناك واحد غير صفري - لذلك ، الحد الأقصى للترتيب غير صفريةطفيفة ويساوي ثلاثة.

السؤال الذي يطرح نفسه ، لماذا لا نحسب المحدد على الفور؟ حسنًا ، أولاً ، في معظم المهام لا تكون المصفوفة مربعة ، وثانيًا ، حتى إذا حصلت على قيمة غير صفرية ، فسيتم رفض المهمة باحتمالية عالية ، نظرًا لأنها تتضمن عادةً "من أسفل إلى أعلى" المحلول. وفي المثال المدروس ، يسمح لنا المحدد الصفري من الرتبة الرابعة بالتأكيد على أن رتبة المصفوفة أقل من أربعة فقط.

يجب أن أعترف بأنني توصلت بنفسي إلى المشكلة التي تم تحليلها من أجل شرح أفضل لطريقة تجاور القاصرين. في الممارسة الواقعية ، كل شيء أبسط:

مثال 2

أوجد مرتبة المصفوفة بطريقة تهديب القاصرين

الحل والجواب في نهاية الدرس.

متى يتم تشغيل الخوارزمية بشكل أسرع؟ لنعد إلى نفس مصفوفة أربعة في أربعة . من الواضح أن الحل سيكون الأقصر في حالة "الخير" ركن القصر: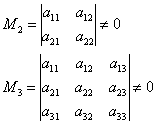

وإذا ، إذن ، خلاف ذلك -.

التفكير ليس افتراضيًا على الإطلاق - هناك العديد من الأمثلة حيث يقتصر الأمر برمته على القصر الزاوي فقط.

ومع ذلك ، في بعض الحالات ، هناك طريقة أخرى أكثر فعالية وأفضل:

كيف تجد رتبة المصفوفة باستخدام طريقة غاوس؟

هذا القسم مخصص للقراء الذين هم على دراية بالفعل طريقة جاوسوشيئًا فشيئًا وضعوا أيديهم عليها.

من الناحية الفنية ، الطريقة ليست جديدة:

1) باستخدام التحولات الأولية ، نأتي بالمصفوفة إلى شكل تدريجي ؛

2) رتبة المصفوفة تساوي عدد الصفوف.

من الواضح أن استخدام طريقة غاوس لا يغير رتبة المصفوفة، والجوهر هنا بسيط للغاية: وفقًا للخوارزمية ، في سياق التحولات الأولية ، يتم تحديد وإزالة جميع الخطوط المتناسبة غير الضرورية (المعتمدة خطيًا) ، ونتيجة لذلك تبقى "البقايا الجافة" - الحد الأقصى لعدد خطوط مستقلة خطيًا.

لنحول المصفوفة القديمة المألوفة بإحداثيات ثلاثة متجهات خطية:

(1) تمت إضافة الصف الأول إلى الصف الثاني ، مضروبًا في -2. تمت إضافة السطر الأول إلى السطر الثالث.

(2) يتم إزالة الخطوط الصفرية.

إذن هناك سطر واحد متبقي ، إذن. وغني عن القول ، أن هذا أسرع بكثير من حساب تسعة صفر قاصرين من الدرجة الثانية وبعد ذلك فقط استخلاص نتيجة.

أذكرك بهذا في حد ذاته مصفوفة جبريةلا شيء يمكن تغييره ، والتحولات تتم فقط لغرض معرفة الرتبة! بالمناسبة ، دعنا نتناول السؤال مرة أخرى ، لماذا لا؟ مصفوفة المصدر 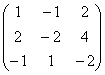يحمل معلومات تختلف اختلافًا جوهريًا عن معلومات المصفوفة والصف. في بعض النماذج الرياضية (بدون مبالغة) ، يمكن أن يكون الاختلاف في رقم واحد مسألة حياة أو موت. ... تذكرت معلمي الرياضيات بالمدرسة في الصفوف الابتدائية والثانوية ، الذين قطعوا الصف بلا رحمة بمقدار 1-2 نقطة لأدنى قدر من عدم الدقة أو الانحراف عن الخوارزمية. وكان الأمر مخيباً للآمال بشكل رهيب عندما تبين أنه "جيد" أو أسوأ من ذلك ، بدلاً من "الخمسة" التي تبدو مضمونة على ما يبدو. جاء التفاهم بعد ذلك بكثير - وإلا فكيف نعهد إلى شخص ما بالأقمار الصناعية والرؤوس الحربية النووية ومحطات الطاقة؟ لكن لا تقلق ، فأنا لا أعمل في هذه المجالات =)

دعنا ننتقل إلى مهام أكثر أهمية ، حيث ، من بين أمور أخرى ، سوف نتعرف على تقنيات حسابية مهمة طريقة جاوس:

مثال 3

أوجد مرتبة المصفوفة باستخدام التحولات الأولية

المحلول: بمصفوفة أربعة في خمسة ، مما يعني أن رتبتها بالتأكيد لا تزيد عن 4.

في العمود الأول ، لا يوجد 1 أو -1 ، لذلك هناك حاجة إلى خطوات إضافية للحصول على وحدة واحدة على الأقل. طوال فترة وجود الموقع ، سئلني مرارًا وتكرارًا السؤال التالي: "هل من الممكن إعادة ترتيب الأعمدة أثناء التحولات الأولية؟". هنا - أعيد ترتيب العمود الأول أو الثاني ، وكل شيء على ما يرام! في معظم المهام حيث طريقة جاوس، يمكن إعادة ترتيب الأعمدة حقًا. لكن لا تفعل. والنقطة ليست حتى خلطًا محتملًا مع المتغيرات ، فالنقطة هي أنه في الدورة الكلاسيكية لتدريس الرياضيات العليا ، لا يُنظر إلى هذا الإجراء تقليديًا ، لذلك ، سيتم النظر إلى مثل هذا الانحناء بشكل ملتوي للغاية (أو حتى يُجبر على إعادة كل شيء) .

النقطة الثانية تتعلق بالأرقام. في سياق القرار ، من المفيد الاسترشاد بالقاعدة الأساسية التالية: يجب أن تقلل التحويلات الأولية ، إذا أمكن ، من أعداد المصفوفة. في الواقع ، من الأسهل بكثير العمل مع واحد - اثنان - ثلاثة من ، على سبيل المثال ، مع 23 و 45 و 97. والإجراء الأول لا يهدف فقط إلى الحصول على وحدة في العمود الأول ، ولكن أيضًا للقضاء على الأرقام 7 و 11.

أولاً الحل الكامل ، ثم التعليقات:

(1) تمت إضافة الصف الأول إلى الصف الثاني ، مضروبًا في -2. تمت إضافة السطر الأول إلى السطر الثالث ، مضروبًا في -3. وإلى الكومة: تمت إضافة السطر الأول ، مضروبًا في -1 ، إلى السطر الرابع.

(2) الأسطر الثلاثة الأخيرة متناسبة. تم حذف الخطين الثالث والرابع ، وتم نقل السطر الثاني إلى المركز الأول.

(3) تم إضافة الصف الأول إلى الصف الثاني ، مضروبًا في -3.

المصفوفة التي تم تقليلها إلى شكل متدرج تتكون من صفين.

إجابه:

الآن حان دورك لتعذيب مصفوفة أربعة في أربعة:

مثال 4

أوجد مرتبة مصفوفة باستخدام طريقة جاوس

أذكرك بذلك طريقة جاوسلا يعني صلابة لا لبس فيها ، ومن المرجح أن يكون حلك مختلفًا عن الحل الذي قدمته. عينة موجزة من المهمة في نهاية الدرس.

ما هي الطريقة التي يجب استخدامها لإيجاد رتبة المصفوفة؟

في الممارسة العملية ، غالبًا ما لا يُقال على الإطلاق الطريقة التي يجب استخدامها للعثور على الرتبة. في مثل هذه الحالة ، يجب على المرء أن يحلل الشرط - بالنسبة لبعض المصفوفات ، من المنطقي تنفيذ الحل من خلال قاصرين ، بينما بالنسبة للآخرين ، يكون تطبيق التحولات الأولية أكثر ربحية:

مثال 5

أوجد مرتبة المصفوفة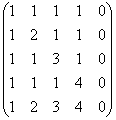

المحلول: الطريقة الأولى تختفي على الفور بطريقة أو بأخرى =)

أعلى قليلاً ، نصحت بعدم لمس أعمدة المصفوفة ، ولكن عندما يكون هناك عمود صفري ، أو أعمدة متناسبة / متطابقة ، فلا يزال الأمر يستحق البتر:

(1) العمود الخامس هو صفر ، نقوم بإزالته من المصفوفة. وبالتالي ، فإن رتبة المصفوفة هي أربعة على الأكثر. يتم ضرب الصف الأول في -1. هذه ميزة توقيع أخرى للطريقة الغاوسية ، مما يجعل الإجراء التالي نزهة ممتعة:

(2) تم إضافة السطر الأول إلى جميع الأسطر ، بدءًا من السطر الثاني.

(3) تم ضرب الصف الأول في -1 ، وتم تقسيم الصف الثالث على 2 ، وتم تقسيم الصف الرابع على 3. تمت إضافة الصف الثاني مضروبًا في -1 إلى الصف الخامس.

(4) تم إضافة السطر الثالث إلى السطر الخامس ، مضروبًا في -2.

(5) السطران الأخيران متناسبان ، نحذف السطر الخامس.

والنتيجة هي 4 صفوف.

إجابه:

مبنى قياسي من خمسة طوابق لاستكشاف الذات:

مثال 6

أوجد مرتبة المصفوفة

حل قصير والإجابة في نهاية الدرس.

وتجدر الإشارة إلى أن عبارة "رتبة المصفوفة" ليست شائعة في الممارسة ، وفي معظم المشاكل يمكنك الاستغناء عنها. ولكن هناك مهمة واحدة يكون فيها المفهوم قيد النظر هو الشخصية الرئيسية ، وفي ختام المقال سننظر في هذا التطبيق العملي:

كيف تتحقق من نظام المعادلات الخطية من أجل التوافق؟

في كثير من الأحيان ، بالإضافة إلى حل أنظمة المعادلات الخطيةوفقًا للشرط ، يجب أولاً فحصه للتأكد من توافقه ، أي لإثبات وجود أي حل على الإطلاق. يتم لعب دور رئيسي في هذا التحقق نظرية كرونيكر كابيليوالتي سأقوم بصياغتها بالشكل المطلوب:

إذا كانت مرتبة مصفوفات النظاميساوي الرتبة نظام المصفوفة المعزز، إذن يكون النظام متسقًا ، وإذا تطابق الرقم المحدد مع عدد المجهولين ، فإن الحل يكون فريدًا.

وبالتالي ، لدراسة نظام التوافق ، من الضروري التحقق من المساواة ، أين - مصفوفة النظام(تذكر المصطلحات من الدرس طريقة جاوس)، أ - نظام المصفوفة المعزز(أي مصفوفة ذات معاملات عند المتغيرات + عمود المصطلحات الحرة).

ستناقش هذه المقالة مفهومًا مثل رتبة المصفوفة والمفاهيم الإضافية الضرورية. سنقدم أمثلة وإثباتات لإيجاد رتبة مصفوفة ، ونخبرك أيضًا ما هي مصفوفة ثانوية وسبب أهميتها.

مصفوفة ثانوية

لفهم ما هي رتبة المصفوفة ، من الضروري فهم مفهوم مثل مصفوفة ثانوية.

التعريف 1

تحت السن القانونيكمصفوفة الترتيب - محدد المصفوفة المربعة بالترتيب k × k ، والذي يتكون من عناصر المصفوفة A ، الموجودة في صفوف k وأعمدة k محددة مسبقًا ، مع الحفاظ على موضع عناصر المصفوفة A.

ببساطة ، إذا قمنا في المصفوفة A بحذف الصفوف (p-k) والأعمدة (n-k) ، ومن العناصر المتبقية ، نصنع مصفوفة ، مع الاحتفاظ بترتيب عناصر المصفوفة A ، ثم محدد المصفوفة الناتجة هو القاصر من أجل ك من المصفوفة أ.

ويترتب على المثال أن العناصر الثانوية من الدرجة الأولى للمصفوفة A هي عناصر المصفوفة نفسها.

يمكننا إعطاء عدة أمثلة للقصر من الدرجة الثانية. دعنا نختار صفين وعمودين. على سبيل المثال ، الصف الأول والثاني ، العمود الثالث والرابع.

مع اختيار العناصر هذا ، سيكون الترتيب الثانوي من الدرجة الثانية - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2

ثانوية أخرى من الرتبة الثانية للمصفوفة A هي 0 0 1 1 = 0

دعونا نقدم الرسوم التوضيحية لبناء القصر من الدرجة الثانية من المصفوفة أ:

يتم الحصول على الرتبة الثالثة من خلال حذف العمود الثالث من المصفوفة أ:

0 0 3 1 1 2-1-4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9

توضيح لكيفية الحصول على الرتبة الثالثة من المصفوفة أ:

بالنسبة لمصفوفة معينة ، لا يوجد قاصر أعلى من الترتيب الثالث ، لأن

ك ≤ م أنا ن (ص ، ن) = م أنا ن (3 ، 4) = 3

كم عدد الصغرى من المرتبة k للمصفوفة A من الرتبة p × n؟

يتم حساب عدد القاصرين باستخدام الصيغة التالية:

C p k × C n k، g e C p k = p! ك! (ع - ك)! و C nk = n! ك! (ن - ك)! - عدد التوليفات من p إلى k ، من n إلى k ، على التوالي.

بعد أن قررنا ما هي صغرى المصفوفة A ، يمكننا المضي قدمًا في تحديد رتبة المصفوفة A.

رتبة المصفوفة: طرق البحث

التعريف 2

رتبة المصفوفة - أعلى ترتيب للمصفوفة ، بخلاف الصفر.

التعيين 1

رتبة (أ) ، Rg (A) ، Rang (A).

من تعريف رتبة المصفوفة والصغرى للمصفوفة ، يتضح أن رتبة المصفوفة الصفرية تساوي الصفر ، وأن رتبة المصفوفة غير الصفرية تختلف عن الصفر.

إيجاد مرتبة المصفوفة بالتعريف

التعريف 3

طريقة العد الصغرى - طريقة تعتمد على تحديد رتبة المصفوفة.

خوارزمية الإجراءات عن طريق تعداد القصر :

من الضروري إيجاد رتبة المصفوفة أ من الترتيب ص× ن. إذا كان هناك عنصر واحد غير صفري على الأقل ، فإن رتبة المصفوفة تساوي واحدًا على الأقل ( لان هو قاصر من الدرجة الأولى لا يساوي صفرًا).

ثم يلي ذلك تعداد القصر من الدرجة الثانية. إذا كان كل الصغار من الدرجة الثانية يساوي صفرًا ، فإن الرتبة تساوي واحدًا. إذا كان هناك قاصر واحد على الأقل ليس صفريًا من الترتيب الثاني ، فمن الضروري الذهاب إلى تعداد القصر من الدرجة الثالثة ، وستكون رتبة المصفوفة ، في هذه الحالة ، اثنين على الأقل.

لنفعل الشيء نفسه مع المرتبة الثالثة: إذا كانت جميع العناصر الثانوية في المصفوفة تساوي صفرًا ، فستكون الرتبة مساوية لاثنين. إذا كان هناك واحد على الأقل من الرتبة الثالثة غير صفرية ، فإن رتبة المصفوفة هي ثلاثة على الأقل. وهكذا ، عن طريق القياس.

مثال 2

أوجد رتبة المصفوفة:

أ \ u003d - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7

نظرًا لأن المصفوفة ليست صفرية ، فإن رتبتها تساوي واحدًا على الأقل.

الدرجة الثانية الثانوية - 1 1 2 2 = (- 1) × 2-1 × 2 = 4 ليست صفرية. هذا يعني أن رتبة المصفوفة A لا تقل عن اثنين.

نقوم بالفرز من خلال القاصرين من الترتيب الثالث: C 3 3 × C 5 3 \ u003d 1 5! 3! (5 - 3)! = 10 قطع.

1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (-1) × 6 × 3 = 0

1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 - (- 1) × 0 × 11 = 0

1 1 - 2 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (-1) × 0 × 3 = 0

1 - 1 0 2 6-4 4 11-7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0

1 - 1 0 2 6 - 4 3 11-7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (- 7) - 1 × (- 4) × 11 = 0

1 - 2 0 2 0 - 4 3 1-7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) - 1 × (- 4) × 1 = 0

1 - 2 0 6 0-4 11 1-7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0

الدرجة الثالثة الصغرى هي صفر ، لذا فإن رتبة المصفوفة هي اثنان.

إجابه : المرتبة (أ) = 2.

إيجاد مرتبة المصفوفة بطريقة تهديب القصر

التعريف 3

طريقة التهذيب الصغرى - طريقة تسمح لك بالحصول على نتيجة بعمل حسابي أقل.

هدب قاصر - M o k (k + 1) - الترتيب الثالث للمصفوفة A ، الذي يحد M الصغرى من الرتبة k من المصفوفة A ، إذا كانت المصفوفة التي تتوافق مع القاصر M o k "تحتوي على" المصفوفة التي تتوافق مع القاصر م.

ببساطة ، يتم الحصول على المصفوفة المقابلة لحدود M الصغيرة من المصفوفة المقابلة للصغرى الحدودية M o k عن طريق حذف عناصر صف واحد وعمود واحد.

مثال 3

أوجد رتبة المصفوفة:

أ = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5

لإيجاد الرتبة ، نأخذ المرتبة الثانية الثانوية M = 2 - 1 4 1

نكتب جميع القاصرين المجاورين:

1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .

لإثبات طريقة تجاور القاصرين ، نقدم نظرية لا تتطلب صياغتها أساس إثبات.

نظرية 1

إذا كان كل القاصرين الذين يحدون من الرتبة k-th من المصفوفة A من الرتبة p في n يساوي صفرًا ، فإن كل العناصر الثانوية (k + 1) للمصفوفة A تساوي صفرًا.

خوارزمية العمل :

للعثور على مرتبة المصفوفة ، ليس من الضروري المرور عبر كل القصر ، فقط انظر إلى الحدود.

إذا كانت الحدود الصغرى تساوي صفرًا ، فإن رتبة المصفوفة تساوي صفرًا. إذا كان هناك قاصر واحد على الأقل لا يساوي صفرًا ، فإننا نعتبر قاصرين متجاورين.

إذا كانت جميعها صفراً ، فإن الرتبة (أ) هي اثنان. إذا كان هناك قاصر واحد على الأقل ليس صفراً على الحدود ، فإننا ننتقل إلى اعتبار القاصرين المجاورين له. وهكذا ، بطريقة مماثلة.

مثال 4

أوجد مرتبة المصفوفة بطريقة تهديب القاصرين

أ = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14

كيف تقرر؟

نظرًا لأن العنصر a 11 في المصفوفة A لا يساوي صفرًا ، فإننا نأخذ العنصر الأصغر من الترتيب الأول. لنبدأ في البحث عن حد أدنى غير الصفر:

2 1 4 2 = 2 × 2-1 × 4 = 0 2 0 4 1 = 2 × 1 - 0 × 4 = 2

لقد وجدنا قاصرًا حدوديًا من الرتبة الثانية لا يساوي صفرًا 2 0 4 1.

لنعد القاصرين المجاورين - (هناك (4 - 2) × (5 - 2) = 6 قطع).

2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0

إجابه : المرتبة (أ) = 2.

إيجاد رتبة مصفوفة بطريقة غاوس (باستخدام التحولات الأولية)

تذكر ما هي التحولات الأولية.

التحولات الأولية:

عن طريق إعادة ترتيب صفوف (أعمدة) المصفوفة ؛
بضرب جميع عناصر أي صف (عمود) من المصفوفة بعدد تعسفي غير صفري ك ؛

عن طريق إضافة عناصر أي صف (عمود) تتوافق مع صف آخر (عمود) من المصفوفة ، والتي يتم ضربها برقم تعسفي ك.

التعريف 5

إيجاد رتبة مصفوفة باستخدام طريقة غاوس - طريقة تعتمد على نظرية تكافؤ المصفوفة: إذا تم الحصول على المصفوفة B من المصفوفة A باستخدام عدد محدود من التحويلات الأولية ، فإن الرتبة (A) = الرتبة (B).

صحة هذا البيان يتبع من تعريف المصفوفة:

في حالة تبديل صفوف أو أعمدة المصفوفة ، علامة التغييرات المحددة لها. إذا كانت تساوي صفرًا ، فعند تبديل الصفوف أو الأعمدة تظل مساوية للصفر ؛
في حالة ضرب جميع عناصر أي صف (عمود) من المصفوفة برقم تعسفي ك ، والذي لا يساوي الصفر ، فإن محدد المصفوفة الناتجة يساوي محدد المصفوفة الأصلية ، والذي يتم ضربه بواسطة k ؛

في حالة إضافة عناصر صف أو عمود معين من المصفوفة ، فإن العناصر المقابلة لصف أو عمود آخر ، والتي يتم ضربها بالرقم k ، لا تغير محددها.

جوهر طريقة التحولات الأولية : اختزل المصفوفة ، التي يمكن إيجاد رتبتها ، إلى شبه منحرف باستخدام التحولات الأولية.

لماذا؟

من السهل جدًا العثور على ترتيب المصفوفات من هذا النوع. إنه يساوي عدد الصفوف التي تحتوي على عنصر واحد غير فارغ على الأقل. وبما أن الرتبة لا تتغير أثناء التحولات الأولية ، فستكون هذه هي رتبة المصفوفة.

دعنا نوضح هذه العملية:

بالنسبة للمصفوفات المستطيلة A بالترتيب p في n ، يكون عدد صفوفها أكبر من عدد الأعمدة:

أ ~ 1 ب 12 ب 13 ⋯ ب 1 ن - 1 ب 1 ن 0 1 ب 23 ⋯ ب 2 ن - 2 ب 2 ن ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 ب ن - 1 ن 0 0 0 0 1 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 0 0، R a n k (A) = n

أ ~ 1 ب 12 ب 13 ⋯ ب 1 ك ب 1 ك + 1 ⋯ ب 1 ن 0 1 ب 23 ⋯ ب 2 ك ب 2 ك + 1 ب 2 ن ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 1 ب ك ك + 1 ⋯ ب ك ن 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 ، R a n k (A) = k

للمصفوفات المستطيلة A بالترتيب p في n ، وعدد صفوفها أقل من عدد الأعمدة:

A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 1 b p p + 1 ⋯ ب ف ن ، ر أ ن ك (أ) = ص

أ ~ 1 ب 12 ب 13 ⋯ ب 1 ك ب 1 ك + 1 ⋯ ب 1 ن 0 1 ب 23 ⋯ ب 2 ك ب 2 ك + 1 ب 2 ن ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 1 ب ك ك + 1 ⋯ ب ك ن 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 0

للمصفوفات المربعة A من أجل n بواسطة n:

أ ~ 1 ب 12 ب 13 ⋯ ب 1 ن - 1 ب 1 ن 0 1 ب 23 ⋯ ب 2 ن - 1 ب 2 ن ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 1 ب ن - 1 ن 0 0 0 0 1 ، R a n k (A) = n

أ ~ 1 ب 12 ب 13 ⋯ ب 1 ك ب 1 ك + 1 ⋯ ب 1 ن 0 1 ب 23 ⋯ ب 2 ك ب 2 ك + 1 ب 2 ن ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 1 ب ك ك + 1 ⋯ ب ك ن 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0، R a n k (A) = k، k< n

مثال 5

أوجد رتبة المصفوفة أ باستخدام التحولات الأولية:

أ = ٢ ١ - ٢ ٦ ٣ ٠ ٠ - ١ ١ - ١ ٢ - ٧ ٥ - ٢ ٤ - ١٥ ٧ ٢ - ٤ ١١

كيف تقرر؟

نظرًا لأن العنصر a 11 غير صفري ، فمن الضروري مضاعفة عناصر الصف الأول من المصفوفة A في 1 a 11 \ u003d 1 2:

أ = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~

نضيف إلى عناصر الصف الثاني العناصر المقابلة للصف الأول ، والتي يتم ضربها في (-3). إلى عناصر الصف الثالث نضيف عناصر الصف الأول ، والتي يتم ضربها ب (-1):

~ A (1) \ u003d 1 1 2-1 3 3 0 0 - 1 1 - 1 2-7 5-2 4-15 7 2-4 11 ~ A (2) \ u003d \ u003d 1 1 2-1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5) ) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =

1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10

العنصر a 22 (2) ليس صفريًا ، لذلك نضرب عناصر الصف الثاني من المصفوفة A في A (2) في a 1 a 22 (2) = - 2 3:

أ (3) \ u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0-9 2 9-30 0 - 3 2 3 - 10 ~ A (4) \ u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2-30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0

إلى عناصر الصف الثالث من المصفوفة الناتجة ، نضيف العناصر المقابلة للصف الثاني ، والتي يتم ضربها في 3 2 ؛
إلى عناصر الصف الرابع - عناصر الصف الثاني ، والتي يتم ضربها في 9 2 ؛
لعناصر الصف الخامس - عناصر الصف الثاني ، والتي يتم ضربها في 3 2.

جميع عناصر الصف صفر. وهكذا ، بمساعدة التحولات الأولية ، قمنا بتقليل المصفوفة إلى شكل شبه منحرف ، يمكن من خلاله ملاحظة أن R a n k (A (4)) = 2. ويترتب على ذلك أن مرتبة المصفوفة الأصلية تساوي أيضًا اثنين.

تعليق

إذا قمت بإجراء تحويلات أولية ، فلن يُسمح بالقيم التقريبية!

إذا لاحظت وجود خطأ في النص ، فيرجى تمييزه والضغط على Ctrl + Enter

في كل مصفوفة ، يمكن ربط رتبتين: رتبة صف (رتبة نظام الصف) ورتبة عمود (رتبة نظام العمود).

نظرية

رتبة صف المصفوفة تساوي رتبة عمودها.

رتبة المصفوفة

تعريف

رتبة المصفوفة$ A $ هو ترتيب نظام الصفوف أو الأعمدة.

يُرمز إليه بـ $ \ operatorname (رن) A $

في الممارسة العملية ، لإيجاد رتبة المصفوفة ، يتم استخدام العبارة التالية: رتبة المصفوفة تساوي عدد الصفوف غير الصفرية بعد أن تم تقليل المصفوفة إلى شكل متدرج.

التحويلات الأولية على صفوف (أعمدة) مصفوفة لا تغير ترتيبه.

رتبة مصفوفة الخطوة تساوي عدد صفوفها غير الصفرية.

مثال

ممارسه الرياضه.أوجد رتبة المصفوفة $ A = \ left (\ begin (array) (cccc) (0) & (4) & (10) & (1) \\ (4) & (8) & (18) & ( 7) \ (10) & (18) & (40) & (17) \\ (1) & (7) & (17) & (3) \ نهاية (مجموعة) \ حق) $

المحلول.باستخدام التحويلات الأولية في صفوفها ، نقوم بتقليل المصفوفة $ A $ إلى نموذج خطوة. للقيام بذلك ، اطرح أولًا ثاني اثنين من السطر الثالث:

$$ A \ sim \ left (\ start (array) (cccc) (0) & (4) & (10) & (1) \\ (4) & (8) & (18) & (7) \\ (2) & (2) & (4) & (3) \\ (1) & (7) & (17) & (3) \ end (array) \ right) $$

من السطر الثاني نطرح السطر الرابع مضروبًا في 4 ؛ من الثالث - ربعان:

$$ A \ sim \ left (\ begin (array) (rrrr) (0) & (4) & (10) & (1) \\ (0) & (-20) & (-50) & (-5 ) \\ (0) & (-12) & (-30) & (-3) \\ (1) & (7) & (17) & (3) \ end (array) \ right) $$

نضيف الخمسة الأولى إلى السطر الثاني ، وثلاثة أثلاث إلى السطر الثالث:

$$ A \ sim \ left (\ start (array) (cccc) (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3) \ end (array) \ right) $$

قم بتبديل الخطين الأول والثاني:

$$ A \ sim \ left (\ start (array) (cccc) (0) & (0) & (0) & (0) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (1) & (7) & (17) & (3) \ end (array) \ right) $$

$$ A \ sim \ left (\ start (array) (cccc) (1) & (7) & (17) & (3) \\ (0) & (4) & (10) & (1) \\ (0) & (0) & (0) & (0) \\ (0) & (0) & (0) & (0) \ end (array) \ right) \ Rightarrow \ operatorname (rang) A = 2 $$

إجابه.$ \ اسم المشغل (المرتبة) A = 2 دولار

طريقة الحدود البسيطة

تعتمد طريقة أخرى لإيجاد رتبة المصفوفة على هذه النظرية - طريقة الحدود الطفيفة. جوهر هذه الطريقة هو العثور على القاصرين ، بدءًا من الطلبات الدنيا والانتقال إلى الأوامر الأعلى. إذا كانت الرتبة الثانوية $ n $ -th ليست صفرية ، وكل $ n + 1 $ الصغرى تساوي صفرًا ، فإن رتبة المصفوفة ستكون مساوية لـ $ n $.

مثال

ممارسه الرياضه.أوجد رتبة المصفوفة $ A = \ left (\ begin (array) (rrrr) (1) & (2) & (-1) & (-2) \\ (2) & (4) & (3) & (0) \\ (-1) & (-2) & (6) & (6) \ end (array) \ right) $ باستخدام طريقة الحدود الثانوية.

المحلول.صغار الترتيب الأدنى هم من الدرجة الأولى الثانوية ، والتي تساوي عناصر المصفوفة $ A $. ضع في اعتبارك ، على سبيل المثال ، $ M_ (1) = 1 \ neq 0 $. يقع في الصف الأول والعمود الأول. على حدود الصف الثاني والعمود الثاني ، نحصل على الصغرى $ M_ (2) ^ (1) = \ left | \ start (array) (ll) (1) & (2) \\ (2) & (4) \ end (array) \ right | = 0 $؛ ضع في اعتبارك ثانويًا آخر من الدرجة الثانية ، لهذا نحدد الصغرى $ M_1 $ بمساعدة الصف الثاني والعمود الثالث ، ثم لدينا الصغرى $ M_ (2) ^ (2) = \ left | \ start (array) (rr) (1) & (-1) \\ (2) & (3) \ end (array) \ right | = 5 \ neq 0 $ ، أي أن رتبة المصفوفة هي اثنان على الأقل. بعد ذلك ، نعتبر القاصرين من الدرجة الثالثة الذين يحيطون بالقاصر $ M_ (2) ^ (2) $. هناك نوعان من القاصرين: مزيج من الصف الثالث مع العمود الثاني أو مع العمود الرابع. نحسب هؤلاء القصر.

§3. رتبة المصفوفة

تحديد رتبة المصفوفة

صفوف خطية تابعة

تحولات المصفوفة الأولية

المصفوفات المكافئة

خوارزمية لإيجاد رتبة مصفوفة باستخدام التحولات الأولية

§ أربعة. محددات الرتب الأولى والثانية والثالثة

محدد من الدرجة الأولى

محدد من الدرجة الثانية

محدد من الدرجة الثالثة

حكم ساروس

§5. حساب محددات الطلبات الكبيرة

الجمع الجبري

نظرية لابلاس

محدد المصفوفة المثلثية

طلب. مفهوم المحدد صالترتيب ال بشكل عام.

§ 3. رتبة المصفوفة

تتميز كل مصفوفة برقم معين مهم في حل أنظمة المعادلات الخطية. هذا الرقم يسمى رتبة المصفوفة.

رتبة المصفوفةيساوي عدد الصفوف (الأعمدة) المستقلة خطيًا ، والتي يتم من خلالها التعبير عن جميع الصفوف (الأعمدة) الأخرى خطيًا.

تسمى صفوف (أعمدة) المصفوفة تعتمد خطياإذا كانت العناصر المقابلة لها متناسبة.

بمعنى آخر ، فإن عناصر أحد الصفوف التابعة خطيًا تساوي عناصر الآخر ، مضروبة في نفس العدد. على سبيل المثال ، الصفوف 1 و 2 من المصفوفة لكنتعتمد خطيًا إذا ، أين (رقم ما).

مثال. أوجد مرتبة المصفوفة

المحلول.

يتم الحصول على الصف الثاني من الأول إذا تم ضرب عناصره في -3 ، ويتم الحصول على الصف الثالث من الأول إذا تم ضرب عناصره في 0 ، ولا يمكن التعبير عن الصف الرابع بدلالة الأول. اتضح أن المصفوفة بها صفان مستقلان خطيًا ، لأن الصفوف الأول والرابع غير متناسبين ، وبالتالي فإن رتبة المصفوفة هي 2.

رتبة المصفوفة لكنيعني رتبة أأو ص(أ).

من تعريف رتبة المصفوفة ما يلي:

1. لا تتجاوز مرتبة المصفوفة أصغر أبعادها ، أي للمصفوفة أكون × ن .

2. رتبة المصفوفة تساوي صفرًا فقط إذا كانت مصفوفة صفرية.

في الحالة العامة ، يعد تحديد رتبة المصفوفة أمرًا شاقًا للغاية. لتسهيل هذه المهمة ، يتم استخدام التحويلات التي تحافظ على رتبة المصفوفة ، والتي تسمى التحولات الأولية:

1) تجاهل صف صفر (عمود) ؛

2) ضرب جميع عناصر الصف (العمود) بعدد آخر غير الصفر ؛

3) تغيير ترتيب الصفوف (الأعمدة) ؛

4) إضافة إلى عناصر صف واحد (عمود) العناصر المقابلة لصف آخر (عمود) ، مضروبًا في أي رقم ؛

5) تبديل المصفوفة.

يتم استدعاء المصفوفتين ما يعادلإذا تم الحصول على أحدهما من الآخر بعدد محدود من التحولات الأولية.

تتم الإشارة إلى معادلة المصفوفات بعلامة "~" (مكافئة).

بمساعدة التحولات الأولية ، يمكن تصغير أي مصفوفة إلى شكل مثلث ، وبالتالي فإن حساب رتبتها ليس بالأمر الصعب.

عملية حساب رتبة المصفوفة باستخدام التحولات الأوليةلنلقي نظرة على مثال.

مثال. أوجد مرتبة المصفوفة

أ =

المحلول.

مهمتنا هي إحضار المصفوفة إلى شكل مثلث ، أي باستخدام تحويلات أولية ، تأكد من أن الأصفار فقط هي تحت القطر الرئيسي في المصفوفة.

1. النظر في السطر الأول. إذا كان العنصر أ 11 = 0 ، ثم عند تبديل الصفوف أو الأعمدة ، نحقق ذلك أ 11 ¹ 0. في مثالنا ، دعنا نتبادل ، على سبيل المثال ، الصفين الأول والثاني من المصفوفة:

أ =

الآن العنصر أ 11 ¹ 0. بضرب الصف الأول بأرقام مناسبة وإضافتها مع صفوف أخرى ، سنضمن أن جميع عناصر العمود الأول (باستثناء أ 11) تساوي الصفر.

2. لننظر الآن في السطر الثاني. إذا كان العنصر أ 22 = 0 ، ثم عند تبديل الصفوف أو الأعمدة ، نحقق ذلك أ 22 ¹ 0. إذا كان العنصر أ 22 ¹ 0 (ولدينا أ 22 = –1 ¹ 0) ، ثم بضرب الصف الثاني بأرقام مناسبة وإضافتها إلى صفوف أخرى ، سنضمن أن جميع عناصر العمود الثاني (باستثناء أ 22) تساوي صفرًا.

3. إذا تم الحصول على صفوف (أعمدة) تتكون بالكامل من أصفار أثناء عملية التحويل ، فإننا نتجاهلها. في مثالنا ، سنتجاهل السطرين 3 و 4:

المصفوفة الأخيرة لها شكل متدرج وتحتوي على صفين. إنها مستقلة خطيًا ، وبالتالي فإن مرتبة المصفوفة هي 2.

§ أربعة. محددات الرتب الأولى والثانية والثالثة

من بين مجموعة متنوعة من المصفوفات ، يتم تحديد المصفوفات المربعة بشكل منفصل. هذا النوع من المصفوفات جيد للأسباب التالية:

1. مصفوفات الهوية مربعة.

2. يمكنك ضرب وإضافة أي مصفوفات مربعة من نفس الترتيب ، وستحصل على مصفوفة من نفس الترتيب.

3. يمكن رفع المصفوفات المربعة إلى قوة.

أيضًا ، يمكن أن تحتوي المصفوفات المربعة فقط على محدد.

محدد المصفوفةهو رقم خاص محسوب وفقًا لبعض القواعد. محدد المصفوفة لكنيعني:

أو بأقواس مستقيمة: ،

أو الحرف اليوناني الكبير "دلتا": Δ ( أ),

أو الرمز "المحدد": det ( أ).

محدد مصفوفة من الدرجة الأولى لكن= (أ 11) أو محدد من الدرجة الأولى، هو رقم يساوي عنصر المصفوفة:

∆1 = =أ 11

محدد مصفوفة من الدرجة الثانية أو محدد من الدرجة الثانية

مثال:

محدد مصفوفة من الرتبة الثالثة أو محدد من الدرجة الثالثة، هو رقم يتم حسابه بواسطة الصيغة:

يمكن حساب محدد الترتيب الثالث باستخدام حكم ساروس .

حكم ساروس. يتم توقيع العمودين الأولين على محدد الترتيب الثالث على اليمين وبعلامة زائد (+) يأخذون مجموع منتجات العناصر الثلاثة الموجودة على القطر الرئيسي للمحدد وعلى الخطوط المتوازية "المستقيمة" إلى القطر الرئيسي ، بعلامة الطرح (-) يأخذون مجموع حاصل ضرب العناصر الموجودة على القطر الثاني وعلى "الخطوط المستقيمة" الموازية له.

مثال:

من السهل أن ترى أن عدد المصطلحات في المحدد يزداد بترتيبها. بشكل عام ، في المحدد صالترتيب ، عدد المصطلحات هو 1 2 3. ص = ص!.

دعنا نتحقق: بالنسبة إلى 1 ، فإن عدد المصطلحات يساوي 1! = 1 ،

بالنسبة إلى Δ 2 ، فإن عدد الحدود هو 2! = 1 2 = 2 ،

لعدد Δ 3 عدد المصطلحات هو 3! = 1 2 3 = 6.

ويترتب على ذلك أنه بالنسبة لمحدد الرتبة الرابعة ، فإن عدد المصطلحات هو 4! = 1 2 3 4 = 24 ، مما يعني أن حساب مثل هذا المحدد شاق للغاية ، ناهيك عن محددات الترتيب الأعلى. بالنظر إلى ذلك ، يحاولون تقليل حساب محددات الطلبات الكبيرة لحساب محددات الطلبات الثانية أو الثالثة.

§ 5. حساب محددات الطلبات الكبيرة

دعونا نقدم عددا من المفاهيم.

دعنا نعطي مصفوفة مربعة ا نالترتيب الثالث:

أ =

تحت السن القانوني معنصر ij أ ij يسمى المحدد ( ص- 1) الترتيب الذي تم الحصول عليه من المصفوفة لكنالإضراب أنا-الخط و يالعمود.

على سبيل المثال ، العنصر الثانوي أ 12 مصفوفة من الدرجة الثالثة ستكون:

الجمع الجبري لكنعنصر ij أ ij هو صغرها ، مأخوذ بعلامة (1) أنا + ي:

لكن ij = (−1) أنا + جماي جاي

بعبارات أخرى، لكن ij = م ij إذا أنا+يرقم زوجي،

لكن ij = - م ij إذا أنا+يعدد فردي.

مثال. أوجد المكملات الجبرية لعناصر الصف الثاني من المصفوفة

المحلول.

بمساعدة المكملات الجبرية ، يمكن للمرء حساب محددات الطلبات الكبيرة ، بناءً على نظرية لابلاس.

نظرية لابلاس. محدد المصفوفة المربعة يساوي مجموع حاصل ضرب عناصر أي من صفوفها (أعمدتها) ومكملاتها الجبرية:

– التحلل على الخط الأول ؛

( هو التوسع في العمود j).

مثال. احسب محدد المصفوفة التحلل في السطر الأول.

المحلول.

وبالتالي ، يمكن اختزال محدد أي طلب إلى حساب عدة محددات لترتيب أصغر. من الواضح أنه بالنسبة للتوسيع ، من الملائم اختيار صف أو عمود يحتوي على أكبر عدد ممكن من الأصفار.

لنفكر في مثال آخر.

مثال. احسب محدد مصفوفة مثلثة

المحلول.

فهمت محدد المصفوفة المثلثية يساوي حاصل ضرب عناصر قطرها الرئيسي .

هذا الاستنتاج المهم يجعل من السهل حساب محدد أي مصفوفة مثلثة. هذا أكثر فائدة لأنه ، إذا لزم الأمر ، يمكن اختزال أي محدد إلى شكل مثلث. في هذه الحالة ، يتم استخدام بعض خصائص المحددات.

طلب

مفهوم المحدد صالترتيب ال بشكل عام.

بشكل عام ، يمكن للمرء أن يعطي تعريفًا صارمًا لمُحدد المصفوفة صمن أجل ذلك ، من الضروري تقديم عدد من المفاهيم.

التقليبالأرقام 1 ، 2 ، ... ، نأي ترتيب لهذه الأرقام بترتيب معين يسمى. في الجبر الابتدائي ، ثبت أن عدد جميع التباديل التي يمكن تشكيلها من نالأرقام هي 12 ... n = ن!. على سبيل المثال ، ثلاثة أرقام 1 ، 2 ، 3 يمكن أن تشكل 3! = 6 تباديل: 123 ، 132 ، 312 ، 321 ، 231 ، 213.

يقولون ذلك في تقليب معين للعدد أناو يتشكل انعكاس(اضطراب) إذا أنا> ي، لكن أنايقف في هذا التقليب من قبل ي، أي إذا كان الرقم الأكبر على يسار الرقم الأصغر.

التقليب يسمى حتى(أو الفردية) إذا كان العدد الإجمالي للانعكاسات زوجيًا (فرديًا) ، على التوالي.

عملية ينتقل بواسطتها المرء من تبديل إلى آخر ، وتتألف من نفس نالأرقام تسمى الاستبدال نالدرجة ال.

الاستبدال الذي يحول تبديلًا إلى آخر مكتوب في سطرين بين قوسين مشتركين ، والأرقام التي تشغل نفس الأماكن في التباديل قيد الدراسة تسمى متطابقة ويتم كتابتها واحدة تحت الأخرى. على سبيل المثال ، الرمز

يشير إلى تبديل حيث 3 يذهب إلى 4 ، 1 إلى 2 ، 2 إلى 1 ، 4 إلى 3. يسمى التقليب زوجي (أو فردي) إذا كان العدد الإجمالي للانعكاسات في كلا صفوف الاستبدال زوجي (فردي). أي استبدال نيمكن كتابة الدرجة

أولئك. مع الترتيب الطبيعي للأرقام في السطر العلوي.

دعونا نحصل على مصفوفة مربعة للترتيب ن

ضع في اعتبارك جميع المنتجات الممكنة نعناصر هذه المصفوفة ، مأخوذة واحدًا واحدًا فقط من كل صف وكل عمود ، أي أعمال النموذج:

أين المؤشرات ف 1 , ف 2 ,..., ف نتشكل بعض التقليب في الأرقام
1, 2,..., ن. عدد هذه المنتجات يساوي عدد التباديل المختلفة من نالشخصيات ، أي يساوي ن!. علامة العمل ، يساوي (-1) ف، أين فهو عدد الانقلابات في التقليب للمؤشرات الثانية للعناصر.

محدد نالترتيبيسمى المجموع الجبري لجميع المنتجات الممكنة أكثر نعناصر المصفوفة ، مأخوذة واحدًا وواحدًا فقط من كل صف وكل عمود ، أي أعمال النموذج: . في نفس الوقت ، علامة العمل يساوي (-1) ف، أين فهو عدد الانقلابات في التقليب للمؤشرات الثانية للعناصر.

الجبر الخطي

ضع في اعتبارك مصفوفة A بالحجم.

أ =
حدد k الصفوف و k الأعمدة فيه (
).

التعريف 26:تحت السن القانونيالترتيب k للمصفوفة A هو محدد المصفوفة المربعة ، والتي يتم الحصول عليها من المصفوفة المعطاة بالاختيار فيها.

صفوف ك وأعمدة ك.

التعريف 27:مرتبةتسمى المصفوفة الأكبر من الترتيب غير الصفري لأبنائها الصغار ، r (A).

التعريف 28:يسمى القاصر الذي تماثل رتبته ثانوي أساسي.

بيان - تصريح:

1. يتم التعبير عن الرتبة بعدد صحيح. (
)

2.r = 0 ،
عندما يكون A صفرًا.

التحولات الأولية للمصفوفات.

تشمل التحولات الأولية للمصفوفات ما يلي:

1) ضرب جميع عناصر أي صف (عمود) من المصفوفة بنفس العدد.

2) إضافة عناصر أي صف (عمود) من المصفوفة للعناصر المقابلة لصف آخر (عمود) مضروبة في نفس العدد ؛

3) تبديل صفوف (أعمدة) المصفوفة ؛

4) تجاهل الصف الصفري (العمود) ؛

5) استبدال صفوف المصفوفة بالأعمدة المقابلة.

التعريف 29:تسمى المصفوفات التي تم الحصول عليها من بعضها البعض ، في إطار التحولات الأولية ، المصفوفات المكافئة ، والتي يُشار إليها بـ "~"

الخاصية الرئيسية للمصفوفات المكافئة: رتب المصفوفات المتكافئة متساوية.

المثال 18:احسب r (A)،

المحلول:اضرب السطر الأول خطوة في (-4) (- 2)

(-7) ثم نضيفها إلى الصفوف الثاني والثالث والرابع على التوالي.

تبديل الخطين الثاني والرابع
اضرب الصف الثاني في (-2) وأضف الصف الرابع ؛ أضف الصفين الثاني والثالث.

أضف الصفين الثالث والرابع.

~
تجاهل السطر الفارغ

~
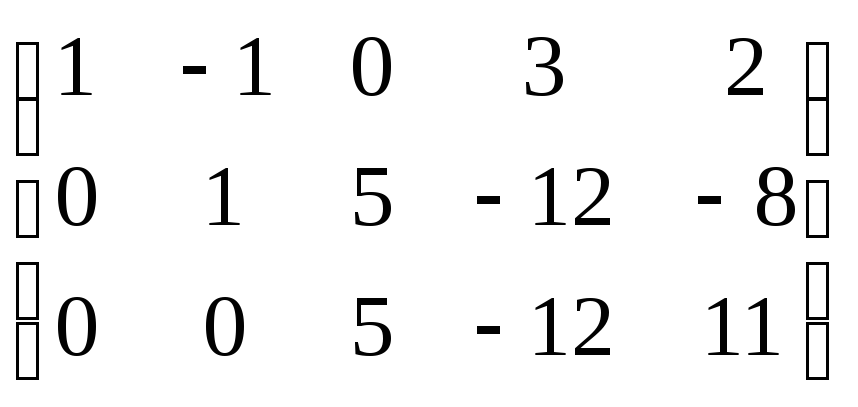ص (أ) = 3
رتبة المصفوفة الأصلية

يساوي ثلاثة.

التعريف 30:نسمي المصفوفة A مصفوفة الخطوة إذا كانت جميع عناصر القطر الرئيسي 0 ، والعناصر الموجودة أسفل القطر الرئيسي هي صفر.

جملة او حكم على:

1) رتبة مصفوفة الخطوة تساوي عدد صفوفها ؛

2) يمكن اختزال أي مصفوفة إلى شكل تدريجي بمساعدة التحولات الأولية.

المثال 19:في أي قيم  مصفوفة
رتبته تساوي واحد؟

المحلول:الرتبة تساوي واحدًا إذا كان محدد الدرجة الثانية يساوي صفرًا ، أي

§6. نظم المعادلات الخطية ذات الشكل العام.

عرض النظام
--- (9) يسمى نظام الشكل العام.

التعريف 31:يقال أن نظامين متكافئان (مكافئان) إذا كان كل حل للنظام الأول هو الحل الثاني والعكس صحيح.

في النظام (1) المصفوفة A =
ستسمى المصفوفة الرئيسية للنظام ، و =
نظام المصفوفة الموسعة

نظرية.كرونيكر كابيلي

لكي يكون النظام (9) متسقًا ، من الضروري والكافي أن تكون رتبة المصفوفة الرئيسية للنظام مساوية لرتبة المصفوفة الممتدة ، أي r (A) = r ( )

نظرية 1.إذا كانت رتبة مصفوفة نظام مشترك مساوية لعدد المجهول ، فإن النظام لديه حل فريد.

نظرية 2.إذا كانت رتبة مصفوفة نظام مشترك أقل من عدد المجهولين ، فإن النظام لديه عدد لا حصر له من الحلول.

قاعدة حل نظام تعسفي من المعادلات الخطية:

1) ابحث عن رتب المصفوفات الرئيسية والممتدة للنظام. اذا كان
، فإن النظام غير متسق.

2) إذا
= r ، إذن النظام متوافق. العثور على بعض الأساسيات من أجل ص. سوف نسمي القاصر الأساسي ، على أساسه تم تحديد رتبة المصفوفة.

تسمى المجهولات التي تم تضمين معاملاتها في الأساسي الثانوي الرئيسي (الأساسي) واليسار على اليسار ، بينما تسمى المجهولات المتبقية مجانًا ويتم نقلها إلى الجانب الأيمن من المعادلة.

3) ابحث عن تعبيرات المجهول الأساسي من حيث المجاهيل الحرة. يتم الحصول على الحل العام للنظام.

المثال 20:تحقق من النظام ، وفي حالة توافقه ، ابحث عن حل فريد أو عام