Inverzna matrica i njena svojstva. inverzna matrica

Pronalaženje inverzne matrice- problem koji se najčešće rješava na dva načina:

• metoda algebarskih sabiranja, u kojoj je potrebno pronaći determinante i transponirati matrice;
• metoda eliminacije nepoznati gaus, u kojem je potrebno izvršiti elementarne transformacije matrica (dodavanje redova, množenje redova istim brojem, itd.).

Za one koji su posebno znatiželjni, postoje i druge metode, na primjer, metoda linearnih transformacija. U ovoj lekciji ćemo analizirati tri navedene metode i algoritme za pronalaženje inverzne matrice ovim metodama.

inverzna matrica ALI, takva matrica se zove

ALI
. (1)

inverzna matrica , koje je potrebno pronaći za datu kvadratnu matricu ALI, takva matrica se zove

proizvod kojim su matrice ALI desno je matrica identiteta, tj.
. (1)

Matrica identiteta je dijagonalna matrica u kojoj su svi dijagonalni unosi jednaki jedan.

Teorema.Za svaku nesingularnu (nesingularnu, nesingularnu) kvadratnu matricu može se pronaći inverzna matrica, i štaviše, samo jedna. Za specijalnu (degenerisanu, singularnu) kvadratnu matricu, inverzna matrica ne postoji.

Kvadratna matrica se zove nespecijalan(ili nedegenerisan, ne-jednina) ako njegova determinanta nije jednaka nuli, i poseban(ili degenerisati, jednina) ako je njegova determinanta nula.

inverzna matrica može se naći samo za kvadratnu matricu. Naravno, inverzna matrica će također biti kvadratna i istog reda kao i data matrica. Matrica za koju se može naći inverzna matrica naziva se invertibilna matrica.

Za inverzna matrica postoji prikladna analogija s recipročnim brojem. Za svaki broj a, koji nije jednak nuli, postoji broj b da je posao a i b jednako jedan: ab= 1 . Broj b naziva se recipročna vrednost broja b. Na primjer, za broj 7, inverzni je broj 1/7, jer je 7*1/7=1.

Pronalaženje inverzne matrice metodom algebarskih sabiranja (matrica sindikata)

Za nesingularnu kvadratnu matricu ALI inverz je matrica

gdje je determinanta matrice ALI, a je matrica pridružena matrici ALI.

Povezano sa kvadratnom matricom A je matrica istog reda čiji su elementi algebarski dodaci odgovarajući elementi determinante matrice transponovane u odnosu na matricu A. Dakle, ako

onda

i

Algoritam za pronalaženje inverzne matrice metodom algebarskih sabiranja

1. Pronađite determinantu ove matrice A. Ako je determinanta jednaka nuli, pronalaženje inverzne matrice prestaje, jer je matrica degenerirana i za nju ne postoji inverzna.

2. Pronađite matricu transponovanu u odnosu na A.

3. Izračunajte elemente matrice unije kao algebarske komplemente marite pronađene u koraku 2.

4. Primijenite formulu (2): pomnožite broj, inverzna determinanta matrice A, na matricu ujedinjenja koja se nalazi u koraku 4.

5. Provjerite rezultat dobiven u koraku 4 množenjem ovu matricu A na inverznu matricu. Ako je proizvod ovih matrica jednak matrici identiteta, tada je inverzna matrica pronađena ispravno. U suprotnom pokrenite postupak rješenja ponovo.

Primjer 1 Za matricu

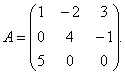
pronađite inverznu matricu.

Rješenje. Da biste pronašli inverznu matricu, potrebno je pronaći determinantu matrice ALI. Po pravilu trouglova nalazimo:

Dakle, matrica ALI je nesingularan (nedegenerisan, nesingularan) i za njega postoji inverz.

Nađimo matricu pridruženu datoj matrici ALI.

Nađimo matricu transponovanu u odnosu na matricu A:

Izračunavamo elemente matrice unije kao algebarske komplemente matrice transponovane u odnosu na matricu A:

Dakle, matrica je konjugirana sa matricom A, ima oblik

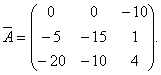
Komentar. Redoslijed izračunavanja elemenata i transpozicije matrice može biti različit. Prvo se mogu izračunati algebarski komplementi matrice A, a zatim transponirati matricu algebarskih komplementa. Rezultat bi trebali biti isti elementi matrice sindikata.

Primjenom formule (2) nalazimo matricu inverznu matrici ALI:

Pronalaženje inverzne matrice Gaussovom eliminacijom nepoznanica

Prvi korak za pronalaženje inverzne matrice Gaussovom eliminacijom je pripisivanje matrici A matrica identiteta istog reda, odvajajući ih okomitom trakom. Dobijamo dualnu matricu. Pomnožite oba dijela ove matrice sa , onda ćemo dobiti

,

Algoritam za pronalaženje inverzne matrice Gaussovom eliminacijom nepoznatih

1. Na matricu A dodijeliti matricu identiteta istog reda.

2. Transformirajte rezultirajuću dualnu matricu tako da se matrica identiteta dobije u njenom lijevom dijelu, tada će se inverzna matrica automatski dobiti u desnom dijelu umjesto matrice identiteta. Matrix A na lijevoj strani se pretvara u matricu identiteta pomoću elementarne transformacije matrice.

2. Ako je u procesu transformacije matrice A u matricu identiteta u bilo kojem retku ili u bilo kojoj koloni bit će samo nule, tada je determinanta matrice jednaka nuli i, prema tome, matrica Aće biti degenerisan i nema inverznu matricu. U ovom slučaju, daljnje pronalaženje inverzne matrice prestaje.

Primjer 2 Za matricu

pronađite inverznu matricu.

a mi ćemo ga transformirati tako da se matrica identiteta dobije na lijevoj strani. Započnimo transformaciju.

Pomnožite prvi red lijeve i desne matrice sa (-3) i dodajte ga drugom redu, a zatim pomnožite prvi red sa (-4) i dodajte ga trećem redu, onda ćemo dobiti

.

Da se izbjegne, ako je moguće razlomci brojeva u kasnijim transformacijama, prvo ćemo kreirati jedinicu u drugom redu na lijevoj strani dualne matrice. Da biste to učinili, pomnožite drugi red sa 2 i oduzmite treći red od njega, a zatim dobijemo

.

Dodajmo prvi red drugom, a zatim pomnožimo drugi red sa (-9) i dodajmo ga trećem redu. Onda dobijamo

.

Zatim podijelite treći red sa 8

.

Pomnožite treći red sa 2 i dodajte ga drugom redu. Ispada:

.

Zamenivši mesta drugog i trećeg reda, konačno dobijamo:

.

Vidimo da je matrica identiteta dobijena na lijevoj strani, dakle, inverzna matrica se dobija na desnoj strani. Na ovaj način:

.

Ispravnost proračuna možete provjeriti množenjem originalne matrice pronađenom inverznom matricom:

Rezultat bi trebao biti inverzna matrica.

Primjer 3 Za matricu

pronađite inverznu matricu.

Rješenje. Sastavljanje dualne matrice

i mi ćemo ga transformisati.

Pomnožimo prvi red sa 3, a drugi sa 2, i oduzmemo od drugog, a zatim prvi red pomnožimo sa 5, a treći sa 2 i oduzmemo od trećeg reda, onda dobijemo

.

Prvi red pomnožimo sa 2 i dodamo ga drugom, a zatim oduzmemo drugi od trećeg reda i dobijemo

.

Vidimo da su u trećem redu na lijevoj strani svi elementi ispali jednaki nuli. Dakle, matrica je degenerisana i nema inverznu matricu. Zaustavljamo dalje pronalaženje obrnute marije.

Ova tema je jedna od najomraženijih među studentima. Još gore, vjerovatno, samo odrednice.

Trik je u tome što nas sam koncept inverznog elementa (a sada ne govorim samo o matricama) upućuje na operaciju množenja. Čak i unutra školski program razmatra se množenje komplikovana operacija, a množenje matrica je generalno posebna tema, kojoj imam cijeli pasus i video tutorijal posvećen tome.

Danas nećemo ulaziti u detalje matričnih proračuna. Samo zapamtite: kako se označavaju matrice, kako se množe i šta iz toga slijedi.

Pregled: Množenje matrica

Prije svega, dogovorimo se oko notacije. Matrica $A$ veličine $\left[ m\times n \right]$ je jednostavno tabela brojeva sa tačno $m$ redova i $n$ kolona:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrica) \desno])_(n)\]

Da ne biste slučajno pomešali redove i kolone na mestima (verujte mi, na ispitu možete da pobrkate jednu sa dvojkom - šta da kažemo o nekim linijama tamo), samo pogledajte sliku:

Određivanje indeksa za ćelije matriksa

Šta se dešava? Ako postavimo standardni koordinatni sistem $OXY$ u lijevo gornji ugao i usmjerite osi tako da pokrivaju cijelu matricu, tada svaka ćelija ove matrice može biti jedinstveno povezana sa koordinatama $\left(x;y \right)$ - to će biti broj reda i broj stupca.

Zašto je koordinatni sistem postavljen tačno u gornjem levom uglu? Da, jer odatle počinjemo čitati bilo kakve tekstove. Vrlo je lako zapamtiti.

Zašto je osa $x$ usmjerena prema dolje, a ne udesno? Opet, jednostavno je: uzmite standardni koordinatni sistem ($x$ osa ide udesno, $y$ osa ide gore) i rotirajte ga tako da obuhvata matricu. Ovo je rotacija za 90 stepeni u smeru kazaljke na satu - njen rezultat vidimo na slici.

Općenito, shvatili smo kako odrediti indekse matričnih elemenata. Sada se pozabavimo množenjem.

Definicija. Matrice $A=\left[ m\times n \right]$ i $B=\left[ n\times k \right]$, kada se broj kolona u prvoj poklapa sa brojem redova u drugoj, su naziva konzistentan.

To je tim redosledom. Može se biti dvosmislen i reći da matrice $A$ i $B$ formiraju uređeni par $\left(A;B \right)$: ako su konzistentne u ovom redoslijedu, onda uopće nije potrebno da $B $ i $A$, oni. par $\left(B;A \right)$ je takođe konzistentan.

Samo konzistentne matrice se mogu množiti.

Definicija. Proizvod konzistentnih matrica $A=\left[ m\times n \right]$ i $B=\left[ n\times k \right]$ je nova matrica $C=\left[ m\times k \right ]$, čiji se elementi $((c)_(ij))$ izračunavaju po formuli:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Drugim riječima: da biste dobili element $((c)_(ij))$ matrice $C=A\cdot B$, trebate uzeti $i$-red prve matrice, $j$ -ti stupac druge matrice, a zatim pomnožiti u parovima elemente iz ovog reda i kolone. Zbrojite rezultate.

Da, to je oštra definicija. Iz toga odmah slijedi nekoliko činjenica:

1. Množenje matrice je, općenito govoreći, nekomutativno: $A\cdot B\ne B\cdot A$;
2. Međutim, množenje je asocijativno: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
3. Čak i distributivni: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. I opet distributivno: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Distributivnost množenja je morala biti opisana odvojeno za levi i desni zbir množenja samo zbog nekomutativnosti operacije množenja.

Ako se ipak ispostavi da je $A\cdot B=B\cdot A$, takve matrice se nazivaju permutabilne.

Među svim matricama koje se tamo nečim množe, postoje posebne - one koje, kada se pomnože bilo kojom matricom $A$, opet daju $A$:

Definicija. Matrica $E$ se naziva identitetom ako je $A\cdot E=A$ ili $E\cdot A=A$. U slučaju kvadratne matrice $A$ možemo napisati:

Matrica identiteta je čest gost u rješavanju matrične jednačine. I općenito čest gost u svijetu matrica. :)

I zbog ovog $E$, neko je smislio svu igru ​​koja će biti sledeća.

Šta je inverzna matrica

Budući da je množenje matrice vrlo dugotrajna operacija (morate pomnožiti gomilu redaka i stupaca), koncept inverzne matrice također nije najtrivijalniji. I treba neko objašnjenje.

Ključna definicija

Pa, vrijeme je da saznamo istinu.

Definicija. Matrica $B$ se zove inverzna matrici $A$ if

Inverzna matrica je označena sa $((A)^(-1))$ (ne treba je brkati sa stepenom!), tako da se definicija može prepisati ovako:

Čini se da je sve krajnje jednostavno i jasno. Ali kada analiziramo takvu definiciju, odmah se postavlja nekoliko pitanja:

1. Da li inverzna matrica uvijek postoji? I ako ne uvijek, kako onda odrediti: kada postoji, a kada ne?
2. A ko je rekao da je takva matrica upravo jedna? Šta ako za neku originalnu matricu $A$ postoji čitava gomila inverza?
3. Kako izgledaju svi ti "preokreti"? I kako ih zapravo brojite?

Što se tiče algoritama proračuna - o tome ćemo govoriti malo kasnije. Ali na ostala pitanja ćemo odmah odgovoriti. Složimo ih u obliku zasebnih tvrdnji-lema.

Osnovna svojstva

Počnimo s tim kako bi matrica $A$ trebala izgledati da bi imala $((A)^(-1))$. Sada ćemo se pobrinuti da obje ove matrice moraju biti kvadratne i iste veličine: $\left[ n\times n \right]$.

Lema 1. Date matricu $A$ i njen inverzni $((A)^(-1))$. Tada su obje ove matrice kvadratne i imaju isti red $n$.

Dokaz. Sve je jednostavno. Neka je matrica $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Pošto proizvod $A\cdot ((A)^(-1))=E$ postoji po definiciji, matrice $A$ i $((A)^(-1))$ su konzistentne u tom redosledu:

\[\begin(poravnati) & \left[ m\puta n \desno]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( poravnati)\]

Ovo je direktna posljedica algoritma množenja matrice: koeficijenti $n$ i $a$ su "tranzitni" i moraju biti jednaki.

Istovremeno je definirano i obrnuto množenje: $((A)^(-1))\cdot A=E$, pa su matrice $((A)^(-1))$ i $A$ također dosljedan ovim redoslijedom:

\[\begin(poravnati) & \left[ a\puta b \desno]\cdot \left[ m\times n \right]=\left[ a\puts n \right] \\ & b=m \end( poravnati)\]

Dakle, bez gubitka opštosti, možemo pretpostaviti da je $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Međutim, prema definiciji $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, tako da su dimenzije matrica potpuno iste:

\[\početak(poravnati) & \lijevo[ m\puta n \desno]=\lijevo[ n\puta m \desno] \\ & m=n \end(poravnati)\]

Dakle, ispada da su sve tri matrice - $A$, $((A)^(-1))$ i $E$ - kvadratna veličina$\lijevo[ n\puta n \desno]$. Lema je dokazana.

Pa, to je već dobro. Vidimo da su samo kvadratne matrice invertibilne. Sada se uvjerimo da je inverzna matrica uvijek ista.

Lema 2. Date matricu $A$ i njen inverzni $((A)^(-1))$. Tada je ova inverzna matrica jedinstvena.

Dokaz. Počnimo od suprotnog: neka matrica $A$ ima najmanje dvije instance inverza — $B$ i $C$. Tada su, prema definiciji, tačne sljedeće jednakosti:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(poravnati)\]

Iz leme 1 zaključujemo da su sve četiri matrice $A$, $B$, $C$ i $E$ kvadrati istog reda: $\left[ n\times n \right]$. Dakle, proizvod je definiran:

Pošto je množenje matrice asocijativno (ali ne i komutativno!), možemo napisati:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \desno)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end(poravnati)\]

Samo primljeno moguća varijanta: dvije instance inverzne matrice su jednake. Lema je dokazana.

Gornje rezonovanje gotovo doslovno ponavlja dokaz jedinstvenosti inverznog elementa za sve realni brojevi$b\ne 0$. Jedini značajan dodatak je uzimanje u obzir dimenzije matrica.

Međutim, još uvijek ne znamo ništa o tome da li ih ima kvadratna matrica je reverzibilan. Ovdje nam u pomoć priskače determinanta - ovo je ključna karakteristika za sve kvadratne matrice.

Lema 3. Zadana je matrica $A$. Ako postoji matrica $((A)^(-1))$ njoj inverzna, tada je determinanta originalne matrice različita od nula:

\[\lijevo| A \right|\ne 0\]

Dokaz. Već znamo da su $A$ i $((A)^(-1))$ kvadratne matrice veličine $\left[ n\puta n \right]$. Stoga je za svaki od njih moguće izračunati determinantu: $\left| A \right|$ i $\left| ((A)^(-1)) \right|$. Međutim, determinanta proizvoda jednak je proizvodu odrednice:

\[\lijevo| A\cdot B \desno|=\lijevo| A \desno|\cdot \levo| B \right|\Rightarrow \levo| A\cdot ((A)^(-1)) \desno|=\lijevo| A \desno|\cdot \levo| ((A)^(-1)) \desno|\]

Ali prema definiciji $A\cdot ((A)^(-1))=E$, a determinanta $E$ je uvijek jednaka 1, tako da

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \lijevo| A\cdot ((A)^(-1)) \desno|=\lijevo| E\desno|; \\ & \lijevo| A \desno|\cdot \levo| ((A)^(-1)) \right|=1. \\ \end(poravnati)\]

Proizvod dva broja jednak je jedan samo ako je svaki od ovih brojeva različit od nule:

\[\lijevo| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Dakle, ispada da je $\left| A \right|\ne 0$. Lema je dokazana.

Zapravo, ovaj zahtjev je sasvim logičan. Sada ćemo analizirati algoritam za pronalaženje inverzne matrice - i biće potpuno jasno zašto, u principu, ne može postojati inverzna matrica sa nultom determinantom.

Ali prvo, hajde da formulišemo "pomoćnu" definiciju:

Definicija. Degenerisana matrica je kvadratna matrica veličine $\left[ n\puts n \right]$ čija je determinanta nula.

Dakle, možemo tvrditi da je bilo koja invertibilna matrica nedegenerirana.

Kako pronaći inverznu matricu

Sada ćemo razmotriti univerzalni algoritam za pronalaženje inverznih matrica. Generalno, postoje dva općeprihvaćena algoritma, a danas ćemo razmotriti i drugi.

Ova koja će se sada razmatrati je vrlo efikasna za matrice veličine $\left[ 2\times 2 \right]$ i - dijelom - veličine $\left[ 3\times 3 \right]$. Ali počevši od veličine $\left[ 4\times 4 \right]$ bolje je ne koristiti je. Zašto - sada ćete sve razumeti.

Algebarski dodaci

Spremiti se. Sada će biti bola. Ne, ne brini: prelepa medicinska sestra u suknji, čarapama sa čipkom ne dolazi do tebe i neće ti dati injekciju u zadnjicu. Sve je mnogo prozaičnije: algebarski dodaci i Njeno Veličanstvo "Union Matrix" dolaze vam.

Počnimo s glavnim. Neka postoji kvadratna matrica veličine $A=\left[ n\times n \right]$ čiji se elementi nazivaju $((a)_(ij))$. Tada se za svaki takav element može definirati algebarski komplement:

Definicija. Algebarski komplement $((A)_(ij))$ elementu $((a)_(ij))$ u $i$-tom redu i $j$-tom stupcu matrice $A=\left [ n \times n \right]$ je konstrukcija forme

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Gdje je $M_(ij)^(*)$ determinanta matrice dobijene iz originalnog $A$ brisanjem istog $i$-tog reda i $j$-te kolone.

Opet. Algebarski komplement matričnom elementu sa koordinatama $\left(i;j \right)$ označava se kao $((A)_(ij))$ i izračunava se prema šemi:

1. Prvo, brišemo $i$-red i $j$-tu kolonu iz originalne matrice. Dobijamo novu kvadratnu matricu i njenu determinantu označavamo sa $M_(ij)^(*)$.
2. Zatim pomnožimo ovu determinantu sa $((\left(-1 \right))^(i+j))$ - u početku ovaj izraz može izgledati zapanjujuće, ali u stvari samo saznajemo znak ispred $ M_(ij)^(*) $.
3. Računamo - dobijamo određeni broj. One. algebarsko sabiranje je samo broj, a ne neka nova matrica i tako dalje.

Sama matrica $M_(ij)^(*)$ naziva se komplementarnim minorom elementu $((a)_(ij))$. I u tom smislu, gornja definicija algebarskog komplementa je poseban slučaj više složena definicija- šta smo razmatrali u lekciji o odrednici.

Važna napomena. Zapravo, u matematici "odraslih" algebarski sabirci se definiraju na sljedeći način:

1. Uzimamo $k$ redova i $k$ kolona u kvadratnoj matrici. Na njihovom preseku dobijamo matricu veličine $\left[ k\times k \right]$ — njena determinanta se naziva minor reda $k$ i označava se sa $((M)_(k))$.
2. Zatim precrtavamo ove "odabrane" $k$ redove i $k$ kolone. Opet, dobijamo kvadratnu matricu - njena determinanta se zove komplementarni minor i označava se sa $M_(k)^(*)$.
3. Pomnožite $M_(k)^(*)$ sa $((\left(-1 \right))^(t))$, gdje je $t$ (pažnja!) zbir brojeva svih odabranih redova i kolone. Ovo će biti algebarski dodatak.

Pogledajte treći korak: zapravo postoji zbir termina od $2k$! Druga stvar je da za $k=1$ dobijamo samo 2 člana - to će biti isti $i+j$ - "koordinate" elementa $((a)_(ij))$, za koji smo tražeći algebarski komplement.

Zato danas koristimo malo pojednostavljenu definiciju. Ali kako ćemo kasnije vidjeti, to će biti više nego dovoljno. Mnogo važnije je sledeće:

Definicija. Matrica unije $S$ na kvadratnu matricu $A=\left[ n\times n \right]$ je nova matrica veličine $\left[ n\times n \right]$, koja se dobija iz $A$ zamjenom $(( a)_(ij))$ algebarskim komplementima $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrica) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrica) \desno]\]

Prva pomisao koja se nameće u trenutku kada se shvati ova definicija je „ovo je koliko ukupno morate izbrojati!“ Opustite se: morate računati, ali ne toliko. :)

Pa, sve je ovo jako lepo, ali zašto je potrebno? Ali zašto.

Glavna teorema

Vratimo se malo unazad. Zapamtite, Lema 3 kaže da je invertibilna matrica $A$ uvijek nesingularna (to jest, njena determinanta nije nula: $\left| A \right|\ne 0$).

Dakle, i obrnuto je tačno: ako matrica $A$ nije degenerisana, onda je uvek invertibilna. A postoji čak i šema pretraživanja $((A)^(-1))$. Provjeri:

Teorema inverzne matrice. Neka je data kvadratna matrica $A=\left[ n\times n \right]$, a njena determinanta je različita od nule: $\left| A \right|\ne 0$. Tada inverzna matrica $((A)^(-1))$ postoji i izračunava se po formuli:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

A sada - sve isto, ali čitljivim rukopisom. Da biste pronašli inverznu matricu, trebate:

1. Izračunajte determinantu $\left| \right|$ i uvjerite se da nije nula.
2. Sastavite matricu unije $S$, tj. izbroj 100500 algebarskih dodataka $((A)_(ij))$ i stavite ih na mjesto $((a)_(ij))$.
3. Transponirajte ovu matricu $S$ i zatim je pomnožite nekim brojem $q=(1)/(\left| A \right|)\;$.

I to je to! Pronađena je inverzna matrica $((A)^(-1))$. Pogledajmo primjere:

\[\left[ \begin(matrica) 3 & 1 \\ 5 & 2 \\\end(matrica) \right]\]

Rješenje. Hajde da proverimo reverzibilnost. Izračunajmo determinantu:

\[\lijevo| A \desno|=\lijevo| \begin(matrica) 3 & 1 \\ 5 & 2 \\\end(matrica) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Odrednica se razlikuje od nule. Dakle, matrica je invertibilna. Kreirajmo matricu sindikata:

Izračunajmo algebarske sabirke:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2\desno|=2; \\ & ((A)_(12))=((\lijevo(-1 \desno))^(1+2))\cdot \lijevo| 5\desno|=-5; \\ & ((A)_(21))=((\lijevo(-1 \desno))^(2+1))\cdot \lijevo| 1 \right|=-1; \\ & ((A)_(22))=((\lijevo(-1 \desno))^(2+2))\cdot \lijevo| 3\desno|=3. \\ \end(poravnati)\]

Obratite pažnju: determinante |2|, |5|, |1| i |3| su determinante matrica veličine $\left[ 1\puts 1 \right]$, a ne moduli. One. ako su determinante bile negativni brojevi, nije potrebno ukloniti "minus".

Ukupno, naša sindikalna matrica izgleda ovako:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(niz)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(niz) \desno])^(T))=\left[ \begin (niz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(niz) \desno]\]

OK, sve je gotovo. Problem riješen.

Odgovori. $\left[ \begin(niz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(niz) \right]$

Zadatak. Pronađite inverznu matricu:

\[\left[ \begin(niz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(niz) \desno] \]

Rješenje. Opet, uzimamo u obzir determinantu:

\[\početi(poravnati) & \lijevo| \begin(niz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(niz) \right|=\begin(matrica ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matrica)= \ \ & =\left(2+1+0 \desno)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Determinanta se razlikuje od nule - matrica je inverzibilna. Ali sada će biti najsitniji: morate izbrojati čak 9 (devet, prokletstvo!) algebarskih sabiraka. I svaki od njih će sadržavati kvalifikator $\left[ 2\times 2 \right]$. leteo:

\[\begin(matrica) ((A)_(11))=((\left(-1 \desno))^(1+1))\cdot \left| \begin(matrica) 2 & -1 \\ 0 & 1 \\\end(matrica) \right|=2; \\ ((A)_(12))=((\lijevo(-1 \desno))^(1+2))\cdot \lijevo| \begin(matrix) 0 & -1 \\ 1 & 1 \\\end(matrix) \right|=-1; \\ ((A)_(13))=((\lijevo(-1 \desno))^(1+3))\cdot \lijevo| \begin(matrica) 0 & 2 \\ 1 & 0 \\\end(matrica) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \desno))^(3+3))\cdot \left| \begin(matrica) 1 & -1 \\ 0 & 2 \\\end(matrica) \right|=2; \\ \end(matrica)\]

Ukratko, matrica sindikata će izgledati ovako:

Dakle, inverzna matrica će biti:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrica) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrica) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\kraj (niz) \desno]\]

Pa, to je sve. Evo odgovora.

Odgovori. $\left[ \begin(niz)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(niz) \right ]$

Kao što vidite, na kraju svakog primjera izvršili smo provjeru. S tim u vezi, važna napomena:

Ne budite lijeni provjeriti. Pomnožite originalnu matricu sa pronađenim inverzom - trebali biste dobiti $E$.

Mnogo je lakše i brže izvršiti ovu provjeru nego tražiti grešku u daljim proračunima, kada, na primjer, rješavate matričnu jednačinu.

Alternativni način

Kao što sam rekao, teorema inverzne matrice dobro radi za veličine $\left[ 2\times 2 \right]$ i $\left[ 3\times 3 \right]$ (u poslednji slučaj- nije više tako "savršeno"), ali za matrice velikih dimenzija počinje tuga.

Ali ne brinite: postoji alternativni algoritam koji se može koristiti da se mirno pronađe inverz čak i za matricu $\left[ 10\puts 10 \right]$. Ali, kao što je često slučaj, da bismo razmotrili ovaj algoritam, potrebno nam je malo teorijske pozadine.

Elementarne transformacije

Među različitim transformacijama matrice postoji nekoliko posebnih - nazivaju se elementarnim. Postoje tačno tri takve transformacije:

1. Množenje. Možete uzeti $i$-ti red (kolona) i pomnožiti ga bilo kojim brojem $k\ne 0$;
2. Dodatak. Dodajte u $i$-ti red (kolona) bilo koji drugi $j$-ti red (kolona) pomnožen sa bilo kojim brojem $k\ne 0$ (naravno, $k=0$ je također moguće, ali u čemu je poenta od toga? ?Ništa se ipak neće promijeniti).
3. Permutacija. Uzmite $i$-ti i $j$-ti red (kolone) i zamijenite ih.

Zašto se ove transformacije nazivaju elementarnim (za velike matrice ne izgledaju tako elementarne) i zašto ih ima samo tri - ova pitanja su izvan okvira današnje lekcije. Stoga, nećemo ulaziti u detalje.

Još jedna stvar je važna: sve ove perverzije moramo izvesti na pridruženoj matrici. Da, da, dobro ste čuli. Sada će biti još jedna definicija - posljednja u današnjoj lekciji.

Attached Matrix

Sigurno ste u školi rješavali sisteme jednačina metodom sabiranja. E, eto, oduzmite drugu od jedne linije, pomnožite neki red brojem - to je sve.

Dakle: sada će sve biti isto, ali već „na odrasli način“. Spreman?

Definicija. Neka su data matrica $A=\left[ n\times n \right]$ i matrica identiteta $E$ iste veličine $n$. Tada pridružena matrica $\left[ A\left| U redu. \right]$ je nova $\left[ n\times 2n \right]$ matrica koja izgleda ovako:

\[\lijevo[ A\lijevo| U redu. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & (a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(niz) \desno]\]

Ukratko, uzimamo matricu $A$, desno joj dodjeljujemo matricu identiteta $E$ tražene veličine, odvajamo ih vertikalnom trakom radi ljepote - evo priložene. :)

u čemu je kvaka? A evo šta:

Teorema. Neka je matrica $A$ invertibilna. Razmotrimo pridruženu matricu $\left[ A\left| U redu. \right]$. Ako koristite elementarne transformacije stringova dovedite ga u oblik $\left[ E\left| Svijetao. \right]$, tj. množenjem, oduzimanjem i preuređivanjem redova da se od $A$ dobije matrica $E$ s desne strane, tada je matrica $B$ dobijena s lijeve strane inverzna od $A$:

\[\lijevo[ A\lijevo| U redu. \desno]\na \lijevo[ E\lijevo| Svijetao. \right]\Rightarrow B=((A)^(-1))\]

To je tako jednostavno! Ukratko, algoritam za pronalaženje inverzne matrice izgleda ovako:

1. Napišite pridruženu matricu $\left[ A\left| U redu. \right]$;
2. Izvodite elementarne konverzije nizova sve dok se desno umjesto $A$ ne pojavi $E$;
3. Naravno, nešto će se pojaviti i na lijevoj strani - određena matrica $B$. Ovo će biti obrnuto;
4. PROFIT! :)

Naravno, mnogo lakše reći nego učiniti. Dakle, pogledajmo nekoliko primjera: za veličine $\left[ 3\times 3 \right]$ i $\left[ 4\times 4 \right]$.

Zadatak. Pronađite inverznu matricu:

\[\left[ \begin(niz)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(niz) \desno]\ ]

Rješenje. Sastavljamo priloženu matricu:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\kraj (niz) \desno]\]

Budući da je posljednja kolona originalne matrice popunjena jedinicama, oduzmite prvi red od ostatka:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\kraj(niz) \desno]\početak(matrica) \strelica prema dolje \\ -1 \\ -1 \\\kraj(matrica)\do \\ & \na \lijevo [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(niz) \desno] \\ \end(poravnati)\]

Nema više jedinica, osim prve linije. Ali mi to ne diramo, inače će se novouklonjene jedinice početi "množavati" u trećoj koloni.

Ali možemo dva puta oduzeti drugi red od posljednjeg - dobivamo jedinicu u donjem lijevom uglu:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\kraj(niz) \desno]\početak(matrica) \ \\ \strelica prema dolje \\ -2 \\\kraj(matrica)\do \\ & \lijevo [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno] \\ \end(poravnati)\]

Sada možemo oduzeti posljednji red od prvog i dva puta od drugog - na taj način ćemo prvi stupac "izbrisati nulom":

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno]\početak(matrica) -1 \\ -2 \\ \uparrow \\\end(matrica)\do \\ & \ na \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\kraj (niz) \desno] \\ \end(poravnanje)\]

Pomnožite drugi red sa −1, a zatim ga oduzmite 6 puta od prvog i dodajte 1 put poslednjem:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\kraj(niz) \desno]\početak(matrica) \ \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \ \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\kraj(niz) \desno]\početak(matrica) -6 \\ \strelica nagore \\ +1 \\\end (matrica)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\kraj (niz) \desno] \\ \end(poravnanje)\]

Ostaje samo zamijeniti redove 1 i 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\kraj (niz) \desno]\]

Spremni! Desno je tražena inverzna matrica.

Odgovori. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

Zadatak. Pronađite inverznu matricu:

\[\left[ \begin(matrica) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\kraj (matrica) \desno]\]

Rješenje. Opet sastavljamo priloženu:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\kraj (niz) \desno]\]

Pozajmimo malo, brinemo se o tome koliko sada moramo brojati ... i počnite brojati. Za početak, prvu kolonu "nuliramo" oduzimanjem reda 1 od reda 2 i 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(niz) \desno]\begin(matrica) \downarrow \\ -1 \\ -1 \\ \ \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(niz) \desno] \\ \end(align)\]

Uočavamo previše "minusa" u redovima 2-4. Pomnožite sva tri reda sa −1, a zatim spalite treći stupac oduzimanjem reda 3 od ostatka:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(niz) \desno]\početak(matrica) \ \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (niz) \desno]\početak(matrica) -2 \\ -1 \\ \strelica nagore \\ -2 \\\kraj(matrica)\na \\ & \na \levo[ \begin(niz)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno] \\ \end(align)\]

Sada je vrijeme da se "prži" posljednji stupac originalne matrice: oduzmite red 4 od ostatka:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz ) \desno]\begin(matrica) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrica)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\kraj (niz) \desno] \\ \end(poravnanje)\]

Završno kotrljanje: "sapalite" drugu kolonu oduzimanjem reda 2 od reda 1 i 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( niz) \desno]\početak(matrica) 6 \\ \strelica nagore \\ -5 \\ \ \\\end(matrica)\to \\ & \to \left[ \begin(niz)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno] \\ \end(align)\]

I opet, matrica identiteta lijevo, dakle inverzna desno. :)

Odgovori. $\left[ \begin(matrica) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matrica) \desno]$

Definicija 1: Matrica se naziva degenerisana ako je njena determinanta nula.

2. definicija: Matrica se naziva nesingularnom ako njena determinanta nije jednaka nuli.

Matrica "A" se zove inverzna matrica, ako je uvjet A*A-1 = A-1 *A = E (matrica identiteta) zadovoljen.

Kvadratna matrica je invertibilna samo ako je nesingularna.

Šema za izračunavanje inverzne matrice:

1) Izračunajte determinantu matrice "A" ako ∆ A = 0, onda inverzna matrica ne postoji.

2) Pronađite sve algebarske komplemente matrice "A".

3) Sastavite matricu algebarskih sabiranja (Aij)

4) Transponirajte matricu algebarskih komplementa (Aij )T

5) Pomnožite transponovanu matricu recipročnom vrednošću determinante ove matrice.

6) Pokrenite provjeru:

Na prvi pogled može izgledati da je teško, ali u stvari sve je vrlo jednostavno. Sva rješenja su bazirana na jednostavnim aritmetičke operacije, glavna stvar pri rješavanju je da se ne zbunite sa znakovima "-" i "+", a ne da ih izgubite.

Hajde da odlučimo zajedno praktični zadatak, izračunavanje inverzne matrice.

Zadatak: pronađite inverznu matricu "A", prikazanu na slici ispod:

Sve rješavamo tačno onako kako je navedeno u planu za izračunavanje inverzne matrice.

1. Prva stvar koju treba učiniti je pronaći determinantu matrice "A":

Objašnjenje:

Pojednostavili smo našu determinantu koristeći njene glavne funkcije. Prvo smo dodali u 2. i 3. red elemente prvog reda, pomnožene sa jednim brojem.

Drugo, promijenili smo 2. i 3. kolonu determinante, a prema njenim svojstvima promijenili smo znak ispred nje.

Treće, izvadili smo zajednički faktor (-1) drugog reda, čime smo ponovo promijenili predznak i on je postao pozitivan. Također smo pojednostavili red 3 na isti način kao na samom početku primjera.

Imamo trokutastu determinantu u kojoj su elementi ispod dijagonale jednaki nuli, a po svojstvu 7 jednak je proizvodu elemenata dijagonale. Kao rezultat, dobili smo ∆ A = 26, dakle inverzna matrica postoji.

A11 = 1*(3+1) = 4

A12 = -1 * (9 + 2) = -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. Sljedeći korak je sastavljanje matrice od rezultirajućih dodataka:

5. Ovu matricu množimo recipročnom vrijednosti determinante, odnosno sa 1/26:

6. Pa, sada samo trebamo provjeriti:

Prilikom verifikacije dobili smo matricu identiteta, tako da je odluka donesena apsolutno ispravno.

2 način za izračunavanje inverzne matrice.

1. Elementarna transformacija matrica

2. Inverzna matrica kroz elementarni pretvarač.

Elementarna transformacija matrice uključuje:

1. Množenje niza brojem koji nije nula.

2. Dodavanje u bilo koji red drugog reda, pomnoženo brojem.

3. Zamjena redova matrice.

4. Primjenom lanca elementarnih transformacija dobijamo drugu matricu.

ALI -1 = ?

1. (A|E) ~ (E|A -1 )

2. A -1*A=E

Razmotrite to praktični primjer sa realnim brojevima.

vježba: Pronađite inverznu matricu.

Rješenje:

provjerimo:

Malo pojašnjenje rješenja:

Prvo smo zamijenili redove 1 i 2 matrice, a zatim smo prvi red pomnožili sa (-1).

Nakon toga, prvi red je pomnožen sa (-2) i dodan drugom redu matrice. Zatim smo 2. red pomnožili sa 1/4.

završna faza transformacija je bila množenje drugog reda sa 2 i sabiranje iz prvog. Kao rezultat, imamo matricu identiteta na lijevoj strani, dakle, inverzna matrica je matrica s desne strane.

Nakon provjere uvjerili smo se u ispravnost rješenja.

Kao što vidite, izračunavanje inverzne matrice je vrlo jednostavno.

Završavajući ovo predavanje, također bih želio posvetiti malo vremena osobinama takve matrice.

Metode za pronalaženje inverzne matrice, . Razmotrimo kvadratnu matricu

Označimo Δ = det A.

Kvadratna matrica A se naziva nedegenerisan, ili nespecijalan ako je njegova determinanta različita od nule, i degenerisati, ili poseban, akoΔ = 0.

Kvadratna matrica B postoji za kvadratnu matricu A istog reda ako je njihov proizvod A B = B A = E, gdje je E matrica identiteta istog reda kao i matrice A i B.

Teorema . Da bi matrica A imala inverznu matricu, potrebno je i dovoljno da njena determinanta bude različita od nule.

Inverzna matrica prema matrici A, označena sa A- 1 pa B = A - 1 a izračunava se po formuli

, (1)

gdje je A i j - algebarski komplementi elemenata a i j matrice A..

Proračun A -1 po formuli (1) za matrice high order vrlo naporno, pa je u praksi zgodno pronaći A -1 metodom elementarnih transformacija (EP). Bilo koja nesingularna matrica A može se reducirati pomoću EP samo stupaca (ili samo redova) na matricu identiteta E. Ako se EP-ovi izvedeni na matrici A primjenjuju istim redoslijedom na matricu identiteta E, tada je rezultat inverzna matrica. Pogodno je izvesti EP na matricama A i E istovremeno, pišući obje matrice jednu do druge kroz liniju. Još jednom napominjemo da se prilikom traženja kanonskog oblika matrice, da bismo ga pronašli, mogu koristiti transformacije redova i stupaca. Ako trebate pronaći inverznu matricu, trebali biste koristiti samo redove ili samo stupce u procesu transformacije.

Primjer 2.10. Za matricu naći A -1 .

Rješenje.Prvo ćemo pronaći determinantu matrice A
tako da inverzna matrica postoji i možemo je pronaći po formuli: , gdje je A i j (i,j=1,2,3) - algebarski komplementi elemenata a i j originalne matrice.

Gdje .

Primjer 2.11. Koristeći metodu elementarnih transformacija, pronađite A -1 za matricu: A=.

Rješenje.Originalnoj matrici s desne strane dodjeljujemo matricu identiteta istog reda: . Uz pomoć elementarnih transformacija stupaca, lijevu “polovinu” reduciramo na identičnu, istovremeno obavljajući upravo takve transformacije na desnoj matrici.
Da biste to učinili, zamijenite prvi i drugi stupac: ~ . Dodamo prvu u treću kolonu, a prvu pomnoženu sa -2 u drugu: . Od prve kolone oduzimamo udvostručeni drugi, a od trećeg - drugi pomnožen sa 6; . Dodajmo treću kolonu prvom i drugom: . Pomnožite posljednju kolonu sa -1: . Kvadratna matrica dobijena desno od vertikalne trake je inverzna matrica datoj matrici A. Dakle,
.

Za bilo koje nedegenerisana matrica I postoji i, štaviše, jedinstvena matrica A -1 takva da

A*A -1 =A -1 *A = E,

gdje je E matrica identiteta istih redova kao i A. Matrica A -1 se naziva inverzna matrici A.

Ako je neko zaboravio, u matrici identiteta, osim dijagonale popunjene jedinicama, sve ostale pozicije su popunjene nulama, primjer matrice identiteta:

Pronalaženje inverzne matrice metodom spojene matrice

Inverzna matrica je definirana formulom:

gdje je A ij - elementi a ij .

One. Da biste izračunali inverznu vrijednost matrice, morate izračunati determinantu ove matrice. Zatim pronađite algebarske dodatke za sve njegove elemente i napravite novu matricu od njih. Zatim morate prenijeti ovu matricu. I podijelite svaki element nove matrice determinantom originalne matrice.

Pogledajmo nekoliko primjera.

Naći A -1 za matricu

Rješenje: Naći A -1 metodom adjuktirane matrice. Imamo det A = 2. Pronađite algebarske komplemente elemenata matrice A. U ovaj slučaj algebarski komplementi elemenata matrice bit će odgovarajući elementi same matrice, uzeti sa predznakom u skladu s formulom

Imamo A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Formiramo pridruženu matricu

Prevozimo matricu A*:

Inverznu matricu nalazimo po formuli:

Dobijamo:

Koristite metodu spojene matrice da pronađete A -1 if

Rješenje Prije svega izračunavamo datu matricu da bismo bili sigurni da inverzna matrica postoji. Imamo

Ovdje smo elementima drugog reda dodali elemente trećeg reda, prethodno pomnožene sa (-1), a zatim proširili determinantu za drugi red. Pošto je definicija ove matrice drugačija od nule, onda postoji matrica inverzna njoj. Da bismo konstruisali pridruženu matricu, nalazimo algebarske komplemente elemenata ove matrice. Imamo

Prema formuli

transportiramo matricu A*:

Zatim prema formuli

Pronalaženje inverzne matrice metodom elementarnih transformacija

Pored metode pronalaženja inverzne matrice, koja slijedi iz formule (metoda pridružene matrice), postoji i metoda za pronalaženje inverzne matrice koja se zove metoda elementarnih transformacija.

Elementarne matrične transformacije

Sljedeće transformacije se nazivaju transformacije elementarnih matrica:

1) permutacija redova (kolona);

2) množenje reda (kolone) brojem koji nije nula;

3) dodavanjem elementima reda (kolone) odgovarajućih elemenata drugog reda (kolone), prethodno pomnoženih određenim brojem.

Da bismo pronašli matricu A -1, konstruišemo pravougaone matrice B = (A|E) redova (n; 2n), dodeljujući matrici A na desnoj strani matricu identiteta E kroz liniju razdvajanja:

Razmotrimo primjer.

Koristeći metodu elementarnih transformacija, pronaći A -1 if

Rješenje Formiramo matricu B:

Označimo redove matrice B kroz α 1 , α 2 , α 3 . Izvršimo sljedeće transformacije na redovima matrice B.