Cosine of the angle between two planes. Finding the angle between planes (dihedral angle)

Goals:

develop the ability to consider different approaches to solving problems and analyze the “effect” of using these methods of solution;
develop the student’s ability to choose a method for solving a problem in accordance with his mathematical preferences, based on more solid knowledge and confident skills;
develop the ability to draw up a plan of successive stages to achieve results;
develop the ability to justify all steps and calculations taken;
repeat and reinforce various topics and issues of stereometry and planimetry, typical stereometric structures related to solving current problems;
develop spatial thinking.

analysis various methods problem solving: coordinate vector method, application of the cosine theorem, application of the theorem of three perpendiculars;
comparison of the advantages and disadvantages of each method;
repetition of the properties of a cube, triangular prism, regular hexagon;
preparation for passing the Unified State Exam;
development of independence in decision making.

Lesson outline

Cubed ABCDA 1 B 1 C 1 D 1 with edge 1 point O – center of face ABCD.

a) the angle between straight lines A 1 D And B.O.;

b) distance from point B to the middle of the segment A 1 D.

Solution to point a).

Let's place our cube in rectangular system coordinates as shown in the figure, vertices A 1 (1; 0; 1), D (1; 1; 0), B 1 (0; 0; 1), O (½; ½; 0).

Direction vectors of straight lines A 1 D And B 1 O:

(0; 1; -1) and (½; ½; -1);

we find the desired angle φ between them using the formula:

cos∠φ = ,
whence ∠φ = 30°.

Method 2. We use the cosine theorem.

1) Let's draw a straight line B 1 C parallel to the line A 1 D. Corner CB 1 O will be what you are looking for.

2) From a right triangle BB 1 O according to the Pythagorean theorem:

3) By the theorem of cosines from a triangle CB 1 O calculate the angle CB 1 O:

cos CB 1 O = , the required angle is 30°.

Comment. When solving the problem in the 2nd way, you can notice that according to the theorem of three perpendiculars COB 1 = 90°, therefore from rectangular ∆ CB 1 O It is also easy to calculate the cosine of the desired angle.

Solution to point b).

1 way. Let's use the formula for the distance between two points

Let the point E– middle A 1 D, then the coordinates E (1; 1/2; ½), B (0; 0; 0).

BE = .

Method 2. According to the Pythagorean theorem

From rectangular ∆ B.A.E. with direct B.A.E. we find BE = .

In the right triangular prism ABCA 1 B 1 C 1 all edges are equal a. Find the angle between lines AB And A 1 C.

1 way. Coordinate vector method

Coordinates of the vertices of the prism in a rectangular system when the prism is positioned as in the figure: A (0; 0; 0), B (a; ; 0), A 1 (0; 0; a), C (0; a; 0).

Direction vectors of straight lines A 1 C And AB:

(0; a; -a) And (a; ; 0} ;

cos φ = ;

Method 2. We use the cosine theorem

We consider ∆ A 1 B 1 C, in which A 1 B 1 || AB. We have

cos φ = .

(From the collection of Unified State Exam-2012. Mathematics: typical exam options edited by A.L. Semenova, I.V. Yashchenko)

In a regular hexagonal prism ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, all edges of which are equal to 1, find the distance from the point E to a straight line B 1 C 1.

1 way. Coordinate vector method

1) Place the prism in a rectangular coordinate system, placing the coordinate axes as shown in the figure. SS 1, NE And SE are perpendicular in pairs, so you can direct the coordinate axes along them. We get the coordinates:

C 1 (0; 0; 1), E (; 0; 0), B 1 (0;1;1).

2) Find the coordinates of the direction vectors for the lines From 1 to 1 And C 1 E:

(0;1;0), (;0;-1).

3) Find the cosine of the angle between From 1 to 1 And C 1 E using scalar product vectors and :

cos β = = 0 => β = 90° => C 1 E – the required distance.

4)C 1 E = = 2.

Conclusion: knowledge different approaches to solving stereometric problems allows you to choose the preferred method for any student, i.e. one that the student masters confidently, helps to avoid mistakes, leads to successful solution of the problem and getting a good score on the exam. Coordinate method has an advantage over other methods in that it requires less stereometric considerations and vision, and is based on the use of formulas that have many planimetric and algebraic analogies that are more familiar to students.

The form of the lesson is a combination of the teacher’s explanation with the frontal collective work of students.

The polyhedra in question are shown on the screen using a video projector, which allows comparison various ways solutions.

Homework: solve problem 3 in another way, for example using the three perpendicular theorem .

Literature

1. Ershova A.P., Goloborodko V.V. Independent and test papers in geometry for grade 11. – M.: ILEKSA, – 2010. – 208 p.

2. Geometry, 10-11: textbook for educational institutions: basic and profile levels / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev et al. - M.: Education, 2007. - 256 p.

3. Unified State Exam-2012. Mathematics: standard exam options: 10 options / ed. A.L. Semenova, I.V. Yashchenko. – M.: National education, 2011. – 112 p. – (USE-2012. FIPI - school).

The article talks about finding the angle between planes. After giving the definition, let’s give a graphic illustration and consider detailed method finding by coordinate method. We obtain a formula for intersecting planes, which includes the coordinates normal vectors.

Yandex.RTB R-A-339285-1

The material will use data and concepts that were previously studied in articles about the plane and line in space. First, it is necessary to move on to reasoning that allows us to have a certain approach to determining the angle between two intersecting planes.

Two intersecting planes γ 1 and γ 2 are given. Their intersection will take the designation c. The construction of the χ plane is associated with the intersection of these planes. The plane χ passes through the point M as a straight line c. The intersection of the planes γ 1 and γ 2 will be made using the plane χ. We take the designation of the line intersecting γ 1 and χ as line a, and the line intersecting γ 2 and χ as line b. We find that the intersection of lines a and b gives the point M.

The location of point M does not affect the angle between intersecting lines a and b, and point M is located on line c, through which the plane χ passes.

It is necessary to construct a plane χ 1 perpendicular to the line c and different from the plane χ. The intersection of the planes γ 1 and γ 2 with the help of χ 1 will take the designation of lines a 1 and b 1.

It can be seen that when constructing χ and χ 1, lines a and b are perpendicular to line c, then a 1, b 1 are located perpendicular to line c. Finding straight lines a and a 1 in the plane γ 1 with perpendicularity to straight line c, then they can be considered parallel. In the same way, the location of b and b 1 in the γ 2 plane with perpendicularity to straight line c indicates their parallelism. This means that it is necessary to make a parallel transfer of the plane χ 1 to χ, where we get two coinciding straight lines a and a 1, b and b 1. We find that the angle between intersecting lines a and b is 1 equal to angle intersecting lines a and b.

Let's look at the figure below.

This proposition is proven by the fact that between the intersecting lines a and b there is an angle that does not depend on the location of the point M, that is, the point of intersection. These lines are located in the planes γ 1 and γ 2. In fact, the resulting angle can be considered the angle between two intersecting planes.

Let's move on to determining the angle between the existing intersecting planes γ 1 and γ 2.

Definition 1

The angle between two intersecting planes γ 1 and γ 2 called the angle formed by the intersection of lines a and b, where the planes γ 1 and γ 2 intersect with the plane χ perpendicular to line c.

Consider the figure below.

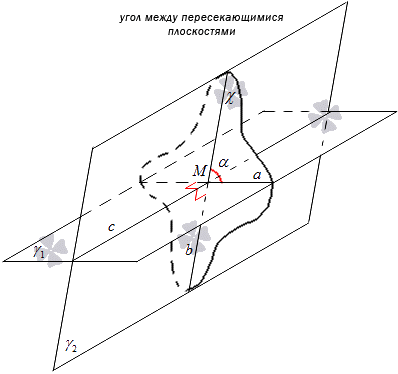
The determination may be submitted in another form. When the planes γ 1 and γ 2 intersect, where c is the line on which they intersected, mark a point M through which draw lines a and b perpendicular to line c and lying in the planes γ 1 and γ 2, then the angle between lines a and b will be the angle between the planes. In practice, this is applicable to constructing an angle between planes.

When crossing, an angle is formed that is less than 90 degrees, that is degree measure angle is valid on an interval of this type (0, 90]. At the same time, these planes are called perpendicular if a right angle is formed at the intersection. The angle between parallel planes is considered equal to zero.

The usual way to find the angle between intersecting planes is to perform additional constructions. This helps to determine it with accuracy, and this can be done using signs of equality or similarity of a triangle, sines, and cosines of an angle.

Let's consider solving problems using an example from Unified State Exam problems block C 2.

Example 1

Set cuboid A B C D A 1 B 1 C 1 D 1, where side A B = 2, A D = 3, A A 1 = 7, point E divides side A A 1 in a ratio of 4: 3. Find the angle between planes A B C and B E D 1.

Solution

For clarity, it is necessary to make a drawing. We get that

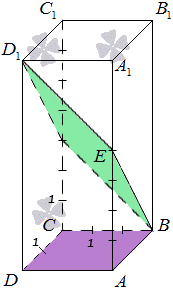
A visual representation is necessary to make it more convenient to work with the angle between planes.

We determine the straight line along which the intersection of planes A B C and B E D 1 occurs. Point B is a common point. We should find another one common point intersections. Let's consider the straight lines D A and D 1 E, which are located in the same plane A D D 1. Their location does not indicate parallelism; it means that they have a common point of intersection.

However, straight line D A is located in the plane A B C, and D 1 E in B E D 1. From this we get that the straight lines D A And D 1 E have a common intersection point, which is common for planes A B C and B E D 1. Indicates the point of intersection of lines D A and D 1 E letter F. From this we obtain that B F is the straight line along which planes A B C and B E D 1 intersect.

Let's look at the figure below.

To obtain the answer, it is necessary to construct straight lines located in planes A B C and B E D 1 passing through a point located on line B F and perpendicular to it. Then the resulting angle between these straight lines is considered the desired angle between planes A B C and B E D 1.

From this we can see that point A is the projection of point E onto the plane A B C. It is necessary to draw a straight line intersecting line B F at a right angle at point M. It can be seen that straight line A M is the projection of straight line E M onto the plane A B C, based on the theorem about those perpendiculars A M ⊥ B F . Consider the figure below.

∠ A M E is the desired angle formed by planes A B C and B E D 1. From the resulting triangle A E M we can find the sine, cosine or tangent of the angle, and then the angle itself, only if its two sides are known. By condition, we have that the length A E is found in this way: straight line A A 1 is divided by point E in the ratio 4: 3, which means the total length of the straight line is 7 parts, then A E = 4 parts. We find A M.

Need to consider right triangle A B F . We have a right angle A with height A M. From the condition A B = 2, then we can find the length A F by the similarity of triangles D D 1 F and A E F. We get that A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

It is necessary to find the length of side B F of triangle A B F using the Pythagorean theorem. We get that B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . The length of side A M is found through the area of triangle A B F. We have that the area can be equal to both S A B C = 1 2 · A B · A F and S A B C = 1 2 · B F · A M .

We get that A M = A B A F B F = 2 4 2 5 = 4 5 5

Then we can find the value of the tangent of the angle of the triangle A E M. We get:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

The desired angle obtained by the intersection of planes A B C and B E D 1 is equal to a r c t g 5, then upon simplification we obtain a r c t g 5 = a r c sin 30 6 = a r c cos 6 6.

Answer: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Some cases of finding the angle between intersecting lines are specified using coordinate plane O x y z and the coordinate method. Let's take a closer look.

If a problem is given where it is necessary to find the angle between intersecting planes γ 1 and γ 2, we denote the desired angle as α.

Then given system coordinates shows that we have the coordinates of the normal vectors of the intersecting planes γ 1 and γ 2. Then we denote that n 1 → = n 1 x, n 1 y, n 1 z is the normal vector of the plane γ 1, and n 2 → = (n 2 x, n 2 y, n 2 z) - for the plane γ 2. Let us consider the detailed determination of the angle located between these planes according to the coordinates of the vectors.

It is necessary to designate the straight line along which the planes γ 1 and γ 2 intersect with the letter c. On the line c we have a point M through which we draw a plane χ perpendicular to c. The plane χ along the lines a and b intersects the planes γ 1 and γ 2 at point M. from the definition it follows that the angle between the intersecting planes γ 1 and γ 2 is equal to the angle of the intersecting lines a and b belonging to these planes, respectively.

In the χ plane we plot normal vectors from the point M and denote them n 1 → and n 2 → . Vector n 1 → is located on a line perpendicular to line a, and vector n 2 → is located on a line perpendicular to line b. From here we get that given planeχ has a normal vector of line a equal to n 1 → and for line b equal to n 2 →. Consider the figure below.

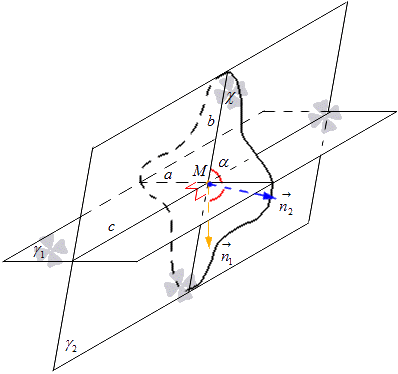
From here we obtain a formula by which we can calculate the sine of the angle of intersecting lines using the coordinates of vectors. We found that the cosine of the angle between straight lines a and b is the same as the cosine between intersecting planes γ 1 and γ 2, which is derived from cos formulasα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, where we have that n 1 → = (n 1 x, n 1 y, n 1 z) and n 2 → = (n 2 x, n 2 y, n 2 z) are the coordinates of the vectors of the represented planes.

The angle between intersecting lines is calculated using the formula

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

Example 2

According to the condition, the parallelepiped A B C D A 1 B 1 C 1 D 1 is given , where A B = 2, A D = 3, A A 1 = 7, and point E divides side A A 1 4: 3. Find the angle between planes A B C and B E D 1.

Solution

From the condition it is clear that its sides are pairwise perpendicular. This means that it is necessary to introduce a coordinate system O x y z with the vertex at point C and coordinate axes O x, O y, O z. It is necessary to set the direction to the appropriate sides. Consider the figure below.

Intersecting planes A B C And B E D 1 form an angle that can be found by the formula α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2, in which n 1 → = (n 1 x, n 1 y, n 1 z) and n 2 → = (n 2 x, n 2 y, n 2 z ) are normal vectors of these planes. It is necessary to determine the coordinates. From the figure we see that coordinate axis O x y coincides in the plane A B C, this means that the coordinates of the normal vector k → are equal to the value n 1 → = k → = (0, 0, 1).

The normal vector of the plane B E D 1 is taken to be the vector product B E → and B D 1 →, where their coordinates are found by coordinates extreme points B, E, D 1, which are determined based on the conditions of the problem.

We get that B (0, 3, 0), D 1 (2, 0, 7). Because A E E A 1 = 4 3, from the coordinates of points A 2, 3, 0, A 1 2, 3, 7 we find E 2, 3, 4. We find that B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 · i → - 6 j → - 6 k → ⇔ n 2 → = (12 , - 6 , - 6)

It is necessary to substitute the found coordinates into the formula for calculating the angle through the arc cosine. We get

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

The coordinate method gives a similar result.

Answer: a r c cos 6 6 .

The final problem is considered with the goal of finding the angle between intersecting planes with the existing known equations of the planes.

Example 3

Calculate the sine, cosine of the angle and the value of the angle formed by two intersecting lines, which are defined in the coordinate system O x y z and given by the equations 2 x - 4 y + z + 1 = 0 and 3 y - z - 1 = 0.

Solution

When studying a topic general equation straight line of the form A x + B y + C z + D = 0 revealed that A, B, C are coefficients equal to the coordinates of the normal vector. This means that n 1 → = 2, - 4, 1 and n 2 → = 0, 3, - 1 are normal vectors of the given lines.

It is necessary to substitute the coordinates of the normal vectors of the planes into the formula for calculating the desired angle of intersecting planes. Then we get that

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

From here we have that the cosine of the angle takes the form cos α = 13 210. Then the angle of intersecting lines is not obtuse. Substituting in trigonometric identity, we find that the value of the sine of the angle is equal to the expression. Let us calculate and find that

sin α = 1 - cos 2 α = 1 - 13,210 = 41,210

Answer: sin α = 41,210, cos α = 13,210, α = a r c cos 13,210 = a r c sin 41,210.

If you notice an error in the text, please highlight it and press Ctrl+Enter

In assignment C2 in mathematics, you most often need to solve a problem in which you need to determine:

Distance between two points
Distance from point to line
Distance from point to plane
Distance between crossing lines
Angle between two straight lines
Angle between a straight line and a plane
Angle between planes

The tasks are elementary if you follow the solution algorithm C2 and remember the basics trigonometric properties, such as the properties of diagonals or the surface area of a polyhedron. Basic tasks will help you remember these basic properties.

Now let's move directly to the algorithms.

1. To determine the distance between two points A and B, we use one of two methods:

We include AB in some triangle and find its length as the side of the triangle
According to the formula

Moreover, the coordinate method, in my opinion, is the simplest; you just need to carefully determine the coordinates of each point.

2. To determine the distance from a point to a line, calculate

as the length of a perpendicular segment, if it is possible to include this segment in some triangle as one of the heights

using the coordinate method using formulas for calculating the area, in which the required distance will be the height and

3. The distance from a point to a plane is

the length of the perpendicular dropped from this point onto the plane. To do this, we carefully construct a section that is perpendicular to the plane and passes through given point. The required distance will be equal to the height of the resulting new polyhedron.
Using the coordinate method

The equation is found by substituting the coordinates of three points belonging to this plane

Using the vector method

To do this, you need to remember the rules for adding and subtracting vectors, that the product perpendicular vectors equals zero.

Using the volume method, if there is a pyramid ABCM, then the distance from point M to the plane containing the triangle ABC is calculated by the formula

Using the method of reference problems, which can be viewed

4. The distance between crossing lines can be solved using

4.1. Step-by-step computational method:

construct a common perpendicular of two intersecting lines and find its length;
construct a plane containing one of the lines and parallel to the second. Then the required distance will be equal to the distance from the point to the straight line constructed in the plane;
enclose given lines in parallel planes passing through given intersecting lines, find the distance between these planes
construct a plane perpendicular to one of these lines and construct an orthogonal projection of the second line

4.2. Vector coordinate method

Find the coordinates of the ends of a segment that is a common perpendicular to two intersecting lines
Finding the distance between two points

4.3. Vector method
We reduce the problem to determining the length of a vector belonging to a perpendicular that is the common perpendicular of two skew lines

6. Angle between a straight line and a plane determined by including it in a right triangle as one of the acute angles, or by the vector-coordinator method

We'll look at how the angle between planes is determined in the next lesson. These algorithms for solving C2 contribute to a comprehensive understanding of the method for solving the problem. "A magazine for schoolchildren and their parents to help schoolchildren." Read more: http://education-club.ru/#ixzz2IXf5GOJU

7. Angle between planes(geometric method)

1. Find the straight line along which the planes intersect.
2. Select a point on this line and draw two perpendiculars to it lying in these planes. Or draw a plane perpendicular to the line of intersection of the planes.
3. Find the trigonometric function of the angle formed by perpendiculars to the line of intersection of the planes. As a rule, we do this through a triangle that includes the desired angle.
4. Write down the value of the angle in your answer, or trigonometric function corner.

Angle between planes. Coordinate method. Task C2

Two intersecting planes form two pairs of equal dihedral angles:

The magnitude of the dihedral angle is measured by the magnitude of the corresponding linear angle.

To construct a linear angle of a dihedral angle, you need to take on the line of intersection of the planes arbitrary point, and in each plane draw a ray to this point perpendicular to the line of intersection of the planes. The angle formed by these rays is the linear angle of the dihedral angle:

The magnitude of the angle between planes is the magnitude of the less than dihedral angle.

Let our planes be defined by the equations:

The cosine of the angle between the planes is found by the following formula:

In the answer we write , since the value of the angle between the planes is the value of the smaller dihedral angle.

In a regular quadrangular prism with a base side of 12 and a height of 21, a point M is taken on the edge so that . Point K is taken on the edge so that . Find the angle between the plane and the plane.

Let's make a drawing. Since we will use the coordinate method, we will immediately introduce a coordinate system: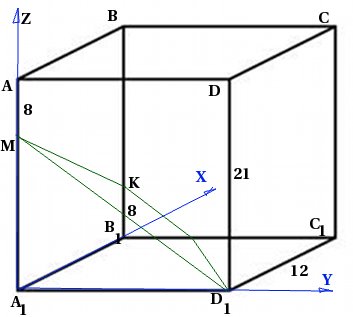

Now we are faced with the task of writing the equations of plane and plane.

I described a detailed algorithm for finding the equation of a plane using three points.

After we find the coefficients in the plane and plane equations, we substitute them into the formula to find the cosine of the angle between the planes, and find the angle.

I suggest you watch a detailed video solution to this problem:

Another task from Inna Vladimirovna Feldman

Video lessons "Coordinate method for solving problems s-2"

Lesson 2 http://youtu.be/dKQWG8OZRGo
Lesson 3 http://youtu.be/ddgr0PnbFno
Lesson 4 http://youtu.be/n6yx2pQC0Lo
Lesson 5 http://youtu.be/JkWbxAw1YLI
Lesson 6 http://youtu.be/gybIqCMKBiI
lesson 7 http://youtu.be/_LpARpYxp5g
Lesson 8 http://youtu.be/XJhyZQoofD8

The angle between two different planes can be determined for any relative position planes.

A trivial case if the planes are parallel. Then the angle between them is considered equal to zero.

A non-trivial case if the planes intersect. This case is the subject of further discussion. First we need the concept of a dihedral angle.

9.1 Dihedral angle

A dihedral angle is two half-planes with a common straight line (which is called the edge of the dihedral angle). In Fig. 50 shows a dihedral angle formed by half-planes and; the edge of this dihedral angle is the straight line a, common to these half-planes.

Rice. 50. Dihedral angle

The dihedral angle can be measured in degrees or radians in a word, enter the angular value of the dihedral angle. This is done as follows.

On the edge of the dihedral angle formed by the half-planes and, we take an arbitrary point M. Let us draw rays MA and MB, respectively lying in these half-planes and perpendicular to the edge (Fig. 51).

Rice. 51. Linear dihedral angle

The resulting angle AMB is the linear angle of the dihedral angle. The angle " = \AMB is precisely the angular value of our dihedral angle.

Definition. The angular magnitude of a dihedral angle is the magnitude of the linear angle of a given dihedral angle.

All linear angles of a dihedral angle are equal to each other (after all, they are obtained from each other by a parallel shift). That's why this definition correct: the value "does not depend on specific choice points M on the edge of a dihedral angle.

9.2 Determining the angle between planes

When two planes intersect, four dihedral angles are obtained. If they all have the same size(by 90), then the planes are called perpendicular; The angle between the planes is then 90.

If not all dihedral angles are the same (that is, there are two acute and two obtuse), then the angle between the planes is the value of the acute dihedral angle (Fig. 52).

Rice. 52. Angle between planes

9.3 Examples of problem solving

Let's look at three problems. The first is simple, the second and third are approximately at level C2 on the Unified State Examination in mathematics.

Problem 1. Find the angle between two faces of a regular tetrahedron.

Solution. Let ABCD be a regular tetrahedron. Let us draw the medians AM and DM of the corresponding faces, as well as the height of the tetrahedron DH (Fig. 53).

Rice. 53. To task 1

Being medians, AM and DM are also heights of equilateral triangles ABC and DBC. Therefore, the angle " = \AMD is the linear angle of the dihedral angle formed by the faces ABC and DBC. We find it from the triangle DHM:

			1 AM

Answer: arccos 1 3 .

Problem 2. In a regular quadrangular pyramid SABCD (with vertex S), the side edge is equal to the side of the base. Point K is the middle of edge SA. Find the angle between the planes

Solution. Line BC is parallel to AD and thus parallel to plane ADS. Therefore, plane KBC intersects plane ADS along straight line KL parallel to BC (Fig. 54).

Rice. 54. To task 2

In this case, KL will also be parallel to line AD; hence KL middle line triangle ADS, and point L is the midpoint of DS.

Let's find the height of the pyramid SO. Let N be the middle of DO. Then LN is the middle line of triangle DOS, and therefore LN k SO. This means LN is perpendicular to plane ABC.

From point N we lower the perpendicular NM to the straight line BC. The straight line NM will be the projection of the inclined LM onto the ABC plane. From the three perpendicular theorem it then follows that LM is also perpendicular to BC.

Thus, the angle " = \LMN is the linear angle of the dihedral angle formed by the half-planes KBC and ABC. We will look for this angle from the right triangle LMN.

Let the edge of the pyramid be equal to a. First we find the height of the pyramid:

SO=p

Solution. Let L be the intersection point of lines A1 K and AB. Then plane A1 KC intersects plane ABC along straight line CL (Fig.55).

A C

Rice. 55. To problem 3

Triangles A1 B1 K and KBL are equal in leg and acute angle. Therefore, the other legs are equal: A1 B1 = BL.

Consider triangle ACL. In it BA = BC = BL. Angle CBL is 120; therefore, \BCL = 30 . Also, \BCA = 60 . Therefore \ACL = \BCA + \BCL = 90 .

So, LC? AC. But line AC serves as a projection of line A1 C onto plane ABC. By the theorem of three perpendiculars we then conclude that LC ? A1 C.

Thus, angle A1 CA is the linear angle of the dihedral angle formed by the half-planes A1 KC and ABC. This is the desired angle. From the isosceles right triangle A1 AC we see that it is equal to 45.

\(\blacktriangleright\) Dihedral angle is an angle formed by two half-planes and a straight line \(a\), which is their common boundary.

\(\blacktriangleright\) To find the angle between the planes \(\xi\) and \(\pi\) , you need to find the linear angle (and spicy or straight) dihedral angle formed by the planes \(\xi\) and \(\pi\) :

Step 1: let \(\xi\cap\pi=a\) (the line of intersection of the planes). In the plane \(\xi\) we mark an arbitrary point \(F\) and draw \(FA\perp a\) ;

Step 2: carry out \(FG\perp \pi\) ;

Step 3: according to TTP (\(FG\) – perpendicular, \(FA\) – oblique, \(AG\) – projection) we have: \(AG\perp a\) ;

Step 4: The angle \(\angle FAG\) is called the linear angle of the dihedral angle formed by the planes \(\xi\) and \(\pi\) .

Note that the triangle \(AG\) is right-angled.
Note also that the plane \(AFG\) constructed in this way is perpendicular to both planes \(\xi\) and \(\pi\) . Therefore, we can say it differently: angle between planes\(\xi\) and \(\pi\) is the angle between two intersecting lines \(c\in \xi\) and \(b\in\pi\) forming a plane perpendicular to and \(\xi\ ) , and \(\pi\) .

Task 1 #2875

Task level: More difficult than the Unified State Exam

Dana quadrangular pyramid, all edges of which are equal, and the base is a square. Find \(6\cos \alpha\) , where \(\alpha\) is the angle between its adjacent side faces.

Let \(SABCD\) be a given pyramid (\(S\) is a vertex) whose edges are equal to \(a\) . Therefore, everything side faces are equal equilateral triangles. Let's find the angle between the faces \(SAD\) and \(SCD\) .

Let's do \(CH\perp SD\) . Because \(\triangle SAD=\triangle SCD\), then \(AH\) will also be the height of \(\triangle SAD\) . Therefore, by definition, \(\angle AHC=\alpha\) is the linear angle of the dihedral angle between the faces \(SAD\) and \(SCD\) .
Since the base is a square, then \(AC=a\sqrt2\) . Note also that \(CH=AH\) is the height equilateral triangle with side \(a\) , therefore, \(CH=AH=\frac(\sqrt3)2a\) .
Then, by the cosine theorem from \(\triangle AHC\) : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Answer: -2

Task 2 #2876

Task level: More difficult than the Unified State Exam

The planes \(\pi_1\) and \(\pi_2\) intersect at an angle whose cosine is equal to \(0.2\). The planes \(\pi_2\) and \(\pi_3\) intersect at right angles, and the line of intersection of the planes \(\pi_1\) and \(\pi_2\) is parallel to the line of intersection of the planes \(\pi_2\) and \(\ pi_3\) . Find the sine of the angle between the planes \(\pi_1\) and \(\pi_3\) .

Let the line of intersection of \(\pi_1\) and \(\pi_2\) be a straight line \(a\), the line of intersection of \(\pi_2\) and \(\pi_3\) be a straight line \(b\), and the line of intersection \(\pi_3\) and \(\pi_1\) – straight line \(c\) . Since \(a\parallel b\) , then \(c\parallel a\parallel b\) (according to the theorem from the section of the theoretical reference “Geometry in space” \(\rightarrow\) “Introduction to stereometry, parallelism”).

Let's mark the points \(A\in a, B\in b\) so that \(AB\perp a, AB\perp b\) (this is possible since \(a\parallel b\) ). Let us mark \(C\in c\) so that \(BC\perp c\) , therefore, \(BC\perp b\) . Then \(AC\perp c\) and \(AC\perp a\) .
Indeed, since \(AB\perp b, BC\perp b\) , then \(b\) is perpendicular to the plane \(ABC\) . Since \(c\parallel a\parallel b\), then the lines \(a\) and \(c\) are also perpendicular to the plane \(ABC\), and therefore to any line from this plane, in particular, the line \ (AC\) .

It follows that \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). It turns out that \(\triangle ABC\) is rectangular, which means \[\sin \angle BCA=\cos \angle BAC=0.2.\]

Answer: 0.2

Task 3 #2877

Task level: More difficult than the Unified State Exam

Given straight lines \(a, b, c\) intersecting at one point, and the angle between any two of them is equal to \(60^\circ\) . Find \(\cos^(-1)\alpha\) , where \(\alpha\) is the angle between the plane formed by lines \(a\) and \(c\) and the plane formed by lines \(b\ ) and \(c\) . Give your answer in degrees.

Let the lines intersect at the point \(O\) . Since the angle between any two of them is equal to \(60^\circ\), then all three straight lines cannot lie in the same plane. Let us mark the point \(A\) on the line \(a\) and draw \(AB\perp b\) and \(AC\perp c\) . Then \(\triangle AOB=\triangle AOC\) as rectangular along the hypotenuse and acute angle. Therefore, \(OB=OC\) and \(AB=AC\) .
Let's do \(AH\perp (BOC)\) . Then by the theorem about three perpendiculars \(HC\perp c\) , \(HB\perp b\) . Since \(AB=AC\) , then \(\triangle AHB=\triangle AHC\) as rectangular along the hypotenuse and leg. Therefore, \(HB=HC\) . This means that \(OH\) is the bisector of the angle \(BOC\) (since the point \(H\) is equidistant from the sides of the angle).

Note that in this way we also constructed the linear angle of the dihedral angle formed by the plane formed by the lines \(a\) and \(c\) and the plane formed by the lines \(b\) and \(c\) . This is the angle \(ACH\) .

Let's find this angle. Since we chose the point \(A\) arbitrarily, let us choose it so that \(OA=2\) . Then in rectangular \(\triangle AOC\) : \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Since \(OH\) is a bisector, then \(\angle HOC=30^\circ\) , therefore, in a rectangular \(\triangle HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Then from the rectangular \(\triangle ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Answer: 3

Task 4 #2910

Task level: More difficult than the Unified State Exam

The planes \(\pi_1\) and \(\pi_2\) intersect along the straight line \(l\) on which the points \(M\) and \(N\) lie. The segments \(MA\) and \(MB\) are perpendicular to the straight line \(l\) and lie in the planes \(\pi_1\) and \(\pi_2\) respectively, and \(MN = 15\) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Find \(3\cos\alpha\) , where \(\alpha\) is the angle between the planes \(\pi_1\) and \(\pi_2\) .

The triangle \(AMN\) is right-angled, \(AN^2 = AM^2 + MN^2\), whence \ The triangle \(BMN\) is right-angled, \(BN^2 = BM^2 + MN^2\), from which \We write the cosine theorem for the triangle \(AMB\): \ Then \ Since the angle \(\alpha\) between the planes is sharp corner, and \(\angle AMB\) turned out to be obtuse, then \(\cos\alpha=\dfrac5(12)\) . Then \

Answer: 1.25

Task 5 #2911

Task level: More difficult than the Unified State Exam

\(ABCDA_1B_1C_1D_1\) is a parallelepiped, \(ABCD\) is a square with side \(a\), point \(M\) is the base of the perpendicular dropped from the point \(A_1\) to the plane \((ABCD)\) , in addition, \(M\) is the point of intersection of the diagonals of the square \(ABCD\) . It is known that \(A_1M = \dfrac(\sqrt(3))(2)a\). Find the angle between the planes \((ABCD)\) and \((AA_1B_1B)\) . Give your answer in degrees.

Let's construct \(MN\) perpendicular to \(AB\) as shown in the figure.

Since \(ABCD\) is a square with side \(a\) and \(MN\perp AB\) and \(BC\perp AB\) , then \(MN\parallel BC\) . Since \(M\) is the point of intersection of the diagonals of the square, then \(M\) is the middle of \(AC\), therefore, \(MN\) is the middle line and \(MN =\frac12BC= \frac(1)(2)a\).
\(MN\) is the projection of \(A_1N\) onto the plane \((ABCD)\), and \(MN\) is perpendicular to \(AB\), then, by the theorem of three perpendiculars, \(A_1N\) is perpendicular to \(AB \) and the angle between the planes \((ABCD)\) and \((AA_1B_1B)\) is \(\angle A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

Answer: 60

Task 6 #1854

Task level: More difficult than the Unified State Exam

In a square \(ABCD\) : \(O\) – the point of intersection of the diagonals; \(S\) – does not lie in the plane of the square, \(SO \perp ABC\) . Find the angle between the planes \(ASD\) and \(ABC\) if \(SO = 5\) and \(AB = 10\) .

Right triangles \(\triangle SAO\) and \(\triangle SDO\) are equal in two sides and the angle between them (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) , because \(O\) – point of intersection of the diagonals of the square, \(SO\) – common side) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\triangle ASD\) – isosceles. Point \(K\) is the middle of \(AD\), then \(SK\) is the height in the triangle \(\triangle ASD\), and \(OK\) is the height in the triangle \(AOD\) \(\ Rightarrow\) plane \(SOK\) is perpendicular to planes \(ASD\) and \(ABC\) \(\Rightarrow\) \(\angle SKO\) – linear angle equal to the desired dihedral angle.

In \(\triangle SKO\) : \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) – isosceles right triangle \(\Rightarrow\) \(\angle SKO = 45^\circ\) .

Answer: 45

Task 7 #1855

Task level: More difficult than the Unified State Exam

Right triangles \(\triangle SAO\) , \(\triangle SDO\) , \(\triangle SOB\) and \(\triangle SOC\) are equal in two sides and the angle between them (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\), because \(O\) – point of intersection of the diagonals of the square, \(SO\) – common side) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \(\triangle ASD\) and \(\triangle BSC\) are isosceles. Point \(K\) is the middle of \(AD\), then \(SK\) is the height in the triangle \(\triangle ASD\), and \(OK\) is the height in the triangle \(AOD\) \(\ Rightarrow\) plane \(SOK\) is perpendicular to plane \(ASD\) . Point \(L\) is the middle of \(BC\), then \(SL\) is the height in the triangle \(\triangle BSC\), and \(OL\) is the height in the triangle \(BOC\) \(\ Rightarrow\) plane \(SOL\) (aka plane \(SOK\)) is perpendicular to the plane \(BSC\) . Thus, we obtain that \(\angle KSL\) is a linear angle equal to the desired dihedral angle.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Rightarrow\) \(OL = 5\) ; \(SK = SL\) – equal heights isosceles triangles, which can be found using the Pythagorean theorem: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). It can be noticed that \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Rightarrow\) for a triangle \(\triangle KSL\) is satisfied converse theorem Pythagoras \(\Rightarrow\) \(\triangle KSL\) – right triangle \(\Rightarrow\) \(\angle KSL = 90^\circ\) .

Answer: 90

Preparing students to take the Unified State Exam in mathematics, as a rule, begins with repeating basic formulas, including those that allow you to determine the angle between planes. Despite the fact that this section of geometry is covered in sufficient detail within school curriculum, many graduates need to repeat basic material. Understanding how to find the angle between planes, high school students will be able to quickly calculate the correct answer when solving a problem and count on receiving decent scores on the results of passing the unified state exam.

Main nuances

To ensure that the question of how to find a dihedral angle does not cause difficulties, we recommend following a solution algorithm that will help you cope with Unified State Examination tasks.

First you need to determine the straight line along which the planes intersect.

Then you need to select a point on this line and draw two perpendiculars to it.

The next step is to find the trigonometric function of the dihedral angle formed by the perpendiculars. The most convenient way to do this is with the help of the resulting triangle, of which the angle is a part.

The answer will be the value of the angle or its trigonometric function.

Preparing for the exam test with Shkolkovo is the key to your success

During classes the day before passing the Unified State Exam Many schoolchildren are faced with the problem of finding definitions and formulas that allow them to calculate the angle between 2 planes. A school textbook is not always at hand exactly when needed. And to find necessary formulas and examples of their correct use, including for finding the angle between planes on the Internet online, which sometimes requires spending a lot of time.

The mathematical portal "Shkolkovo" offers new approach to prepare for the state exam. Classes on our website will help students identify the most difficult sections for themselves and fill gaps in knowledge.

We have prepared and clearly presented all the necessary material. Basic Definitions and formulas are presented in the “Theoretical Information” section.

In order to better understand the material, we also suggest practicing the appropriate exercises. Large selection of tasks varying degrees complexity, for example, is presented in the “Catalog” section. All tasks contain a detailed algorithm for finding the correct answer. The list of exercises on the website is constantly supplemented and updated.

While practicing solving problems that require finding the angle between two planes, students have the opportunity to save any task online as “Favorites.” Thanks to this they will be able to return to him required amount time and discuss the progress of its decision with school teacher or a tutor.