Fundamentals of probability theory and mathematical statistics. Basic concepts of probability theory and mathematical statistics
Theory of Probability and Mathematical Statistics
- Agekyan T.A. Fundamentals of Error Theory for Astronomers and Physicists (2nd ed.). M.: Nauka, 1972 (djvu, 2.44 M)
- Agekyan T.A. Probability theory for astronomers and physicists. M.: Nauka, 1974 (djvu, 2.59 M)
- Anderson T. Statistical analysis of time series. M.: Mir, 1976 (djvu, 14 M)
- Bakelman I.Ya. Werner A.L. Kantor B.E. Introduction to differential geometry "in general". M.: Nauka, 1973 (djvu, 5.71 M)
- Bernstein S.N. Probability theory. M.-L.: GI, 1927 (djvu, 4.51 M)
- Billingsley P. Convergence of probability measures. M.: Nauka, 1977 (djvu, 3.96 M)
- Box J. Jenkins G. Time series analysis: forecast and management. Issue 1. M.: Mir, 1974 (djvu, 3.38 M)
- Box J. Jenkins G. Time series analysis: forecast and management. Issue 2. M.: Mir, 1974 (djvu, 1.72 M)
- Borel E. Probability and reliability. M.: Nauka, 1969 (djvu, 1.19 M)
- Van der Waerden B.L. Math statistics. M.: IL, 1960 (djvu, 6.90 M)
- Vapnik V.N. Recovering dependencies based on empirical data. M.: Nauka, 1979 (djvu, 6.18M)
- Ventzel E.S. Introduction to Operations Research. M.: Soviet radio, 1964 (djvu, 8.43M)
- Ventzel E.S. Elements of Game Theory (2nd ed.). Series: Popular lectures on mathematics. Issue 32. M.: Nauka, 1961 (djvu, 648 K)
- Ventstel E.S. Probability theory (4th ed.). M.: Nauka, 1969 (djvu, 8.05 M)
- Ventstel E.S., Ovcharov L.A. Probability theory. Tasks and exercises. M.: Nauka, 1969 (djvu, 7.71 M)
- Vilenkin N.Ya., Potapov V.G. A practical workbook on probability theory with elements of combinatorics and mathematical statistics. M.: Education, 1979 (djvu, 1.12M)
- Gmurman V.E. A guide to solving problems in probability theory and mathematical statistics (3rd ed.). M.: Higher. school, 1979 (djvu, 4.24 M)
- Gmurman V.E. Probability theory and mathematical statistics (4th ed.). M.: Higher School, 1972 (djvu, 3.75 M)
- Gnedenko B.V., Kolmogorov A.N. Limit distributions for sums of independent random variables. M.-L.: GITTL, 1949 (djvu, 6.26 M)
- Gnedenko B.V., Khinchin A.Ya. An Elementary Introduction to Probability Theory (7th ed.). M.: Nauka, 1970 (djvu, 2.48 M)
- Oak J.L. Probabilistic processes. M.: IL, 1956 (djvu, 8.48 M)
- David G. Ordinal statistics. M.: Nauka, 1979 (djvu, 2.87 M)
- Ibragimov I.A., Linnik Yu.V. Independent and stationary related quantities. M.: Nauka, 1965 (djvu, 6.05 M)
- Idier V., Dryard D., James F., Rus M., Sadoulet B. Statistical methods in experimental physics. M.: Atomizdat, 1976 (djvu, 5.95 M)
- Kamalov M.K. Distribution of quadratic forms in samples from a normal population. Tashkent: Academy of Sciences of the UzSSR, 1958 (djvu, 6.29M)
- Kassandra O.N., Lebedev V.V. Processing of observation results. M.: Nauka, 1970 (djvu, 867 K)
- Katz M. Probability and related issues in physics. M.: Mir, 1965 (djvu, 3.67 M)
- Katz M. Several probabilistic problems of physics and mathematics. M.: Nauka, 1967 (djvu, 1.50 M)
- Katz M. Statistical independence in probability theory, analysis and number theory. M.: IL, 1963 (djvu, 964 K)
- Kendall M., Moran P. Geometric probabilities. M.: Nauka, 1972 (djvu, 1.40 M)
- Kendall M., Stewart A. Volume 2. Statistical inference and connections. M.: Nauka, 1973 (djvu, 10 M)
- Kendall M., Stewart A. Volume 3. Multivariate statistical analysis and time series. M.: Nauka, 1976 (djvu, 7.96M)
- Kendall M., Stewart A. Vol. 1. Theory of distributions. M.: Nauka, 1965 (djvu, 6.02M)
- Kolmogorov A.N. Basic concepts of probability theory (2nd ed.) M.: Nauka, 1974 (djvu, 2.14M)
- Kolchin V.F., Sevastyanov B.A., Chistyakov V.P. Random placements. M.: Nauka, 1976 (djvu, 2.96 M)
- Kramer G. Mathematical methods of statistics (2nd ed.). M.: Mir, 1976 (djvu, 9.63M)
- Leman E. Testing statistical hypotheses. M.: Science. 1979 (djvu, 5.18M)
- Linnik Yu.V., Ostrovsky I.V. Decompositions of random variables and vectors. M.: Nauka, 1972 (djvu, 4.86M)
- Likholetov I.I., Matskevich I.P. A guide to solving problems in higher mathematics, probability theory and mathematical statistics (2nd ed.). Mn.: Vysh. school, 1969 (djvu, 4.99 M)
- Loev M. Theory of Probability. M.: IL, 1962 (djvu, 7.38 M)
- Malakhov A.N. Cumulant analysis of random non-Gaussian processes and their transformations. M.: Sov. radio, 1978 (djvu, 6.72 M)
- Meshalkin L.D. Collection of problems on probability theory. M.: MSU, 1963 (djvu, 1 004 K)
- Mitropolsky A.K. Theory of moments. M.-L.: GIKSL, 1933 (djvu, 4.49 M)
- Mitropolsky A.K. Techniques of statistical computing (2nd ed.). M.: Nauka, 1971 (djvu, 8.35 M)
- Mosteller F., Rurke R., Thomas J. Probability. M.: Mir, 1969 (djvu, 4.82 M)
- Nalimov V.V. Application of mathematical statistics in the analysis of matter. M.: GIFML, 1960 (djvu, 4.11M)
- Neveu J. Mathematical foundations of probability theory. M.: Mir, 1969 (djvu, 3.62 M)
- Preston K. Mathematics. New in foreign science No.7. Gibbs states on countable sets. M.: Mir, 1977 (djvu, 2.15 M)
- Savelyev L.Ya. Elementary probability theory. Part 1. Novosibirsk: NSU, 2005 (
Many, when faced with the concept of “probability theory,” get scared, thinking that it is something overwhelming, very complex. But everything is actually not so tragic. Today we will look at the basic concept of probability theory and learn how to solve problems using specific examples.
The science
What does such a branch of mathematics as “probability theory” study? She notes patterns and quantities. Scientists first became interested in this issue back in the eighteenth century, when they studied gambling. The basic concept of probability theory is an event. It is any fact that is established by experience or observation. But what is experience? Another basic concept of probability theory. It means that this set of circumstances was created not by chance, but for a specific purpose. As for observation, here the researcher himself does not participate in the experiment, but is simply a witness to these events; he does not influence what is happening in any way.
Events
We learned that the basic concept of probability theory is an event, but we did not consider the classification. All of them are divided into the following categories:
- Reliable.
- Impossible.
- Random.
Regardless of what kind of events they are, observed or created during the experience, they are all subject to this classification. We invite you to get acquainted with each type separately.
Reliable event

This is a circumstance for which the necessary set of measures has been taken. In order to better understand the essence, it is better to give a few examples. Physics, chemistry, economics, and higher mathematics are subject to this law. The theory of probability includes such an important concept as a reliable event. Here are some examples:
- We work and receive compensation in the form of wages.
- We passed the exams well, passed the competition, and for this we receive a reward in the form of admission to an educational institution.
- We invested money in the bank, and if necessary, we will get it back.
Such events are reliable. If we have fulfilled all the necessary conditions, we will definitely get the expected result.
Impossible events
Now we are considering elements of probability theory. We propose to move on to an explanation of the next type of event, namely the impossible. First, let's stipulate the most important rule - the probability of an impossible event is zero.
One cannot deviate from this formulation when solving problems. For clarification, here are examples of such events:
- The water froze at a temperature of plus ten (this is impossible).
- The lack of electricity does not affect production in any way (just as impossible as in the previous example).
It is not worth giving more examples, since those described above very clearly reflect the essence of this category. An impossible event will never occur during an experiment under any circumstances.
Random Events

When studying the elements, special attention should be paid to this particular type of event. This is what science studies. As a result of the experience, something may or may not happen. In addition, the test can be carried out an unlimited number of times. Vivid examples include:
- The toss of a coin is an experience or test, the landing of heads is an event.
- Pulling a ball out of a bag blindly is a test; getting a red ball is an event, and so on.
There can be an unlimited number of such examples, but, in general, the essence should be clear. To summarize and systematize the knowledge gained about the events, a table is provided. Probability theory studies only the last type of all presented.
Name | definition | |
Reliable | Events that occur with a 100% guarantee if certain conditions are met. | Admission to an educational institution upon passing the entrance exam well. |
Impossible | Events that will never happen under any circumstances. | It is snowing at an air temperature of plus thirty degrees Celsius. |
Random | An event that may or may not occur during an experiment/test. | A hit or miss when throwing a basketball into a hoop. |
Laws
Probability theory is a science that studies the possibility of an event occurring. Like the others, it has some rules. The following laws of probability theory exist:
- Convergence of sequences of random variables.
- Law of large numbers.
When calculating the possibility of something complex, you can use a set of simple events to achieve a result in an easier and faster way. Note that the laws of probability theory are easily proven using certain theorems. We suggest that you first get acquainted with the first law.
Convergence of sequences of random variables

Note that there are several types of convergence:
- The sequence of random variables converges in probability.
- Almost impossible.
- Mean square convergence.
- Distribution convergence.
So, right off the bat, it’s very difficult to understand the essence. Here are definitions that will help you understand this topic. Let's start with the first view. The sequence is called convergent in probability, if the following condition is met: n tends to infinity, the number to which the sequence tends is greater than zero and close to one.
Let's move on to the next view, almost certainly. The sequence is said to converge almost certainly to a random variable with n tending to infinity and P tending to a value close to unity.
The next type is mean square convergence. When using SC convergence, the study of vector random processes is reduced to the study of their coordinate random processes.
The last type remains, let's look at it briefly so that we can move directly to solving problems. Convergence in distribution has another name - “weak”, and we will explain why later. Weak convergence is the convergence of distribution functions at all points of continuity of the limiting distribution function.
We will definitely keep our promise: weak convergence differs from all of the above in that the random variable is not defined in the probability space. This is possible because the condition is formed exclusively using distribution functions.
Law of Large Numbers
Theorems of probability theory, such as:
- Chebyshev's inequality.
- Chebyshev's theorem.
- Generalized Chebyshev's theorem.
- Markov's theorem.
If we consider all these theorems, then this question may drag on for several dozen sheets. Our main task is to apply probability theory in practice. We suggest you do this right now. But before that, let’s look at the axioms of probability theory; they will be the main assistants in solving problems.
Axioms

We already met the first one when we talked about an impossible event. Let's remember: the probability of an impossible event is zero. We gave a very vivid and memorable example: snow fell at an air temperature of thirty degrees Celsius.
The second is as follows: a reliable event occurs with a probability equal to one. Now we will show how to write this using mathematical language: P(B)=1.
Third: A random event may or may not happen, but the possibility always ranges from zero to one. The closer the value is to one, the greater the chances; if the value approaches zero, the probability is very low. Let's write this in mathematical language: 0<Р(С)<1.
Let's consider the last, fourth axiom, which sounds like this: the probability of the sum of two events is equal to the sum of their probabilities. We write it in mathematical language: P(A+B)=P(A)+P(B).
The axioms of probability theory are the simplest rules that are not difficult to remember. Let's try to solve some problems based on the knowledge we have already acquired.
Lottery ticket

First, let's look at the simplest example - a lottery. Imagine that you bought one lottery ticket for good luck. What is the probability that you will win at least twenty rubles? In total, a thousand tickets are participating in the circulation, one of which has a prize of five hundred rubles, ten of them have a hundred rubles each, fifty have a prize of twenty rubles, and one hundred have a prize of five. Probability problems are based on finding the possibility of luck. Now together we will analyze the solution to the above task.
If we use the letter A to denote a win of five hundred rubles, then the probability of getting A will be equal to 0.001. How did we get this? You just need to divide the number of “lucky” tickets by their total number (in this case: 1/1000).
B is a win of one hundred rubles, the probability will be 0.01. Now we acted on the same principle as in the previous action (10/1000)
C - the winnings are twenty rubles. We find the probability, it is equal to 0.05.
We are not interested in the remaining tickets, since their prize fund is less than that specified in the condition. Let's apply the fourth axiom: The probability of winning at least twenty rubles is P(A)+P(B)+P(C). The letter P denotes the probability of the occurrence of a given event; we have already found them in previous actions. All that remains is to add up the necessary data, and the answer we get is 0.061. This number will be the answer to the task question.
Card deck
Problems in probability theory can be more complex; for example, let’s take the following task. In front of you is a deck of thirty-six cards. Your task is to draw two cards in a row without shuffling the stack, the first and second cards must be aces, the suit does not matter.
First, let's find the probability that the first card will be an ace, for this we divide four by thirty-six. They put it aside. We take out the second card, it will be an ace with a probability of three thirty-fifths. The probability of the second event depends on which card we drew first, we wonder whether it was an ace or not. It follows from this that event B depends on event A.
The next step is to find the probability of simultaneous occurrence, that is, we multiply A and B. Their product is found as follows: we multiply the probability of one event by the conditional probability of another, which we calculate, assuming that the first event occurred, that is, we drew an ace with the first card.
To make everything clear, let’s give a designation to such an element as events. It is calculated assuming that event A has occurred. It is calculated as follows: P(B/A).
Let's continue solving our problem: P(A * B) = P(A) * P(B/A) or P(A * B) = P(B) * P(A/B). The probability is equal to (4/36) * ((3/35)/(4/36). We calculate by rounding to the nearest hundredth. We have: 0.11 * (0.09/0.11) = 0.11 * 0, 82 = 0.09. The probability that we will draw two aces in a row is nine hundredths. The value is very small, it follows that the probability of the event occurring is extremely small.
Forgotten number
We propose to analyze several more variants of tasks that are studied by probability theory. You have already seen examples of solving some of them in this article. Let’s try to solve the following problem: the boy forgot the last digit of his friend’s phone number, but since the call was very important, he began to dial everything one by one. We need to calculate the probability that he will call no more than three times. The solution to the problem is simplest if the rules, laws and axioms of probability theory are known.
Before looking at the solution, try solving it yourself. We know that the last digit can be from zero to nine, that is, ten values in total. The probability of getting the right one is 1/10.
Next, we need to consider the options for the origin of the event, suppose that the boy guessed right and immediately typed the right one, the probability of such an event is 1/10. Second option: the first call misses, and the second one is on target. Let's calculate the probability of such an event: multiply 9/10 by 1/9, and as a result we also get 1/10. The third option: the first and second calls turned out to be at the wrong address, only with the third the boy got to where he wanted. We calculate the probability of such an event: 9/10 multiplied by 8/9 and 1/8, resulting in 1/10. We are not interested in other options according to the conditions of the problem, so we just have to add up the results obtained, in the end we have 3/10. Answer: the probability that the boy will call no more than three times is 0.3.
Cards with numbers

There are nine cards in front of you, on each of which a number from one to nine is written, the numbers are not repeated. They were put in a box and mixed thoroughly. You need to calculate the probability that
- an even number will appear;
- two-digit.
Before moving on to the solution, let's stipulate that m is the number of successful cases, and n is the total number of options. Let's find the probability that the number will be even. It won’t be difficult to calculate that there are four even numbers, this will be our m, there are nine possible options in total, that is, m=9. Then the probability is 0.44 or 4/9.
Let's consider the second case: the number of options is nine, and there can be no successful outcomes at all, that is, m equals zero. The probability that the drawn card will contain a two-digit number is also zero.
INTRODUCTION
Many things are incomprehensible to us not because our concepts are weak;
but because these things are not included in the range of our concepts.
Kozma Prutkov
The main goal of studying mathematics in secondary specialized educational institutions is to give students a set of mathematical knowledge and skills necessary for studying other program disciplines that use mathematics to one degree or another, for the ability to perform practical calculations, for the formation and development of logical thinking.
In this work, all the basic concepts of the section of mathematics “Fundamentals of Probability Theory and Mathematical Statistics”, provided for by the program and the State Educational Standards of Secondary Vocational Education (Ministry of Education of the Russian Federation. M., 2002), are consistently introduced, the main theorems are formulated, most of which are not proven . The main problems and methods for solving them and technologies for applying these methods to solving practical problems are considered. The presentation is accompanied by detailed comments and numerous examples.
Methodological instructions can be used for initial familiarization with the material being studied, when taking notes on lectures, to prepare for practical classes, to consolidate acquired knowledge, skills and abilities. In addition, the manual will also be useful for undergraduate students as a reference tool, allowing them to quickly recall what was previously studied.
At the end of the work there are examples and tasks that students can perform in self-control mode.
The guidelines are intended for part-time and full-time students.
BASIC CONCEPTS
Probability theory studies the objective patterns of mass random events. It is the theoretical basis for mathematical statistics, which deals with the development of methods for collecting, describing and processing observational results. Through observations (tests, experiments), i.e. experience in the broad sense of the word, knowledge of the phenomena of the real world occurs.
In our practical activities, we often encounter phenomena the outcome of which cannot be predicted, the outcome of which depends on chance.
A random phenomenon can be characterized by the ratio of the number of its occurrences to the number of trials, in each of which, under the same conditions of all trials, it could occur or not occur.
Probability theory is a branch of mathematics in which random phenomena (events) are studied and patterns are identified when they are repeated en masse.
Mathematical statistics is a branch of mathematics that deals with the study of methods for collecting, systematizing, processing and using statistical data to obtain scientifically based conclusions and make decisions.
In this case, statistical data is understood as a set of numbers that represent the quantitative characteristics of the characteristics of the objects under study that interest us. Statistical data is obtained as a result of specially designed experiments and observations.
Statistical data by their essence depends on many random factors, therefore mathematical statistics is closely related to probability theory, which is its theoretical basis.
I. PROBABILITY. THEOREMS OF ADDITION AND MULTIPLICATION OF PROBABILITIES
1.1. Basic concepts of combinatorics
In the branch of mathematics, which is called combinatorics, some problems related to the consideration of sets and the composition of various combinations of elements of these sets are solved. For example, if we take 10 different numbers 0, 1, 2, 3,: , 9 and make combinations of them, we will get different numbers, for example 143, 431, 5671, 1207, 43, etc.
We see that some of these combinations differ only in the order of the digits (for example, 143 and 431), others - in the digits included in them (for example, 5671 and 1207), and others also differ in the number of digits (for example, 143 and 43).
Thus, the resulting combinations satisfy various conditions.
Depending on the rules of composition, three types of combinations can be distinguished: permutations, placements, combinations.
Let's first get acquainted with the concept factorial.
The product of all natural numbers from 1 to n inclusive is called n-factorial and write.
Calculate: a) ; b) ; V) .
Solution. A) .
b) Since ![]() , then we can put it out of brackets
, then we can put it out of brackets
Then we get
V) ![]() .
.
Rearrangements.
A combination of n elements that differ from each other only in the order of the elements is called a permutation.
Permutations are indicated by the symbol P n , where n is the number of elements included in each permutation. ( R- first letter of a French word permutation- rearrangement).
The number of permutations can be calculated using the formula
or using factorial:
Let's remember that 0!=1 and 1!=1.
Example 2. In how many ways can six different books be arranged on one shelf?
Solution. The required number of ways is equal to the number of permutations of 6 elements, i.e.
Placements.
Postings from m elements in n in each, such compounds are called that differ from each other either by the elements themselves (at least one), or by the order of their arrangement.
Placements are indicated by the symbol, where m- the number of all available elements, n- the number of elements in each combination. ( A- first letter of a French word arrangement, which means “placement, putting in order”).
At the same time, it is believed that nm.
The number of placements can be calculated using the formula
![]() ,
,
those. number of all possible placements from m elements by n equals the product n consecutive integers, of which the largest is m.
Let's write this formula in factorial form:
Example 3. How many options for distributing three vouchers to sanatoriums of various profiles can be compiled for five applicants?
Solution. The required number of options is equal to the number of placements of 5 elements of 3 elements, i.e.
![]() .
.
Combinations.
Combinations are all possible combinations of m elements by n, which differ from each other by at least one element (here m And n- natural numbers, and n m).
Number of combinations of m elements by n are denoted by ( WITH-the first letter of a French word combination- combination).
In general, the number of m elements by n equal to the number of placements from m elements by n, divided by the number of permutations from n elements:
Using factorial formulas for the numbers of placements and permutations, we obtain:
![]()
Example 4. In a team of 25 people, you need to allocate four to work in a certain area. In how many ways can this be done?
Solution. Since the order of the four people chosen does not matter, there are ways to do this.
We find using the first formula
![]() .
.
In addition, when solving problems, the following formulas are used, expressing the basic properties of combinations:
(by definition they assume and);
![]() .
.
1.2. Solving combinatorial problems
Task 1. There are 16 subjects studied at the faculty. You need to put 3 subjects on your schedule for Monday. In how many ways can this be done?
Solution. There are as many ways to schedule three items out of 16 as you can arrange placements of 16 items by 3.
Task 2. Out of 15 objects, you need to select 10 objects. In how many ways can this be done?

Task 3. Four teams took part in the competition. How many options for distributing seats between them are possible?
![]() .
.
Problem 4. In how many ways can a patrol of three soldiers and one officer be formed if there are 80 soldiers and 3 officers?
Solution. You can choose a soldier on patrol
ways, and officers in ways. Since any officer can go with each team of soldiers, there are only so many ways.
Task 5. Find , if it is known that .
Since , we get
![]() ,
,
![]() ,
,
![]()
By definition of a combination it follows that , . That. .
1.3. The concept of a random event. Types of events. Probability of event
Any action, phenomenon, observation with several different outcomes, realized under a given set of conditions, will be called test.
The result of this action or observation is called event .
If an event under given conditions can happen or not happen, then it is called random . When an event is certain to happen, it is called reliable , and in the case when it obviously cannot happen, - impossible.
The events are called incompatible , if only one of them is possible to appear each time.
The events are called joint , if, under given conditions, the occurrence of one of these events does not exclude the occurrence of another during the same test.
The events are called opposite , if under the test conditions they, being the only outcomes, are incompatible.
Events are usually denoted in capital letters of the Latin alphabet: A, B, C, D, : .
A complete system of events A 1 , A 2 , A 3 , : , A n is a set of incompatible events, the occurrence of at least one of which is obligatory during a given test.
If a complete system consists of two incompatible events, then such events are called opposite and are designated A and .
Example. The box contains 30 numbered balls. Determine which of the following events are impossible, reliable, or contrary:
took out a numbered ball (A);
got a ball with an even number (IN);
got a ball with an odd number (WITH);
got a ball without a number (D).
Which of them form a complete group?
Solution . A- reliable event; D- impossible event;
In and WITH- opposite events.
The complete group of events consists of A And D, V And WITH.
The probability of an event is considered as a measure of the objective possibility of the occurrence of a random event.
1.4. Classic definition of probability
A number that expresses the measure of the objective possibility of an event occurring is called probability this event and is indicated by the symbol R(A).
Definition. Probability of the event A is the ratio of the number of outcomes m that favor the occurrence of a given event A, to the number n all outcomes (inconsistent, only possible and equally possible), i.e. .
Therefore, to find the probability of an event, it is necessary, having considered various outcomes of the test, to calculate all possible inconsistent outcomes n, choose the number of outcomes m we are interested in and calculate the ratio m To n.
The following properties follow from this definition:
The probability of any test is a non-negative number not exceeding one.
Indeed, the number m of the required events is within . Dividing both parts into n, we get
2. The probability of a reliable event is equal to one, because .
3. The probability of an impossible event is zero, since .
Problem 1. In a lottery of 1000 tickets, there are 200 winning ones. One ticket is taken out at random. What is the probability that this ticket is a winner?
Solution. The total number of different outcomes is n=1000. The number of outcomes favorable to winning is m=200. According to the formula, we get
![]() .
.
Problem 2. In a batch of 18 parts there are 4 defective ones. 5 parts are selected at random. Find the probability that two of these 5 parts will be defective.
Solution. Number of all equally possible independent outcomes n equal to the number of combinations of 18 by 5 i.e.
Let's count the number m that favors event A. Among 5 parts taken at random, there should be 3 good ones and 2 defective ones. The number of ways to select two defective parts from 4 existing defective ones is equal to the number of combinations of 4 by 2:
The number of ways to select three quality parts from 14 available quality parts is equal to
![]() .
.
Any group of good parts can be combined with any group of defective parts, so the total number of combinations m amounts to
The required probability of event A is equal to the ratio of the number of outcomes m favorable to this event to the number n of all equally possible independent outcomes:
![]() .
.
The sum of a finite number of events is an event consisting of the occurrence of at least one of them.
The sum of two events is denoted by the symbol A+B, and the sum n events with the symbol A 1 +A 2 + : +A n.
Probability addition theorem.
The probability of the sum of two incompatible events is equal to the sum of the probabilities of these events.
Corollary 1. If the event A 1, A 2, :,A n form a complete system, then the sum of the probabilities of these events is equal to one.
Corollary 2. The sum of the probabilities of opposite events and is equal to one.
![]() .
.
Problem 1. There are 100 lottery tickets. It is known that 5 tickets win 20,000 rubles, 10 tickets win 15,000 rubles, 15 tickets win 10,000 rubles, 25 tickets win 2,000 rubles. and nothing for the rest. Find the probability that the purchased ticket will receive a winning of at least 10,000 rubles.
Solution. Let A, B, and C be events consisting in the fact that the purchased ticket receives a winning equal to 20,000, 15,000, and 10,000 rubles, respectively. since events A, B and C are incompatible, then
Task 2. The correspondence department of a technical school receives tests in mathematics from cities A, B And WITH. Probability of receiving a test from the city A equal to 0.6, from the city IN- 0.1. Find the probability that the next test will come from the city WITH.
Mom washed the frame
At the end of the long summer holidays, it’s time to slowly return to higher mathematics and solemnly open the empty Verdov file to begin creating a new section - . I admit, the first lines are not easy, but the first step is half the way, so I suggest everyone carefully study the introductory article, after which mastering the topic will be 2 times easier! I'm not exaggerating at all. …On the eve of the next September 1st, I remember first grade and the primer…. Letters form syllables, syllables form words, words form short sentences - Mom washed the frame. Mastering turver and math statistics is as easy as learning to read! However, for this you need to know key terms, concepts and designations, as well as some specific rules, which are the subject of this lesson.
But first, please accept my congratulations on the beginning (continuation, completion, mark as appropriate) of the school year and accept the gift. The best gift is a book, and for independent work I recommend the following literature:
1) Gmurman V.E. Theory of Probability and Mathematical Statistics
A legendary textbook that has gone through more than ten reprints. It is distinguished by its intelligibility and extremely simple presentation of the material, and the first chapters are completely accessible, I think, already for students in grades 6-7.
2) Gmurman V.E. Guide to solving problems in probability theory and mathematical statistics
A solution book by the same Vladimir Efimovich with detailed examples and problems.
NECESSARILY download both books from the Internet or get their paper originals! The version from the 60s and 70s will also work, which is even better for dummies. Although the phrase “probability theory for dummies” sounds rather ridiculous, since almost everything is limited to elementary arithmetic operations. They skip, however, in places derivatives And integrals, but this is only in places.
I will try to achieve the same clarity of presentation, but I must warn that my course is aimed at problem solving and theoretical calculations are kept to a minimum. Thus, if you need a detailed theory, proofs of theorems (theorems-theorems!), please refer to the textbook. Well, who wants learn to solve problems in probability theory and mathematical statistics in the shortest possible time, follow me!
That's enough for a start =)
As you read the articles, it is advisable to become acquainted (at least briefly) with additional tasks of the types considered. On the page Ready-made solutions for higher mathematics The corresponding pdfs with examples of solutions will be posted. Significant assistance will also be provided IDZ 18.1 Ryabushko(simpler) and solved IDZ according to Chudesenko’s collection(more difficult).
1) Amount two events and the event is called which is that it will happen or event or event or both events at the same time. In the event that events incompatible, the last option disappears, that is, it may occur or event or event .
The rule also applies to a larger number of terms, for example, the event ![]() is what will happen at least one from events
is what will happen at least one from events ![]() , A if events are incompatible – then one thing and only one thing event from this amount: or event , or event , or event , or event , or event .
, A if events are incompatible – then one thing and only one thing event from this amount: or event , or event , or event , or event , or event .
There are plenty of examples:
Events (when throwing a dice, 5 points will not appear) is what will appear or 1, or 2, or 3, or 4, or 6 points.
Event (will drop no more two points) is that 1 will appear or 2points.
Event ![]() (there will be an even number of points) is what appears or 2 or 4 or 6 points.
(there will be an even number of points) is what appears or 2 or 4 or 6 points.
The event is that a red card (heart) will be drawn from the deck or tambourine), and the event ![]() – that the “picture” will be extracted (jack or lady or king or ace).
– that the “picture” will be extracted (jack or lady or king or ace).
A little more interesting is the case with joint events:
The event is that a club will be drawn from the deck or seven or seven of clubs According to the definition given above, at least something- or any club or any seven or their “intersection” - seven of clubs. It is easy to calculate that this event corresponds to 12 elementary outcomes (9 club cards + 3 remaining sevens).
The event is that tomorrow at 12.00 will come AT LEAST ONE of the summable joint events, namely:
– or there will be only rain / only thunderstorm / only sun;
– or only some pair of events will occur (rain + thunderstorm / rain + sun / thunderstorm + sun);
– or all three events will appear simultaneously.
That is, the event includes 7 possible outcomes.
The second pillar of the algebra of events:
2) The work two events and call an event which consists in the joint occurrence of these events, in other words, multiplication means that under some circumstances there will be And event , And event . A similar statement is true for a larger number of events, for example, a work implies that under certain conditions it will happen And event , And event , And event , …, And event .
Consider a test in which two coins are tossed and the following events:
– heads will appear on the 1st coin;
– the 1st coin will land heads;
– heads will appear on the 2nd coin;
– the 2nd coin will land heads.
Then:
And on the 2nd) heads will appear;
– the event is that on both coins (on the 1st And on the 2nd) it will be heads;
– the event is that the 1st coin will land heads And the 2nd coin is tails;
– the event is that the 1st coin will land heads And on the 2nd coin there is an eagle.
It is easy to see that events incompatible (because, for example, it cannot be 2 heads and 2 tails at the same time) and form full group (since taken into account All possible outcomes of tossing two coins). Let's summarize these events: . How to interpret this entry? Very simple - multiplication means a logical connective AND, and addition – OR. Thus, the amount is easy to read in understandable human language: “two heads will appear or two heads or the 1st coin will land heads And on the 2nd tails or the 1st coin will land heads And on the 2nd coin there is an eagle"
This was an example when in one test several objects are involved, in this case two coins. Another common scheme in practical problems is retesting , when, for example, the same die is rolled 3 times in a row. As a demonstration, consider the following events:
– in the 1st throw you will get 4 points;
– in the 2nd throw you will get 5 points;
– in the 3rd throw you will get 6 points.
Then the event ![]() is that in the 1st throw you will get 4 points And in the 2nd throw you will get 5 points And on the 3rd roll you will get 6 points. Obviously, in the case of a cube there will be significantly more combinations (outcomes) than if we were tossing a coin.
is that in the 1st throw you will get 4 points And in the 2nd throw you will get 5 points And on the 3rd roll you will get 6 points. Obviously, in the case of a cube there will be significantly more combinations (outcomes) than if we were tossing a coin.
...I understand that perhaps the examples being analyzed are not very interesting, but these are things that are often encountered in problems and there is no escape from them. In addition to a coin, a cube and a deck of cards, urns with multi-colored balls, several anonymous people shooting at a target, and a tireless worker who is constantly turning out some details await you =)
Probability of event
Probability of event is the central concept of probability theory. ...A killer logical thing, but we had to start somewhere =) There are several approaches to its definition:
;
Geometric definition of probability
;
Statistical definition of probability
.
In this article I will focus on the classical definition of probability, which is most widely used in educational tasks.
Designations. The probability of a certain event is indicated by a capital Latin letter, and the event itself is taken in brackets, acting as a kind of argument. For example:
Also, the small letter is widely used to denote probability. In particular, you can abandon the cumbersome designations of events and their probabilities ![]() in favor of the following style::
in favor of the following style::
– the probability that a coin toss will result in heads;
– the probability that a dice roll will result in 5 points;
– the probability that a card of the club suit will be drawn from the deck.
This option is popular when solving practical problems, since it allows you to significantly reduce the recording of the solution. As in the first case, it is convenient to use “talking” subscripts/superscripts here.
Everyone has long guessed the numbers that I just wrote down above, and now we will find out how they turned out:
Classic definition of probability:
The probability of an event occurring in a certain test is called the ratio , where:
– total number of all equally possible, elementary outcomes of this test, which form full group of events;
- quantity elementary outcomes, favorable event.
When tossing a coin, either heads or tails can fall out - these events form full group, thus, the total number of outcomes; at the same time, each of them elementary And equally possible. The event is favored by the outcome (heads). According to the classical definition of probability: ![]() .
.
Similarly, as a result of throwing a die, elementary equally possible outcomes may appear, forming a complete group, and the event is favored by a single outcome (rolling a five). That's why: ![]() THIS IS NOT ACCEPTED TO DO (although it is not forbidden to estimate percentages in your head).
THIS IS NOT ACCEPTED TO DO (although it is not forbidden to estimate percentages in your head).
It is customary to use fractions of a unit, and, obviously, the probability can vary within . Moreover, if , then the event is impossible, If - reliable, and if , then we are talking about random event.
! If, while solving any problem, you get some other probability value, look for the error!
In the classical approach to determining probability, extreme values (zero and one) are obtained through exactly the same reasoning. Let 1 ball be drawn at random from a certain urn containing 10 red balls. Consider the following events:
in a single trial a low-possibility event will not occur.
This is why you will not hit the jackpot in the lottery if the probability of this event is, say, 0.00000001. Yes, yes, it’s you – with the only ticket in a particular circulation. However, a larger number of tickets and a larger number of drawings will not help you much. ...When I tell others about this, I almost always hear in response: “but someone wins.” Okay, then let's do the following experiment: please buy a ticket for any lottery today or tomorrow (don't delay!). And if you win... well, at least more than 10 kilorubles, be sure to sign up - I will explain why this happened. For a percentage, of course =) =)
But there is no need to be sad, because there is an opposite principle: if the probability of some event is very close to one, then in a single trial it will almost certain will happen. Therefore, before jumping with a parachute, there is no need to be afraid, on the contrary, smile! After all, completely unthinkable and fantastic circumstances must arise for both parachutes to fail.
Although all this is lyricism, since depending on the content of the event, the first principle may turn out to be cheerful, and the second – sad; or even both are parallel.
Perhaps that's enough for now, in class Classical probability problems we will get the most out of the formula. In the final part of this article, we will consider one important theorem:
The sum of the probabilities of events that form a complete group is equal to one. Roughly speaking, if events form a complete group, then with 100% probability one of them will happen. In the simplest case, a complete group is formed by opposite events, for example:
– as a result of a coin toss, heads will appear;
– the result of a coin toss will be heads.
According to the theorem: ![]()
It is absolutely clear that these events are equally possible and their probabilities are the same ![]() .
.
Due to the equality of probabilities, equally possible events are often called equally probable . And here is a tongue twister for determining the degree of intoxication =)
Example with a cube: events are opposite, therefore ![]() .
.
The theorem under consideration is convenient in that it allows you to quickly find the probability of the opposite event. So, if the probability that a five is rolled is known, it is easy to calculate the probability that it is not rolled:
![]()
This is much simpler than summing up the probabilities of five elementary outcomes. For elementary outcomes, by the way, this theorem is also true:
. For example, if is the probability that the shooter will hit the target, then is the probability that he will miss.
! In probability theory, it is undesirable to use letters for any other purposes.
In honor of Knowledge Day, I will not assign homework =), but it is very important that you can answer the following questions:
– What types of events exist?
– What is chance and equal possibility of an event?
– How do you understand the terms compatibility/incompatibility of events?
– What is a complete group of events, opposite events?
– What does addition and multiplication of events mean?
– What is the essence of the classical definition of probability?
– Why is the theorem for adding the probabilities of events that form a complete group useful?
No, you don’t need to cram anything, these are just the basics of probability theory - a kind of primer that will quickly fit into your head. And for this to happen as soon as possible, I suggest you familiarize yourself with the lessons
Theory of Probability and Mathematical Statistics
1. THEORETICAL PART
1 Convergence of sequences of random variables and probability distributions
In probability theory one has to deal with different types of convergence of random variables. Let's consider the following main types of convergence: by probability, with probability one, by mean of order p, by distribution.
Let,... be random variables defined on some probability space (, Ф, P).
Definition 1. A sequence of random variables, ... is said to converge in probability to a random variable (notation:), if for any > 0
Definition 2. A sequence of random variables, ... is said to converge with probability one (almost certainly, almost everywhere) to a random variable if
those. if the set of outcomes for which () do not converge to () has zero probability.
This type of convergence is denoted as follows: , or, or.
Definition 3. A sequence of random variables ... is called mean-convergent of order p, 0< p < , если
Definition 4. A sequence of random variables... is said to converge in distribution to a random variable (notation:) if for any bounded continuous function
Convergence in the distribution of random variables is defined only in terms of the convergence of their distribution functions. Therefore, it makes sense to talk about this type of convergence even when random variables are specified in different probability spaces.
Theorem 1.
a) In order for (P-a.s.), it is necessary and sufficient that for any > 0
) The sequence () is fundamental with probability one if and only if for any > 0.
Proof.
a) Let A = (: |- | ), A = A. Then
Therefore, statement a) is the result of the following chain of implications:
P(: )= 0 P() = 0 = 0 P(A) = 0, m 1 P(A) = 0, > 0 P() 0, n 0, > 0 P( ) 0,
n 0, > 0.) Let us denote = (: ), = . Then (: (()) is not fundamental ) = and in the same way as in a) it is shown that (: (()) is not fundamental ) = 0 P( ) 0, n.
The theorem is proven
Theorem 2. (Cauchy criterion for almost certain convergence)
In order for a sequence of random variables () to be convergent with probability one (to some random variable), it is necessary and sufficient that it be fundamental with probability one.
Proof.
If, then +
from which follows the necessity of the conditions of the theorem.
Now let the sequence () be fundamental with probability one. Let us denote L = (: (()) not fundamental). Then for all the number sequence () is fundamental and, according to the Cauchy criterion for number sequences, () exists. Let's put
This defined function is a random variable and.
The theorem has been proven.
2 Method of characteristic functions
The method of characteristic functions is one of the main tools of the analytical apparatus of probability theory. Along with random variables (taking real values), the theory of characteristic functions requires the use of complex-valued random variables.
Many of the definitions and properties relating to random variables are easily transferred to the complex case. So, the mathematical expectation M ?complex-valued random variable ?=?+?? is considered certain if the mathematical expectations M are determined ?them ?. In this case, by definition we assume M ?= M ? + ?M ?. From the definition of independence of random elements it follows that complex-valued quantities ?1 =?1+??1 , ?2=?2+??2are independent if and only if pairs of random variables are independent ( ?1 , ?1) And ( ?2 , ?2), or, which is the same thing, independent ?-algebra F ?1, ?1 and F ?2, ?2.
Along with the space L 2real random variables with finite second moment, we can introduce into consideration the Hilbert space of complex-valued random variables ?=?+?? with M | ?|2?|2= ?2+?2, and the scalar product ( ?1 , ?2)= M ?1?2¯ , Where ?2¯ - complex conjugate random variable.
In algebraic operations, vectors Rn are treated as algebraic columns,
As row vectors, a* - (a1,a2,…,an). If Rn , then their scalar product (a,b) will be understood as a quantity. It's clear that
If aRn and R=||rij|| is a matrix of order nхn, then
Definition 1. Let F = F(x1,....,xn) - n-dimensional distribution function in (, ()). Its characteristic function is called the function
Definition 2 . If? = (?1,…,?n) is a random vector defined on a probability space with values in, then its characteristic function is called the function
where is F? = F?(х1,….,хn) - vector distribution function?=(?1,…, ?n).
If the distribution function F(x) has density f = f(x), then
In this case, the characteristic function is nothing more than the Fourier transform of the function f(x).
From (3) it follows that the characteristic function ??(t) of a random vector can also be defined by the equality
Basic properties of characteristic functions (in the case of n=1).
Let be? = ?(?) - random variable, F? =F? (x) is its distribution function and is the characteristic function.
It should be noted that if, then.
Indeed,
where we took advantage of the fact that the mathematical expectation of the product of independent (bounded) random variables is equal to the product of their mathematical expectations.
Property (6) is key when proving limit theorems for sums of independent random variables by the method of characteristic functions. In this regard, the distribution function is expressed through the distribution functions of individual terms in a much more complex way, namely, where the * sign means a convolution of the distributions.
Each distribution function in can be associated with a random variable that has this function as its distribution function. Therefore, when presenting the properties of characteristic functions, we can limit ourselves to considering the characteristic functions of random variables.
Theorem 1. Let be? - a random variable with distribution function F=F(x) and - its characteristic function.
The following properties take place:
) is uniformly continuous in;
) is a real-valued function if and only if the distribution of F is symmetric
)if for some n? 1 , then for all there are derivatives and
)If exists and is finite, then
) Let for all n ? 1 and
then for all |t| The following theorem shows that the characteristic function uniquely determines the distribution function. Theorem 2 (uniqueness). Let F and G be two distribution functions having the same characteristic function, that is, for all The theorem says that the distribution function F = F(x) can be uniquely restored from its characteristic function. The following theorem gives an explicit representation of the function F in terms of. Theorem 3 (generalization formula). Let F = F(x) be the distribution function and be its characteristic function. a) For any two points a, b (a< b), где функция F = F(х) непрерывна, ) If then the distribution function F(x) has density f(x), Theorem 4. In order for the components of a random vector to be independent, it is necessary and sufficient that its characteristic function be the product of the characteristic functions of the components: Bochner-Khinchin theorem .
Let be a continuous function. In order for it to be characteristic, it is necessary and sufficient that it be non-negative definite, that is, for any real t1, ... , tn and any complex numbers Theorem 5. Let be the characteristic function of a random variable. a) If for some, then the random variable is lattice with a step, that is ) If for two different points, where is an irrational number, then is it a random variable? is degenerate: where a is some constant. c) If, then is it a random variable? degenerate. 1.3 Central limit theorem for independent identically distributed random variables Let () be a sequence of independent, identically distributed random variables. Expectation M= a, variance D= , S = , and Ф(х) is the distribution function of the normal law with parameters (0,1). Let us introduce another sequence of random variables Theorem. If 0<<, то при n P(< x) Ф(х) равномерно относительно х (). In this case, the sequence () is called asymptotically normal. From the fact that M = 1 and from the continuity theorems it follows that, along with the weak convergence, FM f() Mf() for any continuous bounded f, there is also convergence M f() Mf() for any continuous f, such that |f(x)|< c(1+|x|) при каком-нибудь. Proof. Uniform convergence here is a consequence of weak convergence and continuity of Ф(x). Further, without loss of generality, we can assume a = 0, since otherwise we could consider the sequence (), and the sequence () would not change. Therefore, to prove the required convergence it is enough to show that (t) e when a = 0. We have (t) = , where =(t). Since M exists, then the decomposition exists and is valid Therefore, for n The theorem has been proven. 1.4 The main tasks of mathematical statistics, their brief description The establishment of patterns that govern mass random phenomena is based on the study of statistical data - the results of observations. The first task of mathematical statistics is to indicate ways of collecting and grouping statistical information. The second task of mathematical statistics is to develop methods for analyzing statistical data, depending on the objectives of the study. When solving any problem of mathematical statistics, there are two sources of information. The first and most definite (explicit) is the result of observations (experiment) in the form of a sample from some general population of a scalar or vector random variable. In this case, the sample size n can be fixed, or it can increase during the experiment (i.e., so-called sequential statistical analysis procedures can be used). The second source is all a priori information about the properties of interest of the object being studied, which has been accumulated up to the current moment. Formally, the amount of a priori information is reflected in the initial statistical model that is chosen when solving the problem. However, there is no need to talk about an approximate determination in the usual sense of the probability of an event based on the results of experiments. By approximate determination of any quantity it is usually meant that it is possible to indicate error limits within which an error will not occur. The frequency of the event is random for any number of experiments due to the randomness of the results of individual experiments. Due to the randomness of the results of individual experiments, the frequency may deviate significantly from the probability of the event. Therefore, by defining the unknown probability of an event as the frequency of this event over a large number of experiments, we cannot indicate the limits of error and guarantee that the error will not exceed these limits. Therefore, in mathematical statistics we usually talk not about approximate values of unknown quantities, but about their suitable values, estimates. The problem of estimating unknown parameters arises in cases where the population distribution function is known up to a parameter. In this case, it is necessary to find a statistic whose sample value for the considered implementation xn of a random sample could be considered an approximate value of the parameter. A statistic whose sample value for any realization xn is taken as an approximate value of an unknown parameter is called a point estimate or simply an estimate, and is the value of the point estimate. A point estimate must satisfy very specific requirements in order for its sample value to correspond to the true value of the parameter. Another approach to solving the problem under consideration is also possible: find such statistics and, with probability? the following inequality holds: In this case we talk about interval estimation for. Interval is called the confidence interval for with the confidence coefficient?. Having assessed one or another statistical characteristic based on the results of experiments, the question arises: how consistent is the assumption (hypothesis) that the unknown characteristic has exactly the value that was obtained as a result of its evaluation with the experimental data? This is how the second important class of problems in mathematical statistics arises - problems of testing hypotheses. In a sense, the problem of testing a statistical hypothesis is the inverse of the problem of parameter estimation. When estimating a parameter, we know nothing about its true value. When testing a statistical hypothesis, for some reason its value is assumed to be known and it is necessary to verify this assumption based on the results of the experiment. In many problems of mathematical statistics, sequences of random variables are considered, converging in one sense or another to some limit (random variable or constant), when. Thus, the main tasks of mathematical statistics are the development of methods for finding estimates and studying the accuracy of their approximation to the characteristics being assessed and the development of methods for testing hypotheses. 5 Testing statistical hypotheses: basic concepts The task of developing rational methods for testing statistical hypotheses is one of the main tasks of mathematical statistics. A statistical hypothesis (or simply a hypothesis) is any statement about the type or properties of the distribution of random variables observed in an experiment. Let there be a sample that is a realization of a random sample from a general population, the distribution density of which depends on an unknown parameter. Statistical hypotheses regarding the unknown true value of a parameter are called parametric hypotheses. Moreover, if is a scalar, then we are talking about one-parameter hypotheses, and if it is a vector, then we are talking about multi-parameter hypotheses. A statistical hypothesis is called simple if it has the form where is some specified parameter value. A statistical hypothesis is called complex if it has the form where is a set of parameter values consisting of more than one element. In the case of testing two simple statistical hypotheses of the form where are two given (different) values of the parameter, the first hypothesis is usually called the main one, and the second one is called the alternative or competing hypothesis. The criterion, or statistical criterion, for testing hypotheses is the rule by which, based on sample data, a decision is made about the validity of either the first or second hypothesis. The criterion is specified using a critical set, which is a subset of the sample space of a random sample. The decision is made as follows: ) if the sample belongs to the critical set, then reject the main hypothesis and accept the alternative hypothesis; ) if the sample does not belong to the critical set (i.e., it belongs to the complement of the set to the sample space), then the alternative hypothesis is rejected and the main hypothesis is accepted. When using any criterion, the following types of errors are possible: 1) accept a hypothesis when it is true - an error of the first kind; )accepting a hypothesis when it is true is a type II error. The probabilities of committing errors of the first and second types are denoted by: where is the probability of an event provided that the hypothesis is true. The indicated probabilities are calculated using the distribution density function of a random sample: The probability of committing a type I error is also called the criterion significance level. The value equal to the probability of rejecting the main hypothesis when it is true is called the power of the test. 1.6 Independence criterion There is a sample ((XY), ..., (XY)) from a two-dimensional distribution L with an unknown distribution function for which it is necessary to test the hypothesis H: , where are some one-dimensional distribution functions. A simple goodness-of-fit test for hypothesis H can be constructed based on the methodology. This technique is used for discrete models with a finite number of outcomes, so we agree that the random variable takes a finite number s of some values, which we will denote by letters, and the second component - k values. If the original model has a different structure, then the possible values of random variables are preliminarily grouped separately into the first and second components. In this case, the set is divided into s intervals, the value set into k intervals, and the value set itself into N=sk rectangles. Let us denote by the number of observations of the pair (the number of sample elements belonging to the rectangle, if the data are grouped), so that. It is convenient to arrange the observation results in the form of a contingency table of two signs (Table 1.1). In applications and usually mean two criteria by which observation results are classified. Let P, i=1,…,s, j=1,…,k. Then the independence hypothesis means that there are s+k constants such that and, i.e. Table 1.1 Sum . . .. . .. . . . . .. . .. . . . . . . . . . . . . . .Sum . . .n Thus, hypothesis H comes down to the statement that frequencies (their number is N = sk) are distributed according to a polynomial law with probabilities of outcomes having the specified specific structure (the vector of probabilities of outcomes p is determined by the values r = s + k-2 of unknown parameters. To test this hypothesis, we will find maximum likelihood estimates for the unknown parameters that determine the scheme under consideration. If the null hypothesis is true, then the likelihood function has the form L(p)= where the multiplier c does not depend on the unknown parameters. From here, using the Lagrange method of indefinite multipliers, we obtain that the required estimates have the form Therefore, statistics L() at, since the number of degrees of freedom in the limit distribution is equal to N-1-r=sk-1-(s+k-2)=(s-1)(k-1). So, for sufficiently large n, the following hypothesis testing rule can be used: hypothesis H is rejected if and only if the t statistic value calculated from the actual data satisfies the inequality This criterion has an asymptotically (at) given level of significance and is called the independence criterion. 2. PRACTICAL PART 1 Solutions to problems on types of convergence 1. Prove that convergence almost certainly implies convergence in probability. Provide a test example to show that the converse is not true. Solution. Let a sequence of random variables converge to a random variable x almost certainly. So, for anyone? > 0 Since then and from the convergence of xn to x it almost certainly follows that xn converges to x in probability, since in this case But the opposite statement is not true. Let be a sequence of independent random variables having the same distribution function F(x), equal to zero at x? 0 and equal for x > 0. Consider the sequence This sequence converges to zero in probability, since tends to zero for any fixed? And. However, convergence to zero will almost certainly not take place. Really tends to unity, that is, with probability 1 for any and n there will be realizations in the sequence that exceed ?. Note that in the presence of some additional conditions imposed on the quantities xn, convergence in probability implies convergence almost certainly. Let xn be a monotone sequence. Prove that in this case the convergence of xn to x in probability entails the convergence of xn to x with probability 1. Solution. Let xn be a monotonically decreasing sequence, that is. To simplify our reasoning, we will assume that x º 0, xn ³ 0 for all n. Let xn converge to x in probability, but convergence almost certainly does not take place. Does it exist then? > 0, such that for all n But what has been said also means that for all n which contradicts the convergence of xn to x in probability. Thus, for a monotonic sequence xn, which converges to x in probability, also converges with probability 1 (almost certainly). Let the sequence xn converge to x in probability. Prove that from this sequence it is possible to isolate a sequence that converges to x with probability 1 at. Solution. Let be some sequence of positive numbers, and let and be positive numbers such that the series. Let's construct a sequence of indices n1 Then the series Since the series converges, then for any? > 0 the remainder of the series tends to zero. But then it tends to zero and Prove that convergence in average of any positive order implies convergence in probability. Give an example to show that the converse is not true. Solution. Let the sequence xn converge to a value x on average of order p > 0, that is Let us use the generalized Chebyshev inequality: for arbitrary? > 0 and p > 0 Directing and taking into account that, we obtain that that is, xn converges to x in probability. However, convergence in probability does not entail convergence in average of order p > 0. This is illustrated by the following example. Consider the probability space áW, F, Rñ, where F = B is the Borel s-algebra, R is the Lebesgue measure. Let's define a sequence of random variables as follows: The sequence xn converges to 0 in probability, since but for any p > 0 that is, it will not converge on average. Let, what for all n . Prove that in this case xn converges to x in the mean square. Solution. Note that... Let's get an estimate for. Let's consider a random variable. Let be? - an arbitrary positive number. Then at and at. If, then and. Hence, . And because? arbitrarily small and, then at, that is, in the mean square. Prove that if xn converges to x in probability, then weak convergence occurs. Provide a test example to show that the converse is not true. Solution. Let us prove that if, then at each point x, which is a point of continuity (this is a necessary and sufficient condition for weak convergence), is the distribution function of the value xn, and - the value of x. Let x be a point of continuity of the function F. If, then at least one of the inequalities or is true. Then Similarly, for at least one of the inequalities or and If, then for as small as desired? > 0 there exists N such that for all n > N On the other hand, if x is a point of continuity, is it possible to find something like this? > 0, which for arbitrarily small So, for as small as you like? and there exists N such that for n >N or, what is the same, This means that convergence and takes place at all points of continuity. Consequently, weak convergence follows from convergence in probability. The converse statement, generally speaking, does not hold. To verify this, let us take a sequence of random variables that are not equal to constants with probability 1 and have the same distribution function F(x). We assume that for all n the quantities and are independent. Obviously, weak convergence occurs, since all members of the sequence have the same distribution function. Consider: |From the independence and identical distribution of values, it follows that Let us choose among all distribution functions of non-degenerate random variables such F(x) that will be non-zero for all sufficiently small ?. Then it does not tend to zero with unlimited growth of n and convergence in probability will not take place. 7. Let there be weak convergence, where with probability 1 there is a constant. Prove that in this case it will converge to in probability. Solution. Let probability 1 be equal to a. Then weak convergence means convergence for any. Since, then at and at. That is, at and at. It follows that for anyone? > 0 probability tend to zero at. It means that tends to zero at, that is, converges to in probability. 2.2 Solving problems on the central heating center The value of the gamma function Г(x) at x= is calculated by the Monte Carlo method. Let us find the minimum number of tests necessary so that with a probability of 0.95 we can expect that the relative error of calculations will be less than one percent. For up to an accuracy we have It is known that Having made a change in (1), we arrive at the integral over a finite interval: With us, therefore As can be seen, it can be represented in the form where, and is distributed uniformly on. Let statistical tests be carried out. Then the statistical analogue is the quantity where, are independent random variables with a uniform distribution. Wherein From the CLT it follows that it is asymptotically normal with the parameters. This means that the minimum number of tests that ensures with probability the relative error of the calculation is no more than equal. A sequence of 2000 independent identically distributed random variables with a mathematical expectation of 4 and a variance of 1.8 is considered. The arithmetic mean of these quantities is a random variable. Determine the probability that the random variable will take a value in the interval (3.94; 4.12). Let, …,… be a sequence of independent random variables that have the same distribution with M=a=4 and D==1.8. Then the CLT is applicable to the sequence (). Random value Probability that it will take a value in the interval (): For n=2000, 3.94 and 4.12 we get 3 Testing hypotheses using the independence criterion As a result of the study, it was found that 782 light-eyed fathers also have light-eyed sons, and 89 light-eyed fathers have dark-eyed sons. 50 dark-eyed fathers also have dark-eyed sons, and 79 dark-eyed fathers have light-eyed sons. Is there a relationship between the eye color of fathers and the eye color of their sons? Take the confidence level to be 0.99. Table 2.1 ChildrenFathersSumLight-eyedDark-eyedLight-eyed78279861Dark-eyed8950139Sum8711291000 H: There is no relationship between the eye color of children and fathers. H: There is a relationship between the eye color of children and fathers. s=k=2 =90.6052 with 1 degree of freedom The calculations were made in Mathematica 6. Since > , then hypothesis H, about the absence of a relationship between the eye color of fathers and children, at the level of significance, should be rejected and the alternative hypothesis H should be accepted. It is stated that the effect of the drug depends on the method of application. Check this statement using the data presented in table. 2.2 Take the confidence level to be 0.95. Table 2.2 Result Method of application ABC Unfavorable 111716 Favorable 202319 Solution. To solve this problem, we will use a contingency table of two characteristics. Table 2.3 Result Method of application Amount ABC Unfavorable 11171644 Favorable 20231962 Amount 314035106 H: the effect of drugs does not depend on the method of administration H: the effect of drugs depends on the method of application Statistics are calculated using the following formula s=2, k=3, =0.734626 with 2 degrees of freedom. Calculations made in Mathematica 6 From the distribution tables we find that. Because the< , то гипотезу H, про отсутствия зависимости действия лекарств от способа применения, при уровне значимости, следует принять. Conclusion This paper presents theoretical calculations from the section “Independence Criterion”, as well as “Limit Theorems of Probability Theory”, the course “Probability Theory and Mathematical Statistics”. During the work, the independence criterion was tested in practice; Also, for given sequences of independent random variables, the fulfillment of the central limit theorem was checked. This work helped improve my knowledge of these sections of probability theory, work with literary sources, and firmly master the technique of checking the criterion of independence. probabilistic statistical hypothesis theorem List of links 1. Collection of problems from probability theory with solutions. Uch. allowance / Ed. V.V. Semenets. - Kharkov: KhTURE, 2000. - 320 p. Gikhman I.I., Skorokhod A.V., Yadrenko M.I. Theory of Probability and Mathematical Statistics. - K.: Vishcha school, 1979. - 408 p. Ivchenko G.I., Medvedev Yu.I., Mathematical statistics: Textbook. allowance for colleges. - M.: Higher. school, 1984. - 248 p., . Mathematical statistics: Textbook. for universities / V.B. Goryainov, I.V. Pavlov, G.M. Tsvetkova and others; Ed. V.S. Zarubina, A.P. Krischenko. - M.: Publishing house of MSTU im. N.E. Bauman, 2001. - 424 p. Need help studying a topic?
Our specialists will advise or provide tutoring services on topics that interest you. Tutoring
Submit your application indicating the topic right now to find out about the possibility of obtaining a consultation.
 Collection of Russian freaks and bodymodifiers
Collection of Russian freaks and bodymodifiers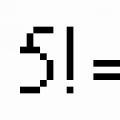 Theory of Probability and Mathematical Statistics
Theory of Probability and Mathematical Statistics Basic concepts of probability theory and mathematical statistics
Basic concepts of probability theory and mathematical statistics