Bernoulli valem erinevate tõenäosuste jaoks. Bernoulli skeemi üldistus
Olgu sündmuse A suhtes läbi viidud n katset. Tutvustame järgmisi sündmusi: Аk -- sündmus А realiseerus k-nda testi käigus, $ k=1,2,\dots , n$. Siis $\bar(A)_(k) $ on vastupidine sündmus (sündmus A ei toimunud k-nda testi käigus, $k=1,2,\dots , n$).
Mis on vastastikused ja sõltumatud katsed
Definitsioon
Teste kutsutakse sündmuse A suhtes sama tüüpi, kui sündmuste $A1, A2, \dots , An$ tõenäosused on samad: $P(A1)=P(A2)= \dots =P(An) $ (st sündmuse A esinemise tõenäosus ühes katses on kõigis katsetes konstantne).
Ilmselgelt antud juhul tõenäosused vastupidised sündmused sobivad ka: $P(\bar(A)_(1))=P(\bar(A)_(2))=...=P(\bar(A)_(n))$.
Definitsioon
Katseid nimetatakse sündmuse A suhtes sõltumatuteks, kui sündmused $A1, A2, \dots , An$ on sõltumatud.
Sel juhul
Sel juhul säilib võrdsus, kui mis tahes sündmus Ak asendatakse $\bar(A)_(k) $-ga.
Olgu sündmuse A suhtes n-i sarnane jada sõltumatud testid. Kanname tähistust: p - sündmuse A tõenäosus ühes testis; q on vastupidise sündmuse tõenäosus. Seega P(Ak)=p, $P(\bar(A)_(k))=q$ mis tahes k korral ja p+q=1.
Tõenäosus, et n-st katsest koosnevas reas toimub sündmus A täpselt k korda (0 ≤ k ≤ n), arvutatakse järgmise valemiga:
$P_(n) (k)=C_(n)^(k) p^(k) q^(n-k) $ (1)
Võrdsust (1) nimetatakse Bernoulli valemiks.
Tõenäosus, et n sama tüüpi sõltumatu katse seerias toimub sündmus A vähemalt k1 korda ja kõige rohkem k2 korda, arvutatakse järgmise valemiga:
$P_(n) (k_(1) \le k\le k_(2))=\sum \limits _(k=k_(1) )^(k_(2) )C_(n)^(k) p ^(k) q^(n-k) $ (2)
Bernoulli valemi rakendamine suured väärtused n põhjustab tülikaid arvutusi, nii et nendel juhtudel on parem kasutada muid valemeid - asümptootilisi.
Bernoulli skeemi üldistus
Mõelge Bernoulli skeemi üldistusele. Kui reas n sõltumatut katset, millest igaühel on m paarikaupa kokkusobimatu ja võimalikud tulemused Ak vastavate tõenäosustega Рk= рk(Аk). Siis kehtib polünoomjaotuse valem:
Näide 1
Epideemia ajal grippi haigestumise tõenäosus on 0,4. Leia tõenäosus, et ettevõtte 6 töötajast haigestub
- täpselt 4 töötajat;
- mitte rohkem kui 4 töötajat.
Lahendus. 1) Ilmselt on selle ülesande lahendamiseks rakendatav Bernoulli valem, kus n=6; k = 4; p = 0,4; q = 1-p = 0,6. Rakendades valemit (1), saame: $P_(6) (4)=C_(6)^(4) \cdot 0.4^(4) \cdot 0.6^(2) \ca 0.138$.
Selle ülesande lahendamiseks kasutatakse valemit (2), kus k1=0 ja k2=4. Meil on:
\[\begin(massiiv)(l) (P_(6) (0\le k\le 4)=\sum \limits _(k=0)^(4)C_(6)^(k) p^( k) q^(6-k) =C_(6)^(0) \cpunkt 0,4^(0) \cpunkt 0,6^(6) +C_(6)^(1) \cpunkt 0,4 ^(1) \cpunkt 0,6^(5) +C_(6)^(2) \cpunkt 0,4^(2) \cpunkt 0,6^(4) +) \\ (+C_(6) ^(3) \cpunkt 0,4^(3) \ cdot 0.6^(3) +C_(6)^(4) \cdot 0.4^(4) \cdot 0.6^(2) \ ligikaudu 0.959.) \end(massiivi)\]
Tuleb märkida, et seda ülesannet on lihtsam lahendada vastupidise sündmuse abil - haigestus üle 4 töötaja. Seejärel, võttes arvesse valemit (7) vastupidiste sündmuste tõenäosuste kohta, saame:
Vastus: $ \ $ 0,959.
Näide 2
Urnis on 20 valget ja 10 musta palli. Võetakse välja 4 palli ja iga väljavõetud pall viiakse urni tagasi enne järgmise loosimist ja urnis olevate pallide segamist. Leia tõenäosus, et joonisel 1 on neljast tõmmatud kuulist 2 valget palli.
1. pilt.
Lahendus. Olgu sündmus A seisneb selles, et - sai valge pall. Siis tõenäosused $D (A)=\frac(2)(3) ,\, \, D (\overline(A))=1-\frac(2)(3) =\frac(1)(3) $ .
Bernoulli valemi järgi on nõutav tõenäosus $D_(4) (2)=N_(4)^(2) \left(\frac(2)(3) \right)^(2) \left(\frac (1)( 3) \parem)^(2) =\frac(8)(27) $.
Vastus: $\frac(8)(27) $.
Näide 3
Määrake tõenäosus, et 5 lapsega peres sünnib kuni 3 tüdrukut. Eeldatakse, et poisi ja tüdruku sünni tõenäosus on sama.
Lahendus. Tüdruku saamise tõenäosus $\partial =\frac(1)(2) ,\, q=\frac(1)(2) $-poissi saamise tõenäosus. Tüdrukuid ei ole peres rohkem kui kolm, mis tähendab, et perre sündis kas üks, kaks või kolm tüdrukut või kõik poisid.
Leidke tõenäosus, et peres ei ole tüdrukuid, sündis üks, kaks või kolm tüdrukut: $D_(5) (0)=q^(5) =\frac(1)(32) $,
\ \ \
Seetõttu on nõutav tõenäosus $D =D_(5) (0)+D_(5) (1)+D_(5) (2)+D_(5) (3)=\frac(13)(16) $ .
Vastus: $\frac(13)(16)$.
Näide 4
Esimene laskur ühe lasuga saab esikümnesse tabada tõenäosusega 0,6, üheksa tõenäosusega 0,3 ja kaheksasse tõenäosusega 0,1. Kui suur on tõenäosus, et ta tabab kümne viskega kümme kuus, üheksa kolm ja kaheksa kaheksa korda?
Kaaluge Binoomjaotus, arvutage selle matemaatiline ootus, dispersioon, moodus. MS EXCEL funktsiooni BINOM.DIST() abil joonistame jaotusfunktsiooni ja tõenäosustiheduse graafikud. Hindame jaotuse parameetrit p, matemaatiline ootus levitamine ja standardhälve. Võtke arvesse ka Bernoulli jaotust.
Definitsioon. Las nad hoitakse n testid, millest igaühes võib toimuda ainult 2 sündmust: sündmus "eduneb" tõenäosusega lk või sündmus "tõrge" tõenäosusega q =1-p (nn Bernoulli skeem,Bernoullikatsumused).
Tõenäosus saada täpselt x edu nendes n testid on võrdne:
Valimi õnnestumiste arv x on juhuslik muutuja, millel on Binoomjaotus(Inglise) Binoomlevitamine) lk Ja n– on selle jaotuse parameetrid.
Kandideerimiseks tuletage see meelde Bernoulli skeemid ja vastavalt binoomjaotus, peavad olema täidetud järgmised tingimused:
- igal katsel peab olema täpselt kaks tulemust, mida tinglikult nimetatakse "edu" ja "ebaõnnestumine".
- iga testi tulemus ei tohiks sõltuda eelmiste testide tulemustest (testi sõltumatus).
- õnnestumise tõenäosus lk peaks olema kõigi testide jaoks konstantne.
Binoomjaotus MS EXCELIS
MS EXCELIS, alates versioonist 2010, jaoks Binoomjaotus on funktsioon BINOM.DIST() , Ingliskeelne pealkiri- BINOM.DIST(), mis võimaldab arvutada tõenäosuse, et valim on täpselt X"edu" (st. tõenäosustiheduse funktsioon p(x), vt ülaltoodud valemit) ja integraalne jaotusfunktsioon(tõenäosus, et proovis on x või vähem "edu", sealhulgas 0).
Enne MS EXCEL 2010 oli EXCELis funktsioon BINOMDIST(), mis võimaldab ka arvutada jaotusfunktsioon Ja tõenäosustihedus p(x). BINOMDIST() on ühilduvuse tagamiseks jäetud MS EXCEL 2010-sse.
Näidisfail sisaldab graafikuid tõenäosusjaotuse tihedus Ja .

Binoomjaotus omab tähistust B(n; lk) .
Märge: Ehitamiseks integraalne jaotusfunktsioon ideaalse sobivuse diagrammi tüüp Ajakava, Sest jaotustihedus – Histogramm koos rühmitamisega. Lisateavet diagrammide ehitamise kohta leiate artiklist Diagrammide peamised tüübid.
Märge: Näidisfaili valemite kirjutamise mugavuse huvides on loodud parameetrite nimed Binoomjaotus: n ja p.

Näidisfail näitab erinevaid tõenäosusarvutusi, kasutades MS EXCELi funktsioone:

Nagu ülaltoodud pildil näha, eeldatakse, et:
- Lõpmatu üldkogum, millest valim tehakse, sisaldab 10% (või 0,1) häid elemente (parameeter lk, funktsiooni kolmas argument =BINOM.DIST() )
- Arvutada tõenäosus, et 10 elemendist koosnevas valimis (parameeter n, funktsiooni teine argument) on täpselt 5 kehtivat elementi (esimene argument), peate kirjutama valemi: =BINOM.DIST(5, 10, 0,1, VÄÄR)
- Viimane, neljas element on seatud = FALSE, st. funktsiooni väärtus tagastatakse jaotustihedus.
Kui neljanda argumendi väärtus on TRUE, tagastab funktsioon BINOM.DIST() väärtuse integraalne jaotusfunktsioon või lihtsalt jaotusfunktsioon. Sel juhul saame arvutada tõenäosuse, et heade elementide arv valimis pärineb teatud vahemik, näiteks 2 või vähem (sh 0).
Selleks peate kirjutama valemi:
= BINOM.DIST(2, 10, 0,1, TÕENE)
Märge: x mittetäisarvulise väärtuse korral . Näiteks järgmised valemid tagastavad sama väärtuse:
=BINOM.DIST( 2
; 10; 0,1; TÕSI)
=BINOM.DIST( 2,9
; 10; 0,1; TÕSI)
Märge: Näidisfailis tõenäosustihedus Ja jaotusfunktsioon arvutatakse ka definitsiooni ja funktsiooni COMBIN() abil.
Jaotusnäitajad
IN näidisfail lehel Näide Mõnede jaotusnäitajate arvutamiseks on olemas valemid:
- =n*p;
- (ruut standardhälve) = n*p*(1-p);
- = (n+1)*p;
- =(1-2*p)*JUUR(n*p*(1-p)).
Tuletame valemi matemaatiline ootus Binoomjaotus kasutades Bernoulli skeem.
A-prioor juhuslik väärtus X sisse Bernoulli skeem(Bernoulli juhuslik muutuja) on jaotusfunktsioon:

Seda jaotust nimetatakse Bernoulli jaotus.
Märge: Bernoulli jaotus – erijuhtum Binoomjaotus parameetriga n=1.
Loome 3 massiivi 100 numbrist koos erinevad tõenäosused edu: 0,1; 0,5 ja 0,9. Selleks aknas Juhuslike arvude genereerimine seatud järgmised parameetrid iga tõenäosuse p kohta:

Märge: kui määrate valiku Juhuslik hajumine (Juhuslik seeme), siis saate valida konkreetse juhuslik komplekt genereeritud numbrid. Näiteks määrates selle valiku =25, saate genereerida erinevates arvutites samu juhuslike arvude komplekte (juhul, kui muud jaotusparameetrid on muidugi samad). Suvandi väärtus võib võtta täisarvud vahemikus 1 kuni 32 767. Suvandi nimi Juhuslik hajumine võib segadusse ajada. Parem oleks see tõlkida kui Määrake arv juhuslike numbritega.
Selle tulemusena saame 3 veergu 100 numbriga, mille põhjal saame näiteks hinnata edu tõenäosust lk valemi järgi: Õnnestumiste arv/100(cm. näidisfailileht Bernoulli genereerimine).

Märge: Sest Bernoulli distributsioonid kui p=0,5, saate kasutada valemit =RANDBETWEEN(0;1) , mis vastab .
Juhuslike arvude genereerimine. Binoomjaotus
Oletame, et proovis on 7 defektset eset. See tähendab, et on "väga tõenäoline", et defektsete toodete osakaal on muutunud. lk, mis on meie tootmisprotsessile iseloomulik. Kuigi see olukord on "väga tõenäoline", on olemas võimalus (alfa risk, 1. tüüpi viga, "valehäire"). lk jäi muutumatuks ning defektsete toodete arvu suurenemine oli tingitud juhuslikust proovivõtust.
Nagu on näha alloleval joonisel, on 7 defektsete toodete arv, mis on vastuvõetav protsessi jaoks, mille p=0,21 sama väärtuse juures Alfa. See näitab, et kui proovis on defektsete esemete piirmäär ületatud, lk"tõenäoliselt" suurenenud. Väljend "kõige tõenäolisemalt" tähendab, et on vaid 10% tõenäosus (100%-90%), et defektsete toodete osakaalu hälve üle läve on tingitud ainult juhuslikest põhjustest.

Seega võib proovis olevate defektsete toodete künnise ületamine olla signaaliks, et protsess on häiritud ja hakkas tootma b. O suurem defektsete toodete protsent.
Märge: Enne MS EXCEL 2010 oli EXCELil funktsioon CRITBINOM() , mis on samaväärne funktsiooniga BINOM.INV() . CRITBINOM() jäetakse ühilduvuse tagamiseks MS EXCEL 2010 ja uuemates versioonides.
Binoomjaotuse seos teiste jaotustega
Kui parameeter n Binoomjaotus kipub lõpmatusse ja lk kipub olema 0, siis antud juhul Binoomjaotus saab ligikaudselt hinnata.
Tingimusi on võimalik sõnastada, kui lähendus Poissoni jaotus töötab hästi:
- lk<0,1 (vähem lk ja veel n, seda täpsem on lähendus);
- lk>0,9 (võttes arvesse, et q=1- lk, tuleb sel juhul arvutused teha kasutades q(A X tuleb asendada n- x). Seetõttu, mida vähem q ja veel n, seda täpsem on lähendus).
Kell 0,1<=p<=0,9 и n*p>10 Binoomjaotus saab ligikaudselt hinnata.
Omakorda Binoomjaotus võib olla hea ligikaudne väärtus, kui populatsiooni suurus on N Hüpergeomeetriline jaotus palju suurem kui valimi suurus n (st N>>n või n/N<<1).
Lisateavet ülaltoodud jaotuste seoste kohta saate lugeda artiklist. Seal tuuakse ka näiteid lähendusest ning selgitatakse tingimusi, millal see võimalik on ja millise täpsusega.
NÕUANNE: MS EXCELi muude distributsioonide kohta saate lugeda artiklist.
Lühike teooria
Tõenäosusteooria käsitleb katseid, mida saab korrata (vähemalt teoreetiliselt) piiramatu arv kordi. Mõnda katset korratakse üks kord ja iga korduse tulemused ei sõltu eelnevate korduste tulemustest. Selliseid korduste seeriaid nimetatakse sõltumatuteks katseteks. Selliste testide erijuhtum on sõltumatud Bernoulli kohtuprotsessid, mida iseloomustavad kaks tingimust:
1) iga testi tulemus on üks kahest võimalikust tulemusest, mida nimetatakse vastavalt "edu" või "ebaõnnestumine".
2) iga järgneva testi "edusaamise" tõenäosus ei sõltu eelnevate testide tulemustest ja jääb konstantseks.
Bernoulli teoreem
Kui tehakse rida sõltumatuid Bernoulli katseid, millest igaühes saavutatakse "edu" tõenäosusega , siis tõenäosus, et "edu" toimub katsetes täpselt üks kord, väljendatakse valemiga:
kus on ebaõnnestumise tõenäosus.
- elementide kombinatsioonide arv (vt kombinatoorika põhivalemeid)
Seda valemit nimetatakse Bernoulli valem.
Bernoulli valem võimaldab vabaneda suurest arvust arvutustest – tõenäosuste liitmisest ja korrutamisest – piisavalt suure hulga testidega.
Bernoulli testi skeemi nimetatakse ka binoomskeemiks ja vastavaid tõenäosusi binoomseks, mida seostatakse binoomkoefitsientide kasutamisega.
Bernoulli skeemi kohane jaotus võimaldab eelkõige leida sündmuse kõige tõenäolisema esinemise arvu.
Kui katsete arv n suurepärane, siis naudi:
Probleemilahenduse näide
Ülesanne
Teatud taime seemnete idanevus on 70%. Kui suur on tõenäosus, et 10 külvatud seemnest: 8, vähemalt 8; vähemalt 8?
Probleemi lahendus
Kasutame Bernoulli valemit:
Meie puhul
Laske sündmusel - 10 seemnest tärkab 8:
Laske sündmusel tõusta vähemalt 8 (see tähendab 8, 9 või 10)
Laske sündmusel tõusta vähemalt 8 (see tähendab 8,9 või 10)
Vastus
Keskmine kontrolltööde lahendamise maksumus on 700 - 1200 rubla (kuid mitte vähem kui 300 rubla kogu tellimuse kohta). Hinda mõjutab tugevalt otsuse kiireloomulisus (päevadest mitme tunnini). Eksami / testi veebiabi maksumus - alates 1000 rubla. piletilahenduse eest.
Rakenduse saab jätta otse vestlusse, olles eelnevalt ülesannete seisukorrast välja visanud ja teavitades selle lahendamise tähtaegadest. Reaktsiooniaeg on mitu minutit.
Ärgem mõelgem pikalt kõrgele – alustame kohe definitsiooniga.
- see on siis, kui tehakse n sama tüüpi sõltumatut katset, millest igaühes võib ilmneda meile huvipakkuv sündmus A ja selle sündmuse tõenäosus P (A) \u003d p on teada. On vaja kindlaks määrata tõenäosus, et sündmus A toimub täpselt k korda n katse jooksul.
Bernoulli skeemi järgi lahendatavad ülesanded on äärmiselt mitmekesised: lihtsatest (näiteks "leia tõenäosus, et laskur tabab 1 kord 10-st") kuni väga raskete ülesanneteni (näiteks protsentide või mängukaartide ülesanded) . Tegelikkuses kasutatakse seda skeemi sageli toodete kvaliteedikontrolli ja erinevate mehhanismide töökindlusega seotud probleemide lahendamiseks, mille kõik omadused peavad olema teada enne töö alustamist.
Lähme tagasi definitsiooni juurde. Kuna me räägime sõltumatutest katsetest ja igas katses on sündmuse A tõenäosus sama, on võimalikud ainult kaks tulemust:
- A on sündmuse A toimumine tõenäosusega p;
- "mitte A" - sündmust A ei ilmnenud, mis juhtub tõenäosusega q = 1 − p.
Kõige olulisem tingimus, ilma milleta Bernoulli skeem kaotab oma tähenduse, on püsivus. Ükskõik kui palju katseid me ka ei teeks, oleme huvitatud samast sündmusest A, mis toimub sama tõenäosusega p.
Muide, kõiki tõenäosusteooria probleeme ei saa taandada konstantsetele tingimustele. Iga pädev kõrgema matemaatika juhendaja räägib teile sellest. Isegi nii lihtne asi nagu värviliste pallide karbist välja korjamine ei ole pidevate tingimustega eksperiment. Nad võtsid välja veel ühe palli – värvide suhe kastis muutus. Seetõttu on ka tõenäosused muutunud.
Kui tingimused on konstantsed, saab täpselt määrata tõenäosuse, et sündmus A toimub täpselt k korda n-st võimalikust. Sõnastame selle fakti teoreemi kujul:
Olgu sündmuse A toimumise tõenäosus igas katses konstantne ja võrdne p-ga. Seejärel arvutatakse valemiga tõenäosus, et n sõltumatus katses ilmub sündmus A täpselt k korda:
kus C n k on kombinatsioonide arv, q = 1 − p.
Seda valemit nimetatakse: Huvitav on märkida, et alltoodud probleemid lahendatakse täielikult ilma seda valemit kasutamata. Näiteks saate rakendada tõenäosuse liitmise valemeid. Arvutuste maht on aga lihtsalt ebareaalne.
Ülesanne. Tõenäosus, et masinal tekib defektne toode, on 0,2. Määrake tõenäosus, et antud masinal toodetud kümnest detailist koosnevas partiis on täpselt k defektideta. Lahendage ülesanne k = 0, 1, 10 korral.
Tingimuse järgi huvitab meid defektideta toodete vabastamise sündmus A, mis juhtub iga kord tõenäosusega p = 1 − 0,2 = 0,8. Peame määrama tõenäosuse, et see sündmus toimub k korda. Sündmus A vastandub sündmusele "mitte A", st. defektse toote tootmine.
Seega on meil: n = 10; p = 0,8; q = 0,2.
Seega leiame tõenäosuse, et kõik partii osad on defektsed (k = 0), et ainult üks osa on defektne (k = 1) ja defektseid osi pole üldse (k = 10):

Ülesanne. Münti visatakse 6 korda. Sama tõenäoline on vapi ja saba kadumine. Leidke tõenäosus, et:
- vapp langeb kolm korda;
- vapp langeb üks kord;
- vapp ilmub vähemalt kaks korda.
Niisiis, meid huvitab sündmus A, mil vapp kukub välja. Selle sündmuse tõenäosus on p = 0,5. Sündmusele A vastandub sündmus “mitte A”, kui see tekib sabad, mis juhtub tõenäosusega q = 1 − 0,5 = 0,5. Tuleb määrata tõenäosus, et vapp kukub välja k korda.
Seega on meil: n = 6; p = 0,5; q = 0,5.
Määrame tõenäosuse, et vapp kukkus välja kolm korda, s.o. k = 3:
Nüüd määrame tõenäosuse, et vapp kukkus välja vaid korra, s.o. k = 1:
Jääb veel kindlaks teha, kui suure tõenäosusega kukub vapp välja vähemalt kaks korda. Peamine tõrge on fraasis "mitte vähem". Selgub, et meile sobib iga k, välja arvatud 0 ja 1, s.t. peate leidma summa X \u003d P 6 (2) + P 6 (3) + ... + P 6 (6).
Pange tähele, et see summa võrdub ka (1 − P 6 (0) − P 6 (1)), s.o. kõigist võimalikest variantidest piisab, kui “välja lõigata” need, mil vapp kukkus välja 1 korra (k = 1) või ei kukkunud üldse välja (k = 0). Kuna P 6 (1) me juba teame, jääb üle leida P 6 (0):

Ülesanne. Tõenäosus, et teleris on varjatud defekte, on 0,2. Ladu sai 20 telerit. Kumb sündmus on tõenäolisem: kas selles partiis on kaks varjatud defektidega telerit või kolm?
Huvipakkuv sündmus A on varjatud defekti olemasolu. Telereid kokku n = 20, varjatud defekti tõenäosus p = 0,2. Vastavalt sellele on tõenäosus saada teler ilma varjatud defektita q = 1 − 0,2 = 0,8.
Bernoulli skeemi lähtetingimused saame: n = 20; p = 0,2; q = 0,8.
Leiame kahe "defektse" teleri (k = 2) ja kolme (k = 3) saamise tõenäosuse:
\[\begin(massiivi)(l)(P_(20))\left(2 \right) = C_(20)^2(p^2)(q^(18)) = \frac((20)}{{2!18!}} \cdot {0,2^2} \cdot {0,8^{18}} \approx 0,137\\{P_{20}}\left(3 \right) = C_{20}^3{p^3}{q^{17}} = \frac{{20!}}{{3!17!}} \cdot {0,2^3} \cdot {0,8^{17}} \approx 0,41\end{array}\]!}
Ilmselgelt P 20 (3) > P 20 (2), s.o. tõenäosus saada kolm varjatud defektidega telerit on tõenäolisemalt ainult kaks sellist telerit. Pealegi pole erinevus nõrk.
Väike märkus faktoriaalide kohta. Paljud inimesed kogevad ebamäärast ebamugavustunnet, kui nad näevad kirjet "0!" (loe "nullfaktoriaal"). Niisiis, 0! = 1 definitsiooni järgi.
P.S. Ja viimase ülesande suurim tõenäosus on saada neli varjatud defektidega telerit. Arvutage ja vaadake ise.
Vaata ka:
Täname, et lugesite ja jagate teistega
Tõenäosusprobleemide lahendamisel tuleb sageli ette olukordi, kus sama katset korratakse mitu korda ja iga katse tulemus on sõltumatu teiste tulemustest. Seda katset nimetatakse ka korduvate sõltumatute testide skeem või Bernoulli skeem.
Kordustestide näited:
1) ühe palli urnist mitmekordne väljatõmbamine tingimusel, et pärast selle värvi registreerimist välja võetud pall pannakse urni tagasi;
2) laskude kordamine ühe laskuri poolt samasse märklauda, eeldusel, et iga lasuga eduka tabamise tõenäosus loetakse samaks (nullimise rolli ei arvestata).
Niisiis, lase katse tulemusena võimalik kaks tulemust: kas ilmub sündmus A või selle vastupidine sündmus. Viime läbi n Bernoulli katset. See tähendab, et kõik n katset on sõltumatud; sündmuse $A$ esinemise tõenäosus igas üksikus või üksikus testis on konstantne ega muutu testiti (st testid viiakse läbi samadel tingimustel). Tähistame sündmuse $A$ toimumise tõenäosust ühes katses tähega $p$, s.o. $p=P(A)$ ja vastupidise sündmuse (sündmust $A$ ei toimunud) tõenäosus on antud tähega $q=P(\overline(A))=1-p$.
Siis tõenäosus, et sündmus A ilmub neis n testid täpselt k korda, väljendatud Bernoulli valem
$$P_n(k)=C_n^k \cdot p^k \cdot q^(n-k), \quad q=1-p.$$
Õnnetuste (sündmuse esinemiste) arvu jaotust nimetatakse binoomjaotus.
Interneti-kalkulaatorid Bernoulli valemi jaoks
Mõnda kõige populaarsemat Bernoulli valemit kasutavat probleemitüüpi analüüsitakse artiklites ja need on varustatud veebikalkulaatoriga, mille juurde saate linke kasutades:
Bernoulli valemi ülesannete lahendusnäited
Näide. Urnis on 20 valget ja 10 musta palli. Võetakse välja 4 palli ja iga väljavõetud pall viiakse urni tagasi enne järgmise loosimist ja urnis olevate pallide segamist.
Bernoulli valem. Probleemi lahendamine
Leidke tõenäosus, et 4 joonistatud kuulist 2 on valged.
Lahendus. Sündmus A- sain valge palli. Siis tõenäosused
, .
Bernoulli valemi järgi on nõutav tõenäosus ![]() .
.
Näide. Määrake tõenäosus, et 5 lapsega peres sünnib kuni 3 tüdrukut. Eeldatakse, et poisi ja tüdruku sünni tõenäosus on sama.
Lahendus. Tüdruku saamise tõenäosus
, Siis.
Leiame tõenäosused, et peres pole tüdrukuid, sündis üks, kaks või kolm tüdrukut:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Seega soovitud tõenäosus
![]() .
.
Näide. Töötaja poolt töödeldud detailide hulgas on keskmiselt 4% ebastandardseid. Leidke tõenäosus, et 30 testimiseks võetud osast kaks on mittestandardsed.
Lahendus. Siin seisneb kogemus kõigi 30 osa kvaliteedi kontrollimises.
Sündmus A on "mittestandardse osa ilmumine", selle tõenäosus on siis . Siit leiame Bernoulli valemi järgi
.
Näide. Iga püssist tehtud lasu korral on sihtmärki tabamise tõenäosus 0,9. Leidke tõenäosus, et 20 löögist on õnnestunud löökide arv vähemalt 16 ja kõige rohkem 19.
Lahendus. Arvutame Bernoulli valemiga:

Näide. Sõltumatud katsed jätkuvad kuni sündmuseni A ei juhtu küks kord. Leidke tõenäosus, et see võtab n katsed (n ³ k), kui igas neist .
Lahendus. Sündmus IN- täpselt n testid enne k- sündmuse toimumine A on kahe järgmise sündmuse tulemus:
D-in n th test A juhtus;
C - esimene (n–1) th test A ilmunud (k-1)üks kord.
Korrutusteoreem ja Bernoulli valem annavad vajaliku tõenäosuse:
Tuleb märkida, et binoomseaduse kasutamine on sageli seotud arvutusraskustega. Seetõttu kasvavate väärtustega n Ja m otstarbekaks muutub ligikaudsete valemite kasutamine (Poisson, Moivre-Laplace), millest tuleb juttu järgmistes osades.
Videoõpetus Bernoulli valem
Neile, kes on järjestikuses videoselgituses visuaalsemad, 15-minutiline video:
Kogutõenäosuse valem: probleemide lahendamise teooria ja näited
Kogutõenäosuse valem ja sündmuste tingimuslikud tõenäosused
Kogutõenäosuse valem on tõenäosusteooria põhireeglite – liitmise ja korrutamise reegli – tagajärg.
Kogutõenäosuse valem võimaldab leida sündmuse tõenäosuse A, mis võib esineda ainult kõigiga nüksteist välistavad sündmused, mis moodustavad tervikliku süsteemi, kui nende tõenäosused on teada, ja tingimuslikud tõenäosused sündmused A süsteemi iga sündmuse puhul on võrdsed .
Sündmusi nimetatakse ka hüpoteesideks, need välistavad üksteist. Seetõttu leiate kirjandusest ka nende tähistuse mitte tähe järgi B, aga kirjaga H(hüpotees).
Selliste tingimustega seotud probleemide lahendamiseks on vaja arvestada 3, 4, 5 või üldiselt n sündmuse võimalus A iga sündmusega.
Kasutades tõenäosuste liitmise ja korrutamise teoreeme, saame süsteemi iga sündmuse tõenäosuse korrutiste summa tingimuslik tõenäosus sündmused A iga süsteemi sündmuse kohta.
21 Bernoulli kohtuprotsess. Bernoulli valem
See tähendab sündmuse tõenäosust A saab arvutada valemiga

või üldiselt
![]() ,
,
mida nimetatakse kogu tõenäosuse valem .
Kogutõenäosuse valem: näited probleemide lahendamisest
Näide 1Ühesuguse välimusega urne on kolm: esimeses on 2 valget ja 3 musta palli, teises 4 valget ja üks must, kolmandas kolm valget kuuli. Keegi läheneb juhuslikult ühele urnile ja võtab sealt ühe palli välja. Kasu lõikama kogu tõenäosuse valem, leidke tõenäosus, et pall on valge.
Lahendus. Sündmus A- valge palli välimus. Esitame kolm hüpoteesi:
— valitakse esimene urn;
— valitakse teine urn;
— valitakse kolmas urn.
Tingimuslikud sündmuse tõenäosused A iga hüpoteesi jaoks:
![]() ,
, ![]() , .
, .
Rakendame kogu tõenäosuse valemit, mille tulemusena - nõutav tõenäosus:
![]() .
.
Näide 2 Esimeses tehases toodetakse igast 100 lambipirnist keskmiselt 90 tavalist, teises - 95, kolmandas - 85 ning nende tehaste toodang on vastavalt 50%, 30% ja 20% elektripirnist. kõik elektripirnid, mis tarnitakse teatud piirkonna kauplustesse. Leidke tavalise lambipirni ostmise tõenäosus.
Lahendus. Tähistame standardse lambipirni omandamise tõenäosust kui A, ja sündmused, mille kaudu ostetud lambipirn on valmistatud vastavalt esimeses, teises ja kolmandas tehases. Tingimuste järgi on teada nende sündmuste tõenäosused: , , ja sündmuse tingimuslikud tõenäosused A igaühe kohta neist: ![]() ,
, ![]() ,
, ![]() . Need on tavalise lambipirni omandamise tõenäosused eeldusel, et see on toodetud vastavalt esimeses, teises ja kolmandas tehases.
. Need on tavalise lambipirni omandamise tõenäosused eeldusel, et see on toodetud vastavalt esimeses, teises ja kolmandas tehases.
Sündmus A toimub sündmuse toimumisel või K– pirn on valmistatud esimeses tehases ja on standardne või üritus L- pirn on valmistatud teises tehases ja on standardne või üritus M- pirn on toodetud kolmandas tehases ja on standardne.
Muud sündmuse toimumise võimalused A Ei. Seetõttu üritus A on sündmuste summa K, L Ja M mis on kokkusobimatud. Tõenäosuste liitmise teoreemi rakendades esitame sündmuse tõenäosuse A nagu

ja tõenäosuste korrutamise teoreemiga saame

see on, kogutõenäosuse valemi erijuhtum.
Asendades tõenäosused valemi vasakpoolsesse serva, saame sündmuse tõenäosuse A:
![]()
Kas teil pole aega lahendusse süveneda? Tööd saab tellida!
Näide 3 Lennuk maandub lennujaamas. Kui ilm lubab, maandab piloot lennuki, kasutades lisaks instrumentidele ka visuaalset vaatlust. Sel juhul on eduka maandumise tõenäosus . Kui lennuväljal on pilves madal pilvisus, siis piloot maandab lennuki, orienteerudes ainult instrumentidel. Sel juhul on eduka maandumise tõenäosus ; .
Pimemaandumist võimaldavatel seadmetel on töökindlus (tõrgeteta töötamise tõenäosus) P. Madala pilvisusega ja ebaõnnestunud pimemaandumise instrumentide olemasolul on eduka maandumise tõenäosus ; . Statistika näitab, et aastal k% maandumistest on lennuväli kaetud madalate pilvedega. Otsi sündmuse täieliku tõenäosusegaA- õhusõiduki ohutu maandumine.
Lahendus. Hüpoteesid:
— madalaid pilvi pole;
- Pilvisus on madal.
Nende hüpoteeside (sündmuste) tõenäosused:
![]() ;
;
Tingimuslik tõenäosus.
Tingimuslik tõenäosus leitakse jällegi kogutõenäosuse valemiga koos hüpoteesidega
- töötavad pimemaandumisseadmed;
- pimemaandumisseadmed ebaõnnestusid.
Nende hüpoteeside tõenäosused on järgmised:
Kogutõenäosuse valemi järgi
Näide 4 Seade võib töötada kahes režiimis: tavaline ja ebanormaalne. Tavalist režiimi täheldatakse 80% kõigist seadme tööjuhtudest ja ebanormaalset - 20% juhtudest. Seadme rikke tõenäosus teatud aja jooksul t võrdne 0,1; ebanormaalses 0,7. Otsi täieliku tõenäosusega seadme rike õigel ajal t.
Lahendus. Seadme rikke tõenäosust tähistame jälle kui A. Niisiis, mis puudutab seadme töötamist igas režiimis (sündmused), siis on tõenäosused teada tingimuse järgi: tavarežiimi puhul on see 80% (), ebanormaalse režiimi puhul - 20% (). Sündmuse tõenäosus A(see tähendab, et seadme rike) olenevalt esimesest sündmusest (tavarežiim) on 0,1 (); sõltuvalt teisest sündmusest (ebanormaalne režiim) - 0,7 ( ![]() ). Asendame need väärtused kogutõenäosuse valemiga (st süsteemi iga sündmuse tõenäosuse ja sündmuse tingimusliku tõenäosuse korrutistega A süsteemi iga sündmuse kohta) ja meil on nõutav tulemus.
). Asendame need väärtused kogutõenäosuse valemiga (st süsteemi iga sündmuse tõenäosuse ja sündmuse tingimusliku tõenäosuse korrutistega A süsteemi iga sündmuse kohta) ja meil on nõutav tulemus.
Bernoulli valem- tõenäosusteooria valem, mis võimaldab leida sündmuse toimumise tõenäosust A (\displaystyle A) sõltumatutes testides. Bernoulli valem võimaldab vabaneda suurest arvust arvutustest – tõenäosuste liitmisest ja korrutamisest – piisavalt suure hulga testidega. Nimetatud silmapaistva Šveitsi matemaatiku Jacob Bernoulli järgi, kes selle valemi tuletas.
Entsüklopeediline YouTube
1 / 3
✪ Tõenäosusteooria. 22. Bernoulli valem. Probleemi lahendamine
✪ Bernoulli valem
✪ 20 kordustesti Bernoulli valem
Subtiitrid
Sõnastus
Teoreem. Kui tõenäosus p (\displaystyle p) sündmus A (\displaystyle A) on igas katses konstantne, siis tõenäosus P k , n (\displaystyle P_(k,n)) et sündmus A (\displaystyle A) tuleb täpselt k (\displaystyle k)ükskord n (\displaystyle n) sõltumatud testid on võrdne: P k , n = C n k ⋅ p k ⋅ q n − k (\displaystyle P_(k,n)=C_(n)^(k)\cdot p^(k)\cdot q^(n-k)), Kus q = 1 – p (\displaystyle q=1-p).
Tõestus
Las see peetakse n (\displaystyle n) sõltumatud testid ja on teada, et iga testi tulemusena sündmus A (\displaystyle A) kaasneb tõenäosusega P (A) = p (\displaystyle P\left(A\right)=p) ja seetõttu ei esine seda tõenäoliselt P (A ¯) = 1 − p = q (\displaystyle P\left((\bar (A))\right)=1-p=q). Olgu ka tõenäosustestide käigus p (\displaystyle p) Ja q (\displaystyle q) jäävad muutumatuks. Kui suur on tõenäosus, et selle tulemusena n (\displaystyle n) sõltumatu test, sündmus A (\displaystyle A) tuleb täpselt k (\displaystyle k)üks kord?
Selgub, et on võimalik täpselt välja arvutada testitulemuste "edukate" kombinatsioonide arv, mille puhul sündmus A (\displaystyle A) tuleb k (\displaystyle k)ükskord n (\displaystyle n) sõltumatud katsed, on täpselt kombinatsioonide arv n (\displaystyle n) Kõrval k (\displaystyle k) :
C n (k) = n! k! (n − k) ! (\displaystyle C_(n)(k)=(\frac (n{k!\left(n-k\right)!}}} !}.
Samal ajal, kuna kõik katsed on sõltumatud ja nende tulemused ei ühildu (sündmus A (\displaystyle A) kas esineb või mitte), siis on "eduka" kombinatsiooni saamise tõenäosus täpselt: .
Lõpuks, et leida tõenäosus, et n (\displaystyle n) sõltumatu testüritus A (\displaystyle A) tuleb täpselt k (\displaystyle k) korda, peate liitma kõigi "edukate" kombinatsioonide saamise tõenäosused. Tõenäosused saada kõik "edukad" kombinatsioonid on ühesugused ja võrdsed p k ⋅ q n − k (\displaystyle p^(k)\cdot q^(n-k)), "edukate" kombinatsioonide arv on C n (k) (\displaystyle C_(n) (k)), nii et lõpuks saame:
P k , n = C n k ⋅ p k ⋅ q n − k = C n k ⋅ p k ⋅ (1 − p) n − k (\displaystyle P_(k,n)=C_(n)^(k)\cdot p^( k)\cdot q^(n-k)=C_(n)^(k)\cdot p^(k)\cdot (1-p)^(n-k)).
Viimane väljend pole midagi muud kui Bernoulli valem. Samuti on kasulik märkida, et sündmuste rühma täielikkuse tõttu on see tõsi:
∑ k = 0 n (P k , n) = 1 (\kuvastiil \summa _(k=0)^(n)(P_(k,n))=1).
 Kümnendmurru teisendamine tavaliseks murruks ja vastupidi: reegel, näited
Kümnendmurru teisendamine tavaliseks murruks ja vastupidi: reegel, näited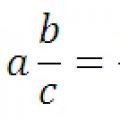 Kümnendarvude teisendamine harilikeks murdudeks
Kümnendarvude teisendamine harilikeks murdudeks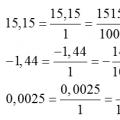 Hariliku murru teisendamine kümnendmurruks ja vastupidi, reeglid, näited
Hariliku murru teisendamine kümnendmurruks ja vastupidi, reeglid, näited