Binom distribucije. Distribucije vjerojatnosti diskretnih slučajnih varijabli

Teorija vjerojatnosti nevidljivo je prisutna u našim životima. Ne obraćamo pažnju na to, ali svaki događaj u našem životu ima jednu ili drugu vjerojatnost. Obrati pozornost na veliki iznos scenarija, postaje neophodno da odredimo najvjerojatnije i najmanje vjerojatne od njih. Najprikladnije je takve vjerojatnosne podatke analizirati grafički. U tome nam može pomoći distribucija. Binom je jedan od najjednostavnijih i najpreciznijih.

Prije nego što prijeđemo izravno na matematiku i teoriju vjerojatnosti, shvatimo tko je prvi smislio ovu vrstu distribucije i koja je povijest razvoja matematički aparat za ovaj koncept.

Priča

Pojam vjerojatnosti poznat je od davnina. Međutim, stari matematičari tome nisu pridavali veliku važnost i uspjeli su samo postaviti temelje za teoriju koja je kasnije postala teorija vjerojatnosti. Stvorili su neke kombinatorne metode, što je uvelike pomoglo onima koji su kasnije stvarali i razvijali samu teoriju.

U drugoj polovici sedamnaestog stoljeća počinje formiranje osnovnih pojmova i metoda teorije vjerojatnosti. Uvedene su definicije slučajnih varijabli, metode za izračunavanje vjerojatnosti jednostavnih i nekih složenih neovisnih i ovisni događaji. Takav interes za slučajne varijable i vjerojatnosti diktirao je Kockanje: Svaka je osoba htjela znati kolike su mu šanse za pobjedu u igri.

Sljedeći korak bila je primjena metoda matematičke analize u teoriji vjerojatnosti. Eminentni matematičari kao što su Laplace, Gauss, Poisson i Bernoulli preuzeli su ovaj zadatak. Upravo su oni unaprijedili ovo područje matematike nova razina. James Bernoulli je otkrio zakon binomne distribucije. Inače, kako ćemo kasnije saznati, na temelju ovog otkrića napravljeno je još nekoliko, što je omogućilo stvaranje zakona normalne raspodjele i mnogih drugih.

Sada, prije nego počnemo opisivati binomnu distribuciju, malo ćemo osvježiti sjećanje na pojmove teorije vjerojatnosti, vjerojatno već zaboravljene iz školske klupe.

Osnove teorije vjerojatnosti

Razmotrit ćemo takve sustave, kao rezultat kojih su moguća samo dva ishoda: "uspjeh" i "neuspjeh". To je lako razumjeti na primjeru: bacamo novčić, pogađajući da će ispasti repovi. Vjerojatnosti svakog od mogućih događaja (padanje repova - "uspjeh", padanje glava - "neuspjeh") jednake su 50 posto ako je novčić savršeno uravnotežen i nema drugih čimbenika koji mogu utjecati na eksperiment.

Bio je to najjednostavniji događaj. Ali postoje i složeni sustavi, u kojem se izvode sekvencijalne radnje, a vjerojatnosti ishoda tih radnji će se razlikovati. Na primjer, razmotrimo sljedeći sustav: u kutiji čiji sadržaj ne vidimo nalazi se šest apsolutno identičnih kuglica, tri para plavih, crvenih i bijelo cvijeće. Moramo dobiti nekoliko lopti nasumce. Sukladno tome, izvlačenjem prve bijele kuglice nekoliko puta ćemo smanjiti vjerojatnost da će i sljedeća također dobiti bijelu kuglicu. To se događa jer se broj objekata u sustavu mijenja.

U sljedeći odjeljak smatrati složenijim matematički pojmovi, približavajući nam riječi " normalna distribucija"," binomna distribucija "i slično.

Elementi matematičke statistike

U statistici, koja je jedno od područja primjene teorije vjerojatnosti, ima mnogo primjera gdje podaci za analizu nisu dati eksplicitno. Odnosno, ne u brojevima, već u obliku podjele prema karakteristikama, na primjer, prema spolu. Da bi se primijenio matematički aparat na takve podatke i izvukli neki zaključci iz dobivenih rezultata, potrebno je početne podatke pretvoriti u format broja. U pravilu, za provedbu toga, pozitivnom ishodu se dodjeljuje vrijednost 1, a negativnom se dodjeljuje vrijednost 0. Na taj način dobivamo statističke podatke koji se mogu analizirati matematičkim metodama.

Sljedeći korak u razumijevanju binomne distribucije slučajne varijable je određivanje varijance slučajne varijable i matematičko očekivanje. O tome ćemo govoriti u sljedećem odjeljku.

Očekivana vrijednost

Zapravo, nije teško razumjeti što je matematičko očekivanje. Razmotrimo sustav u kojem postoji mnogo različite događaje s njihovim različite vjerojatnosti. Matematičko očekivanje će se zvati vrijednost, jednak zbroju proizvodi vrijednosti tih događaja (i matematički oblik, o čemu smo govorili u prethodnom odjeljku) o vjerojatnosti njihove provedbe.

Matematičko očekivanje binomne distribucije izračunava se po istoj shemi: uzmemo vrijednost slučajne varijable, pomnožimo je s vjerojatnošću pozitivnog ishoda, a zatim sumiramo dobivene podatke za sve varijable. Vrlo je zgodno te podatke prikazati grafički - na taj način se bolje uočava razlika između matematičkih očekivanja različitih vrijednosti.

U sljedećem ćemo vam odjeljku reći nešto o drugom konceptu - varijanci slučajne varijable. Također je usko povezan s takvim konceptom kao što je binomna distribucija vjerojatnosti i njegova je karakteristika.

Varijanca binomne distribucije

Ova je vrijednost usko povezana s prethodnom i također karakterizira distribuciju statističkih podataka. Ona predstavlja srednji trg odstupanja vrijednosti od njihovog matematičkog očekivanja. Odnosno, varijanca slučajne varijable je zbroj kvadrata razlika između vrijednosti slučajne varijable i njezinog matematičkog očekivanja, pomnožen s vjerojatnošću tog događaja.

Općenito, ovo je sve što trebamo znati o varijanci da bismo razumjeli što je binomna distribucija vjerojatnosti. Sada prijeđimo na našu glavnu temu. Naime, ono što se iza ovoga krije naizgled je dovoljno složena fraza"binomni zakon distribucije".

Binomna distribucija

Prvo shvatimo zašto je ova distribucija binomna. Dolazi od riječi "binom". Možda ste čuli za Newtonov binom - formulu koja se može koristiti za proširenje zbroja bilo koja dva broja a i b na bilo koju nenegativnu potenciju od n.

Kao što ste vjerojatno već pogodili, Newtonova binomna formula i formula binomne distribucije gotovo su iste formule. S jedinom iznimkom koju drugi ima primijenjena vrijednost Za specifične količine, a prvi je samo opći matematički alat čije primjene u praksi mogu biti različite.

Formule raspodjele

Funkcija binomne distribucije može se napisati kao zbroj sljedećih članova:

(n!/(n-k)!k!)*p k *q n-k

Ovdje je n broj neovisnih slučajnih eksperimenata, p je broj uspješnih ishoda, q je broj neuspješnih ishoda, k je broj eksperimenta (može poprimiti vrijednosti od 0 do n),! - oznaka faktorijela, takve funkcije broja, čija je vrijednost jednaka umnošku svih brojeva koji idu do njega (na primjer, za broj 4: 4!=1*2*3*4= 24).

Osim toga, funkcija binomne distribucije može se napisati kao nepotpuna beta funkcija. Međutim, to je već složenija definicija, koja se koristi samo pri rješavanju složenih statističkih problema.

Binomna distribucija, čije smo primjere ispitali gore, jedan je od najvažnijih jednostavne vrste distribucije u teoriji vjerojatnosti. Postoji i normalna distribucija, koja je vrsta binomne distribucije. Najčešće se koristi i najlakše ga je izračunati. Postoji i Bernoullijeva distribucija, Poissonova distribucija, uvjetna distribucija. Svi oni grafički karakteriziraju područja vjerojatnosti određenog procesa u različitim uvjetima.

U sljedećem odjeljku razmotrit ćemo aspekte vezane uz primjenu ovog matematičkog aparata u stvaran život. Na prvi pogled, naravno, izgleda da je riječ o još jednoj matematičkoj stvari, koja, kao i obično, ne nalazi primjenu u stvarnom životu, i uglavnom ne treba nikome osim samim matematičarima. Međutim, nije tako. Uostalom, sve vrste distribucija i njihove grafički prikazi stvoreni su isključivo za praktične ciljeve, a ne kao hir znanstvenika.

Primjena

Daleko najvažnija primjena distribucije nalazi se u statistici, jer zahtijeva složena analiza puno podataka. Kao što pokazuje praksa, vrlo mnogo nizova podataka ima približno istu raspodjelu vrijednosti: kritična područja vrlo niskih i vrlo visokih vrijednosti u pravilu sadrže manje elemenata od prosječnih vrijednosti.

Analiza velikih nizova podataka potrebna je ne samo u statistici. Nezaobilazan je npr. u fizička kemija. U ovoj se znanosti koristi za određivanje mnogih veličina koje su povezane s nasumičnim vibracijama i kretanjem atoma i molekula.

U sljedećem odjeljku raspravljat ćemo o tome koliko je važno koristiti ih statistički pojmovi, kao binom distribucija slučajne varijable u Svakidašnjica za tebe i mene.

Zašto mi to treba?

Mnogi ljudi sebi postavljaju ovo pitanje kada je u pitanju matematika. I usput, matematiku ne zovu uzalud kraljicom znanosti. Ona je osnova fizike, kemije, biologije, ekonomije, au svakoj od tih znanosti koristi se i neka vrsta distribucije: je li to diskretna binomna distribucija ili normalna, svejedno je. A ako malo bolje pogledamo svijet oko nas, vidjet ćemo da se matematika primjenjuje posvuda: u svakodnevnom životu, na poslu, pa čak i ljudski odnosi mogu se predstaviti u obliku statističkih podataka i analizirati (to, usput, rade oni koji rade u posebne organizacije prikupljanje informacija).

Sada razgovarajmo malo o tome što učiniti ako trebate znati mnogo više o ovoj temi od onoga što smo naveli u ovom članku.

Podaci koje smo dali u ovom članku daleko su od potpunih. Postoji mnogo nijansi o tome kakav oblik distribucije može biti. Binomna distribucija, kao što smo već saznali, jedna je od glavnih vrsta na kojoj se temelji cjelina matematička statistika i teorija vjerojatnosti.

Ako se zainteresirate, ili u vezi s vašim radom, morate znati mnogo više o ovoj temi, morat ćete proučiti stručnu literaturu. Počnite sa sveučilišnim tečajem matematička analiza i doći tamo do odjeljka teorije vjerojatnosti. Također će biti korisno znanje u području nizova, jer binomna distribucija vjerojatnosti nije ništa više od niza uzastopnih članova.

Zaključak

Prije nego završimo članak, htjeli bismo vam reći još jednu zanimljivost. To se izravno tiče teme našeg članka i cijele matematike općenito.

Mnogi ljudi kažu da je matematika beskorisna znanost i ništa što su naučili u školi nije im koristilo. Ali znanje nikad nije suvišno, a ako vam nešto ne koristi u životu, znači da se toga jednostavno ne sjećate. Ako imate znanja, oni vam mogu pomoći, ali ako ih nemate, ne možete očekivati pomoć od njih.

Dakle, ispitali smo koncept binomne distribucije i sve definicije povezane s njom i razgovarali o tome kako se primjenjuje u našim životima.

Razmotrite binomnu distribuciju, izračunajte njezino matematičko očekivanje, varijancu, modus. Pomoću MS EXCEL funkcije BINOM.DIST() iscrtat ćemo grafove funkcije distribucije i gustoće vjerojatnosti. Procijenimo parametar distribucije p, matematičko očekivanje distribucije i standardna devijacija. Također razmotrite Bernoullijevu distribuciju.

Definicija. Neka se drže n testovi, u svakom od kojih se mogu dogoditi samo 2 događaja: događaj "uspjeh" s vjerojatnošću str ili događaj "neuspjeh" s vjerojatnošću q =1-p (tzv Bernoullijeva shema,Bernoullisuđenja).

Vjerojatnost dobivanja točno x uspjeh u ovim n testovi jednaki su:

Broj uspjeha u uzorku x je slučajna varijabla koja ima Binomna distribucija(Engleski) Binomnidistribucija) str I n– su parametri ove distribucije.

Prisjetite se toga kako biste se prijavili Bernoullijeve sheme i shodno tome binomna distribucija, moraju biti ispunjeni sljedeći uvjeti:

svaki pokušaj mora imati točno dva ishoda, uvjetno nazvana "uspjeh" i "neuspjeh".
rezultat svakog testa ne smije ovisiti o rezultatima prethodnih testova (nezavisnost testa).
stopa uspjeha str treba biti konstantan za sve testove.

Binomna distribucija u MS EXCEL-u

U MS EXCEL-u, počevši od verzije 2010, za Binomna distribucija postoji funkcija BINOM.DIST() , engleski naslov- BINOM.DIST(), koji vam omogućuje izračunavanje vjerojatnosti da će uzorak biti točan x"uspjesi" (tj. funkcija gustoće vjerojatnosti p(x), vidi gornju formulu), i funkcija integralne distribucije(vjerojatnost da će uzorak imati x ili manje "uspjeha", uključujući 0).

Prije MS EXCEL-a 2010, EXCEL je imao funkciju BINOMDIST(), koja vam također omogućuje izračunavanje distribucijska funkcija I gustoća vjerojatnosti p(x). BINOMDIST() je ostavljen u MS EXCEL 2010 radi kompatibilnosti.

Datoteka primjera sadrži grafikone gustoća distribucije vjerojatnosti I .

Binomna distribucija ima oznaku B(n; str) .

Bilješka: Za izgradnju funkcija integralne distribucije tip karte savršenog pristajanja Raspored, Za gustoća distribucije – Histogram s grupiranjem. Za više informacija o izradi grafikona pročitajte članak Glavne vrste grafikona.

Bilješka: Radi lakšeg pisanja formula u datoteku primjera, stvoreni su nazivi za parametre Binomna distribucija: n i str.

Datoteka primjera prikazuje različite izračune vjerojatnosti pomoću MS EXCEL funkcija:

Kao što se vidi na gornjoj slici, pretpostavlja se da:

Beskonačna populacija iz koje je napravljen uzorak sadrži 10% (ili 0,1) dobrih elemenata (parametar str, treći argument funkcije =BINOM.DIST() )
Za izračunavanje vjerojatnosti da će u uzorku od 10 elemenata (parametar n, drugi argument funkcije) bit će točno 5 valjanih elemenata (prvi argument), trebate napisati formulu: =BINOM.DIST(5, 10, 0,1, FALSE)
Posljednji, četvrti element postavljen je = FALSE, tj. vraća se vrijednost funkcije gustoća distribucije.

Ako je vrijednost četvrtog argumenta = TRUE, tada funkcija BINOM.DIST() vraća vrijednost funkcija integralne distribucije ili jednostavno distribucijska funkcija. U ovom slučaju možemo izračunati vjerojatnost da će broj dobrih elemenata u uzorku biti od određeni raspon, na primjer, 2 ili manje (uključujući 0).

Da biste to učinili, morate napisati formulu:
= BINOM.DIST(2, 10, 0,1, TRUE)

Bilješka: Za vrijednost x koja nije cijeli broj, . Na primjer, sljedeće formule vratit će istu vrijednost:
=BINOM.DIST( 2 ; 10; 0,1; PRAVI)
=BINOM.DIST( 2,9 ; 10; 0,1; PRAVI)

Bilješka: U primjeru datoteke gustoća vjerojatnosti I distribucijska funkcija također izračunati pomoću definicije i funkcije COMBIN().

Pokazatelji distribucije

U primjer datoteke na listu Primjer postoje formule za izračun nekih pokazatelja distribucije:

=n*p;
(kvadrat standardne devijacije) = n*p*(1-p);
= (n+1)*p;
=(1-2*p)*ROOT(n*p*(1-p)).

Izvodimo formulu matematičko očekivanje Binomna distribucija korištenjem Bernoullijeva shema.

A-priorat slučajna vrijednost X in Bernoullijeva shema(Bernoullijeva slučajna varijabla) ima distribucijska funkcija:

Ova distribucija se zove Bernoullijeva distribucija.

Bilješka: Bernoullijeva distribucija – poseban slučaj Binomna distribucija s parametrom n=1.

Generirajmo 3 niza od 100 brojeva s različitim vjerojatnostima uspjeha: 0,1; 0,5 i 0,9. Da biste to učinili, u prozoru Generacija slučajni brojevi postaviti sljedeće parametre za svaku vjerojatnost p:

Bilješka: Ako postavite opciju Nasumično rasipanje (Nasumično sjeme), tada možete odabrati određeni slučajni skup generirani brojevi. Na primjer, postavljanjem ove opcije =25, možete generirati iste skupove nasumičnih brojeva na različitim računalima (ako su, naravno, ostali parametri distribucije isti). Vrijednost opcije može imati cjelobrojne vrijednosti od 1 do 32 767. Naziv opcije Nasumično rasipanje može zbuniti. Bolje bi bilo prevesti kao Postavite broj s nasumičnim brojevima.

Kao rezultat, imat ćemo 3 stupca od 100 brojeva, na temelju kojih npr. možemo procijeniti vjerojatnost uspjeha str prema formuli: Broj uspjeha/100(cm. list primjera datoteke Generiranje Bernoullija).

Bilješka: Za Bernoullijeve distribucije s p=0,5, možete koristiti formulu =RANDBETWEEN(0;1) , što odgovara .

Generiranje slučajnih brojeva. Binomna distribucija

Pretpostavimo da u uzorku ima 7 neispravnih artikala. To znači da je "vrlo vjerojatno" da se udio neispravnih proizvoda promijenio. str, što je karakteristika našeg proizvodnog procesa. Iako je ova situacija "vrlo vjerojatna", postoji mogućnost (alfa rizik, pogreška tipa 1, "lažni alarm") da str ostala nepromijenjena, a do povećanog broja neispravnih proizvoda došlo je zbog slučajnog uzorkovanja.

Kao što se može vidjeti na donjoj slici, 7 je broj neispravnih proizvoda koji je prihvatljiv za proces s p=0,21 pri istoj vrijednosti Alfa. Ovo ilustrira da kada se prekorači prag neispravnih artikala u uzorku, str“vjerojatno” povećao. Izraz "najvjerojatnije" znači da postoji samo 10% šanse (100%-90%) da je odstupanje postotka neispravnih proizvoda iznad praga uzrokovano samo slučajnim uzrocima.

Prema tome, prekoračenje praga broja neispravnih proizvoda u uzorku može poslužiti kao signal da je proces poremećen i počeo proizvoditi b O veći postotak neispravnih proizvoda.

Bilješka: Prije MS EXCEL-a 2010, EXCEL je imao funkciju CRITBINOM() , koja je ekvivalentna BINOM.INV() . CRITBINOM() je ostavljen u MS EXCEL 2010 i novijim verzijama radi kompatibilnosti.

Odnos binomne distribucije s drugim distribucijama

Ako je parametar n Binomna distribucija teži beskonačnosti i str teži 0, onda u ovom slučaju Binomna distribucija može se približno odrediti.
Moguće je formulirati uvjete kada aproksimacija Poissonova distribucija radi dobro:

str<0,1 (manje str i više n, što je aproksimacija točnija);
str>0,9 (s obzirom na to q=1- str, izračuni u ovom slučaju moraju se izvesti pomoću q(A x treba zamijeniti s n- x). Stoga, što manje q i više n, što je aproksimacija točnija).

Na 0,1<=p<=0,9 и n*p>10 Binomna distribucija može se približno odrediti.

Sa svoje strane, Binomna distribucija može poslužiti kao dobra aproksimacija kada je veličina populacije N Hipergeometrijska raspodjela mnogo veći od veličine uzorka n (tj. N>>n ili n/N<<1).

Više o odnosu navedenih raspodjela možete pročitati u članku. Tu su također navedeni primjeri aproksimacije te su objašnjeni uvjeti kada je to moguće i s kojom točnošću.

SAVJET: O ostalim distribucijama MS EXCEL-a možete pročitati u članku.

Binomna distribucija je jedna od najvažnijih distribucija vjerojatnosti za diskretno promjenjivu slučajnu varijablu. Binomna distribucija je distribucija vjerojatnosti broja m događaj A V n međusobno neovisna opažanja. Često događaj A naziva se "uspjeh" promatranja, a suprotni događaj - "neuspjeh", ali ova je oznaka vrlo uvjetna.

Uvjeti binomne distribucije:

provedeno ukupno n suđenja u kojima događaj A može se ili ne mora pojaviti;
događaj A u svakom od pokusa može se dogoditi s istom vjerojatnošću str;
testovi su međusobno neovisni.

Vjerojatnost da u n ispitni događaj A točno m puta, može se izračunati pomoću Bernoullijeve formule:

Gdje str- vjerojatnost nastanka događaja A;

q = 1 - str je vjerojatnost da će se dogoditi suprotni događaj.

Hajdemo shvatiti zašto je binomna distribucija povezana s Bernoullijevom formulom na gore opisan način . Događaj - broj uspjeha na n testovi su podijeljeni u niz opcija, u svakoj od kojih se postiže uspjeh m kušnje, i neuspjeh - in n - m testovi. Razmotrite jednu od ovih opcija - B1 . Prema pravilu zbrajanja vjerojatnosti množimo vjerojatnosti suprotnih događaja:

a ako označimo q = 1 - str, To

Istu vjerojatnost će imati bilo koja druga opcija u kojoj m uspjeh i n - m kvarovi. Broj takvih opcija jednak je broju načina na koje je to moguće n test dobiti m uspjeh.

Zbroj vjerojatnosti svih m broj događaja A(brojevi od 0 do n) jednako je jedan:

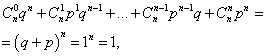
gdje je svaki član član Newtonovog binoma. Stoga se razmatrana distribucija naziva binomna distribucija.

U praksi je često potrebno izračunati vjerojatnosti "najviše m uspjeh u n testovi" ili "barem m uspjeh u n testovi". Za to se koriste sljedeće formule.

Integralna funkcija, tj vjerojatnost F(m) to u n događaj promatranja A više neće doći m jednom, može se izračunati pomoću formule:

Sa svoje strane vjerojatnost F(≥m) to u n događaj promatranja A dođi barem m jednom, izračunava se formulom:

Ponekad je prikladnije izračunati vjerojatnost da u n događaj promatranja A više neće doći m puta, kroz vjerojatnost suprotnog događaja:

Koju od formula koristiti ovisi o tome koja od njih sadrži manje članova.

Obilježja binomne distribucije izračunavaju se pomoću sljedećih formula .

Očekivana vrijednost: .

disperzija: .

Standardna devijacija: .

Binomna distribucija i izračuni u MS Excelu

Vjerojatnost binomne distribucije P n ( m) i vrijednost integralne funkcije F(m) može se izračunati pomoću MS Excel funkcije BINOM.DIST. Dolje je prikazan prozor za odgovarajući izračun (kliknite lijevom tipkom miša za povećanje).

MS Excel zahtijeva da unesete sljedeće podatke:

broj uspjeha;
broj testova;
vjerojatnost uspjeha;
integral - logička vrijednost: 0 - ako trebate izračunati vjerojatnost P n ( m) i 1 - ako je vjerojatnost F(m).

Primjer 1 Direktor tvrtke sažeo je podatke o broju prodanih kamera u proteklih 100 dana. U tablici su sažeti podaci i izračunate vjerojatnosti da će određeni broj kamera biti prodan dnevno.

Dan završava s dobiti ako se proda 13 ili više kamera. Vjerojatnost da će se dan završiti s dobiti:

Vjerojatnost da će dan biti odrađen bez profita:

Neka je vjerojatnost da se dan završi s dobiti konstantna i jednaka 0,61, a broj prodanih kamera po danu ne ovisi o danu. Zatim možete koristiti binomnu distribuciju, gdje događaj A- dan će biti odrađen s dobiti, - bez dobiti.

Vjerojatnost da će od 6 dana svi biti odrađeni s dobiti:

Isti rezultat dobivamo pomoću MS Excel funkcije BINOM.DIST (vrijednost integralne vrijednosti je 0):

P 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.

Vjerojatnost da će se od 6 dana 4 ili više dana raditi s dobiti:

Gdje ,

Pomoću MS Excel funkcije BINOM.DIST izračunavamo vjerojatnost da od 6 dana najviše 3 dana neće završiti s dobiti (vrijednost integralne vrijednosti je 1):

P 6 (≤3 ) = BINOM.DIST(3, 6, 0,61, 1) = 0,435.

Vjerojatnost da će od 6 dana svi biti odrađeni s gubicima:

Isti pokazatelj izračunavamo pomoću MS Excel funkcije BINOM.DIST:

P 6 (0 ) = BINOM.DIST(0; 6; 0,61; 0) = 0,0035.

Sami riješite problem i onda vidite rješenje

Primjer 2 Urna sadrži 2 bijele kugle i 3 crne. Iz urne se izvadi kuglica, namjesti se boja i vrati. Pokušaj se ponavlja 5 puta. Broj pojavljivanja bijelih kuglica je diskretna slučajna varijabla x, raspodijeljen prema binomnom zakonu. Sastavite zakon raspodjele slučajne varijable. Odredite modus, matematičko očekivanje i varijancu.

Nastavljamo zajedno rješavati probleme

Primjer 3 Od kurirske službe otišao do objekata n= 5 kurira. Svaki kurir s vjerojatnošću str= 0.3 kasni za objekt bez obzira na ostale. Diskretna slučajna varijabla x- broj zakašnjelih dostavljača. Konstruirajte niz distribucije ove slučajne varijable. Nađite njegovo matematičko očekivanje, varijancu, standardnu devijaciju. Nađite vjerojatnost da će najmanje dva kurira zakasniti na predmete.

Binomna distribucija

distribucija vjerojatnosti broja pojavljivanja nekog događaja u ponovljenim neovisnim ispitivanjima. Ako je za svaki pokušaj vjerojatnost događanja događaja R, i 0 ≤ str≤ 1, tada je broj μ pojavljivanja ovog događaja za n neovisna ispitivanja, postoji slučajna varijabla koja uzima vrijednosti m = 1, 2,.., n s vjerojatnostima

Gdje q= 1 - p, a - binomni koeficijenti (odatle naziv B. r.). Gornja formula se ponekad naziva Bernoullijeva formula. Matematičko očekivanje i varijanca veličine μ, koja ima B. R., jednaki su M(μ) = np I D(μ) = npq, odnosno. U cjelini n, na temelju Laplaceovog teorema (Vidi Laplaceov teorem), B. r. blizu normalne distribucije (vidi Normalna distribucija), što se i koristi u praksi. Na malom n potrebno je koristiti tablice B. r.

Lit.: Bolshev L. N., Smirnov N. V., Tablice matematičke statistike, M., 1965.

Velika sovjetska enciklopedija. - M.: Sovjetska enciklopedija. 1969-1978 .

Pogledajte što je "binomna distribucija" u drugim rječnicima:

Funkcija vjerojatnosti ... Wikipedia

- (binomna distribucija) Distribucija koja vam omogućuje izračunavanje vjerojatnosti pojavljivanja bilo kojeg slučajnog događaja dobivenog kao rezultat promatranja niza neovisnih događaja, ako je vjerojatnost pojavljivanja njegovog sastavnog elementa ... ... Ekonomski rječnik

- (Bernoullijeva distribucija) distribucija vjerojatnosti broja pojavljivanja nekog događaja u ponovljenim neovisnim pokušajima, ako je vjerojatnost pojavljivanja tog događaja u svakom pokušaju jednaka p(0 p 1). Točno, broj? postoje pojave ovog događaja ... ... Veliki enciklopedijski rječnik

binomna distribucija- - Telekomunikacijske teme, osnovni pojmovi EN binomna distribucija ...

- (Bernoullijeva distribucija), distribucija vjerojatnosti broja pojavljivanja nekog događaja u ponovljenim neovisnim pokusima, ako je vjerojatnost pojavljivanja tog događaja u svakom pokusu p (0≤p≤1). Naime, broj μ pojavljivanja ovog događaja… … enciklopedijski rječnik

binomna distribucija- 1,49. binomska distribucija Distribucija vjerojatnosti diskretne slučajne varijable X, uzimajući bilo koje cjelobrojne vrijednosti od 0 do n, tako da je za x = 0, 1, 2, ..., n i parametre n = 1, 2, ... i 0< p < 1, где Источник … Rječnik-priručnik pojmova normativne i tehničke dokumentacije

Bernoullijeva distribucija, distribucija vjerojatnosti slučajne varijable X, koja uzima cjelobrojne vrijednosti s vjerojatnostima (binomni koeficijent; p parametar B. R., koji se naziva vjerojatnost pozitivnog ishoda, koji uzima vrijednosti ... Matematička enciklopedija

- (Bernoullijeva distribucija), distribucija vjerojatnosti broja pojavljivanja određenog događaja u ponovljenim neovisnim pokusima, ako je vjerojatnost pojavljivanja tog događaja u svakom pokusu p (0<или = p < или = 1). Именно, число м появлений … Prirodna znanost. enciklopedijski rječnik

Binomna distribucija vjerojatnosti- (binomna distribucija) Distribucija promatrana u slučajevima kada ishod svakog neovisnog eksperimenta (statističko promatranje) ima jednu od dvije moguće vrijednosti: pobjedu ili poraz, uključivanje ili isključenje, plus ili ... Ekonomski i matematički rječnik

binomna distribucija vjerojatnosti- Distribucija koja se promatra u slučajevima kada ishod svakog neovisnog eksperimenta (statističko promatranje) poprima jednu od dvije moguće vrijednosti: pobjedu ili poraz, uključenje ili isključenje, plus ili minus, 0 ili 1. To je ... ... Tehnički prevoditeljski priručnik

knjige

Teorija vjerojatnosti i matematička statistika u problemima. Više od 360 zadataka i vježbi, D. A. Borzykh. Predloženi priručnik sadrži zadatke različitih razina složenosti. Ipak, glavni naglasak stavljen je na zadatke srednje složenosti. Ovo je namjerno učinjeno kako bi se studenti potaknuli na...
Teorija vjerojatnosti i matematička statistika u zadacima: više od 360 zadataka i vježbi, Borzykh D. Predloženi priručnik sadrži probleme različitih razina složenosti. Ipak, glavni naglasak stavljen je na zadatke srednje složenosti. Ovo je namjerno učinjeno kako bi se studenti potaknuli na...

Poglavlje 7

Specifični zakoni raspodjele slučajnih varijabli

Vrste zakona distribucije diskretnih slučajnih varijabli

Neka diskretna slučajna varijabla poprima vrijednosti x 1 , x 2 , …, x n, … . Vjerojatnosti ovih vrijednosti mogu se izračunati pomoću različitih formula, na primjer, pomoću osnovnih teorema teorije vjerojatnosti, Bernoullijeve formule ili nekih drugih formula. Za neke od ovih formula zakon raspodjele ima svoje ime.

Najčešći zakoni distribucije diskretne slučajne varijable su binomni, geometrijski, hipergeometrijski, Poissonov zakon distribucije.

Binomni zakon distribucije

Neka se proizvodi n neovisna ispitivanja, u svakom od njih se događaj može ili ne mora dogoditi A. Vjerojatnost pojave ovog događaja u svakom pojedinačnom pokusu je konstantna, ne ovisi o broju pokusa i jednaka je R=R(A). Otuda vjerojatnost da se događaj neće dogoditi A u svakom testu je također konstantan i jednak q=1–R. Razmotrimo slučajnu varijablu x jednak broju pojavljivanja događaja A V n testovi. Očito je da su vrijednosti ove količine jednake

x 1 =0 - događaj A V n testovi se nisu pojavili;

x 2 =1 – događaj A V n suđenja su se pojavila jednom;

x 3 =2 - događaj A V n suđenja su se pojavila dva puta;

…………………………………………………………..

x n +1 = n- događaj A V n testovi su se pojavili sve n jednom.

Vjerojatnosti ovih vrijednosti mogu se izračunati pomoću Bernoullijeve formule (4.1):

Gdje Do=0, 1, 2, …,n .

Binomni zakon distribucije x jednak broju uspjeha u n Bernoullijeva ispitivanja, s vjerojatnošću uspjeha R.

Dakle, diskretna slučajna varijabla ima binomnu distribuciju (ili je raspoređena prema binomnom zakonu) ako su njene moguće vrijednosti 0, 1, 2, …, n, a odgovarajuće vjerojatnosti izračunavaju se formulom (7.1).

Binomna distribucija ovisi o dva parametri R I n.

Niz distribucije slučajne varijable raspodijeljen prema binomnom zakonu ima oblik:

x			…	k	…	n
R			…		…

Primjer 7.1 . U metu se ispaljuju tri neovisna hica. Vjerojatnost pogađanja svakog udarca je 0,4. Slučajna vrijednost x- broj pogodaka u metu. Konstruirajte njegovu distribucijsku seriju.

Riješenje. Moguće vrijednosti slučajne varijable x su x 1 =0; x 2 =1; x 3 =2; x 4=3. Odredite odgovarajuće vjerojatnosti pomoću Bernoullijeve formule. Lako je pokazati da je primjena ove formule ovdje potpuno opravdana. Imajte na umu da će vjerojatnost da ne pogodite metu jednim hicem biti jednaka 1-0,4=0,6. Dobiti

Distribucijska serija ima sljedeći oblik:

x
R	0,216	0,432	0,288	0,064

Lako je provjeriti da je zbroj svih vjerojatnosti jednak 1. Sama slučajna varijabla x raspoređeni prema binomnom zakonu. ■

Nađimo matematičko očekivanje i varijancu slučajne varijable raspodijeljene prema binomnom zakonu.

Prilikom rješavanja primjera 6.5 pokazalo se da je matematičko očekivanje broja pojavljivanja događaja A V n neovisna ispitivanja, ako je vjerojatnost pojave A u svakom testu konstantan i jednak R, jednako n· R

U ovom primjeru korištena je slučajna varijabla raspoređena prema binomnom zakonu. Stoga je rješenje primjera 6.5, zapravo, dokaz sljedećeg teorema.

Teorem 7.1. Matematičko očekivanje diskretne slučajne varijable raspodijeljene prema binomnom zakonu jednako je umnošku broja pokušaja i vjerojatnosti "uspjeha", tj. M(x)=n· R.

Teorem 7.2. Varijanca diskretne slučajne varijable raspodijeljene prema binomnom zakonu jednaka je umnošku broja pokušaja s vjerojatnošću "uspjeha" i vjerojatnosti "neuspjeha", tj. D(x)=npq.

Asimetrija i kurtoza slučajne varijable raspodijeljene prema binomnom zakonu određuju se formulama

Ove formule mogu se dobiti korištenjem koncepta početnog i središnjeg momenta.

Zakon binomne distribucije je temelj mnogih stvarnih situacija. Za velike vrijednosti n binomna distribucija može se aproksimirati drugim distribucijama, posebno Poissonovom distribucijom.

Poissonova distribucija

Neka bude n Bernoullijevi pokusi, s brojem pokusa n dovoljno velik. Prethodno je pokazano da u ovom slučaju (ako je, osim toga, vjerojatnost R događanja A vrlo mala) kako bi se pronašla vjerojatnost da događaj A da se pojavi T jednom u testovima, možete koristiti Poissonovu formulu (4.9). Ako je slučajna varijabla x označava broj pojavljivanja događaja A V n Bernoullijeva ispitivanja, zatim vjerojatnost da x poprimit će značenje k može se izračunati po formuli

, (7.2)

Gdje λ = np.

Poissonov zakon distribucije naziva se distribucija diskretne slučajne varijable x, za koje su moguće vrijednosti nenegativni cijeli brojevi, i vjerojatnosti p t te se vrijednosti nalaze formulom (7.2).

Vrijednost λ = np nazvao parametar Poissonova distribucija.

Slučajna varijabla raspodijeljena prema Poissonovom zakonu može poprimiti beskonačan broj vrijednosti. Budući da je za ovu distribuciju vjerojatnost R pojava događaja u svakom pokušaju mala, onda se ova raspodjela ponekad naziva zakonom rijetkih pojava.

Niz distribucije slučajne varijable raspodijeljen prema Poissonovom zakonu ima oblik

x					…	T	…
R					…		…

Lako je provjeriti da je zbroj vjerojatnosti drugog retka jednak 1. Da bismo to učinili, moramo zapamtiti da se funkcija može proširiti u Maclaurinov niz, koji konvergira za bilo koji x. U ovom slučaju imamo

. (7.3)

Kao što je navedeno, Poissonov zakon u određenim ograničavajućim slučajevima zamjenjuje binomni zakon. Primjer je slučajna varijabla x, čije su vrijednosti jednake broju kvarova u određenom vremenskom razdoblju s ponovljenom uporabom tehničkog uređaja. Pretpostavlja se da je ovaj uređaj visoke pouzdanosti, tj. vjerojatnost neuspjeha u jednoj aplikaciji je vrlo mala.

Osim takvih ograničavajućih slučajeva, u praksi postoje slučajne varijable raspodijeljene prema Poissonovom zakonu, koje nisu povezane s binomnom distribucijom. Na primjer, Poissonova distribucija se često koristi kada se radi o broju događaja koji se dogode u određenom vremenskom razdoblju (broj poziva telefonskoj centrali tijekom sata, broj automobila koji su stigli u autopraonicu tijekom dana, broj zaustavljanja stroja tjedno, itd. .). Svi ovi događaji moraju tvoriti tzv. tok događaja, što je jedan od temeljnih pojmova teorije čekanja. Parametar λ karakterizira prosječni intenzitet toka događaja.